EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 672 (April 2023) A&A, 672 (2023) A132 Full HTML
Open Access
Issue
A&A
Volume 672, April 2023
Article Number A132
Number of page(s) 10
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202244905
Published online 12 April 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Active galactic nuclei (AGNs) are among the most luminous sources of radiation in the Universe, and understanding their interior structure has been one of the major goals of extragalactic astrophysics. The current picture of the schematic sub-parsec-scale structure of an AGN includes three main components: a hot, X-ray emitting corona; an accretion disk around a supermassive black hole (SMBH), and a broad-line region (BLR) consisting of fast-orbiting photoionized gas and clouds. On scales of parsec to hundreds of parsecs, the AGN consists of an obscuring dusty torus and a narrow-line region (NLR) comprised of small, low-density gas clouds moving at lower velocities. Gravitational potential energy and viscous heating is converted into heat and radiation by the accretion of matter onto the central SMBH (e.g., Page & Thorne 1974; Rees 1984; Balbus & Hawley 1998). The accretion disk thereby reaches temperatures of 105 − 106 K at its inner edge with a gradient to cooler temperatures at larger radii, leading to a continuum emission spectrum spanning from the extreme ultraviolet (UV) to the infrared (IR). The hottest parts of the accretion disk provide the ionizing photons that cause Doppler-broadened emission lines in the BLRs and NLRs (Davidson & Netzer 1979; Veilleux & Osterbrock 1987). Although this basic picture can explain most of the observational properties of AGNs (Burbidge 1967; Weedman 1977; Shields 1978; Elvis et al. 1994; Telfer et al. 2002), the detailed geometry and kinematics of the interior structure remain poorly understood. Since the sub-parsec-scale structures are unresolved in even the closest AGN, information must be obtained by indirect means.

Reverberation mapping (RM; Bahcall et al. 1972; Blandford & McKee 1982; Peterson 1993, 2014) is a powerful tool to probe compact structures in the central parts of AGNs. The basic principle of RM is to search for temporal correlations between the time-variable flux signals (intrinsic variability) and their light echoes at different wavelengths. Combined with the speed of light, the lag between those light echoes determines the characteristic size of the reverberation structure in the AGN. For example, gas in the outer part of the accretion disk reprocesses (as variable optical flux) variations emitted in the far and extreme UV by the inner parts of the accretion disk. Measuring the lag between the primary UV signal and light echoes at longer wavelengths provides an estimate of the accretion disk’s spatial extent. Recent findings suggest that the disk sizes are larger than the predictions from standard models (e.g., Fian et al. 2022; Fausnaugh et al. 2017, 2018; Edelson et al. 2015, 2019). Accretion disk sizes considerably larger than predicted by theory have also been found in microlensing studies of gravitationally lensed quasars (e.g., Morgan et al. 2010; Blackburne et al. 2011; Fian et al. 2016, 2018, 2021; Cornachione et al. 2020a,b). In addition, continuum time lags across the accretion disk provide information about the disk’s temperature gradient, and it appears that they are flatter than expected (Motta et al. 2017; Cornachione & Morgan 2020; Jiménez-Vicente et al. 2014).

Measuring inter-band continuum lags is extremely challenging, because the predicted size of accretion disks is only about one light day and monitoring campaigns require comparable or better cadence (i.e., on the order of one day or less) on timescales of weeks to months to resolve such short lags. In this work, we analyzed six months of densely sampled (daily cadence) photometric monitoring data of the Seyfert 1 galaxy MCG 08-11-011, and we present detections of optical and near-IR inter-band continuum time lags. In Sect. 2, we discuss our observations, the data reduction, and the light curves taken in multiple photometry bands. In Sect. 3, we describe our time series analysis and compare several tools to measure the inter-band continuum time lags. The results are presented in Sect. 4, including the time delays, the lag spectrum, the host-subtracted AGN luminosity, and a comparison with the theoretical disk sizes. Finally, we discuss and conclude our findings in Sect. 5.

2. Observations and data reduction

The ground-based photometric monitoring was conducted between October 2019 and April 2020 with the robotic C18 telescope (Brosch et al. 2008) of the Wise Observatory located in the Negev desert in southern Israel. We used the QSI 683 CCD (image sensor KAF-8300), which has 3326 × 2504 pixels of 5.4 μm in size. The pixel scale is 0.882 arcsec pix−1, which gives a field of view of 48.9 × 36.8 arcmin (0.815 × 0.613 deg, corresponding to an area of 0.5 deg2). The observations were carried out on a daily basis (∼4 exposures per night in each filter) for a duration of almost six months. To trace the AGN continuum variations free of emission lines at the object’s rest frame (MCG 08-11-011 is at a redshift of z ∼ 0.02051), five relatively narrow bands (NBs) at 4250, 5700, 6200, 7320, and 8025 Å were carefully chosen. In Table 1 we list the object’s characteristics. In Table 2 we summarize the filter and observation information, and Fig. 1 shows the position of the NB filters together with the quasars’ composite spectrum of Glikman et al. (2006). The images were reduced following standard procedures performed with IRAF (including bias subtraction, dark current correction, and flat fielding for each filter), and we used the traditional point-spread function (PSF) fitting photometry to obtain the light curves.

Table 1.

MCG 08-11-011 characteristics.

Table 2.

Filter and observation information.

thumbnail Fig. 1.

Composite AGN spectrum of Glikman et al. (2006) shown at the quasar’s redshift of z = 0.0205. The five emission-line-free NB passes of the filters which mainly trace the AGN continuum variations (and are used for the photometric monitoring presented in this work) are shaded in different colors (blue for NB4250, green for NB5700, orange for NB6200, red for NB7320, and dark red for NB8025).

We used the DAOPHOT (Stetson 1987) package as implemented in IRAF and DAOSTAT (Netzer et al. 1996) to measure the magnitude of the objects in the images and to compute the light curves of the Seyfert 1 galaxy (see Fian et al. 2022 for a detailed description). To obtain accurate measures for the magnitude at a given epoch, we discarded problematic exposures (due to low S/N, condensation rings on the CCD, and/or elongated stars caused by telescope tracking or auto-guider issues) from each night. After comparing consecutive points and removing points above a certain threshold, we are left with a set of good measurements per night (only one night has been discarded). Finally, we averaged the outlier-free exposures for each night, resulting in high S/N light curves consisting of ∼90 data points. In Fig. 2 we show the normalized-to-mean and unit standard deviation light curves for the different bands, and in Table 3 we present the variability measures for each light curve2.

thumbnail Fig. 2.

PSF photometry light curves of the AGN continuum at 4250, 5700, 6200, 7320, and 8025 Å (from top to bottom) for the period between October 2019 and April 2020. The light curves are normalized to zero mean and unit standard deviation, and the fluxes are in arbitrary units.

Table 3.

Variability measures for the host-subtracted PSF photometry light curves.

3. Time series analysis

The primary objective of this paper is to estimate the time delays between the NB passes located at 4250, 5700, 6200, 7320, and 8025 Å, which to a large extent trace the AGN continuum variations relatively free of contamination from the broad-emission lines. We used several methods to robustly determine the reverberation lags between the multiwavelength bands, as outlined below. All time lags are measured relative to the NB4250 light curve. A more detailed description of the methods (a)–(e) can be found in Fian et al. (2022).

(a) ICCF. A well-known method to estimate reverberation lags is the traditional interpolated cross-correlation function (ICCF) of Gaskell & Sparke (1986) and Gaskell & Peterson (1987), as implemented by White & Peterson (1994); see also review by Gaskell (1994). To properly perform cross-correlation function (CCF) analysis, uneven sampled light curves have to be interpolated. The time lag is determined by measuring the centroid of the points around the ICCF peak (above a certain threshold), and to estimate the errors of the inferred time lags we used the flux randomization and random subset selection (FR/RSS) method of Peterson et al. (1998, 2004).

(b) ZDCF. One way to bypass interpolation is the use of a discrete correlation function (DCF; Edelson & Krolik 1988), which evaluates the correlation function in bins of time delay. In this work, we used the z-transformed discrete correlation function (ZDCF) of Alexander (1997), which applies Fisher’s z transformation to the correlation coefficients. To measure the time delays between the multiband light curves, we took the centroid of the correlation function above 60% or 80% of the peak, and we estimated the errors using a maximum likelihood method that takes into account the uncertainty in the ZDCF points.

(c) Von Neumann Estimator. The von Neumann estimator (von Neumann 1941; Chelouche et al. 2017) does not depend on interpolation or binning of the light curves but is based on the regularity of randomness of the data. In this work, we used von Neumann’s statistical estimator to find the relative time shift between two light curves that minimizes the level of randomness.

(d) JAVELIN. JAVELIN stands for “Just Another Vehicle for Estimating Lags in Nuclei”, and is a popular (parametric) Bayesian tool to measure reverberations lags (Zu et al. 2011, 2013, 2016). Instead of extracting peaks from empirical cross-correlation functions, it models the continuum variability of the quasar itself by assuming a damped random walk (DRW) process (Kelly et al. 2009; MacLeod et al. 2010, 2012; Kozłowski et al. 2010; Kozłowski 2016). In this work, we used JAVELIN in spectroscopic and photometric RM mode. In the spectroscopic mode, we have two parameters for the continuum DRW model (amplitude and timescale of the quasar’s stochastic variability) and three parameters for each lagging light curve (time delay, width of the smoothing function, and scaling factor). In photometric mode, JAVELIN models light curves in two different bands and estimates the contamination of the leading light curve to the longer wavelength band (additional parameter) and the corresponding time delay simultaneously.

(e) MICA. MICA3 (Li et al. 2016) is a nonparametric method that determines the so-called transfer functions (see Blandford & McKee 1982) for RM data, which reflect the structure of AGNs since the temporal behavior of spatially extended regions (outer parts of the accretion disk, BLR) is assumed to involve blurred echoes of the central ionizing continuum variations. The time lags are given by the first moment of the transfer functions, and the associated uncertainties are estimated as the standard deviation of the generated Markov chains.

(f) PRM. The photometric RM (PRM) developed by Chelouche & Zucker (2013) is a generalized approach to RM and is based on multivariate correlation analysis techniques. It is able to identify reverberation signals across the accretion disk and simultaneously identifies the relative contribution of an additional, slowly varying component (associated with the BLR) to the continuum signal. Observationally, neither the time lag nor the contribution of the BLR to the lagging continuum light curve is known. Those values are constrained by the requirement for a maximal Pearson correlation coefficient within the computational domain. A more detailed explanation of the performance of this method is given in Chelouche & Zucker (2013).

We used 1000 Monte Carlo runs to obtain the lag distributions for methods (a)–(c) and (f). In the case of JAVELIN and MICA, we ran 10.000 Markov Chain Monte Carlo simulations. We applied a common time-lag search interval of [τmin, τmax]=[−15, 10] days, and, for methods that required interpolation, we adopted a time step of 0.15 days.

4. Results and discussion

In the subsequent section, we report the results of the multiband photometric study of the AGN MCG 08-11-011, including the derived continuum time lags between the different NBs, the corresponding lag spectrum, an estimate for the host-subtracted AGN luminosity, and the theoretical disk size as a function of luminosity.

4.1. Continuum time lags

We calculated the time lags (and their uncertainties) between the varying AGN continuum light curves at five different wavelengths using the various methods discussed in Sect. 3. All lags are measured with respect to the bluest (NB4250) light curve, and, for validation purposes, we also include the lag estimations of the 4250 Å NB relative to itself. In Fig. 3, we show the lag distributions or transfer functions for each light curve and method, and Table 4 lists the corresponding lags and uncertainties. The last four rows give the overall mean time delay of all time-lag determination techniques, and the final uncertainties were obtained by estimating the standard deviation from the mean of all methods. From Fig. 3, we see that the lag distributions of the reference light curve relative to itself are symmetric and concentrated around zero as expected, while for the rest of the NB light curves the distributions are clearly shifted away from zero, and RM lags can be detected at high significance.

thumbnail Fig. 3.

From top to bottom: partially interpolated CCFs, z-transformed DCFs, FR/RSS centroid distributions (for centroid ≥0.8 rmax), von Neuman estimator peak distributions, JAVELIN posterior distributions of lags (spectroscopic mode), MICA transfer functions, and PRM lag distributions for each NB relative to the 4250 Å band. In the bottom panel all time delays are plotted (in the same order as described before) on a vertical axis for illustration. The solid lines show the mean time delay of all methods together, and the shaded regions represent the corresponding standard deviation. These values are presented in Table 4.

Table 4.

Summary of the time lags expressed in light days in the observer’s frame between the five continuum light curves of MCG 08-11-011.

For the ICCF, ZDCF, and FR/RSS, we computed the centroid time lags from all points above 60% and 80% of the peak value, leading to similar results. The lags derived from the ICCF, and ZDCF methods are consistent, indicating that the interpolation done in the ICCF does not introduce any artificial correlation. Also, the light-curve modeling techniques are able to capture reverberation lags, as can be seen for the JAVELIN and PRM posterior distributions, as well as for the MICA transfer functions. The lag distributions obtained from the von Neumann method after Monte Carlo simulation of FR/RSS as done for the ICCF analysis, yield similar results to those derived from the cross-correlation and light-curve modeling approaches. Thus, we find general agreements within uncertainties among the results of all methods used in this work. Combining all the lag estimates listed in Table 4, we obtain the mean time delays in the observer’s frame relative to the 4250 Å NB, τ = 1.0 ± 0.5 days for NB5700, τ = 2.0 ± 0.6 days for NB6200, τ = 4.5 ± 0.6 days for NB7320, and τ = 7.1 ± 1.1 days for NB8025. We note that in the case of the PRM, the contribution of the additional component is close to unity (∼0.85) for all wavelength bands, thereby justifying the inclusion of the inferred lag estimates in the mean time delay calculation. Applying a weighted mean, we obtain slightly larger values for the time delays of the bluer wavelength bands (τ = 1.1 days for NB5700 and τ = 2.2 days for NB6200) and somewhat smaller values for the two reddest wavelength bands used in our RM campaign (τ = 3.9 days for NB7320 and τ = 6.2 days for NB8025); however, these are consistent (within errors) with the time lags obtained when using the ordinary mean.

4.2. Lag spectrum

Figure 4 displays the inter-band continuum time lags (relative to the 4250 Å light curve) as a function of wavelength for each of the methods discussed in Sect. 3. For a disk reprocessing model, we can translate the observed time-lag-wavelength relation to a wavelength-dependent emissivity profile, which in turn depends on the temperature profile of the accretion disk. To quantify this, we fit the observed continuum lags in the five different photometric NBs with a disk model of the following form:

τ = τ 0 [ ( λ λ 0 ) β − y 0 ] , $$ \begin{aligned} \tau = \tau _0 \left[ \left( \frac{\lambda }{\lambda _0} \right)^\beta - { y}_0 \right], \end{aligned} $$(1)

thumbnail Fig. 4.

Time lags (black circles) between multiband continuum light curves as a function of wavelength for the various methods described in Sect. 3. All lags are measured relative to variations at 4250 Å. The dashed blue lines show the best fit to the observed relation τ = τ0/ [(λ/λ0) β − y0] with τ0, β, and y0 as free parameters (these values are presented in Table 5).

where λ is the observed wavelength, λ0 is the reference band wavelength (here 4250 Å), and τ0, β, and y0 are free parameters. The normalization τ0 = Rλ0/c measures the light crossing time across an accretion disk emitting at a reference wavelength, λ0; the power-law index, β, quantifies the temperature profile of the disk, T ∝ R−1/β; and y0 allows the model lag at λ0 to differ from 0. A list of best-fitting parameters is shown in Table 5. From Fig. 5 and Table 5, we infer that the observed time lags, as well as the physical models, clearly favor a steeper slope than predicted by the standard disk temperature profile.

Table 5.

Best-fitting parameters to the inter-band lag spectra presented in Fig. 4.

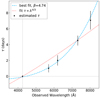thumbnail Fig. 5.

Mean time lags (black circles) between multiband continuum light curves as a function of wavelength. All lags are measured relative to variations at 4250 Å. The dashed blue line shows the best fit to the observed relation τ = τ0/ [(λ/λ0) β − y0], with τ0, β, and y0 as free parameters (these values are presented in Table 5). The red dotted line is a fit with fixed theoretical power-law index β = 4/3, as expected for an optically thick and geometrically thin disk.

In Fig. 5, we show the average time lag spectrum, and fit models with both τ0, β, and y0 free to vary, as well as with β fixed to 4/3, corresponding to a standard thin accretion disk. The best fit yields β = 4.74 (dashed blue line in Fig. 5), resulting in a very steep lag-wavelength relation. The dotted red fit indicates that a disk reprocessing model with β = 4/3 cannot reproduce our data very well, contradicting the prediction for a geometrically thin disk with temperature profile of T ∝ R−3/4. In previous RM studies several authors observed similar trends in the lag spectra of AGNs (see, e.g., Gaskell et al. 2007; Chelouche et al. 2019; Fian et al. 2022) and attributed this to possible contamination by light being reprocessed from further away.

4.3. Host-subtracted AGN luminosity

To determine the AGN’s luminosity at a wavelength of 5100Å, the contribution of the host galaxy to the nuclear flux has to be subtracted. To achieve this, we disentangled the constant host from the variable AGN flux inside our aperture by using the flux variation gradient (FVG) method originally proposed by Choloniewski (1981) and further established by Winkler et al. (1992) and Sakata et al. (2010). We plot data points for different filter pairs collected throughout the monitoring program in flux-flux diagrams in units of mJy (see Fig. 6). As the observed source varies in luminosity, the fluxes in the FVG diagram will follow a linear relation with a slope (denoted by the symbol Γ; representing the AGN color) given by the host-free AGN continuum. The host, however, will show no variation. While the host slope passes through the origin, a linear least-squares fit to the data points yields the AGN slope. The intersection of the two slopes then allows us to determine the host flux contribution and to calculate the host-subtracted AGN luminosity at the time of the monitoring campaign – even without the need for high spatial resolution images (Haas et al. 2011). We note that the FVG diagrams were calculated taking into account the previously estimated time delays (in Sect. 4.1) between the different wavelength bands. The absolute flux calibration was carried out on the reference images (built from the individual NB frames) by comparison with the Pan-STARRS1 Catalog4 (within a 20′ distance of the target). Since the field is crowded, we obtained up to ∼150 comparison stars in the red filters. For each calibration star, we fit a black-body curve between the known griz values and interpolate the flux to obtain the flux values for the central wavelengths of our NB filters. Finally, we calibrated and estimate the flux of MCG 08-11-011 in each NB and corrected the value for the Galactic foreground extinction (Schlafly & Finkbeiner 2011).

thumbnail Fig. 6.

FVG diagram of MCG 08-11-011 between NB4250 and NB5700, NB6200, NB7320, and NB8025 (from left to right). Each data point is drawn as a thin cross in which the line length corresponds to the photometric uncertainties in the respective filters. A linear least-squares fit to the data points yields the AGN slope, plotted with the steep blue line. The cyan shaded area denotes the host color range from our multi-aperture photometry. The intersection between the AGN and the host galaxy slope gives the host contribution in the respective band within the aperture.

Figure 6 shows the NB4250 vs. NB5700, NB4250 vs. NB6200, NB4250 vs. NB7320, and NB4250 vs. NB8025 fluxes of MCG 08-11-011. Linear least-squares fits to the flux variations in each NB filter pair yield ΓAGN = 1.18 ± 0.02 for NB4250 vs. NB5700, ΓAGN = 1.15 ± 0.02 for NB4250 vs. NB6200, ΓAGN = 1.10 ± 0.02 for NB4250 vs. NB7320, and ΓAGN = 1.04 ± 0.03 for NB4250 vs. NB8025. The host slope was determined by applying multi-aperture photometry on the stacked reference images as proposed by Winkler et al. (1992). Fluxes measured at different apertures are used to infer the host galaxy color, and since the host galaxy contribution increases with the aperture, a linear fit between the fluxes approximates the host slope. We list the total (AGN + host) fluxes for each filter in Table 6 together with the mean host galaxy fluxes (obtained by averaging over the intersection area between the AGN and the host galaxy slopes) and the nuclear flux (calculated by subtracting the constant host galaxy component from the total flux). The listed uncertainties include the median errors of the calibration stars and errors caused by the black-body interpolation. The host contributes ∼5% in NB4250, ∼30% in NB5700, ∼36% in NB6200, ∼47% in NB7320, and ∼54% in NB8025 to the total (AGN + host) observed fluxes.

Table 6.

Total (AGN + host), host galaxy, and AGN continuum fluxes.

To obtain the host-subtracted AGN flux of MCG 08-11-011 at a rest-frame of 5100 Å, we interpolated between the filters NB4250 and NB5700, adopting for the interpolation that the AGN has a power-law spectral shape (Fν ∝ να). At a distance of DL = 93.10 Mpc (Yoshii et al. 2014), this yields a host-subtracted AGN luminosity of λLλ(5100Å) = (4.21 ± 0.65) × 1043 erg s−1. The ∼15% uncertainty includes the measurement errors, the uncertainty of the AGN and host slopes, and the AGN variations. In Fig. 7, we show the total (AGN + host) fluxes, the host-subtracted AGN fluxes, and the host fluxes as a function of wavelength. The power-law fit to the pure AGN fluxes yields Fν ∼ λ−α, with α = 0.02 ± 0.12, which is shallower than (but consistent within uncertainties with) the spectral index predicted by a standard Shakura-Sunyaev disk (α = 1/3). The host-subtracted rms spectrum (values listed in Table 3) shows no spectral variation, which is accordant with the use of the Choloniewski diagrams. Thus, all fractional variability amplitude values are consistent with each other within their uncertainties.

thumbnail Fig. 7.

SED of MCG 08-11-011. Blue points show the host-subtracted AGN continuum with a power-law spectral shape of Fν ∝ λ−0.02 ± 0.12 (dashed blue line). The dotted light blue line corresponds to a spectral shape as predicted by a standard Shakura–Sunyaev disk (with a spectral index of 1/3).

It is worth mentioning that MCG 08-11-011 was previously monitored over four months in 2014 by Fausnaugh et al. (2017, 2018), with the light curves spanning the broad-band ugriz filters. Unlike our work, they observe a lag-spectrum consistent with geometrically thin accretion-disk models that predict a lag-wavelength relation of τ ∝ λ4/3. They report significantly smaller lags (up to ∼2.6 days) than the ones inferred in the present paper using NB light curves, and they find that the disk is a factor of 3.3 larger than predictions based on standard thin-disk theory. However, it is interesting to notice that Fausnaugh et al. (2017) estimated an (host-subtracted) AGN luminosity of λLλ(5100Å) ∼ 1.99 × 1043 erg s−1, which is ∼2.1 times lower than our optical luminosity estimate. These differences in luminosity and measured reverberation lags indicate that the reprocessing may undergo changes on timescales of years. Up to now, only very few AGNs comprise high-cadence continuum RM data spanning timescales long enough to search for temporal changes in lags (one example is Mrk 110 which has shown evidence for a time-varying BLR contribution; Vincentelli et al. 2021, 2022).

4.4. Theoretical disk size

A standard, geometrically thin, optically thick accretion disk radiates thermally and has a temperature profile of T ∼ R−3/4 (Shakura & Sunyaev 1973). The hot inner parts of the accretion disk emit in the UV (∼100 − 3000 Å), while the cooler outer annuli emit in the optical and near-IR (∼3000 − 10 000 Å). As the short-wavelength emission from the X-ray-emitting corona and the inner edge of the disk varies, it irradiates the outer annuli and drives variations at longer wavelengths delayed by the light travel time across the disk (e.g., Krolik et al. 1991). Therefore, this model predicts (based on the object’s SMBH mass and mass-accretion rate) theoretical time delays between short-wavelength and long-wavelength variations according to a given temperature-radius relation.

We compared the observed inter-band continuum lags with model predictions for thermal reprocessing following the method described by Fausnaugh et al. (2016) and Edelson et al. (2017). Since the SMBH mass is highly uncertain, we substituted the product of the SMBH mass and mass-accretion rate with the target’s optical luminosity, Lopt (see Eq. (7) in Davis & Laor 2011; for a detailed derivation, see Fian et al. 2022). Hence, we used the Shakura–Sunyaev model self-consistently and without the need to assume radiative efficiencies. The predicted light travel time τ (in days) relative to a reference time delay τ0 at a wavelength of λ0 = 5100 Å can then be written as follows:

( τ − τ 0 ) ≃ 2 ( L opt 10 45 e r g s s − 1 ) 1 / 2 × [ ( λ 5100 Å ) 4 / 3 − 1 ] days . $$ \begin{aligned} (\tau -\tau _0) \simeq 2 \ \left( \frac{L_{\rm opt}}{10^{45}\,\mathrm ergs\,s^{-1} }\right)^{1/2}\times \ \left[\left(\frac{\lambda }{5100\,\mathrm \AA }\right)^{4/3}-1\right]\,\mathrm{days} . \end{aligned} $$(2)

We find that the inferred time lags are much larger (by a factor of ∼3 − 7) than the theoretical lag estimates, which has been reported in previous works as well (Jha et al. 2022; Fian et al. 2022; Montano et al. 2022; Edelson et al. 2019; Fausnaugh et al. 2018). However, an accretion disk larger than predictions by a factor of 7.4 for the longest optical wavelength band used in this work is striking since optical continuum RM campaigns typically find that continuum emission region sizes are ∼2 − 3 times larger than expected from disk reprocessing models (Cackett et al. 2022). The discrepancy in MCG 08-11-011 is difficult to explain, and it is not clear that host contamination (even for an ∼50% contribution from the extended host galaxy to the observed PSF photometry light curve at that wavelength) and/or intrinsic reddening could fully account for the mismatch between theory and observations. One possible explanation is that AGN accretion disks are larger than model predictions and that their implied physics (e.g., the accretion disk temperature profile) is markedly different from that expected in the thin-disk scheme. Another possible explanation for the longer-than-expected continuum lags and their wavelength dependences is a substantial contribution of diffuse continuum emission from the BLR to the observed continuum signals and reverberation lags (e.g., Cackett et al. 2018; Chelouche et al. 2019; Korista & Goad 2019; Netzer 2022). Since we were not able to constrain higher moments of the transfer functions than the lags (i.e., the first moment), we could not test the pure accretion disk versus accretion disk-BLR origin for the time delays.

5. Conclusions

We carried out photometric RM of the Seyfert 1 galaxy MCG 08-11-011 using specially designed optical NB filters at the C18 telescope of the Wise Observatory, allowing us to trace the emission-line-free continuum at different wavelengths and measure inter-band continuum time lags. According to the disk-reprocessing lamppost model (Martocchia & Matt 1996; Petrucci & Henri 1997; Bao et al. 1998; Reynolds et al. 1999; Dabrowski & Lasenby 2001), photons arising from the innermost regions are reprocessed in the form of emission from the outer regions, resulting in a lag. The reverberation lags represent the light travel time across different regions of the disk and their trend with wavelength contains information about the disk’s temperature profile. The high-cadence multi-wavelength observations at the Wise Observatory provide an excellent dataset to constrain inter-band reverberation lags efficiently. Our main results and conclusions are summarized below.

  • (i)

    All continuum light curves show significant correlated flux variations, which enabled us to carry out time series analysis to estimate the accretion disk size of MCG 08-11-011 using different cross-correlation and light-curve modeling methods.

  • (ii)

    We chose to measure lags relative to the NB4250 band as this is our bluest light curve, and we obtain mean time delays in the observer’s frame of τ = 1.0 ± 0.5 days for NB5700, τ = 2.0 ± 0.6 days for NB6200, τ = 4.5 ± 0.6 days for NB7320, and τ  =  7.1 ± 1.1 days for NB8025. The inferred disk sizes are larger (by a factor of ∼5 on average) than predicted by the Shakura–Sunyaev accretion disk model, which is consistent with recent findings (Jha et al. 2022; Fausnaugh et al. 2017, 2018; Fian et al. 2022; Pozo Nuñez et al. 2019; Edelson et al. 2019; Cackett et al. 2018).

  • (iii)

    The inter-band lags increase with wavelength, which provides strong evidence of disk reprocessing. However, the trend of lag versus wavelength does not match the τ ∝ λ4/3 prediction of a standard geometrically thin disk. Phenomenological modeling shows that the data prefer a steeper lag-wavelength relation instead. This is in agreement with recent findings for Mrk 279, in which a diffuse continuum emission component was detected at the light curve level (Chelouche et al. 2019).

  • (iv)

    A significant contribution of the host-galaxy was found in the reddest bands, and we estimated a monochromatic host-corrected AGN luminosity at 5100 Å of (4.21 ± 0.65) × 1043 erg s−1.

  • (v)

    Interestingly, our results corroborate those from gravitational microlensing of strongly lensed quasars, which also find larger disk sizes than expected and a range of temperature profiles (Jiménez-Vicente et al. 2014; Motta et al. 2017; Fian et al. 2016, 2018, 2021; Cornachione et al. 2020a,b; Cornachione & Morgan 2020; Rojas et al. 2020). While microlensing can only probe the continuum emitting regions in distant high-luminosity quasars, RM provides a complementary approach to investigate the accretion disk structure in low-luminosity AGNs.

Accretion disk sizes obtained through both gravitational microlensing and continuum RM indicate that the standard Shakura–Sunyaev disk assumption does not hold for the majority of AGNs studied so far, and it raises the question of the usage of the simple standard-disk model for AGN accretion disks. Thus, the discrepancy between theory and observations reinforces the suggestion that additional components (such as a contribution of the diffuse BLR continuum emission) may be needed while modeling the accretion disks in AGNs (Jha et al. 2022; Montano et al. 2022; Vincentelli et al. 2021, 2022; Fian et al. 2022). Evidence of a non-disk component in the optical continuum of Mrk 279 was reported by Chelouche et al. (2019), indicating a possible explanation for the larger-than-expected continuum time lags. Vincentelli et al. (2021, 2022) show, for the first time, that the BLR contribution may even vary in a single object, confirming the importance of considering the effect of emitting components different from the disk when studying the lag phenomenology in AGNs. Further multi-epoch observations over a broader range of wavelengths and a longer time baseline would be particularly valuable to search for evidence of diffuse continuum emission from the BLR and to better understand short-timescale variations in reprocessing behavior. Although mapping the entire accretion disk profile is only possible with intensive multiwavelength campaigns such as the AGN STORM (Edelson et al. 2015; Fausnaugh et al. 2016; Kara et al. 2021) with observations ranging from X-ray over UV/optical up to the far IR, the RM campaign at the Wise Observatory provides us with the opportunity to use well-sampled NB light curves free of prominent line emission to study inter-band continuum lags and to reach a more detailed understanding of their physical origin, albeit with a smaller wavelength coverage. This work can be extended to a larger sample of low-luminosity sources that are not accessible through microlensing, allowing us to further research the structure of AGN accretion disks and accretion mechanisms.

Acknowledgments

We thank the anonymous referee for the constructive remarks on this manuscript. This work was financially supported by the DFG grant HA3555-14/1 and CH71-34-3 to Tel Aviv University and University of Haifa. This research also has been partly supported by the Israeli Science Foundation grant no. 2398/19. T.L. is supported by an appointment to the NASA Postdoctoral Program at Goddard Space Flight Center, administered by Oak Ridge Associated Universities under contract with NASA.

References

  1. Alexander, T. 1997, ASSL, 218, 163 [NASA ADS] [Google Scholar]
  2. Bahcall, J. N., Kozlovsky, B.-Z., & Salpeter, E. E. 1972, ApJ, 171, 467 [NASA ADS] [CrossRef] [Google Scholar]
  3. Balbus, S. A., & Hawley, J. F. 1998, Rev. Mod. Phys., 70, 1 [Google Scholar]
  4. Bao, G., Wiita, P. J., & Hadrava, P. 1998, ApJ, 504, 58 [NASA ADS] [CrossRef] [Google Scholar]
  5. Blackburne, J. A., Pooley, D., Rappaport, S., & Schechter, P. L. 2011, ApJ, 729, 34 [Google Scholar]
  6. Blandford, R. D., & McKee, C. F. 1982, ApJ, 255, 419 [Google Scholar]
  7. Brosch, N., Polishook, D., Shporer, A., et al. 2008, Ap&SS, 314, 163 [NASA ADS] [CrossRef] [Google Scholar]
  8. Burbidge, E. M. 1967, ARA&A, 5, 399 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cackett, E. M., Chiang, C.-Y., McHardy, I., et al. 2018, ApJ, 857, 53 [NASA ADS] [CrossRef] [Google Scholar]
  10. Cackett, E. M., Zoghbi, A., & Ulrich, O. 2022, ApJ, 925, 29 [NASA ADS] [CrossRef] [Google Scholar]
  11. Chelouche, D., & Zucker, S. 2013, ApJ, 769, 124 [NASA ADS] [CrossRef] [Google Scholar]
  12. Chelouche, D., Pozo-Nuñez, F., & Zucker, S. 2017, ApJ, 844, 146 [CrossRef] [Google Scholar]
  13. Chelouche, D., Pozo Nuñez, F., & Kaspi, S. 2019, Nat. Astron., 3, 251 [NASA ADS] [CrossRef] [Google Scholar]
  14. Choloniewski, J. 1981, Acta Astron., 31, 293 [NASA ADS] [Google Scholar]
  15. Cornachione, M. A., & Morgan, C. W. 2020, ApJ, 895, 93 [Google Scholar]
  16. Cornachione, M. A., Morgan, C. W., Burger, H. R., et al. 2020a, ApJ, 905, 7 [NASA ADS] [CrossRef] [Google Scholar]
  17. Cornachione, M. A., Morgan, C. W., Millon, M., et al. 2020b, ApJ, 895, 125 [Google Scholar]
  18. Dabrowski, Y., & Lasenby, A. N. 2001, MNRAS, 321, 605 [CrossRef] [Google Scholar]
  19. Davidson, K., & Netzer, H. 1979, Rev. Mod. Phys., 51, 715 [NASA ADS] [CrossRef] [Google Scholar]
  20. Davis, S. W., & Laor, A. 2011, ApJ, 728, 98 [NASA ADS] [CrossRef] [Google Scholar]
  21. Edelson, R. A., & Krolik, J. H. 1988, ApJ, 333, 646 [Google Scholar]
  22. Edelson, R., Turner, T. J., Pounds, K., et al. 2002, ApJ, 568, 610 [CrossRef] [Google Scholar]
  23. Edelson, R., Gelbord, J. M., Horne, K., et al. 2015, ApJ, 806, 129 [NASA ADS] [CrossRef] [Google Scholar]
  24. Edelson, R., Gelbord, J., Cackett, E., et al. 2017, ApJ, 840, 41 [NASA ADS] [CrossRef] [Google Scholar]
  25. Edelson, R., Gelbord, J., Cackett, E., et al. 2019, ApJ, 870, 123 [NASA ADS] [CrossRef] [Google Scholar]
  26. Elvis, M., Wilkes, B. J., McDowell, J. C., et al. 1994, ApJS, 95, 1 [Google Scholar]
  27. Fausnaugh, M. M., Denney, K. D., Barth, A. J., et al. 2016, ApJ, 821, 56 [Google Scholar]
  28. Fausnaugh, M. M., Peterson, B. M., Starkey, D. A., Horne, K., & AGN Storm Collaboration 2017, Front. Astron. Space Sci., 4, 55 [NASA ADS] [CrossRef] [Google Scholar]
  29. Fausnaugh, M. M., Starkey, D. A., Horne, K., et al. 2018, ApJ, 854, 107 [NASA ADS] [CrossRef] [Google Scholar]
  30. Fian, C., Mediavilla, E., Hanslmeier, A., et al. 2016, ApJ, 830, 149 [Google Scholar]
  31. Fian, C., Mediavilla, E., Jiménez-Vicente, J., Muñoz, J. A., & Hanslmeier, A. 2018, ApJ, 869, 132 [NASA ADS] [CrossRef] [Google Scholar]
  32. Fian, C., Mediavilla, E., Jiménez-Vicente, J., et al. 2021, A&A, 654, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Fian, C., Chelouche, D., Kaspi, S., et al. 2022, A&A, 659, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Gaskell, C. M. 1994, ASP Conf. Ser., 69, 111 [NASA ADS] [Google Scholar]
  35. Gaskell, C. M. 2007, ASP Conf. Ser., 373, 596 [NASA ADS] [Google Scholar]
  36. Gaskell, C. M., & Peterson, B. M. 1987, ApJS, 65, 1 [NASA ADS] [CrossRef] [Google Scholar]
  37. Gaskell, C. M., & Sparke, L. S. 1986, ApJ, 305, 175 [NASA ADS] [CrossRef] [Google Scholar]
  38. Glikman, E., Helfand, D. J., & White, R. L. 2006, ApJ, 640, 579 [NASA ADS] [CrossRef] [Google Scholar]
  39. Haas, M., Chini, R., Ramolla, M., et al. 2011, A&A, 535, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Jha, V. K., Joshi, R., Chand, H., et al. 2022, MNRAS, 511, 3005 [NASA ADS] [CrossRef] [Google Scholar]
  41. Jiménez-Vicente, J., Mediavilla, E., Kochanek, C. S., et al. 2014, ApJ, 783, 47 [Google Scholar]
  42. Kara, E., Mehdipour, M., Kriss, G. A., et al. 2021, ApJ, 922, 151 [NASA ADS] [CrossRef] [Google Scholar]
  43. Kelly, B. C., Bechtold, J., & Siemiginowska, A. 2009, ApJ, 698, 895 [Google Scholar]
  44. Korista, K. T., & Goad, M. R. 2019, MNRAS, 489, 5284 [CrossRef] [Google Scholar]
  45. Kozłowski, S. 2016, MNRAS, 459, 2787 [CrossRef] [Google Scholar]
  46. Kozłowski, S., Kochanek, C. S., Udalski, A., et al. 2010, ApJ, 708, 927 [CrossRef] [Google Scholar]
  47. Krolik, J. H., Horne, K., Kallman, T. R., et al. 1991, ApJ, 371, 541 [Google Scholar]
  48. Li, Y.-R., Wang, J.-M., & Bai, J.-M. 2016, ApJ, 831, 206 [NASA ADS] [CrossRef] [Google Scholar]
  49. MacLeod, C. L., Ivezić, Ž., Kochanek, C. S., et al. 2010, ApJ, 721, 1014 [Google Scholar]
  50. MacLeod, C. L., Ivezić, Ž., Sesar, B., et al. 2012, ApJ, 753, 106 [NASA ADS] [CrossRef] [Google Scholar]
  51. Martocchia, A., & Matt, G. 1996, MNRAS, 282, L53 [NASA ADS] [CrossRef] [Google Scholar]
  52. Montano, J.W., Guo, H., Barth, A.J., et al. 2022, ApJ, 934, L37 [NASA ADS] [CrossRef] [Google Scholar]
  53. Morgan, C. W., Kochanek, C. S., Morgan, N. D., & Falco, E. E. 2010, ApJ, 712, 1129 [Google Scholar]
  54. Motta, V., Mediavilla, E., Rojas, K., et al. 2017, ApJ, 835, 132 [NASA ADS] [CrossRef] [Google Scholar]
  55. Netzer, H. 2022, MNRAS, 509, 2637 [NASA ADS] [Google Scholar]
  56. Netzer, H., Heller, A., Loinger, F., et al. 1996, MNRAS, 279, 429 [NASA ADS] [CrossRef] [Google Scholar]
  57. Page, D. N., & Thorne, K. S. 1974, ApJ, 191, 499 [NASA ADS] [CrossRef] [Google Scholar]
  58. Peterson, B. M. 1993, PASP, 105, 247 [NASA ADS] [CrossRef] [Google Scholar]
  59. Peterson, B. M. 2014, Space Sci. Rev., 183, 253 [Google Scholar]
  60. Peterson, B. M., Wanders, I., Horne, K., et al. 1998, PASP, 110, 660 [Google Scholar]
  61. Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [Google Scholar]
  62. Petrucci, P. O., & Henri, G. 1997, A&A, 326, 99 [NASA ADS] [Google Scholar]
  63. Pozo Nuñez, F., Gianniotis, N., Blex, J., et al. 2019, MNRAS, 490, 3936 [Google Scholar]
  64. Rees, M. J. 1984, ARA&A, 22, 471 [Google Scholar]
  65. Reynolds, C. S., Young, A. J., Begelman, M. C., & Fabian, A. C. 1999, ApJ, 514, 164 [NASA ADS] [CrossRef] [Google Scholar]
  66. Rodríguez-Pascual, P. M., Alloin, D., Clavel, J., et al. 1997, ApJS, 110, 9 [CrossRef] [Google Scholar]
  67. Rojas, K., Motta, V., Mediavilla, E., et al. 2020, ApJ, 890, 3 [Google Scholar]
  68. Sakata, Y., Minezaki, T., Yoshii, Y., et al. 2010, ApJ, 711, 461 [NASA ADS] [CrossRef] [Google Scholar]
  69. Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
  70. Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
  71. Shields, G. A. 1978, Nature, 272, 706 [NASA ADS] [CrossRef] [Google Scholar]
  72. Stetson, P. B. 1987, PASP, 99, 191 [Google Scholar]
  73. Telfer, R. C., Zheng, W., Kriss, G. A., & Davidsen, A. F. 2002, ApJ, 565, 773 [NASA ADS] [CrossRef] [Google Scholar]
  74. Veilleux, S., & Osterbrock, D. E. 1987, ApJS, 63, 295 [Google Scholar]
  75. Véron-Cetty, M. P., & Véron, P. 2010, A&A, 518, A10 [Google Scholar]
  76. Vincentelli, F. M., McHardy, I., Cackett, E. M., et al. 2021, MNRAS, 504, 4337 [CrossRef] [Google Scholar]
  77. Vincentelli, F. M., McHardy, I., Hernández Santisteban, J. V., et al. 2022, MNRAS, 512, L33 [NASA ADS] [CrossRef] [Google Scholar]
  78. von Neumann, J. 1941, Ann. Math. Statist., 12, 367 [CrossRef] [Google Scholar]
  79. Weedman, D. W. 1977, ARA&A, 15, 69 [NASA ADS] [CrossRef] [Google Scholar]
  80. White, R. J., & Peterson, B. M. 1994, PASP, 106, 879 [NASA ADS] [CrossRef] [Google Scholar]
  81. Winkler, H., Glass, I. S., van Wyk, F., et al. 1992, MNRAS, 257, 659 [NASA ADS] [Google Scholar]
  82. Yoshii, Y., Kobayashi, Y., Minezaki, T., Koshida, S., & Peterson, B. A. 2014, ApJ, 784, L11 [NASA ADS] [CrossRef] [Google Scholar]
  83. Zu, Y., Kochanek, C. S., & Peterson, B. M. 2011, ApJ, 735, 80 [NASA ADS] [CrossRef] [Google Scholar]
  84. Zu, Y., Kochanek, C. S., Kozłowski, S., & Udalski, A. 2013, ApJ, 765, 106 [NASA ADS] [CrossRef] [Google Scholar]
  85. Zu, Y., Kochanek, C. S., Kozłowski, S., & Peterson, B. M. 2016, ApJ, 819, 122 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

MCG 08-11-011 characteristics.

In the text
Table 2.

Filter and observation information.

In the text
Table 3.

Variability measures for the host-subtracted PSF photometry light curves.

In the text
Table 4.

Summary of the time lags expressed in light days in the observer’s frame between the five continuum light curves of MCG 08-11-011.

In the text
Table 5.

Best-fitting parameters to the inter-band lag spectra presented in Fig. 4.

In the text
Table 6.

Total (AGN + host), host galaxy, and AGN continuum fluxes.

In the text

All Figures

thumbnail Fig. 1.

Composite AGN spectrum of Glikman et al. (2006) shown at the quasar’s redshift of z = 0.0205. The five emission-line-free NB passes of the filters which mainly trace the AGN continuum variations (and are used for the photometric monitoring presented in this work) are shaded in different colors (blue for NB4250, green for NB5700, orange for NB6200, red for NB7320, and dark red for NB8025).
In the text
thumbnail Fig. 2.

PSF photometry light curves of the AGN continuum at 4250, 5700, 6200, 7320, and 8025 Å (from top to bottom) for the period between October 2019 and April 2020. The light curves are normalized to zero mean and unit standard deviation, and the fluxes are in arbitrary units.
In the text
thumbnail Fig. 3.

From top to bottom: partially interpolated CCFs, z-transformed DCFs, FR/RSS centroid distributions (for centroid ≥0.8 rmax), von Neuman estimator peak distributions, JAVELIN posterior distributions of lags (spectroscopic mode), MICA transfer functions, and PRM lag distributions for each NB relative to the 4250 Å band. In the bottom panel all time delays are plotted (in the same order as described before) on a vertical axis for illustration. The solid lines show the mean time delay of all methods together, and the shaded regions represent the corresponding standard deviation. These values are presented in Table 4.
In the text
thumbnail Fig. 4.

Time lags (black circles) between multiband continuum light curves as a function of wavelength for the various methods described in Sect. 3. All lags are measured relative to variations at 4250 Å. The dashed blue lines show the best fit to the observed relation τ = τ0/ [(λ/λ0) β − y0] with τ0, β, and y0 as free parameters (these values are presented in Table 5).
In the text
thumbnail Fig. 5.

Mean time lags (black circles) between multiband continuum light curves as a function of wavelength. All lags are measured relative to variations at 4250 Å. The dashed blue line shows the best fit to the observed relation τ = τ0/ [(λ/λ0) β − y0], with τ0, β, and y0 as free parameters (these values are presented in Table 5). The red dotted line is a fit with fixed theoretical power-law index β = 4/3, as expected for an optically thick and geometrically thin disk.
In the text
thumbnail Fig. 6.

FVG diagram of MCG 08-11-011 between NB4250 and NB5700, NB6200, NB7320, and NB8025 (from left to right). Each data point is drawn as a thin cross in which the line length corresponds to the photometric uncertainties in the respective filters. A linear least-squares fit to the data points yields the AGN slope, plotted with the steep blue line. The cyan shaded area denotes the host color range from our multi-aperture photometry. The intersection between the AGN and the host galaxy slope gives the host contribution in the respective band within the aperture.
In the text
thumbnail Fig. 7.

SED of MCG 08-11-011. Blue points show the host-subtracted AGN continuum with a power-law spectral shape of Fν ∝ λ−0.02 ± 0.12 (dashed blue line). The dotted light blue line corresponds to a spectral shape as predicted by a standard Shakura–Sunyaev disk (with a spectral index of 1/3).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.