| Issue |
A&A
Volume 672, April 2023
Solar Orbiter First Results (Nominal Mission Phase)
|
|
|---|---|---|
| Article Number | A14 | |
| Number of page(s) | 7 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202244069 | |
| Published online | 23 March 2023 | |
In-flight validation of the Metis visible-light polarimeter coronagraph on board Solar Orbiter
1
INAF – Astrophysical Observatory of Turin, Via Osservatorio 20, 10025 Pino Torinese, Turin, Italy
e-mail: alessandro.liberatore@inaf.it
2
The Catholic University of America at NASA-GSFC, 620 Michigan Ave NE, Washington, DC 20064, USA
3
INAF – Astronomical Observatory of Capodimonte, Salita Moiariello 16, 80131 Naples, Italy
4
CNR – Institute for Photonics and Nanotechnologies, Via Trasea 7, 35131 Padua, Italy
5
University of Urbino Carlo Bo and INFN, Via Aurelio Saffi 2, 61029 Urbino, Italy
6
INAF – Trieste Astronomical Observatory, Via Giambattista Tiepolo 11, 34149 Trieste, Italy
7
US Naval Research Laboratory, 4555 Overlook Ave SW, Washington, DC 20375, USA
8
University of Padua, Via VIII Febbraio 2, 35122 Padua, Italy
9
University of Florence, Via Nello Carrara 1, 50019 Sesto Fiorentino, Florence, Italy
10
INAF – Astrophysical Observatory of Catania, Via S. Sofia 78, 95123 Catania, Italy
11
ASI – Italian Space Agency, Via del Politecnico, 00133 Rome, Italy
12
Max-Planck-Institut für Sonnensystemforschung, Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany
13
INAF – Institute for Space Astrophysics and Cosmic Physics, Via Giovanni Celoria 16, 20133 Milan, Italy
Received:
20
May
2022
Accepted:
5
February
2023
Context. The Metis coronagraph is one of the remote sensing instruments of the ESA-NASA Solar Orbiter mission. The goal for the instrument is to enable the study of the solar atmosphere and solar wind by simultaneously acquiring images of the solar corona at two different wavelengths: visible light (VL), within a band ranging from 580 nm to 640 nm, and ultraviolet light, in the HI Lyα 121.6 ± 10 nm. The visible-light channel of the coronagraph includes a polarimeter with electro-optically modulating liquid crystal variable retarders to measure the linearly polarized brightness of the K-corona and derive the electron density.
Aims. In this paper, we present the first in-flight validation results of the Metis polarimetric channel together with a comparison to the on-ground calibrations. This paper seeks to validate the first use of an electro-optical device, the liquid crystal-based polarimeter, in deep space and within a hard radiation environment.
Methods. We used the orientation of the K-corona’s linear polarization vector during the roll maneuvers of the Space Orbiter spacecraft for the in-flight calibration.
Results. The Metis coronagraph on board the Solar Orbiter shows good agreement with the on-ground measurements. The in-flight validation confirms the expected performance of the visible-light channel polarimeter. Furthermore, a comparison between the first polarized brightness value obtained by Metis and the polarized brightness values obtained by the space-based coronagraph LASCO and the ground-based coronagraph K-Cor shows the consistency of the Metis calibrated results.
Key words: Sun: corona / space vehicles: instruments / telescopes / polarization / techniques: polarimetric / instrumentation: polarimeters
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The Sun provides the only opportunity to study in detail the magnetically driven activity in solar-like and late main-sequence stars. Moreover, the diagnostics of the physical parameters of the coronal magnetized plasma is a crucial tool for understanding phenomena that can affect the Earth’s magnetosphere. For this reason, many space missions are aimed at collecting data about our star. Solar Orbiter is one of those missions1.
The scientific goal of the Solar Orbiter mission is to perform detailed measurements of the inner heliosphere and solar wind by combining observations from all ten of the Solar Orbiter spacecraft’s onboard instruments. The Solar Orbiter mission will, for the first time, allow for the remote sensing of the Sun from as close as 0.28 AU. Thanks to several gravitational assists from Venus and Earth, the inclination of the Solar Orbiter spacecraft will be increased with respect to the ecliptic plane until approximately 30deg, enabling the spacecraft to observe the Sun’s polar regions (Müller et al. 2020). Among the Solar Orbiter’s remote sensing instruments is the Metis2 coronagraph, for the study of the solar corona (Antonucci et al. 2020; Fineschi et al. 2020).
One of the observational goals of Metis is to measure the linear polarization of the Kontinuum component of the corona (K-corona). The linear polarization of the K-corona is caused by the Thomson diffusion from coronal free electrons of the photospheric radiation, and it is linearly polarized (Inhester 2016; Raouafi 2011). The coronal emission is optically thin and contains not only the linearly polarized K-corona but also a component that is mostly unpolarized due to the scattering of photospheric light from dust (F-corona). Instrumental stray light would also add to the coronal signal3. In order to eliminate these components, Metis measures the polarized brightness (pB) through the acquisition of four images with different polarization angles. A polarimeter assembly with an electro-optically modulating liquid crystal variable retarder (LCVR) is situated along the optical path of the visible channel of Metis. From the images of the K-corona polarized brightness, a map of the coronal electron density can be derived, as shown in Van De Hulst (1950). The electron density is essential to obtaining other physical parameters, such as the solar wind speed, and to helping determine the origin and acceleration of solar wind.
In Sect. 2, we describe the Metis coronagraph and its polarimeter assembly comprising the LCVR in more detail. In Sect. 3, we present the first in-flight validation results of the Metis LCVR. And in Sect. 4, we report the pB cross-calibration between Metis and SOHO/LASCO.
2. Metis coronagraph
Metis is the coronagraph on board the Solar Orbiter spacecraft for the observation of the Sun’s inner corona, that is, within heliocentric heights of less than nine solar radii (R⊙). During its mission, the Solar Orbiter spacecraft will cover a wide range of distances from the Sun. For this reason, all the instruments aboard have a particular design in order to deal with a high thermal flux when they are at the perihelion. In order to reduce the high thermal load on the instrument when it is near the Sun, the Metis occultation scheme was based on an “inverted” externally occulted configuration. The coronal light is collected by an on-axis aplanatic Gregorian telescope, while the solar disk light is rejected back by a mirror (M0 in Fig. 1). The inverted external occulter (IEO) consists of a circular aperture that reduces the thermal load on the rejection mirror by two orders of magnitude, compared to that of the annular aperture in classical coronagraphs (Fineschi et al. 2020). The suppression of the diffracted light off the edges of the IEO and M0 is achieved, respectively, with an internal occulter (IO) and a Lyot trap (LS).
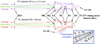 |
Fig. 1. Metis ray trace for the UV and VL channels. The solar disk light is rejected by the mirror M0, while the coronal light is collected by an on-axis aplanatic Gregorian telescope. |
Metis can simultaneously acquire images in visible and ultraviolet light (Fig. 1). The coronal light is split by a UV interferential filter that works by selecting the UV Lyα (121.6 nm) in transmission and by reflecting the visible light (VL) passing through a bandpass filter at 580 − 640 nm to a polarimeter. The polarimeter consists of the following elements: a collimating doublet (CD), a VL bandpass filter (BP), a quarter-wave (QW) plate retarder, a polarization modulation package (PMP) comprising two LCVRs, a linear polarizer (LP) and a focusing lens system (FLS). The detectors are positioned on the focal planes (FPs). All the details about the optical design and performance can be found in the References section (Antonucci et al. 2020; Fineschi et al. 2020).
The VL optical path comprises a polarimeter assembly with two electro-optically modulating LCVRs4 (Fig. 2; Fineschi et al. 2005; Zangrilli et al. 2009). An LCVR consists of optically anisotropic liquid crystal molecules embedded between two glasses with a conductive film and an ordered orientation. The liquid crystal molecules have an effective birefringence value that can be changed by applying an electric field to the cells, which rotates the molecules. The technology of LCVRs has many advantages: Retarders based on liquid crystals do not use moving mechanical parts, thus reducing noise, failure probability, and mass. The power consumption of the liquid crystal-based retarders is also reduced, and their response is very fast (on the order of milliseconds), thus providing a fast modulation of the polarization state of light. The Space Orbiter mission is the first time that such technology has been used in a space mission5.
 |
Fig. 2. Schematic representation of a Liquid Crystal Variable Retarders operation. |
An LCVR device is sensitive to temperature (Fig. 3). Indeed, the retardance depends on the temperature of the liquid crystals cells because different temperatures can facilitate (if higher) or inhibit (if lower) the rotation of the molecules. For this reason, the Metis polarization modulation package (PMP) has a temperature controller to guarantee the temperature stability of the liquid crystal cells. Nominally, the LCVR works at a temperature of 30deg C. However, a characterization of the LCVR performance at different temperatures was performed during on-ground calibrations and can be found in Casti et al. (2018).
 |
Fig. 3. Optical retardances for different applied voltages and verification of the PMP performance for different temperatures (Casti et al. 2018). |
During the on-ground calibrations, we were able to test the Metis polarimeter and evaluate the performance of the LCVR. These calibrations yielded the Metis polarimeter demodulation tensor X†. This tensor was obtained by computing and inverting the modulation matrix X associated with each pixel of the acquired polarimetric images. The elements of these demodulation matrices were collected in images, each relating to an element of the matrix. Because the demodulation matrices have a 3 × 4 dimension, we finally obtained a tensor of 12 images.
The demodulation tensor polarimetrically characterizes the incoming light by returning its Stokes vector S = (S0, S1, S2) = (I, Q, U)6. In accordance with the considered Polarimeter Instrument Level System (PILS) reference frame7 (Figs. 4 and 5), we can define the Stokes parameters as:
-
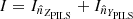 ≡ Intensity of the linearly polarized radiation beams along
≡ Intensity of the linearly polarized radiation beams along 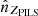 and
and 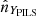 ;
; -
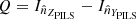 ≡ Intensity of linearly polarized radiation along
≡ Intensity of linearly polarized radiation along 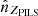 minus intensity of linearly polarized radiation along
minus intensity of linearly polarized radiation along 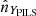 ;
; -
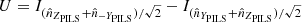 ≡ Intensity of linearly polarized radiation along
≡ Intensity of linearly polarized radiation along 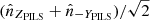 minus intensity of linearly polarized radiation along
minus intensity of linearly polarized radiation along 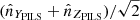 ;
;
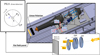 |
Fig. 4. Schematic view of the set up used for data acquisition and Metis polarimeter optical elements relative orientations in PILS reference frame [compared with the Unit Reference Frame (URF)]. The arrows in the optical elements represent, respectively: the fast axes for both the QW and the LP, and the PMP polarization axis. |
 |
Fig. 5. Positions of the sensor’s elements, H(r, α), for the LCVR retardances evaluation in Eq. (5). We considered different heliocentric distances, r, from 3.14 R⊙ to 3.63 R⊙ and different polar angles, α. The PILS reference frame position relative to the Sun is shown in blue. In particular, the zPILS axis results were found to be at −45deg from the west solar limb. |
where 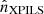 ,
, 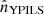 , and
, and 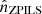 are the unit vectors parallel to the x, y, and z-axes in the PILS reference frame. From the Stokes parameters, it is possible to then define the polarized brightness:
are the unit vectors parallel to the x, y, and z-axes in the PILS reference frame. From the Stokes parameters, it is possible to then define the polarized brightness:
Four images m =[m1, m2, m3, m4] at different retardance values were obtained by varying the voltage applied to the LCVRs, and they were then combined through the relation m = XS → S = X†m. The theoretical modulation matrix is given by Eq. (2):
where the values of the quadruplet retardances, δi, i = 1, 2, 3, 4, of the LCVR in the polarimeter are δ1 = 90deg, δ2 = 180deg, δ3 = 270deg, and δ4 = 0deg.
The theoretical demodulation matrix X† (Eq. (3)) was obtained as the Moore-Penrose inverse of the theoretical modulation matrix X:
As mentioned, the experimental demodulation tensor associated with the Metis polarimeter was derived during the on-ground calibration by acquiring images of a known polarized source modulated by applying different voltages to the LCVR cell. By considering the elements of the Stokes vectors associated with the known polarized source (generated by a rotating linear pre-polarizer), a linear system was solved for at each detector pixel to derive the demodulation tensor (Casti et al. 2018; Liberatore et al. 2021). More information about the on-ground calibration of the Metis VL polarimetric channel can be found in the references (Casti et al. 2019; Fineschi et al. 2020).
3. Polarimeter in-flight validation
In this section, we analyze the in-flight validation of the Metis polarimeter carried out during the first image acquisition by the Metis coronagraph. In particular, we use the geometrical properties of the K-corona polarization vector to perform in-flight validation of the LCVR retardances.
3.1. LCVR retardances evaluation
The K-corona is due to the Thomson diffusion of the photospheric radiation and it is linearly polarized with a polarization vector tangent to the solar limb.
The K-corona polarization vector crossing the transmission axis of the polarimeter analyzer with an angle α, the “polar angle” (shown in Fig. 5), results in an intensity modulation in each i-th image of the set of four coronal images acquired at different voltages of the polarimeter (Fig. 6). We calculated this modulation from the recorded signal, mi, for each sensor element, P(r, α), detrended of the total intensity, I(0), and normalized by the pB(0) (Elmore et al. 2000):
 |
Fig. 6. Intensity modulation in each i-th image of the polarization set of four coronal images expressed in Eq. (4) as a function of the “polar angle”, α, shown in Fig. 5. The LCVR retardances, δi, were derived from the regression in Eq. (5). The data come from a quadruplet acquired during the “roll n.0” of the IT-7 campaign (June 8, 2020; Fig. 8) for a fixed heliocentric height (620 pixels from the Sun center in this particular case). |
where mi is the in-flight data (for i = 1, 2, 3, 4) and the angle ρi is equivalent to the effective polarizer rotations equal to half the LCVR’s retardances, ρ = δ/2. The initial evaluations of I(0) and pB(0) were carried out by using the ground-calibrated effective polarizer rotation angles, 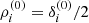 . The in-flight retardance values, δi, were retrieved through the following three-parameter (P0, P1, P2) regression:
. The in-flight retardance values, δi, were retrieved through the following three-parameter (P0, P1, P2) regression:
where yi = (2mi − I)/pB, x is the polar angle α, P0 is the bias of the fitting curve, and P1 is the modulation amplitude. The P2 parameter is defined as:
where the shift of −45deg is introduced to align the PILS reference frame with the solar coordinate system (aligning the zPILS-axis with the solar east-west direction; Fig. 5).
The values of the retardances of the LCVR measured in flight are within the uncertainty due to the flat field in the on-ground derived retardances. Even if these values have a lower error than those obtained from the on-ground calibration, we decided to continue to use the latter because they were obtained through a pixel-by-pixel process (with a demodulation tensor). Moreover, the in-flight values of the retardances were evaluated just for some fixed heliocentric heights and polar angles. Nevertheless, our results show the consistency between the on-ground and in-flight values.
This is the first in-flight validation of a polarimeter with a liquid crystal-based polarimeter. We believe that it may be useful to repeat this validation process in the future to check the status of the polarimeter over time.
3.2. Different voltage configurations
During the first remote sensing checkout window (RSCW1; June 18, 2020; distance to the Sun, 0.52 A.U.), we acquired polarimetric sequences with different quadruplets of PMP voltages. A quadruplet consists of four images at four different LVCR voltages (i.e., effective “polarization angles”) separated by approximately 45deg from each other. The ground calibration yielded the demodulation tensor associated with each image (in addition to the nominal one). The goal of having these different acquisitions was to check the polarimeter’s response for the other set of four voltage configurations. Table 1 summarizes the considered quadruplets with an effective angle error of approximately 1deg.
Retardances of the different LCVR quadruplets Q.
The demodulation tensor associated with each quadruplet returned a corresponding pB(1) that is a refined value with respect to the initial pB(0) obtained from the ground calibration8 In the following sections, these refined values of polarized brightness are indicated as pB ≡ pB(1). By considering the four different coronal regions (i.e., near the streamers, regions 1 and 3, and near the coronal holes, regions 2 and 4) and performing an average over the pixels inside these regions (Fig. 7), we compared the measured polarized brightness with different voltage configurations. The resulting polarized brightness should be the same for each configuration. Figure 7 shows that the difference between the measures of polarized brightness returned by different quadruplets is ≤2%.
 |
Fig. 7. Comparison between the average of the four pB regions for the different quadruplets Qi. The effective angles for each quadruplet are reported in Table 1. The differences between the different pBs are less than 2%. |
4. Validation during spacecraft roll
We acquired different image sets during a complete roll performed by the Solar Orbiter spacecraft on June 8, 2020 (IT-7 campaign; S/C; Sun distance: 0.52 A.U.). During the roll maneuver, the Metis polarimeter acquired a total of eight K-corona pB images (one for each roll position; see Fig. 8). A comparison of these images gave the differences in the polarimetric response at different positions across the polarimeter and the detector.
 |
Fig. 8. Degree of linear polarization (pB/I) of the K-corona for the eight different S/C roll positions and the considered region (white rectangles). The white circle inside the internal occulter shows the Sun’s size and position. |
The degree of linear polarization is derived from the ratio between a pB and the first Stokes parameter I. Figure 8 shows the pB/I images for different spacecraft roll positions. Specifically, the pB/I is plotted as a function of the roll angle for a few selected coronal regions in the frame (along a streamer) at different heliocentric9 distances.
4.1. Check on the LCVR retardances during S/C roll
By analyzing the data acquired during the spacecraft rolls, we could repeat the same type of analysis performed in Sect. 3.1. For a given region in the solar corona, the spacecraft roll acts as a “rotating polarizer.” Therefore, the recorded intensity of a selected region follows the Malus law (Fig. 9). The fitting parameters of this function give an estimation of the LCVR retardances that can be compared with those from the ground calibration and with those obtained from the method presented in Sect. 3. Table 2 summarizes the retardances from the on-ground calibration, the Malus curve fitting (Eq. (4); see Fig. 6), and the Malus curve obtained from the roll maneuver (see Fig. 9).
 |
Fig. 9. Malus curve obtained from yi = (2mi − I)/pB average values over the pixels in a fixed region in the solar corona during each roll. |
Comparison between the LCVR polarization angles from on-ground calibration and in-flight validation.
4.2. Polarized flat field verification
We verified the in-flight polarized flat field by considering the pB of coronal structures measured as they moved to different locations across the detector during roll maneuvers of the Solar Orbiter spacecraft, as shown in Fig. 8. Figure 10 shows, as a function of the roll angle, the pB/I derived from the demodulation tensor, X†, measured during the on-ground calibrations. The quality of the polarization flat fielding obtained by applying the on-ground calibrated demodulation tensor is indicated by the constant pB/I values (i.e., < 5%, except for the heliocentric height 3.39 R⊙ with a percentage variation of approximately 12%) for different roll angles at the same heliocentric height. The degree of linear polarization decreased for increasing heliocentric distances, from (0.24 ± 0.01) at 3.39 R⊙ to (0.14 ± 0.01) at 4.91 R⊙. We note that at higher heliocentric heights, the behavior of the pB/I during the roll maneuvers tended to be less flat due to the decrease in the S/N.
 |
Fig. 10. Average pB/I values over the pixels inside the selected regions for each roll. Data were obtained by using the demodulation tensor from the ground calibration. The bars represent the intensity uncertainty inside the considered area. |
For comparison, Fig. 11 shows, as a function of the roll angle, the pB/I derived from the theoretical demodulation tensor X† given by Eq. (3). The uncertainty of the pB/I mean values using the theoretical X† is two to three times higher than the ones obtained by using the demodulation tensor from the on-ground calibration. Table 3 summarizes the pB/I values for the two cases.
 |
Fig. 11. Average pB/I values over the pixels inside the selected regions. The data are based on the theoretical demodulation tensor. The bars represent the uncertainty inside the considered area. |
Average values of pB/I with standard deviation.
Data reduction with the theoretical X† would return the state of polarization with an accuracy of only about 10% (best case). This value would be the dominant uncertainty, considering that the dispersion error is approximately 2% in the considered regions. On the other hand, the uncertainty in deriving the pB/I values with the experimental X† drops to less than 5%. This percentage is comparable to the approximately 1 − 3% error due to the data uncertainty. In conclusion, the experimental demodulation tensor from ground calibration returns polarization measurements with an accuracy of less than 5%. As estimated in Fineschi et al. (2005), with an accuracy of approximately 1% for the pB (to be compared with the obtained 1–3% due to data uncertainty), we can expect a 1% error on the electron density evaluation. Finally, the retardances calculated from the fitting of the Malus curves acquired during the spacecraft rolls are: 46deg ± 4deg, 82deg ± 4deg, 130deg ± 5deg, and 176deg ± 5deg.
5. Metis first light pB comparison
A preliminary verification of the in-flight validation was obtained from a comparison of the coronal polarized brightness measured by Metis with that obtained by other instruments. In particular, we compared the Metis pB with the pB of the K-Cor (Hou et al. 2013) and LASCO C2/C3 coronagraphs (Brueckner et al. 1995). We performed this comparison by using the data of May 15, 2020. At this time, the Solar Orbiter was almost along the Sun-Earth axis, and for this reason, LASCO C2 and C3, K-Cor, and Metis can be considered as aligned (Fig. 12). Only LASCO-C3 data for May 14 and 16, 2020, were available. Figure 13, shows the Metis pB value compared to the LASCO and K-Cor measurements. For the east streamer, Metis pB values are in agreement with those of LASCO-C3, while they are less than a factor of two higher than that of LASCO-C2. For the west limb, the Metis and LASCO-C2 measured values show better agreement. As the Solar Orbiter mission will progress, more Metis pB measurements will allow for refinement of cross-calibration with other instruments. These initial measurements are a first check of the performance of the Metis polarimeter, and they succeed in confirming the validity of its on-ground and in-flight validation (Fineschi et al. 2021).
 |
Fig. 12. Position of SolO (SO), STEREO-A (A), and Parker Solar Probe (PSP) with respect to Earth on May 15, 2020 (00:00 UT). From STEREO website. |
 |
Fig. 13. Comparison of pB values along the east and west streamer between Metis, LASCO C2/C3, and K-Cor. The images were acquired during an almost Sun-S/C-Earth alignment on 2020-05-15 (Sun-S/C distance: 0.64 A.U.; Fineschi et al. 2021). (a) East streamer. (b) West streamer. |
6. Conclusion
After a summary of the Metis on-ground calibration, we report its first in-flight validation. The first step in the calibration was the validation of the LCVR retardances. We considered the geometry of the physical process that polarizes the K-corona radiation with a polarization vector tangent to the solar limb. At four LCVR retardance values, we acquired four images from which we obtained four Malus curves. From these curves, we were able to derive the effective LCVR retardances. We obtained the retardances, that is, the “polarization angles,” 45.0deg ± 0.1deg, 81.4deg ± 0.1deg, 128.7deg ± 0.1deg, and 175.4deg ± 0.1deg. We also considered a fixed region in the solar corona during a complete S/C rotation as an ulterior check. This gave the same result as “rotating the polarizer.” We obtained 46deg ± 4deg, 82deg ± 4deg, 130deg ± 5deg, and 176deg ± 5deg, which is consistent with the on-ground calibration and with what we obtained by analyzing the polarization of the K-corona tangent to the solar limb.
We acquired polarimetric sequences from different quadruplets of the LCVR voltages used to evaluate the polarimetric response at different voltage configurations. We considered four fixed coronal regions and obtained the polarized brightness by using the demodulation tensor associated with each quadruplet. A comparison of the polarized brightness of the quadruplets with different applied tensions to the polarimeter yielded differences within 2%.
We also evaluated the polarimetric flat field by considering a given coronal region as it was imaged across different locations of the detector focal plane during a complete S/C roll. In particular, we considered different heliocentric heights in the pB/I images. As expected, these values had a small percentage of variation (i.e., < 5%) at the same heliocentric height during the roll maneuver. The percentage variation of the pB/I mean values using the theoretical demodulation tensor is higher than the one obtained using the on-ground calibrations. Quantitatively, by using the demodulation tensor from ground calibrations, the accuracy of the polarization measurement improves by a factor of approximately three. Indeed, the accuracy of the pB/I values when using the theoretical X† is about 10%, while using the X† obtained during on-ground calibrations gives an accuracy of 3 − 5%. Finally, a comparison of the Metis polarized brightness with what has been obtained by other instruments (LASCO C2 and C3 K-Cor) confirms the validity of the Metis polarimeter calibration.
The LCVR cells that compose the Metis PMP were assembled with the fast axes aligned and the pre-tilt angle of the liquid crystal molecules in opposite directions in order to obtain a wider acceptance angle (equal to ±4deg (Alvarez-Herrero et al. 2011; Casti et al. 2018).
It is also used in the Polarimetric and Helioseismic Imager on board Solar Orbiter (Solanki et al. 2020).
Acknowledgments
This paper has been possible thanks to the whole Metis team and the contributions of the many listed authors. Among the others, a particular acknowledgment to E. Antonucci, who led this Project as Principal Investigator until the delivery of the instrument to ESA in September 2017, when M. Romoli took over this role. This work has been supported by the Italian Space Agency - ASI. The industrial contractor for the Metis project has been a temporary consortium between OHB Italia (for opto-mechanical design, electronics and the software) and Thales Alenia Space Italia (for telescope thermal and structural design and realization, application software, instrument integration, alignment and test). The primary and secondary mirrors were provided as Czech contribution to Metis; the mirror hardware development and manufacturing was possible thanks to the Czech PRODEX Programme. The authors thank also ALTEC Company for providing logistic and technical support.
References
- Alvarez-Herrero, A., Uribe-Patarroyo, N., Parejo, P. G., et al. 2011, SPIE Conf. Ser., 8160, 312 [Google Scholar]
- Antonucci, E., Romoli, M., Andretta, V., et al. 2020, A&A, 642, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brueckner, G. E., Howard, R. A., Koomen, M. J., et al. 1995, Sol. Phys., 162, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Casti, M., Fineschi, S., Capobianco, G., et al. 2018, SPIE Conf. Ser., 10698, 930 [Google Scholar]
- Casti, M., Fineschi, S., Capobianco, G., et al. 2019, SPIE Conf. Ser., 11180, 1255 [Google Scholar]
- Elmore, D. F., Card, G. L., Lecinski, A. R., et al. 2000, SPIE Conf. Ser., 4139, 370 [NASA ADS] [Google Scholar]
- Fineschi, S., Zangrilli, L., Rossi, G., et al. 2005, SPIE Conf. Ser., 5901, 389 [NASA ADS] [Google Scholar]
- Fineschi, S., Naletto, G., Romoli, M., et al. 2020, Exp. Astron., 49, 239 [Google Scholar]
- Fineschi, S., Romoli, M., Andretta, V., et al. 2021, SPIE Conf. Ser., 11852, 1185211 [NASA ADS] [Google Scholar]
- Hou, J., de Wijn, A. G., & Tomczyk, S. 2013, ApJ, 774, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Inhester, B. 2016, Solar Stellar Astrophys., 2, 104 [Google Scholar]
- Liberatore, A., Fineschi, S., Casti, M., et al. 2021, SPIE Conf. Ser., 11852, 1793 [Google Scholar]
- Müller, D., St. Cyr, O. C. Zouganelis, I., et al. 2020, A&A, 642, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raouafi, N. E. 2011, ASP Conf. Ser., 437, 99 [NASA ADS] [Google Scholar]
- Solanki, S. K., del Toro Iniesta, J. C., Woch, J., et al. 2020, A&A, 642, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van De Hulst, H. C. 1950, B.A.N., 11, 135 [Google Scholar]
- Zangrilli, L., Fineschi, S., & Capobianco, G. 2009, SPIE Conf. Ser., 7438, 74380W [NASA ADS] [Google Scholar]
All Tables
Comparison between the LCVR polarization angles from on-ground calibration and in-flight validation.
All Figures
 |
Fig. 1. Metis ray trace for the UV and VL channels. The solar disk light is rejected by the mirror M0, while the coronal light is collected by an on-axis aplanatic Gregorian telescope. |
| In the text | |
 |
Fig. 2. Schematic representation of a Liquid Crystal Variable Retarders operation. |
| In the text | |
 |
Fig. 3. Optical retardances for different applied voltages and verification of the PMP performance for different temperatures (Casti et al. 2018). |
| In the text | |
 |
Fig. 4. Schematic view of the set up used for data acquisition and Metis polarimeter optical elements relative orientations in PILS reference frame [compared with the Unit Reference Frame (URF)]. The arrows in the optical elements represent, respectively: the fast axes for both the QW and the LP, and the PMP polarization axis. |
| In the text | |
 |
Fig. 5. Positions of the sensor’s elements, H(r, α), for the LCVR retardances evaluation in Eq. (5). We considered different heliocentric distances, r, from 3.14 R⊙ to 3.63 R⊙ and different polar angles, α. The PILS reference frame position relative to the Sun is shown in blue. In particular, the zPILS axis results were found to be at −45deg from the west solar limb. |
| In the text | |
 |
Fig. 6. Intensity modulation in each i-th image of the polarization set of four coronal images expressed in Eq. (4) as a function of the “polar angle”, α, shown in Fig. 5. The LCVR retardances, δi, were derived from the regression in Eq. (5). The data come from a quadruplet acquired during the “roll n.0” of the IT-7 campaign (June 8, 2020; Fig. 8) for a fixed heliocentric height (620 pixels from the Sun center in this particular case). |
| In the text | |
 |
Fig. 7. Comparison between the average of the four pB regions for the different quadruplets Qi. The effective angles for each quadruplet are reported in Table 1. The differences between the different pBs are less than 2%. |
| In the text | |
 |
Fig. 8. Degree of linear polarization (pB/I) of the K-corona for the eight different S/C roll positions and the considered region (white rectangles). The white circle inside the internal occulter shows the Sun’s size and position. |
| In the text | |
 |
Fig. 9. Malus curve obtained from yi = (2mi − I)/pB average values over the pixels in a fixed region in the solar corona during each roll. |
| In the text | |
 |
Fig. 10. Average pB/I values over the pixels inside the selected regions for each roll. Data were obtained by using the demodulation tensor from the ground calibration. The bars represent the intensity uncertainty inside the considered area. |
| In the text | |
 |
Fig. 11. Average pB/I values over the pixels inside the selected regions. The data are based on the theoretical demodulation tensor. The bars represent the uncertainty inside the considered area. |
| In the text | |
 |
Fig. 12. Position of SolO (SO), STEREO-A (A), and Parker Solar Probe (PSP) with respect to Earth on May 15, 2020 (00:00 UT). From STEREO website. |
| In the text | |
 |
Fig. 13. Comparison of pB values along the east and west streamer between Metis, LASCO C2/C3, and K-Cor. The images were acquired during an almost Sun-S/C-Earth alignment on 2020-05-15 (Sun-S/C distance: 0.64 A.U.; Fineschi et al. 2021). (a) East streamer. (b) West streamer. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



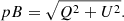
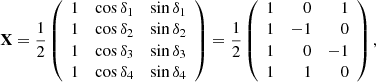
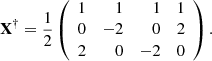
![$$ \begin{aligned} \frac{2m_i - I^{(0)}}{pB^{(0)}} = \cos [2(\alpha - \rho _i)], \end{aligned} $$](/articles/aa/full_html/2023/04/aa44069-22/aa44069-22-eq16.gif)
![$$ \begin{aligned} { y}_i = P_0 + P_1 \cos {[2(x - P_2)],} \end{aligned} $$](/articles/aa/full_html/2023/04/aa44069-22/aa44069-22-eq18.gif)