| Issue |
A&A
Volume 672, April 2023
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 13 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202141918 | |
| Published online | 31 March 2023 | |
Using the “least-deflected” subsamples of ultra-high energy cosmic rays to constrain source population(s)
Astronomy Department, Universidad de Concepción, Casilla 160-C, Concepción 4030000, Chile
e-mail: matiassotomayor@udec.cl
Received:
30
July
2021
Accepted:
4
December
2022
Context. The source population(s) of ultra-high energy cosmic rays (UHECRs) with energies of ≥57 × 1018 eV (57 EeV) are still unknown and continue to be a subject of debate. The published arrival directions and energies of 303 UHECRs from the Pierre Auger Observatory and Telescope Array enable correlations with astronomical sources. However, deflections of UHECRs in the Galactic Magnetic Field (GMF) can be considerable, especially for heavy UHECR compositions.
Aims. We aim to constrain the source(s) of UHECRs by focusing on the subset of UHECRs that experience minimal deflections by the Galactic magnetic field (GMF).
Methods. We used Monte Carlo simulations of UHECR trajectories in a total of eight posited GMF models (and six UHECR compositions from H to Fe) to identify two subsamples of about 40 UHECRs. The H compositions of these subsamples suffer deflections of less than a few degrees in one (or most) of the GMFs. Both the total UHECR sample and the “least-deflected” (vs. the remaining “more-deflected”) subsamples of UHECRs were cross-correlated with catalogs of astronomical sources (at D ≲ 100 Mpc) and neutrino arrival directions.
Results. For H compositions, the full sample of UHECRs is most closely correlated with Cen A, nearby (< 75 Mpc) radiogalaxies, and optically selected active galactic nuclei (AGNs); the least-deflected sub sample shows a most consistent correlation with nearby (D ≲ 25 Mpc) galaxies, although some GMF models show a preference for the IceCube muon-neutrino arrival detections. For oxygen compositions, the out-of-galaxy arrival directions of least-deflected UHECRs fall on the extragalactic plane (and thus close to nearby galaxies) in many GMFs. For Fe compositions, the out-of-galaxy UHECR arrival directions typically originate in a region ∼30 deg offset from Cen A, except in the case of the JF12 model; this offset can be decreased by re-scaling (by ∼50%) the magnitudes of the dipole and disk fields of the relevant GMFs.
Key words: astroparticle physics / acceleration of particles / magnetic fields / catalogs / cosmic rays / galaxies: magnetic fields
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Cosmic rays (CRs) are highly energetic, fully ionized nuclei that permeate Galactic interstellar space (Grenier et al. 2015). Since the discovery of their extraterrestrial origin by Victor Hess over a century ago (for the english transcript, see Hess 2018), an extensive body of work has been dedicated to uncover their nature and their source(s), but many unknowns remain, particularly at the highest energies. The energy spectrum of CRs (Aab et al. 2020; Abbasi et al. 2018a) covers thirteen orders of magnitude and is well approximated by broken power-laws. It is widely accepted that CRs with energy below 5 × 1018 eV (below the break in the energy spectrum referred to as the “ankle”) predominantly come from the sun (Miroshnichenko 2001) and Galactic sources, such as core-collapse supernovae (Marcowith et al. 2018) and Wolf-Rayet stars (Thoudam et al. 2016). Higher energy CRs show arrival-direction anisotropies and have large Larmor radii, so they are believed to have an extragalactic origin (Pierre Auger Collaboration 2017; Aloisio et al. 2012). Cosmic rays with energies above ∼1018 eV (1 Exa electron volt; EeV) are referred to as ultra-high energy cosmic rays (UHECRs). However, in this work, we use UHECR to refer to only those CRs with energies of ≳57 EeV. Research in this energy regime started in 1960 with the CR event observed at Volcano Ranch (Linsley et al. 1961), but given the low flux of these particles at Earth, their fundamental properties (e.g., compositions and acceleration sites) are still uncertain (Anchordoqui 2019).
A UHECR that enters the Earth’s atmosphere excites fluorescence in atmospheric molecules and produces a cascade of secondary particles, that is, the so-called extensive air shower (EAS) over a ∼km radius. The former can be detected via wide-angle fluorescent light detectors (night time) and the latter via Cerenkov detectors on the ground (24-h cycles). This hybrid detection of showers allows high accuracy spatial (∼one degree) and energy (∼10%) constraints on the originating UHECR (Pierre Auger Collaboration 2015; Martens 2007; Shibata 2008).
The largest currently operating UHECR observatories are the Pierre Auger (PAO) and Telescope Array (TA) observatories (see more in Sect. 2.1).
The acceleration mechanism of UHECRs is an active topic of discussion: the most popular processes are the Fermi first- and second-order accelerations, in which particles are accelerated when passing repeatedly through magnetic field irregularities inside astrophysical plasmas, resulting in a power-law UHECR spectrum that is consistent with observations (e.g., Lemoine 2019). Moreover, continuous and long term acceleration can only take place when the magnetic field is strong enough and the source is large enough, to contain the particle’s Larmor radius.
Extensive works in the literature have been dedicated to answering the question of UHECR origin, with diverse astrophysical objects theoretically proposed as sources of UHECRs. Radio galaxies satisfy both the above requirements; here, particles could be accelerated in the lobes (Fraschetti & Melia 2008; Hardcastle et al. 2009; Matthews & Taylor 2021; Hardcastle 2010), jets (Lyutikov & Ouyed 2007), central engine (Norman et al. 1995), and/or hot-spots in the jets (Rachen & Biermann 1993).
Galaxies closest to the Milky Way, specifically the local volume (D < 11 Mpc), are strong candidate sources. Here, UHECRs could be accelerated via processes such as low- and high-luminosity γ-ray bursts (Murase et al. 2006), magnetars (Murase et al. 2009), or the decay of superheavy dark matter (SHDM) particles (Supanitsky & Medina-Tanco 2019). In the latter scenario, the contribution from the Galactic dark matter halo will likely dominate, but anisotropies would be seen due to the nearby extragalactic dark matter distribution, which nearby dwarfs are believed to greatly contribute to (Côté et al. 2000). In addition, UHECRs have been proposed to be accelerated inside galaxy clusters (Brunetti & Jones 2014; Kang et al. 1997), where they likely remain confined by the clusters magnetic field, interacting with the intracluster medium until they can eventually escape (Rordorf et al. 2004).
It is expected that the sources of high energy neutrinos and UHECRs are related (Murase 2019) and the neutral nature of former messengers means they are not affected by magnetic deflections. In order to test for a multimessenger signature in UHECR arrival directions, we correlate our UHECR simulation results with the directions of high-energy muon neutrinos. If indeed UHECRs and high energy neutrinos are produced simultaneously, then a candidate site for UHECR acceleration is the accretion disk around massive black holes (Uryson 2019; Tursunov et al. 2020). A motivation for testing this scenario has been boosted by the multi-messenger detection of high energy neutrinos and γ-rays from the blazar TXS 0506+056 (IceCube Collaboration 2018).
Since UHECRs are expected to be fully ionized nuclei, when travelling through a magnetic field, they are deflected via the Lorentz force. Within the Galaxy, this deflection is significant (from a few to few tens of degrees for hydrogen compositions and few tens to hundreds of degrees for Fe compositions) if the magnetic field is ordered (e.g., Takami & Sato 2008; Nagar & Matulich 2010; Jansson & Farrar 2012). Deflections are typically highest if the particle crosses close to the Galactic center or Galactic plane (both due to the large path length through the Galactic GMF, and since the ordered magnetic field is strongest in the Galactic plane in most models) or if the UHECR has a heavy (e.g., Fe) composition. While it is clearly important to consider these deflections when correlating UHECR Earth-arrival directions with source populations, the morphology and intensity of the GMF is still not definitely determined, with several differing GMF models developed from observational constraints (Sect. 2.3).
On larger scales, a propagating UHECR is subject to energy losses caused by the adiabatic expansion of the universe, photo-disintegration, pair production (Bhattacharjee 2000), and photo-pion production due to interaction with photons of the cosmic microwave background (CMB). The latter, referred to as the Greisen-Zatsepin Kuzmin (GZK) effect (Greisen 1966; Zatsepin & Kuz’min 1966) implies a ∼30% loss of energy of the UHECR and, thus, a suppression of the UHECR energy spectrum at the highest energies (the “GZK cutoff”). The UHECR mean-free path in the GZK scenario (propagation distance between photo-pion production) is estimated to be ∼75–150 Mpc, depending on UHECR composition, initial energy, and the cross-section of ions at these high energies. For example, following Figs. 1 and 2 of Aloisio (2017), the CMB photodisintegration mean-free path for a 1020 eV Iron composition UHECR is approximately 100 Mpc (for the H composition, the photo-pion production mean-free path is 135 Mpc). Heavier cosmic rays are considerably more susceptible to attenuation (Bhattacharjee 2000), however, information on UHECR composition cannot yet be well constrained from EAS development, since this method relies on models of hadronic interaction that are confirmed only up to 1017 EeV (Razzaque 2020).
The usual method to infer UHECR sources involves statistical correlations between astronomical source samples and the UHECR’s Earth-arrival directions. Several correlations of UHECR samples with different astrophysical objects have been attempted; the most recent include starburst galaxies and active galactic nuclei (AGNs, Aab et al. 2018), tidal disruption events (Farrar & Piran 2014), IR-luminous galaxies (Berlind et al. 2010), blazars (Murase et al. 2012), local volume galaxies (Ghisellini et al. 2008; Cuesta & Prada 2009), nearby AGNs, (Jiang et al. 2010), nearby extended radio galaxies (Nagar & Matulich 2008, 2010), high-energy muon neutrinos (Barbano 2020), Centaurus A (Isola et al. 2002, hereafter Cen A) and large-scale structures such as the supergalactic plane (Stanev 2008). Joint analyses of PAO and Telescope Array (TA) UHECRs have also been carried out to test for correlations with high energy neutrinos detected by IceCube and Antares (IceCube Collaboration 2016). However, few of these studies consider magnetic deflections and very few consider, holistically, the wide range of possible scenarios, such as diverse Galactic magnetic field (GMF) models and different potential UHECR compositions.
The first UHECR data release by PAO in 2007 consisted of 27 UHECRs: from this sample, the PAO Collaboration concluded that the events are not isotropic with 99% confidence Pierre Auger Collaboration (2007; hereafter PAO07), this result was confirmed with the second PAO data release of 69 events (PAO10). The TA has published arrival directions and energies for 72 UHECRs detected between 2008 and 2013, with energies above 57 EeV and with a shower zenith angle smaller than 55 degrees (Abbasi et al. 2014). The authors discuss an intermediate scale anisotropy seen in the TA data as a hot-spot near the Galactic anti-center (Abbasi et al. 2014).
In Nagar & Matulich (2008) we used the PAO first release of 27 UHECRs to show a correlation between the Earth-arrival directions of a subset of UHECRs with a small sample of nearby extended radiogalaxies, including Cen A. In Nagar & Matulich (2010), this idea was further developed via Monte Carlo simulations of UHECR propagation in popular GMF models. The results allowed us to argue that about a third of the UHECR sample were closely correlated with the small sample of nearby extended radiogalaxies; the remaining UHECR sample could also be explained as originating in the same radiogalaxy sample if a heavy UHECR composition for these was invoked.
The 2015 PAO release of an enlarged sample of UHECRs (now 231 UHECRs; Aab et al. 2015, PAO15) together with the 72 events reported by TA (Abbasi et al. 2014), allow us to expand our previous work into new directions. The main motivating factors for this new approach are (a) the evidence from PAO and TA of a mixed composition favoured against a pure-light UHECR composition at the ankle region (Aab et al. 2016; Abbasi et al. 2018b; b) the importance of taking into account small deflections in light compositions as well as the large (many tens of degrees) deflections suffered by heavy composition UHECRs in popular GMF models; and (c) the large size of the sample when combining both PAO and TA UHECRs (303 published to date), which allows us to select a subsample that is expected to be least-deflected in all posited GMF models – and use this “least deflected” sample to better constrain the origin of UHECRs. We use Monte Carlo simulations of UHECR propagation through different GMF models and consider different UHECR compositions between H and Fe. The method (and the majority of the GMF models) are detailed in Nagar & Matulich (2008, 2010). Here, we have updated the UHECR samples to the latest samples publicly available and updated model parameters (as relevant), and added the GMF model of Jansson & Farrar (2012, hereafter JF12).
This paper is organized as follows. Section 2 describes the UHECR and astronomical samples, Galactic magnetic field models, and the simulation methods. Section 3 describes the selection of the least-deflected subsamples, and our results when correlating the full UHECR sample, as well as the least-deflected subsamples, with astronomical catalogs. Here, we distinguish the results for hydrogen and heavier UHECR compositions. Finally, Sect. 4 provides a short discussion and summary of our results. Distances and luminosities in this work are calculated using H0 = 72 km s−1 Mpc−1, k = 0, ΩM = 0.3, Λ0 = 0.7, and q0 = − 0.5.
2. Samples and methods
In this section, we describe the UHECR and astronomical source catalogs, the Galactic magnetic field (GMF) models used and our numerical and statistical correlation methods.
2.1. UHECR sample
We used all 231 UHECRs with energies above 50 EeV detected by PAO between January 2004 and March 2014 (Aab et al. 2015). Arrival directions of these are determined to better than 1° when the zenith angle of the cascade is less than 60° (around 50 of these were detected at zenith angles between 60 and 80°). We also used the 72 UHECRs detected by the TA between May 2008 and May 2013, with energies above 57 EeV and with a shower zenith angle smaller than 55° (Abbasi et al. 2014). A combined working group of the PAO and TA collaborations has concluded that re-scaling the PAO energies by +5.2% and the TA energies by −5.2% corrects the shift observed between the UHECR energy spectrum of both observatories (Ivanov et al. 2017). Thus, we scaled the published energies of the PAO and TA UHECRs by these factors.
We refer to the combined PAO and TA UHECR sample : 303 UHECRs with (re-scaled) energies between 57 and 160 EeV as the “full UHECR sample” (Fig. 1). Together, the PAO and TA samples provide an almost full sky coverage, although the exposure time in the northern sky (TA) is less than that in the south (PAO). We account for this by considering a statistical weight for each UHECR that is equal to the inverse of the summed sky exposures of the two observatories.
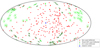 |
Fig. 1. Pierre Auger Observatory (PAO) and Telescope Array (TA) UHECR samples in an Aitoff projection of Galactic coordinates. Light green (dark green) dots and corresponding circles represent UHECRs, which we consider as least-deflected according to the JF12 model (mix of other GMF models; see text). Only four UHECRs are present in both least-deflected subsamples. Red symbols represent the remaining UHECR sample. As expected, the mix-GMF least-deflected sample are primarily at high Galactic latitudes, while the JF12 least-deflected sample are at longitudes that are opposite to the Galactic center. |
2.2. Astronomical source catalogues
We required that the out-of-galaxy arrival directions of UHECRs are correlated with several relevant astronomical catalogs and arrival directions of other multi-messengers. Given the estimated GZK attenuation horizon – unless otherwise noted – all catalogs are filtered to a maximum source distance of ∼75 Mpc. Figure 2 shows the sky distribution in Galactic coordinates of all astronomical catalogs used in this work: each is briefly described in the following paragraphs.
 |
Fig. 2. Astronomical samples used in this work. As in Fig. 1, these are plotted in an Aitoff projection of Galactic coordinates. Light (dark) green circles are used for sources at small (large) distances following the legend. The panels show the following samples: nearby AGN from the Swift-BAT 105 month X-ray catalog (Swift; Oh et al. 2018), Van Velzen radiogalaxy sample (VanVelzen; van Velzen et al. 2012), sample of nearby galaxies (nearby gals; Karachentsev et al. 2013), sample of spectroscopically identified nearby AGN (Zaw AGN; Zaw et al. 2019), sample of high energy muon neutrinos detected by IceCube (IceCube; Plavin et al. 2020), sample of nearby supermassive black holes (SMBH; Caramete & Biermann 2014), galaxy clusters from the Swift-BAT 105 month X-ray catalog (GalCluster; Oh et al. 2018) at D < 75 Mpc, and nearby dwarf galaxies (nearby dwarfs; Karachentsev et al. 2013). |
Swift BAT catalog (Swift): we used the 105 month catalog of the Swift-BAT survey (Fig. 2), which contains 1632 hard X-ray sources (Oh et al. 2018). From this, we chose all Seyfert galaxies, LINERs, and beamed AGNs within 75 Mpc, resulting in a total of 186 galaxies.
Galaxy clusters: we extracted all objects classified as galaxy clusters in the Swift-BAT 105-month survey (Oh et al. 2018). This is the only sample in which we do not apply a distance cutoff.
Van Velzen radiogalaxy catalog (hereafter VanVelzen): we used the catalog of nearby radiogalaxies (RGs) of van Velzen et al. (2012), which is drawn from 2MRS, NVSS and SUMSS. The catalog contains radio-galaxies with flux greater than 213 mJy at 1.4 GHz. This catalog was specifically constructed to select a limited-volume sample of galaxies capable of accelerating UHECRs. Considering only those objects classified as jets+lobes at D < 75 Mpc, we obtained a subcatalog of 28 radiogalaxies, which we refer to as the VanVelzen sample.
Zaw optical AGN catalog: we used the all-sky catalog of uniformly selected optical AGN galaxies of Zaw et al. (2019). These were selected from the 2MRS (2MASS Redshift Survey), and is thus reasonably complete out to 75 Mpc. Zaw identified 1929 broad line AGN, and 6562 narrow line AGN that satisfy either the Kauffmann (Kauffmann et al. 2003) or Kewley (Kewley et al. 2001) criteria. Both Kewley and Kauffman use optical emission line ratios to separate starburst galaxies from AGN (Seyferts and LINERs); the Kauffman criterion classifies more galaxies as AGN as compared to the Kewley criterion. We selected all Zaw AGN classified as Type I (broad line AGN), and Type II (narrow line AGN) that satisfy the Kewley criteria, applying a distance limit of 75 Mpc results in 121 AGN in the sample.
Nearby galaxies and nearby dwarfs: we used the all-sky catalog of 869 nearby galaxies of Karachentsev et al. (2013), with distances up to 25 Mpc. We note that this catalog is complete in the zone of avoidance of the Galaxy. From these, we constructed two subsamples: the nearby dwarf sample (643 dwarfs, classified morphologically following Corwin 1994) and the nearby galaxy sample (226 normal, i.e., non-dwarf, galaxies).
IceCube: muon neutrinos, detected by IceCube (IceCube Collaboration 2006), produce clear track-like signatures, which allow for precise determinations of arrival directions. Other neutrino flavors produce showers which do not allow precise arrival directions of the originating neutrino. We thus used the catalog of high energy muon neutrinos compiled by Plavin et al. (2020), which contains 56 muon neutrino events with energies above 200 TeV and arrival directions accurate to ∼1°.
The SMBH catalog: to test for correlations with supermassive black holes, we used the catalog of Caramete & Biermann (2014), which was compiled specifically to test associations between black holes and UHECRs. Their sample, based on early type galaxies and 2MASS photometry, includes 5916 sources. Using our cut-off of 75 Mpc results in 4103 supermassive black holes.
Finally we also considered specific regions of the sky for our analysis: the nearby radio galaxy Cen A plus its radio jets and lobes, and the supergalactic plane.
2.3. Magnetic field models
The UHECRs detected at the Earth have already suffered deflections due to magnetic fields within their source environment (e.g., source galaxy or cluster), inter-galactic space, and our Galaxy.
In this work, we did not consider deflections by inter-galactic magnetic fields (IGMF; e.g., Sigl et al. 2003; van Vliet et al. 2021) for two main reasons: they are expected to be weak, (e.g., ≲9 × 10−12 G Alves Batista & Saveliev 2021; Jedamzik & Saveliev 2019), and disordered. While ordered magnetic fields can produce systematic deflections of large magnitude, weak disordered fields likely produce a dispersion of a few degrees, even for heavy compositions.
Considering this upper limit for the IGMF and using Eq. (1) of Kachelriess (2022), the average dispersion expected to be introduced by the IGMF is less than 1 deg for Fe nuclei.
Models of the Galaxy’s ordered magnetic field are constructed via fits to the measured optical polarization of stars and the Faraday rotation of polarized emission from pulsars and extragalactic radio sources (e.g., Sun et al. 2008). Additionally, Zeeman splitting of radio spectral lines and synchrotron emission depolarization are used to measure the local and turbulent magnetic fields (Beck & Wielebinski 2013).
The Galactic magnetic field (GMF) is usually modelled with two components: regular and turbulent. The regular component is typically divided into a disk field, which follows the matter distribution and can be bisymmetric (BS) or axisymmetric (AS), and a halo field that can be symmetric (S) or asymmetric (A). A dipole field is often added to account for the observed vertical (z) component in the vicinity of the Solar System and the Galactic Center. Reviews of proposed GMF models and their derivations can be found in Brown (2010), Beck (2008), Sun et al. (2008), and Sun & Reich (2010).
In this work we use a total of eight proposed GMF models. As in Nagar & Matulich (2010) we use the four “traditional” models (AS-S,AS-A,BS-S,BS-A; Takami & Sato 2008) and the three models – which we refer to as AS-S Ring, AS-S Arm, and BS-S Sun – proposed by Sun et al. (2008), using the updated parameters listed in Sun & Reich (2010). Finally we implement the model from Jansson & Farrar (2012, hereafter JF12), which has been constructed to reproduce the most updated observations and, unlike previous models, incorporates an X-shape field component that has a very distinctive influence on UHECR deflections.
The most up-to-date analytic description of the Milky Way GMF, the model is composed of three main components, which will be briefly described here. This model, like the Sun ones, makes use of the NE2001 electron density model and was made to fit observations of galactic polarized synchrotron emission from WMAP7 and over 40.000 Faraday rotation measures from extragalactic sources. Thus, giving a much better fit to the observable data than previous models in the literature. Consistent with the other models considered here, the JF12 model includes a disk and extended halo fields, but unlike the others, and motivated by observations of external galaxies, they include an out of plane ‘X shape’ field. The authors argue that this has particular influence on UHECR deflections.
2.4. Methods
Our simulations, which are detailed in Nagar & Matulich (2010), backtrack the Earth-arrival directions of UHECRs through the deflections suffered by the GMF model in steps of 0.01 kpc, until they reach a distance of 40 kpc from the Galactic center, at which point their velocity vector is used to determine their “out-of-Galaxy” arrival direction. We use all eight models detailed in Sect. 2.3 and six different UHECR compositions: hydrogen (H), helium (He), oxygen (O), aluminium (Al), calcium (Ca), and iron (Fe). This simulation is initially performed once for each UHECR, for each GMF, and for each composition, and without considering errors in the GMF. Given the relatively high energies of the UHECRs, out-of-galaxy arrival directions are obtained for all UHECRs, namely, even Fe composition UHECRs leave the galaxy without multiple closed orbits within the Galaxy.
For our Monte Carlo (MC) simulations, we ran the above simulations 50 times for each UHECR (for details, see Nagar & Matulich 2010). At each 0.01 kpc step of the simulation, we added a random error in the ordered GMF field (uniformly distributed between 0 and 50% of the value of the GMF at that location), plus a turbulent field component. The turbulent field scale is 50 pc, with a maximum value of 10 μGauss, and the probability of its existence is 20% for scale heights of ≤5 pc from the disk plane and 80% in the spiral arms. The spread in the out-of-galaxy arrival directions of the 50 MC points thus trace the magnitude of the expected error in the out-of-galaxy arrival direction of the UHECR for a given GMF and composition. Density plots and the statistical correlations shown here thus use 303 UHECRs × 50 MC points per UHECR.
For statistical comparisons between astronomical catalogs and out-of-galaxy UHECR arrival directions, we calculated the normalized fraction of our MC out-of-galaxy arrival directions that fall within a circle of a given (varying) radius around all sources in a given catalog. The normalization accounts for the total sky area inside vs. outside the circles around all catalog sources and (optionally) a weight which depends on the sky exposure time of the PAO+TA observatories at the declination of the Earth-arrival-direction of the UHECR, that is, a UHECR with Earth-arrival-direction in an area with low sky exposure is considered with a higher weight. Error bars in this case are taken from propagating Poisson errors of the MC counts inside and outside the circles.
3. Results
In this section, we first outline our selection of the “least-deflected” UHECR sub-samples. We then present comparisons between the out-of-galaxy arrival directions of the full UHECR sample and sources in astronomical catalogs. This analysis is then repeated but now separating the results for the least-deflected and the other (more-deflected) subsamples.
3.1. Identifying the least-deflected UHECR samples
From the full sample of 303 UHECRs, we identified the subsamples that suffer from the least amount of deflection in GMF models when considering a hydrogen UHECR composition. This subsample should provide the best candidate UHECRs for positional correlations with extragalactic sources.
To construct the least-deflected sample, we took the difference between the simulated out-of-galaxy and the observed Earth-arrival directions (final deflection, deffin). The azimuthal symmetry in many of the GMF models means that deflection on the near-side and far-side of the galaxy can cancel out. Thus, it can be dangerous to rely only on the values of deffin unless we had complete confidence in the azimuthal symmetry of the GMF. For this reason, we additionaly defined the variable defabs, calculated for each UHECR by summing, as scalars, the magnitudes of the deflection angles suffered in each 10 pc step of our simulation. This accounts for the total deflection suffered by each particle, independent of these getting canceled out in a vector summation during the 3D propagation.
The JF12 GMF model is intrinsically very different from the other seven GMF models: in the former, the “X-shaped” component of the GMF is the dominant contributor to deflections, while in the latter the disk field is the dominant deflector for most UHECRs. The magnitude of the deflections suffered by a given hydrogen UHECR in the latter models is relatively similar, but is significantly different from the equivalent deflection in the JF12 model. We thus created two “least-deflected samples”, namely the JF12 least-deflected sample and the “mix-GMF” least-deflected sample (considering a mix of the other seven models).
We selected the “JF12 least-deflected” sample as follows: all UHECRs for which a hydrogen composition in the JF12 GMF gives defabs < 7°, and deffin < 3°. This yielded a sample of 36 least-deflected UHECRs (dark green circles in Fig. 1). These are primarily at anti-Galactic-center longitudes (and do not necessarily avoid the Galactic plane). When necessary, we refer to the remaining 267 UHECRs as the JF12 more-deflected sample.
We selected the “mix-GMF” least-deflected sample as follows: all UHECRs for which a hydrogen composition gave defabs < 7° and deffin < 6° in at least four of the seven non-JF12 GMF models. This resulted in 41 events in the “mix-GMF least-deflected” sample, shown as light green circles in Fig. 1. Given the dominance of the disk field component in these seven models, this least-deflected UHECR subsample avoids both the Galactic plane and Galactic-center longitudes. When necessary we refer to the remaining 262 UHECRs as the mix-GMF more-deflected sample.
Figure 3 shows the (re-scaled) energy and sky exposure weighting distributions for the UHECR samples used in this work. The mix-GMF least-deflected sample has, on average, slightly higher energies than the JF12 least-deflected sample. The JF12 least-deflected sample is – relative to the mix-GMF least-deflected sample – found in areas with lower sky exposure. The figures showing statistical results in the rest of this work shows those without sky exposure weights.
 |
Fig. 3. Histograms for the UHECR samples used in this work. Top: energy distribution of the full (PAO and TA) UHECR sample (after re-scaling), together with those of the two least-deflected samples. Energies range between 57 and 160 EeV. Bottom: histogram of the exposure weight (the inverse of the combined sky-exposures of the PAO and TA) for the arrival directions of the UHECRs used in this work. Since exposure weights vary by factor 6–10 over the different sub-samples we preferentially use the statistical results without weighting for the sky exposure time of the observatories. |
3.2. Hydrogen full-sample UHECRs and astronomical catalogs
In this subsection, we consider a hydrogen composition for the full sample of 303 detected UHECRs, all GMFs, and all astronomical catalogs.
Figure 4 shows the out-of-galaxy arrival directions of UHECRs, specifically a density plot of the resulting MC points from our trajectory simulations, assuming a hydrogen composition, and in all GMFs considered. For illustration, we overplot our nearby galaxy sample (described in Sect. 2.2) by distinguishing the closest (D < 11 Mpc) galaxies. This MC density can be compared to other astronomical samples using Fig. 2. As noted previously (e.g., Nagar & Matulich 2010; Giaccari & Pierre Auger Collaboration 2017) in all GMF models we see a concentration towards the Cen A region, which is also a region which includes a high density of D < 11 Mpc (red dots) galaxies. The GMF models with an Galactic-plane asymmetry (e.g., BS-A) also show a southern counterpart to this concentration around the Cen A region.
 |
Fig. 4. Density plots of the Monte Carlo points for hydrogen UHECR composition and for different GMF models (as marked), following the color bar on the right. The black outline represents Centaurus A. The red (orange) dots in each panel show the distribution of our nearby galaxy sample at D < 11 Mpc (11 Mpc < D < 25 Mpc). |
A zoom of the top left panel of Fig. 4 in the Cen A region is shown in the left panel of Fig. 5. Here we also show the outline of the large scale lobes in Cen A (Hardcastle et al. 2003) and the density colors show only those MC points within 30° of Cen A. This highest density of MC points shows a double shape that roughly aligns with the twin lobes of Cen A. Changing the BS-S dipole and disk fields by ∼50% (see Sect. 4) can bring the two into even better alignment.
 |
Fig. 5. Figure for the special case of Cen A, considering a mixed composition scenario. Left: density plot of hydrogen UHECR MC points closer than 30° from the Cen A nucleus for the BS-S model. Right: aitoff projected density plot of iron UHECR MC points, but UHECRs for which ≥50% of hydrogen MC points are already matched to Cen A (left panel) are not considered. In both panels galaxies in the VanVelzen RG catalog at distances D < 75 Mpc (75 < D < 150 Mpc) are shown in orange (red) dots; the overall extent of the radio lobes of Cen A are outlined in red. |
As detailed in Sect. 2.4, we tested for correlations between astronomical catalogs and the out-of-galaxy MC arrival directions by counting the MC points which fall within a circle of a given radius around each source in a given catalog. Example results are shown in Fig. 6. The left panel shows the normalized counts when comparing all astronomical catalogs with the hydrogen composition MC points obtained for the BS-S GMF model, as the match radius is varied. Values greater than one imply that MC points preferentially fall inside, rather than outside, the circles around the catalog members. Here, the Zaw AGN and VanVelzen nearby RGs (and perhaps nearby clusters) are the most favored at radii smaller than 10°, while clearly the least favored is the IceCube neutrino catalog. In the middle (right) panels, we show the correlation between VanVelzen RGs (nearby galaxies) for all GMFs. For BS-S and BS-A models, nearby RGs are favored as the source of UHECRs for match radii ≲8°. The match with Zaw AGN is much tighter: in almost all GMFs (and especially AS-A) the MC points preferentially fall close to optical AGN at relatively small (≲ few degrees) match distances. The preferential clustering of the hydrogen MC points for several GMFs, around nearby AGN and nearby RGs is an important result of this work.
 |
Fig. 6. Results for our statistical correlations at different radii. Left: normalized counts of MC points which fall within circles around source in a given catalog, for the BS-S GMF, hydrogen composition, and all astronomical catalogs used in this work. A normalized count of > 1 implies that MC points prefer to fall inside, rather than outside, the circles around a given catalog’s sources (see Sect. 2.4). Error bars are from Poisson errors (Sect. 2.4). Middle: as in the left panel but for all radiogalaxies in the Van Velzen catalog within 75 Mpc, and for different GMF models. Right: same as in the middle panel but for the Zaw AGN catalog. |
3.3. Heavy-composition full-sample UHECRs and astronomical catalogs
In this subsection, we present results for the full sample of 303 UHECRs, for compositions heavier than hydrogen, and for all GMFs. Figure 7 shows the density distribution of MC points for the different UHECR compositions used and for the BS-S GMF model. As the composition increases all MC points are driven to a “focal point” that is located ∼20–30° to the East (in Galactic coordinates) of Cen A. This overdensity, particularly for compositions heavier than Oxygen, is relatively close to the highest density of RGs from the VanVelzen catalog and a high density in the nearby galaxy catalog. This correlation can also be clearly noted in the left panel of Fig. 8.
 |
Fig. 7. Density plots of our MC simulations for the BS-S GMF model, and different UHECR compositions, and here the orange (red) points show galaxies from the Van Velzen RG catalog at D < 75 Mpc (75 Mpc < D < 150 Mpc). The black outline represents Centaurus A. |
 |
Fig. 8. Correlation results for different scenarios considered. Left: same as the left panel of Fig. 6, i.e., correlations for all astronomical catalogs considering deflections in the BS-S GMF, but for an Fe UHECR composition. Middle: correlations between Fe composition UHECRs and the nearby galaxy catalog for different GMF models. Right: correlations between the nearby galaxy catalog and different UHECR compositions for the BS-S GMF. |
The predictions of out-of-galaxy arrival directions for a Fe UHECR composition can be significantly different between the GMF models considered (Fig. 9). For reference we overlay in this figure the arrival directions of IceCube high energy muon neutrinos. The large deflections suffered by Fe UHECRs make any correlation with extragalactic sources more uncertain, but the overall trends seen here are nevertheless instructive. The strongest correlation to IceCube neutrinos occur for two of the Sun et al. models: AS-S Ring, and AS-S Arm, whose deflections produce out-of-galaxy arrival directions preferentially towards the Galactic anti-center. The JF12 model also exhibits this Galactic anti-center tendency, but with positions closer to the north Galactic pole, likely due to the X-shape field component; this produces a strong correlation with the nearby galaxy sample (middle panel of Fig. 8).
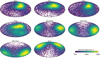 |
Fig. 9. Density plot of our MC simulations for Fe composition and different GMF models. Red points show neutrino arrival directions from IceCube. Centaurus A is represented by the black outline. |
In Sect. 3.2 and the left panel of Fig. 5 we present all UHECRs whose out-of-galaxy arrival directions, assuming a hydrogen composition, fall within 30° of Cen A. We eliminated all UHECRs for which ≥50% of MC points fall within 30° of Cen A and for the remaining UHECRs, we plot the distribution of out-of-galaxy arrival directions, assuming an Fe composition and BS-S model, in the right panel of Fig. 5. As in the total UHECR sample, the points are clustered about 30° from Cen A. In Sect. 4, we illustrate that ∼50% changes in the normalizing magnitudes of the dipole and disk components of the GMF would shift the distribution of both the H and Fe composition UHECR out-of-galaxy overdensity closer towards Cen A: in this case, most UHECRs could be attributed to the Cen A lobes, for a mixed H and Fe composition. Alternatively, a mix of hydrogen and oxygen (for which case the offset between Cen A and the MC concentration is smaller; e.g., Fig. 7) is another possibility which requires smaller changes in the normalization of the BS-S model. While Fe nuclei are easier to accelerate, carbon, nitrogen, and oxygen have significantly higher abundances in the ISM and they are therefore most likely to be swept up from the nuclear starburst in Cen A and into its radio lobes.
Illustrative plots of the correlations between heavy UHECRs and astronomical sample are shown in Fig. 8. In the BS-S model, nearby RGs are most closely correlated with Fe composition UHECRs over a large range of separations (left panel). For Fe compositions and all GMFs considered (middle panel), the strongest correlation is seen between the nearby galaxy sample in the JF12 GMF – over a large range of distances, though several other GMFs including BS-S also show preference at separations of < 1°. The right panel compares correlations between BS-S GMF and nearby galaxies, for different compositions. As noted earlier, hydrogen compositions show a clear trend of correlation increasing as the separation decreases, however, in general, the correlations remain strong for all compositions except helium.
3.4. Hydrogen least-deflected UHECRs and astronomical catalogs
We now present the correlations found among each of the two least-deflected samples and our astronomical catalogs for the case of hydrogen-composition UHECRs. These correlations were performed both with and without sky-exposure weighting. The results of the two cases show quantitative differences (and the case of using sky-exposure weighting shows more variance between GMF models), but the overall correlation results do not change. For brevity, we present and discuss only the results in the case where sky-exposure weighting was not applied.
In Fig. 10, we show the correlations for the mix-GMF least-deflected UHECR sample and all astronomical catalogs, considering the BS-A GMF model and without applying the sky exposure weights of the observatories. In most GMF models, including the BSA-A model shown here the mix-GMF least-deflected sample shows a clear preference, at ≲4° separations, for the nearby galaxy and IceCube neutrino catalogs. In some GMFs, including the BSA-A model shown here, the mix-GMF least-deflected sample also shows a preference for AGN in the Swift catalog at ≲4° separations (left panel). The UHECRs not in the mix-GMF least-deflected sample (middle panel) do show consistent or clear trends across all GMF models; in the BSA-A model shown here, there is a preference for nearby RGs in the Van Velzen sample. The ratio of the two left panels is shown in the rightmost panel, illustrating the preferences shown in the least-deflected sample that are not seen in the other UHECRs. As compared to the other UHECRs, the mix-GMF least-deflected sample is highly preferentially correlated at distances of ≲2° with nearby galaxies and (to a lesser extent) with IceCube neutrinos and Swift AGN across most GMF models.
 |
Fig. 10. Normalized number (left two panels) or ratio (right panel) of MC points, for a hydrogen composition and BS-A GMF model, which fall within a certain radius of any source in a given astronomical sample, for several samples as noted in the legend. Left (middle) panel shows the statistics for the mix-GMF least-deflected sample (all other UHECRs). The normalization in the left two panels is done based on the ratio of sky area within and outside the circles around all sources in a given astronomical catalog. Right panel shows the ratio of the numbers in the left and middle panels. |
We do not show the equivalent results of the other GMF models as they are relatively consistent with those shown for the BS-A model in in Fig. 10. Across all GMFs, the catalog that most consistently shows the least correlation for the mix-GMF least-deflected sample is the VanVelzen RG catalog.
We show a similar analysis to the above-described one, but for the JF12 least-deflected sample, in Fig. 11. The JF12 least-deflected sample (left panel) also shows a general preference for the nearby galaxy and IceCube neutrino catalogs. For the JF12 least-deflected sample, we see a preference for the Zaw AGN catalog in more GMFs as compared to the case of the mix-GMF least-deflected sample. The non least-deflected sample (middle panel) shows a preference for IceCube neutrinos at < 3° separations. Thus, in the ratio (right panel), the JF12 least-deflected UHECRs show a much greater affinity for IceCube neutrinos at intermediate (∼8–12°) as compared to those that are the most deflected. The other catalogs show no strong gradients with distance.
 |
Fig. 11. Correlation results As in Fig. 10, but for the JF12 least-deflected sample, and the BS-S Sun model. |
3.5. Heavy composition least-deflected UHECRs and astronomical catalogs
In this section, we present our results for both least-deflected subsamples assuming heavier compositions. Heavier compositions of course suffer larger deflections, thus making the concept of “least-deflected” moot. Nevertheless, it is instructive – to be open to the scenario where all detected UHECRs are of heavy composition – to test how these least-deflected UHECRs, which suffer minimal deflections if hydrogen, change their out-of-galaxy arrival directions when assuming increasingly heavier compositions.
In Fig. 12, we show our least-deflected subsamples and their corresponding out of galaxy arrival directions for compositions of hydrogen, helium, and oxygen. We do not show compositions heavier than oxygen to avoid cluttering these plots and since the “focal points” seen for Fe composition – for the full UHECR sample, however – have already been explored in Sect. 3.3. For easy visualization the Earth arrival direction and the different out of galaxy arrival directions for a given UHECR are connected with lines.
 |
Fig. 12. Out-of-galaxy arrival directions of least-deflected UHECRs for compositions of hydrogen, helium, and oxygen, in all GMFs considered. Earth arrival directions of the mix-GMF (JF12) least-deflected sample are shown as dark green (light green) filled circles following the legend. Out of galaxy arrival directions for compositions of hydrogen (yellow), helium (orange), and oxygen (red) are shown as filled circles. For visualization ease, lines in the same color as the Earth arrival direction of the respective least-deflected sample (light and dark green) join the Earth arrival direction and out of galaxy arrival directions of a given UHECR. |
For both least-deflected samples, the deflections for He compositions (orange circles) remain relatively small, but for oxygen compositions (red circles) the out of galaxy arrival directions, while significantly offset, begin to form several overall patterns. In the four models at the top of the figure, BS-S, BS-A, AS-S, and AS-A, the least-deflected UHECRs in the northern Galactic hemisphere have their oxygen compositions lined up with the supergalactic plane. A similar (but not as tight) pattern is also seen in the southern Galactic hemisphere: here, the symmetric versus the axi-symmetric GMFs move the oxygen UHECR out of galaxy directions to different parts of the supergalactic plane. This comparison with the supergalactic plane is also relevant as the catalog of nearby galaxies (Fig. 2) also traces the supergalactic plane as expected. In fact, the red points in the top four panels of Fig. 12, which do not lie close to the supergalactic plane, still lie close to other overdensities in the nearby galaxy sample. This is one of the reasons for the consistently good correlation seen between arrival directions and the nearby galaxy catalog over several models and compositions (e.g., Figs. 6, 8, and 10).
As noted in Sect. 3.3, for the Sun et al. models, increasing the composition moves the out of galaxy arrival directions towards the Galactic anti-center for UHECRs in the northern Galactic hemisphere, while those in the southern Galactic hemisphere move closer to the SuperGalactic plane. For the JF12 GMF, as noted earlier, increasing the composition moves the out of galaxy arrival directions to longitudes away from the Galactic center, but intermediate latitudes.
Figure 12 also illustrates the large incompatibility of the two least-deflected samples we used: the mix-GMF and the JF12 least-deflected samples. The JF12 least-deflected sample suffers relatively large deflections in the other GMFs (and vice versa). It is also notable that the JF12 least-deflected sample suffers much smaller deflections in the JF12 GMF, as compared to the mix-GMF least deflected sample in any other GMF. That is to say, in the case that the JF12 model truly represents the true GMF, then future expanded JF12 least deflected samples may provide the strongest constraints on the origin of UHECRs, even if most UHECRs have a heavy composition.
4. Discussion and conclusions
With PAO and the TA in full operation, the sample of detected UHECRs at energies greater than 57 EeV is steadily growing. With 303 published (∼2014 and earlier) UHECRs with accurate energies and arrival directions in this range, the full PAO+TA sample is likely almost double this size as of today. Given the uncertainties in GMF models and UHECR compositions, the primary aim of this work is to demonstrate the potential of using a subsample of UHECRs which are least deflected in current GMFs, so that we may identify the source population(s) of UHECRs in the most reliable way. In this exploratory work, we have already found several interesting correlations with astronomical catalogs – both for the full sample of UHECRs and for the least-deflected subsamples.
To be open to most alternative scenarios, our simulations of UHECR trajectories included most currently accepted GMF models in the literature, several compositions between hydrogen and iron, and physically motivated samples of galaxies: hard X-ray selected AGNs, optically selected AGNs, nearby galaxies and dwarfs, radiogalaxies with jets and lobes, nearby supermassive black holes, and X-ray detected galaxy clusters. Given the current estimates of the GZK horizon, we have filtered all samples except for galaxy clusters, at a distance of 75 Mpc; we note that the sample of nearby galaxies and dwarfs are much closer: D < 11 Mpc. Apart from extragalactic source catalogs we also used the arrival directions of muon-neutrinos detected by the IceCube observatory, given current evidence that the source of UHECRs and neutrinos may be correlated.
Our numerical simulations back-tracked the Earth arrival directions of UHECRs detected by PAO and TA, in several posited GMFs and for several compositions between hydrogen and iron. We used the deflections for hydrogen composition UHECRs to select UHECRs that are the least deflected (due to a combination of their energy and Earth arrival direction) in all GMF models used. While most of the GMF models considered give relatively consistent (in magnitude) deflections for hydrogen composition UHECRs, the JF12 model, with its X-shaped magnetic field, gives very different results. We compromised in this regard by using two least deflected samples: one selected to be least deflected in the JF12 GMF, and one selected to have small deflections in most of the other seven GMFs (the mix-GMF least deflected sample). For trajectories along certain Galactic longitudes, axisymmetric GMFs produce deflections on the near side of the Galaxy disc which cancel out – as vectors – with the deflections produced on the far side of the Galactic disk. Our selection of the least deflected sample therefore considers both the final deflection produced (the vector difference between Earth arrival and out-of-galaxy arrival directions) and the sum of the absolute deflections suffered by the UHECR during our simulated trajectory. Both are required to be small (≲7°) in order for the UHECR to be considered least deflected.
For the full sample of 303 UHECRs we have found the following:
-
When UHECR compositions are primarily hydrogen: from a revision of Fig. 6 and the equivalent for other GMFs, we conclude that nearby optically selected AGN (Zaw catalog) is most consistently seen as a favorite, closely followed by nearby RGs (VanVelzen catalog; which tends to be favoured at larger separations) and by nearby galaxies (which are favored in some of the Sun and JF12 models). Clearly the least favored for most GMFs are the IceCube neutrino and Galaxy clusters catalog. From the second panel of Fig. 6: if nearby RGs are the true (hydrogen) UHECR source population, the BS-S and BS-A models best represent the true GMF. In the specific case of only Cen A, a large fraction of MC points (which even appear to form a double structure) are concentrated within 10° of its extended radio lobes in most models (see left panel of Fig. 5 for the case of the BS-S GMF). Modifying the normalizing constants of the BS-S model (e.g., top panel of Fig. 13) can move this concentration even closer to the Cen A lobes. We note that this latter figure and analysis is shown only in an illustrative sense.
-
When UHECR compositions are a mix of hydrogen and heavier compositions: we find that for He, the results still show a consistently strong preference for the RG and optically selected AGN catalogs. however, when moving to increasingly heavier compositions (as discussed in Sect. 3.3 and Figs. 9 and 8), the greatest concentration of MC points moves around the sky: specifically, it falls relatively close to the Cen A region for the first four GMF models, towards mid to low anti-galactic latitudes in the Sun et al. models, and towards high Galactic latitude, anti-Galactic longitudes in the JF12 model, producing different correlations in each case. We note (e.g., Fig. 13 for the BS-S case) that in the case of the first four GMF model(s), changes in the normalizing magnitude of the dipole and disk components of the GMF would attribute an even larger number of the full UHECR sample to the nearby radiogalaxy Cen A.
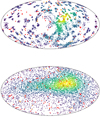 |
Fig. 13. Same as the top left and bottom right panel of Fig. 7, i.e. out of galaxy arrival directions of H and Fe composition UHECRs in the BS-S GMF, but here the strengths of the dipole field (μg) and disk field (B0) components have both been increased by 50%; see Eqs. (3) and (6) of Takami & Sato (2008). This change in GMF normalization is not physical, and is done only to illustrate a potential systematic uncertainty in our analysis. Here only 20 MC simulations were performed for each UHECR. In both panels galaxies in the VanVelzen RG catalog at distances D < 75 Mpc (75 < D < 150 Mpc) are shown in orange (red) dots; the overall extent of the radio lobes of Cen A are outlined in red. |
For the least-deflected samples we find the following:
-
When UHECR compositions are primarily hydrogen: for the mix-GMF least-deflected sample the catalogs that show the strongest correlation in most GMFs are the nearby galaxy catalog, the Swift catalog, and (in some cases) the IceCube neutrinos. These results are consistent among different GMF models with and without sky exposure weighting. In the case of the JF12 least-deflected sample we see the same three catalogs as favoured in most models but when using sky exposure weights, the results are a bit more inconsistent between different GMFs than they were for the mix-GMF.
-
When UHECR compositions are a mix of hydrogen and heavier compositions: we find that for deflections of intermediate masses (e.g., C, N, O), the out-of-galaxy arrival directions of our least-deflected subsamples align with the supergalactic plane remarkably well. This is particularly true for the AS-A GMF, which produces deflections towards the supergalactic plane in the northern and southern Galactic hemispheres, as seen in Fig. 12. This result is of interest since we know that these intermediate compositions are abundant in interstellar space and, thus, readily available for acceleration.
The methodology followed in this work can lead to even more promising results in the coming years. The UHECR samples are being rapidly expanded, the planned AugerPrime upgrade for PAO (Castellina & Pierre Auger Collaboration 2019) will allow for better constrains on the mass composition of each detected UHECR. In addition, the Square Kilometer Array (SKA) polarisation survey (Heald et al. 2020) is expected to improve the exploration of magnetic field observables on both large and small scales, thus enabling the development of improved and more accurate GMF models.
Acknowledgments
We acknowledge funding from ANID Nucleo Milenio TITANs (NCN19−058), Fondecyt 1221421 and BASAL FB210003 and AFB-170002. We thank Glennys Farrar for sharing the code of their GMF model with us.
References
- Aab, A., Abreu, P., Aglietta, M., et al. 2015, ApJ, 804, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Aab, A., Abreu, P., Aglietta, M., et al. 2016, Phys. Lett. B, 762, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Aab, A., Abreu, P., Aglietta, M., et al. 2018, ApJ, 853, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Aab, A., Abreu, P., Aglietta, M., et al. 2020, Phys. Rev. D, 102, 062005 [NASA ADS] [CrossRef] [Google Scholar]
- Abbasi, R. U., Abe, M., Abu-Zayyad, T., et al. 2014, ApJ, 790, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Abbasi, R. U., Abe, M., Abu-Zayyad, T., et al. 2018a, ApJ, 858, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Abbasi, R. U., Abe, M., Abu-Zayyad, T., et al. 2018b, ApJ, 865, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Aloisio, R. 2017, Progr. Theoret. Exp. Phys., 2017, 12A102 [Google Scholar]
- Aloisio, R., Berezinsky, V., & Gazizov, A. 2012, Astropart. Phys., 39–40, 129 [CrossRef] [Google Scholar]
- Alves Batista, R., & Saveliev, A. 2021, Universe, 7, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Anchordoqui, L. A. 2019, Phys. Rep., 801, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Barbano, A. 2020, ArXiv e-prints [arXiv:2001.09057] [Google Scholar]
- Beck, R. 2008, in American Institute of Physics Conf. Ser., 1085, 83 [NASA ADS] [Google Scholar]
- Beck, R., & Wielebinski, R. 2013, Magnetic Fields in Galaxies (Dordrecht: Springer Science+Business Media), 5, 641 [NASA ADS] [Google Scholar]
- Berlind, A. A., Farrar, G. R., & Zaw, I. 2010, ApJ, 716, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Bhattacharjee, P. 2000, Phys. Rep., 327, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C. 2010, ASP Conf. Ser., 438, 216 [NASA ADS] [Google Scholar]
- Brunetti, G., & Jones, T. W. 2014, Int. J. Mod. Phys. D, 23, 1430007 [Google Scholar]
- Caramete, L. I., & Biermann, P. L. 2014, VizieR Online Data Catalog: J/A+A/521/A55 [Google Scholar]
- Castellina, A., & Pierre Auger Collaboration 2019, Eur. Phys. J. Web Conf., 210, 06002 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Corwin, Harold G. J., & Buta, R. J., & de Vaucouleurs, G., 1994, AJ, 108, 2128 [NASA ADS] [CrossRef] [Google Scholar]
- Côté, S., Carignan, C., & Freeman, K. C. 2000, AJ, 120, 3027 [CrossRef] [Google Scholar]
- Cuesta, A. J., & Prada, F. 2009, MNRAS, submitted [arXiv:0910.2702] [Google Scholar]
- Farrar, G. R., & Piran, T. 2014, ArXiv e-prints [arXiv:1411.0704] [Google Scholar]
- Fraschetti, F., & Melia, F. 2008, MNRAS, 391, 1100 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Ghirlanda, G., Tavecchio, F., Fraternali, F., & Pareschi, G. 2008, MNRAS, 390, L88 [NASA ADS] [Google Scholar]
- Giaccari, G. U., & Pierre Auger Collaboration 2017, Int. Cosmic Ray Conf., 301, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Greisen, K. 1966, Phys. Rev. Lett., 16, 748 [Google Scholar]
- Grenier, I. A., Black, J. H., & Strong, A. W. 2015, ARA&A, 53, 199 [Google Scholar]
- Hardcastle, M. J. 2010, MNRAS, 405, 2810 [NASA ADS] [Google Scholar]
- Hardcastle, M. J., Worrall, D. M., Kraft, R. P., et al. 2003, ApJ, 593, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. J., Cheung, C. C., Feain, I. J., & Stawarz, Ł. 2009, MNRAS, 393, 1041 [NASA ADS] [CrossRef] [Google Scholar]
- Heald, G., Mao, S., Vacca, V., et al. 2020, Galaxies, 8, 53 [Google Scholar]
- Hess, V. 2018, ArXiv e-prints [arXiv:1808.02927] [Google Scholar]
- IceCube Collaboration (Aartsen, M. G., et al.) 2018, Science, 361, eaat1378 [NASA ADS] [Google Scholar]
- IceCube Collaboration (Achterberg, A., et al.) 2006, Astropart. Phys., 26, 155 [NASA ADS] [CrossRef] [Google Scholar]
- IceCube Collaboration, Pierre Auger Collaboration, & Telescope Array Collaboration 2016, J. Cosmology Astropart. Phys., 2016, 037 [Google Scholar]
- Isola, C., Lemoine, M., & Sigl, G. 2002, Phys. Rev. D, 65 [CrossRef] [Google Scholar]
- Ivanov, D., Pierre Auger Collaboration,& Telescope Array Collaboration 2017, International Cosmic Ray Conference, 301, 498 [NASA ADS] [Google Scholar]
- Jansson, R., & Farrar, G. R. 2012, ApJ, 757, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Jedamzik, K., & Saveliev, A. 2019, Phys. Rev. Lett., 123, 021301 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, Y.-Y., Hou, L. G., Han, J. L., Sun, X. H., & Wang, W. 2010, ApJ, 719, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Kachelriess, M. 2022, 37th International Cosmic Ray Conference, 12–23 July 2021, Berlin, 18 [Google Scholar]
- Kang, H., Rachen, J. P., & Biermann, P. L. 1997, MNRAS, 286, 257 [NASA ADS] [Google Scholar]
- Karachentsev, I. D., Makarov, D. I., & Kaisina, E. I. 2013, AJ, 145, 101 [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [Google Scholar]
- Kewley, L. J., Dopita, M. A., Sutherland, R. S., Heisler, C. A., & Trevena, J. 2001, ApJ, 556, 121 [Google Scholar]
- Lemoine, M. 2019, Phys. Rev. D, 99 [CrossRef] [Google Scholar]
- Linsley, J., Scarsi, L., & Rossi, B. 1961, Phys. Rev. Lett., 6, 485 [Google Scholar]
- Lyutikov, M., & Ouyed, R. 2007, Astropart. Phys., 27, 473 [NASA ADS] [CrossRef] [Google Scholar]
- Marcowith, A., Dwarkadas, V. V., Renaud, M., Tatischeff, V., & Giacinti, G. 2018, MNRAS, 479, 4470 [CrossRef] [Google Scholar]
- Martens, K., & Telescope Array Collaboration 2007, Nucl. Phys. B Proc. Suppl., 165, 33 [Google Scholar]
- Matthews, J. H., & Taylor, A. M. 2021, MNRAS, 503, 5948 [NASA ADS] [CrossRef] [Google Scholar]
- Miroshnichenko, L. I. 2001, Solar Cosmic Rays (Berlin: Springer), 260 [CrossRef] [Google Scholar]
- Murase, K. 2019, Int. Cosmic Ray Conf., 36, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Murase, K., Ioka, K., Nagataki, S., & Nakamura, T. 2006, ApJ, 651, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Murase, K., Mészáros, P., & Zhang, B. 2009, Phys. Rev. D, 79, 103001 [Google Scholar]
- Murase, K., Dermer, C. D., Takami, H., & Migliori, G. 2012, ApJ, 749, 63 [Google Scholar]
- Nagar, N. M., & Matulich, J. 2008, A&A, 488, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nagar, N. M., & Matulich, J. 2010, A&A, 523, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Norman, C. A., Melrose, D. B., & Achterberg, A. 1995, ApJ, 454, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Oh, K., Koss, M., Markwardt, C. B., et al. 2018, ApJS, 235, 4 [Google Scholar]
- Pierre Auger Collaboration 2015, Nucl. Instrum. Methods Phys. Res. A, 798, 172 [Google Scholar]
- Pierre Auger Collaboration (Aab, A., et al.) 2017, Science, 357, 1266 [NASA ADS] [CrossRef] [Google Scholar]
- Pierre Auger Collaboration (Abraham, J., et al.) 2007, Science, 318, 938 [NASA ADS] [CrossRef] [Google Scholar]
- Plavin, A., Kovalev, Y. Y., Kovalev, Y. A., & Troitsky, S. 2020, ApJ, 894, 101 [Google Scholar]
- Rachen, J. P., & Biermann, P. L. 1993, A&A, 272, 161 [NASA ADS] [Google Scholar]
- Razzaque, S. 2020, Phys. Online J., 13, 145 [NASA ADS] [Google Scholar]
- Rordorf, C., Grasso, D., & Dolag, K. 2004, Astropart. Phys., 22, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Sigl, G., Miniati, F., & Ensslin, T. A. 2003, Phys. Rev. D, 68, 043002 [NASA ADS] [CrossRef] [Google Scholar]
- Stanev, T. 2008, ArXiv e-prints [arXiv:0805.1746] [Google Scholar]
- Sun, X.-H., & Reich, W. 2010, RAA, 10, 1287 [NASA ADS] [Google Scholar]
- Sun, X. H., Reich, W., Waelkens, A., & Enßlin, T. A. 2008, A&A, 477, 573 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Supanitsky, A. D., & Medina-Tanco, G. 2019, J. Cosmol. Astropart. Phys., 2019, 036 [CrossRef] [Google Scholar]
- Shibata, T. 2008, Nucl. Instrum. Methods Phys. Res. A, 597, 61 [CrossRef] [Google Scholar]
- Takami, H., & Sato, K. 2008, ApJ, 681, 1279 [NASA ADS] [CrossRef] [Google Scholar]
- Thoudam, S., Rachen, J. P., van Vliet, A., et al. 2016, A&A, 595, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tursunov, A., Stuchlík, Z., Kološ, M., Dadhich, N., & Ahmedov, B. 2020, ApJ, 895, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Uryson, A. V. 2019, J. Phys. Conf. Ser., 1390, 012065 [CrossRef] [Google Scholar]
- van Velzen, S., Falcke, H., Schellart, P., Nierstenhöfer, N., & Kampert, K.-H. 2012, A&A, 544, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Vliet, A., Palladino, A., Taylor, A., & Winter, W. 2021, MNRAS, 510, 1289 [CrossRef] [Google Scholar]
- Zatsepin, G. T., & Kuz’min, V. A. 1966, Sov. J. Exp. Theoret. Phys. Lett., 4, 78 [NASA ADS] [Google Scholar]
- Zaw, I., Chen, Y.-P., & Farrar, G. R. 2019, ApJ, 872, 134 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Pierre Auger Observatory (PAO) and Telescope Array (TA) UHECR samples in an Aitoff projection of Galactic coordinates. Light green (dark green) dots and corresponding circles represent UHECRs, which we consider as least-deflected according to the JF12 model (mix of other GMF models; see text). Only four UHECRs are present in both least-deflected subsamples. Red symbols represent the remaining UHECR sample. As expected, the mix-GMF least-deflected sample are primarily at high Galactic latitudes, while the JF12 least-deflected sample are at longitudes that are opposite to the Galactic center. |
| In the text | |
 |
Fig. 2. Astronomical samples used in this work. As in Fig. 1, these are plotted in an Aitoff projection of Galactic coordinates. Light (dark) green circles are used for sources at small (large) distances following the legend. The panels show the following samples: nearby AGN from the Swift-BAT 105 month X-ray catalog (Swift; Oh et al. 2018), Van Velzen radiogalaxy sample (VanVelzen; van Velzen et al. 2012), sample of nearby galaxies (nearby gals; Karachentsev et al. 2013), sample of spectroscopically identified nearby AGN (Zaw AGN; Zaw et al. 2019), sample of high energy muon neutrinos detected by IceCube (IceCube; Plavin et al. 2020), sample of nearby supermassive black holes (SMBH; Caramete & Biermann 2014), galaxy clusters from the Swift-BAT 105 month X-ray catalog (GalCluster; Oh et al. 2018) at D < 75 Mpc, and nearby dwarf galaxies (nearby dwarfs; Karachentsev et al. 2013). |
| In the text | |
 |
Fig. 3. Histograms for the UHECR samples used in this work. Top: energy distribution of the full (PAO and TA) UHECR sample (after re-scaling), together with those of the two least-deflected samples. Energies range between 57 and 160 EeV. Bottom: histogram of the exposure weight (the inverse of the combined sky-exposures of the PAO and TA) for the arrival directions of the UHECRs used in this work. Since exposure weights vary by factor 6–10 over the different sub-samples we preferentially use the statistical results without weighting for the sky exposure time of the observatories. |
| In the text | |
 |
Fig. 4. Density plots of the Monte Carlo points for hydrogen UHECR composition and for different GMF models (as marked), following the color bar on the right. The black outline represents Centaurus A. The red (orange) dots in each panel show the distribution of our nearby galaxy sample at D < 11 Mpc (11 Mpc < D < 25 Mpc). |
| In the text | |
 |
Fig. 5. Figure for the special case of Cen A, considering a mixed composition scenario. Left: density plot of hydrogen UHECR MC points closer than 30° from the Cen A nucleus for the BS-S model. Right: aitoff projected density plot of iron UHECR MC points, but UHECRs for which ≥50% of hydrogen MC points are already matched to Cen A (left panel) are not considered. In both panels galaxies in the VanVelzen RG catalog at distances D < 75 Mpc (75 < D < 150 Mpc) are shown in orange (red) dots; the overall extent of the radio lobes of Cen A are outlined in red. |
| In the text | |
 |
Fig. 6. Results for our statistical correlations at different radii. Left: normalized counts of MC points which fall within circles around source in a given catalog, for the BS-S GMF, hydrogen composition, and all astronomical catalogs used in this work. A normalized count of > 1 implies that MC points prefer to fall inside, rather than outside, the circles around a given catalog’s sources (see Sect. 2.4). Error bars are from Poisson errors (Sect. 2.4). Middle: as in the left panel but for all radiogalaxies in the Van Velzen catalog within 75 Mpc, and for different GMF models. Right: same as in the middle panel but for the Zaw AGN catalog. |
| In the text | |
 |
Fig. 7. Density plots of our MC simulations for the BS-S GMF model, and different UHECR compositions, and here the orange (red) points show galaxies from the Van Velzen RG catalog at D < 75 Mpc (75 Mpc < D < 150 Mpc). The black outline represents Centaurus A. |
| In the text | |
 |
Fig. 8. Correlation results for different scenarios considered. Left: same as the left panel of Fig. 6, i.e., correlations for all astronomical catalogs considering deflections in the BS-S GMF, but for an Fe UHECR composition. Middle: correlations between Fe composition UHECRs and the nearby galaxy catalog for different GMF models. Right: correlations between the nearby galaxy catalog and different UHECR compositions for the BS-S GMF. |
| In the text | |
 |
Fig. 9. Density plot of our MC simulations for Fe composition and different GMF models. Red points show neutrino arrival directions from IceCube. Centaurus A is represented by the black outline. |
| In the text | |
 |
Fig. 10. Normalized number (left two panels) or ratio (right panel) of MC points, for a hydrogen composition and BS-A GMF model, which fall within a certain radius of any source in a given astronomical sample, for several samples as noted in the legend. Left (middle) panel shows the statistics for the mix-GMF least-deflected sample (all other UHECRs). The normalization in the left two panels is done based on the ratio of sky area within and outside the circles around all sources in a given astronomical catalog. Right panel shows the ratio of the numbers in the left and middle panels. |
| In the text | |
 |
Fig. 11. Correlation results As in Fig. 10, but for the JF12 least-deflected sample, and the BS-S Sun model. |
| In the text | |
 |
Fig. 12. Out-of-galaxy arrival directions of least-deflected UHECRs for compositions of hydrogen, helium, and oxygen, in all GMFs considered. Earth arrival directions of the mix-GMF (JF12) least-deflected sample are shown as dark green (light green) filled circles following the legend. Out of galaxy arrival directions for compositions of hydrogen (yellow), helium (orange), and oxygen (red) are shown as filled circles. For visualization ease, lines in the same color as the Earth arrival direction of the respective least-deflected sample (light and dark green) join the Earth arrival direction and out of galaxy arrival directions of a given UHECR. |
| In the text | |
 |
Fig. 13. Same as the top left and bottom right panel of Fig. 7, i.e. out of galaxy arrival directions of H and Fe composition UHECRs in the BS-S GMF, but here the strengths of the dipole field (μg) and disk field (B0) components have both been increased by 50%; see Eqs. (3) and (6) of Takami & Sato (2008). This change in GMF normalization is not physical, and is done only to illustrate a potential systematic uncertainty in our analysis. Here only 20 MC simulations were performed for each UHECR. In both panels galaxies in the VanVelzen RG catalog at distances D < 75 Mpc (75 < D < 150 Mpc) are shown in orange (red) dots; the overall extent of the radio lobes of Cen A are outlined in red. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


