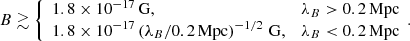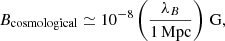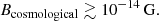| Issue |
A&A
Volume 670, February 2023
|
|
|---|---|---|
| Article Number | A145 | |
| Number of page(s) | 8 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202244126 | |
| Published online | 17 February 2023 | |
A lower bound on intergalactic magnetic fields from time variability of 1ES 0229+200 from MAGIC and Fermi/LAT observations
1
Instituto de Astrofísica de Canarias and Dpto. de Astrofísica, Universidad de La Laguna, 38200 La Laguna, Tenerife, Spain
2
National Institute for Astrophysics (INAF), 00136 Rome, Italy
3
Università di Udine and INFN Trieste, 33100 Udine, Italy
4
Max-Planck-Institut für Physik, 80805 München, Germany
5
Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology (BIST), 08193 Bellaterra, Barcelona, Spain
6
Japanese MAGIC Group: Institute for Cosmic Ray Research (ICRR), The University of Tokyo, Kashiwa, 277-8582 Chiba, Japan
7
Technische Universität Dortmund, 44221 Dortmund, Germany
8
Croatian MAGIC Group: University of Zagreb, Faculty of Electrical Engineering and Computing (FER), 10000 Zagreb, Croatia
9
IPARCOS Institute and EMFTEL Department, Universidad Complutense de Madrid, 28040 Madrid, Spain
10
Centro Brasileiro de Pesquisas Físicas (CBPF), 22290-180 URCA, Rio de Janeiro, RJ, Brazil
11
Università di Padova and INFN, 35131 Padova, Italy
12
University of Lodz, Faculty of Physics and Applied Informatics, Department of Astrophysics, 90-236 Lodz, Poland
13
Deutsches Elektronen-Synchrotron (DESY), 15738 Zeuthen, Germany
14
ETH Zürich, 8093 Zürich, Switzerland
15
Instituto de Astrofísica de Andalucía-CSIC, Glorieta de la Astronomía s/n, 18008 Granada, Spain
16
Università di Pisa and INFN Pisa, 56126 Pisa, Italy
17
Universitat de Barcelona, ICCUB, IEEC-UB, 08028 Barcelona, Spain
18
Armenian MAGIC Group: A. Alikhanyan National Science Laboratory, 0036 Yerevan, Armenia
19
Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas, 28040 Madrid, Spain
20
Department for Physics and Technology, University of Bergen, Bergen, Norway
21
INFN MAGIC Group: INFN Sezione di Catania and Dipartimento di Fisica e Astronomia, University of Catania, 95123 Catania, Italy
22
INFN MAGIC Group: INFN Sezione di Torino and Università degli Studi di Torino, 10125 Torino, Italy
23
INFN MAGIC Group: INFN Sezione di Bari and Dipartimento Interateneo di Fisica dell’Università e del Politecnico di Bari, 70125 Bari, Italy
24
Croatian MAGIC Group: University of Rijeka, Department of Physics, 51000 Rijeka, Croatia
25
Universität Würzburg, 97074 Würzburg, Germany
26
Finnish MAGIC Group: Finnish Centre for Astronomy with ESO, University of Turku, 20014 Turku, Finland
27
Departament de Física, and CERES-IEEC, Universitat Autònoma de Barcelona, 08193 Bellaterra, Spain
28
Japanese MAGIC Group: Physics Program, Graduate School of Advanced Science and Engineering, Hiroshima University, 739-8526 Hiroshima, Japan
29
Armenian MAGIC Group: ICRANet-Armenia at NAS RA, 0019 Yerevan, Armenia
30
Croatian MAGIC Group: University of Split, Faculty of Electrical Engineering, Mechanical Engineering and Naval Architecture (FESB), 21000 Split, Croatia
31
Croatian MAGIC Group: Josip Juraj Strossmayer University of Osijek, Department of Physics, 31000 Osijek, Croatia
32
Japanese MAGIC Group: Department of Physics, Kyoto University, 606-8502 Kyoto, Japan
33
Japanese MAGIC Group: Department of Physics, Tokai University, Hiratsuka, 259-1292 Kanagawa, Japan
34
Università di Siena and INFN Pisa, 53100 Siena, Italy
35
Saha Institute of Nuclear Physics, HBNI, 1/AF Bidhannagar, Salt Lake, Sector-1, Kolkata 700064, India
36
Inst. for Nucl. Research and Nucl. Energy, Bulgarian Academy of Sciences, 1784 Sofia, Bulgaria
37
Japanese MAGIC Group: Department of Physics, Yamagata University, Yamagata 990-8560, Japan
38
Finnish MAGIC Group: Astronomy Research Unit, University of Oulu, 90014 Oulu, Finland
39
Croatian MAGIC Group: Ruđer Bošković Institute, 10000 Zagreb, Croatia
40
INFN MAGIC Group: INFN Sezione di Perugia, 06123 Perugia, Italy
41
INFN MAGIC Group: INFN Roma Tor Vergata, 00133 Roma, Italy
42
Japanese MAGIC Group: Department of Physics, Konan University, Kobe, Hyogo 658-8501, Japan
43
International Center for Relativistic Astrophysics (ICRA), Rome, Italy
44
University of Innsbruck, 6020 Innsbruck, Austria
45
Port d’Informació Científica (PIC), 08193 Bellaterra, Barcelona, Spain
46
Ruhr-Universität Bochum, Fakultät für Physik und Astronomie, Astronomisches Institut (AIRUB), 44801 Bochum, Germany
47
Dipartimento di Fisica, Università di Trieste, 34127 Trieste, Italy
48
Max-Planck-Institut für Physik, 80805 München, Germany
49
INAF Trieste and Dept. of Physics and Astronomy, University of Bologna, Bologna, Italy
50
Université de Paris, CNRS, Astroparticule et Cosmologie, 75006 Paris, France
51
Institute for Nuclear Research of the Russian Academy of Sciences, 60th October Anniversary Prospect 7a, Moscow 117312, Russia
52
Novosibirsk State University, Pirogova 2, Novosibirsk 630090, Russia
53
Laboratory of Astrophysics, Ecole Polytechnique Federale de Lausanne, 1015 Lausanne, Switzerland
54
National Research Nuclear University MEPHI (Moscow Engineering Physics Institute), Kashirskoe Highway 31, 115409 Moscow, Russia
Received:
27
May
2022
Accepted:
29
September
2022
Context. Extended and delayed emission around distant TeV sources induced by the effects of propagation of γ ray s through the intergalactic medium can be used for the measurement of the intergalactic magnetic field (IGMF).
Aims. We search for delayed GeV emission from the hard-spectrum TeV γ-ray emitting blazar 1ES 0229+200, with the goal of detecting or constraining the IGMF-dependent secondary flux generated during the propagation of TeV γ rays through the intergalactic medium.
Methods. We analysed the most recent MAGIC observations over a 5 year time span, and complemented them with historic data of the H.E.S.S. and VERITAS telescopes, along with a 12-year-long exposure of the Fermi/LAT telescope. We used them to trace source evolution in the GeV–TeV band over a decade and a half. We used Monte Carlo simulations to predict the delayed secondary γ-ray flux, modulated by the source variability, as revealed by TeV-band observations. We then compared these predictions for various assumed IGMF strengths to all available measurements of the γ-ray flux evolution.
Results. We find that the source flux in the energy range above 200 GeV experiences variations around its average on the 14-year time span of observations. No evidence for the flux variability is found in the 1 − 100 GeV energy range accessible to Fermi/LAT. The non-detection of variability due to delayed emission from electromagnetic cascade developing in the intergalactic medium imposes a lower bound of B > 1.8 × 10−17 G for the long-correlation-length IGMF and B > 10−14 G for an IGMF of cosmological origin. Though weaker than the one previously derived from the analysis of Fermi/LAT data, this bound is more robust, being based on a conservative intrinsic source spectrum estimate and accounting for the details of source variability in the TeV energy band. We discuss implications of this bound for cosmological magnetic fields that might explain the baryon asymmetry of the Universe.
Key words: intergalactic medium / galaxies: active / gamma rays: galaxies / early Universe
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
Teraelectronvolt γ rays propagating from distant extragalactic sources suffer from attenuation due to pair production in interactions with the extragalactic background light (EBL). The pair production effect leads to the deposition of electron-positron pairs in the intergalactic medium. These pairs lose their energy via inverse Compton scattering of cosmic microwave background (CMB) photons and in this way produce a secondary γ-ray flux that could be detected as extended and time-delayed γ-ray ‘glow’ around extragalactic TeV γ-ray sources (Aharonian et al. 1994). Properties of this secondary γ-ray flux are sensitive to weak magnetic fields present in the intergalactic medium (Plaga 1995; Neronov & Semikoz 2007, 2009; Neronov et al. 2010). This provides us an opportunity to measure such weak magnetic fields using γ-ray observation techniques.
The non-detection of extended or delayed GeV band emission from several extragalactic TeV sources has been previously used to derive a lower bound on the intergalactic magnetic field (IGMF) strength. Indeed, the lower bound on the IGMF represents the minimum magnetic field strength needed to suppress the cascade emission in the GeV domain, which makes it negligible with respect to the source emission. The bound on the long-correlation-length magnetic field, B > 10−16 G (Neronov & Vovk 2010; Tavecchio et al. 2011), has been derived under the assumption that the present day measurements of the TeV γ-ray flux from selected blazars (a class of active galactic nuclei – AGNs – with the jet pointing towards the observer) are representative for the entire AGN duty cycle period of the order of 10 Myr. A weaker bound of B > 10−17 G was derived after relaxing this assumption and assuming instead that the selected TeV sources were active only during the historical TeV γ-ray observation time span (Dermer et al. 2011; Taylor et al. 2011; Vovk et al. 2012). An update of this approach yielding a lower bound B > 3 × 10−16 G on long-correlation-length magnetic fields was reported by Ackermann et al. (2018), based on 7.5 years of the Fermi/LAT telescope data (Atwood et al. 2009). This updated analysis was also based on the unverified assumption of stability of the TeV band flux on a decade-long time span. Limits on extended emission around bright blazars Mrk 421 and Mrk 501 were also derived from the MAGIC telescope data (Aleksić et al. 2010) at energies above 300 GeV, excluding IGMF strengths in the range 4 × 10−15 G − 1.3 × 10−14 G, under a strong assumption of the existence of persistent intrinsic source flux above 20 TeV. Several other blazars were observed by the H.E.S.S. telescopes (H.E.S.S. Collaboration 2014), yielding similar results – IGMF strengths in the range (0.3 − 3)×10−15 G were excluded, under similar assumptions regarding (unmeasured) intrinsic source fluxes above 20 TeV.
In this paper, we report a significant improvement upon these previous results. We used the data of systematic long-term GeV–TeV band monitoring data on a specific source providing the most stringent IGMF lower limits to date, 1ES 0229+200, owing to its distance (redshift of z ≈ 0.14, Woo et al. 2005), hard GeV–TeV spectrum, and apparent absence of high-energy cut-off (Aharonian et al. 2007). The data collected over more than a decade allowed us to substantially relax assumptions about the intrinsic source flux properties over that period. The TeV band monitoring data allowed us to make precise predictions of the cascade flux timing properties at lower energies, that is, those accessible to the Fermi/LAT telescope. The combination of the imaging atmospheric telescope and Fermi/LAT measurements allowed us to test the model prediction against the data. We show that the non-detection of delayed cascade emission in Fermi/LAT data yields a robust lower bound on the IGMF strength and correlation length, free of the assumptions above.
This paper is organised as follows. In Sect. 2 we describe the reduction of the MAGIC and Fermi/LAT data, followed by the numerical modelling of the time-delayed cascade emission. In Sect. 3 we assess the 1ES 0229+200 variability and apply the developed model to evaluate the corresponding bounds on IGMF strength. Finally, in Sect. 4 we discuss the implications of this measurement for the IGMF origin and outline prospects for its further improvements with future observations.
2. Data analysis
2.1. MAGIC data analysis
The MAGIC telescope is a stereoscopic system of two 17-m diameter Imaging Atmospheric Cherenkov Telescopes (IACTs). It is located at 2200 m above sea level in the observatory of the Roque de los Muchachos, on the Canary island of La Palma, Spain. It can register γ ray s from about 50 GeV to more than 50 TeV. For low-zenith angle observations, the sensitivity of MAGIC for point sources reaches 0.7% of the Crab Nebula flux above 220 GeV in 50 h of exposure (Aleksić et al. 2016).
The MAGIC observations of the 1ES 0229+200 were conducted during the period September 2013–December 20171. The dataset used in our analysis has 145.5 hr of accumulated exposure with the zenith angle below 50 degrees, where the MAGIC energy threshold is lower.
The data were analysed using the standard MAGIC software MARS (Zanin et al. 2013). Standard event cuts were used to improve the signal-to-background ratio, as described in Aleksić et al. (2016). We used standard MAGIC angular cuts to select the source events in the field of view as for time delays shorter than ∼10 years, which we discuss below, no significant cascade emission is expected to extend beyond the MAGIC point spread function (PSF).
2.2. Fermi/LAT data analysis
Our analysis of Fermi/LAT data is based on the P8R3 SOURCE type γ-ray event selection in the energy range 100 MeV to 200 GeV, collected between August 2008 and September 2020. We processed the data using the Fermitools package and FermiPy framework2 v0.17.3 (Wood et al. 2017), as described in the FermiPy documentation3.
To extract the source spectrum we considered the events in the 25°-wide region-of-interest around the source position, collected under the zenith angles below 90°. We accounted for the galactic (gll_iem_v07.fits) and extragalactic (iso_P8R3_SOURCE_V2_v1.txt) diffuse backgrounds and included other sources from the Fermi/LAT fourth source catalogue (4FGL, Abdollahi et al. 2020). The shapes of the sources’ spectra were taken from the 4FGL catalogue with their normalisation left free. We constructed likelihood components separately for each of the four Fermi/LAT PSF classes (event types 4, 8, 16, and 32) and used them jointly in the fit, accounting for the instrument’s energy dispersion. The spectra and light curves were extracted using two complementary techniques: the binned likelihood analysis and the aperture photometry (for the latter a smaller 5° region and ‘source’ event type 3 selection was used). The consistency of the results was verified via the crosscheck of the spectra and light curves obtained with these two techniques.
We restricted the aperture photometry analysis to the energy range 1–200 GeV (the highest-energy photon from the source direction had the energy E ≃ 180 GeV). All over this energy range, the diffuse background event count becomes comparable to or lower than that of the source only in the narrow angular bin range 0 < θ < 0.25°. Taking this into account, we chose the region of extraction of the source signal θ < 0.25° in the aperture photometry method of spectral extraction. Given that the 95% containment radius of the Fermi/LAT PSF4 above 2 GeV is ≈1.5°, we used the gtexposure tool with parameter apcorr=y, which assured that the source flux estimate from small region of θ < 0.25° was properly corrected for the source flux fraction contained in this circle.
2.3. Numerical modelling
Propagation of γ ray s through the intergalactic medium leads to the development of electromagnetic cascades initiated by pair production of the highest-energy γ rays on the far-infrared photons of the extragalactic background light. The cascade emission appears as a delayed γ-ray emission following an intrinsic flare of a γ-ray source. To model the delayed emission signal, we used two fully 3D Monte Carlo codes that trace the development of the cascade in the intergalactic medium: the CRPropa v3.1.7 code (Alves Batista et al. 2016) and the CRbeam code developed in Berezinsky & Kalashev (2016), also tested via comparison with the alternative cascade simulations (Taylor et al. 2011; Kalashev & Kido 2015; Kachelriess et al. 2012). Detailed comparison of these codes was performed by Kalashev et al. (2022), who showed that simulations with CRPropa and CRbeam agree with each other with an accuracy of the order of 10% for relatively nearby sources with z < 0.3; for the modelling below, we fixed the issue with the inverse Compton interaction rate in CRPropa, identified there. We used these codes to calculate the cascade signal G(Eγ, 0, Eγ, t, τ, B, λB) at the energy Eγ produced by propagation of primary γ rays of energy Eγ, 0, injected instantaneously by the source and arriving at the time t. The codes give the estimate of the cascade signal as a function of the time delay τ. The cascade ‘Green’s function’ G depends on the strength B and correlation length λB of the IGMF and, in principle, also on the spatial-domain power spectrum of the Fourier expansion of B. Throughout the paper we assume all of the IGMF power is concentrated in a single mode at k = 1/λB scale.
The cascade flux at an energy Eγ in the observer’s frame, based on the known flux variability pattern Fs(Eγ, 0, t) can be then expressed as follows:
In our calculations we parametrised the intrinsic source light curve (namely the variability pattern) Fs as 14 steps (bins) in the time interval MJD 53000 – MJD 59000, covering all of the IACT and Fermi/LAT observations. The step size was chosen so as to suppress the appearance of the bins with no observation counterparts while still matching the observed source variability (see Sect. 3.1 below). The combined contribution of these time bins (as described by the Green’s function above) was used to estimate both the primary and delayed fluxes in each time and energy bin.
As available data do not reveal any variability in the 1ES 0229+200 spectral shape in the ≳100 GeV energy range, when converting Fs to primary and secondary flux estimates, we made a simplifying assumption that the intrinsic source spectrum follows the power law shape with an exponential cut-off:
and varies only in normalisation (see Sect. 3.2 for the details on the chosen spectral shape parameters.
To simulate the secondary emission for 1ES 0229+200 with CRPropa, we assumed the source distance of Ds = 580 Mpc (corresponding to the sources’ redshift of z ≈ 0.14) and recorded all photons injected within a 10° cone, arriving to the sphere of the same radius r = Ds and centred on the source. The CMB and the far-infrared backgrounds (model from Franceschini et al. 2008) served as the target fields for both γ-ray photon absorption and inverse Compton scattering of the created secondary e+/e− pairs. All particles were traced with the required relative integration step accuracy of ϵ = 10−12 and a minimal step size of Δd = 1014 cm, which were sufficient to reproduce time delays with an accuracy better than 1 day.
3. Analysis results
3.1. Spectrum and light curve
Spectral energy distribution and light curves of 1ES 0229+200 in the GeV–TeV energy range, obtained here, are shown in Figs. 1 and 2 (see Sect. 3.3 for full description), respectively, along with the archival measurements from H.E.S.S. (Aharonian et al. 2007) and VERITAS (Aliu et al. 2014).
 |
Fig. 1. Spectral energy distribution of 1ES 0229+200 in the 100 MeV–100 TeV energy range. The Fermi/LAT and MAGIC data were obtained here; H.E.S.S and VERITAS measurements were taken from Aharonian et al. (2007) and Aliu et al. (2014) correspondingly. |
 |
Fig. 2. Light curve of 1ES 0229+200 in several energy bands along with an exemplary fit with an IGMF with strength B = 10−16 G and a coherence scale of λB = 1 Mpc. The top panel represents the best-fit model light curve (along with its uncertainties) used to make the predictions in the energy bands where the measurements were taken (the panels below). The Fermi/LAT and MAGIC data are reported in the text; H.E.S.S. and VERITAS measurements were taken from Cologna et al. (2015) and Aliu et al. (2014) correspondingly. The primary, cascade, and total source fluxes are denoted with green triangles, orange squares, and red circles, correspondingly. Solid and dashed lines represent calculations with CRPropa (Alves Batista et al. 2016) and CRbeam (Berezinsky & Kalashev 2016) Monte Carlo codes respectively; the latter use the small point-like markers to distiguish themselves. |
The joint Fermi/LAT and MAGIC spectrum is well described by a simple EBL-absorbed power law with a cut-off model (χ2 = 2.5/8 degrees of freedom) with best-fit intrinsic values of Γ = 1.72 ± 0.05 and Ecut > 2.6 TeV at a 95% confidence level. In general, MAGIC, H.E.S.S., and VERITAS spectra in the 0.1 − 10 TeV energy range agree well with each other in shape, though differ in normalisation. The joint spectrum (including Fermi/LAT measurements) is still described well with the same simple spectral model (χ2 = 14.2/22 degrees of freedom) with a compatible spectral index Γ = 1.74 ± 0.07 and a larger cut-off energy (Ecut > 10 TeV at a 95% confidence level).
The source’s light curve below ∼100 GeV from Fermi/LAT data does not indicate any significant time variability of the flux. On the contrary, the TeV band measurements from H.E.S.S., VERITAS, and MAGIC suggest notable variations with respect to the mean flux by a factor of approximately two. The flux is variable on timescales of ∼500 days, with several brightening and dimming episodes identifiable. The significance of this variability was assessed from a joint χ2 fit of H.E.S.S., VERITAS, and MAGIC light curves, using an EBL-absorbed power law with cut-off spectral model to compute the fluxes in the respective energy bins. The parameters of the model were left free in the fit. In addition, an 11% point-to-point systematical uncertainly, characteristic for MAGIC (Aleksić et al. 2016), and a 25% inter-instrument calibration uncertainty (corresponding to a typical ∼15% uncertainty on the IACT energy scale and a power law source spectrum with the measured index Γ = 2.6 – similar to that of 1ES 0229+200 after absorption on EBL) were also accounted for. This joint fit results in χ2 = 47/11 degrees of freedom, which rejects the constant flux assumption at the 4.8σ level. The MAGIC data alone, with monthly binning, hint at the variability at a marginal 2.7σ level (χ2 = 14.2/4 degrees of freedom) when the measurement systematical uncertainty is taken into account. Estimated fractional variability and corresponding χ2 contributions to the joint fit are given in Table 1.
Summary of the variability study with IACT data, estimated from their joint fit with the exponentially cut-off power law model.
3.2. Minimal expected cascade estimate
Following the arguments of Neronov & Vovk (2010), a conservative lower bound on the IGMF strength should be based on the minimal possible cascade contribution allowed by the data, for example the softest intrinsic spectrum with the lowest cut-off:
In order to estimate the values of Γlow and 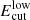 , we fitted the GeV–TeV spectrum of the source, scanning the Γ − Ecut space by means of χ2. In the scan we combined the GeV data from Fermi/LAT and TeV measurements of MAGIC, H.E.S.S., and VERITAS. Each spectrum was allowed to have a different normalisation during the fit, accounting for the variability of the source. For each combination of Γ − Ecut, we also computed the expected cascade power in terms of the total absorbed flux. This allowed us to select the intrinsic spectrum parameters that lead to the minimal possible cascade contribution in the ≲100 GeV energy band.
, we fitted the GeV–TeV spectrum of the source, scanning the Γ − Ecut space by means of χ2. In the scan we combined the GeV data from Fermi/LAT and TeV measurements of MAGIC, H.E.S.S., and VERITAS. Each spectrum was allowed to have a different normalisation during the fit, accounting for the variability of the source. For each combination of Γ − Ecut, we also computed the expected cascade power in terms of the total absorbed flux. This allowed us to select the intrinsic spectrum parameters that lead to the minimal possible cascade contribution in the ≲100 GeV energy band.
The outcome of this scan is shown in Fig. 3. The best χ2 values correspond to Ecut ≫ 10 TeV and a hard spectrum with Γ ≈ −1.70. Still, at a 90% confidence level, the lowest cascade flux is provided by the intrinsic source spectrum with Γlow ≈ −1.72 and 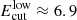 TeV (in the observer reference frame, otherwise it should be corrected for the source redshift by a factor of [1 + z]).
TeV (in the observer reference frame, otherwise it should be corrected for the source redshift by a factor of [1 + z]).
 |
Fig. 3. Scan of the cascade power in the Γ − Ecut parameter space along with the 68% and 90% confidence contours from the χ2 fit. At a 90% confidence level, the minimal cascade, marked with the yellow dashed lines, corresponds to Γ ≈ 1.72 and Ecut ≈ 6.9 TeV. |
3.3. Light curve modelling and accounting for the IGMF
To model the GeV–TeV light curves, we used the model introduced in Sect. 2.3. For each IGMF configuration (i.e., strength and coherence length), we performed a fit of all H.E.S.S., VERITAS, MAGIC, and Fermi/LAT light curves together. This combination of TeV and GeV data allowed us to self-consistently estimate the ‘primary’ and ‘delayed’ flux contribution in each time and energy bin.
In our ‘minimal cascade’ modelling, we assumed zero intrinsic source flux before MJD = 53000 (just before the first H.E.S.S. flux data point in Fig. 2). The non-zero flux at MJD < 53000 would produce extra cascade flux during the observation time span MJD > 53000. In addition, we used the Γ and Ecut values that minimise the expected delayed contribution, estimated in Sect. 3.2. The constructed model is the most conservative with respect to the IGMF constraints.
The minimal cascade model is not free from uncertainties (e.g., on the source jet orientation and opening angle). The characteristic delay of the off-centre emission of 1ES 0229+200 is Td ≃ 1(θ/10−3 deg)2 yr (with θ being the offset angle); this value is set by the geometry of the e+/e− pairs deflection and is independent of the IGMF configuration. For the time delays allowed to be probed by the data at hand (below ≈16 years), the characteristic off-centre angle of the delayed secondary emission would be ≲4 × 10−3 deg – much less than PSF of the considered instruments or a typical opening angle of AGN jets.
The result of the IGMF strength scan, assuming a randomly orientated IGMF with a coherence scale in the range λB = 10−3 − 1 Mpc, is shown in Fig. 4. For IGMF strengths below ∼10−18 G, the secondary emission suffers minimal lag (below ∼1 yr), so that there is almost no suppression due to the time delay. For IGMF stronger than ∼10−16 G, the time delay is large enough to suppress the secondary emission well below the expected primary one, so that the model light curves at GeV energies start to simply mirror the variability at the higher-energy, TeV spectrum end. The minimal χ2 value here represents the ability of the constructed model to reproduce the short timescale (< 400 days) variability of 1ES 0229+200, suggested by the data points in Fig. 2.
 |
Fig. 4. Intergalactic magnetic field strength scan for several different assumed coherence lengths λB. The scan is performed via a simultaneous fit of GeV–TeV observations at hand. Calculations with both CRPropa (Alves Batista et al. 2016) and CRbeam (Berezinsky & Kalashev 2016) Monte Carlo codes are presented. Lines of different colours depict the χ2 values estimated for different non-zero IGMF strengths. The solid black line represents the case of zero IGMF, in which case the secondary emission dominates in the Fermi/LAT energy range; the dashed black line represents the reference fit with the cascade contribution disabled. |
This scan in Fig. 4 indicates that with very few assumptions made here, the IGMF is constrained to have strength B ≳ 1.8 × 10−17 G at a 95% confidence level (corresponding to Δχ2 ≈ 2.71 from the the minimal χ2 value).
The scaling of the above constraint with the IGMF correlation length is set by the cooling distance of the injected electrons and positrons, and for randomly orientated IGMF cells it can be derived analytically (Neronov & Semikoz 2009). The cooling distance of e+/e− pairs (due to radiative loss through inverse Compton scattering) is
for electrons and positrons up-scattering CMB photons to the energy EIC. The scan performed above is most sensitive to the delayed emission contribution in the lowest-energy 1–10 GeV light curve. This suggests that the derived lower limit holds for IGMF coherence lengths λB > 0.2 Mpc and scales for shorter correlation lengths inversely proportionally to 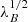 , so that it can be summarised as:
, so that it can be summarised as:
This conclusion is supported by the scan of the simulated λB < 1 Mpc cases that we performed.
It is wort noting that the presented analysis does not favour a specific value of B or λB as every IGMF satisfying the limit in Eq. (5) would result in the same secondary flux time delay. This degeneracy, in principle, can be broken if an accurate measurement of the cascade flux time evolution is obtained (Neronov et al. 2013); in the absence of such a firm detection, we are not in a position to do this here.
3.4. Effect of the possible spectral variations
The assumption of the fixed source spectral shape, used here, may not be justified if the 1ES 0229+200 spectral shape varies over the 14 years of Fermi/LAT observations. However, no indications for its change have been found in earlier H.E.S.S. and VERITAS data with possible spectral index variations ΔΓ ≲ 0.2 (Aharonian et al. 2007; Aliu et al. 2014); we have not found such indications in the MAGIC data either. Such small variations do not have a noticeable impact on the derived IGMF bound value.
Still, given the lower source flux during the MAGIC observations (see Fig. 2), the cut-off energy is poorly constrained for the time period MJD 56500–58000 and may be substantially lower than the assumed 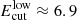 TeV. Conservatively assuming that no detectable cascade was thus generated during the MAGIC observations, we have found that lower limit on IGMF strength is relaxed to B ≳ 6 × 10−18 G for λB > 0.2 Mpc.
TeV. Conservatively assuming that no detectable cascade was thus generated during the MAGIC observations, we have found that lower limit on IGMF strength is relaxed to B ≳ 6 × 10−18 G for λB > 0.2 Mpc.
4. Discussion and conclusions
A range of lower bounds on the IGMF strength has been previously reported based on the non-observation of delayed emission in the 1–100 GeV band, assuming that the TeV sources remain active on year-to-decade timescales (Dermer et al. 2011; Taylor et al. 2011; Vovk et al. 2012; Ackermann et al. 2018)5. An important limitation of all previously reported bounds is that none of the previously reported analyses used strictly contemporaneous monitoring of the source in the 1–100 GeV and TeV bands.
The bound derived in the present paper is based on a combination of long-term simultaneous monitoring of 1ES 0229+200 in the 1–100 GeV energy range with Fermi/LAT and in the E > 200 GeV range with Cherenkov telescopes: H.E.S.S., VERITAS, and MAGIC. This combination alleviates, for the first time, the dependence of the bound on an uncertainty related to possible variability of the TeV band source flux. This makes the bound more robust and almost free from uncertainties of the intrinsic primary source flux variability.
We would like to note that a certain fraction of the deposited electron-positron power may be carried away via plasma instabilities, which develop as a result of interaction between the generated particle stream and the intergalactic medium (Broderick et al. 2012). Such instabilities may mimic the effect of the IGMF, reducing the expected cascade flux. Presently there is no self-consistent description of the problem, given the large density gradient between the stream and the surrounding plasma, so that conclusions on its importance for the IGMF measurements vary substantially, depending on the assumptions adopted (Broderick et al. 2012; Miniati & Elyiv 2013; Chang et al. 2014; Shalaby et al. 2018; Vafin et al. 2018, 2019; Alves Batista & Saveliev 2019; Perry & Lyubarsky 2021). Furthermore, the instability development may be affected by the source emission lifetime (Broderick et al. 2012) and by the IGMF itself (Alawashra & Pohl 2022). Given these uncertainties, a quantitative analysis of this issue is beyond the scope of this work.
Figure 5 puts our bound in the context of other measurements and theoretical models of IGMF. The cosmological evolution of magnetic fields that might have been present in the early Universe drives the field strength and correlation length towards
 |
Fig. 5. Lower bound on IGMF strength derived from Fermi/LAT and Cherenkov telescope datasets (thick blue curve and red data points, respectively). The green dot-dashed and dashed curves show previous Fermi/LAT limits derived for the full source sample and 1ES 0229+200 only, respectively (Ackermann et al. 2018). The light-grey shaded upper bound shows previously known limits on the IGMF strength and correlation length from radio telescope data (Kronberg 1994) and CMB (Planck Collaboration XIII 2016) analysis, as well as from theoretical estimates (Durrer & Neronov 2013). The inclined orange stripe shows the locus of end points of evolution of cosmological magnetic fields (Banerjee & Jedamzik 2004). The red stripe marks the possible range of the magnetic field produced by the chiral dynamo (Joyce & Shaposhnikov 1997; Neronov & Semikoz 2020). The dark green stripe denotes the range of electroweak phase transition magnetic fields that might explain the observed baryonic asymmetry of the Universe (Giovannini & Shaposhnikov 1998; Fujita & Kamada 2016; Kamada & Long 2016). The filled vertical green and violet boxes show favoured regions of IGMF generated by a frozen-in magnetic field, originating from AGN outflows (Furlanetto & Loeb 2001) or galactic winds (Bertone et al. 2006) as labelled in the figure. |
shown by the inclined orange band in Fig. 5 (Banerjee & Jedamzik 2004; Durrer & Neronov 2013). The non-observation of Faraday rotation of the radio waves’ polarisation from distant AGNs and of magnetic field imprint on the CMB constrains the IGMF strength from above for large λB (Kronberg 1994; Durrer & Neronov 2013). The γ-ray observations reported here constrain the field from below. For the particular case of cosmological magnetic field, equating Eqs. (5) and (6) we find
The bound derived here (Eq. (5)) is weaker than the one reported by Ackermann et al. (2018) based on the stacking analysis of a number of blazars. However, one should note that the effect of the IACT and Fermi/LAT energy scale calibration uncertainties relaxes that bound threefold (Ackermann et al. 2018). Moreover, the IGMF limit presented here is based on a prior conservative estimate of the intrinsic 1ES 0229+200 spectrum, with the aim of minimising the expected cascade regardless of the IGMF. Finally, the bound of Ackermann et al. (2018) relied on a strong assumption about the properties of the TeV band γ-ray fluxes of the stacked sources, rather than on real measurements of the TeV flux. In contrast, the bound reported here is free from this assumption. Instead, it relies on precise measurements of the flux history of the source in the GeV–TeV energy range.
The robust lower bound on the IGMF strongly constrains a range of testable models of cosmological magnetogenesis, and specifically the models of magnetic field production at or before the electroweak phase transition (EWPT) in the hot Universe at the temperature close to T ∼ 100 GeV, during the first nanosecond after the Big Bang (see Vachaspati 1991; Neronov & Semikoz 2009; Durrer & Neronov 2013, and references therein). These models are particularly interesting in the context of the problem of the origin of baryon asymmetry of the Universe (BAU). It is possible that the BAU has been generated through the transfer of hypermagnetic helicity to the baryon number at the moment of EWPT (Giovannini & Shaposhnikov 1998; Vachaspati 2001; Fujita & Kamada 2016; Kamada & Long 2016). If this is the case, the hypermagnetic field should have been present in the Universe before the EWPT, when the temperature was still higher. This is possible, for example, through the ‘chiral dynamo’ magnification of thermal fluctuations of hypermagnetic field at temperatures T > 80 TeV (Joyce & Shaposhnikov 1997; Neronov & Semikoz 2020). Estimates of possible initial parameters of the cosmological hypermagnetic field at the moment of chiral dynamo action are shown by the red stripe in Fig. 5. At the moment of the EWPT, the chiral dynamo field parameters fall into a range of fields needed for successful BAU generation (Fujita & Kamada 2016; Kamada & Long 2016). Subsequent evolution of the field to the present epoch results in the cosmological fields with strength from ∼10−15 G to ∼5 × 10−14 G, close to the lower bound derived here.
The analysis presented above indicates that the chiral dynamo magnetic field, possibly responsible for BAU, can be measured using the technique of the search of time-delayed emission in the signal of extragalactic sources of TeV γ rays. In the specific case of sources at the redshift z ∼ 0.1 similar to that of 1ES 0229+200, detection of the ∼10 yr delayed signal requires systematic monitoring of the sources in both the TeV and in the 1–100 GeV bands.
Shorter time delays are expected at higher energies, because the delay time shortens as 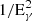 (Neronov & Semikoz 2009). In the specific case of 1ES 0229+200, it goes down to ∼1 yr at 100 GeV. This opens up the possibility of detecting the BAU-related magnetic field through the regular monitoring of source variability at intra-year timescales with Cherenkov telescopes. The detection of a specifically energy-dependent ‘afterglow’ of a bright, short pronounced flare of the source would be a ‘smoking gun’ of the effect in question. Unfortunately, 1ES 0229+200 does not exhibit intense flaring episodes. Other candidate sources could be considered for this approach. A necessary condition is that the candidate sources should have strong intrinsic luminosity above 10 TeV (the energy of primary γ rays, which induce cascade emission at 100 GeV, Neronov & Semikoz 2009). Measurement of such time delays through long-term monitoring is challenging, but not impossible with existing and planned γ-ray observation facilities, including Fermi/LAT (Atwood et al. 2009), CTA (Actis et al. 2011) and HERD (Zhang et al. 2014).
(Neronov & Semikoz 2009). In the specific case of 1ES 0229+200, it goes down to ∼1 yr at 100 GeV. This opens up the possibility of detecting the BAU-related magnetic field through the regular monitoring of source variability at intra-year timescales with Cherenkov telescopes. The detection of a specifically energy-dependent ‘afterglow’ of a bright, short pronounced flare of the source would be a ‘smoking gun’ of the effect in question. Unfortunately, 1ES 0229+200 does not exhibit intense flaring episodes. Other candidate sources could be considered for this approach. A necessary condition is that the candidate sources should have strong intrinsic luminosity above 10 TeV (the energy of primary γ rays, which induce cascade emission at 100 GeV, Neronov & Semikoz 2009). Measurement of such time delays through long-term monitoring is challenging, but not impossible with existing and planned γ-ray observation facilities, including Fermi/LAT (Atwood et al. 2009), CTA (Actis et al. 2011) and HERD (Zhang et al. 2014).
The spectral energy distribution obtained processing the data sample from 2013 to January 2017 has been already published by MAGIC coll. (Acciari et al. 2020). Here we added the data taken in 2017, showing also the overall light curve.
The difference between the lower bounds derived by Dermer et al. (2011) and Taylor et al. (2011), 10−18 G and 10−17 G is due to more precise modelling of the cascade emission by Taylor et al. (2011, Monte Carlo) compared to Dermer et al. (2011, approximate analytic model).
Acknowledgments
We would like to thank the Instituto de Astrofísica de Canarias for the excellent working conditions at the Observatorio del Roque de los Muchachos in La Palma. The financial support of the German BMBF, MPG and HGF; the Italian INFN and INAF; the Swiss National Fund SNF; the ERDF under the Spanish Ministerio de Ciencia e Innovación (MICINN) (PID2019-104114RB-C31, PID2019-104114RB-C32, PID2019-104114RB-C33, PID2019-105510GB-C31,PID2019-107847RB-C41, PID2019-107847RB-C42, PID2019-107847RB-C44, PID2019-107988GB-C22); the Indian Department of Atomic Energy; the Japanese ICRR, the University of Tokyo, JSPS, and MEXT; the Bulgarian Ministry of Education and Science, National RI Roadmap Project DO1-400/18.12.2020 and the Academy of Finland grant nr. 320045 is gratefully acknowledged. This work was also supported by the Spanish Centro de Excelencia “Severo Ochoa” (SEV-2016-0588, SEV-2017-0709, CEX2019-000920-S), the Unidad de Excelencia “María de Maeztu” (CEX2019-000918-M, MDM-2015-0509-18-2) and by the CERCA program of the Generalitat de Catalunya; by the Croatian Science Foundation (HrZZ) Project IP-2016-06-9782 and the University of Rijeka Project uniri-prirod-18-48; by the DFG Collaborative Research Centers SFB823/C4 and SFB876/C3; the Polish National Research Centre grant UMO-2016/22/M/ST9/00382; and by the Brazilian MCTIC, CNPq and FAPERJ. Author contributions Ie. Vovk: methodology, simulations, Fermi/LAT and MAGIC data reduction/analysis, statistical analysis; A. Neronov: methodology; P. Da Vela: MAGIC data analysis; A. Stamerra: project supervision, coordination of MAGIC observations, MAGIC data analysis; D. Semikoz: interpretation; A. Korochkin: simulations, statistical analysis. The rest of the authors have contributed in one or several of the following ways: design, construction, maintenance and operation of the MAGIC telescopes; preparation and/or evaluation of the observation proposals; data acquisition, processing, calibration and/or reduction; production of analysis tools and/or related Monte Carlo simulations; discussion and approval of the contents of the draft.
References
- Abdollahi, S., Acero, F., Ackermann, M., et al. 2020, ApJS, 247, 33 [Google Scholar]
- Acciari, V. A., Ansoldi, S., Antonelli, L. A., et al. 2020, ApJS, 247, 16 [Google Scholar]
- Ackermann, M., Ajello, M., Baldini, L., et al. 2018, ApJS, 237, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Actis, M., Agnetta, G., Aharonian, F., et al. 2011, Exp. Astron., 32, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F. A., Coppi, P. S., & Voelk, H. J. 1994, ApJ, 423, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Barres de Almeida, U., et al. 2007, A&A, 475, L9 [CrossRef] [EDP Sciences] [Google Scholar]
- Alawashra, M., & Pohl, M. 2022, ApJ, 929, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Aleksić, J., Antonelli, L. A., Antoranz, P., et al. 2010, A&A, 524, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aleksić, J., Ansoldi, S., Antonelli, L. A., et al. 2016, Astropart. Phys., 72, 76 [Google Scholar]
- Aliu, E., Archambault, S., Arlen, T., et al. 2014, ApJ, 782, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Alves Batista, R., Dundovic, A., Erdmann, M., et al. 2016, J. Cosmol. Astropart. Phys., 5, 038 [CrossRef] [Google Scholar]
- Alves Batista, R., Saveliev, A., & de Gouveia Dal Pino, E. M., 2019, MNRAS, 489, 3836 [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [CrossRef] [Google Scholar]
- Banerjee, R., & Jedamzik, K. 2004, Phys. Rev. D, 70, 123003 [NASA ADS] [CrossRef] [Google Scholar]
- Berezinsky, V., & Kalashev, O. 2016, Phys. Rev. D, 94, 023007 [NASA ADS] [CrossRef] [Google Scholar]
- Bertone, S., Vogt, C., & Enßlin, T. 2006, MNRAS, 370, 319 [NASA ADS] [Google Scholar]
- Broderick, A. E., Chang, P., & Pfrommer, C. 2012, ApJ, 752, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, P., Broderick, A. E., Pfrommer, C., et al. 2014, ApJ, 797, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Cologna, G., Mohamed, M., Wagner, S., et al. 2015, in 34th International Cosmic Ray Conference (ICRC2015), eds. A. S. Borisov, V. G. Denisova, Z. M. Guseva, et al., 34, 762 [NASA ADS] [Google Scholar]
- Dermer, C. D., Cavadini, M., Razzaque, S., et al. 2011, ApJ, 733, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Durrer, R., & Neronov, A. 2013, A&ARv, 21, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Edelson, R., Turner, T. J., Pounds, K., et al. 2002, ApJ, 568, 610 [CrossRef] [Google Scholar]
- Franceschini, A., Rodighiero, G., & Vaccari, M. 2008, A&A, 487, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fujita, T., & Kamada, K. 2016, Phys. Rev. D, 93, 083520 [NASA ADS] [CrossRef] [Google Scholar]
- Furlanetto, S. R., & Loeb, A. 2001, ApJ, 556, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Giovannini, M., & Shaposhnikov, M. E. 1998, Phys. Rev. D, 57, 2186 [Google Scholar]
- H. E. S. S. Collaboration (Abramowski, A., et al.) 2014, A&A, 562, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joyce, M., & Shaposhnikov, M. 1997, Phys. Rev. Lett., 79, 1193 [NASA ADS] [CrossRef] [Google Scholar]
- Kachelriess, M., Ostapchenko, S., & Tomas, R. 2012, Comput. Phys. Commun., 183, 1036 [NASA ADS] [CrossRef] [Google Scholar]
- Kalashev, O., & Kido, E. 2015, J. Exp. Theor. Phys., 120, 790 [NASA ADS] [CrossRef] [Google Scholar]
- Kalashev, O., Korochkin, A., Neronov, A., & Semikoz, D. 2022, A&A, submitted [arXiv:2201.03996] [Google Scholar]
- Kamada, K., & Long, A. J. 2016, Phys. Rev. D, 94, 063501 [NASA ADS] [CrossRef] [Google Scholar]
- Kronberg, P. P. 1994, Rep. Progr. Phys., 57, 325 [CrossRef] [Google Scholar]
- Miniati, F., & Elyiv, A. 2013, ApJ, 770, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Neronov, A., & Semikoz, D. 2020, ArXiv e-prints [arXiv:2010.13571] [Google Scholar]
- Neronov, A., & Semikoz, D. V. 2007, JETP Lett., 85, 579 [Google Scholar]
- Neronov, A., & Semikoz, D. V. 2009, Phys. Rev. D, 80, 123012 [NASA ADS] [CrossRef] [Google Scholar]
- Neronov, A., & Vovk, I. 2010, Science, 328, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Neronov, A., Semikoz, D., Kachelriess, M., Ostapchenko, S., & Elyiv, A. 2010, ApJ, 719, L130 [NASA ADS] [CrossRef] [Google Scholar]
- Neronov, A., Taylor, A. M., Tchernin, C., & Vovk, I. 2013, A&A, 554, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perry, R., & Lyubarsky, Y. 2021, MNRAS, 503, 2215 [NASA ADS] [CrossRef] [Google Scholar]
- Plaga, R. 1995, Nature, 374, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shalaby, M., Broderick, A. E., Chang, P., et al. 2018, ApJ, 859, 45 [Google Scholar]
- Tavecchio, F., Ghisellini, G., Bonnoli, G., & Foschini, L. 2011, MNRAS, 414, 3566 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, A. M., Vovk, I., & Neronov, A. 2011, A&A, 529, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vachaspati, T. 1991, Phys. Lett. B, 265, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Vachaspati, T. 2001, Phys. Rev. Lett., 87, 251302 [Google Scholar]
- Vafin, S., Rafighi, I., Pohl, M., & Niemiec, J. 2018, ApJ, 857, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Vafin, S., Deka, P. J., Pohl, M., & Bohdan, A. 2019, ApJ, 873, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Vovk, I., Taylor, A. M., Semikoz, D., & Neronov, A. 2012, ApJ, 747, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Woo, J.-H., Urry, C. M., van der Marel, R. P., Lira, P., & Maza, J. 2005, ApJ, 631, 762 [Google Scholar]
- Wood, M., Caputo, R., Charles, E., et al. 2017, Int. Cosmic Ray Conf., 301, 824 [Google Scholar]
- Zanin, R., Carmona, E., Sitarek, J., et al. 2013, Int. Cosmic Ray Conf., 33, 2937 [NASA ADS] [Google Scholar]
- Zhang, S. N., Adriani, O., Albergo, S., et al. 2014, in Space Telescopes and Instrumentation 2014: Ultraviolet to Gamma Ray, eds. T. Takahashi, J. W. A. den Herder, & M. Bautz, SPIE Conf. Ser., 9144, 91440X [NASA ADS] [Google Scholar]
All Tables
Summary of the variability study with IACT data, estimated from their joint fit with the exponentially cut-off power law model.
All Figures
 |
Fig. 1. Spectral energy distribution of 1ES 0229+200 in the 100 MeV–100 TeV energy range. The Fermi/LAT and MAGIC data were obtained here; H.E.S.S and VERITAS measurements were taken from Aharonian et al. (2007) and Aliu et al. (2014) correspondingly. |
| In the text | |
 |
Fig. 2. Light curve of 1ES 0229+200 in several energy bands along with an exemplary fit with an IGMF with strength B = 10−16 G and a coherence scale of λB = 1 Mpc. The top panel represents the best-fit model light curve (along with its uncertainties) used to make the predictions in the energy bands where the measurements were taken (the panels below). The Fermi/LAT and MAGIC data are reported in the text; H.E.S.S. and VERITAS measurements were taken from Cologna et al. (2015) and Aliu et al. (2014) correspondingly. The primary, cascade, and total source fluxes are denoted with green triangles, orange squares, and red circles, correspondingly. Solid and dashed lines represent calculations with CRPropa (Alves Batista et al. 2016) and CRbeam (Berezinsky & Kalashev 2016) Monte Carlo codes respectively; the latter use the small point-like markers to distiguish themselves. |
| In the text | |
 |
Fig. 3. Scan of the cascade power in the Γ − Ecut parameter space along with the 68% and 90% confidence contours from the χ2 fit. At a 90% confidence level, the minimal cascade, marked with the yellow dashed lines, corresponds to Γ ≈ 1.72 and Ecut ≈ 6.9 TeV. |
| In the text | |
 |
Fig. 4. Intergalactic magnetic field strength scan for several different assumed coherence lengths λB. The scan is performed via a simultaneous fit of GeV–TeV observations at hand. Calculations with both CRPropa (Alves Batista et al. 2016) and CRbeam (Berezinsky & Kalashev 2016) Monte Carlo codes are presented. Lines of different colours depict the χ2 values estimated for different non-zero IGMF strengths. The solid black line represents the case of zero IGMF, in which case the secondary emission dominates in the Fermi/LAT energy range; the dashed black line represents the reference fit with the cascade contribution disabled. |
| In the text | |
 |
Fig. 5. Lower bound on IGMF strength derived from Fermi/LAT and Cherenkov telescope datasets (thick blue curve and red data points, respectively). The green dot-dashed and dashed curves show previous Fermi/LAT limits derived for the full source sample and 1ES 0229+200 only, respectively (Ackermann et al. 2018). The light-grey shaded upper bound shows previously known limits on the IGMF strength and correlation length from radio telescope data (Kronberg 1994) and CMB (Planck Collaboration XIII 2016) analysis, as well as from theoretical estimates (Durrer & Neronov 2013). The inclined orange stripe shows the locus of end points of evolution of cosmological magnetic fields (Banerjee & Jedamzik 2004). The red stripe marks the possible range of the magnetic field produced by the chiral dynamo (Joyce & Shaposhnikov 1997; Neronov & Semikoz 2020). The dark green stripe denotes the range of electroweak phase transition magnetic fields that might explain the observed baryonic asymmetry of the Universe (Giovannini & Shaposhnikov 1998; Fujita & Kamada 2016; Kamada & Long 2016). The filled vertical green and violet boxes show favoured regions of IGMF generated by a frozen-in magnetic field, originating from AGN outflows (Furlanetto & Loeb 2001) or galactic winds (Bertone et al. 2006) as labelled in the figure. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



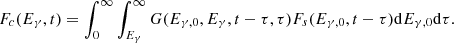
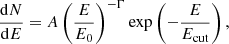
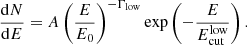
![$$ \begin{aligned} l_{\rm IC}\simeq 160\left[\frac{E_{\rm IC}}{3\,\mathrm{GeV}}\right]^{-1/2}\,\mathrm{kpc} \end{aligned} $$](/articles/aa/full_html/2023/02/aa44126-22/aa44126-22-eq6.gif)