EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 683 (March 2024) A&A, 683 (2024) A25 Full HTML
Open Access
Issue
A&A
Volume 683, March 2024
Article Number A25
Number of page(s) 4
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202347310
Published online 29 February 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Very-high-energy (VHE; ≳100 GeV) γ rays, which propagate from cosmological distances, suffer from absorption in interactions with infrared and optical photons of extragalactic background light (EBL; Blumenthal & Gould 1970; Lee 1998). This leads to the injection of the electron-positron pairs in the intergalactic space and the formation of electromagnetic cascades that release the absorbed power as lower energy γ-ray emission as the pairs up-scatter cosmic microwave background photons via an inverse Compton mechanism (Aharonian et al. 1994). The development of these cascades is sensitive to the intergalactic magnetic field (IGMF), providing means to measure its properties if a spatially extended and/or time-delayed γ-ray ‘pair echo’ is detected from distant VHE sources (Plaga 1995; Neronov & Semikoz 2007, 2009).

A lower bound on the IGMF has previously been derived from the searches of the extended IGMF-dependent emission around blazars, active galactic nuclei (AGN) with jets aligned along the line of sight (Neronov & Vovk 2010; Taylor et al. 2011; Tavecchio et al. 2011; Vovk et al. 2012; Ackermann et al. 2018; Aharonian et al. 2001; Aleksić et al. 2010; H.E.S.S. Collaboration 2014; Archambault et al. 2017). These limits suffer from uncertainties of the intrinsic properties of blazars in the multi-TeV energy range: the time-average spectrum and activity duty cycle.

These uncertainties are reduced in the searches of the delayed IGMF-dependent emission from blazars (Dermer et al. 2011; Taylor et al. 2011; Ackermann et al. 2018). A recent analysis of MAGIC telescope data on the blazar 1ES 0229+200 provides a conservative lower bound on the IGMF from the search of the time-delayed signal at the level of 10−17 G for the long correlation length IGMF (Acciari et al. 2023). This limit still relies on partial information concerning the time-average spectrum of the source on a decade-long time span (it is not possible to continuously monitor the source in the TeV band on such timescales).

In this respect, γ-ray bursts (GRB) may provide a better source type for IGMF searches (Razzaque et al. 2004; Ichiki et al. 2008; Murase et al. 2008, 2009; Takahashi et al. 2008). Their TeV energy range signal is detectable only during a limited time interval (MAGIC Collaboration 2019a,b; Abdalla et al. 2019; H.E.S.S. Collaboration 2021; Blanch et al. 2020), so that the evolution of the intrinsic source spectrum can be monitored in sufficient details. This information can be used for precision calculation of the expected time-delayed IGMF-dependent flux, which is to be compared to the observational data (Vovk 2023).

In this work, we applied this idea to the recent exceptionally bright GRB 221009A that has been detected in the TeV band by LHAASO (Huang et al. 2022). We used publicly available data of the Fermi Large Area Telescope (LAT, Atwood et al. 2009) to search for the pair-echo signal from this GRB. Comparing the GRB afterglow signal detected by Fermi/LAT with model predictions of the time-delayed emission from different IGMF parameters, we derive a lower bound on the IGMF strength at the level 10−19 G. This limit is weaker than the limit from the AGN observations (Acciari et al. 2023), but it provides an independent verification of existence of IGMF in the voids of the large-scale structure, obtained with a different type of source with smaller uncertainties on the primary source flux.

2. Data analysis

We used publicly available Fermi/LAT data on GRB 221009A corresponding to P8R3 SOURCEγ-ray event selection and collected between 2022 September 9 13:00:00 (roughly one month prior to the burst T0= 2022 October 9 13:16:59; Veres et al. 2022) and 2022 October 30 03:02:45 UTC within 20° from the GRB position in the energy range from 100 MeV to 1 TeV. Throughout the analysis we retain events corresponding to the (DATAQUAL>0) (LATCONFIG==1) good time intervals and the maximal telescope zenith angle of 90°. Data reduction was performed with Fermitools package v2.0.8 and FermiPy framework1 v1.0.1 (Wood et al. 2017), as described in the FermiPy documentation2. We accounted for the galactic (gll_iem_v07.fits) and extragalactic (iso_P8R3_SOURCE_V2_v1.txt) diffuse emission and included the sources listed the Fermi/LAT fourth source catalogue (4FGL, Abdollahi et al. 2020). The spectral and spatial models of these sources were taken from the 4FGL catalogue with only their normalisation left free during the fit. To improve the estimate of the catalogue sources’ parameters, we made a joint fit of the pre- (2022 September 9 13:00:00 to T0) and post-burst time intervals, setting the flux from the GRB 221009A position to zero at all times prior to T0.

The pair-echo emission we searched for in the presence of IGMF may appear extended with angular size directly linked to the corresponding time delay as 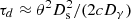, with Ds being the distance to the source, Dγ – γ-ray mean free path and c being the speed of light. In case of GRB 221009A observations in the GeV energy range (Ds ∼ 600 Mpc, Dγ ∼ 100 Mpc), this leads to τd ≈ 1(θ/10−3 deg) yr, so the halo extension observable within the 20 day time window considered here post GRB 221009A explosion is two to three orders of magnitude smaller than the Fermi/LAT point spread function in the entire energy range considered. GRB 221009A was thus modelled here as a simple point source with the spectrum following the power-law form.

The time intervals selected for analysis after the burst T0 were determined from the recorded arrival times of the selected events. We first split them into batches so that there are at least 103 s gaps between the neighbouring ones; then, we grouped the batches that would fall within the same bin of the artificial logarithmically spaced time grid in the T − T0 = 100 − 106.7 s range with four bins per decade. The obtained temporal binning is thus roughly logarithmic while optimally matching the time intervals when GRB 221009A was actually within the Fermi/LAT field of view.

The derived GRB 221009A spectra, exemplified in Fig. 1, do not indicate any significant (test statistics TS > 9) source detection at energies E ≳ 30 GeV; furthermore, we find no significant GRB detection after T − T0 ≈ 2 days from the burst in the entire energy range studied. At earlier times the source spectrum is flat with the slope Γ ∼ 2, roughly corresponding to that measured with LHAASO within the first 3000 s (LHAASO Collaboration 2023). The most stringent energy flux upper limits corresponds to E ≲ 10 GeV, setting the energy range we thus focused upon. The GRB 221009A light curve, extracted in it, is shown in Fig. 2.

thumbnail Fig. 1.

GRB 221009A Fermi/LAT spectra in the few selected time intervals within the first day from the burst. Where source detection is not significant (TS < 9), the 95% confidence level upper limits are plotted. Shaded bands denote the 68% uncertainty of the best-fit power-law model.

thumbnail Fig. 2.

Time evolution of the expected ‘pair echo’ and registered GRB 221009A signal. Top: comparison of measured GRB 221009A Fermi/LAT signal in the 0.1 − 10 GeV energy range with the models of the pair echo emission for different IGMF correlation length and strength combinations, stemming from the LHAASO measurements of its multi-TeV flux. For the time intervals with no significant detection (TS < 9), the 95% confidence level upper limits are given. Short timescale fluctuations visible in the curves are numerical artifacts of the ‘echo’ signal calculation. Bottom: GRB 221009A detection test statistics (TS). Horizontal lines denote the TS = 25 and TS = 9 levels, roughly reflecting the 5σ and 3σ detection significances correspondingly.

3. Pair echo modelling

The temporal dependence of the pair-echo signal is set by angular scatter of the cascade electron-positron pairs, caused by both IGMF and angular spreads of the pair production and inverse Compton emission, which are intrinsic to the cascade. The latter alone may result in time delays comparable to the GRB duration (Takahashi et al. 2008; Neronov & Semikoz 2009); however, for numerical reasons it may be challenging to account for using general-purpose Monte Carlo codes (Vovk 2023). We thus used a mixed approach to calculate the expected ‘echo’ light curve.

First, we used the approach of Vovk (2023) to model the intrinsically time-delayed emission from from GRB 221009A. This model incorporates the exact angular and energy dependencies of the pair production and inverse Compton scattering cross-sections that define the intrinsic scatter of the generated electromagnetic cascade, and thus the inherent time delay of the pair echo in the absence of IGMF. We assume that the source is located at z = 0.15, corresponding to the GRB 221009A redshift derived from spectroscopic observations (de Ugarte Postigo et al. 2022; Castro-Tirado et al. 2022) and its intrinsic spectrum in the TeV range follows a power-law shape as suggested by LHAASO measurements (LHAASO Collaboration 2023). Using the reported slope and normalisation for each of the time bins identified in LHAASO analysis, we then calculate the total ‘echo’ flux in 50 logarithmically spaced time intervals spanning the 10 − 106 s time range after the burst. Though no high-energy cut-off was found in the LHAASO data, we conservatively limited the maximal intrinsic photon energy to Emax = 10 TeV; given the soft GRB spectrum in the multi-TeV energy range with the slope Γ ∼ 2.3 (LHAASO Collaboration 2023), this artificially reduces the time-delayed emission flux by a up to a factor of two compared to the uninterrupted spectrum above Emax.

We then ran the publicly available CRPropa code (Alves Batista et al. 2021) to model the time-delayed signal expected in presence of IGMF. Here, we modelled the GRB 221009A as a point source of jetted emission with the half-opening angle of 10° located at the same redshift of z = 0.15. Given the shortness of the target time delay τd ≲ 10 days, the exact location of the observer within jet cone plays a minor role, so we arbitrarily located it on the jet axis. We explored different configurations of the intergalactic magnetic field characterised by strength B = 10−21 − 10−17 G and correlation length l = 10−3 − 1 Mpc. We modelled this field as cell-like, with the field being constant within each ‘cell’, but randomly changing the orientation from one cell to another. The CRPropa code was cross-validated with the other Monte Carlo modelling codes (Kalashev et al. 2023) and is known to provide sufficient precision for sources at moderate redshifts, such as GRB 221009A. It does not, however, account for the intrinsic time delay of the pair echo that we estimate above. We thus only used its output to determine the IGMF-induced time spread of the echo signal in the energy range of our analysis.

Finally, to account for both intrinsic and IGMF-induced time delays, we convolved the echo light curve determined at the first step with the temporal spread computed obtained from CRPropa. The resulting models of the delayed signal for several values of IGMF strength B and coherence scale l are shown in Fig. 2.

4. IGMF limit

The expected echo signal for weak (or even zero) IGMF substantially exceeds the Fermi/LAT measurements, as is evident from Fig. 2. This rules out the possibility of zero IGMF along the line of sight towards the GRB.

At the same time, all the models with IGMF strength below 10−19 G are also inconsistent with the Fermi/LAT measurements of GRB 221009A flux. The possibility of B ≃ 10−19 G is marginally inconsistent with the data in the case of the correlation length l = 1 Mpc. The expected secondary emission flux is still well above the observed flux limits in the case l = 1 kpc. This is explained by the fact that shorter correlation length field is less efficient in deflections of electrons and positrons. The secondary flux in the 0.1–10 GeV range is produced via inverse Compton scattering of the Cosmic Microwave Background photons by electrons with energies in the Ee ≃ 0.3 − 3 TeV range (Neronov & Semikoz 2009). Such electrons lose energy on the inverse Compton scattering on the distance scale of about De ≃ 0.1 − 1 Mpc (Neronov & Semikoz 2009). If the magnetic field correlation length is longer than De, electrons and positrons are deflected by an angle α = De/RL, where RL = Ee/eB is the giro-radius in magnetic field B and e is the electron charge. The deflection angle does not depend on the magnetic field correlation length. On the contrary, if l ≪ De, the deflection direction changes n = De/l times on the cooling distance scales, so the overall deflection pattern is a random walk in the pitch angle, with the resulting deflection angle 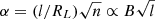. Stronger magnetic field is required to sufficiently deflect the electrons and reduce the pair-echo signal.

Overall, we find that the lower bound on the IGMF is l-independent for l > 1 Mpc and scales as B > 10−19(l/1 Mpc)−1/2 G for shorter correlation lengths, as shown in Fig. 3.

thumbnail Fig. 3.

Lower bound on IGMF derived from GRB 221009A (red line) compared to existing bounds from γ-ray, radio, CMB, and UHECR observations and predictions of the cosmological evolution models. The CMB upper bounds are from Planck (Planck Collaboration XIX 2016) and from the analysis of Jedamzik & Saveliev (2019). UHECR upper bound is from Neronov et al. (2023). MAGIC lower bound is from Acciari et al. (2023). Green shaded area shows the range of predictions for the endpoints of cosmological evolution of primordial magnetic fields. BJ04 is from Banerjee & Jedamzik (2004) and HS22 is from Hosking & Schekochihin (2023).

5. Discussion

The lower bound on IGMF derived from a combination of LHAASO and Fermi/LAT data on GRB 221009A, at B ≃ 10−19 G level, is weaker than that derived from MAGIC observations of the blazar 1ES 0229+200. The difference between the two bounds is somewhat smaller at shorter correlation lengths because of the different correlation length dependence of the bounds. The two sources, GRB 221009A and 1ES 0229+200, are at comparable redshifts. The difference in the correlation length dependence of the lower bound on IGMF is explained by the different energy range in which the time-delayed secondary emission was searched for the two sources. The MAGIC search of the pair echo was concentrated on the 100 GeV range, while the Fermi/LAT analysis reported in our paper was for the 1 GeV energy range. The cooling distance of electrons generating the inverse Compton emission at 1 GeV is larger so that they can accumulate random deflection by IGMF on longer distance scales.

The γ-ray observations constrain the magnetic field in the voids of the large-scale structure. Recent modelling of magnetised outflows from galaxies suggests that the strength of these outflows is not sufficient for filling the voids, so the void field is most probably of cosmological origin (Marinacci et al. 2018). The GRB 221009A Fermi/LAT pair-echo limit on the short correlation length magnetic fields provides a limit on such cosmological IGMF (green-shaded region in Fig. 3) that is of the same order of magnitude as the AGN limit.

The cosmological magnetic fields may be produced during the epochs of electroweak and quantum chromodynamics (QCD) transitions in the early Universe or during the period of inflation (see Grasso & Rubinstein 2001 and Durrer & Neronov 2013 for reviews). The maximal initial correlation length of these fields does not exceed the size of the cosmological horizon at the moment of the field generation. This limits the comoving correlation length of the fields from the electroweak epoch to about 102 au and the QCD epoch field to about a parsec. Turbulent decay of the field from the moment of generation up to the recombination epoch leads to decrease of the field strength and increase of the correlation length up to the scale of the largest processed eddies: l ≃ 1(B/10−8 G) Mpc (Banerjee & Jedamzik 2004; the boundary of the green-shaded region marked BJ04). If the turbulent decay is governed by the magnetic reconnection, a somewhat shorter final correlation length is expected (Hosking & Schekochihin 2023; the boundary marked HS22). The GRB pair-echo γ-ray data limit the parameters of the cosmological magnetic field to B > 10−15 G, λB > 0.1 pc for the Banerjee & Jedamzik (2004) evolution model and B > 10−14 G, λB > 10−5 pc for the Hosking & Schekochihin (2023) evolution model.

When this study was in the final stage and awaiting LHAASO data, two other publications arrived using the Elmag code (Dzhatdoev et al. 2024; Huang et al. 2023) and suggest somewhat stronger IGMF limits of B > (3 − 10)×10−19 G. In comparison, our result benefits from a cross-check between CRpropa and CRbeam codes and, importantly, accounts for the intrinsic time delay, substantially diluting the ‘echo’ flux on timescales below a day and thus yielding a more conservative limit B > 10−19 G.

Acknowledgments

The work of D.S. and A.N. has been supported in part by the French National Research Agency (ANR) grant ANR-19-CE31-0020. Ie.V. gratefully acknowledges the support of the Institute for Cosmic Ray Research (ICRR), the University of Tokyo in realization of this study and thanks the CTA-North computing center at La Palma, Spain for providing the necessary computational resources. The work of A.K. has been supported by the IISN project No. 4.4501.18.

References

  1. Abdalla, H., Adam, R., Aharonian, F., et al. 2019, Nature, 575, 464 [Google Scholar]
  2. Abdollahi, S., Acero, F., Ackermann, M., et al. 2020, ApJS, 247, 33 [Google Scholar]
  3. Acciari, V. A., Agudo, I., Aniello, T., et al. 2023, A&A, 670, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Ackermann, M., Ajello, M., Baldini, L., et al. 2018, ApJS, 237, 32 [NASA ADS] [CrossRef] [Google Scholar]
  5. Aharonian, F. A., Coppi, P. S., & Voelk, H. J. 1994, ApJ, 423, L5 [NASA ADS] [CrossRef] [Google Scholar]
  6. Aharonian, F. A., Akhperjanian, A. G., Barrio, J. A., et al. 2001, A&A, 366, 746 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Aleksić, J., Antonelli, L. A., Antoranz, P., et al. 2010, A&A, 524, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Alves Batista, R., Erdmann, M., Evoli, C., et al. 2021, PoS, ICRC2021, 978 [Google Scholar]
  9. Archambault, S., Archer, A., Benbow, W., et al. 2017, ApJ, 835, 288 [NASA ADS] [CrossRef] [Google Scholar]
  10. Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [CrossRef] [Google Scholar]
  11. Banerjee, R., & Jedamzik, K. 2004, Phys. Rev. D, 70, 123003 [NASA ADS] [CrossRef] [Google Scholar]
  12. Blanch, O., Longo, F., Berti, A., et al. 2020, GRB Coordinates Network, 29075 [Google Scholar]
  13. Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [Google Scholar]
  14. Castro-Tirado, A. J., Sanchez-Ramirez, R., Hu, Y. D., et al. 2022, GRB Coordinates Network, 32686 [Google Scholar]
  15. Dermer, C. D., Cavadini, M., Razzaque, S., et al. 2011, ApJ, 733, L21 [NASA ADS] [CrossRef] [Google Scholar]
  16. de Ugarte Postigo, A., Izzo, L., Pugliese, G., et al. 2022, GRB Coordinates Network, 32648 [Google Scholar]
  17. Durrer, R., & Neronov, A. 2013, A&ARv, 21, 62 [NASA ADS] [CrossRef] [Google Scholar]
  18. Dzhatdoev, T. A., Podlesnyi, E. I., & Rubtsov, G. I. 2024, MNRAS, 527, L95 [Google Scholar]
  19. Grasso, D., & Rubinstein, H. R. 2001, Phys. Rep., 348, 163 [NASA ADS] [CrossRef] [Google Scholar]
  20. H.E.S.S. Collaboration (Abdalla, H. et al.) 2021, Science, 372, 1081 [NASA ADS] [CrossRef] [Google Scholar]
  21. H.E.S.S. Collaboration (Abramowski, A. et al.) 2014, A&A, 562, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Hosking, D. N., & Schekochihin, A. A. 2023, Nat. Comm., 14, 7523 [NASA ADS] [CrossRef] [Google Scholar]
  23. Huang, Y., Hu, S., Chen, S., et al. 2022, GRB Coordinates Network, 32677 [Google Scholar]
  24. Huang, Y.-Y., Dai, C.-Y., Zhang, H.-M., Liu, R.-Y., & Wang, X.-Y. 2023, ApJ, 955, L10 [NASA ADS] [CrossRef] [Google Scholar]
  25. Ichiki, K., Inoue, S., & Takahashi, K. 2008, ApJ, 682, 127 [NASA ADS] [CrossRef] [Google Scholar]
  26. Jedamzik, K., & Saveliev, A. 2019, Phys. Rev. Lett., 123, 021301 [NASA ADS] [CrossRef] [Google Scholar]
  27. Kalashev, O., Korochkin, A., Neronov, A., & Semikoz, D. 2023, A&A, 675, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Lee, S. 1998, Phys. Rev. D, 58, 043004 [NASA ADS] [CrossRef] [Google Scholar]
  29. LHAASO Collaboration (Cao, Z., et al.) 2023, Science, 380, 1390 [NASA ADS] [CrossRef] [Google Scholar]
  30. MAGIC Collaboration (Acciari, V. A., et al.) 2019a, Nature, 575, 455 [Google Scholar]
  31. MAGIC Collaboration (Acciari, V. A., et al.) 2019b, Nature, 575, 459 [Google Scholar]
  32. Marinacci, F., Vogelsberger, M., Pakmor, R., et al. 2018, MNRAS, 480, 5113 [NASA ADS] [Google Scholar]
  33. Murase, K., Takahashi, K., Inoue, S., Ichiki, K., & Nagataki, S. 2008, ApJ, 686, L67 [NASA ADS] [CrossRef] [Google Scholar]
  34. Murase, K., Zhang, B., Takahashi, K., & Nagataki, S. 2009, MNRAS, 396, 1825 [Google Scholar]
  35. Neronov, A., & Semikoz, D. V. 2007, JETP Lett., 85, 473 [NASA ADS] [CrossRef] [Google Scholar]
  36. Neronov, A., & Semikoz, D. V. 2009, Phys. Rev. D, 80, 123012 [NASA ADS] [CrossRef] [Google Scholar]
  37. Neronov, A., & Vovk, I. 2010, Science, 328, 73 [NASA ADS] [CrossRef] [Google Scholar]
  38. Neronov, A., Semikoz, D., & Kalashev, O. 2023, Phys. Rev. D, 108, 103008 [NASA ADS] [CrossRef] [Google Scholar]
  39. Plaga, R. 1995, Nature, 374, 430 [NASA ADS] [CrossRef] [Google Scholar]
  40. Planck Collaboration XIX. 2016, A&A, 594, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Razzaque, S., Mészáros, P., & Zhang, B. 2004, ApJ, 613, 1072 [NASA ADS] [CrossRef] [Google Scholar]
  42. Takahashi, K., Murase, K., Ichiki, K., Inoue, S., & Nagataki, S. 2008, ApJ, 687, L5 [NASA ADS] [CrossRef] [Google Scholar]
  43. Tavecchio, F., Ghisellini, G., Bonnoli, G., & Foschini, L. 2011, MNRAS, 414, 3566 [NASA ADS] [CrossRef] [Google Scholar]
  44. Taylor, A. M., Vovk, I., & Neronov, A. 2011, A&A, 529, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Veres, P., Burns, E., Bissaldi, E., et al. 2022, GRB Coordinates Network, 32636 [Google Scholar]
  46. Vovk, I. 2023, Phys. Rev. D, 107, 043020 [NASA ADS] [CrossRef] [Google Scholar]
  47. Vovk, I., Taylor, A. M., Semikoz, D., & Neronov, A. 2012, ApJ, 747, L14 [NASA ADS] [CrossRef] [Google Scholar]
  48. Wood, M., Caputo, R., Charles, E., et al. 2017, Int. Cosmic Ray Conf., 301, 824 [Google Scholar]

All Figures

thumbnail Fig. 1.

GRB 221009A Fermi/LAT spectra in the few selected time intervals within the first day from the burst. Where source detection is not significant (TS < 9), the 95% confidence level upper limits are plotted. Shaded bands denote the 68% uncertainty of the best-fit power-law model.
In the text
thumbnail Fig. 2.

Time evolution of the expected ‘pair echo’ and registered GRB 221009A signal. Top: comparison of measured GRB 221009A Fermi/LAT signal in the 0.1 − 10 GeV energy range with the models of the pair echo emission for different IGMF correlation length and strength combinations, stemming from the LHAASO measurements of its multi-TeV flux. For the time intervals with no significant detection (TS < 9), the 95% confidence level upper limits are given. Short timescale fluctuations visible in the curves are numerical artifacts of the ‘echo’ signal calculation. Bottom: GRB 221009A detection test statistics (TS). Horizontal lines denote the TS = 25 and TS = 9 levels, roughly reflecting the 5σ and 3σ detection significances correspondingly.
In the text
thumbnail Fig. 3.

Lower bound on IGMF derived from GRB 221009A (red line) compared to existing bounds from γ-ray, radio, CMB, and UHECR observations and predictions of the cosmological evolution models. The CMB upper bounds are from Planck (Planck Collaboration XIX 2016) and from the analysis of Jedamzik & Saveliev (2019). UHECR upper bound is from Neronov et al. (2023). MAGIC lower bound is from Acciari et al. (2023). Green shaded area shows the range of predictions for the endpoints of cosmological evolution of primordial magnetic fields. BJ04 is from Banerjee & Jedamzik (2004) and HS22 is from Hosking & Schekochihin (2023).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.