| Issue |
A&A
Volume 667, November 2022
|
|
|---|---|---|
| Article Number | A114 | |
| Number of page(s) | 10 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/202243820 | |
| Published online | 15 November 2022 | |
SPHERE adaptive optics performance for faint targets
1
European Southern Observatory,
Alonso de Córdova 3107, Vitacura, Casilla
19001
Santiago, Chile
e-mail: mjones@eso.org
2
Université Grenoble Alpes, CNRS, IPAG,
38000
Grenoble, France
3
Astronomical Observatory, University of Warsaw,
Al. Ujazdowskie 4,
00-478
Warsaw, Poland
Received:
20
April
2022
Accepted:
27
August
2022
Context. High-contrast imaging is a powerful technique for detecting and characterizing planetary companions at orbital separations ≳100 mas from their parent stars.
Aims. We aim to study the limiting magnitude of the VLT/SPHERE adaptive optics (AO) system and the corresponding instrument performance for faint targets (G ≥ 11.0 mag).
Methods. We computed the coronagraphic H-band raw contrast and the full width at half maximum (FWHM) of the non-coronagraphic point spread function (PSF), for a total of 111 different stars observed between 2016 and 2022 with IRDIS. For this, we processed a large number of individual frames that were obtained under different atmospheric conditions. We then compared the resulting raw contrast and the PSF shape as a function of the visible wave front sensor (WFS) instant flux, which scales with the G-band stellar magnitude. We repeated this analysis for the top 10% (TCAT10) and top 30% (TCAT38) best turbulence conditions on Cerro Paranal.
Results. We found a strong decrease in the coronagraphic contrast for stars fainter than G ∼ 12.5 mag, even under the best atmospheric conditions. In this regime, the AO correction is dominated by the read-out noise of the WFS detector. In particular we found roughly a factor of 10 decrease in the raw contrast ratio between stars with G ∼ 12.5 and G ∼ 14.0 mag. Similarly, we observed a sharp increase in the FWHM of the non-coronagraphic PSF beyond G ∼ 12.5 mag, and a corresponding decrease in the strehl ratio from ∼0.5 to ∼0.2 for the faintest stars. The decrease in the contrast ratio and PSF sharpness is slightly more pronounced for TCAT38 than for TCAT18.
Key words: instrumentation: adaptive optics / atmospheric effects
© M. I. Jones et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
High-contrast direct imaging (DI) is a powerful technique for detecting and characterizing young and self-luminous giant planets, reflected light planets, highly polarized disks, Solar System objects, among other interesting objects. Thanks to its extreme adaptive optics (AO) system, called SAXO (Fusco et al. 2006), the Spectro-Polarimetric High-contrast Exoplanet REsearch instrument (SPHERE; Beuzit et al. 2019) is one of the most powerful instruments in the world for direct imaging science, and after more than 6 yr of operations, it has led to the detection and characterization of a variety of (forming) planetary systems and protoplanet disks. Notable examples of these include β Pictoris b (Lagrange et al. 2018), the PDS 70 planet-forming system (Müller et al. 2018; Keppler et al. 2018), the multiplanet systems around HD 8799 (Zurlo et al. 2016) and YSES 1 (Bohn et al. 2020), and the TW Hydrae disk (van Boekel et al. 2017), among others.
While different long-term SPHERE DI programs have mainly studied relatively bright stars (e.g., SHARDDS: Milli et al. 2017a; SHINE: Desidera et al. 2021; YSES: Bohn et al. 2021; BEAST: Janson et al. 2021), there is still a large population of faint stars located in young (age ≲ 10−20 Myr) stellar associations, which are ideal laboratories for studying in-situ planet formation inside protoplanetary disks. However, these stars are embedded in gas- and dust-rich disks, which absorb a large fraction of the stellar visible light, making these objects very red (see a discussion in Boccaletti et al. 2020). This effect is even stronger for M-type stars, which are intrinsically fainter in the optical when compared to the near infrared (NIR). The main disadvantage of targeting these kinds of stars with SPHERE is that the instant flux recorded in the visible wave front sensor (WFS) is strongly reduced, and thus the AO correction is highly degraded. As increasing number of such faint stars (in visible light) are routinely being observed with SPHERE, we are able to better characterize the SAXO limiting magnitude. Motivated by this idea, we studied the SPHERE performance for targets fainter than G = 11.0 mag, where G corresponds to the Gaia Early Data Release 3 (Gaia EDR3) magnitude (Riello et al. 2021).
This paper is organized as follows: in Sect. 2 we present the data used for the analysis and we describe our methods in detail. In Sect. 3, we discuss about the instant flux received by the WFS. In Sect. 4, we present the results of the raw contrast (from coro-nagraphic images) and the full width at half maximum (FWHM) of the non-coronagraphic point spread function (PSF), as a function of the WFS flux and the stellar G-band magnitude. Similarly, we computed the strehl ratio (SR) for a handful of selected stars and we compare the resulting values with the FWHM previously measured. In Sect. 5, we compare the contrast from the raw images to that obtained in post-processing data. Finally, the summary, discussion and conclusions are presented in Sect. 6.
2 Data and method
We analyzed a total of 111 different stars observed with SPHERE between 2016 and 2022, all of them fainter than G = 11.0 mag, which are listed in Table A.1. Figure 1 shows the Gaia EDR3 color-magnitude diagram (CMD) with the positions of all of the targets. Similarly, Fig. 2 shows a Two Micron All Sky Survey (2MASS; Cutri et al. 2003) NIR CMD for our stars. The median G-band and H-band magnitudes of the sample are 12.4 mag and 8.9 mag, respectively. We included in the analysis only H-band (λc ~ 1.63 μm) observations taken with the visible (WFS) in the high-gain (M = 1000) low-frequency mode (300 Hz), with the WFS spectral filter in the OPEN position. We also included both imaging and polarimetric observations. In the case of the coronagraphic observations, we included individual frames with detector integration time (DIT) longer than 2 s. We note that the vast majority of the faint star observations were made using these setups. The list of header keywords used to filter the data are summarized in Table 1. We note that all of the raw data (non-coronagraphic FLUX and coronagraphic OBJECT data cubes) and their corresponding AO files (FITS binary tables containing atmospheric and SAXO telemetry data; see Milli et al. 2017b) were downloaded from the ESO archive. For the analysis, we developed an IDL-based code, which computes the contrast for each individual raw frame, following the steps listed below.
First, we fitted a 2D Gaussian function to each individual non-coronagraphic FLUX frames. From the fit we estimated the peak flux (fnc) and the corresponding FWHM in the x- and y-pixels direction. The final fnc value was computed from the mean of all individual flux frames. We then used the mean fnc to predict the peak flux (fc) in each individual coronagraphic OBJECT frame, by scaling the DIT, neutral density filters and other optical elements with different transmissions (e.g. when a sequence is obtained with and without the apodizer). We then estimated the noise level (σ300) at 24 pixels from the coronagraph center (corresponding to ~300 mas), by computing the standard deviation in a 5-pixels-wide annulus. The resulting 5σ raw contrast at 300 mas (RC300) was obtained from:
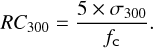 (1)
(1)
We note that for the broad-band observations (B_H filter) and the differential polarimetry (DP_0_BB_H filter), we used only the left side of the Infra-Red Dual-beam Imaging and Spectroscopy (IRDIS; Dohlen et al. 2008) detector, while for the dual-imaging mode (DB_H23 filter) we independently analyzed the left (λc ~ 1.59 μm) and the right (λc ~ 1.67 μm) sides of the detector, and we then computed the mean value from the two channels. Finally, to study the effect of the atmospheric conditions on the contrast and the PSF, we retrieved the Differential Image Motion Monitor (DIMM) seeing and coherence time (τ0) at the beginning of each exposure, directly from the image header.
Header keywords used to filter the data for the flux and coronagraphic observations.
 |
Fig. 1 Gala EDR3 color-magnitude diagram of all 111 stars included in the analysis. The typical uncertainties are smaller than the symbol size. The position of the reddest star in the sample (AX Cha) is also labeled. The corresponding histogram of the G-band magnitude distribution is overplotted on the right side. |
3 Instant flux on the visible WFS
The SPHERE instrument is equipped with a 40 × 40 Shack-Hartmann WFS, (with a total of 1240 effective subapertures imaging the SPHERE entrance pupil). The light reaching the WFS is recorded by a 240 × 240 pixel electron multiplying charge-coupled device (EMCCD) detector, sensitive to visible light (~0.45–0.95 μm). The main advantage of this detector is that it can operate at very high frequencies (up to 1380 Hz), low read-out noise (<0.2 e−/pixel/frame), and high multiplication gains (up to M = 1000; Sauvage et al. 2016b). However, as mentioned before, for our analysis we included only data taken with the EMCCD operating at 300 Hz and M = 1000, which is the mode automatically selected by the real-time computing system (SPARTA; Fedrigo et al. 2006) for faint targets (R > 10.5 mag).
The instant flux in the WFS EMCCD detector (fWFS) is recorded by SPARTA, and it is saved in the AO files. These files (among other telemetry data) contain the total flux per pupil (i.e., integrated in all 1240 subapertures). This flux (tagged FLUX_AVG in the binary tables) is thus expressed in units of [ADU/pupil/frame]. To convert FLUX_AVG into [e−1/subaperture/frame], we used:
![${f_{{\rm{WFS}}}}\left[ {{{\rm{e}}^{{\rm{ - 1}}}}{\rm{/subaperture/frame}}} \right]{\rm{ = }}{{{\rm{g \times FLUX\_AVG}}} \over {{{\rm{n}}_{\rm{s}}}{\rm{ \times M}}}}{\rm{,}}$](/articles/aa/full_html/2022/11/aa43820-22/aa43820-22-eq2.png) (2)
(2)
where g = 16.5 [e−/ADU], ns = 1240 [subapertures/pupil], and M = 1000 (unit-less).
 |
Fig. 3 H-band 5σ raw contrast at 300 mas as a function of the visible WFS flux. The black and red lines correspond to atmospheric turbulence categories TCAT10 and TCAT38, respectively. |
4 Results
4.1 Raw contrast and FWHM as a function of the WFS flux
After computing the raw contrast, we cleaned up the sample by removing those frames that lead to very deviant values. Typical examples of these included cases with the stars out of the coronagraph, AO loop open, contamination from close binary companions, extreme cases of low-wind effect (Sauvage et al. 2016a; Milli et al. 2018), among others. We then compared the raw contrast as a function of fWFS. Figure 3 shows the RC300 versus the fWFS binned in 1 [e−/subaperture/frame] flux bins. We note that only frames with header values listed in Table 1 were included (as explained in Sect. 2). The black dots represent the atmospheric turbulence category TCAT10, corresponding to a seeing <0.6arcsec and a coherence time (τ0) >5.2 ms, and the red dots represent TCAT30 (corresponding to a seeing <0.8arcsec and a τ0 > 4.1ms). The error bars correspond to a 1σ equal-tailed confidence interval for each bin. In total, we included ~12000 individual OBJECT frames in Fig. 3.
As can be seen, there is a sharp decrease in the achievable contrast for fBFS below ~3 [e−/subaperture/frame]. In this regime, the AO correction is degraded due to the lack of photons collected by the WFS. Above this value the RC300 is nearly constant. We also note that the RC388 achieved under TCAT10 conditions is slightly better than that under TCAT30. Similarly, Fig. 4 shows the mean FWHM (from the x- and y-direction) measured on non-coronagraphic FLUX frames as a function of fWFS. Again, this quantity was computed on the left side of the IRDIS detectors in the dual-band mode (see Table 1), and includes a total of ~9000 individual frames. It can be seen that for fWFS level above ~3 [e−/subaperture/frame] the PSF is nearly flat, with a FWHM of ~ 53 mas, for both TCAT10 and TCAT30. On the other hand, for lower fWFS values, the AO correction degrades, and thus the FWHM increases with a decreasing flux level, reaching a mean value larger than ~ 100 mas, when reaching the subelectron per frame regime, for both TCAT10 and TCAT30.
 |
Fig. 4 Mean FWHM as a function of the visible WFS flux. The black and red lines correspond to the atmospheric turbulence categories TCAT10 and TCAT38, respectively. |
4.2 Correlation between stellar magnitude and WFS flux
To understand the SPHERE performance not only as a function of fWFS, but also as a function of the target magnitude, we investigated the correlation between fWFS and the stellar G-band magnitude. We chose this particular band because the transmission curve of the WFS detector is very close to the G-band one, and also since nearly all of the targets observed by SPHERE show a G-band entry in the EDR3 catalog. Figure 5 shows the normalized transmission of the Gaia EDR3 bands1, the Johnson R broad-band filter (Bessell 1990), and the WFS response, including all of the upstream optical elements and with the WFS spectral filter in the OPEN position (which is the case for faint stars). It can be seen that the G-band transmission function is the closest one to the WFS response function, although the latter one is slightly more sensitive to longer wavelengths. For this reason, to predict the expected fWFS value during an observing sequence of a faint target, the G-band should be used, instead of the R-band (as currently implemented in SPARTA). In fact, even though the value of these two magnitudes are generally very close, there are cases where the difference is as large as one magnitude (corresponding to a factor of ~2.5 in flux). For this analysis, we first corrected the flux in the WFS for the target airmass, using an extinction coefficient of 0.12 (Patat et al. 2011). We then compared this value with the stellar G-band magnitude. We note that to minimize the stellar color effect, we only included stars with 1 < GB − GR < 3 (see Fig. 1). The results are shown in Fig. 6. The error bars in the WFS flux correspond to the standard deviation from all individual measurements. The solid line corresponds to the WFS magnitude scale (mWFS), given by:
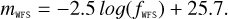 (3)
(3)
We note that we removed outliers beyond 2.5 σ from the fit (18 stars in total), leading to a scatter of 0.18 mag. This value is mainly explained by observations performed under different observing conditions (e.g., sky transparency, seeing) and, more importantly, due to the fact that we included observations using different spatial filters (Fusco et al. 2016), as listed in Table 1, meaning that a different amount of the light was blocked for different observations. Ideally, this analysis should be repeated with data taken under photometric conditions and using the WFS spatial filter in the LARGE position, as opposed to the majority of the observations analyzed here that were done using either the SMALL or the MEDIUM spatial filter. In addition, variable stars or intrinsically red stars, such as AX Cha, might introduce extra scatter to this correlation.
Using this correlation, we can directly compare the stellar G magnitude and the expected raw contrast, under different atmospheric conditions. We therefore replicated Figs. 3 and 4, but this time we replaced fWFS by the stellar G magnitude. The results are shown in Figs. 7 and 8. As can be seen, there is a decrease of roughly one order of magnitude in the contrast ratio beyond G ~ 12.5. For stars brighter than this, the contrast is nearly constant, meaning that is it limited by the atmospheric conditions and by the ability of the AO system to correct for the atmospheric turbulence. In this regime (G ~ 10.5-12 mag), the medium AO frequency mode (600 Hz) should be used, while currently the 300 Hz frequency mode is set automatically by the real-time computer. This is confirmed by recent SPHERE technical observations of stars with G between 11 and 12, which yielded a systematic improvement in SR and contrast, even in atmospheric conditions worse than TCAT30. Similarly, there is an increase in the FWHM of the PSF from ~53mas to ≳ 100 mas between G ~ 12.5 mag and ~ 14mag.
 |
Fig. 5 Normalized transmission curves for the Gaia EDR3 G (solid black line), GB (dotted blue line), GR (dotted red line) and Johnson R (solid green line) broad-band filters. The total transmission curve (including upstream optics) of the WFS is overplotted (solid black dots). |
 |
Fig. 6 Stellar G-band magnitude versus the logarithm of the WFS flux. The solid line corresponds to the best linear fit between these two quantities. The position of AX cha is also shown (red dot). The corresponding fWFS values expressed in linear scale and units of [e−1 /subaperture/frame] are labeled in the upper x-axis. |
 |
Fig. 7 H-band 5σ raw contrast at 300 mas as a function of the stellar G-band magnitude. The black and red lines correspond to the atmospheric turbulence categories TCAT10 and TCAT38, respectively. |
 |
Fig. 8 Mean FWHM as a function of the stellar G-band magnitude. The solid black and red dots (lines) correspond to the atmospheric turbulence categories TCAT10 and TCAT38, respectively. |
 |
Fig. 9 Normalized diffraction-limited theoretical PSF of the VLT pupil at 1.63 μm, as seen by IRDIS/SPHERE. |
4.3 Strehl ratio
In addition to the FWHM values, we investigated the dependence of the strehl ratio (SR) on fwfs and the stellar magnitude. For this, we first computed a theoretical diffraction-limited PSF for the VLT as seen by SPHERE, (i.e., including the effect of the Lyot stop and the apodizer in the optical path) at 1.63 μm. The PSF was computed over an area of 29 × 29 pixels (including light up to the third airy ring) with the IRDIS plate scale of 12.27 mas pix−1, and was then normalized by the total integrated flux in the whole 29 × 29 pixels area. A 3D view of the resulting normalized PSF is shown in Fig. 9. We then fitted a 2D Moffat profile (Moffat 1969) of the form:
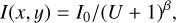 (4)
(4)
The resulting coefficients are listed in Table 2. We then repeated the Moffat fit, but this time for a total of 332 observed FLUX frames. We note that, in this case, we also included brighter stars (leading to a higher SR) that were not part of the sample presented in Sect. 2, only to cover the full range of FWHM and SR values. The resulting SR was simply estimated by taking the ratio between the peak of the Moffat fit (corresponding to I0 in Eq. (4)) of the observed FLUX frames and that from the theoretical PSF. An example of an observed PSF leading to SR =0.78 and its corresponding Moffat fit is shown in Fig. 10.
In addition, we measured the FWHM to the FLUX frames (as explained in Sect. 4.1), and we compared them with the measured SR. The results are presented in Fig. 11. We finally obtained a correlation between the SR and FWHM by fitting a function of the form:
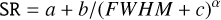 (6)
(6)
The resulting coefficients are listed in Table 3. The RMS of the post-fit residuals is 0.023. The best-fit is also over plotted in Fig. 11. Using this correlation, we then converted the FWHM values into SR values. We note that this conversion is more accurate for faint stars, which leads to relatively low SR values. On the other hand, for brighter targets that lead to a SR ≳ 0.5, this conversion is less suited, since in this regime the FWHM varies very slowly, asymptotically approaching the full diffraction limit value of ~ 43 mas. We therefore replicated Figs. 4 and 8, but this time we replaced the FWHM by the SR. The results are presented in Figs. 12 and 13. As expected, we observed a similar result to that seen in the raw contrast and FWHM, that is, a plateau for stars brighter than G ~ 12.5 mag, and a sharp decrease in the SR beyond this value. By comparing our findings with the expected AO performance for SPHERE and commissioning data (see Fig. 13 in Fusco et al. 2016 and Fig. 7 in Beuzit et al. 2019), we found that, although the overall trend in the SR with the stellar magnitude is also predicted, we see two main differences. Firstly, we found a nearly constant SR between G ~ 11 and G ~ 12.5 mag, and then a sharp decrease, at the 35% per magnitude level, beyond this value. In contrast, they found a nearly constant decrease in SR between R ~ 11-16 mag, at the ~20% per magnitude level. Secondly, we measured an overall lower SR in the full range of stellar flux. However, this is partly explained by the different methods used to compute this quantity (see Roberts et al. 2004). In addition, we note that they used the R-band instead of the G-band, which might introduce some small systematic differences, although it cannot solely explain this trend. Moreover, other parameters such as the WFS gain, the frequency or spatial filter used, as well as the atmospheric conditions during the commissioning (which are not discussed in their paper), might be partially responsible for these differences.
5 Final contrast
To investigate the achievable final contrast as a function of the stellar magnitude, we compared the raw contrast with the contrast measured on post-processing data. We included in this analysis 19 different stars, leading to RC300 values covering roughly two orders of magnitude (between ~2 × 10−2 and 2 × 10−4). For this we retrieved the post-processing contrast curves (corrected for the throughput of the algorithm) produced by the SPHERE Data Center (Delorme et al. 2017), for the classical Angular Differential Imaging (cADI; Marois et al. 2006) and the Template Local Optimized Combination of Images (TLOCI; Marois et al. 2010; Galicher et al. 2018) techniques. We note that we only included relatively long observing sequences, leading to a total field of view (FoV) rotation >15deg, to avoid strong self-subtraction, and thus avoid a low throughput of the reduction algorithm. These results are presented in Fig. 14. The black dots and blue stars correspond to cADI and TLOCI reduction techniques. The dashed black and blue lines correspond to the median conversion factors, which were 2.7 and 12.4 for the cADI and TLOCI techniques, respectively. We could then use this result to estimate the final contrast on post-processing data by scaling RC300 using these two values (to convert Figs. 3 and 7 into final contrast). Finally, we repeated this conversion, but this time from RC388 to final contrast at 500 mas. The results are presented in Fig. 15. Similarly, we obtained median conversion factors of 11.0 and 43.5 for the cADI and TLOCI techniques, respectively.
 |
Fig. 10 Observed PSF of a star leading to a Strehl ratio of 0.78 (left) and its corresponding Moffat fit (right). |
 |
Fig. 11 Strehl ratio versus the FWHM measured from FLUX frame. The solid line corresponds to the fit following Eq. (6). |
 |
Fig. 12 Strehl ratio as a function of the visible WFS flux, using the SR-FWHM correlation. The black and red lines correspond to the atmospheric turbulence categories TCAT10 and TCAT38, respectively. |
 |
Fig. 13 Strehl ratio as a function of the stellar G-band magnitude, using the SR-FWHM correlation. The solid black and red dots (lines) correspond to the atmospheric turbulence categories TCAT10 and TCAT38, respectively. |
 |
Fig. 14 Comparison between the contrast measured at 300 mas from individual raw frames and the post-reduction full observing sequence. The black dots and blue stars correspond to cADI and TLOCI reduction techniques, respectively. |
6 Summary and discussion
In this paper, we have analyzed a sample of 111 relatively faint stars (G ≥ 11.0 mag) observed with IRDIS/SPHERE between 2016 and 2022, with the aim of investigating how the AO correction (and thus the final performance in terms of achievable contrast) degrades when approaching the limiting magnitude regime. For this, we measured the H-band RC300 from coronagraphic frames and we compared this quantity to the instant flux received by the visible WFS. We found that the RC300 is at the ~10−3 level for fWFS >3 [e−1/subaperture/frame]. For fWFS below this value, the AO correction strongly degrades, decreasing the RC300 by a factor of roughly ten when reaching the 1 [e−1/subaperture/frame] level. In terms of stellar magnitude, this turning point is observed at G ~ 12.5 mag. At G ~ 14 mag, the measured RC300 is at the 10−2 level. We observed this behavior in the data taken under both TCAT10 and TCAT30 atmospheric conditions, with the former performing slightly better.
Similarly, we computed the FWHM and SR from the FLUX frames. We observed a very similar trend above and below the ~3 [e−1/subaperture/frame] limit. In particular, we measured an increase of a factor of roughly two and three in the FWHM from this limit and the ~1 [e−1/subaperture/frame] fWFS level, for TCAT10 and TCAT30, respectively. Similarly, the SR drops from above 0.5 to less than 0.2, for both TCAT10 and TCAT30.
Finally, we computed the final contrast at 300 mas and 500 mas, in a selected sample of stars, using the post-reduction contrast curves. We obtained median conversion factors of roughly three and 12, at 300 mas, for the cADI and TLOCI techniques, respectively. Similarly, we found scaling factors of ~11 and 44, to 500 mas, for cADI and TLOCI, respectively. Using these conversion factors, we can then estimate the final contrast achievable at 300 mas and 500 mas, by scaling the results presented in this work.
As an example, we can consider a star with the exact same luminosity and colors of the well-known planet host star PDS70 (Keppler et al. 2018). We can also consider that such a star is located at ~213 pc from the Earth, so that it has: G = 13.0mag and H = 11.2 mag. Following Fig. 7, we can expect a RC300 of ~4 × 10-3 under good atmospheric conditions (TCAT30 or better). If we perform a relatively long (FoV rotation ≳ 15 deg) ADI sequence, we can then estimate a 5σ final contrast at 500 mas using the TLOCI technique of ~10−4. If we compare these numbers with the AMES-COND models (Allard et al. 2001), this limit corresponds to a 10-Myr planet with a ~4.8 MJ mass, located at a physical separation of ~107 AU from the host star.
Improving the contrast on faint targets and reaching fainter or redder stars represent one of the primary scientific drivers for the instrument upgrade called SPHERE+ (Boccaletti et al. 2022). Indeed, ALMA surveys such as DSHARP (Andrews et al. 2018) revealed dozens of star-forming disks with structures such as gaps, rings, or spirals, suggesting planet formation is on-going. PDS70 represents one of the brightest examples of this population, the bulk of which is currently out of reach for SPHERE (see Fig. 12 of Boccaletti et al. 2020). Coupling the current AO correction stage to a more sensitive second-stage AO in cascade represents the main technical improvement of SPHERE+ (Cerpa-Urra et al. 2022), and the characterization of the current performance on faint targets presented here is crucial in order to make informed technical choices in the design of the second stage AO for SPHERE+.
Acknowledgements.
This work has made use of the SPHERE Data Centre, jointly operated by OSUG/IPAG (Grenoble), PYTHEAS/LAM/CESAM (Marseille), OCA/Lagrange (Nice), Observatoire de Paris/LESIA (Paris), and Observatoire de Lyon. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the GaiaMultilateral Agreement.
Appendix A Targets' apparent magnitudes
Gaia EDR3 and 2MASS JHK stellar magnitudes, listed in ascending order.
References
- Allard, F., Hauschildt, P. H., Alexander, D. R., Tamanai, A., & Schweitzer, A. 2001, ApJ, 556, 357 [Google Scholar]
- Andrews, S. M., Huang, J., Pérez, L. M., et al. 2018, ApJ, 869, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Bessell, M. S. 1990, PASP, 102, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Beuzit, J. L., Vigan, A., Mouillet, D., et al. 2019, A&A, 631, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boccaletti, A., Chauvin, G., Mouillet, D., et al. 2020, ESO, submitted [arXiv: 2003.05714] [Google Scholar]
- Boccaletti, A., Chauvin, G., Wildi, F., et al. 2022, ArXiv e-prints [arXiv:2209.02092] [Google Scholar]
- Bohn, A. J., Kenworthy, M. A., Ginski, C., et al. 2020, ApJ, 898, L16 [Google Scholar]
- Bohn, A. J., Ginski, C., Kenworthy, M. A., et al. 2021, A&A, 648, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cerpa-Urra, N., Kasper, M., Kulcsár, C., Raynaud, H.-F., & Taïssir Heritier, C. 2022, J. Astron. Telescopes Instrum. Syst., 8, 019001 [NASA ADS] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, 2MASS All Sky Catalog of point sources. [Google Scholar]
- Delorme, P., Meunier, N., Albert, D., et al. 2017, in SF2A-2017: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, eds. C. Reylé, P. Di Matteo, F. Herpin, E. Lagadec, A. Lançon, Z. Meliani, & F. Royer, Di [Google Scholar]
- Desidera, S., Chauvin, G., Bonavita, M., et al. 2021, A&A, 651, A70 [EDP Sciences] [Google Scholar]
- Dohlen, K., Langlois, M., Saisse, M., et al. 2008, SPIE Conf. Ser., 7014, 70143L [Google Scholar]
- Fedrigo, E., Donaldson, R., Soenke, C., et al. 2006, SPIE Conf. Ser., 6272, 627210 [Google Scholar]
- Fusco, T., Petit, C., Rousset, G., et al. 2006, SPIE Conf. Ser., 6272, 62720K [NASA ADS] [Google Scholar]
- Fusco, T., Sauvage, J. F., Mouillet, D., et al. 2016, SPIE Conf. Ser., 9909, 99090U [NASA ADS] [Google Scholar]
- Galicher, R., Boccaletti, A., Mesa, D., et al. 2018, A&A, 615, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janson, M., Squicciarini, V., Delorme, P., et al. 2021, A&A, 646, A164 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keppler, M., Benisty, M., Müller, A., et al. 2018, A&A, 617, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagrange, A. M., Keppler, M., Meunier, N., et al. 2018, A&A, 612, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marois, C., Lafrenière, D., Doyon, R., Macintosh, B., & Nadeau, D. 2006, ApJ, 641, 556 [Google Scholar]
- Marois, C., Macintosh, B., & Véran, J.-P. 2010, SPIE Conf. Ser., 7736, 77361J [Google Scholar]
- Milli, J., Kasper, M., Bourget, P., et al. 2018, SPIE Conf. Ser., 10703, 107032A [Google Scholar]
- Milli, J., Hibon, P., Christiaens, V., et al. 2017a, A&A, 597, A2 [Google Scholar]
- Milli, J., Mouillet, D., Fusco, T., et al. 2017b, Adaptive Optics for Extremely Large Telescopes 5, Conference Proceeding, Tenerife, Canary Islands, Spain https://doi.org/10.26698/AO4ELT5.0034 [Google Scholar]
- Moffat, A. F. J. 1969, A&A, 3, 455 [NASA ADS] [Google Scholar]
- Müller, A., Keppler, M., Henning, T., et al. 2018, A&A, 617, A2 [Google Scholar]
- Patat, F., Moehler, S., O’Brien, K., et al. 2011, A&A, 527, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riello, M., De Angeli, F., Evans, D. W., et al. 2021, A&A, 649, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roberts, Lewis C. J., Perrin, M. D., Marchis, F., et al. 2004, SPIE Conf. Ser., 5490, 504 [NASA ADS] [Google Scholar]
- Sauvage, J.-F., Fusco, T., Lamb, M., et al. 2016a, SPIE Conf. Ser., 9909, 990916 [Google Scholar]
- Sauvage, J.-F., Fusco, T., Petit, C., et al. 2016b, J. Astron. Telescopes Instrum. Syst., 2, 025003 [Google Scholar]
- van Boekel, R., Henning, T., Menu, J., et al. 2017, ApJ, 837, 132 [Google Scholar]
- Zurlo, A., Vigan, A., Galicher, R., et al. 2016, A&A, 587, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Header keywords used to filter the data for the flux and coronagraphic observations.
All Figures
 |
Fig. 1 Gala EDR3 color-magnitude diagram of all 111 stars included in the analysis. The typical uncertainties are smaller than the symbol size. The position of the reddest star in the sample (AX Cha) is also labeled. The corresponding histogram of the G-band magnitude distribution is overplotted on the right side. |
| In the text | |
 |
Fig. 2 Same as for Fig. 1, but for the J and H bands. |
| In the text | |
 |
Fig. 3 H-band 5σ raw contrast at 300 mas as a function of the visible WFS flux. The black and red lines correspond to atmospheric turbulence categories TCAT10 and TCAT38, respectively. |
| In the text | |
 |
Fig. 4 Mean FWHM as a function of the visible WFS flux. The black and red lines correspond to the atmospheric turbulence categories TCAT10 and TCAT38, respectively. |
| In the text | |
 |
Fig. 5 Normalized transmission curves for the Gaia EDR3 G (solid black line), GB (dotted blue line), GR (dotted red line) and Johnson R (solid green line) broad-band filters. The total transmission curve (including upstream optics) of the WFS is overplotted (solid black dots). |
| In the text | |
 |
Fig. 6 Stellar G-band magnitude versus the logarithm of the WFS flux. The solid line corresponds to the best linear fit between these two quantities. The position of AX cha is also shown (red dot). The corresponding fWFS values expressed in linear scale and units of [e−1 /subaperture/frame] are labeled in the upper x-axis. |
| In the text | |
 |
Fig. 7 H-band 5σ raw contrast at 300 mas as a function of the stellar G-band magnitude. The black and red lines correspond to the atmospheric turbulence categories TCAT10 and TCAT38, respectively. |
| In the text | |
 |
Fig. 8 Mean FWHM as a function of the stellar G-band magnitude. The solid black and red dots (lines) correspond to the atmospheric turbulence categories TCAT10 and TCAT38, respectively. |
| In the text | |
 |
Fig. 9 Normalized diffraction-limited theoretical PSF of the VLT pupil at 1.63 μm, as seen by IRDIS/SPHERE. |
| In the text | |
 |
Fig. 10 Observed PSF of a star leading to a Strehl ratio of 0.78 (left) and its corresponding Moffat fit (right). |
| In the text | |
 |
Fig. 11 Strehl ratio versus the FWHM measured from FLUX frame. The solid line corresponds to the fit following Eq. (6). |
| In the text | |
 |
Fig. 12 Strehl ratio as a function of the visible WFS flux, using the SR-FWHM correlation. The black and red lines correspond to the atmospheric turbulence categories TCAT10 and TCAT38, respectively. |
| In the text | |
 |
Fig. 13 Strehl ratio as a function of the stellar G-band magnitude, using the SR-FWHM correlation. The solid black and red dots (lines) correspond to the atmospheric turbulence categories TCAT10 and TCAT38, respectively. |
| In the text | |
 |
Fig. 14 Comparison between the contrast measured at 300 mas from individual raw frames and the post-reduction full observing sequence. The black dots and blue stars correspond to cADI and TLOCI reduction techniques, respectively. |
| In the text | |
 |
Fig. 15 Same as for Fig. 14, but for the final contrast at 500 mas. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$U = {\left[ {\left( {x - {x_0}} \right)/{A_x}} \right]^2} + {\left[ {\left( {y - {y_0}} \right){A_y}} \right]^2}.$](/articles/aa/full_html/2022/11/aa43820-22/aa43820-22-eq5.png)