| Issue |
A&A
Volume 680, December 2023
|
|
|---|---|---|
| Article Number | A34 | |
| Number of page(s) | 8 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/202346984 | |
| Published online | 05 December 2023 | |
Empirical contrast model for high-contrast imaging A VLT/SPHERE case study
1
European Southern Observatory,
Alonso de Córdova 3107, Vitacura, Casilla
19001,
Santiago, Chile
e-mail: bcourtne@eso.org
2
Research School of Astronomy and Astrophysics, Australian National University,
Canberra, ACT
2611, Australia
3
Institute of Astronomy and National Astronomical Observatory, Bulgarian Academy of Sciences,
72 Tsarigradsko Shose Blvd.,
Sofia
1784, Bulgaria
4
Université Grenoble Alpes, CNRS, IPAG,
38000
Grenoble, France
Received:
24
May
2023
Accepted:
26
September
2023
Context. The ability to accurately predict the contrast achieved with high-contrast imagers is important for efficient scheduling and quality control measures in modern observatories.
Aims. We aim to consistently predict and measure the raw contrast achieved by SPHERE/IRDIS on a frame-by-frame basis in order to improve the efficiency of SPHERE at the Very Large Telescope (VLT) and maximise scientific yield.
Methods. Contrast curves were calculated for over 5 yr of archival data obtained using the most common SPHERE/IRDIS corona-graphic mode in the H2/H3 dual-band filter. These data consist of approximately 80 000 individual frames, which were merged and interpolated with atmospheric data to create a large database of contrast curves with associated features. An empirical power-law model for contrast – motivated by physical considerations – was then trained and finally tested on an out-of-sample test dataset.
Results. At an angular separation of 300 mas, the contrast model achieved a mean (out-of-sample) test error of 0.13 magnitude with the 5th and 95th percentiles of the residuals equal to −0.23 and 0.64 magnitude respectively. The models test-set root mean square error (RMSE) between 250 and 600 mas was between 0.31 and 0.40 magnitude, which is equivalent to that of other state-of-the-art contrast models presented in the literature. In general, the model performed best for targets of between 5 and 9 G-band magnitude, with degraded performance for targets outside this range. This model is currently being incorporated into the Paranal SCUBA software for first-level quality control and real-time scheduling support.
Key words: methods: data analysis / methods: statistical / instrumentation: adaptive optics / atmospheric effects
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
High-contrast imagers have become central tools for the discovery and understanding of exoplanets and protoplanetary disk formation, demographics, and dynamics around young stars. Instruments such as the Spectro-Polarimetric High-contrast Exoplanet REsearcher (SPHERE) at the Very Large Telescope (VLT) (Beuzit et al. 2019; Fusco et al. 2015), The Gemini Planet Imager (GPI) at the Gemini observatory (Macintosh et al. 2014), and the Subaru Coronagraphic Extreme Adaptive Optics (SCExAO) at the Subaru telescope (Sahoo et al. 2018) can achieve typical raw contrasts in the range of 10−4 to 10−6 between 0.1″ and 0.5″ from the central star at near-infrared (NIR) wavelengths. The instruments foreseen for the epoch of extremely large telescopes will push these boundaries even further (e.g., Brandl et al. 2021). The outstanding capabilities of these current and future instruments attached to world-class telescopes are in great demand, making the optimisation of telescope time an important task. This optimization generally requires accurate models to predict observational performance indicators (e.g., contrast for high-contrast imagers) both prior and/or early on during the observation in order to select observations that optimally exploit the atmospheric conditions. Traditionally, short-term scheduling and quality control in queue observations for high-contrast imagers such as SPHERE are carried out primarily based on atmospheric, sidereal, and/or airmass constraints. While strong correlations exist between turbulence and adaptive optics (AO) performance, there are often outliers where the measured contrast is considerably lower than what would be expected from the observed atmospheric conditions. This is typically due to local effects within the telescope or instrument. Without the ability to properly predict and measure the contrast, such observations may be scheduled and pass basic quality-control checks despite not meeting the users scientific requirements. Therefore, to optimise telescope time and the ultimate data quality provided to users, high-contrast imagers may benefit greatly from precise models to predict scientifically meaningful metrics, such as contrast or signal-to-noise ratio (S/N), which can then be measured in almost real time in order to evaluate the quality of the data. The ultimate goal is to perform short-term scheduling and quality control based on predicted and measured metrics that are of scientific significance. This, combined with significant efforts to improve quality-control software and standards (Thomas et al. 2020), as well as forecasting models at Paranal (Milli et al. 2020, 2019; Masciadri et al. 2020; Osborn & Sarazin 2018), will greatly advance real-time decision making and quality control measures. The ability to accurately predict contrast for high-contrast imagers on large telescopes is not a trivial task. While fundamental atmospheric limits are well characterized (Conan et al. 1995; Fusco & Conan 2004; Aime & Soummer 2004; Males et al. 2021), typically nontrivial local effects can dominate achievable contrast; for example, quasi-static speckles caused by opto-mechanical imperfections and thermal drifts (Bloemhof et al. 2001; Soummer et al. 2007; Martinez et al. 2013; Vigan et al. 2022) or dome seeing (Tallis et al. 2020) and low wind effects (Milli et al. 2018; Sauvage et al. 2015). Given the maturity of instruments such as SPHERE, data-driven analysis and empirical models are a practical way to understand these limitations and the uncertainty that random telescope and instrumental processes have on observations. Some good examples of this are the work of Martinez et al. (2013), using SPHERE data to characterize speckle temporal stability in high-Strehl regimes; that of Milli et al. (2018), who characterized the low wind effect on SPHERE; and Jones et al. (2022), who presented a data-driven analysis of SPHERE performance for faint targets. In the case of predicting contrast, various models have been explored in the literature to empirically predict the on-sky observed contrast given atmospheric and instrumental conditions (Bailey et al. 2016; Courtney-Barrer et al. 2019; Xuan et al. 2018). In particular, initial work at the GPI used linear regression of AO telemetry and astronomical site monitoring data to predict contrast (Bailey et al. 2016), which was further advanced with neural networks that were able to predict the measured contrast using six input parameters available pre-observation with a contrast root mean square error (RMSE) of 0.45 magnitude at 0.25″ (Savransky et al. 2018). Correlations between measured contrast and AO error terms have also been shown in other work (e.g., Poyneer & Macintosh 2006; Poyneer et al. 2016), and in general have been shown to provide good predictive capacity of the contrast in atmospherically limited regimes (Fusco et al. 2016; Sauvage et al. 2016; Macintosh et al. 2014). In this work, we present a simple empirical model to predict the raw contrast measured by SPHERE with the goal to assist on-site quality control measures and short- to mid-term scheduling decisions. This paper begins with a brief overview of the SPHERE instrument followed by the motivation of an empirical model to which contrast data is fitted. Section 4 outlines the data preparation and pre-processing that was done before fitting the contrast model, along with the algorithms used for fitting. Section 5 presents the results along with some discussion. In Sect. 6, we present our conclusions and future outlook.
2 SPHERE/IRDIS
SPHERE is an extreme AO instrument installed on the Unit Telescope 3 (Melipal) at the Paranal Observatory. Its primary science goal is imaging and low-resolution spectroscopic and polarimetric characterization of extra-solar planetary systems at optical and NIR wavelengths. SPHERE consists of three science channels: the Integral Field Spectrograph (IFS) and the Infra-Red Dual-band Imager and Spectrograph (IRDIS), which both observe in the NIR, and the Zurich Imaging Polarimeter (ZIMPOL) for visible polarimetric observations. Each subinstrument has a series of coronagraphs and filters available in addition to having an extreme AO system called SAXO (Fusco et al. 2016; Sauvage et al. 2016) placed in the common path of all subinstrument channels. SAXO operates up to a frequency of 1.38 kHz on bright targets with a 40 × 40 spatially filtered Shack-Hartmann (SH) wavefront sensor (WFS) measuring in the optical, and a 41 × 41 piezoelectric high-order deformable mirror for AO actuation. SAXO also uses a dedicated differential tip/tilt sensor (Baudoz et al. 2010) in the NIR to correct for wavelength-dependent tip/tilt between the NIR and optical channels. In the present work, we tested our model on the most common SPHERE/IRDIS mode, which uses an apodised Lyot coronagraph with the H2/H3 dual-band filters centered at wavelengths 1.593 µm and 1.667 µm, respectively.
3 Contrast model
We begin by outlining our motivation to build an empirical model for contrast with some statistical considerations of the measured intensity in the focal plane. It can easily be shown using Fourier optics that a phase aberration at some spatial frequency k in a pupil plane of a telescope gets mapped to a so-called speckle in the focal plane at an angular coordinate of kλ, where λ is the wavelength of the light (Roddier 2004). Such speckles are typically classified based on their temporal behavior, which ultimately determines whether or not (or how well) they can be suppressed by post-processing reduction methods. This sets the fundamental contrast limits on ground-based high-contrast imagers (Males et al. 2021). The detection of real signals (such as a planet) within the circumstellar environment of a star requires statistical knowledge of the probability of some intensity measurement in the focal plane. Various authors (e.g., Canales & Cagigal (1999) and references therein) have shown – under the assumption of long exposures – that a point-wise intensity measurement (I) generally follows a modified Rician probability density function:
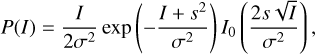 (1)
(1)
where I0 is the zero-order modified Bessel function of the first kind, and s2 and 2σ2 are related to the (long-exposure) intensity of the deterministic and random speckle components of the wavefront, respectively. Soummer et al. (2007) developed this statistical framework to derive a general expression for the expected point-wise variance in a coronagraphic image as:
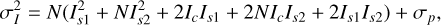 (2)
(2)
where we have kept the notation used in Soummer et al. (2007). Here, “I” generally denotes the intensity, ***(-eq3)*****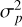 the variance of the photon noise, and N the ratio of fast-speckle to slow-speckle lifetimes. Ic is the intensity produced by the deterministic part of the wavefront, including static aberrations, while the Is terms correspond to the halo produced by random intensity variations; that is, atmospheric (Is1) and quasi-static contributions (Is2). In this generalized expression of the variance, several contributions can be identified by order of appearance: (1) the atmospheric halo; (2) the quasi-static halo; (3) the atmospheric pinning term, the speckle pinning of the static aberrations by the fast-evolving atmospheric speckles; (4) the speckle pinning of the static by quasi-static speckles; and finally (5) the speckle pinning of the atmospheric speckles by quasi-static speckles. Converting this to the expected contrast as a general function of radius (e.g., a typical contrast curve) requires calculation of the sum of the pixel-wise modified Rician density functions within a given annulus. No closed-form analytic solution to this exists, although there are closed-form approximations (Lopez-Salcedo 2009). Under a strong assumption of independence between pixels and, for a given spatial frequency, equal probability of the directions of aberrations (i.e. angular position of a speckle at a fixed radius), where θ is the angular position of a speckle at a given radius, we can estimate the expected intensity variance within a thin annulus at radius r by simply scaling by the number of pixels in the annulus, in which case we can make the proportional approximation of the 1 σ contrast:
the variance of the photon noise, and N the ratio of fast-speckle to slow-speckle lifetimes. Ic is the intensity produced by the deterministic part of the wavefront, including static aberrations, while the Is terms correspond to the halo produced by random intensity variations; that is, atmospheric (Is1) and quasi-static contributions (Is2). In this generalized expression of the variance, several contributions can be identified by order of appearance: (1) the atmospheric halo; (2) the quasi-static halo; (3) the atmospheric pinning term, the speckle pinning of the static aberrations by the fast-evolving atmospheric speckles; (4) the speckle pinning of the static by quasi-static speckles; and finally (5) the speckle pinning of the atmospheric speckles by quasi-static speckles. Converting this to the expected contrast as a general function of radius (e.g., a typical contrast curve) requires calculation of the sum of the pixel-wise modified Rician density functions within a given annulus. No closed-form analytic solution to this exists, although there are closed-form approximations (Lopez-Salcedo 2009). Under a strong assumption of independence between pixels and, for a given spatial frequency, equal probability of the directions of aberrations (i.e. angular position of a speckle at a fixed radius), where θ is the angular position of a speckle at a given radius, we can estimate the expected intensity variance within a thin annulus at radius r by simply scaling by the number of pixels in the annulus, in which case we can make the proportional approximation of the 1 σ contrast:
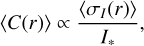 (3)
(3)
where I* is the stellar intensity in the science channel and 〈..〉 is the expected value. As mentioned, this is a strong assumption that does not generally hold. For example, experience shows that there is typically anisotropy in the aberrations at a given spatial frequency, especially from biased wind directions of dominant turbulent layers. Nevertheless, this basic assumption is useful for deriving first-order contrast estimates. Analytically predicting each term in Eq. (2) prior to observation would require full knowledge of internal aberrations and wind velocity profiles, as well as the ability to reconstruct the modal distribution of the incoming phase front in order to predict AO residuals, which would difficult to achieve. Nevertheless, noting that any first-order expansion of the coronagraph PSF term (Ic) and atmospheric speckle terms (Is1) with regard to the typical AO error budget terms would lead to various cross products of the AO error-budget terms in the pinned speckles; we could make the assumption that typically one of these terms will dominate the halo at a given radius and therefore propose to model the contrast as a product of AO cross terms, each with a power law to give an appropriate weighting at a given radius, that is,
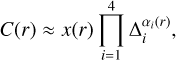 (4)
(4)
where x(r) and αi(r) are the fitted parameters for a given radius. From a basic leave-one-out analysis, the ∆ terms considered for the following model are a combination of typical (unitless) AO error-budget-like terms:
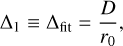 (5)
(5)
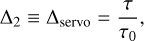 (6)
(6)
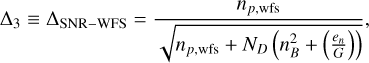 (7)
(7)
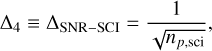 (8)
(8)
where D is the telescope diameter, r0 is the atmospheric coherence length (Fried parameter), τ and τ0 are the AO latency and atmospheric coherence time, respectively, np is the number of detected photoelectrons per defined subaperture (sum of all pixels); ND is the number of pixels in a subaperture, nB is the number of detected background photoelectrons per subaperture; en is the read noise in electrons per pixel, and G is the gain (Robert K. Tyson 2012). The values np, are generally inferred through fitted zero points and extinction coefficients to convert stellar magnitude (mag) to flux (see Sect. 4.1). The residuals of such a model would therefore be due to the variance in non-AO related terms in Eq. (2). We also note that in a shot-noise-limited regime, the product of
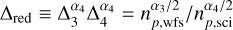
can be seen as the reddening parameter. In the case of equal flux, that is, np,wfs = np,sci = np, we get ***(-eq11)*****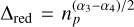 and therefore one would expect α4 > α3 to maintain the situation where brighter targets generally achieve better contrast. However, in general np,wfs ≠ np,sci and chromatic effects of red stars may play an important role (especially with the performance of the differential tip/tilt controller). This general model confers a considerable advantage in that it can capture nonlinearities in the contrast performance and furthermore can be fitted linearly by simply considering the contrast magnitude: Cm = −5/2log10(C), such that
and therefore one would expect α4 > α3 to maintain the situation where brighter targets generally achieve better contrast. However, in general np,wfs ≠ np,sci and chromatic effects of red stars may play an important role (especially with the performance of the differential tip/tilt controller). This general model confers a considerable advantage in that it can capture nonlinearities in the contrast performance and furthermore can be fitted linearly by simply considering the contrast magnitude: Cm = −5/2log10(C), such that
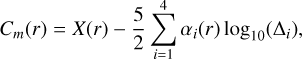 (9)
(9)
where X(r) = −5/2log10(x(r)) is the fitted intercept. On the training dataset, we also allowed for a linear calibration of the fitted intercept Xf (r) with the model residuals given the partitioned instrumental state such that X(r) = Xf (r) – ∆c(r|state), where ∆c(r|store) is the training model residual when filtering for a given observational state. The state filters considered were the sky transparency classification (e.g., thick, thin, clear, photometric), the AO gain and frequency setting, and the wavefront sensor spatial filter size (e.g., small, medium, large). This significantly improved the cross-validation performance of the model on the training dataset, while maintaining a significant sample size for the general fitting of α parameters. These calibrated offsets were then used for the out-of-sample model test (without recalibration).
Header keywords used to filter the data for the coronagraphic observations.
4 Data preparation
We developed a database of all public observations taken between 2015 and 2019, which were downloaded from the ESO SPHERE archive. In this particular study, we focused on fitting the model described above for the most commonly observed SPHERE/IRDIS mode. This mode uses an apodised Lyot coronagraph with the H2 (λc = 1.593 µm) filter, which corresponds to the left detector in the H2/H3 dual band mode. The general FITS headers used to filter these data are displayed in Table 1. After filtering and outlier rejection (described below), train (75%) and test (25%) datasets were split to have nonoverlapping observation nights; meaning for any given sample in the train set, there did not exist a sample in the test set that was observed on the same night (and vice versa). This corresponded to 149 and 47 unique stars in the train and test sets, respectively, with only 4 stars shared between the two sets, totalling nearly 80k raw coronagraphic frames to analyze. A 75%:25% split provided a sufficient parameter space density to perform ten-fold cross validation on the training set, while allowing sufficient samples to avoid biases in the out-of-sample test. One-sigma noise levels were estimated as a function of radius in coronagraphic data cubes (DPR TYPE = OBJECT) after some basic reduction (e.g., background subtraction, flat fielding, bad pixel masking, and high-pass filtering). The standard deviation was calculated in an annulus with 4 pixels (~λ/D) from 82 to 1800 mas, where radii that had pixels in the nonlinear regime of the IRDIS detector (ADU > 20k) were masked. Additionally, each coronagraphic (OBJECT) frame was cross correlated with a median corona-graphic image across the filtered dataset to provide an additional criterion for outlier removal. From visual inspection of individual frames, anything with a cross correlation below 0.5 seemed to correspond to frames that had obvious issues, such as bright companions in the field or where AO loops temporarily opened during an exposure. Therefore, frames that had a cross correlation with the median image of less than 0.5 were dropped from the analysis. In short exposures, there were noticeable pinned speckles that were initially difficult to predict from atmospheric conditions. This was significantly improved by co-adding coronagraph frames that had exposure times of ≤64 s to roughly 64 s. An example of this is shown in Fig. 1. A 2D Gaussian function was then fitted to the corresponding noncoronagraphic flux frames (DPR TYPE = OBJECT,FLUX) of the observation to estimate the peak flux. The contrast curve was then calculated by dividing the 1σ noise levels at a given radius by the estimated peak flux when adjusting for the different integration times and neutral density filters. To correct for changing transparency between the noncoronagraphic (flux) and coronagraphic (object) frames, the measured contrast was multiplied by the ratio of the aggregated wavefront sensor (SPARTA telemetry) flux data between the two periods. While no specific sky classifications (e.g., thin or thick clouds) were excluded from the data, we neglected data where there was significant (>50%) variability in the wavefront sensor flux during an exposure, because this caused significant variability in the measured contrast that was unpredictable from a pre-observation perspective.
The initial contrast curve database consisted of 27 135 co-added contrast frames. Each contrast curve was associated with various features, including the FITS headers from the initial files and the full available range of atmospheric parameters available from ESO MASS-DIMM and meteorological archives, which were interpolated to the mean coronagraphic frame time-stamp. This included important parameters such as atmospheric seeing and coherence time. Atmospheric data prior to the last MASS-DIMM upgrade (April 2016) were neglected due to instrumental biases between the old and new systems. Data were then further filtered to exclude observations that were outside of standard operational conditions and/or where feature outliers were detected. Basic filters included the following:
All SPARTA AO loops were closed.
SPARTA differential tip/tilt loop is closed.
Telescope was guiding on a guidestar.
Atmospheric seeing and coherence time measurements were in the ranges of 0–5″ and 0–30 ms, respectively.
Raw coronagraphic image cross-correlation with median image > 0.5.
No low wind effected data (typically V < 3m s−1 in data before Nov.-2017).
Wavefront sensor flux variability did not exceed more than 50% between frames.
Data taken prior to the M2 spider re-coating carried out in November 2017 show significantly different contrast statistics for wind speeds below 3 m s−1 due to the low wind effect, which was largely resolved by the re-coating intervention (Milli et al. 2018; Sauvage et al. 2015). Figure 2 shows the measured raw contrast at 0.3″ before and after the M2 spider re-coat for low (left plot) and nominal (right plot) wind speeds. It is clear that there was a large statistical improvement in the measured contrast from the intervention in the low wind case, while there was a statistically insignificant difference when observing in wind speeds of >3 m s−1 after the re-coating. We note that data taken with fast AO modes (1200 Hz, 1380 Hz) were neglected in these histograms to avoid biases, because the 1380 Hz AO mode was an upgrade that was not used in earlier data, particularly before the M2 spider re-coat. This prompted us to only neglect data taken before November 2017 with wind speeds of <3 m s−1. After this filtering process, 8494 co-added frames remained with which to train and test the model.
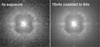 |
Fig. 1 Example of co-adding short exposure frames to 64 s. |
 |
Fig. 2 Normalized histogram of raw contrast at 0.3″ in [left] low wind conditions (<3m s−1) and [right] nominal (>3 m s−1) wind conditions before (red) and after (green) the M2 spider re-coat that was completed in November 2017. |
4.1 Flux model
Calibrated instrumental zero points and extinction coefficients were required to estimate the photocurrent (ADUs−1) received in both the wavefront sensor and science detector for a given SIMBAD magnitude and airmass prior to observation. Data were first filtered to consider SPHERE flux sequences and WFS data taken during periods classified as photometric using either the LP780 or OPEN spectral filter without restrictions on the WFS spatial filter size. From these filtered data, the following model was fitted:
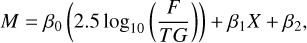 (10)
(10)
where M is the Simbad magnitude of the target star, F is the flux (ADUs−1) measured in either the WFS (G band) – which is summed over all subapertures – or the flux template from the science detector (H band), T is a scalar to represent the relative transmission of the spectral filter, G the detector gain, X is the targets airmass, and β0,β1, and β2 are the fitted parameters corresponding to the telescope-instrument transfer function, extinction coefficient, and zero point, respectively. Fitted parameters from data taken in photometric conditions are outlined in Table 2 and are consistent with previously measured extinction coefficients at Paranal (Patat et al. 2011).
To account for sky transparency in the contrast model, sky category offsets were calibrated on the train dataset via the contrast residuals of the respective sky-category-partitioned data as described in Sect. 3. Additionally, Fig. 3 displays the results when the data were partitioned into sky-transparency categories as classified by the weather officer and the above fitted photometric model was applied to each respective sky category. Figure 4 shows that the mean absolute error between the measured and predicted WFS flux given the target magnitude scales monotonically with the weather officer classification of the sky transparency. These results suggest that the models could be used for automatic sky-transparency classification. This would be advantageous over the standard method of the weather officer going outside every 30 min to visually classify the whole sky, because the WFS measurements would be in real time directly within the SPHERE field of view.
Parameters for the WFS (G band) and science flux frame (H band) magnitude fitted to the flux model in photometric conditions.
 |
Fig. 3 G and H band photometric models applied to different sky transparency categories defined as photometric (PH), clear (CL), thin (TN), and thick (TH). |
 |
Fig. 4 Mean absolute error in the WFS flux model vs. weather officer sky classification. |
 |
Fig. 5 Train and test contrast curve residual heatmaps (2D histograms) with sample ID histograms shown at a radius of 300 mas. |
 |
Fig. 6 Test set results. [Left] measured vs. predicted raw 5σ contrasts plotted in magnitudes. [Right] RMSE for the raw 5σ contrast magnitude vs. radius. |
4.2 Model fitting
The empirical contrast model presented in Sect. 3 was fitted with the Python scikit-learn package (Pedregosa et al. 2011) using Bayesian regression. This model was tuned and ultimately fitted to the training dataset (75% of the data) using 10-fold cross validation. The best-fit parameters are reported as the mean of the ten-fold fit on the training set for the given radius, and respective uncertainties are ±2 standard deviations. After tuning via cross validation on the training dataset, the model was evaluated on the test dataset (25% of the data). The results are presented in the following sections.
5 Results and discussion
Figure 5 shows the residuals of the contrast model as a function of separation from the central star for the training and testing datasets, which shows good generalization to the out-of-sample test. It can also be seen that mean model residuals were well centered near zero, with a mean error of 0.13 mag, and the 5th and 95th percentiles in the residuals were –0.23 and 0.64 magnitude respectively on the test set at 300 mas. Figure 6 shows the general measured versus predicted raw 5σ contrast on the out-of-sample test set across all radii, along with the respective model RMSE at a given radial separation from the central star. Between 0.25″ and 1.00″, the model achieves a RMSE of between 0.17 and 0.40 magnitude on the out-of-sample test set.
We also analyze the model performance over an aggregated grid of atmospheric and star brightness categories in Fig. 7. The atmospheric categories considered are those currently used (ESO period p106) as user constraints for grading observations. The categories are defined from cuts in the atmospheric seeing– coherence time joint probability distribution, with T.Cat10 corresponding to the best (top 10%) atmospheric conditions, and T.Cat85 to the worst. We also simply consider three star magnitude categories of bright (Gmag < 5), mid (5 < Gmag < 9), and faint (Gmag > 9) targets. There is excellent agreement (<0.15 mag residual at 0.5″) in the mid category range across all atmospheric conditions; however, there is poorer performance for the bright and faint categories, particularly when in better atmospheric conditions. This would indicate that the underlying assumption that pinned atmospheric residuals dominate contrast is most valid in the mid category, while the worst performance is seen for bright and faint target where, for example, static or quasi-static pinning may become dominant. The fitted parameters are shown in Fig. 8. We find that fitted power indices deviate considerably from the five-thirds power laws typically encountered in AO error budgets for phase residuals arising from limited spatial or temporal bandwidths. Between 250 and 500 mas, these typically range between 10% and 30% of the five-thirds value for fitting errors and servo-lag-related terms. The fitted parameter typically approach zero (minimum sensitivity) near a radius of 800 mas. This corresponds to the radius determined by the inter-actuator spacing of the deformable mirror. Interestingly, the fitting term has two zero-crossing points, becoming negative (albeit very near zero) between 750 and 1000 mas, which is around the scattering halo. This implies that contrast within this radius slightly degrades with lower seeing. Outside of this region, we see the expected behavior that contrast improves with lower seeing. However, it is clear that SPHERE contrast is much more sensitive to the atmospheric coherence time than to coherence length (seeing). For example, at 300 mas, doubling the atmospheric coherence time (keeping all other variables equal) leads to an expected ∼30% reduction (improvement) in contrast, while doubling the Fried parameter (halving the seeing) only leads to a ~6% reduction in contrast. Similar results were also found for the Gemini Planet Imager (Bailey et al. 2016). As expected, αSNR-WFS < αSNR-SCI for all radii, which, as discussed in Sect. 3, implies that contrast generally improves with brightness assuming equal partitioning of flux between WFS and science channels in a shot-noise-limited regime. Analyzing the reddening parameter, we see that contrast generally degrades as targets become redder. For example, around 300 mas, considering the train set median Gmag = 7, contrast degrades by roughly 20% per magnitude difference between WFS and Science channels.
To compare results to other contrast models found in the literature, we achieved a test contrast RMSE of between 0.31 and 0.40 magnitude between 250 and 600 mas, or equivalently a log10 contrast RMSE of 0.13–0.16, respectively. This is comparable to the results of Savransky et al. (2018), who, when using a feedforward neural network with pre-observation data as input, achieved a test log10 contrast RMSE of 0.18 at 250 mas. Such comparable results are encouraging given the relative simplicity and physical interpretability of the model presented in this work compared to more complex neural networks. Comparing the predictions of our model at 400 mas to the current SPHERE exposure time calculator (ETC) offered by ESO (as of May 2023) when considering raw image predictions (EXPTIME=64s) without differential imaging (neglecting field rotation), we see in Fig. 9 that the ETC appears to provide very optimistic predictions for bright targets, and pessimistic predictions for faint targets relative to those of the model presented here across all turbulence categories. Our model also predicts that the contrast is less sensitive to changes in H-band flux compared to the ETC, which seems to also be reflected in the data at hand. The inclusion of these data in the ETC in short exposure time limits could be used to ultimately improve the predictive accuracy of an ETC for SPHERE users. The contrast model presented here is currently being incorporated into Paranal’s SCUBA software (Thomas et al. 2020) to be used as first-level quality control and to help improve the real-time decision process for SPHERE at Paranal. Figure 10 shows a real example of how this model could be used in operations for providing quick checks to ensure the measured raw contrast (~60 s frame) is within the expected 95% test residual range of the model given the target and current atmospheric conditions. Statistics on the frame-by-frame contrast could then be used to grade the OB based on potential user constraints. Abnormal aberrations caused from instrumental effects that impact the contrast can also easily be detected and evaluated by users and/or operators in the context of expected performance. Based on the out-of-sample test results; at 0.3″ the operator should be able to predict the contrast to less than 0.5 magnitude at a 2 sigma level.
 |
Fig. 7 Predicted vs. measured test data contrast, binned by star magnitude (faint, mid, bright), along with the atmospheric categories currently used for ranking and grading SPHERE observations in Paranal. |
 |
Fig. 8 The fitted contrast model parameters. Top: The mean fitted alpha power indices ±2σ as a function of separation. Bottom: The fitted intercept X(r) (in log space) as a function of separation. |
 |
Fig. 9 Comparison between the 400 mas contrast predictions made by the model of this work vs. the current (as of the publication of this paper) ETC on the ESO website. The ETC options were set to match the observed mode of the model developed here: DBH23 filter with coronagraph. Both the ETC and model were set with no neutral densities, exptime ~64 s, DIT ≤ 64 s, without differential imaging and considered a spectral type of around GV2. |
 |
Fig. 10 Example of how the contrast model could be used in operations for providing quick checks to ensure the measured raw contrast (~60 s frame) is within the expected 95% range of model residuals given the target and current atmospheric conditions. |
6 Conclusions
A simple model was trained and tested on SPHERE/IRDIS coronagraphic data to predict contrast as a function of radius in the most commonly used H-band filter. When testing on out-of-sample test data, the model achieved a mean error of 0.13 magnitude with the 5th and 95th percentiles in the residuals equal to −0.23 and 0.64 magnitude respectively when considering a separation of 300 mas. The test set RMSE between 250 and 600 mas was between 0.31 and 0.40 magnitude, which is similar to that of other state-of-the-art contrast models presented in the literature. This model is currently being incorporated into the Paranal SCUBA software for first-level quality control and realtime scheduling support. Future work will consider fitting this model to other SPHERE instrumental modes.
Acknowledgements
This work has made use of the SPHERE Data Centre, jointly operated by OSUG/IPAG (Grenoble), PYTHEAS/LAM/CESAM (Marseille), OCA/Lagrange (Nice), Observatoire de Paris/LESIA (Paris), and Observatoire de Lyon.
References
- Aime, C., & Soummer, R. 2004, ApJ, 612, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Bailey, V. P., Poyneer, L. A., Macintosh, B. A., et al. 2016, SPIE Conf. Ser., 9909, 99090V [NASA ADS] [Google Scholar]
- Baudoz, P., Dorn, R. J., Lizon, J.-L., et al. 2010, SPIE Conf. Ser., 7735, 77355B [Google Scholar]
- Beuzit, J. L., Vigan, A., Mouillet, D., et al. 2019, A & A, 631, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bloemhof, E. E., Dekany, R. G., Troy, M., & Oppenheimer, B. R. 2001, ApJ, 558, L71 [Google Scholar]
- Brandl, B., Bettonvil, F., van Boekel, R., et al. 2021, ESO Messenger, 182, 22 [NASA ADS] [Google Scholar]
- Canales, V. F., & Cagigal, M. P. 1999, Appl. Opt., 38, 766 [NASA ADS] [CrossRef] [Google Scholar]
- Conan, J. M., Rousset, G., & Madec, P. Y. 1995, J. Opt. Soc. Am. A, 12, 1559 [NASA ADS] [CrossRef] [Google Scholar]
- Courtney-Barrer, B., Wahhaj, Z., Mouillet, D., & Milli, J. 2019, in AO4ELT6 Proceedings [Google Scholar]
- Fusco, T., & Conan, J.-M. 2004, J. Opt. Soc. Am. A, 21, 1277 [NASA ADS] [CrossRef] [Google Scholar]
- Fusco, T., Sauvage, J.-F., Mouilelt, D., et al. 2015, in Adaptive Optics for Extremely Large Telescopes IV (AO4ELT4), E11 [Google Scholar]
- Fusco, T., Sauvage, J.-F., Mouillet, D. et al. 2016, in Proc. SPIE, 9909, Adaptive Optics Systems V Series [Google Scholar]
- Jones, M. I., Milli, J., Blanchard, I., et al. 2022, A & A, 667, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lopez-Salcedo, J. A. 2009, IEEE Signal Process. Lett., 16, 153 [CrossRef] [Google Scholar]
- Macintosh, B. A., Patience, J. Graham, J. R., & Gpies Team. 2014, in Search for Life Beyond the Solar System. Exoplanets, Biosignatures, & Instruments, eds. D. Apai, & P. Gabor, 4.3 [Google Scholar]
- Males, J. R., Fitzgerald, M. P., Belikov, R., & Guyon, O. 2021, PASP, 133, 104504 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez, P., Kasper, M., Costille, A., et al. 2013, A & A, 554, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masciadri, E., Martelloni, G., & Turchi, A. 2020, MNRAS, 492, 140 [CrossRef] [Google Scholar]
- Milli, J., Kasper, M., Bourget P., et al. 2018, in Proc. SPIE, 10703, Adaptive Optics Systems VI, 107032A [Google Scholar]
- Milli, J., Gonzalez, R., Fluxa, P. R., et al. 2019, ArXiv e-prints [arXiv:1918.13767] [Google Scholar]
- Milli, J., Rojas, T., Courtney-Barrer, B., et al. 2020, SPIE Conf. Ser., 11448, 114481J [NASA ADS] [Google Scholar]
- Osborn, J., & Sarazin, M. 2018, MNRAS, 480, 1278 [NASA ADS] [CrossRef] [Google Scholar]
- Patat, F., Moehler, S., O’Brien, K., et al. 2011, A & A, 527, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
- Poyneer, L. A., & Macintosh, B. A. 2006, Opt. Exp., 14, 7499 [NASA ADS] [CrossRef] [Google Scholar]
- Poyneer, L. A., Palmer, D. W., Macintosh, B., et al. 2016, Appl. Opt., 55, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Robert K. Tyson, B. W. F. 2012, Field Guide to Adaptive Optics, 2nd ed. (SPIE) [CrossRef] [Google Scholar]
- Roddier, F. 2004, Adaptive Optics in Astronomy (Cambridge, UK: Cambridge) [Google Scholar]
- Sahoo, A., Guyon, O., Clergeon, C. S., et al. 2018, SPIE Conf. Ser., 10703, 1070350 [Google Scholar]
- Sauvage, J., Fusco, T., Guesalaga, A., et al. 2015, in Adaptive Optics for Extremely Large Telescopes 4 – Conference Proceedings [Google Scholar]
- Sauvage, J.-F., Fusco, T., Petit, C., et al. 2016, J. Astron. Telescopes Instrum. Syst., 2, 025003 [Google Scholar]
- Savransky, D., Shapiro, J., Bailey, V., et al. 2018, SPIE Conf. Ser., 10703, 107030H [NASA ADS] [Google Scholar]
- Soummer, R., Ferrari, A., Aime, C., & Jolissaint, L. 2007, ApJ, 669, 642 [Google Scholar]
- Tallis, M., Bailey, V. P., Macintosh, B., et al. 2020, J. Astron. Telescopes Instrum. Syst., 6, 015002 [NASA ADS] [Google Scholar]
- Thomas, R., Berg, T. A. M., Mehner, A., de Wit, W.-J., & Brillant, S. 2020, SPIE Conf. Ser., 11449, 114490C [NASA ADS] [Google Scholar]
- Vigan, A., Dohlen, K., N’Diaye, M., et al. 2022, A & A, 660, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xuan, W. J., Mawet, D., Ngo, H., et al. 2018, AJ, 156, 156 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Parameters for the WFS (G band) and science flux frame (H band) magnitude fitted to the flux model in photometric conditions.
All Figures
 |
Fig. 1 Example of co-adding short exposure frames to 64 s. |
| In the text | |
 |
Fig. 2 Normalized histogram of raw contrast at 0.3″ in [left] low wind conditions (<3m s−1) and [right] nominal (>3 m s−1) wind conditions before (red) and after (green) the M2 spider re-coat that was completed in November 2017. |
| In the text | |
 |
Fig. 3 G and H band photometric models applied to different sky transparency categories defined as photometric (PH), clear (CL), thin (TN), and thick (TH). |
| In the text | |
 |
Fig. 4 Mean absolute error in the WFS flux model vs. weather officer sky classification. |
| In the text | |
 |
Fig. 5 Train and test contrast curve residual heatmaps (2D histograms) with sample ID histograms shown at a radius of 300 mas. |
| In the text | |
 |
Fig. 6 Test set results. [Left] measured vs. predicted raw 5σ contrasts plotted in magnitudes. [Right] RMSE for the raw 5σ contrast magnitude vs. radius. |
| In the text | |
 |
Fig. 7 Predicted vs. measured test data contrast, binned by star magnitude (faint, mid, bright), along with the atmospheric categories currently used for ranking and grading SPHERE observations in Paranal. |
| In the text | |
 |
Fig. 8 The fitted contrast model parameters. Top: The mean fitted alpha power indices ±2σ as a function of separation. Bottom: The fitted intercept X(r) (in log space) as a function of separation. |
| In the text | |
 |
Fig. 9 Comparison between the 400 mas contrast predictions made by the model of this work vs. the current (as of the publication of this paper) ETC on the ESO website. The ETC options were set to match the observed mode of the model developed here: DBH23 filter with coronagraph. Both the ETC and model were set with no neutral densities, exptime ~64 s, DIT ≤ 64 s, without differential imaging and considered a spectral type of around GV2. |
| In the text | |
 |
Fig. 10 Example of how the contrast model could be used in operations for providing quick checks to ensure the measured raw contrast (~60 s frame) is within the expected 95% range of model residuals given the target and current atmospheric conditions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


