EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 667 (November 2022) A&A, 667 (2022) C1 Full HTML
Open Access
Erratum
This article is an erratum for:
[https://doi.org/10.1051/0004-6361/202142164]

Issue
A&A
Volume 667, November 2022
Article Number C1
Number of page(s) 3
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202142164e
Published online 08 November 2022

Erratum for: A&A, 658, A112 (2022), https://doi.org/10.1051/0004-6361/202142164

In Stapper et al. (2022), which presents Atacama Large Millimeter/submillimeter Array (ALMA) archival continuum images of a sample of Herbig Ae/Be stars, an incorrect data file was accidentally used for one target, R CrA. As a result, a detection was erroneously reported for this source. Using the correct image results in a non-detection of millimeter flux for R CrA and an associated upper limit on the mass. This results in only minor changes in many of the values reported in Stapper et al. (2022), and none of the conclusions from Stapper et al. (2022) are affected.

R CrA has been removed from Fig. 2, see Fig. 1, and the entry of R CrA in Table 1 in Stapper et al. (2022) changes in Table 1. Figure 3 changes only marginally, see Fig. 2, the low-mass end of the distribution goes down slightly further. This changes the log-normal fitting results from a mean of 1.34 to 1.32 and a standard deviation of 0.53 to 0.57, both given in log10(M/M⊕). The confidence intervals do not change. The mean dust mass for the Herbigs mentioned in Sect. 4.2 changes from 39 ± 6 M⊕ into 38 ± 5 M⊕. The percentage of disks with masses above 10 M⊙ should be 63% instead of 67%.

Due to the non-detection, the radius is not known and the cumulative distributions of the dust radii presented in Fig. 6 change, see Fig. 3. The first of the p-values mentioned in the last paragraph of Sect. 4.3 changes from 1.8 × 10−4 into 9.5 × 10−5, the second value reported does not change.

The mean dust mass of the unresolved disks mentioned in Sect. 5.1 changes from 25 ± 5 M⊕ into 19 ± 3 M⊕. Because no radius is known, R CrA is removed from Fig. 7, see Fig. 4. The modified dust mass distribution of the group I and group II Herbig disks is shown in Fig. 5, only the distribution of the group II disks changes slightly. Table 4 should have a mean of 0.61 instead of 0.63 and a standard deviation of 0.68 instead of 0.67; the confidence intervals do not change. Lastly, the corrected values of the frequency, beam size, and root-mean-square noise (RMS) of the observation in Table C.1 can be found in Table 2.

Table 1

Coordinates and spectral types of the Herbig stars used in this work and the calculated Band 6 and 7 flux densities and dust masses of each Herbig disk.

Table 2

Project IDs of the data used in this work with the corresponding observation frequency of the continuum data.

thumbnail Fig. 1

ALMA Band 6 and 7 continuum images of all objects. The size of the beam is shown in the bottom left of each plot and a scale bar of 100 au in size together with the angular scale in arcseconds is shown in the bottom right. Each image is normalized with an asinh stretch to make the fainter details of the disk more visible. HD 53367, HD 176386, and R CrA, which are not detected, are not shown.
thumbnail Fig. 2

Left: cumulative distribution functions of the dust masses contained inside the disks of our Herbig sample, Upper Sco (Barenfeld et al. 2016) and Lupus (Ansdell et al. 2016). Right: log-normal fit through the cumulative distributions. The solid line represents the best-fit distribution, while the light lines show a sub-sample of distributions from a bootstrapping method, showing the spread in possible fits.
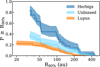thumbnail Fig. 3

Cumulative distribution functions of the 90% dust radii of the Herbig and Lupus samples (Ansdell et al. 2018). The unbiased distribution is made by assuming that all unresolved and unobserved disks are smaller than or equal in size to the smallest disk present in the sample.
thumbnail Fig. 4

R68% radius plotted against the dust mass for the full sample in this work. Unlike Fig. 3, we use R68% values here for consistency with the work of van der Marel & Mulders (2021). The Herbig disks are divided into the Meeus et al. (2001) group I and II disks. Disks with one (⊙) and two or more (aa42164e-21) (visible) rings are indicated as well. The upper limits on the radius are plotted as triangles. The grey scatter points and radius upper limits are the Τ Tauri disks of van der Marel & Mulders (2021). The large arrow shows the range of upper limits on the undetected disks. Three pairs of Herbig group I and II disks are circled and numbered 1–3; these are further discussed in Sect. 5.4 and Fig. 10 in Stapper et al. (2022). For extra context, the positions of the large Τ Tauri disks IM Lup and V1094 Sco are shown as green stars (Ansdell et al. 2016, 2018; van Terwisga et al. 2018; Cleeves et al. 2016).
thumbnail Fig. 5

Left: cumulative distributions of the dust masses of the group I and group II sources. Right: log-normal fit through the cumulative distributions. The solid line represents the best-fit distribution, while the light lines show a sub-sample of distributions from a bootstrapping method, showing the spread in possible fits. The orange log-normal distribution shows the best-fit distribution of Lupus shown in Fig. 2.

References

  1. Ansdell, M., Williams, J. P., van der Marel, N., et al. 2016, ApJ, 828, 46 [Google Scholar]
  2. Ansdell, M., Williams, J. P., Trapman, L., et al. 2018, ApJ, 859, 21 [NASA ADS] [CrossRef] [Google Scholar]
  3. Barenfeld, S. A., Carpenter, J. M., Ricci, L., & Isella, A. 2016, ApJ, 827, 142 [Google Scholar]
  4. Cleeves, L. I., Öberg, K. I., Wilner, D. J., et al. 2016, ApJ, 832, 110 [Google Scholar]
  5. Meeus, G., Waters, L. B. F. M., Bouwman, J., et al. 2001, A&A, 365, 476 [CrossRef] [EDP Sciences] [Google Scholar]
  6. Stapper, L. M., Hogerheijde, M. R., van Dishoeck, E. F., & Mentel, R. 2022, A&A, 658, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. van der Marel, N., & Mulders, G. D. 2021, AJ, 162, 28 [NASA ADS] [CrossRef] [Google Scholar]
  8. van Terwisga, S. E., van Dishoeck, E. F., Ansdell, M., et al. 2018, A&A, 616, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

© L. M. Stapper et al. 2022

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.

All Tables

Table 1

Coordinates and spectral types of the Herbig stars used in this work and the calculated Band 6 and 7 flux densities and dust masses of each Herbig disk.

In the text
Table 2

Project IDs of the data used in this work with the corresponding observation frequency of the continuum data.

In the text

All Figures

thumbnail Fig. 1

ALMA Band 6 and 7 continuum images of all objects. The size of the beam is shown in the bottom left of each plot and a scale bar of 100 au in size together with the angular scale in arcseconds is shown in the bottom right. Each image is normalized with an asinh stretch to make the fainter details of the disk more visible. HD 53367, HD 176386, and R CrA, which are not detected, are not shown.
In the text
thumbnail Fig. 2

Left: cumulative distribution functions of the dust masses contained inside the disks of our Herbig sample, Upper Sco (Barenfeld et al. 2016) and Lupus (Ansdell et al. 2016). Right: log-normal fit through the cumulative distributions. The solid line represents the best-fit distribution, while the light lines show a sub-sample of distributions from a bootstrapping method, showing the spread in possible fits.
In the text
thumbnail Fig. 3

Cumulative distribution functions of the 90% dust radii of the Herbig and Lupus samples (Ansdell et al. 2018). The unbiased distribution is made by assuming that all unresolved and unobserved disks are smaller than or equal in size to the smallest disk present in the sample.
In the text
thumbnail Fig. 4

R68% radius plotted against the dust mass for the full sample in this work. Unlike Fig. 3, we use R68% values here for consistency with the work of van der Marel & Mulders (2021). The Herbig disks are divided into the Meeus et al. (2001) group I and II disks. Disks with one (⊙) and two or more (aa42164e-21) (visible) rings are indicated as well. The upper limits on the radius are plotted as triangles. The grey scatter points and radius upper limits are the Τ Tauri disks of van der Marel & Mulders (2021). The large arrow shows the range of upper limits on the undetected disks. Three pairs of Herbig group I and II disks are circled and numbered 1–3; these are further discussed in Sect. 5.4 and Fig. 10 in Stapper et al. (2022). For extra context, the positions of the large Τ Tauri disks IM Lup and V1094 Sco are shown as green stars (Ansdell et al. 2016, 2018; van Terwisga et al. 2018; Cleeves et al. 2016).
In the text
thumbnail Fig. 5

Left: cumulative distributions of the dust masses of the group I and group II sources. Right: log-normal fit through the cumulative distributions. The solid line represents the best-fit distribution, while the light lines show a sub-sample of distributions from a bootstrapping method, showing the spread in possible fits. The orange log-normal distribution shows the best-fit distribution of Lupus shown in Fig. 2.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.