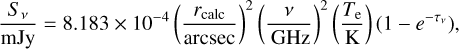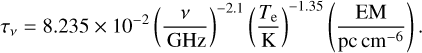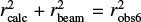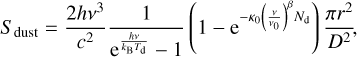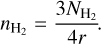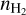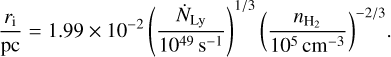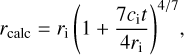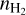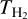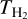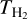| Issue |
A&A
Volume 666, October 2022
|
|
|---|---|---|
| Article Number | A31 | |
| Number of page(s) | 16 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202243674 | |
| Published online | 04 October 2022 | |
The physical and chemical structure of Sagittarius B2
VI. UCHii regions in Sgr B2★
1
University of Chinese Academy of Sciences,
Beijing
100049, PR China
e-mail: mengfanyi@ucas.ac.cn;meng@ph1.uni-koeln.de
2
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Str. 77,
50937
Köln, Germany
3
Department of Astronomy, University of Florida,
PO Box 112055
Gainesville, FL, USA
4
NRAO,
520 Edgemont Rd,
Charlottesville, VA
22903, USA
5
Agnes Scott College,
141 E. College Ave.,
Decatur, GA
30030, USA
6
Max Planck Institute for Extraterrestrial Physics,
Giessenbachstrasse 1,
85748
Garching, Germany
7
Max Planck Institute for Radio Astronomy,
Auf dem Hügel 69,
53121
Bonn, Germany
Received:
30
March
2022
Accepted:
8
July
2022
Context. The giant molecular cloud Sagittarius B2 (hereafter SgrB2) is the most massive region with ongoing high-mass star formation in the Galaxy. Two ultra-compact Hii (UCHii ) regions were identified in SgrB2’s central hot cores, SgrB2(M) and SgrB2(N).
Aims. Our aim is to characterize the properties of the Hii regions in the entire SgrB2 cloud. Comparing the Hii regions and the dust cores, we aim to depict the evolutionary stages of different parts of SgrB2.
Methods. We use the Very Large Array in its A, CnB, and D configurations, and in the frequency band C (~6GHz) to observe the whole SgrB2 complex. Using ancillary VLA data at 22.4 GHz and ALMA data at 96 GHz, we calculated the physical parameters of the UCHii regions and their dense gas environment.
Results. We identify 54 UCHii regions in the 6 GHz image, 39 of which are also detected at 22.4 GHz. Eight of the 54 UCHii regions are newly discovered. The UCHii regions have radii between 0.006 pc and 0.04 pc, and have emission measure between 106 pc cm6 and 109 pc cm6. The UCHii regions are ionized by stars of types from B0.5 to O6. We found a typical gas density of ~106–109 cm3 around the UCHii regions. The pressure of the UCHii regions and the dense gas surrounding them are comparable. The expansion timescale of these UCHii regions is determined to be ~104–105 yr. The percentage of the dust cores that are associated with Hii regions are 33%, 73%, 4%, and 1% for SgrB2(N), SgrB2(M), SgrB2(S), and SgrB2(DS), respectively. Two-thirds of the dust cores in SgrB2(DS) are associated with outflows.
Conclusions. The electron densities of the UCHii regions we identified are in agreement with that of typical UCHii regions, while the radii are smaller than those of the typical UCHii regions. The dust cores in SgrB2(M) are more evolved than in SgrB2(N). The dust cores in SgrB2(DS) are younger than in SgrB2(M) or SgrB2(N).
Key words: stars: formation / stars: massive / radio continuum: ISM / radio lines: ISM / ISM: individual objects: Sgr B2 / ISM: clouds
The reduced image is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/666/A31
© F. Meng et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
The giant molecular cloud Sagittarius B2 (Sgr B2) is the most massive (~ 107 M⊙) region with ongoing high-mass star formation in the Galaxy (see e.g., Goldsmith et al. 1990). SgrB2 has a higher density (>105 cm−3) and dust temperature (≳50–70 K) compared to other star forming regions in the Galactic plane (see e.g., Ginsburg et al. 2016; Schmiedeke et al. 2016; Sánchez-Monge et al. 2017). SgrB2 is located at a distance of 8.34 ± 0.16 pc, and only ~100pc in projection from the Galactic center (Reid et al. 2014)1. These features make Sgr B2 an excellent case to study high-mass star formation in an extreme high-pressure environment. Such an environment resembles nearby starburst galaxies (Leroy et al. 2018). Understanding the structure of the SgrB2 molecular cloud complex is necessary to comprehend the most massive star forming region in our Galaxy, which at the same time provides a unique opportunity to study in detail the nearest counterpart of the extreme environments that dominate star formation in the Universe (see, e.g., Kruijssen & Longmore 2013; Henshaw et al. 2022). This paper continues our series of studies on Sgr B2 (Schmiedeke et al. 2016; Sánchez-Monge et al. 2017; Pols et al. 2018; Schwörer et al. 2019; Meng et al. 2019). In Meng et al. (2019), we presented the observations of Sgr B2(DS), which is a part of Sgr B2 giant cloud, and analyzed the physical properties of the non-thermal emission within it. In this work we study the whole Sgr B2 region.
In the central 2pc of SgrB2 there are the two well-known and well-studied hot cores SgrB2(N) and SgrB2(M) (see, e.g., Schmiedeke et al. 2016; Sánchez-Monge et al. 2017), which contain at least 70 high-mass stars with spectral types from O5 to B0 (see, e.g., Gaume et al. 1995; De Pree et al. 1998; De Pree et al. 2014). Surrounding the two hot cores, there is a larger envelope (hereafter the envelope) with a radius of 20 pc that contains more than 99% of the total mass of SgrB2 (Schmiedeke et al. 2016). Along with the active high-mass star forming activity discovered in Sgr B2(N) and Sgr B2(M), hints of star formation happening in the envelope are also revealed. Ginsburg et al. (2018), with ALMA at 3 mm, revealed 271 high-mass protostellar cores distributed throughout the entire SgrB2 region, including the envelope. The luminosities of these dust cores suggest that they must contain objects with stellar masses higher than 8 Mθ.
Due to the high extinction in the infrared bands toward SgrB2 (see Meng et al. 2019), there is no direct evidence of the existence of high-mass stars embedded in the dust cores detected by Ginsburg et al. (2018). However, since high-mass stars ionize the neutral material surrounding them, the presence and properties of the associated Hii regions reflect the evolutionary stages of these dust cores (see, e.g., González-Avilés et al. 2005; Breen et al. 2010). Additionally, since the free-free emission from Hi i regions may extend from centimeter to millimeter wavelengths in the spectral domain (see, e.g., Sánchez-Monge et al. 2013), measuring the luminosities of the associated Hii regions can help us better constrain the luminosities of the dust cores. Therefore, to further characterize the evolutionary stages and physical properties of these dust cores, we investigate the possible Hii regions associated with them.
The Hii regions in SgrB2 were targeted by several previous studies. Mehringer et al. (1993) observed the entire SgrB2 with VLA in the 20, 6, and 3.6 cm bands and identified 15 Hii regions. The resolutions range from -20″ to -3″ when the wavelength changes from 20 to 3.6cm, which correspond to the range 0.8–0.12 pc. The 15 Hii regions, except two unresolved cases, all have sizes >2″. Since the 271 dust cores may contain newly formed high-mass stars (Ginsburg et al. 2018), the associated Hii regions may be ultra-compact Hii (UCHii) and hyper-compact Hii (HCHii) regions, which typically have sizes from ~0.03 pc to ~0.1 pc (see, e.g., Kurtz 2002, 2005; González-Avilés et al. 2005; Breen et al. 2010). Thus, the resolution of Mehringer et al. (1993) is not sufficient to resolve the UCHii and HCHii regions. Gaume & Claussen (1990); Gaume et al. (1995) observed Sgr B2(N) and SgrB2(M) at 7 mm and 1.3 cm and achieved resolutions of 0.065″ and 0.25″, respectively. Rolffs et al. (2011) observed SgrB2(N) and SgrB2(M) in 40GHz with a resolution of 0.1″. Unfortunately, these high-resolution observations do not cover the entire envelope. For example, SgrB2(DS), where ~80 of dust cores reside (see, e.g., Ginsburg et al. 2018; Meng et al. 2019), is left out of these observations. LaRosa et al. (2000); Law et al. (2008a,b) also observed the entire SgrB2 at centimeter wavelengths, but the resolutions were not high enough to study the UCHii and HCHii regions.
In this paper, we present Very Large Array (VLA) observations of the entire SgrB2 cloud in the frequency regime 4–8 GHz, with configurations A, BnC, and D. The high resolution (≲0.01 pc) and large spatial coverage (~20 pc) of our data sets make a systemic and complete study of the UCHii and HCHii regions in SgrB2 possible. We also include analysis of the 3 mm image (Ginsburg et al. 2018) as well as the newly acquired SiO (5–4) data, both of which were observed with the Atacama Large Millimeter/submillimeter Array (ALMA). Thus, we can disentangle the contributions of ionized gas and dust at millimeter wavelengths and better constrain the evolutionary stages of the dust cores.
This paper is organized as follows. In Sect. 2, we describe the observations and the data reduction process. In Sect. 3, we present the results. In Sect. 4, we discuss the results. Finally, we summarize this paper in Sect. 5.
2 Observations and data reduction
We used the VLA in its A, CnB, and D configurations to observe the entire SgrB2 complex in frequency band C (4–8 GHz). In the following we call this band 6 GHz. The observations with the CnB and D configurations were described in Meng et al. (2019). The observations with the A configuration were conducted from October 1 to 12, 2016 (project 16B-031, PI: F. Meng). We used 64 spectral windows with a bandwidth of 128 MHz each. Mosaic mode was used, with ten pointings for C band. The primary beam of each pointing is 7.5′. Quasar 3C286 was used as the flux and bandpass calibrator, the SED of which is Sν = 5.059 ± 0.021 Jy × (S/8.435 GHz)−0.46 from 0.5 to 50 GHz (Perley & Butler 2013). Quasar J1820-2528, whose flux is 1.3 Jy in the C Band, was used as phase calibrator. The calibration was done using the standard VLA pipelines provided by the NRAO2.
Calibration and imaging were done in Common Astronomy Software Applications (CASA 4.7.2, McMullin et al. 2007). The details of the data processing from the CnB and D configurations are described in Meng et al. (2019). The A configuration data were originally taken every 2 s. To shorten the time of processing, we applied timebin in CASA to the measurement sets, which averaged the data taken within 10 s into one data point. All the pointings of the mosaic in each band were primary beam corrected and the mosaic was imaged using the CASA task tclean. With a robust factor of 0, the image of C band has a synthesized beam of 0.62″×0.28″, with a position angle (PA) of 7.27°. The PA is defined positive north to east. To mitigate the spatial filtering effect of the A configuration image, we applied the feather algorithm to combine the images from A configuration and from CnB and D configurations. The combined image of the three configurations is shown in Fig. 1. The combined image has a resolution identical to that of the A configuration images, while being sensitive to spatial scales up to ~240″. The sensitivities of the observations are described in Sect. 3.
Ancillary data include the 22.4 GHz data, the 3 mm continuum, and SiO (5–4) data. The observations of the 22.4 GHz data are described in Gaume et al. (1995), with a resolution of 0.27″ × 0.23″ (PA = 70°). The root mean square (RMS) noise is 0.38 mJy beam−1. The spatial coverage of the 22.4 GHz data is shown as the blue dashed box in Fig. 1. The 96 GHz continuum data covers the frequency range from 89.5 to 103.3 GHz. The image in 96 GHz has a resolution of 0.54″ × 0.46″ (PA = 68.31°), the observational details of which are described in Ginsburg et al. (2018). Unlike the 22.4 GHz image, the 96 GHz image covers the entire area shown in Fig. 1. The 22.4GHz observations were performed 27 yr prior to the 6 GHz and 96 GHz observations. If we assume that SgrB2 has a proper motion of ~50 km s−1 (Henshaw et al. 2016), the corresponding position shift in 27 yr is 0.04″, which is only ~10% of the beam sizes of our images. In addition, we did not find any visible shift in the positions of the compact sources positions between the 6 and 22.4 GHz images. Thus, we do not take the astrometry difference into account when analyzing the 6 and 22.4 GHz data in the following sections. The SiO (5–4) emission was observed with ALMA (Project 2017.1.00114.S, P.I. A. Ginsburg) and has a resolution of 0.35″× 0.24″, with PA of −80°, and spectral resolution of 1.35 km s−1. For the details of the observation and data reduction, see Jeff et al. (in prep.). The typical RMS of the SiO image is 0.9 mJy beam−1 (0.3 K). The observation covers SgrB2(S) and the eastern part of SgrB2(DS).
 |
Fig. 1 Sources identified in the 6 cm image. Those objects shown as white and blue circles have radii of robs6 (see Table B.1). Notable Hii regions are indicated. The Hii regions that are masked out for core identification are shown as white contours. The beam size is given in the lower left corner of the main panel (θmaj, θmin, PA). The spatial coverage of the 22.4 GHz image is shown as a blue dashed box. |
3 Results
In this section, we present the image of Sgr B2 at 6 GHz and the UCHii regions identified in it. For the Hii regions, we calculated their actual sizes and physical properties using the observations at 6 GHz and at 22.4 GHz. With the 96 GHz data we characterized the properties of the dense gas that the UCHii regions reside in.
3.1 Observed parameters of the 6 GHz sources
Figure 1 displays the image of Sgr B2 at 6 GHz, where the known large-scale Hii regions are denoted N, M, S, AA, DS, and V, following the nomenclature of Mehringer et al. (1992, 1993); Ginsburg et al. (2018); Meng et al. (2019). The maps at 22.4 GHz and 96 GHz are presented by Gaume et al. (1995) and Ginsburg et al. (2018), respectively. Our aim is to study UCHii regions and since the 22.4 GHz image has non-complete spatial coverage, we performed compact source identification at the 6 GHz image only. We used the automatic source extracting algorithm SExtractor (Bertin & Arnouts 1996), which allows us to identify the location of bright compact sources throughout the map. We note that this algorithm also includes a large fraction of artificial sources due to some large-scale artifacts visible in the final image (see the zoomed-in images in Fig. 1). The variable noise (see Fig. A.1) also has an effect on the exclusion of certain sources with the automatic algorithms. After cross-checking the automatically produced lists of sources at 6 GHz and 22.4 GHz, we made the final catalog of continuum sources at 6 GHz by excluding or adding sources by visual inspection (in a similar way to the approach followed in Ginsburg et al. 2018 for the ALMA 96 GHz data). Since we focus on compact sources, extended emission larger than 5″ or 0.2 pc (see contours in Fig. 1) are excluded in the catalog and the following analysis. In total, 54 compact sources are identified throughout the entire SgrB2 cloud (see Table B.1), 8 of which are newly identified. Of these 54 cores, 8 are identified in SgrB2(N), 40 in SgrB2(M), 2 in SgrB2(S), and 1 in SgrB2(DS). All 54 compact sources are covered by the 22.4 GHz image, except core 1.
For each of the 54 compact sources we define a minimal circle that can include as much as the total flux density of it at 6 GHz.3 The observed radius of the core and the flux density within the core are denoted robs6 and S6, respectively. For these 54 sources we followed the same photometry procedure at the 22.4GHz and 96 GHz bands, and obtained robs22, S22, robs96, and S96 that correspond to the observed radii and flux densities. The observed radius and flux density in three bands of all the 54 compact sources are listed in Table B.1.
To match the sources across the three images (6, 22.4, and 96 GHz), we defined that if two sources in two images have a distance (distance between their centers) shorter than either of their radii, they are associated with each other. Afterward, we manually adjust few of the matched sources in the crowed region in SgrB2(M). For all the compact sources at 6 GHz, emission in the 96 GHz band is also detected. Among the 15 sources that have no S22, 14 are without reliable 22.4 GHz detection (S22 < 3RMS), and one (#1 in B.1) is not spatially covered by the 22.4 GHz image. All the 22.4 GHz sources4 reported by Gaume et al. (1995) are associated with the 6 GHz compact sources.
We compared the spatial association of the 54 sources with the 271 dust cores identified at 96 GHz by Ginsburg et al. (2018). Although there is no one-to-one correspondence between the 271 dust cores and the associated dust emission of the 54 compact sources, we can still conclude that at least 217 (80%) dust cores are not associated with compact radio sources that are detectable with our sensitivity.
Most of the compact sources have robs6 from 0.5″ to 1″, which is comparable to the beam size at 6 GHz. Even though the 22.4 GHz image has higher resolution (~0.25″), the measured robs22 are still not significantly larger than the beam size at 22.4 GHz. Therefore, most of the compact sources are not well resolved; in other words, robs6 or robs22 cannot accurately represent the actual radii of most of the compact sources. The 96 GHz compact sources, as indicated by Ginsburg et al. (2018), are also not resolved. The flux densities of the compact sources are distributed in a wide range; S6 ranges from ~3 mJy to ~300 mJy at 6 GHz, as shown in Fig. 2. The mean and median of S6 are 37.3 mJy and 16.2 mJy, respectively.
To test whether the nature of the emission at 6 and 22.4 GHz is free-free emission, we interpolated S6 and S22 to derive a spectral index α6–22 for each of the 39 sources that have 22.4 GHz detection, see the last column of Table B.1. All 39 sources have α6–22 > −0.1, which suggest that their emission at centimeter wavelengths is very probably dominated by thermal free-free emission from ionized gas (see, e.g., Sánchez-Monge et al. 2013). For the 15 sources without 22.4 GHz detections, we find that their are not higher than the values of the other sources. If we treat their emission at 6 GHz as free-free as well5, the derived physical parameters are also within the same ranges as the other sources (see Sect. 3.2). Thus, we treat all 54 sources as thermal free-free sources in the following analysis.
 |
Fig. 2 Probability distribution of S6 (pink), plotted as a kernel density estimation. Mean and median values are indicated. The distributions of S22 (green) and S96 (blue) are also shown. |
3.2 Physical parameters of the HII regions
As we show in Sect. 3.1, most of the compact sources at 6 and 22.4 GHz are not well resolved. Therefore, we first need to determine their actual sizes. The observed flux density (S6 and S22) of an HII region is related to its actual size (rcalc, which is called calculated radius in this paper), its electron temperature (Te), and its emission measure (EM) as (see, e.g., Wilson et al. 2013)
where the optical depth τv is
In our case the frequency v is 6 GHz or 22.4 GHz. We assume that Te is 104 K, following the values given by Mehringer et al. (1993) for SgrB2(N) and SgrB2(M), considering that most of the compact sources are in these two regions. Thus, with the two independent flux density measurements, S6 and S22, we solve Eqs. (1) and (2) to obtain rcalc and EM simultaneously for the 39 sources that are detected at both 6 and 22.4 GHz. For the 15 compact sources that are only detected at 6 GHz, we deconvolved the beam size from robs6 to estimate rcalc, as 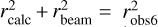 , and
, and 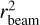 = 0.62″ × 0.28″ for 6GHz. Then we calculated EM using the estimated rcalc. The rcalc and EM of all the compact sources are listed in Table B.2; those derived from the deconvolved rcalc are flagged with asterisk (*) in Table B.2.
= 0.62″ × 0.28″ for 6GHz. Then we calculated EM using the estimated rcalc. The rcalc and EM of all the compact sources are listed in Table B.2; those derived from the deconvolved rcalc are flagged with asterisk (*) in Table B.2.
For all the compact sources that are associated with the 22.4 GHz detection, we plot the robs6 − rcalc diagram (see Fig. 3). We can see that in general rcalc follows the trend of deconvolution (i.e., 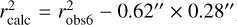 ), which suggests that the method we used to calculate rcalc, although without measuring the compact source size in the image, is in general consistent with the size we observed. The deviation between the rcalc from the dashed curve in Fig. 3 is likely due to some uncertainties in the observations and flux measurements. For example, the determination of robs6 is made by including as much of the flux as possible, which might be larger than the actual observed size. In addition, due to the artifacts in the image, we cannot ideally define the boundaries of the compact sources, but only approximate the compact source as a circle with r = robs.
), which suggests that the method we used to calculate rcalc, although without measuring the compact source size in the image, is in general consistent with the size we observed. The deviation between the rcalc from the dashed curve in Fig. 3 is likely due to some uncertainties in the observations and flux measurements. For example, the determination of robs6 is made by including as much of the flux as possible, which might be larger than the actual observed size. In addition, due to the artifacts in the image, we cannot ideally define the boundaries of the compact sources, but only approximate the compact source as a circle with r = robs.
The probability distribution of EM of all the 54 compact sources is shown in Fig. 4. The EM of these compact sources ranges from ~2 × 106 pc cm−6 to ~3 × 109 pc cm−6. Only eight compact sources have EM < 107 pc cm−6, which means that most of the compact sources are consistent with the parameters derived for UCH∏ regions (see Kurtz 2002). From EM we estimated the electron density ne as ne = [EM/(2rcalc)]1/2. The distribution of ne is shown in Fig. 5. The ne of the 54 HII regions are from ~4 × 103 cm−3 to ~5 × 10s cm−3 with a mean value of ~ 105 cm−3.
Knowing EM, we calculated the flux of Lyman continuum photons 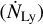 that are needed to ionize these UCHII regions following Eq. (C.18) in Schmiedeke et al. (2016). The derived NLy ranges from 1046 s−1 to 1049 s−1 (see Fig. 6). If we assume that these cores are ionized by single stars, these UCHII regions are ionized by stars from spectral types B0.5 to 06 (Panagia 1973).
that are needed to ionize these UCHII regions following Eq. (C.18) in Schmiedeke et al. (2016). The derived NLy ranges from 1046 s−1 to 1049 s−1 (see Fig. 6). If we assume that these cores are ionized by single stars, these UCHII regions are ionized by stars from spectral types B0.5 to 06 (Panagia 1973).
In this section, we describe a method that is independent of the observed source size to derive the radius (rcalc) and emission measure (EM) of 39 sources detected at 6 and 22.4 GHz. To verify this a method, we compared the rcalc, EM, and NLy values of these 39 sources with the values presented by Gaume et al. (1995), namely rG95, EMG95, and NLy g95∙ Of the 39 sources, 33 are coincident with the UCHII regions reported by Gaume et al. (1995). Twenty of the 33 sources have rcalc > rg95 (see left panel of Fig. 7). The order of magnitude of EM of the UCHII regions is consistent in these two studies. Of the 33 sources, 23 have EM larger than EMG95 (see middle panel of Fig. 7). Most of the sources have NLy similar to NLy G95 (see right panel of Fig. 7), except source 44. The difference between NLy and NLyG95 of source 44 is possibly caused by the time-domain flickering of the radio emission in SgrB2 (see the last paragraph of this section).
In Fig. 8, we plot the diagram of rcalc and ne. It is worth noting that all of the 39 HII regions have typical ne of UCHII regions (i.e., ~104 cm−3 to ~106 cm−3; Kurtz 2005). However, 16 of these have r smaller than that of typical UCHII regions (~0.015 to ~0.05 pc). Although some of the sources have sizes similar to HCHII regions, considering the low density of our HII regions compared to typical HCHII regions, and following the previous nomenclature of most of the sources (e.g., Gaume et al. 1995), we still call all the HII regions in this study UCHII regions.
Recently, Rivera-Soto et al. (2020) identified similar HII regions in W51 that have ne ~ 104–105cm−3 and 2 × r ~ 10−3–10−2 pc. They categorized these sources as HCHII regions, but they are similar to smaller UCHII regions and are ionized by early B-type stars, which is in agreement with the spectral type of the ionizing stars for most of our UCHII regions (see Fig. 6). Unlike the HCHII regions in W51, our UCHII regions do not exactly follow the r − ne relationships of UCHII regions proposed by Garay & Lizano (1999) and Kim & Koo (2001), and have higher ne (by a factor of ~2) than the predicted values (see Fig. 8). Such a discrepancy might be due to the neutral gas surrounding our UCHII regions that is denser («H2 > 106 cm−3) than typical molecular cores (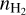 ~ 104–105cm−3; see, e.g., Bergin & Tafalla 2007). In Sect. 3.3, a detailed analysis of the gas density surrounding the UCHII regions is presented.
~ 104–105cm−3; see, e.g., Bergin & Tafalla 2007). In Sect. 3.3, a detailed analysis of the gas density surrounding the UCHII regions is presented.
Since we cannot resolve the detailed morphologies of the UCHII regions, we neglect the possible inhomogeneity of the HII regions. The various morphologies of UCHII regions result in modified SEDs other than that described by Eqs. (1) and (2), (see, e.g., Keto 2003; Keto et al. 2008). Additionally, if there are accretion flows to the HII regions, flickering of the flux on a timescale of ~100yr may occur, which is observed by De Pree et al. (2014) and modeled by Peters et al. (2010b,c). Since the 6 GHz observation (2013) was performed 23 yr after the 22.4 GHz observations (1989), the effects of flickering could be present in some of these cores. Hence, the simultaneous use of 6 GHz and 22.4 GHz fluxes may not be appropriate for the analysis of some sources. However, De Pree et al. (2014) reported the flickering of 4 out of 41 sources in Sgr B2 within a similar time range (1989-2014). Such a rarity of cases (10%) suggests that the flickering may not significantly alter our statistical results.
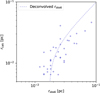 |
Fig. 3 Relation between robs6 and rcaic of the 39 compact sources with 22.4 GHz detection. The dashed curve indicates the deconvolution relationship |
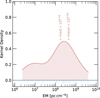 |
Fig. 4 Distribution of EM. The mean and median values are indicated. |
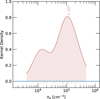 |
Fig. 5 Distribution of ne. The mean and median values, which are both ~105 cm−3, are indicated. |
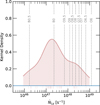 |
Fig. 6 Distribution of NLy. The corresponding spectral type of the ionizing stars (assuming that the Hπ regions are ionized by single stars) are indicated. |
 |
Fig. 7 Comparison between rcalc (left), EM (middle), and NLy (right) of 33 sources and the corresponding parameters found by Gaume et al. (1995). |
 |
Fig. 8 Diagram of rcalc and ne. Previously derived rcalc–ne relationships for UCHII regions from Garay & Lizano (1999), ne = 780 × (2r)−1.19, and from Kim & Koo (2001), ne = 790 × (2r)−∞, are plotted as dashed lines. The green shading indicates the typical ne of UCHII regions, which is from ~104 cm−3 to ~106 cm−3, and the typical r of UCHII regions, which is ~0.015 to ~0.05 pc (Kurtz 2005). |
3.3 Dense gas environment
We extrapolated the HII regions’ SED (Eq. (1)) to subtract the free-free contribution from S96 to get the emission purely from dust, which is denoted Sdust∙ Twelve UCHII regions have Sdust below 3× rms, while the other 42 UCHII regions have detectable dust emission after subtraction of the free-free emission. Using S dust, we evaluated the dust properties in the vicinity of the 42 UCHII regions.
Following Ossenkopf & Henning (1994), we calculated the dust column density Nd as
in which Td is the dust temperature, D is the distance of Sgr B2, and r is the radius of the dust core. Since most of the dust cores are not resolved (Ginsburg et al. 2018), here we use 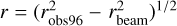 where rbeam = (0.54″ × 0.46″)1/2 is the effective radius of the 96 GHz beam. The dust parameters κ0 and β depend on the dust grain properties. Due to the general high temperature and high density of neutral gas revealed by previous studies (see, e.g., Huttemeister et al. 1993; Schmiedeke et al. 2016), we assume that Td = 100, κ0 = 2.631, and β = 1.05 for v0 = 100 GHz. The assumption of κ0 and β corresponds to dust grains without ice mantles and with a volume density of 108 cm-3. We assume a gas-to-dust mass ratio of 100 (Ott et al. 2014; Giannetti et al. 2017) to estimate the gaseous mass
where rbeam = (0.54″ × 0.46″)1/2 is the effective radius of the 96 GHz beam. The dust parameters κ0 and β depend on the dust grain properties. Due to the general high temperature and high density of neutral gas revealed by previous studies (see, e.g., Huttemeister et al. 1993; Schmiedeke et al. 2016), we assume that Td = 100, κ0 = 2.631, and β = 1.05 for v0 = 100 GHz. The assumption of κ0 and β corresponds to dust grains without ice mantles and with a volume density of 108 cm-3. We assume a gas-to-dust mass ratio of 100 (Ott et al. 2014; Giannetti et al. 2017) to estimate the gaseous mass 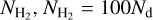 .
.
From the column density of molecular gas, 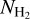 , we obtain the volume density of molecular gas (H2),
, we obtain the volume density of molecular gas (H2),
We list the 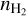 values at the position of the 42 UCHII regions associated with dust emission in Table B.2. The distribution of
values at the position of the 42 UCHII regions associated with dust emission in Table B.2. The distribution of 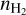 is shown in Fig. 9. The
is shown in Fig. 9. The 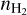 ranges from ~106 to ~108 cm-3. Due to the artifacts and possible small size of the dust core, even a dust core with enough volume density might not be detected by the sensitivity of our data set. We used the method in Ginsburg et al. (2018) to estimate the detection limit of the dust emission. Compared to the typical
ranges from ~106 to ~108 cm-3. Due to the artifacts and possible small size of the dust core, even a dust core with enough volume density might not be detected by the sensitivity of our data set. We used the method in Ginsburg et al. (2018) to estimate the detection limit of the dust emission. Compared to the typical 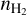 of the molecular clouds surrounding UCHII regions (105 cm-3) (e.g., Wood & Churchwell 1989), our UCHii regions reside in denser neutral gas. The median value obtained in this work is similar to the value (2 × 107 cm-3) measured in the central region of Sgr B2(M) (de Pree et al. 1995; Huettemeister et al. 1995; Sánchez-Monge et al. 2017), although our sources are also distributed in the outskirts of Sgr B2(M).
of the molecular clouds surrounding UCHII regions (105 cm-3) (e.g., Wood & Churchwell 1989), our UCHii regions reside in denser neutral gas. The median value obtained in this work is similar to the value (2 × 107 cm-3) measured in the central region of Sgr B2(M) (de Pree et al. 1995; Huettemeister et al. 1995; Sánchez-Monge et al. 2017), although our sources are also distributed in the outskirts of Sgr B2(M).
 |
Fig. 9 Probability distribution of |
4 Analysis and discussion
4.1 Expansion and equilibrium
Based on the physical properties of the Hπ regions (see Sect. 3.2) and the properties of their surrounding environment (see Sect. 3.3), we now investigate the expansion time for these extremely compact and dense HII regions. The density of the molecular cloud that UCHII regions expand into significantly affects the expansion rate (e.g., Wood & Churchwell 1989; de Pree et al. 1995, de Pree et al. 1998). For the simple case of a spherical UCHII region ionized by the Lyman continuum flux of NLy and expanding in molecular gas with volume density 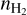 and electron temperature of 104 K, following de Pree et al. (1995, de Pree et al. 1998) we calculate the initial Strömgren radius ri as
and electron temperature of 104 K, following de Pree et al. (1995, de Pree et al. 1998) we calculate the initial Strömgren radius ri as
For the 12 UCHII regions without detected associated dust emission (Sdust, which is S96 subtracting the free-free component), we assumed a uniform dust density of 2 × 107 cm-3 following De Pree et al. (2015). This value is in agreement with the median of 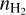 of the 42 sources that have physical Sdust∙ Since we assumed a relatively high gas density compared to typical dust cores (see, e.g., Bergin & Tafalla 2007), the nondetection of Sdust for 12 sources under such an assumption is due to small r but not low
of the 42 sources that have physical Sdust∙ Since we assumed a relatively high gas density compared to typical dust cores (see, e.g., Bergin & Tafalla 2007), the nondetection of Sdust for 12 sources under such an assumption is due to small r but not low 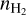 ∙ Then we calculated the expansion timescales of all 54 cores applying the expansion equation by Spitzer (1968); Dyson & Williams (1980),
∙ Then we calculated the expansion timescales of all 54 cores applying the expansion equation by Spitzer (1968); Dyson & Williams (1980),
where c¡ is the sound speed (~10 km s−1). The expansion times, t, of the UCHII regions are listed in Table B.2. In Fig. 10 the cores are color-coded according to their t. In ideal cases most of the cores have an expansion time between 104 yr and 105 yr. The expansion times in this section were dervied under the assumption of ideal conditions (Spitzer 1968). Such derived expansion times should be treated as lower limits and the actual expansion time might be longer for to at least three reasons. First, the expansion of UCHII regions can be halted due to the pressure equilibrium between the ionized gas and the surrounding dense molecular gas (e.g., De Pree et al. 1998). We assume that Te of the ionized gas is 104 K, and the molecular temperature 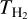 is from 50 K to 100 K. The pressure equilibrium condition
is from 50 K to 100 K. The pressure equilibrium condition 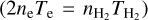 can be expressed as
can be expressed as 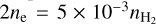 and
and 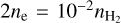 for
for 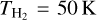 = 50 K and 100 K, respectively. In dust cores with
= 50 K and 100 K, respectively. In dust cores with 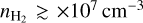 ≳ × 10 cm-3, the UCHII regions are mostly in equilibrium with the neutral gas, evident from Fig. 11, whereas for the lower
≳ × 10 cm-3, the UCHII regions are mostly in equilibrium with the neutral gas, evident from Fig. 11, whereas for the lower 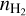 regime, the UCHII regions are in expansion phase owing to ionized gas pressure exceeding the neutral gas pressure. Second, in reality, dust absorption may reduce r¡, and therefore slows down the expansion (see, e.g., Wood & Churchwell 1989; De Pree et al. 1998). Third, accretion flow on to the central star will disrupt the expansion process and cause a sudden decrease in the flux and size of the UCHII region, (see, e.g., Fig. 10 in Peters et al. 2010a). With the current data, we cannot quantify the effect of either of these mechanisms. Future observations, for example high-resolution radio recombination line observations, may provide constraints on the possible effect of accretion on the expansion of the HII regions.
regime, the UCHII regions are in expansion phase owing to ionized gas pressure exceeding the neutral gas pressure. Second, in reality, dust absorption may reduce r¡, and therefore slows down the expansion (see, e.g., Wood & Churchwell 1989; De Pree et al. 1998). Third, accretion flow on to the central star will disrupt the expansion process and cause a sudden decrease in the flux and size of the UCHII region, (see, e.g., Fig. 10 in Peters et al. 2010a). With the current data, we cannot quantify the effect of either of these mechanisms. Future observations, for example high-resolution radio recombination line observations, may provide constraints on the possible effect of accretion on the expansion of the HII regions.
Number of objects associated with dust cores.
4.2 Evolutionary stages
The type of objects that are associated with dust cores suggests the evolutionary stages of the dust cores in star formation activity. In Table 1 we summarize the type and number of objects associated with the dust cores in the subregions SgrB2(N), SgrB2(M), SgrB2(S), and SgrB2(DS), and in the rest of the envelope of Sgr B2.
Of all the 54 UCHII regions, 8 are in SgrB2(N), 40 are in SgrB2(M), 2 are in SgrB2(S), 1 is in SgrB2(DS) and 3 are in the rest of the envelope. Although the dust cores are distributed all over SgrB2 (Ginsburg et al. 2018) and more than 80 of them are associated with the large HII region in SgrB2(DS) (Meng et al. 2019), the dust cores are rarely associated with any UCHII regions outside of SgrB2(N) and SgrB2(M). The percentage of the dust cores that are associated with UCHII regions are 33%, 73%, 4%, and 1% for SgrB2(N), SgrB2(M), Sgr B2(S), and Sgr B2(DS), respectively, while for the remaining part of the envelope the percentage is 3%.
For a dust core, association with the HII region is a sign of that the core is more evolved (see, e.g., Breen et al. 2010). Therefore, the cores in Sgr B2(M) are the most evolved, while the cores in SgrB2(S) and SgrB2(DS) are the least evolved. The evolutionary stages of the cores in Sgr B2(N) are between those of SgrB2(M) and SgrB2(DS) or SgrB2(S).
All the dust cores in SgrB2(DS) appear to be pure dust6. With the sensitivity of our observation (~ 1 mJy, for unresolved sources), we constrain the age of the possibly undetectable embedded Hπ regions in the dust cores. We consider the NLy from the central star are of 1046, 1047, 1048 s−1, and dust densities are 106 and 108 cm−3, which are based on the typical values of the detected UCHII regions. The evolution of S6 of the HII regions, based on the expansion model in Sect. 4.1 and Eq. (8) in (De Pree et al. 1998), are displayed in Fig. 12. The temporal evolution of r and EM leads to increase in S6 (see Eq. (1)). For the dust cores that have 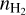 = 106cm-3, the embedded HII regions with NLy ≥ 1047 s−1 will be observable ~100 yr after their birth, which contradicts the nondetection of Hi I regions in SgrB2(DS). For the dust cores that have
= 106cm-3, the embedded HII regions with NLy ≥ 1047 s−1 will be observable ~100 yr after their birth, which contradicts the nondetection of Hi I regions in SgrB2(DS). For the dust cores that have 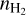 = 108cm-3, the embedded HII regions with NLy ≥ 1047 s−1 will be observable ~103 yr after their birth, which suggests that it is possible that the Hπ regions are already formed but still too dim to be detected. The Hπ regions with NLy ≤ 1046 s−1 will be always undetectable with the current sensitivity. The sizes of the embedded HII regions will reach the typical size of the UCHII regions in this study (~0.01 pc) in 104 yr (de Pree et al. 1995, see Fig. 1 in). Thus, it is possible that stars later than Bl have already formed and ionized the interiors of the dust cores.
= 108cm-3, the embedded HII regions with NLy ≥ 1047 s−1 will be observable ~103 yr after their birth, which suggests that it is possible that the Hπ regions are already formed but still too dim to be detected. The Hπ regions with NLy ≤ 1046 s−1 will be always undetectable with the current sensitivity. The sizes of the embedded HII regions will reach the typical size of the UCHII regions in this study (~0.01 pc) in 104 yr (de Pree et al. 1995, see Fig. 1 in). Thus, it is possible that stars later than Bl have already formed and ionized the interiors of the dust cores.
Collimated outflows are the footprints of the very early stages of star formation activity (see, e.g., Beuther et al. 2002). Outflows can be traced by SiO emission (e.g., Schilke et al. 1997). In a recent project, the SiO (5–4) emission was observed with ALMA (P.I. A. Ginsburg). For the details of the observation and data reduction, see Jeff et. al. (in prep.). The resolution is 0.35″ × 0.24″, with PA of −80°. The spectral resolution is 1.35 km s−1. The typical RMS of the image is 0.9 mfy beam−1. The observation covers SgrB2(S) and the eastern part of SgrB2(DS). The peak intensity map of SiO (5–4) is shown in Fig. C.1. Due to the artifacts around Sgr B2(S), we only analyzed the part of the image with declination <−28:24:00. We generated the moment one map by masking out all the pixels below 3σ (see Fig. C.2). The average velocity difference between the blueshifted and red-shifted lobes is found to be ~10 km s−1 . We visually matched the positions of the dust cores identified by Ginsburg et al. (2018) and the SiO outflows. The dust cores that are (1) spatially associated with an outflow, (2) covered by the SiO image not associated with an outflow, and (3) not covered by the SiO image are indicated in Table B.3. Spatially, most of the outflows are associated with dust cores. On the other hand, of all the 120 dust cores covered by the SiO image, 49 are identified as associated with outflows. Particularly, among all the cores in SgrB2(DS), two-thirds are associated with outflows. Such a high fraction confirms that the cores in SgrB2(DS) are at their very early evolutionary stages.
CH3OH masers serve as additional probes to trace the star formation activity (see, e.g., Breen et al. 2010). We crossmatched the ch3oh masers presented by Caswell et al. (2010) with our dust cores7. In Table 1, the number of masers that are associated with the dust cores that are in each region are listed. The cores in SgrB2(M) and in SgrB2(N) are associated with two ch3oh masers. The cores in SgrB2(DS) have no associated masers. This lack of associated masers also suggests that the cores in SgrB2(DS) are less evolved than those in SgrB2(N) and SgrB2(M).
It is worth noting that the dust cores in Sgr B2(DS) are distributed around the large-scale HII region in SgrB2(DS) (see Fig. 2 in Meng et al. 2019). The large-scale HII region was ionized by a central 07 star and is still in the expansion phase (Meng et al. 2019). The expansion time of this HII region is ~105 yr, which is estimated based on the size of the HII region (0.72 pc) and the sound speed of the ionized gas, 10 km s−1. This timescale, compared to the expansion time of the Hπ regions in SgrB2(M) and SgrB2(N) suggest that the central 07 star possibly formed before the stars in Sgr B2(M) and Sgr B2(N). Another possible scenario is that the 07 star was ejected from a nearby star forming site (e.g., Sgr B1) earlier than 105 yr ago, and Sgr B2 had no star forming activity at that time. The newly formed dust cores in Sgr B2(DS), on the other hand, are signs of star forming activity that possibly was triggered by the expansion of the large-scale HII region in SgrB2(DS).
 |
Fig. 10 Evolution sequence of the HII regions. The circles are calculated with the dust density derived from the 96 GHz image. The triangles are calculated with the dust density of 2 × 107 cm−3. The color of the markers indicates the expansion timescale. |
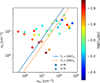 |
Fig. 11 Diagram of ne and |
 |
Fig. 12 Modeled evolution of S6 of HII regions with time. The black line denotes the sensitivity of our 6 GHz observation, which is ~1 mJy, for unresolved sources. |
5 Summary
We observed the SgrB2 complex with VLA A, BnC, and D array at 6 GHz and identified 54 compact radios sources. We found that 39 of the 54 sources are also detected in the 22.4 GHz band (Gaume et al. 1995). Our main results are summarized as follows:
Using the 6 GHz data of all 54 sources, as well as the 22.4 GHz data of 39 sources, we calculated the EM, radius, electron densities, and the spectral type of the ionizing stars of all the 54 UCHII regions. The UCHII regions have radius between 6 × 10−3 pc and 4 × 10−2 pc, and have EM between 106pc cm−6 and 109pc cm−6. We found that the electron densities of these UCHII regions are in agreement with the values of typical UCHII regions, while the radii are smaller than for the typical UCHII regions. We identified that the UCHII regions are ionized by stars with spectral types ranging between B0.5 to O6.
Using the 96 GHz ALMA data, we characterized the dense gas environment where the UCHII regions are located. We found a typical dense gas density of ~106–109 cm-3 around the UCHII regions. Using Spitzer (1968), we estimated the expansion timescale of the UCHII regions as ~104–105yr. More than half of the UCHII regions are close to equilibrium with the neutral gas; this means that the pressure of most UCHii regions and the dense gas surrounding them are comparable. Due to the high pressure of the neutral gas, some natal HII regions might be optically thick and cannot be detected with the sensitivity of this study. Instead, for the lower
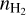 regime (
regime (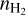 ≲ ×107cm-3) the ionized gas pressure exceeds that of the neutral gas and the UCHII regions are still expanding.
≲ ×107cm-3) the ionized gas pressure exceeds that of the neutral gas and the UCHII regions are still expanding.The percentage of the dust cores that are associated with HII regions are 33%, 73%, 4%, and 1% for SgrB2(N), SgrB2(M), SgrB2(S), and SgrB2(DS), respectively. Among all the dust cores in Sgr B2(DS), two-thirds are associated with outflows that are traced by SiO(5^1). The dust cores in both of SgrB2(M) and SgrB2(N) are associated with two 6.7 GHz ch3oh masers, while the dust cores in SgrB2(DS) have no associated maser. Based on these findings, we suggest that the dust cores in SgrB2(M) are more evolved than those in SgrB2(N). The dust cores in SgrB2(DS) are younger than those in SgrB2(M) or SgrB2(N).
In this work, we calculated the physical properties of the UCHII regions and their surrounding neutral gas in SgrB2. We found that the pressure of the UCHII regions and the dense gas surrounding them are comparable. We also characterized the evolutionary stages of these UCHII regions and obtained their minimum expansion timescales.
A new distance to the Galactic center of 8.127 ± 0.031 kpc has been measured (GRAVITY Collaboration 2018). For consistency with the papers published within the same series of studies of SgrB2, we use the distance reported by Reid et al. (2014).
In Gaume et al. (1995), extended Hπ regions are also included in the catalog. We only compare the compact sources (r < 5″) in their catalog with ours.
For single-dish images, the RMS around a certain null detection spot could be used to derive an upper limit of the possible signal, which in this paper can be translated into an upper limit of α6–22; however, because the artifacts in the 22.4 GHz image contain negative bowls of interferometric images, we do not trust the upper limits derived from the 22.4 GHz RMS map.
One HII region is found associated with a core reported by Ginsburg et al. (2018), but the core emission is pure free-free, which suggests that the core is a dust-free HII region. Therefore, no dust cores in Sgr B2(DS) are associated with HII regions.
Acknowledgements
FM, ASM, PS, ASchw research is carried out within the Collaborative Research Centre 956, sub-projects A6 and C3, funded by the Deutsche Forschungsgemeinschaft (DFG) – project ID 184018867. AG acknowledges support from the NSF via AST 2008101 and CAREER 2142300. This paper makes use of the following ALMA data: 2013.1.00269.S and 2017.1.00114.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. This research made use of Astropy, (http://www.astropy.org) a community-developed core Python package for Astronomy (Astropy Collaboration 2013, 2018).
References
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Benson, J. M., & Johnston, K. J. 1984, ApJ, 277, 181 [Google Scholar]
- Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339 [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuther, H., Schilke, P., Sridharan, T. K., et al. 2002, A&A, 383, 892 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Breen, S. L., Ellingsen, S. P., Caswell, J. L., & Lewis, B. E. 2010, MNRAS, 401, 2219 [NASA ADS] [CrossRef] [Google Scholar]
- Caswell, J. L., Fuller, G. A., Green, J. A., et al. 2010, MNRAS, 404, 1029 [Google Scholar]
- De Pree, C. G., Rodriguez, L. F., & Goss, W. M. 1995, Rev. Mex. Astron. Astrofis., 31, 39 [Google Scholar]
- De Pree, C. G., Goss, W. M., & Gaume, R. A. 1998, ApJ, 500, 847 [NASA ADS] [CrossRef] [Google Scholar]
- De Pree, C. G., Peters, T., Mac Low, M. M., et al. 2014, ApJ, 781, L36 [NASA ADS] [CrossRef] [Google Scholar]
- De Pree, C. G., Peters, T., Mac Low, M. M., et al. 2015, ApJ, 815, 123 [Google Scholar]
- Dyson, J. E., & Williams, D. A. 1980, Physics of the Interstellar Medium (Wiley) [Google Scholar]
- Garay, G., & Lizano, S. 1999, PASP, 111, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Gaume, R. A., & Claussen, M. J. 1990, ApJ, 351, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Gaume, R. A., Claussen, M. J., de Pree, C. G., Goss, W. M., & Mehringer, D. M. 1995, ApJ, 449, 663 [Google Scholar]
- Giannetti, A., Leurini, S., König, C., et al. 2017, A&A, 606, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ginsburg, A., Henkel, C., Ao, Y., et al. 2016, A&A, 586, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ginsburg, A., Bally, J., Barnes, A., et al. 2018, ApJ, 853, 171 [Google Scholar]
- Goldsmith, P. F., Lis, D. C., Hills, R., & Lasenby, J. 1990, ApJ, 350, 186 [Google Scholar]
- González-Avilés, M., Lizano, S., & Raga, A. C. 2005, ApJ, 621, 359 [CrossRef] [Google Scholar]
- Gravity Collaboration (Abuter, R., et al.) 2018, A&A, 615, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henshaw, J. D., Barnes, A. T., Battersby, C., et al. 2022, in Protostars and Planets VII, [arXiv:2203.11223] [Google Scholar]
- Henshaw, J. D., Longmore, S. N., Kruijssen, J. M. D., et al. 2016, MNRAS, 457, 2675 [Google Scholar]
- Huttemeister, S., Wilson, T. L., Henkel, C., & Mauersberger, R. 1993, A&A, 276, 445 [NASA ADS] [Google Scholar]
- Huettemeister, S., Wilson, T. L., Mauersberger, R., et al. 1995, A&A, 294, 667 [NASA ADS] [Google Scholar]
- Keto, E. 2003, ApJ, 599, 1196 [NASA ADS] [CrossRef] [Google Scholar]
- Keto, E., Zhang, Q., & Kurtz, S. 2008, ApJ, 672, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, K.-T., & Koo, B.-C. 2001, ApJ, 549, 979 [Google Scholar]
- Kruijssen, J. M. D., & Longmore, S. N. 2013, MNRAS, 435, 2598 [Google Scholar]
- Kurtz, S. 2002, in Hot Star Workshop III: The Earliest Phases of Massive Star Birth, ASP Conf. Ser., 267, ed. P. Crowther, 81 [NASA ADS] [Google Scholar]
- Kurtz, S. 2005, in Massive Star Birth: A Crossroads of Astrophysics, IAU Symposium, 227, eds. R. Cesaroni, M. Felli, E. Churchwell, & M. Walmsley, 111 [NASA ADS] [CrossRef] [Google Scholar]
- LaRosa, T. N., Kassim, N. E., Lazio, T. J. W., & Hyman, S. D. 2000, AJ, 119, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Law, C. J., Yusef-Zadeh, F., & Cotton, W. D. 2008a, ApJS, 177, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Law, C. J., Yusef-Zadeh, F., Cotton, W. D., & Maddalena, R. J. 2008b, ApJS, 177, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Bolatto, A. D., Ostriker, E. C., et al. 2018, ApJ, 869, 126 [NASA ADS] [CrossRef] [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Data Analysis Software and Systems XVI, ASP Conf. Ser., 376, eds. R. A. Shaw, F. Hill, & D. J. Bell, 127 [NASA ADS] [Google Scholar]
- Mehringer, D. M., Yusef-Zadeh, F., Palmer, P., & Goss, W. M. 1992, ApJ, 401, 168 [Google Scholar]
- Mehringer, D. M., Palmer, P., Goss, W. M., & Yusef-Zadeh, F. 1993, ApJ, 412, 684 [Google Scholar]
- Meng, F., Sánchez-Monge, Á., Schilke, P., et al. 2019, A&A, 630, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Ott, J., Weiß, A., Staveley-Smith, L., Henkel, C., & Meier, D. S. 2014, ApJ, 785, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Panagia, N. 1973, AJ, 78, 929 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, R. A., & Butler, B. J. 2013, ApJS, 204, 19 [Google Scholar]
- Peters, T., Banerjee, R., Klessen, R. S., et al. 2010a, ApJ, 711, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, T., Klessen, R. S., Mac Low, M.-M., & Banerjee, R. 2010b, ApJ, 725, 134 [Google Scholar]
- Peters, T., Mac Low, M.-M., Banerjee, R., Klessen, R. S., & Dullemond, C. P. 2010c, ApJ, 719, 831 [Google Scholar]
- Pols, S., Schwörer, A., Schilke, P., et al. 2018, A&A, 614, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2014, ApJ, 783, 130 [Google Scholar]
- Rivera-Soto, R., Galván-Madrid, R., Ginsburg, A., & Kurtz, S. 2020, ApJ, 899, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Rolffs, R., Schilke, P., Wyrowski, F., et al. 2011, A&A, 529, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez-Monge, Á., Kurtz, S., Palau, A., et al. 2013, ApJ, 766, 114 [Google Scholar]
- Sánchez-Monge, Á., Schilke, P., Schmiedeke, A., et al. 2017, A&A, 604, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schilke, P., Walmsley, C. M., Pineau des Forets, G., & Flower, D. R. 1997, A&A, 321, 293 [NASA ADS] [Google Scholar]
- Schmiedeke, A., Schilke, P., Möller, T., et al. 2016, A&A, 588, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwörer, A., Sánchez-Monge, Á., Schilke, P., et al. 2019, A&A, 628, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitzer, L.J. 1968, Interscience Tracts on Physics and Astronomy, 28 [Google Scholar]
- Wilson, T. L., Rohlfs, K., & Hüttemeister, S. 2013, Tools of Radio Astronomy (Heidelberg: Springer-Verlag Berlin) [Google Scholar]
- Wood, D. O. S., & Churchwell, E. 1989, ApJS, 69, 831 [Google Scholar]
Appendix A RMS maps
The rms maps were generated using SExtractor (Bertin & Arnouts 1996). Although the core identification was performed by eye, SExtractor produces rms maps as side-products of automated core identification. The rms maps are shown in Fig. A.1.
Appendix B: Tables
Appendix C: SiO Images
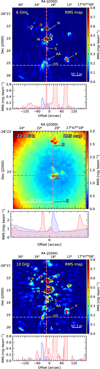 |
Fig. A.1 RMS maps of 6 GHz, 22.4 GHz, and 96 GHz. The resolutions are given in Sect. 2. Each image has two profile cuts, in blue and red. To better show the features and maxima of the rms of each image, the offset is different for each of the three images. The offset of each profile increases from left to right and from bottom to top. The profile is below each image. |
 |
Fig. C.1 Peak intensity map of SiO (5-4) line. The zoomed-in plots are the regions in SgrB2(DS) with abundant outflows. The resolution of the image is 0.35″× 0.24″, with PA. of −80°. The dust cores identified by Ginsburg et al. (2018) are shown as green circles, whose size is not scaled to the size of the cores. |
 |
Fig. C.2 Moment 1 map of SiO (5-4) line. The zoomed-in plots are the regions in SgrB2(DS) with abundant outflows. The resolution of the image is 0.35″× 0.24″, with P.A. of −80°. The dust cores identified by Ginsburg et al. (2018) are shown as green circles, whose size is not scaled to the size of the cores. |
Observed parameters.
Derived parameters
Which cores in Ginsburg et al. (2018) are associates with outflows.
All Tables
All Figures
 |
Fig. 1 Sources identified in the 6 cm image. Those objects shown as white and blue circles have radii of robs6 (see Table B.1). Notable Hii regions are indicated. The Hii regions that are masked out for core identification are shown as white contours. The beam size is given in the lower left corner of the main panel (θmaj, θmin, PA). The spatial coverage of the 22.4 GHz image is shown as a blue dashed box. |
| In the text | |
 |
Fig. 2 Probability distribution of S6 (pink), plotted as a kernel density estimation. Mean and median values are indicated. The distributions of S22 (green) and S96 (blue) are also shown. |
| In the text | |
 |
Fig. 3 Relation between robs6 and rcaic of the 39 compact sources with 22.4 GHz detection. The dashed curve indicates the deconvolution relationship |
| In the text | |
 |
Fig. 4 Distribution of EM. The mean and median values are indicated. |
| In the text | |
 |
Fig. 5 Distribution of ne. The mean and median values, which are both ~105 cm−3, are indicated. |
| In the text | |
 |
Fig. 6 Distribution of NLy. The corresponding spectral type of the ionizing stars (assuming that the Hπ regions are ionized by single stars) are indicated. |
| In the text | |
 |
Fig. 7 Comparison between rcalc (left), EM (middle), and NLy (right) of 33 sources and the corresponding parameters found by Gaume et al. (1995). |
| In the text | |
 |
Fig. 8 Diagram of rcalc and ne. Previously derived rcalc–ne relationships for UCHII regions from Garay & Lizano (1999), ne = 780 × (2r)−1.19, and from Kim & Koo (2001), ne = 790 × (2r)−∞, are plotted as dashed lines. The green shading indicates the typical ne of UCHII regions, which is from ~104 cm−3 to ~106 cm−3, and the typical r of UCHII regions, which is ~0.015 to ~0.05 pc (Kurtz 2005). |
| In the text | |
 |
Fig. 9 Probability distribution of |
| In the text | |
 |
Fig. 10 Evolution sequence of the HII regions. The circles are calculated with the dust density derived from the 96 GHz image. The triangles are calculated with the dust density of 2 × 107 cm−3. The color of the markers indicates the expansion timescale. |
| In the text | |
 |
Fig. 11 Diagram of ne and |
| In the text | |
 |
Fig. 12 Modeled evolution of S6 of HII regions with time. The black line denotes the sensitivity of our 6 GHz observation, which is ~1 mJy, for unresolved sources. |
| In the text | |
 |
Fig. A.1 RMS maps of 6 GHz, 22.4 GHz, and 96 GHz. The resolutions are given in Sect. 2. Each image has two profile cuts, in blue and red. To better show the features and maxima of the rms of each image, the offset is different for each of the three images. The offset of each profile increases from left to right and from bottom to top. The profile is below each image. |
| In the text | |
 |
Fig. C.1 Peak intensity map of SiO (5-4) line. The zoomed-in plots are the regions in SgrB2(DS) with abundant outflows. The resolution of the image is 0.35″× 0.24″, with PA. of −80°. The dust cores identified by Ginsburg et al. (2018) are shown as green circles, whose size is not scaled to the size of the cores. |
| In the text | |
 |
Fig. C.2 Moment 1 map of SiO (5-4) line. The zoomed-in plots are the regions in SgrB2(DS) with abundant outflows. The resolution of the image is 0.35″× 0.24″, with P.A. of −80°. The dust cores identified by Ginsburg et al. (2018) are shown as green circles, whose size is not scaled to the size of the cores. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.