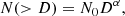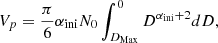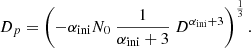| Issue |
A&A
Volume 665, September 2022
|
|
|---|---|---|
| Article Number | L9 | |
| Number of page(s) | 13 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202244590 | |
| Published online | 22 September 2022 | |
Letter to the Editor
Athor asteroid family as the source of the EL enstatite meteorites
1
Université Côte d’Azur, CNRS – Lagrange, Observatoire de la Côte d’Azur, CS 34229, 06304 Nice Cedex 4, France
e-mail: chrysa.avdellidou@oca.eu
2
Southwest Research Institute, 1050 Walnut St. Suite 300, Boulder, CO 80302, USA
3
Université Côte d’Azur, CNRS – Géoazur, Observatoire de la Côte d’Azur, 250 rue Albert Einstein, Sophia Antipolis, 06560 Valbonne, France
4
LESIA, Université Paris Cité, Observatoire de Paris, Université PSL, Sorbonne Université, CNRS, 92190 Meudon, France
5
Arecibo Observatory, University of Central Florida, HC-3 Box 53995 Arecibo, PR 00612, USA
6
Institut Universitaire de France (IUF), 1 rue Descartes, 75231 Paris Cedex 05, France
7
Muséum National d’Histoire Naturelle, Sorbonne Universités, CNRS, IMPMC – UMR CNRS 7590, 57 rue Cuvier, 75005 Paris, France
8
Lowell Observatory, 1400 West Mars Hill Road, Flagstaff, AZ 86001, USA
Received:
24
July
2022
Accepted:
30
August
2022
The identification of meteorite parent bodies provides the context for understanding planetesimal formation and evolution as well as the key Solar System events they have witnessed. However, identifying such links has proven challenging and some appear ambiguous. Here, we identify that the family of asteroid fragments whose largest member is (161) Athor is the unique source of the rare EL enstatite chondrite meteorites, the closest meteorites to Earth in terms of their isotopic ratios. The Athor family was created by the collisional fragmentation of a parent body 3 Gyr ago in the inner main belt. We calculate that the diameter of the Athor family progenitor was 64 km in diameter, much smaller than the putative size of the EL original planetesimal. Therefore, we deduce that the EL planetesimal that accreted in the terrestrial planet region underwent a first catastrophic collision in that region, and one of its fragments suffered a more recent catastrophic collision in the main belt, generating the current source of the EL meteorites.
Key words: minor planets, asteroids: general / meteorites, meteors, meteoroids / techniques: spectroscopic / catalogs
© C. Avdellidou et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
It is established that meteorites were formed inside planetesimals that accreted in our protoplanetary disc 4.5 Gyr ago (Johansen et al. 2015), while current main belt asteroids are derived from the leftovers of the aforementioned planetesimals. In the main belt, subsequent collisional evolution over 4.5 Gyr further destroyed some planetesimals by breaking them to create families of smaller asteroid fragments (Nesvorny et al. 2015), and therefore the few surviving planetesimals currently coexist with millions of asteroid fragments (Delbo et al. 2017, 2019). These small asteroid fragments suffer orbital mobility due to non-gravitational forces (Vokrouhlický et al. 2015), which can drive them into zones of orbital instability, where their orbital eccentricity typically increases, leading to Earth-crossing orbits (Bottke et al. 2006). These fragments can therefore impact Earth, producing meteorites. Meteorites, which are the debris of a primary parent asteroid that broke and produced a family of smaller fragments (secondary parents; Greenwood et al. 2020), can come directly from a main belt source. Another pathway is that whereby the secondary parent asteroids (the family members), via the aforementioned orbital instability zones, become near-Earth asteroids (NEAs), from which debris can detach and produce meteorites.
According to these scenarios, a meteorite or a meteorite type is putatively linkable to a family of secondary parent asteroids, which themselves can be linked to a primary parent asteroid (family progenitor), and ultimately to an original planetesimal (Greenwood et al. 2020). Establishing this linkage allows us to gain insight into planetesimal composition, original size, formation time, and, indirectly, the heliocentric distance of its accretion zone (Henke et al. 2012; Trieloff et al. 2022). The heliocentric distance can be inferred from the isotopic abundance ratio of some elements in meteorites, whereas the planetesimal size can be estimated by fitting size-dependent thermal evolution models to meteorite cooling curves determined by the isotopic thermochronometers (Henke et al. 2012; Trieloff et al. 2022).
The linkage between meteorites and parent bodies requires several conditions to be met: (i) the putative parent should be associated with a family of collisional fragments, and (ii) the reflectance spectra of family members, their albedo, and colours should be consistent with those measured for the meteorites, considering space weathering alteration (Vernazza et al. 2009; Brunetto et al. 2015). Further supporting information may come from the pre-atmospheric orbit of the meteoroid that produced the meteorite (Spurný et al. 2003; Jenniskens et al. 2009) and the cosmic-ray exposure times (CRE) of similar meteorites, indicating common origin from their secondary parent bodies.
The most undisputed linkage is between the Howardites, Eucrites, and Diogenites (HEDs) meteorites, the Vesta asteroid family (Vestoids), and the asteroid (4) Vesta itself (Russell et al. 2012), with the latter being the primary parent as well as the surviving planetesimal. Moreover, the high-albedo Hungaria family is associated with the enstatite achondrite meteorites (aubrites; Lucas et al. 2019). Additionally, broader associations have been made between the asteroids belonging to the spectroscopic S and C complexes and the ordinary and carbonaceous chondrite meteorites, respectively (Reddy et al. 2015; DeMeo et al. 2022). However, the S- and C-complex main belt asteroid families are numerous (Nesvorny et al. 2015), complicating the search for unique linkages between the different subtypes of ordinary and carbonaceous chondrites and their respectively sources.
On the other hand, the search for meteorites linkable to X-complex families benefits from the advantage that (i) such families are far less numerous, and (ii) the different meteorite types with reflectance spectra within the X-complex, such as the enstatite chondrites (ECs; Vernazza et al. 2009), the aubrites (enstatite achondrites; Gaffey et al. 1992), some types of carbonaceous chondrites (DeMeo et al. 2015), the mesosiderites (Vernazza et al. 2009), and the metallic meteorites (Cloutis et al. 1990), can be distinguished on the basis of weak spectral features and absolute reflectance values (related to albedo). Specifically, the ECs correspond to 2% of all chondrites (Norton & Chitwood 2008) and are divided into the higher and lower iron content EH and EL classes respectively, which contribute equal numbers of meteorites to our collection. Both EHs and ELs have similar oxygen isotopic compositions (Clayton & Mayeda 1996; Herwartz et al. 2014), yet some incompatibilities have been emphasised. In particular, Lin & El Goresy (2002) showed that the chemical and petrography of the EHs and ELs are incompatible with a common parent body, where EHs have a higher Mg/Si ratio than the ELs (Keil 1968). EHs and ELs also have very distinct cooling rates and heating histories, suggesting distinct parents (Zhang et al. 1995; Lin & El Goresy 2002). Each class can be subdivided into different petrologic types that experienced specific degrees of thermal metamorphism: for example, type 6 chondrites were heated to higher metamorphic peak temperatures than those of type 3. ECs are all completely dry as no ECs of petrologic types 1 or 2 have been found. A possible model for the early evolution of their parents is an onion-shell-layered body (Trieloff et al. 2003, 2022). On the other hand, the enstatite achondrites formed from EC-like material on at least two separate parent bodies; one indicated from the peculiar Shallowater meteorite and another one for all the other aubrites. They are nearly monomineralic enstatite pyroxenites, consisting mostly of nearly FeO-free enstatite and other rare minerals that formed under highly reducing conditions (Keil 2010).
Here we study the ELs because the new discovery that thermo-chronometers inside them define the cooling history of the original EL planetesimal allows us to constrain its size (Trieloff et al. 2022). Therefore, identifying the main belt source and parenthood of the ELs offers a unique opportunity to study the formation and evolution of the EL original planetesimal.
2. Global search of the EL parent body
There are 15 putative X-complex families (Nesvorny et al. 2015; Delbo et al. 2019) and, as a first criterion, we investigated which of them have geometric albedo values (pV) compatible with those of the ELs. To do so, first we retrieved all the EL spectra from the Reflectance Experiment Laboratory (RELAB) and the Planetary Spectrophotometer Facility (PSF) meteorite spectra databases and using the method of Beck et al. (2021) we calculated their average geometric visible albedo pV and its standard deviation, finding a value between 0.11 and 0.23 (Fig. 1B). For each of these asteroid families, we then retrieved from the Minor Planet Physical Properties Catalogue the pV-values of their members, and computed their average (Table A.1). Twelve families can be excluded as the source of the ELs because their average pV-values are out of the range of the ELs (Fig. 1B). Finally, the San Marcello family has an average pV = 0.177 that is within the range of the ELs (original membership from Nesvorny et al. 2015), but we excluded it as a source of ELs because (i) Broz et al. (2022) proposed that asteroid (22) Kalliope is the potential progenitor of the family, which could be a differentiated body; (ii) the pV-values of its members span a large range between 0.1 and 0.35 (Broz et al. 2022), which could also indicate the presence of a large number of interlopers; and (iii) the position of the San Marcello family in the outer main belt does not favour the delivery of meteorites. The remaining two families with pV-values compatible with the ELs, namely Athor and Zita, are located in the inner main belt, and are therefore dynamically favoured to deliver meteorites (Delbo et al. 2019).
 |
Fig. 1. Reflectance spectrum of the Athor family and meteorites. (A) Average spectra of Athor and Zita family members, which are clearly distinct, while the curve-matching of EL spectra with the average Athor family spectrum is evident. For comparison, we present three spectra of two EL6 meteorites, Hvittis and Pillistfer, that best-matched with the Athor family. (B) 1.8/0.8 μm reflectance ratio versus the geometric visible albedo of the Athor family and the individual meteorite spectra (CM2 and CV) that achieved a curve-matching with Athor in the first step of the analysis. Another curve-matched meteorite is a bright enstatite achondrite (aubrite) that lies out of the range of the plot (Table B.3). For ELs and EHs, we present the respective averages. The properties of the Athor family members and the ELs overlap, whereas the other meteorite classes are clearly distinct. |
3. Spectroscopic observations of potential EL sources
In order to study the potential link between the Athor and Zita families and ELs, we carried out a spectroscopic observational campaign (Appendix B.1, Table B.1), characterised the asteroid reflectances and their spectroscopic types (Appendix B.2, Table B.2), and re-assessed the family membership (Table B.2). Observations were performed mainly in the near-infrared wavelength range using the SpeX instrument at the NASA Infrared Telescope Facility, while in some cases we also performed visible spectroscopic observations using the Copernico Telescope and the Lowell Discovery Telescope (Table B.1). We combined our results with the literature data (Fig. B.1).
In total, we observed 39 members of both families (Appendix B.1) according to the family membership of Delbo et al. (2019), and found a bimodal distribution of their near-infrared spectral reflectance slopes with the two groups clearly separating at 15% μm−1 (Fig. B.2). These groups have mean and standard deviation of 8.3 ± 3% μm−1 and 21 ± 2.3% μm−1, respectively (Fig. B.2), being separated by more than 4σ. Even if we adopt the 4.2% μm−1 SpeX statistical uncertainty of reflectance calibration (Marsset et al. 2020) as standard deviation, the centres of the two groups are separated by more than 3σ. We deduced that the two groups are real, and therefore Athor and Zita families can be distinguished in the near-infrared. The first group predominantly occurs in Athor family and the second in Zita.
Next, we classified each asteroid reflectance in the Bus-DeMeo taxonomy (DeMeo et al. 2009) following established methods (Appendix B.2, Table B.2). The spectrum of the Xc-type is the most recurrent within the Athor-type group. Where applicable, the Xe- and Ch/Cgh-type matches were not preferred as previous dedicated studies showed that Xe-type asteroids have very high pV-values (Lucas et al. 2019), while Ch/Cgh-type have low pV-values, both incompatible with those of Athor family members (Table B.2). In the case of the Zita-type group, the best spectral matches were with Xk-, X-, and T-types.
3.1. Re-assessment of family membership
Given our spectroscopic results, we proceeded to a reassessment of the family membership. This was needed because the identification of family members on the basis of clustering in orbital elements and the correlations between the orbital proper semi-major axis and the inverse diameter (V-shape criterion, see Bolin et al. 2017; Delbo et al. 2017) is only a rough expression of the true membership (Nesvorny et al. 2015). This means that asteroids unrelated to a family can happen to have values of proper elements within the orbital range of that family, and are therefore grouped together with the true members. This problem could be particularly significant for Athor and Zita families, which are extensively overlapping in the orbital elements, and their members have similar pV-values and visible spectrophotometry (Delbo et al. 2019).
It is natural to attempt to assign Athor members with Zita-type spectra to the Zita family and vice versa. However, we carefully inspected (i) whether or not the Zita-type asteroids that were originally assigned to the Athor family (Delbo et al. 2019) are placed inside the V-shape of Athor family, and (ii) whether or not their orbital elements are overlapping with the Zita family as well, and vice versa. We also visually inspected the spectra of each asteroid in order to assess the possibility that they were spectrally misclassified, that is, members of Athor and Zita are required to be within the spectroscopic X-complex. We find that asteroids (10 309) and (21 475), previously classified within the X-complex on the basis of spectrophotometric data and consequently originally included in Zita family, are in reality S-types, and should therefore be excluded from the Zita family. Asteroid (68 750), originally included in the Athor family (Delbo et al. 2019), is likely a low-albedo C-complex object and should therefore be excluded from the Athor family. Asteroid (757) has been reported in the literature as an Xk-type (Clark et al. 2009), but visual inspection shows that this literature spectrum is intermediate between that of an Xk- and an Xc-type. Moreover, we calculated the near-infrared slope of the Clark et al. (2009) spectrum and find that it is within the Athor-type slope range. We also note that asteroid (757) cannot be assigned to Zita on the basis of its position in the (ap, 1/D) space because it is outside the V-shape of Zita family, hence we kept it in Athor family.
We find that 17 out of 21 asteroids observed from the core of the Athor family have an Athor-type spectrum and at 95% significance level; this corresponds to 81 ± 15% of the total Athor core population that counts 110 members. Of these 21 observed asteroids, 3 have a Zita-type spectrum and indeed belong to the Zita family (Table B.2). In the halo of Athor, which is a part of the family that has a far lower member number density than the core, we find that four out of eight asteroids (50%) are Athor-types, the the remaining members being Zita-type. The asteroids with a Zita-type spectrum but originally assigned to the Athor halo could indeed belong to the Zita family because they lay inside the V-shape and the proper element range of the latter. The number of objects that we observed is sufficient to also ensure the statistical significance of our findings.
Finally, we calculated the average spectrum for the members of the families (Appendix B.3, Fig. 1A). The average spectrum of the Athor family is in very good agreement with the Xc-type of the Bus-DeMeo taxonomy, while the average spectrum of the Zita family has a slope similar to the X/T-types but also shows the presence of the 0.9 μm band, a characteristic of the Xk-types, placing Zita in an intermediate position between Bus-DeMeo taxonomic types. Furthermore, we calculated the uncertainty-weighed pV of the Athor and Zita families using the inverse of the uncertainty squared as weights. We selected this method as it combines measurements of the same quantity (pV) obtained with different instruments or phases of space missions, which therefore have different accuracy. For the Athor family, we find that pV = 0.19 ± 0.05, while for Zita we obtain pV = 0.13 ± 0.03. The Zita family appears darker than the Athor family, but their average pVs are within 1σ of uncertainty.
4. Spectral match of the Athor family to the ELs
We followed well-established approaches (Appendix B.3), consisting in (i) curve-matching (Popescu et al. 2012) between the average reflectance spectrum of the Athor family and meteorite spectra from RELAB and PSF, and (ii) comparison of the absolute reflectances of meteorites at 0.56 μm and their reflectance ratio at 1.8/0.8 μm (Cloutis et al. 2010; Beck et al. 2021) against the respective quantities of Athor family members (Fig. 1B). We find that Athor family spectroscopically matches with ELs, EHs, some carbonaceous chondrites, and one aubrite (Table B.3). This is because the reflectance spectral curve of ELs may not be unique amongst meteorites. However, only the ELs have albedo values within the range of the Athor family (Fig. 1), concluding that ELs are the only known meteorites that can be matched to the Athor family. The effects of space weathering are not sufficiently significant to change the spectral slope or albedo of the ELs (Vernazza et al. 2009), implying that the direct match between asteroid and meteorite spectra is satisfactory (Fig. 1).
There is additional evidence of the link between the Athor family and the EL meteorites. First of all, the absence of 3 μm features from the asteroid (161) Athor itself has been reported (Rivkin et al. 2000; Usui et al. 2018), which can be used as an indication that the Athor family progenitor was not hydrated. The uniqueness of the link is also supported by (i) well-established thermal models of EL thermo-chronometers, which show that the meteorites used (all EL6) originate from the same depth of a single parent body (Trieloff et al. 2022), and (ii) the very narrow distribution of the CRE ages of the ELs, which means that they share a common travel history from their source to Earth (Trieloff et al. 2022). The only EL that was observed while entering Earth’s atmosphere is the Neuschwanstein. This meteorite, before reaching the ground, had semi-major axis and inclination values (Spurný et al. 2003) inside the range of the Athor family (Delbo et al. 2019), demonstrating that the latter can deliver ELs to Earth. Moreover, EL pieces are found in the Almahata Sitta multi-lithology meteorites, whose parent body was asteroid 2008 TC3 (Zolensky et al. 2010). This body has 82% probability of being delivered to near-Earth space from the inner main belt, where the Athor family is also located. Therefore, it is reasonable to hypothesise that EL pieces coming from the Athor family were implanted via collisions on the 2008 TC3 parent body. We conclude that Athor is the only asteroidal source of the ELs.
5. The size of the Athor family progenitor
What was the size of the Athor family progenitor, before it was collisionally disrupted forming a family? An asteroid family loses members over time due to their collisional disruption and by orbital semi-major axis drift caused by non-gravitational forces that push them into zones of orbital instability (Nesvorny et al. 2015), as detailed earlier. Starting from different possible initial size distributions of the Athor family, we modelled their dynamical and collisional evolution until we found the one best matching with the observed family members (Appendix C, Fig. C.1). By integrating all of the volume from this initial size distribution, we deduce that the Athor family progenitor had a diameter of 64 km before its catastrophic disruption (Appendix C.1), leading to the formation of the Athor family, which is best fit at 3.0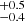 Gyr ago (Delbo et al. 2019). Given the method of Athor family identification (Delbo et al. 2017, 2019), it is likely that those members that contribute most of the volume have been identified.
Gyr ago (Delbo et al. 2019). Given the method of Athor family identification (Delbo et al. 2017, 2019), it is likely that those members that contribute most of the volume have been identified.
6. Discussion
We show that the ELs originate from a family of asteroid fragments (EL secondary parents), where asteroid (161) Athor is the largest fragment. The link that we find between the Athor family and the ELs is consistent with other works (Vernazza et al. 2009; DeMeo et al. 2022), which indicated that ELs have spectra similar to asteroids classified as Xc-types; indeed, we classified the reflectance spectra of (161) Athor and the Athor family as Xc-type.
How unique is this link? We demonstrated that given the Athor family average reflectance spectrum, only ELs, amongst all meteorites, produce a match with the reflectance spectral curve and the albedo values, and that Athor is the only known collisional family with these characteristics. However, the uniqueness of the EL reflectance spectrum amongst main belt asteroids that are outside the Athor family is another open question. In the search for an answer, we proceeded as follows: First, we calculated the average reflectance spectrum of all the ELs present in the RELAB and PSF databases after their normalisation to 1 at 0.55 μm. We find that the EL reflectance spectra have very small dispersion with a relative standard deviation of < 2.5% between 0.7 and 2.5 μm, implying that EL spectra are very similar to each other. Using the method described in Appendix B.2, we then found that only the Xc and the Xe Bus DeMeo spectral types provide a spectral curve match to the normalised reflectance spectra of ELs. However, the absolute reflectance value (pV) of Xe is out of the range of ELs. We therefore deduce that only Xc asteroids with pV between 0.11 and 0.23 provide a good match to the ELs.
In addition to the Athor family members, we also pinpointed nine asteroids that appear to be Xc-types with pV values in the EL range. These are (21) Lutetia, (97) Klotho, (129) Antigone, (224) Oceana, (242) Kriemhild, (1541) Estonia, (2349) Kurchenko, (2567) Elba, and (5632) Ingelehmann (Fig. A.1). Apart from (21), (97), (129), and (224), these asteroids do not have a known near-infrared spectrum to confirm their Xc-type. Of those, only asteroids (21) and (97) were found to spectroscopically match the ELs (Vernazza et al. 2009), but only (21) resides in the inner main belt, which is a condition that dynamically favours the delivery of meteorites. All the rest are located at semi-major axes far from meteorite feeding zones (e.g. ν6 and 3:1 MMR). Moreover, none of the asteroids above are associated with a collisional family; we survey all potential X-complex families in section 2, and find it to be unlikely that any of those are the sources of the ELs that we receive on Earth, although they could indeed have an EL composition.
We calculated that the size of the Athor family progenitor (the parent body of the family), finding a value of 64 km in diameter. However, the most likely diameter of the EL original planetesimal is 240–420 km, as is estimated by best-fitting thermal evolution models to EL thermo-chronometric data (Trieloff et al. 2022). A planetesimal of the size of the Athor family progenitor would have been too small and would therefore have had an excessively fast cooling rate to be consistent with the EL thermo-chronometers, which instead indicate a slow cooling rate (Trieloff et al. 2022).
The only possibility to explain the size difference between the Athor family progenitor and the original EL planetesimal is that the Athor family progenitor was a 64 km-diameter collisional fragment of the much larger EL planetesimal (Fig. 2). If the latter had suffered the break up collision at the current location of Athor, a larger collisional family would have been detected by methods that can identify families as old as our Solar System (Bolin et al. 2017; Delbo et al. 2017, 2019; Deienno et al. 2021). However, this large family does not exist, indicating that the breakup of the EL planetesimal did not occur in the main belt. We therefore deduce that the breakup of the original EL planetesimal happened elsewhere, most likely in the terrestrial planetary region. This is because a planetesimal with EL composition most likely accreted in the terrestrial region of our planetary disc (Kallemeyn & Wasson 1986; Zhang et al. 1995), as suggested from its striking isotopic similarity with the Earth and the similar low-oxygen fugacity (Javoy et al. 2010; Dauphas 2017). Differences in chemical composition between ELs and the Earth can be explained via a fractionated condensation sequence starting from the same parent material (Morbidelli et al. 2020); hence, this should not be interpreted as an argument against the Earth-EL relationship.
 |
Fig. 2. Collisional history of the EL original planetesimal. The EL planetesimal accreted in the terrestrial planet region where it suffered a collisional event. A fragment of it –the Athor family progenitor– was transported to the current location of Athor in the inner main belt by a dynamical process. About 900 Myr later, the Athor family progenitor suffered an additional collisional event that led to the formation of the present Athor family. Meteorites are now transported from the Athor family to Earth via well-established routes. |
Additional evidence that the current source of the ELs is a piece of a larger planetesimal comes from the study of the EL metamorphic grades. According to the thermal-evolution models (Trieloff et al. 2022), the EL planetesimal should have formed a large core of EL material of a high metamorphic grade 6 or 7, which was surrounded by thinner layers of lower metamorphic grades towards the surface (from EL5 to EL3). Although the known ELs sample all metamorphic grades, the EL3, EL4, and EL5 are small fractions of the total collection, which instead is dominated by the EL6. This indicates that the ELs come from a parent body (Athor family progenitor) of mainly EL6 composition, and therefore sample only a fraction of the original EL planetesimal, mostly the interior. This is supported by the fact that during the curve matching with the literature meteoritic spectra, the Athor family average spectrum matches better with EL6 (Table B.3). However, this EL Athor family progenitor should have also re-accumulated lower grade EL material from the upper layers of the EL original planetesimal during the initial collision in the terrestrial region, explaining the small presence of EL3-5 in the collections.
How could the EL Athor family progenitor be transported from the terrestrial planet region to the Athor family current location in the main belt? Several dynamical mechanisms have been proposed that could have led to the implantation of planetesimals from the terrestrial region to the main belt at the very early stages following the formation of the Solar System (Bottke et al. 2006; Raymond & Izidoro 2017). Further analysis of the properties of the EL original planetesimal may provide constraints on the time of its initial breakup and subsequent implantation into the main belt. This will clarify whether the existing implantation mechanisms are valid or a new dynamical mechanism is needed. The fact that original planetesimals underwent catastrophic collisions out of the belt and that their pieces were later implanted into the main belt means that some of the leftover planetesimals from the main belt accreted larger than what is observed. This will have implications for the original size frequency distribution of the planetesimals (Delbo et al. 2017, 2019), which could be conservative at present.
7. Conclusions
We report the discovery of a unique source of the rare EL enstatite chondrite meteorites, namely the Athor asteroid family. The EL original planetesimal accreted in the terrestrial region and a comparison of its size to that of the Athor family progenitor suggests that the former broke via an impact, and a fragment of it (the progenitor of Athor) was transported into the inner main belt. The latter suffered a new catastrophic collision, forming the currently observed Athor family.
Acknowledgments
We acknowledge support from the ANR ORIGINS (ANR-18-CE31-0014). CA was supported by the French National Research Agency under the project “Investissements d’Avenir” UCAJEDI (ANR-15-IDEX-01) and by a European Space Agency Research Fellowship. AM acknowledges support from the ERC advanced grant HolyEarth N. 101019380. KJW acknowledges support through Project ESPRESSO, a NASA SSERVI program at SwRI. CA and MD were Visiting Astronomers at the Infrared Telescope Facility, which is operated by the University of Hawaii under contract 80HQTR19D0030 with the National Aeronautics and Space Administration. This work is partially based on observations collected at Copernico telescope (Asiago, Italy) of the INAF – Osservatorio Astronomico di Padova. These results made use of the Lowell Discovery Telescope at Lowell Observatory. Lowell is a private, non-profit institution dedicated to astrophysical research and public appreciation of astronomy and operates the LDT in partnership with Boston University, the University of Maryland, the University of Toledo, Northern Arizona University and Yale University. The upgrade of the DeVeny optical spectrograph has been funded by a generous grant from John and Ginger Giovale and by a grant from the Mt. Cuba Astronomical Foundation. This work is based on data provided by the Minor Planet Physical Properties Catalogue (MP3C) of the Observatoire de la Côte d’Azur (mp3c.oca.eu). Meteorite spectra acquired from the NASA RELAB facility (Brown University) and Planetary Spectrophotometer Facility (University of Winnipeg) databases. We thank S.J. Bus, A.C.A. Boogert and the IRTF telescope operators for their help during the observations. We thank Thomas Burbine for his comments, allowing us to improve the manuscript.
References
- Alí-Lagoa, V., Müller, T. G., Usui, F., & Hasegawa, S. 2018, A&A, 612, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, P., Schmitt, B., Potin, S., Pommerol, A., & Brissaud, O. 2021, Icarus, 354, 114066 [NASA ADS] [CrossRef] [Google Scholar]
- Bida, T. A., Dunham, E. W., Massey, P., & Roe, H. G. 2014, in Ground-based and Airborne Instrumentation for Astronomy V, eds. S. K. Ramsay, I. S. McLean, & H. Takami, SPIE Conf. Ser., 9147, 91472N [NASA ADS] [Google Scholar]
- Bolin, B. T., Delbo, M., Morbidelli, A., & Walsh, K. J. 2017, Icarus, 282, 290 [CrossRef] [Google Scholar]
- Bottke, W. F., Durda, D. D., Nesvorný, D., et al. 2005, Icarus, 179, 63 [Google Scholar]
- Bottke, W. F., Nesvorný, D., Grimm, R. E., Morbidelli, A., & O’Brien, D. P. 2006, Nature, 439, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Broz, M., Ferrais, M., Vernazza, P., Sevecek, P., & Jutzi, M. 2022, A&A, 664, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brunetto, R., Loeffler, M. J., Nesvorný, D., Sasaki, S., & Strazzulla, G. 2015, in Asteroids IV, eds. P. Michel, F. E. DeMeo, W. F. Bottke, et al., 597 [Google Scholar]
- Bus, S. J., & Binzel, R. P. 2002, Icarus, 158, 106 [CrossRef] [Google Scholar]
- Carvano, J. M., Hasselmann, P. H., Lazzaro, D., & Mothé-Diniz, T. 2010, A&A, 510, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clark, B. E., Ockert-Bell, M. E., Cloutis, E. A., et al. 2009, Icarus, 202, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Clayton, R. N., & Mayeda, T. K. 1996, Geochim. Cosmochim. Acta., 60, 1999 [NASA ADS] [CrossRef] [Google Scholar]
- Cloutis, E. A., Gaffey, M. J., Smith, D. G. W., & Lambert, R. S. J. 1990, J. Geophys. Res., 95, 8323 [NASA ADS] [CrossRef] [Google Scholar]
- Cloutis, E. A., Hardersen, P. S., Bish, D. L., et al. 2010, MAPS, 45, 304 [NASA ADS] [Google Scholar]
- Cushing, M. C., Vacca, W. D., & Rayner, J. T. 2004, PASP, 116, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Dauphas, N. 2017, Nature, 541, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Deienno, R., Walsh, K. J., & Delbo, M. 2021, Icarus, 357, 114218 [NASA ADS] [CrossRef] [Google Scholar]
- Delbo, M., Walsh, K., Bolin, B., Avdellidou, C., & Morbidelli, A. 2017, Science, 357, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Delbo, M., Avdellidou, C., & Morbidelli, A. 2019, A&A, 624, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- DeMeo, F. E., & Carry, B. 2013, Icarus, 226, 723 [NASA ADS] [CrossRef] [Google Scholar]
- DeMeo, F. E., Binzel, R. P., Slivan, S. M., & Bus, S. J. 2009, Icarus, 202, 160 [Google Scholar]
- DeMeo, F. E., Alexander, C. M. O., Walsh, K. J., Chapman, C. R., Binzel, R. P., et al. 2015, in Asteroids IV, eds. P. Michel, F. E. DeMeo, W. F. Bottke, et al. [Google Scholar]
- DeMeo, F. E., Burt, B. J., Marsset, M., et al. 2022, Icarus, 380, 114218 [Google Scholar]
- Devogèle, M., Moskovitz, N., Thirouin, A., et al. 2019, AJ, 158, 196 [CrossRef] [Google Scholar]
- Dohnanyi, J. S. 1969, J. Geophys. Res., 74, 2531 [Google Scholar]
- Fornasier, S., Lazzarin, M., Barbieri, C., & Barucci, M. A. 1999, A&AS, 135, 65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fornasier, S., Clark, B. E., Dotto, E., et al. 2010, Icarus, 210, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Gaffey, M. J., Reed, K. L., & Kelley, M. S. 1992, Icarus, 100, 95 [CrossRef] [Google Scholar]
- Gayon-Markt, J., Delbo, M., Morbidelli, A., & Marchi, S. 2012, MNRAS, 424, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Greenwood, R. C., Burbine, T. H., & Franchi, I. A. 2020, Geochim. Cosmochim. Acta., 277, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Gulbis, A. A. S., Bus, S. J., Elliot, J. L., et al. 2011, PASP, 123, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Henke, S., Gail, H. P., Trieloff, M., Schwarz, W. H., & Kleine, T. 2012, A&A, 545, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herwartz, D., Pack, A., Friedrichs, B., & Bischoff, A. 2014, Science, 344, 1146 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezić, Ž., Tabachnik, S., Rafikov, R., et al. 2001, AJ, 122, 2749 [Google Scholar]
- Javoy, M., Kaminski, E., Guyot, F., et al. 2010, Earth Planet. Sci. Lett., 293, 259 [CrossRef] [Google Scholar]
- Jenniskens, P., Shaddad, M. H., Numan, D., et al. 2009, Nature, 458, 485 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Johansen, A., Jacquet, E., Cuzzi, J. N., Morbidelli, A., Gounelle, M., et al. 2015, in Asteroids IV, eds. P. Michel, F. E. DeMeo, W. F. Bottke, et al., 471 [Google Scholar]
- Kallemeyn, G. W., & Wasson, J. T. 1986, Geochim. Cosmochim. Acta., 50, 2153 [NASA ADS] [CrossRef] [Google Scholar]
- Keil, K. 1968, J. Geophys. Res., 73, 6945 [NASA ADS] [CrossRef] [Google Scholar]
- Keil, K. 2010, Geochemistry, 70, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Lazzaro, D., Angeli, C. A., Carvano, J. M., et al. 2004, Icarus, 172, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., & Duncan, M. J. 1994, Icarus, 108, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y., & El Goresy, A. 2002, MAPS, 37, 577 [NASA ADS] [Google Scholar]
- Lucas, M. P., Emery, J. P., MacLennan, E. M., et al. 2019, Icarus, 322, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Marsset, M., DeMeo, F. E., Binzel, R. P., et al. 2020, ApJS, 247, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., Libourel, G., Palme, H., Jacobson, S. A., & Rubie, D. C. 2020, Earth Planet. Sci. Lett., 538 [Google Scholar]
- Nesvorny, D., Broz, M., Carruba, V., et al. 2015, in Asteroids IV, eds. P. Michel, F. E. DeMeo, W. F. Bottke, et al., 297 [Google Scholar]
- Norton, O. R., & Chitwood, L. A. 2008, Field Guide to Meteors and Meteorites [CrossRef] [Google Scholar]
- Popescu, M., Birlan, M., & Nedelcu, D. A. 2012, A&A, 544, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popescu, M., Licandro, J., Morate, D., et al. 2016, A&A, 591, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raymond, S. N., & Izidoro, A. 2017, Sci. Adv., 3, e1701138 [NASA ADS] [CrossRef] [Google Scholar]
- Rayner, J. T., Toomey, D. W., Onaka, P. M., et al. 2003, PASP, 115, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, V., Emery, J. P., Gaffey, M. J., et al. 2009, MAPS, 44, 1917 [NASA ADS] [Google Scholar]
- Reddy, V., Dunn, T. L., Thomas, C. A., Moskovitz, N. A., Burbine, T. H., et al. 2015, in Asteroids IV, eds. P. Michel, F. E. DeMeo, W. F. Bottke, et al., 43 [Google Scholar]
- Rivkin, A. S., Howell, E. S., Lebofsky, L. A., Clark, B. E., & Britt, D. T. 2000, Icarus, 145, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Rozehnal, J., Brož, M., Nesvorný, D., et al. 2022, Icarus, 383, 115064 [NASA ADS] [CrossRef] [Google Scholar]
- Russell, C. T., Raymond, C. A., Coradini, A., et al. 2012, Science, 336, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Spurný, P., Oberst, J., & Heinlein, D. 2003, Nature, 423, 151 [Google Scholar]
- Tanga, P., Cellino, A., Michel, P., et al. 1999, Icarus, 141, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Trieloff, M., Jessberger, E. K., Herrwerth, I., et al. 2003, Nature, 422, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Trieloff, M., Hopp, J., & Gail, H.-P. 2022, Icarus, 373, 114762 [NASA ADS] [CrossRef] [Google Scholar]
- Usui, F., Hasegawa, S., Ootsubo, T., & Onaka, T. 2018, PASJ, 71, 1 [NASA ADS] [Google Scholar]
- Vernazza, P., Brunetto, R., Binzel, R. P., et al. 2009, Icarus, 202, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., Bottke, W. F., Chesley, S. R., Scheeres, D. J., Statler, T. S., et al. 2015, in Asteroids IV, eds. P. Michel, F. E. DeMeo, W. F. Bottke, et al., 509 [Google Scholar]
- Xu, S., Binzel, R. P., Burbine, T. H., & Bus, S. J. 1995, Icarus, 115, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y., Benoit, P. H., & Sears, D. W. G. 1995, J. Geophys. Res., 100, 9417 [NASA ADS] [CrossRef] [Google Scholar]
- Zolensky, M., Herrin, J., Mikouchi, T., et al. 2010, MAPS, 45, 1618 [NASA ADS] [Google Scholar]
Appendix A: Table of X-complex asteroid families and location of individual Xc-type asteroids
Average pV-values of potential X-complex families.
 |
Fig. A.1. The location in the main belt of nine potential Xc-type asteroids with pV values within the range of the ELs. No one of these belong to an asteroid family. |
Appendix B: Spectroscopic Analysis
B.1. Literature data and observations
Considering the Athor and Zita family membership, we initially searched for literature spectral and spectro-photometric data. Spectra exist in the near-infrared (NIR) only for (161) Athor (Bus & Binzel 2002; Fornasier et al. 2010) and (757) Portlandia (Clark et al. 2009) and in the visible (VIS) for other 22 asteroids (Table B.1). The remaining family members have at least spectrophotometric data from the Sloan Digital Sky Survey (SDSS) (Ivezić et al. 2001) and/or near-infrared colours from VISTA-VHS survey (MOVIS) (Popescu et al. 2016).
We performed new compositionally diagnostic spectroscopic observations (Table B.1) mostly in the NIR, but also in the VIS of Athor and Zita family members. We used the SpeX (Rayner et al. 2003) and MORIS instruments (Gulbis et al. 2011) at the NASA Infrared Telescope Facility (IRTF), the Near-Infrared High-Throughput Spectrograph (NIHTS; Bida et al. 2014) and the DeVeny optical spectrograph (Bida et al. 2014) at the Lowell Discovery Telescope (LDT), as well as the Asiago Faint Object Spectrograph and Camera (AFOSC) at the Copernico Telescope (Table B.1). SpeX was used with a slit 0.8 × 15″ in PRISM mode, covering wavelengths between 0.7 and 2.5 μm with a spectral resolution ∼200 in a single configuration. NIHTS covers the 0.84 to 2.4 μm range and was used with the 1.34"-wide slit. For this slit the spectral resolution is 2194 pix−1 at 1 μm, 667 pix−1 at 1.5 μm and 535 pix−1 at 2 μm. For NIR observations we used the commonly adopted ABBA observation procedure which consists in alternating our targets between two positions along the slit (A and B), therefore allowing us to remove the background contribution. DeVeny was used with the R150 grating providing a dispersion of 0.43 nm pix−1 covering a spectral range between 0.32 to 1 μm. AFOSC was used with the VPH#6 grism covering the 0.4–1.0 μm range and the 4.22"-wide slit resulting in a spectral resolution of 0.295 nm pix−1.
In the NIR, following well-established procedures (Reddy et al. 2009), we calculated the asteroid’s reflectance R(λ) as a function of the wavelength λ using Eq. B.1:
where A(λ), SL(λ), ST(λ) are the wavelength-calibrated raw spectra respectively of the asteroid, a local G2-type star observed within ∼300" of the asteroid, and a well-studied (trusted) solar analogue star that was observed at similar airmass when possible respectively (table S2). The function Poly() represents a polynomial fit of the stars ratio, excluding the regions affected by the telluric water vapour absorption (1.3 < λ< 1.5, 1.78 < λ< 2.1, and λ> 2.4 μm). Asteroid spectra were shifted to sub-pixel accuracy to align with the calibration star spectra. In general, the local star ensures accurate removal of the telluric features, but may require the slope correction 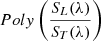 due to difference between the spectrum of the local star and that of the Sun. When the local solar analogue was not observed, the correction of the telluric features was performed directly by dividing the asteroid spectrum by that of the trusted solar analogue, i.e:
due to difference between the spectrum of the local star and that of the Sun. When the local solar analogue was not observed, the correction of the telluric features was performed directly by dividing the asteroid spectrum by that of the trusted solar analogue, i.e: 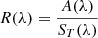 . This latter procedure is also used for visible-light spectroscopy. In the NIR we collected data with the slit oriented to the parallactic angle so that any atmospheric dispersion is along the slit, which minimises the light loss. In the VIS observations from Asiago, the rotator was not used because the 4.22" slit was large enough to compensate for differential refraction.
. This latter procedure is also used for visible-light spectroscopy. In the NIR we collected data with the slit oriented to the parallactic angle so that any atmospheric dispersion is along the slit, which minimises the light loss. In the VIS observations from Asiago, the rotator was not used because the 4.22" slit was large enough to compensate for differential refraction.
 |
Fig. B.1. NIR spectra (black points) were obtained from our survey and are presented after we applied a 2σ clipping in order to eliminate the scattered datapoints inside the telluric bands (grey areas) by as much as possible. We also present their existing VIS counterpart (grey points) obtained also from our survey or retrieved from the literature, as well as the SDSS data (red points). |
 |
Fig. B.1. continued. |
SpeX observations were reduced using the interactive data language (IDL)-based spectral reduction tool Spextool (v4.1 Cushing et al. 2004), while NITHS observations with a version of the Spextool adapted to this instrument. DeVeny data were reduced using standard reduction techniques for spectroscopy as detailed in Devogèle et al. (2019). AFOSC data were analysed using the ESO-MIDAS with standard reduction methods as detailed in Fornasier et al. (1999). In all cases we performed flat fielding and wavelength calibration, while for the VIS we also performed bias and atmospheric extinction corrections.
We also included in our analysis spectrophotometry from the SDSS MOC4 (Ivezić et al. 2001), which contains magnitudes at five spectral bands (u’, g’, r’, i’, z’) centred at 0.354, 0.477, 0.623, 0.763, and 0.913 μm, respectively Carvano et al. (2010), Gayon-Markt et al. (2012). We transformed SDSS magnitudes to reflectance values following the procedure of DeMeo & Carry (2013) and we did not use the u’ magnitudes because of their very large errors.
B.2. Classification of spectra
First, we normalised the NIR reflectances of asteroids at 1 μm and calculated their slopes between 0.8 and 2.4 μm avoiding the telluric absorption regions, as it is commonly done (Marsset et al. 2020; DeMeo et al. 2009). Next, we classified each asteroid reflectance in the Bus-DeMeo taxonomy (DeMeo et al. 2009). To do so, we performed a reflectance curve-matching by minimising value of the χ2-figure of merit (Eq. B.2):
where O(λ) is the observed asteroid reflectance (i.e. O(λ)=R(λ)), σ its uncertainty, and M(λ) the reflectance model of each Bus-DeMeo class DeMeo et al. (2009), downloaded from the Small Main-Belt Asteroid Spectroscopic Survey1. The parameter β is required to take into account that reflectances are arbitrarily normalised. For each asteroid, we calculated independently the 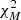 for the NIR and visible spectra as well as the SDSS spectrophotometry where applicable, and sum the results. We present the two best-matching classes in Table B.3, that is, those with the lowest and second-to-lowest
for the NIR and visible spectra as well as the SDSS spectrophotometry where applicable, and sum the results. We present the two best-matching classes in Table B.3, that is, those with the lowest and second-to-lowest 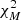 . The definition of the best spectral class is not based only on the output of the best fits, but also on the object’s pV together with the visual inspection of the spectrum. Classes such as Xe, Xk, and Ch/Cgh cannot be proposed as the best ones because the absorption bands at 0.49 μm, 0.9 μm, and 0.7 μm, respectively, are missing.
. The definition of the best spectral class is not based only on the output of the best fits, but also on the object’s pV together with the visual inspection of the spectrum. Classes such as Xe, Xk, and Ch/Cgh cannot be proposed as the best ones because the absorption bands at 0.49 μm, 0.9 μm, and 0.7 μm, respectively, are missing.
 |
Fig. B.2. NIR slopes of the asteroid members of the Athor and Zita families appear to have a bimodal distribution. The separation at around 15% μm−1 distinguishes the members of these two overlapping families, with the Zita members having the redder slopes. |
VIS and NIR observations for asteroids and calibrating stars are reported along with the telescope and instrument that was used each time. The phase angle at the time of the observations is also reported.
Summary of the asteroid members of Athor and Zita families for which either we performed spectroscopic observations or retrieved literature spectra.
B.3. Meteorite spectral matching
For each asteroid, we combined NIR, VIS, and SDSS reflectances by normalising them at 0.85 μm. The normalisation was performed by fitting a natural spline (Python csaps module) with a smoothing coefficient value of 0.9 to each reflectance independently, the values of which were divided by the values of the spline at 0.85 μm. Next, we calculated the median and the absolute median deviation (MAD) of the reflectances of the Athor members in 0.0125 μm-wide wavelength bins between 0.5 and 2.5 μm. We removed in each bin those data-points which distance was > 2 × MAD from the median; next we calculated the mean and standard deviation in each wavelength bin. The result of this computation represents the average spectra of the Athor and Zita families (Fig. 1 A).
Meteorites that satisfied the curve matching with the average spectrum of the Athor family.
In order to match the Athor family average spectrum we used the databases of the meteorite reflectance spectra from RELAB (Brown University) and PSF (University of Winnipeg). For curve matching, we performed a Monte Carlo simulation, where at each iteration, the Athor family average reflectance 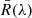 is varied within the standard deviation of the reflectance distribution of the family members
is varied within the standard deviation of the reflectance distribution of the family members 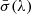 and compared to all meteorite reflectances R(λ)M. For this, we again use Eq. B.2 assigning
and compared to all meteorite reflectances R(λ)M. For this, we again use Eq. B.2 assigning 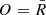 ,
, 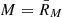 , and
, and 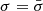 . The meteorite spectrum scoring the best comparison (minimum
. The meteorite spectrum scoring the best comparison (minimum 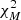 ) was recorded. After 105 Monte Carlo iterations, the distribution of scoring is a good approximation of the probability that a meteorite spectrum matches the average reflectance of Athor family members. There are 17 meteorite spectra that carry 99% of the cumulative probability to match, corresponding to nine individual meteorites of which five are enstatite chondrites (EL, EH groups), three are carbonaceous chondrites (CM2 and CV2 groups), and one is an enstatite achondrite (aubrite).
) was recorded. After 105 Monte Carlo iterations, the distribution of scoring is a good approximation of the probability that a meteorite spectrum matches the average reflectance of Athor family members. There are 17 meteorite spectra that carry 99% of the cumulative probability to match, corresponding to nine individual meteorites of which five are enstatite chondrites (EL, EH groups), three are carbonaceous chondrites (CM2 and CV2 groups), and one is an enstatite achondrite (aubrite).
Curve-matching of the reflectances is a condition necessary but not always sufficient to establish an asteroid-meteorite link (especially in the case of spectra with weak or no absorption bands). A further matching parameter is the absolute value of the reflectance, which is typically calculated at 0.56 μm. We addressed this matching at a second step. Initially, using an established procedure (Eq. 2 from Beck et al. 2021), we corrected the meteorite absolute reflectances, which are typically measured with an emission angle of 30° and incident illuminating angle 0° (phase angle 30°) to 0° of phase in order to compare them with the geometric visible albedo pV of the Athor family members. In addition, we computed the 1.8/0.8 μm reflectance ratio for the meteorites and the Athor family members in order to construct compositionally diagnostic plots (Fig. 1 B); following a well established method (Cloutis et al. 2010), we built the 1.8/0.8 μm reflectance ratio vs. 0.56 μm absolute reflectance plot for the reflectance spectra of those carbonaceous chondrites passing the curve-matching step and for all EL and EH reflectance spectra in the RELAB and PSF databases including those passing the curve-matching step. The filenames of the curve-matched meteorites are given in Table B.3.
Appendix C: Dynamical and collisional loss of Athor family members
Firstly, we estimated the size-dependent probability that an Athor family member is dynamically removed from main belt. To do so, we integrated the orbital evolution of a randomised synthetic Athor family for 3 Gyr, monitoring how many of these bodies leave the inner main belt. The code used is a modified version of SWIFT RMVS3 (Levison & Duncan 1994). Our orbital integrations included all planets except Mercury on their current orbits and also the orbital drift due to the Yarkovsky effect for all the asteroids. The large asteroids, such as Ceres and Vesta, were not included in the integrations because it has been shown (Delbo et al. 2017) that their effect in the dynamical depletion is negligible for our purposes. We modelled 375 asteroids whose diameters (D) were selected randomly from a cumulative size frequency distribution (SFD) given by Eq. C.1
where N is the number of asteroids larger than D, 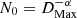 , α the cumulative slope set equal to -3, and 3 < D< 50 km (implying that DMax = 50 km). The cumulative slopes of asteroid families have been measured and modelled to be steeper (Tanga et al. 1999; Rozehnal et al. 2022) than the -2.5, meaning steeper than the collisional equilibrium of Dohnanyi (1969). On the other hand, cumulative family size slopes that are steeper than -3 lead to a mass function that cannot be integrated down to dust sizes. Therefore, we chose to run the simulation with α=-3. The selection of DMax = 50 km was done in order to account for the current largest fragment of the family; asteroid (161) Athor with D = 42±4 km (Alí-Lagoa et al. 2018). Each body was given an orbital drift rate (da/dt, Vokrouhlický et al. 2015) depending on its diameter and on random obliquity (ϵ) with a rate of 1.93 × 10−4 × cos(ϵ)×(1 km/D−1) au Myr−1. A 10-day time step was used for the integrations. Asteroids were eliminated from the simulation if their distance from the Sun reached less than 0.5 au or greater than 30 au or if they passed within a Hill Sphere of a planet (the area where the planet’s gravity dominates). All the asteroids had initial averaged orbital elements (averaged over 20 Myr to approximate proper elements) within the range of eccentricity 0.055 < e< 0.1, and inclination 7.15° < i< 9.2°, typical of the observed Athor family. The initial semi-major axes were centred around a = 2.379 au (the semi-major axis of Athor), and an initial range of semi-major axes was calculated for an initial family velocity dispersion of 65 m s−1. After the 3 Gyr simulation, 254 of the initial 375 bodies were still on orbits in the inner main belt allowing us to estimate the size-dependent probability of the dynamical loss (1 minus the ratio between the initial and the final number of asteroids) in different diameter bins.
, α the cumulative slope set equal to -3, and 3 < D< 50 km (implying that DMax = 50 km). The cumulative slopes of asteroid families have been measured and modelled to be steeper (Tanga et al. 1999; Rozehnal et al. 2022) than the -2.5, meaning steeper than the collisional equilibrium of Dohnanyi (1969). On the other hand, cumulative family size slopes that are steeper than -3 lead to a mass function that cannot be integrated down to dust sizes. Therefore, we chose to run the simulation with α=-3. The selection of DMax = 50 km was done in order to account for the current largest fragment of the family; asteroid (161) Athor with D = 42±4 km (Alí-Lagoa et al. 2018). Each body was given an orbital drift rate (da/dt, Vokrouhlický et al. 2015) depending on its diameter and on random obliquity (ϵ) with a rate of 1.93 × 10−4 × cos(ϵ)×(1 km/D−1) au Myr−1. A 10-day time step was used for the integrations. Asteroids were eliminated from the simulation if their distance from the Sun reached less than 0.5 au or greater than 30 au or if they passed within a Hill Sphere of a planet (the area where the planet’s gravity dominates). All the asteroids had initial averaged orbital elements (averaged over 20 Myr to approximate proper elements) within the range of eccentricity 0.055 < e< 0.1, and inclination 7.15° < i< 9.2°, typical of the observed Athor family. The initial semi-major axes were centred around a = 2.379 au (the semi-major axis of Athor), and an initial range of semi-major axes was calculated for an initial family velocity dispersion of 65 m s−1. After the 3 Gyr simulation, 254 of the initial 375 bodies were still on orbits in the inner main belt allowing us to estimate the size-dependent probability of the dynamical loss (1 minus the ratio between the initial and the final number of asteroids) in different diameter bins.
 |
Fig. C.1. Cumulative size distribution approximated by a power law, N(> D)=N0Dα, where the α-value is the slope of a straight line in the log10N – log10D space. Here we show the actual slope, αact, and its standard error (grey area), of a synthetic Athor family resulting from the dynamical and collisional evolution of an initial distribution of family members with slope αini for 3 Gyr. The horizontal dashed line denotes the actual observed slope of the real Athor family (-1.67). The two curves cross at αini=-2.37, which indicates the initial slope of the cumulative size distribution of the family. |
Given the above, we were able to estimate the dynamical and collisional evolution of a synthetic Athor family using a probabilistic approach: We began by creating an initial family of 1 000 asteroids whose diameters were randomly drawn from a cumulative SFD whose form is given by Eq. C.1. We use αini to refer to the initial slope of the SFD. To apply the dynamical loss we performed the following. For each asteroid we extracted a random number from a uniform distribution between 1 and 0. If this number was smaller than the probability of the dynamical loss of said asteroid (calculated at the previous step), then the latter is eliminated. This procedure resulted in an erosion of the initial SFD. Next, we applied a second SFD erosional step to simulate the elimination of asteroids due to collisions. For this, we adopted a classical method that consists in determining the probability that an asteroid undergoes a catastrophic collision during a time Δt. This probability is equal to the size-dependent inverse collisional lifetime from Bottke et al. (2005), multiplied by the time Δt. Subsequently, we ran a Monte Carlo simulation for a number of steps equal to 3 Gyr/Δt (where Δt=10 Myr). At each step, an asteroid is eliminated from the simulation if a random number, uniformly distributed between 0 and 1, was found smaller than that probability. Next, we measured the dynamical and collisional loss of family members by adjusting the parameters α and N0 to obtain the best fit of Eq. C.1 to the post-evolutionary SFD and we call αact this best fit value of α. We repeated the Monte Carlo simulations and fitting of Eq. C.1 1,000 times for discrete values of αini between -3.7 and -1.7 with a step of 0.1; for each value of αini we recorded the mean value of αact and its standard error. The result is presented in Fig. C.1.
The α-value of the real Athor family was derived using the diameters of its members from Delbo et al. (2019) after having removed the interlopers spectroscopically identified here (Table B.2). Using the α-value of the real Athor family as the αact (-1.67) we indicated the most likely αini-slope of the SFD of the family to be -2.37.
C.1. Initial size of the parent body of the Athor family
We determined the size of the precursor to the Athor family by integrating the initial SFD of this latter given by Eq. C.1 with α equal to the best fit αini (Fig. C1), namely:
where Vp is the volume of Athor family precursor body and DMax is the diameter of the largest family member, which is (161) Athor of ∼42 km in diameter (Alí-Lagoa et al. 2018). Equation C.2 can be solved analytically for αini > −3, which is our case, yielding the diameter of the Athor family progenitor (∼64 km):
All Tables
VIS and NIR observations for asteroids and calibrating stars are reported along with the telescope and instrument that was used each time. The phase angle at the time of the observations is also reported.
Summary of the asteroid members of Athor and Zita families for which either we performed spectroscopic observations or retrieved literature spectra.
Meteorites that satisfied the curve matching with the average spectrum of the Athor family.
All Figures
 |
Fig. 1. Reflectance spectrum of the Athor family and meteorites. (A) Average spectra of Athor and Zita family members, which are clearly distinct, while the curve-matching of EL spectra with the average Athor family spectrum is evident. For comparison, we present three spectra of two EL6 meteorites, Hvittis and Pillistfer, that best-matched with the Athor family. (B) 1.8/0.8 μm reflectance ratio versus the geometric visible albedo of the Athor family and the individual meteorite spectra (CM2 and CV) that achieved a curve-matching with Athor in the first step of the analysis. Another curve-matched meteorite is a bright enstatite achondrite (aubrite) that lies out of the range of the plot (Table B.3). For ELs and EHs, we present the respective averages. The properties of the Athor family members and the ELs overlap, whereas the other meteorite classes are clearly distinct. |
| In the text | |
 |
Fig. 2. Collisional history of the EL original planetesimal. The EL planetesimal accreted in the terrestrial planet region where it suffered a collisional event. A fragment of it –the Athor family progenitor– was transported to the current location of Athor in the inner main belt by a dynamical process. About 900 Myr later, the Athor family progenitor suffered an additional collisional event that led to the formation of the present Athor family. Meteorites are now transported from the Athor family to Earth via well-established routes. |
| In the text | |
 |
Fig. A.1. The location in the main belt of nine potential Xc-type asteroids with pV values within the range of the ELs. No one of these belong to an asteroid family. |
| In the text | |
 |
Fig. B.1. NIR spectra (black points) were obtained from our survey and are presented after we applied a 2σ clipping in order to eliminate the scattered datapoints inside the telluric bands (grey areas) by as much as possible. We also present their existing VIS counterpart (grey points) obtained also from our survey or retrieved from the literature, as well as the SDSS data (red points). |
| In the text | |
 |
Fig. B.1. continued. |
| In the text | |
 |
Fig. B.2. NIR slopes of the asteroid members of the Athor and Zita families appear to have a bimodal distribution. The separation at around 15% μm−1 distinguishes the members of these two overlapping families, with the Zita members having the redder slopes. |
| In the text | |
 |
Fig. C.1. Cumulative size distribution approximated by a power law, N(> D)=N0Dα, where the α-value is the slope of a straight line in the log10N – log10D space. Here we show the actual slope, αact, and its standard error (grey area), of a synthetic Athor family resulting from the dynamical and collisional evolution of an initial distribution of family members with slope αini for 3 Gyr. The horizontal dashed line denotes the actual observed slope of the real Athor family (-1.67). The two curves cross at αini=-2.37, which indicates the initial slope of the cumulative size distribution of the family. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



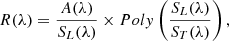
![$$ \begin{aligned} \chi ^2_M = \sum _{\lambda } \frac{ [ O(\lambda )- \beta M(\lambda ) ]^2 }{\sigma (\lambda )^2} \ \ \text{ with}\ \ \ \beta = \frac{\sum _{\lambda } O(\lambda ) M(\lambda )}{\sum _{\lambda } M(\lambda )^2}, \end{aligned} $$](/articles/aa/full_html/2022/09/aa44590-22/aa44590-22-eq5.gif)