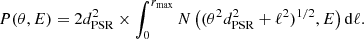| Issue |
A&A
Volume 665, September 2022
|
|
|---|---|---|
| Article Number | A132 | |
| Number of page(s) | 17 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202243481 | |
| Published online | 20 September 2022 | |
Are pulsar halos rare?
Modeling the halos around PSRs J0633+1746 and B0656+14 in the light of Fermi-LAT, HAWC, and AMS-02 observations and extrapolating to other nearby pulsars
1
IRAP, Université de Toulouse, CNRS, CNES, 31028 Toulouse, France
e-mail: pierrick.martin@irap.omp.eu
2
Laboratoire Univers et Particules de Montpellier (LUPM) Université Montpellier, CNRS/IN2P3, CC72, Place Eugène Bataillon, 34095 Montpellier Cedex 5, France
Received:
4
March
2022
Accepted:
8
June
2022
Context. Extended gamma-ray emission, interpreted as halos formed by the inverse-Compton scattering of ambient photons by electron-positron pairs, is observed toward a number of middle-aged pulsars. The physical origin and actual commonness of the phenomenon in the Galaxy remain unclear. The conditions of pair confinement seem extreme compared to what can be achieved in recent theoretical models.
Aims. We searched for scenarios minimizing as much as possible the extent and magnitude of diffusion suppression in the halos in J0633+1746 and B0656+14, and explored the implications on the local positron flux if they are applied to all nearby middle-aged pulsars.
Methods. We used a phenomenological static two-zone diffusion framework, and compared its predictions with Fermi-LAT and HAWC observations of the two halos, and with the local positron flux measured with AMS-02.
Results. While strong diffusion suppression of two to three orders of magnitude at ∼100 TeV is required by the data, it is possible to find solutions with diffusion suppression extents as small as 30 pc for both objects. If all nearby middle-aged pulsars develop such halos, their combined positron flux including the contribution from Geminga would saturate the ≳100 GeV AMS-02 measurement for injection efficiencies that are much smaller than those inferred for the canonical halos in J0633+1746 and B0656+14, and more generally with the values typical of younger pulsar wind nebulae. Conversely, if positrons from other nearby pulsars are released in the interstellar medium without any confinement around the source, their total positron flux fits into the observed spectrum for the same injection efficiencies of a few tens of percent for all pulsars, from objects a few thousand years in age that power bright pulsar wind nebulae to much older objects like J0633+1746 and B0656+14.
Conclusions. It seems simpler to assume that most middle-aged pulsars do not develop halos, although the evidence supporting this scenario depends on the actual properties of the local pulsar population and on the uncertain physics driving the formation and evolution of halos. The occurrence rate of the phenomenon could be as low as ∼5−10%, and the local positron flux in the ∼0.1−1.0 TeV range would thus be attributed to a few dozen nearby middle-aged pulsars rapidly releasing pairs into the interstellar medium, with a possible contribution over part or most of the range by J0633+1746, and at higher energies by B0656+14.
Key words: astroparticle physics / pulsars: general / cosmic rays / gamma rays: ISM
© P. Martin et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
The discovery of extended emission structures around two nearby middle-aged pulsars, with characteristic ages ≳100 kyr, suggests the possibility of efficient electron-positron pair confinement beyond the pulsar wind nebula stage (Abeysekara et al. 2017). Linden et al. (2017) suggest that such sources could be common, and more instances of these teraelectronvolt (TeV) halos or gamma-ray halos have since then been proposed (Di Mauro et al. 2020; Albert et al. 2020). The phenomenon was demonstrated to have a broadband signature, at least in the gamma-ray range from below 10 GeV to above 100 TeV (Di Mauro et al. 2019; Aharonian et al. 2021).
High-Altitude Water Cherenkov (HAWC) observations of PSR J0633+1746 (the Geminga pulsar) and PSR B0656+14 (the pulsar in the Monogem ring) clearly indicate diffusion suppression by factors of ∼100−500 at ∼100 TeV particle energies, with respect to the average conditions in the Galactic plane, over an extent of at least 20−30 pc (Abeysekara et al. 2017). Several subsequent analyses tried to account for the growing ensemble of observations with phenomenological models featuring strong diffusion suppression over scales of at least 100−120 pc (e.g., Di Mauro et al. 2019; Manconi et al. 2020). Alternative scenarios involving shallower diffusion suppression or even no diffusion suppression at all have been proposed (Recchia et al. 2021), but were demonstrated to be only marginally applicable to the case of PSR J0633+1746 and not to be applicable at all to some other halos on energetic grounds (Bao et al. 2021). Therefore, the slow or suppressed diffusion paradigm is still the preferred reference.
Theoretically, the question remains essentially open as to exactly how efficient confinement in the vicinity of a middle-aged pulsar is achieved (in what medium, by what physical mechanism, and over what extent and duration) and how the phenomenon extrapolates to a galactic population of objects located in a variety of environments. The real challenge posed by pulsar halos lies in the scales involved: strong diffusion suppression reaching up to almost three orders of magnitude, potentially over very extended regions of 100 pc or more, for long durations of hundreds of thousands of years, and at very high energies of hundreds of TeV, typically not those at which most sources output the bulk of their nonthermal energy.
Recent theoretical attempts to account for such conditions can be cast into two families. The first is self-confinement, where the gradient of escaping pairs triggers kinetic instabilities out of which turbulence develops so as to scatter the particles themselves; the second is external turbulence, where the pair halo happens to develop in a region of the interstellar medium (ISM) where, for some reason, standard magnetohydrodynamical turbulence has the required properties for efficient confinement of ∼100 TeV particles. A third option could actually be that the pulsar halo develops is preexisting turbulence self-generated by cosmic-ray protons when they escaped the parent supernova remnant (SNR), provided these conditions can be maintained for long enough (Schroer et al. 2021, 2022)
In the scenario of turbulence of fluid origin, the properties of the required turbulence were demonstrated to be consistent with those typical of the ISM, although at the lower end in terms of turbulence correlation length (López-Coto & Giacinti 2018). A possible explanation for such conditions was proposed in Fang et al. (2019a), in which the halo develops in strong turbulence produced in the wake of the expanding shock wave of the parent supernova remnant. The idea is shown to be a valid explanation for J0633+1746, provided 1−10% of the kinetic energy of the remnant is transferred to turbulence with an injection scale of 10 pc. Nevertheless, the calculation of wave transport does not include any term for turbulence damping or a self-consistent treatment of dilution, such that the question of turbulence survival after long times still deserves some attention. In addition, the scenario would predict that turbulence around PSR B0656+14 is more intense because it lies in remnant that is younger (110 vs. 342 kyr, less time for cascading) and smaller (60 vs. 90 pc, less spatial dilution), whereas the opposite trend is inferred from HAWC observations, with a diffusion coefficient that is a few times higher.
In the scenario of turbulence of kinetic origin, the first studies concluded that it cannot account for strong diffusion suppression at very late times (Evoli et al. 2018; Fang et al. 2019a), essentially because pulsar spin-down and proper motion result in streaming at late times that is too weak to generate sufficient turbulence. In Mukhopadhyay & Linden (2022), the authors revisit that scenario and show that a corrected rate of nonlinear wave damping significantly increases both the duration and the suppression of particle diffusion, which accounts for the properties of the Geminga halo. Significant confinement is still produced with additional ion-neutral wave damping terms and a flat instead of hard injection spectrum, but prospects degrade rapidly when particle injection is diluted in three dimensions. These encouraging prospects are, however, based on injection starting right at pulsar birth, thereby maximizing the energy reservoir available for turbulence growth, and not taking into account proper motion, which limits the dilution of the particle stream. It is not clear whether or how often such favorable conditions can be realized in nature since early injection could be expected to come with high proper motion (causing the pulsar to rapidly escape its parent nebula or remnant).
Overall, several promising scenarios have been proposed and explored, but reproducing the confinement inferred for at least the Geminga halo seems to push theoretical models to their limits and require rather optimistic input parameters. This questions the extrapolation of the Geminga halo to the whole Galactic population of pulsars. The theoretical works referred to above demonstrate that pair halos can naturally be produced around middle-aged pulsars, but perhaps not all with the extreme properties inferred for the halo around J0633+1746.
We explore in this paper to what extent the inferred magnitude and extent of diffusion suppression in the halos around J0633+1746 and B0656+14 can be minimized. In the phenomenological framework of a static two-zone diffusion model, our aim is to find the minimum possible values for these parameters in the light of (i) observations of a gamma-ray halo surrounding these systems with Fermi-LAT and HAWC and (ii) measurements of the local positron flux with AMS-02 up to about 1 TeV. In doing so, we incorporate the constraint that the nonthermal particles produced in these two sources are expected to be typical of the conditions inferred for pulsar wind nebulae (PWNe), in terms of injection spectrum, acceleration efficiency, and possible escape age. We then extrapolate these minimalist scenarios to the population of nearby pulsars without currently detected halos to assess the corresponding contribution to the local positron flux.
2. Halo model and parameters
2.1. Halo definition
The nature and physical state of the medium in which the few observed pair halos developed are particularly relevant to any attempt to account for the efficient confinement of particles in the vicinity of the pulsar. Several scenarios have been proposed over the past few years.
Giacinti et al. (2020) define halos as overdensities of relativistic pairs in an ISM essentially unaffected dynamically or energetically by the pulsar, leaving open the question of how efficient confinement is achieved. One possible scenario is that confinement actually results from standard magnetohydrodynamical turbulence with the appropriate properties. López-Coto & Giacinti (2018) determined from first-principles numerical simulations of particle transport that a small enough turbulence correlation length of ∼1 pc and magnetic field strength on the order of 3−5 μG are needed, both conditions being satisfied in the ISM, although at the lower end of the usually assumed range for the turbulence correlation length (Haverkorn et al. 2008).
Alternatively, Tang & Piran (2019) propose that the extended emission around the Geminga pulsar results from pairs trapped in the relic nebula that typically formed when the reverse shock crushed the young pulsar wind nebula (PWN) and shifted it away from the pulsar. In that picture the halo emission would be powered by aging particles injected some time ago, their confinement arising from the specific magnetic topology of the relic nebula, while freshly accelerated particles would be found in the compact bow-shock nebula surrounding the pulsar.
Another option put forward by Fang et al. (2019a) states that the halo around Geminga develops inside the parent SNR, the expansion and evolution of which is a source of fluid turbulence that eventually is responsible for the suppressed diffusion close to the pulsar. A key question here is whether such turbulence imparted in the first few thousand years of the remnant’s evolution can retain beyond 100 kyr a high enough energy density on the scales relevant for ∼10−100 TeV particle scattering.
Irrespective of the specific case of J0633+1746 and B0656+14, the above scenarios are all situations likely to be realized in nature. However, they ought to have different consequences in terms of halo properties and evolution, and extrapolation to a galactic population; for instance, the scenario of a halo developing inside the parent remnant requires a large remnant and/or a low pulsar proper motion, conditions that will not be met by all middle-aged pulsars. It is beyond the scope of this work to explore all these alternatives and their combinations, and instead we restrict ourselves to a physical setup for a halo in the spirit of the picture sketched in Giacinti et al. (2020):
1. The halo phase starts when the pulsar becomes supersonic in its surrounding medium, either when it exits the PWN that initially developed at the center of the parent SNR, that then becomes a relic nebula, or exits the SNR itself. This occurs when the displacement of the pulsar owing to its natal kick exceeds the size of the nebula or remnant, typically after a few tens of kyr (after exit from the initial nebula, the pulsar becomes supersonic and develops a bow-shock morphology in the cooling ejecta at 70% of the remnant radius; see Bucciantini 2008).
2. The pulsar then feeds a compact bow-shock nebula out of which relativistic pairs can easily escape, almost unaffected by energy losses in the nebula; in practice, the whole compact nebula is not resolved in our model and is treated as a point source isotropically injecting particles (in the case of Geminga, the bow-shock nebula is on subparsec scales, much smaller than the few tens of parsec halo; see Posselt et al. 2017).
3. Particles are then free to propagate diffusively in the surrounding medium, either the remnant interior or the ISM, essentially undisturbed except for the possibility of a suppressed diffusion of unspecified origin; in the latter case, the environmental conditions for (radiative) energy losses are therefore typical of the ISM rather than representative of a relic nebula.
This definition provides a clear temporal separation between the classical young PWN and the older halo phases, but is inadequate to properly model transitional objects. Systems in a stage following the dispersion of the original nebula by the remnant’s reverse shock and its subsequent mixing may constitute a fair number of bright and extended gamma-ray sources and can provide an important and specific contribution to the positron flux. Their modeling is quite complex, however, well beyond the scope of the present work, and our focus is restricted to the late stages of fully developed halos. Our scheme, which features delayed particle injection into the halo, offers the advantage of alleviating the dependence of the predictions on the uncertain initial stages in the pulsar’s spin-down history when most of the rotational energy is lost.
2.2. Model framework and parameters
With the above definition, and in the absence of a complete and self-consistent physical picture, pulsar halos were described in the framework of a phenomenological model for the release and propagation of electron-positron pairs in the medium surrounding the pulsar. The exact nature of that medium is not defined (e.g., undisturbed ISM, stellar-wind bubble, or interior of an old SNR), nor is it specified by what physical mechanism enhanced confinement is achieved (e.g., self-confinement of streaming pairs or standard turbulence with small coherence length stirred by an unknown past event).
All these important questions are hidden in the description of particle transport around the system as a two-zone diffusive process in static conditions. Particles diffuse away spherically in a medium characterized by a two-zone concentric structure for diffusion properties, with an outer region typical of the average ISM of the Galactic plane, and an inner region where diffusion is strongly suppressed. The applicability of this framework implicitly means that particles with the relevant energies scatter on mean free paths much smaller than the ∼30−50 pc halo size. Under the interpretation that particle diffusion results from transport in a turbulent magnetic field, this implies a small enough parsec-scale turbulence correlation length (López-Coto & Giacinti 2018).
Similarly, the exact conditions and processes by which pairs are accelerated and released out of the small bow-shock nebula are not detailed. We simply assume, after the pulsar exits from the nebula or the remnant at a time texit, that electron-positron pairs are injected directly into the surrounding medium from a central subparsec source that in practice is point-like in the model, with a spectrum typical of those inferred from the broadband spectral modeling of most PWNe.
The complete formalism for this two-zone individual halo model is presented in Tang & Piran (2019) in the context of Geminga1. We neglected the impact of the pulsar’s proper motion on the halo morphology because the effects are most prominent at low GeV energies, where the morphology remains poorly constrained (for the halo around Geminga; see Di Mauro et al. 2019). So when using the Fermi-LAT data for model fitting, we only considered the total emission spectrum as a constraint. The parameters of the model, grouped into the main aspects of the phenomenon, are listed and discussed below, while selected values for baseline model setups are summarized in Table 1.
Summary of baseline parameters used in modeling the halos around PSR J0633+1746 and PSR B0656+14.
Pulsar. As default pulsar parameters for J0633+1746 and B0656+14, we adopted the values used in Abeysekara et al. (2017). The age, distance, power, and spin-down history of the pulsar are of crucial importance. The distance and true age of the system are key parameters when it comes to predicting the associated local positron flux (see next section), and we discuss the effect of variations from the commonly adopted values. In the case of age the default values are the characteristic ages of the pulsars, which may overestimate the true ages, so we investigated the possibility that the true ages are significantly younger than the characteristic ages.
The spin-down power and history of the pulsar set the maximum power available for particle injection. The present-day power of the pulsar L(t) is computed as
Its value is determined from the current period P and period derivative Ṗ and an assumed neutron star inertia INS = 1045 g cm2. Unless available from other means (e.g., historical observation of the parent supernova), the age of the pulsar is approximated to the characteristic age τc of the pulsar, which is the sum of the true age tage and initial spin-down time scale τ0:
The spin-down history sets the total number of particles released since injection into the halo started and is relevant for long-lived particles that accumulate over long durations and eventually radiate, for example in the Fermi-LAT band. The past spin-down power evolution is assumed to be governed by rotational energy loss from dipole radiation only (i.e., with a braking index n = 3 already folded into the above equations), for an assumed τ0 (to which our model is only marginally sensitive since we consider delayed injection after a few tens of kyr; see below).
Injection. According to our definition for a halo, particles are accelerated at the pulsar wind termination shock and can easily escape from a subparsec bow-shock nebula. However, this process can be quite complex, anisotropic, highly energy-dependent, and charge separated (Bucciantini et al. 2020). In the absence of any solid prescription as to what spectrum should be used for any given system, from observational evidence or numerical investigations, we adopted the commonly accepted particle injection spectrum Q(E, t) for younger PWNe either still in their parent remnant or in the bow-shock phase: a broken power law, typically with a harder or softer shape at low or high energies and a break at Eb in the few hundred GeV range2. We note, however, that the relevance of such a spectral shape for much older pulsars or in the context of halos is not solidly demonstrated, and that harder single power-law shapes seem to be a viable alternative for several objects (Sudoh et al. 2021):
The low-energy part of the spectrum is hardly constrained by the data we are comparing to; the power-law index α1 is inferred to lie in the 1.0−2.0 range from radio observations (Bucciantini et al. 2011; Torres et al. 2014), and we fixed it to a mean value of 1.5. Conversely, the high-energy index α2 strongly influences the predictions for the observables we are considering. It is constrained to values in the range 2.0−2.8 from spectral fits to various PWNe (Bucciantini et al. 2011; Torres et al. 2014; Principe et al. 2020; Abramowski et al. 2015), and we therefore investigated the effect of changing the index within this range. For the break energy Eb, we adopted a typical value of 100 GeV, and checked that values up to 500 GeV have little influence on the qualitative and quantitative conclusions of the study. Finally, the accelerated particle spectrum is expected to feature a cutoff at very high energies reflecting the time evolution of the potential drop, hence decreasing from a few PeV down to a few hundred TeV over the first few hundred kyr of the pulsar (Evoli et al. 2021). However, we adopted a constant spectral cutoff at Ec = 1 PeV since the observables we are comparing to are marginally sensitive to particle energies above a few hundred TeV.
Particle acceleration is powered by the spin-down luminosity of the pulsar and the injection efficiency η (i.e., the fraction of the pulsar spin-down power converted into nonthermal pairs, which is a free parameter in the model):
The modeling of the broadband emission from PWNe suggests relatively high values for η, on the order of a few tens of percent and reaching up to nearly 100% (Bucciantini et al. 2011; Torres et al. 2014). We note that the spin-down power is computed under the hypothesis of a typical moment of inertia of 1045 g cm2, and variations of up to a factor of two are possible depending on the actual mass and internal structure of the neutron star (Worley et al. 2008; Zhao 2016). In this respect, the 100% efficiency is not a strict limit and injection efficiencies moderately in excess of that value could be considered. It seems quite an extrapolation to consider that high injection efficiencies close to 100% inferred for objects that are a few thousand years in age could still hold for the 100 kyr pulsars powering halos. Nevertheless, as we show below, the injection efficiency required for the two canonical halos around J0633+1746 and B0656+14 are on the same order.
Finally, an important parameter is the time when nonthermal particle release into the halo begins; several studies assumed an injection starting at pulsar birth (see Sudoh et al. 2019, for a discussion of the effects of such a parameter in the context of a population synthesis), but this overlooks the PWN phase where particles are injected and trapped into an expanding, highly magnetized nebula for a few tens of kyr. Several studies considered that pairs from pulsars are fed into the ISM when the pulsar exits its parent remnant owing to its natal kick. Estimates for typical exit times are in the 40−60 kyr range (see, e.g., Bykov et al. 2017; Evoli et al. 2021). In this study we assumed by default an injection start time of texit = 60 kyr, but we considered variations from 20 to 80 kyr and assessed their impact on our results.
Diffusion: In the two-zone diffusion framework we are using, particles released from a point-like source diffuse away spherically in a medium characterized by a two-zone concentric structure for diffusion properties, with an outer region typical of the average ISM of the Galactic plane, and an inner region where diffusion is strongly suppressed:
The two key parameters of the problem are the radial extent of the suppressed diffusion region RSDR and the value of the diffusion coefficient therein DSDR, and they are the main focus of our work. We also discuss below the impact of the diffusion index δD.
The particle distribution around the pulsar in the two-zone diffusion framework is computed following the formalism detailed in Tang & Piran (2019):
The full expression for the spatial kernel H(r, E) in the two-zone case is given in Tang & Piran (2019) and Di Mauro et al. (2019), and we do not repeat it here. The integration runs over the full injection history, over all particles released at time t0 with an energy E0 that decreased as a result of losses to E at time tage.
Recent theoretical efforts to quantify the extent of self-confinement of escaping nonthermal particles in the case of SNRs or pulsars suggest that diffusion suppression by 1−2 orders of magnitude could be reached over 50−100 pc distances at most (Malkov et al. 2013; Nava et al. 2016, 2019; Evoli et al. 2018; Schroer et al. 2022). This is consistent with the levels and extents inferred from observations or modeling of other objects (see Tibaldo et al. 2021, for a recent review). Around individual objects such as SNRs or pulsars, sustaining this strong confinement over durations above 100 kyr is a challenge, especially at very high energies (but see Mukhopadhyay & Linden 2022, for recent developments in the case of pulsars).
In the case of particles diffusing inside a very large and possibly relic nebula, a likely maximum extent is suggested by the largest known PWN, HESS J1825−137, which has a radius of 100 pc (Principe et al. 2020). The very nature of that object remains unclear and, interestingly, it was recently suggested that it is a mixed or transitional object evolving from a classical PWN to a halo (Giacinti et al. 2020). In the case of trapping in the enhanced fluid turbulence that could be expected in the interior of an old and large SNR or inside a stellar-wind bubble, the maximum size of such objects is on the same order, 50−100 pc. Supernova remnants with ages ≲20 kyr seem to have radii below 30 pc (Badenes et al. 2010), while older objects ≲100 kyr can reach up to 100−120 pc (Fesen et al. 2021). A reasonable maximum extent for the suppressed diffusion region therefore seems to be 100 pc, and we therefore favor values below such a limit if the data allow.
Overall, the results referred to above suggest that diffusion suppression by up two orders of magnitude over an extent of 50−100 pc at most should be considered a reasonable limit, and we will try to find model setups for J0633+1746 and B0656+14 that comply with such bounds, as much as the data allow. As we show below, however, the magnitude of diffusion suppression seems quite well constrained by HAWC observations, at least at particle energies of a few hundred TeV and in the two-zone diffusion framework, and the halo around Geminga points to diffusion suppression reaching almost 3 orders of magnitude.
The rigidity dependence of the suppressed diffusion parameter, here approximated as an energy dependence, is another possibly important free parameter that may well differ from standard Kolmogorov or Kraichnan scaling, especially in the case of self-confinement (e.g., Evoli et al. 2018); however, this parameter is strongly degenerate with others. HAWC observations pinpoint the diffusion properties for short-lived freshly injected ∼100 TeV particles, but the spatial distribution of the much longer-lived ∼0.1−1 TeV particles contributing to the positron flux or shining in the Fermi-LAT band can be reproduced by several combinations of diffusion coefficient at this energy, injection spectrum, and time when injection started. So for simplicity, we assumed by default that suppressed diffusion is, like average interstellar diffusion, described by a Kolmogorov scaling δD = 1/3, but we discuss below the effect of a harder rigidity dependence. For completeness, we note that the exact shape and extent of the transition from suppressed to average interstellar diffusion also matters, but this is second-order here and would only add unnecessary complexity (Profumo et al. 2018).
The value of the effective diffusion coefficient in the outer region can be considered relatively well determined from studies of cosmic-ray propagation in the Galaxy. One cannot exclude, however, the presence of inhomogeneities in transport properties throughout the disk, even beyond very localized effects around sources (such as those around SNRs or maybe at stake around Geminga). However, this is poorly constrained at the moment so we kept the average value for the Galactic plane, using by default a value consistent with the range in Trotta et al. (2011) for the normalization and a Kolmogorov scaling for the rigidity dependence.
Energy losses and radiation. Synchrotron and inverse-Compton scattering losses drive the propagation range of the ≳1 TeV particles, which are in a loss-dominated regime. The energy loss rate Ė of particle including the Klein-Nishina regime was approximated following Moderski et al. (2005):
The sum is performed over all components of the radiation field, described as graybodies with energy densities Ui and temperatures Ti (see the values in Table 1), yielding normalized photon energies for the fields ϵi = 2.8kBTi/mec2, where kB is the Boltzmann constant, me the electron mass, and c the speed of light. By default, we used the same magnetic and radiation fields as in Abeysekara et al. (2017).
For the magnetic field, we used a baseline value of B = 3 μG, typical of the local ISM, but considered variations of factors of a few since the medium in which the halos develop may not be representative of the average ISM (e.g., if it is the interior of the parent remnant). As an alternative for the radiation field, which sets both the magnitude of losses and the seed photon fields for inverse-Compton scattering, we tested the model of Popescu et al. (2017) for the position of Geminga in the Galaxy and found a limited impact on model predictions. More generally, there are obvious uncertainties in magnetic and radiation fields in the medium surrounding the pulsar, and we investigated the impact of varying the input values, as described in Sect. 3.3.
Inverse-Compton radiation from the halo is computed from the projected particle angular distribution P(θ, E) obtained by integrating the particle spatial distributions along the line of sight for the assumed distance dPSR to the pulsar:
In practice, the particle spatial distribution N(r, E) is computed over a grid of radial positions from 0 to rmax = max(100 pc, RSDR + 20 pc), with a step of 1 pc by default3. The corresponding inverse-Compton radiation is computed from the particle angular distributions using the Naima package (Zabalza 2015), in the approximation of isotropic radiation fields4.
Some of the above parameters are object-specific and only affect the modeling of J0633+1746 or B0656+14 (e.g., the pulsar age), while others are likely to have an impact on a putative halo population if they are taken as representative (e.g., the suppressed diffusion region properties). A population perspective, built on the (still questionable) assumption that all middle-aged pulsars develop at some stage a halo similar to that of J0633+1746 or B0656+14, bear some potential for constraining some of the parameters of the problem, at least in a statistical sense. We illustrate this point in Sect. 4, where we extrapolate the model setups for halos like J0633+1746 or B0656+14 to the population of nearby pulsars to assess the corresponding contribution to the local positron flux. A complementary exercise involving the synthesis of an entire Galactic population of halos around mock or real pulsars and the analysis of the resulting source flux distribution in the light of existing measurements in the GeV and TeV range will be presented in subsequent publications.
3. Results
In this section we start from baseline model setups for the halos around J0633+1746 or B0656+14 and discuss several possibilities for minimizing the extent and magnitude diffusion suppression, while still being in agreement with the HAWC and Fermi-LAT gamma-ray observations, and with the local positron flux measured with AMS-02.
3.1. Baseline model setups
Our baseline model setups for J0633+1746 or B0656+14 are inspired by previous modeling efforts (e.g., Abeysekara et al. 2017; Tang & Piran 2019; Di Mauro et al. 2019; Jóhannesson et al. 2019) and the expectation that particle injection in the halos is similar to that inferred for younger PWNe (Bucciantini et al. 2011; Torres et al. 2014; Zhang et al. 2008). The corresponding parameter sets are summarized in Table 1. The only remaining free parameter is the injection efficiency, which is determined by a joint fit to the LAT spectrum and HAWC intensity distribution.
The predictions for these baseline model setups are shown as dashed blue lines in the curve series presented in Figs. 1 and 2. A good match to the gamma-ray observations is obtained in either case. The optimal suppressed diffusion coefficient normalizations are about 4 × 1027 and 1 × 1028 cm2 s−1 at 100 TeV, for J0633+1746 and B0656+14, respectively, in agreement with estimates from Abeysekara et al. (2017). Even so, while the fit for B0656+14 involves an acceptable injection efficiency of about 60%, that for Geminga requires an excessive value of nearly 200%. This stems from the fact that matching both the LAT and HAWC data calls for a rather soft injection spectrum, with an index of 2.6. Clearly, the baseline setup is not a viable option for Geminga, and we show in the next subsections how solutions with acceptable efficiencies can be found.
 |
Fig. 1. Model fits to HAWC+LAT observations of J0633+1746, and the corresponding predicted local positron fluxes, for different sizes of the suppressed diffusion region RSDR, and different high-energy injection indexes α2. All other parameters have their baseline values, in particular the diffusion coefficient DSDR(100 TeV)=4 × 1027 cm2 s−1. The set of dashed blue curves corresponds to the baseline model setup. The legend indicates the injection efficiency η and the χ2 of the fit. |
 |
Fig. 2. Model fits to HAWC observations of B0656+14, and the corresponding predicted local positron fluxes, for different sizes of the suppressed diffusion region RSDR. All other parameters have their baseline values, in particular the diffusion coefficient DSDR(100 TeV)=1028 cm2 s−1. The set of dashed blue curves corresponds to the baseline model setup. The legend indicates the injection efficiency η and the χ2 of the fit. |
The suppressed diffusion coefficient at ∼100 TeV is set by the intensity profiles observed with HAWC, for the assumed distances and ages of the pulsars, while the LAT data set the slope of the injection spectrum above the break energy Eb and the overall acceleration efficiency (for the assumed broken power-law spectral shape). In all the presented results, the predicted spectrum in the Fermi-LAT range is not shown for B0656+14 because the available upper limits in this range were found to be poorly constraining for all model setups that were investigated. This is due to the relatively young age of the pulsar, which leaves little time for the accumulation of low-energy particles after injection starts at 60 kyr, and thus a relatively weak flux in the GeV band, such that the Fermi-LAT upper limit is easily accommodated.
The bottom panel of Fig. 1 shows that, in addition to requiring an unphysical injection efficiency, the baseline setup for Geminga yields a positron flux exceeding the AMS-02 measurements above ∼100 GeV, while the predicted flux in the case of B0656+14 is fully consistent with it. The qualitative differences between J0633+1746 or B0656+14 in positron flux come mostly from the younger age of the latter (110 vs. 342 kyr) which implies less accumulation of low-energy particles and less time for diffusion, and as a result a positron flux peaking at ∼10 TeV, which is above the current reach of AMS-02.
These results are the direct outcome of using a two-zone diffusion model with a limited extent for the suppressed diffusion region. In the extreme case of an infinitely large confinement region, in practice a one-zone model, the local positron flux is heavily suppressed (Abeysekara et al. 2017). Finite confinement regions with very large sizes of 120 pc or more lead to similar results, although less dramatic, because the region size is much larger than the typical diffusion scale length at all energies (Di Mauro et al. 2019). As discussed in Sect. 4, however, there are several arguments to disfavor such very large extents.
While the observed intensity distributions in the HAWC range can easily be accommodated with confinement region sizes down to 20−30 pc, as will be made clear in the next subsections, the local positron flux constraint seems to require much larger sizes, at least for Geminga and in our baseline scenario. This may not be the only solution to the problem, however, and we explore in the following several alternative possibilities to account for the gamma-ray halo properties while being in agreement with the locally measured positron flux, minimizing the extent and magnitude of suppressed diffusion, and getting acceptable injection efficiencies. Before that, we briefly discuss those features in the predicted spectrum of the local positron flux that can guide the search for an acceptable solution.
The shape of the injection spectrum, with a break at 100 GeV and harder and softer slopes below and above it, can be recognized in the positron flux spectrum. The low-energy slope is hardly constrained by any of the observables considered here, at least for values in the expected 1.0−2.0 range, while the high-energy slope is constrained to values ∼2.3−2.5 in the case of Geminga by the need to reproduce the observed fluxes both in the LAT and HAWC ranges (the nondetection of B0656+14 in the LAT range allows flatter spectra). The peak positron flux reached at about ∼1−2 TeV, in the case of Geminga, corresponds to the particles with the largest propagation range, resulting from a trade-off between diffusion coefficient and energy losses increasing with energy. Above and below that peak, particles are in loss-limited and diffusion-limited regimes, respectively. This is illustrated in Fig. 3, which shows the diffusion radius or diffusion length scale as a function of final energy, for a homogeneous one-zone diffusion scheme. The propagation range of particles in the lower branch is determined by the time allowed for diffusion (from injection start time to pulsar age), while the propagation range of particles in the upper branch is set by the energy loss time (from radiative processes in the magnetic and radiation fields). The normalization of the whole profile is set by the normalization of the suppressed diffusion coefficient, and the momentum dependence of the latter would skew the respective layout of the lower and upper branches.
 |
Fig. 3. Diffusion scale length in three different model setups for J0633+1746: the baseline setup (in blue), an alternative setup with a lower pulsar age (150 kyr instead of 342 kyr, in red), and a setup with a higher radiation field (eight times stronger than baseline, in green). Overlaid are the typical particle energy ranges probed directly or indirectly by the different observables considered in this work. The AMS-02 experiment is sensitive to positrons with energies from below 1 GeV to above 1 TeV, but only the range above 50 GeV is relevant to this work (at lower energies the flux is dominated by cosmic-ray secondaries). |
The case of two-zone diffusion adds some effects depending on whether the suppressed diffusion region size, which acts as some free escape boundary, lies above or below the diffusion radius. When it is above the diffusion radius (e.g., RSDR = 100−120 pc), the particle density at the boundary of the suppressed diffusion region is small and the flux escaping out of it is modest; conversely, with a suppressed diffusion region smaller than the diffusion radius at some of the energies of interest to us (e.g., RSDR = 20−30 pc), the flux leaking out of the halo is higher.
The above discussion points to several possible solutions to reduce the escaping positron flux from the halo of J0633+1746, for example enhancing confinement, reducing the time for diffusion, increasing energy losses, or injecting positrons with a flatter spectrum. We examine these possibilities and others in the following subsections.
We note that an additional option would be to assume a much lower diffusion coefficient for the propagation outside the halos, but we chose to not explore that option and consider instead that the coefficient for diffusion in the average ISM applies locally and is well determined within a factor of two to three, which is much smaller than what would be needed to strongly suppress the flux of positrons from small halos (see Tang & Piran 2019). We also tested an alternative prescription for the momentum dependence of the diffusion coefficient, such as that investigated in Génolini et al. (2019) to account for spectral features in cosmic-ray direct measurements and where the diffusion coefficient has a steeper momentum dependence below about 250 GeV. We implemented the BIG model from that study and found a negligible impact on the predicted signatures.
3.2. Effect of changes in diffusion suppression
We first examine the uncertainty range on the diffusion coefficient to determine how much the magnitude of diffusion suppression can be relaxed in our baseline model. We first note that a solution to suppress the positron flux at ∼0.1−1 TeV while still fitting the intensity profile in the HAWC energy range can be achieved by increasing the momentum dependence of the suppressed diffusion coefficient. Although not reported here, we explored this possibility and concluded that such a choice results in a non-negligible contribution to the positron flux and actually shifts the problem to that of explaining very high suppression factors ≳2000 at ≲1 TeV energies5.
The diffusion suppression level actually is quite well constrained for both objects, as illustrated in Fig. 4. For models with suppressed diffusion region extents of 50 pc, and from the HAWC and LAT constraints alone, the diffusion coefficients could be increased up to nearly 1028 and 1029 cm2 s−1 at 100 TeV, for J0633+1746 and B0656+14, respectively. Even so, this has to be compensated by higher and higher injection efficiencies, rapidly reaching 100% for B0656+14 and largely exceeding 200% for J0633+1746, making the violation of the positron flux constraint even more severe in the latter case. On the other side, smaller values of the diffusion coefficient do not help as they rapidly lead to degraded fits to the HAWC intensity profile.
 |
Fig. 4. Confidence interval in the diffusion normalization and injection index space, for model fits to HAWC+LAT data in the case of J0633+1746 (top panel), and to HAWC data only in the case of B0656+14 (bottom panel). The model setups feature a suppressed diffusion region extent of 50 pc. The color-coding indicates increasing χ2 variations from the optimum of up to 1 and 4 in the orange and yellow regions, respectively. The black vertical hatches indicate the model fits yielding positron fluxes in excess of the AMS-02 measurement in the 0.1−1 TeV range, while the gray slanting hatches indicate model fits implying injection efficiencies in excess of 100% of the spin-down power. |
Eventually, the most straightforward solution to the excessive positron flux issue in the baseline model setup is to enlarge the suppressed diffusion region, as has been explored in other works already (e.g., Di Mauro et al. 2019). More extended suppressed diffusion regions place the boundary at positions where the particle density is lower, especially when it is beyond the diffusion length scale, which reduces the escaping flux, as illustrated in Figs. 1 and 2. This is going in the opposite direction of what we are trying to achieve (i.e., minimizing the conditions of diffusion suppression), but it remains a physically viable solution.
In the case of Geminga, satisfactory fits to the observables required reducing the high-energy injection index, which brought the injection efficiency down to acceptable values. Sizes of 80 pc and above provide good fits to all observables, although the 80 pc case nearly saturates the 1 TeV positron flux inferred from the latest AMS-02 measurements (Aguilar et al. 2019). In the case of B0656+14, the baseline confinement region size of 50 pc already provided a good fit to all observables, and so does the 30 pc case, as illustrated in the bottom panel of Fig. 2.
3.3. Effect of changes in the magnetic/radiation fields
As illustrated in Fig. 4, higher diffusion coefficients lead to progressively degraded fits to the HAWC data because the corresponding intensity distributions are more spread out. This trend can be compensated with (i) a larger distance to the pulsar, to fit a more diluted physical distribution into the observed angular distribution, and (ii) higher energy losses, to reduce the larger diffusion scale length. We examine here the second option, while the first is dealt with in the next subsection.
Compensating for a higher diffusion coefficient with higher energy losses from a stronger magnetic field indeed allows us to fit the HAWC profile, as illustrated in the top panel of Fig. 5. In the case of J0633+1746, variations in the magnetic field of up to ∼10 μG allows the diffusion coefficients to be relaxed up to 1028 cm2 s−1 or more. However, this comes with ever increasing injection efficiencies, to ensure that sufficient energy is channeled into inverse-Compton scattering, which eventually translates into a larger and still excessive positron flux.
 |
Fig. 5. Confidence interval in the diffusion normalization and magnetic field strength space (top panel), and diffusion normalization and radiation field intensity space (bottom panel), for model fits to HAWC+LAT data in the case of J0633+1746, assuming a suppressed diffusion region extent of 50 pc. The meaning of graphical elements is the same as in Fig. 4. |
Increasing instead the intensity of the radiation fields involved in inverse-Compton scattering (except the cosmic microwave background) produces viable solutions for two reasons: (i) when increasing the field intensities, a given level of gamma-ray emission in the HAWC or LAT band can be reproduced with a smaller injection efficiency, hence a correspondingly smaller flux of diffusion-limited particles and an even smaller flux of loss-limited particles; (ii) enhanced energy losses produce a shift of the positron flux peak toward lower energies and smaller fluxes. The net effect is illustrated in Figs. 3 and 6, while the allowed parameter space is shown in the bottom panel of Fig. 5.
 |
Fig. 6. Predicted local positron fluxes for different increases in the infrared and optical photon field densities UIR, Opt (top panel) and different ages for the pulsar tage (bottom panel), assuming a suppressed diffusion region extent of RSDR = 50 pc. The predicted gamma-ray emission is fitted to HAWC+LAT observations of Geminga and the corresponding injection efficiencies η and χ2 of the fits are given in the legend. |
Radiation fields a few times stronger than our baseline assumption can solve the issues of excessive local positron flux and injection efficiency in the model setup with a 50 pc suppressed diffusion region applied to Geminga. Substantiating this possibility would require an investigation of the stellar content in the vicinity of the pulsar to establish whether it is conceivable that the radiation field be at least five to six times higher than the average for the Galaxy at this position (e.g., from the model of Popescu et al. 2017). Such enhancements however leave a significant contribution of Geminga to the ∼0.1−1 TeV positron flux and only allow for a modest relaxing of the diffusion coefficient as it needs to be compensated by a higher injection efficiency, which raises the positron flux above the AMS-02 measurement again.
3.4. Effect of changes in pulsar parameters
Higher diffusion coefficients lead to intensity distributions that are more spread out, an effect that needs to be compensated in some way to fit a more diluted physical distribution into the observed angular distribution. A larger distance to the pulsar is a possible solution.
In the case of Geminga the upper bound of the distance range published in Verbiest et al. (2012) is 480 pc, nearly twice the baseline 250 pc used here. However, as illustrated in the top panel of Fig. 7, a larger distance only allows for a modest increase in the diffusion coefficient when the suppressed diffusion region has a 50 pc size. This comes from the fact that the particles radiating in the HAWC range have a diffusion scale length already close to 50 pc (see Fig. 3), such that relaxing the diffusion coefficient from its baseline value does not significantly modify the intensity distribution within 50 pc of the pulsar. The effect is more significant when the suppressed diffusion region has a 80 pc size. However, in both cases the possible solutions lead to a larger positron flux because the higher diffusion coefficient, and to a lesser extent the larger distance, need to be compensated for by a higher injection efficiency still largely in excess of 100%.
 |
Fig. 7. Confidence interval in the diffusion normalization and pulsar distance space (top panel) and diffusion normalization and pulsar age space (bottom panel), for model fits to HAWC+LAT data in the case of J0633+1746, assuming a suppressed diffusion region extent of 50 pc and injection index of 2.6. The meaning of graphical elements is the same as in Fig. 4. |
Another solution to suppressing the excessive predicted positron flux below 1 TeV is to reduce the time allowed for diffusion. For lower-energy particles in the diffusion-limited regime, this implies reducing the time from the injection start. This could be done with a delayed particle release from the pulsar, but we already use a rather high 60 kyr baseline value. Instead, a significant effect can be obtained by assuming a smaller age for the Geminga pulsar.
The 342 kyr value used as baseline actually corresponds to the characteristic age and is based on the assumption of spin-down driven by magnetic dipole radiation, with a braking index of 3, and the unknown initial spin period being much smaller than the present-day value. Both assumptions may well be inappropriate for the Geminga pulsar, as they were shown to be for other pulsars. In Suzuki et al. (2021), the characteristic ages of pulsars were shown to overestimate alternative, presumably more reliable, historical, light-echo, or kinematic age estimates of their parent systems, by a few factors.
The bottom panels of Figs. 6 and 7 show that ages ≲250 kyr result in a predicted positron flux in agreement with AMS-02 data, while still allowing for solutions consistent with HAWC and Fermi-LAT observations. This, however, does not solve the excessive injection efficiency, which remains close to 200%. Eventually, the best solution for this issue, which is investigated in the next section, is to reduce the injection index at the expense of a poorer fit to the Fermi-LAT data. For a true pulsar age of 190 kyr, reducing the injection index from 2.6 to 2.5 allows for a decent fit to all observables with an injection efficiency of 110%.
A younger age for the Geminga pulsar, in the 150−200 kyr range, has interesting consequences on the birth place of the pulsar, which would be closer to the Galactic mid-plane, and on the morphology of the halo at low energies, with trailing emission at low GeV energies that should be less extended. This point would have to be tested against Fermi-LAT data, although the very large extension of the detected source and its limited significance may preclude disentangling halo models with different pulsar ages (Di Mauro et al. 2019).
3.5. Effect of changes in injection spectrum
In the case of Geminga, reproducing the HAWC+LAT constraints for a confinement region of 50 pc, without exceeding the AMS-02 measurements and while getting an injection efficiency below 100%, turned out to be quite challenging, even with all the options explored above. Beyond a younger pulsar age or higher radiation field density, an alternative solution can be obtained by relaxing one of the constraints. In particular, motivated by the result of Xi et al. (2019), we considered the possibility that the Fermi-LAT measurement in Di Mauro et al. (2019) is overestimating the GeV flux, and turned it into an upper limit instead. The situation then becomes similar to that of B0656+14, for which only upper limits were obtained from LAT observations.
Acceptable solutions for Geminga are then easily found with injection indices of 2.4 or below, and suppressed diffusion regions as small as 30 pc, nearly the minimum value allowed by the HAWC intensity profile. This solves the excessive positron flux issue, as illustrated in Fig. 8, and leads to injection efficiencies of about 70% or below. Interestingly, such injection efficiencies are comparable to those needed for B0656+14 to match the HAWC constraint with a similar model setup featuring suppressed diffusion regions of 30−50 pc (see Fig. 2).
 |
Fig. 8. Predicted local positron fluxes for variations in the injection index α2, assuming a suppressed diffusion region extent RSDR = 30 pc. The predicted gamma-ray emission is fitted to HAWC observations of Geminga only and the corresponding injection efficiencies η and χ2 of the fits are given in the legend. The χ2 includes the deviation from the LAT spectral points to illustrate the effect of neglecting that constraint. |
Relaxing the LAT constraint actually may allow for an even more drastic modification of the injection spectrum by making it possible to drop the broken power-law assumption in favor of a single power-law. In such a scenario, the relatively soft emission in the HAWC band can be reproduced by shifting the cutoff from our default 1 PeV energy to smaller values in the 10−100 TeV range. Such a low-energy cutoff has the effect of softening the spectrum of particles radiating in the ∼5−50 TeV HAWC band, while allowing for a hard injection spectrum overall, with indices in the 1.5−2.0 range. This strongly suppresses the contribution to the local positron flux and requires a very small injection efficiency. The same logic applies to B0656+14 and is reminiscent of the work presented in Hooper et al. (2017). The extension of gamma-ray measurements to 100 TeV energies and above will tell whether this is a viable option (Sudoh et al. 2021).
3.6. Summary
We summarize here the different model setups found to yield acceptable fits to all (or a subset of all) observables for J0633+1746 and B0656+14, under the constraint of minimizing the extent and magnitude of diffusion suppression as much as possible.
In the case of J0633+1746 and suppressed diffusion regions of moderate sizes ≲80 pc, the highly suppressed diffusion coefficient is constrained by both the HAWC and AMS-02 observations and the total energetics of the pulsar. Eventually, the following model setups were found to provide acceptable fits: (i) a 80 pc suppressed diffusion region size with injection index 2.3−2.4; (ii) a 50 pc suppressed diffusion region size with injection index 2.5−2.6, assuming a true pulsar age ≲200 kyr; and (iii) a 30 pc suppressed diffusion region size with injection index 2.3−2.4, relaxing the constraint to fit the claimed detected flux in the Fermi-LAT range. These scenarios feature a suppressed diffusion coefficient in the range 2−6 × 1027 cm2 s−1 at 100 TeV, and involve injection efficiencies in the range 50−110%.
The case of B0656+14 is less constrained, owing to the nondetection in the Fermi-LAT range and younger age and larger distance of the pulsar. These conspire to yield a smaller contribution to the local positron flux, which makes it easier to fit within the AMS-02 measurement. Eventually, we retained the following model setups: (i) a 50 pc suppressed diffusion region size with injection index 2−1 − 2.5, or (ii) a 30 pc suppressed diffusion region size with injection index 2.1−2.3. These scenarios feature a suppressed diffusion coefficient in the range 1−6 × 1028 cm2 s−1 at 100 TeV, and involve injection efficiencies in the range 60−100%.
To limit the computational cost of the work, we did not explore all possible combinations of the parameters, but it is clear that there are more model setups than listed above that could provide similar or even better fits to the observations. For instance, in the case of Geminga, a younger age for the pulsar combined with a 30 pc suppressed diffusion region size and the appropriate injection index to fit (or not) the Fermi-LAT spectrum could be an option.
In all the above scenarios, we note that our assumption of late injection, past a PWN stage lasting for 60 kyr, clearly helps to reduce the predicted positron flux. Injection starting earlier leads to a higher output of ≲1 TeV particles and a bit more time for diffusion, which makes it even more difficult to match all three observables. The important point is that, in all cases, significant contributions to the ≳1 TeV local positron flux are expected from J0633+1746 and B0656+14, unless the suppressed diffusion regions are extremely large.
Future high-precision measurements of the positron flux in the few TeV range may offer a way to discriminate between all the possible scenarios considered here. Observations in the Fermi-LAT core band is also an obvious way to tell the possibilities apart, but we are probably at the limit of what can be done for a very extended source like Geminga. Potentially more promising are the implications at the Galactic population level of the different confinement region sizes in these scenarios. All other things being equal, especially a typical distribution for injection efficiencies from pulsars/PWNe, a larger suppressed diffusion region leads to higher gamma-ray fluxes, and to a brighter population if most or all middle-aged pulsars go through a halo phase similar to J0633+1746 or B0656+14. This aspect is explored in a separate publication (Martin et al. 2022), while the following section deals with the implications on the positron flux of a putative local population of pulsar halos.
4. Positron flux from nearby pulsars
In this section we assess the consequences in terms of local positron flux of a scenario where all nearby pulsars around us develop a halo similar to J0633+1746 or B0656+14. This is complementary to a full Galactic pulsar halo population synthesis, such as Martin et al. (2022).
We extract from the Australia Telescope National Facility (ATNF) data base (Manchester et al. 2005) a selection of pulsars with estimated distances ≤1 kpc, characteristic ages ≥60 kyr, and spin-down power ≥1033 erg s−1. This amounts to 16 objects, including J0633+1746 and B0656+14, which we exclude from the sample as they were treated separately already, taking constraints from their detected gamma-ray emission into account. For the remaining 14 objects, we compute the predicted positron flux for the different halo model setups selected in Sect. 3.6.
Figure 9 shows the total local positron flux from all other known nearby middle-aged pulsars, assuming they develop a halo similar to J0633+1746 or B0656+14. As typical properties for the latter, we assumed a suppressed diffusion coefficient of 4 × 1027 cm2 s−1 and 1 × 1028 cm2 s−1 at 100 TeV, with a power-law scaling in rigidity with index 1/3, and different possible extents of the suppressed diffusion region. Particle injection starts at 60 kyr after pulsar birth, with a high-energy spectral index assumed to have an average value of 2.4 and an efficiency set by default to 100%. Using flatter injection indices does not profoundly modify the picture. For comparison, we show in the same plots the expected local positron flux if all nearby pulsars develop no halo, all particles being directly released in the ISM, diffusing out in average conditions for the Galactic plane without experiencing any kind of strong and extended confinement around the source. Injection efficiency is here again set to 100% by default.
 |
Fig. 9. Total local positron flux from known middle-aged pulsars within 1 kpc, except J0633+1746 and B0656+14, under the assumption that they develop a halo like J0633+1746 (top panel) or B0656+14 (bottom panel) past an age of 60 kyr, with different possible sizes for the suppressed diffusion region. For comparison, both plots also display the expected flux if all nearby pulsars develop no halo and particles released in the ISM diffuse out without experiencing any kind of strong and extended confinement around the source. By default, injection efficiencies of 100% are assumed, and several possibilities were tested for the injection index in the case of plain interstellar diffusion. |
Figure 9 shows that halos around nearby pulsars would yield a positron flux in excess of the AMS-02 measurement for average injection efficiencies ≳10−30%, depending on the extent and magnitude of diffusion suppression. Conversely, if positrons from nearby pulsars diffuse in the ISM without strong and extended confinement around the source, all known nearby pulsars taken together would saturate the local positron flux above 80−100 GeV for an average injection efficiency of 70−100%. It may seem counterintuitive that adding regions of inhibited diffusion around pulsars leads to lower injection efficiencies to match a given particle flux at a distant location. This effect was already discussed in Profumo et al. (2018) in the case of Geminga. For particles suffering little from energy losses, typically ≲1 TeV in the present context, halos actually slow down the release of particles and initially suppress their flux at a distant location. At later times, however, a high density of particles fills the entire suppressed diffusion region, and the diffusive flux escaping from its boundary is higher than it would have been at the same time and position without a halo. For pulsars old enough to be in this stage and close enough to the observer, a smaller injection efficiency is thus required to match a given particle flux.
The possible contribution from Geminga now needs to be folded in. According to the model setups listed in Sect. 3.6, Geminga can be expected to contribute 30−50% or more of the positron flux over part or all of the ∼0.1−1 TeV range. This leaves only about half or less of the positron flux to be accounted for from other pulsars. As above, we consider two extreme scenarios: all other pulsars develop halos (hereafter called the “widespread halos scenario”) or none does (hereafter the “rare halos scenario”). This is illustrated in Figs. 10 and 11 for different halo model setups.
 |
Fig. 10. Total positron flux from the halos around J0633+1746 and B0656+14, and the population of known nearby middle-aged pulsars under two hypotheses for the latter: all pulsars develop a halo (top panel) or none develops a halo and particles are released without confinement around the source (bottom panel). Suppressed diffusion regions of 30 pc for both and an injection index of 2.4 were assumed for all halos. The injection efficiencies in J0633+1746 and B0656+14 were obtained by a fit to HAWC data, while the average value for other nearby pulsars was approximately set so that the sum of all contributions match the AMS-02 measurement in the ∼0.1−1 TeV range. |
 |
Fig. 11. Same as Fig. 10, but for halos with a suppressed diffusion region of 80 pc for Geminga and 50 pc for others. |
In the rare halos scenario the positron flux can be accounted for with all other known nearby pulsars having an average injection efficiency in the 40−70% range, depending on the exact model for the halos around J0633+1746 and B0656+14. Such injection efficiencies are typical of young PWNe and are similar to those for the halos around J0633+1746 and B0656+14. In this scenario all pulsars have similar average properties in terms of injection spectrum and efficiency over the first few hundred kyr of their lifetimes. Conversely, the widespread halos scenario involves low injection efficiencies (10−15%) for all other nearby pulsars, which is at odds with the values given above. This suggests that particle injection efficiency tends to decrease over the first few hundred kyr of a pulsar’s lifetime, except in some cases like J0633+1746 and B0656+14 for some reason (which may explain why these two halos were detected first).
Quantitatively, however, the situation is more complicated. The typical injection efficiencies estimated above depend on the middle-aged population in our neighborhood, on the properties of the objects, and on the details of the formation of a suppressed diffusion region and injection of pairs into it. We discuss below the different features of the local pulsar population that may alter the above numbers and reduce the difference between the widespread and rare halos scenarios.
Distances. As illustrated in Fig. 12, a handful of nearby known objects dominate the positron flux, in particular PSR B1055−52. The estimated distance of 93 pc for this pulsar, combined with its characteristic age of 535 kyr and spin-down power of 3.01 × 1034 erg s−1, guarantee a dominant contribution to the local positron flux whatever the size of the suppressed diffusion region. In the case of a 120 pc size, B1055−52 drives the total positron flux to very high values, well above those obtained for smaller sizes because we then find ourselves inside its halo. The possible predominance of that object in the local positron flux was already noted in Fang et al. (2019b), while the scenario of a single pulsar within 100 pc making up most of the positron flux above 100 GeV (and most of the all-electron flux above 1 TeV), was studied in more general terms in López-Coto et al. (2018). Assuming a distance of 350 pc instead of 93 pc for B1055−52, as suggested in Mignani et al. (2010), the average injection efficiency needed in the widespread halos scenario to account for the observed positron flux increases by a factor 2−3, while it increases by less than a factor of 2 in the rare halos scenario. This reduces the difference between the two scenarios and brings the injection efficiencies for putative nearby halos closer to the typical expected range.
 |
Fig. 12. Individual contributions to the total positron flux from known middle-aged pulsars within 1 kpc, except J0633+1746 and B0656+14, assuming they develop a Geminga-like halo with a size of 50 pc past an age of 60 kyr. A default injection efficiency of 100% is assumed for all pulsars, and only those contributing at the ≳1% level or more are labeled. |
Ages. Figure 12 also shows that the local positron flux is dominated by several rather old objects with characteristic ages ≳500 kyr, such as B1055−52, J2030+4415, and B1742−30. Whether halos can be developed around such old pulsars remains to be proven. They may have moved past the region of enhanced turbulence, or that turbulence may have damped, such that particles are not efficiently confined anymore. In that case the average injection efficiency needed in the widespread halos scenario to account for the observed positron flux from all pulsars younger than 500 kyr is increased by nearly an order of magnitude, and is in agreement with the very high values inferred for young PWNe. Alternatively, the characteristic ages may be overestimating the true ages by a factor of a few, as already discussed in Sect. 3.4. If those pulsars with characteristic ages ≳500 kyr actually have true ages in the 200−300 kyr range, the impact on the required injection efficiency is very limited, a decrease on the order of 10−20% at energies of a few hundred GeV, and the low injection efficiencies are overall preserved.
Completeness. While the existence of very nearby objects like B1055−52 tends to lower the requirement on injection efficiency, so would the existence of more pulsars than considered here. The small sample we use may underestimate the population of relevant objects for two reasons. First, we considered only nearby pulsars within 1 kpc, to simplify the calculations, while some contribution to the positron flux from objects up to 2−3 kpc can be expected just based on the typical diffusion scale length at 1 TeV for average diffusion conditions. Second, pulsars selected from the ATNF catalog were mostly identified in radio or X-rays through beamed emission periodically pointing toward our direction, and many more exist that we could not detect this way but would nevertheless contribute to the positron flux. Including all known middle-aged ATNF pulsars within 2 kpc (41 objects instead of 14) yields an increase in the local positron flux by ∼20% at most, and much less if B1055−52 actually is at a distance of 93 pc and heavily dominates the flux. A more significant effect can be expected from unknown nearby pulsars. From estimates of the pulsar beaming fraction, the full population may count at least three times more objects than currently known (Linden et al. 2017), maybe up to ten times. Including their contribution to the local positron flux would mechanically reduce the average injection efficiencies needed to match the AMS-02 data by the same amount, for both the widespread halos scenario and the rare halos scenario, although possibly in different proportions depending on the exact layout of objects in terms of distances and ages. It may well be, however, that the local population was probed to a relatively high degree of completeness because the proximity of pulsars favored their detection in gamma rays, especially since they are emitted with higher beaming fractions than pulsed radio signals. In Johnston et al. (2020), pulsars with spin-down power in the 1035 − 1036 erg s−1 (i.e., the decade above the one most relevant to us) have radio and gamma-ray beaming fractions of 0.33 and 0.50, respectively, with partial overlap, which suggests a correction for completeness by less than a factor of 2 for a sample of local objects that is not flux-limited, hence a limited correction on the above injection efficiency estimates.
Pair injection. The conditions of particle injection also have an impact on the average injection efficiencies inferred in each scenario. While the high-energy spectral index α2 influences the shape of the predicted contribution to the positron flux in the widespread halos scenario, variations in the 2.0−2.4 range have little effect on the average injection efficiency required to match the AMS-02 data because they preserve a maximum in the positron flux at 0.1−1 TeV energies and at about the same level in the E3F(E) space. A more drastic effect results from assuming a single hard power-law injection spectrum with relatively low cutoff energy, as discussed in Sect. 3.5. A strong impact also arises from the injection start time. Replacing our default assumption of 60 kyr by 20 kyr leads to a predicted positron flux from all other nearby halos that is about twice as high, hence required injection efficiencies to match the AMS-02 measurement that are twice as low. More generally, any contribution to the injection from the early stages of a pulsar’s evolution will push the required injection efficiency to match the AMS-02 data to lower values, potentially very low because the pulsar was much more powerful at early times. In that respect, transitional objects between the classical young PWN and evolved halo stages are potentially very important when it comes to their contribution to the local positron flux. Evaluating how the population of pairs injected in the early stages spreads out following the reverse-shock crushing of the original nebula and its mixing with the remnant’s material would require a more involved modeling framework than the one used here for diffusive halos. To the best of our knowledge, this remains a poorly explored area.
The local population and the positron flux constraint therefore suggest different scenarios regarding the occurrence of pulsar halos. The first scenario is that pulsar halos are rare. Locally, only J0633+1746 and B0656+14 have developed a halo, for some reason. The rest of the middle-aged pulsar population, known already to a high degree of completeness, contributes to the positron flux at Earth without strong confinement around the source. In this scenario the properties of particle injection, spectrum, and efficiency, are the same for all pulsars, from objects that are a few thousand years old and power bright PWNe to 100 kyr objects, including J0633+1746 and B0656+14. This situation is preserved if the very nearby pulsar B1055−52 is located at a distance greater than 93 pc and if, at the same time, the actual local pulsar population exceeds the known population by less than a factor 2.
The second scenario is that pulsar halos are common. Most middle-aged pulsars develop halos similar to those around J0633+1746 and B0656+14, but the average injection efficiency is on the order of 10−15% or less depending on the fraction of unknown local pulsars. This suggests a drop in injection efficiency by nearly one order of magnitude over the first few hundred kyr of a pulsar’s lifetime, on average, with notable exceptions such as J0633+1746 and B0656+14. The required decrease in efficiency, however, can be reduced to just a factor of a few if the very nearby pulsar B1055−52 is located at a distance greater than 93 pc, or even suppressed if pulsars with characteristic ages above approximately 500 kyr do not develop halos. On the other hand, the decrease in efficiency can be even stronger if a fraction of the particles produced at early times, when the pulsar was more powerful, manage to escape into the halo.
Taking the population properties from the ATNF data base at face value, the first option may be favored only for the sake of simplicity, as it requires no exceptional status for J0633+1746 and B0656+14. However, as discussed in the previous paragraphs, the exact properties of the population, especially the most nearby objects, are crucial because a handful of objects have a predominant contribution to the positron flux.
In the case where halos are common, very large halos do not seem favored. As suggested in the top panel of Fig. 9, and this is even more marked in the absence of B1055−52, very large halos around nearby pulsars produce a rather peaked positron flux, with a maximum around 500−600 GeV for an average value of the injection index, very unlike the observed spectral shape, which is flat ≳100 GeV in the E3F(E) space. The very existence of B1055−52, if it is indeed located very close to us, is an even stronger argument. It alone demonstrates that not all middle-aged pulsars develop very large halos of ≳100−120 pc in size, otherwise this would place us within the halo of B1055−52, leading to a positron flux one to two orders of magnitude above the AMS-02 measurement for typical injection efficiencies on the order of a few tens of percent.
The hypothesis that halos could be relatively rare raises the question of their actual occurrence rate among pulsars. Based on the local sample of objects, assuming J0633+1746 and B0656+14 are the only halos, the occurrence rate would lie in the ∼5−10% range depending on the fraction of the local pulsar population that we can assume as known: typically ∼12−13% if the 16 known pulsars within 1 kpc are all those that exist, and half of that if there are twice as many. We note that rarity should probably be understood in a broad sense: either halos are long-lived structures that occur rarely among the pulsar population (the option we most directly test here with our static model) or they are an infrequent evolutionary phase in a larger number of pulsars. Both possibilities could manifest in the same way in terms of contribution to the local positron flux, depending on the parameters of the problem.
While a number of extended TeV sources are positionally coincident with middle-aged pulsars, for instance the list presented in Linden et al. (2017) and updated in Albert et al. (2020), formal identification is lacking in most cases such that the idea that halos are generally rare among middle-aged pulsars is perfectly viable. In the list of candidate halos from Albert et al. (2020), only 8 out of 16 middle-aged pulsars observable with HAWC can be associated with a 3HWC source, despite a very loose criterion of positional coincidence within 1°, and alternative interpretations are available for many of these. For instance, the source associated with PSR J1913+1011 may well be a SNR (see Zhang et al. 2020), while the source associated with PSR J2032+4127 is most likely a classical PWN associated with the gamma-ray binary (see Aliu et al. 2014; Lyne et al. 2015; Albacete Colombo et al. 2020). In several other cases, the associations involve powerful pulsars with spin-down power ≳1036 erg s−1 and characteristic ages ∼100 kyr, like PSR J1831−0952 and PSR J1925+1720, such that a classical PWN is the most likely origin for the gamma-ray emission, as suggested in more general terms in Giacinti et al. (2020). Overall, from the list in Albert et al. (2020), only 3 out of the 16 middle-aged pulsars are associated with sources that can be considered solid halo candidates (J0633+1746, B0656+14, and B0540+23), eventually yielding an occurrence rate similar to that provided above, via a different approach.
The above results suggest a range of possibilities for the composition of the positron flux above 80−100 GeV: (i) if the halos around J0633+1746 and B0656+14 have large extents of 80−100 pc, and the corresponding positron flux is heavily suppressed, the spectrum is dominated by particles freely escaping from nearby middle-aged pulsars and falls off more or less abruptly in the TeV range depending on the actual injection spectrum in nearby pulsars (e.g., spectral index in the 2.4−2.8 range, existence of a cutoff at lower energies than assumed here; see Fig. 11); (ii) if the halos around J0633+1746 and B0656+14 have moderate extents of 30−50 pc, their summed contribution to the positron flux dominates above 100 GeV, with a flat or slightly rising spectrum ≳1 TeV (see Fig. 10 and also Fang et al. 2019b). The actual trend may hopefully be revealed in future releases of AMS-02 data.
Last, we note that the above results and conclusions hold in the adopted model framework. It is perfectly conceivable that the suppressed diffusion region has both time- and energy-dependent properties (e.g., extent or onset of diffusion suppression depending on particle energy). Such solutions would certainly help to relax the local positron flux constraint and thus allow for halos to be more widespread (at the expense of a greater number of free parameters).
5. Conclusions
The discovery of extended gamma-ray emission structures around a growing but still small number of middle-aged pulsars, interpreted as halos formed by the inverse-Compton scattering of ambient photon fields by electron-positron pairs, has raised the question of their commonness in the Galaxy. Observations of the nearby PSR J0633+1746 and PSR B0656+14 almost directly indicate diffusion suppression by factors reaching two to three orders of magnitude at ∼100 TeV, and complementary analyses have suggested that this inhibited diffusion could extend over scales of at least 100−120 pc. These numbers, however, seem extreme when compared to what can be achieved in recent theoretical attempts to account for the phenomenon, under reasonable and representative assumptions for particle acceleration and release in these systems.
Using the phenomenological framework of a static two-zone diffusion model, we searched for parameter setups minimizing as much as possible the extent and magnitude of pair confinement around J0633+1746 and B0656+14. We compared model predictions to data from Fermi-LAT, HAWC, and AMS-02, under the requirement that nonthermal particles released in the halos past an age of 60 kyr are representative of PWNe in terms of injection spectrum and efficiency.
In this framework, the magnitude of diffusion suppression at 100 TeV particle energies, with respect to average conditions in the Galactic plane, appears tightly constrained for both objects. The case of J0633+1746 is the most extreme, with diffusion suppression at a level of ∼500 constrained by both the HAWC and AMS-02 observations and the total energetics of the pulsar. The age and distance of J0633+1746 are such that a suppressed diffusion region of moderate extent ≲50 pc yields an excessive contribution to the local positron flux and requires an excessive injection efficiency for commonly assumed parameters of the problem. These issues can be circumvented if the Geminga pulsar has a true age ≲200 kyr, younger than its characteristic age, and/or if the injection spectrum is relatively flat, which implies a flux in the Fermi-LAT range below the level of the claimed detection. In these cases solutions with suppressed diffusion regions as small as 30 pc can be found. The case of B0656+14, with diffusion suppression at a level of ∼100, is less constrained, owing to the nondetection in the Fermi-LAT range and to the younger age and larger distance of the pulsar compared to Geminga. This translates into a much smaller contribution to the local positron flux, peaking at energies above the current reach of AMS-02, which makes it easier to fit within the positron flux constraint for a wide range of suppressed diffusion region sizes. For both pulsars, depending on the exact model setup, injection efficiencies above a few tens of percent are required, similar to the values inferred for the younger PWNe. In these model setups, the contribution of both pulsar halos to the local positron flux is significant and could even dominate above a few hundred GeV. In particular, Geminga would account for about 30−50% or more of the positron flux over part or all of the ∼0.1−1 TeV range.
If all other nearby middle-aged pulsars develop halos similar to our minimal model setups for J0633+1746 and B0656+14, their combined positron flux complemented by the contribution from Geminga would saturate the AMS-02 measurement above ≳100 GeV for an average injection efficiency that is much lower than the values inferred for the halos around J0633+1746 and B0656+14 or with the values inferred for younger PWNe. In this scenario extremely large suppressed diffusion regions of 100−120 pc or more are disfavored for the following reasons: (i) this would place us inside the halo of PSR B1055−52 with, as a consequence of its proximity and age, an extremely large positron flux overwhelming the AMS-02 measurement for a typical injection efficiency; (ii) it raises the question of what exactly contributes to the local ≳100 GeV positron flux since the cumulative contribution from very large halos is strongly peaked at 0.5−1 TeV, much unlike the flat spectral shape observed with AMS-02; and (iii) is is in tension with what seems achievable in most theoretical models.
Conversely, if positrons from other nearby pulsars are released in the ISM without any kind of confinement around the source, their local flux complements the contribution from Geminga for average injection efficiencies of a few tens of percent for all pulsars, from objects that are a few thousand years in age and power bright PWNe to 100 kyr objects like J0633+1746 and B0656+14. It thus seems a simpler scenario to consider that most middle-aged pulsars do not develop halos similar to those around J0633+1746 and B0656+14, or even no halo at all. Even so, the quantitative difference between the rare or common halos scenarios, in terms of required injection efficiency to fit the positron flux constraint, depends heavily on the actual properties of the local population of pulsars and on the still uncertain physics driving the formation and evolution of halos.
Based on local objects, the occurrence rate of halos among middle-aged pulsars could be as low as ∼5−10%. The local positron flux at ∼0.1−1 TeV energies would therefore be attributed to a few dozen nearby middle-aged pulsars rapidly releasing pairs into the ISM, with a possible contribution over part or most of the range by J0633+1746, and at higher energies by B0656+14, depending on their properties. Positron flux measurements in the TeV range would therefore be instrumental in constraining the size of the halos around J0633+1746 and B0656+14, and the possible existence of other instances of the phenomenon in our neighborhood.
Equation (22) in Tang & Piran (2019) contains a mistake in the arguments of the erf and erfc functions. The correct form of the spatial kernel in the two-zone case can be found in Di Mauro et al. (2019).
The physical mechanism underlying such a spectrum is not fully clear yet, but several proposed scenarios rely on two electron populations: low-energy relic electrons injected during the early rapid spin-down phase of the pulsar and high-energy wind electrons continuously released downstream of the wind termination shock (see Meyer et al. 2010, and references therein, for an application to the Crab nebula); as an alternative, low-energy particles could result from turbulent acceleration downstream of the termination shock, while high-energy particles would be produced by shock acceleration (Bucciantini et al. 2011, this second scenario is more consistent with the model framework used in this work). The physical meaning of the break energy depends on the scenario: either low-energy cutoff of the high-energy population reflecting the Lorentz factor of the bulk upstream flow (Kennel & Coroniti 1984); or high-energy cutoff of the low-energy population reflecting the maximum attainable energy in the turbulent flow (Bucciantini et al. 2011). In either case, a smooth connection of the two populations remains a challenge.
We tested the effect of grid parameters and found them to be negligible except at the lowest energies when diffusion suppression is very low, much lower than the values handled here (because the particle distribution then becomes very extended within the suppressed diffusion region and particle density is non-negligible outside of it).
Inverse-Compton scattering radiation should ideally be computed taking into account the anisotropic nature of the seed photon fields, but the effect was found to be minor and most likely degenerate with other free parameters of the problem (Jóhannesson et al. 2019).
A harder momentum dependence of the diffusion coefficient, with a power-law index increasing from 0.3 to 0.8, can actually bring the positron flux below the ∼1 TeV observed level for values of 0.6−0.7. The effect is nonlinear and depends on the relative values of the energy-dependent diffusion radius and suppressed diffusion region size at the relevant energy. When the former approaches and drops below the latter, the particle density at the halo boundary is progressively cut off exponentially (the erfc term prevails over the 1/r dependence in Eq. (S4) in Abeysekara et al. 2017), and so do the resulting escaping fluxes. In the baseline scenario, the 1 TeV diffusion radius is on the order of 80 pc, and bringing it down to a 50 pc size for the confinement region can be achieved by reducing the diffusion coefficient at 1 TeV by about 3 (the diffusion radius depends on the square root of the diffusion coefficient). This reduction can be obtained using a diffusion index of 0.6 instead of 0.3. If the confinement region is 30 pc in size instead, matching the 1 TeV diffusion radius requires reducing the diffusion coefficient by about 7, which in turn implies a diffusion index of 0.8 instead of 0.3. A stronger momentum dependence is not unexpected theoretically in the self-confinement scenario (see Fig. 2 in Evoli et al. 2018), at least over a selected range of distances from the pulsar and times since particle and/or turbulence injection.
Acknowledgments
The authors acknowledge financial support by CNES for the exploitation of Fermi-LAT observations, and by ANR for support to the GAMALO project under reference ANR-19-CE31-0014. We thank Rúben López-Coto for providing the HAWC intensity data in a convenient format, Carmelo Evoli for insightful discussions and comments on the manuscript, and Benedikt Schroer for spotting a mistake in an initial version of the results. We also thank the anonymous referee for very valuable comments that contributed to improve the quality of the manuscript. This work has made use of the SIMBAD database, operated at CDS, Strasbourg, France, and of NASA’s Astrophysics Data System Bibliographic Services. The preparation of the figures has made use of the following open-access software tools: Astropy (Astropy Collaboration 2013), Matplotlib (Hunter 2007), NumPy (van der Walt et al. 2011), and SciPy (Virtanen et al. 2020).
References
- Abeysekara, A. U., Albert, A., Alfaro, R., et al. 2017, Science, 358, 911 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowski, A., Aharonian, F., Ait Benkhali, F., et al. 2015, Science, 347, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Aguilar, M., Ali Cavasonza, L., Ambrosi, G., et al. 2019, Phys. Rev. Lett., 122, 041102 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., An, Q., Axikegu, et al. 2021, Phys. Rev. Lett., 126, 241103 [NASA ADS] [CrossRef] [Google Scholar]
- Albacete Colombo, J. F., Drake, J. J., Filócomo, A., & Wright, N. J. 2020, Boletin de la Asociacion Argentina de Astronomia La Plata Argentina, 61B, 204 [Google Scholar]
- Albert, A., Alfaro, R., Alvarez, C., et al. 2020, ApJ, 905, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Aliu, E., Aune, T., Behera, B., et al. 2014, ApJ, 783, 16 [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Badenes, C., Maoz, D., & Draine, B. T. 2010, MNRAS, 407, 1301 [NASA ADS] [CrossRef] [Google Scholar]
- Bao, L. Z., Fang, K., Bi, X. J. 2021, ArXiv e-prints [arXiv:2107.07395] [Google Scholar]
- Bucciantini, N. 2008, in 40 Years of Pulsars: Millisecond Pulsars, Magnetars and More, eds. C. Bassa, Z. Wang, A. Cumming, & V. M. Kaspi, AIP Conf. Ser., 983, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Bucciantini, N., Arons, J., & Amato, E. 2011, MNRAS, 410, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Bucciantini, N., Olmi, B., & Del Zanna, L. 2020, J. Phys. Conf. Ser., 1623, 012002 [NASA ADS] [CrossRef] [Google Scholar]
- Bykov, A. M., Amato, E., Petrov, A. E., Krassilchtchikov, A. M., & Levenfish, K. P. 2017, Space Sci. Rev., 207, 235 [CrossRef] [Google Scholar]
- Di Mauro, M., Manconi, S., & Donato, F. 2019, Phys. Rev. D, 100, 123015 [NASA ADS] [CrossRef] [Google Scholar]
- Di Mauro, M., Manconi, S., & Donato, F. 2020, Phys. Rev. D, 101, 103035 [NASA ADS] [CrossRef] [Google Scholar]
- Evoli, C., Linden, T.., Morlino, G., et al. 2018, Phys. Rev. D, 98, 063017 [NASA ADS] [CrossRef] [Google Scholar]
- Evoli, C., Amato, E., Blasi, P., & Aloisio, R. 2021, Phys. Rev. D, 103, 083010 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, K., Bi, X.-J., & Yin, P.-F. 2019a, MNRAS, 488, 4074 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, K., Bi, X.-J., & Yin, P.-F. 2019b, ApJ, 884, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Fesen, R. A., Drechsler, M., Weil, K. E., et al. 2021, ApJ, 920, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Génolini, Y., Boudaud, M., Batista, P. I., et al. 2019, Phys. Rev. D, 99, 123028 [NASA ADS] [CrossRef] [Google Scholar]
- Giacinti, G., Mitchell, A. M. W., López-Coto, R., et al. 2020, A&A, 636, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haverkorn, M., Brown, J. C., Gaensler, B. M., & McClure-Griffiths, N. M. 2008, ApJ, 680, 362 [Google Scholar]
- Hooper, D., Cholis, I., Linden, T., & Fang, K. 2017, Phys. Rev. D, 96, 103013 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Jóhannesson, G., Porter, T. A., & Moskalenko, I. V. 2019, ApJ, 879, 91 [CrossRef] [Google Scholar]
- Johnston, S., Smith, D. A., Karastergiou, A., & Kramer, M. 2020, MNRAS, 497, 1957 [NASA ADS] [CrossRef] [Google Scholar]
- Kennel, C. F., & Coroniti, F. V. 1984, ApJ, 283, 710 [Google Scholar]
- Linden, T., Auchettl, K., Bramante, J., et al. 2017, Phys. Rev. D, 96, 103016 [NASA ADS] [CrossRef] [Google Scholar]
- López-Coto, R., & Giacinti, G. 2018, MNRAS, 479, 4526 [CrossRef] [Google Scholar]
- López-Coto, R., Parsons, R. D., Hinton, J. A., & Giacinti, G. 2018, Phys. Rev. Lett., 121, 251106 [CrossRef] [Google Scholar]
- Lyne, A. G., Stappers, B. W., Keith, M. J., et al. 2015, MNRAS, 451, 581 [Google Scholar]
- Malkov, M. A., Diamond, P. H., Sagdeev, R. Z., Aharonian, F. A., & Moskalenko, I. V. 2013, ApJ, 768, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, AJ, 129, 1993 [Google Scholar]
- Manconi, S., Di Mauro, M., & Donato, F. 2020, Phys. Rev. D, 102, 023015 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, P., Tibaldo, L., Marcowith, A., & Abdollahi, S. 2022, A&A accepted, https://doi.org/10.1051/0004-6361/202244002 [Google Scholar]
- Meyer, M., Horns, D., & Zechlin, H. S. 2010, A&A, 523, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mignani, R. P., Pavlov, G. G., & Kargaltsev, O. 2010, ApJ, 720, 1635 [NASA ADS] [CrossRef] [Google Scholar]
- Moderski, R., Sikora, M., Coppi, P. S., & Aharonian, F. 2005, MNRAS, 363, 954 [Google Scholar]
- Mukhopadhyay, P., & Linden, T. 2022, Phys. Rev. D, 105, 123008 [NASA ADS] [CrossRef] [Google Scholar]
- Nava, L., Gabici, S., Marcowith, A., Morlino, G., & Ptuskin, V. S. 2016, MNRAS, 461, 3552 [NASA ADS] [CrossRef] [Google Scholar]
- Nava, L., Recchia, S., Gabici, S., et al. 2019, MNRAS, 484, 2684 [NASA ADS] [CrossRef] [Google Scholar]
- Popescu, C. C., Yang, R., Tuffs, R. J., et al. 2017, MNRAS, 470, 2539 [NASA ADS] [CrossRef] [Google Scholar]
- Posselt, B., Pavlov, G. G., Slane, P. O., et al. 2017, ApJ, 835, 66 [CrossRef] [Google Scholar]
- Principe, G., Mitchell, A. M. W., Caroff, S., et al. 2020, A&A, 640, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Profumo, S., Reynoso-Cordova, J., Kaaz, N., & Silverman, M. 2018, Phys. Rev. D, 97, 123008 [NASA ADS] [CrossRef] [Google Scholar]
- Recchia, S., Di Mauro, M., Aharonian, F. A., et al. 2021, Phys. Rev. D, 104, 123017 [NASA ADS] [CrossRef] [Google Scholar]
- Schroer, B., Pezzi, O., Caprioli, D., Haggerty, C., & Blasi, P. 2021, ApJ, 914, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Schroer, B., Pezzi, O., Caprioli, D., Haggerty, C. C., & Blasi, P. 2022, MNRAS, 512, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Sudoh, T., Linden, T., & Beacom, J. F. 2019, Phys. Rev. D, 100, 043016 [NASA ADS] [CrossRef] [Google Scholar]
- Sudoh, T., Linden, T., & Hooper, D. 2021, JCAP, 2021, 010 [CrossRef] [Google Scholar]
- Suzuki, H., Bamba, A., & Shibata, S. 2021, ApJ, 914, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Tang, X., & Piran, T. 2019, MNRAS, 484, 3491 [CrossRef] [Google Scholar]
- Tibaldo, L., Gaggero, D., & Martin, P. 2021, Universe, 7, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, D. F., Cillis, A., Martín, J., & de Oña Wilhelmi, E. 2014, J. High Energy Astrophys., 1, 31 [NASA ADS] [Google Scholar]
- Trotta, R., Jóhannesson, G., Moskalenko, I. V., et al. 2011, ApJ, 729, 106 [NASA ADS] [CrossRef] [Google Scholar]
- van der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
- Verbiest, J. P. W., Weisberg, J. M., Chael, A. A., Lee, K. J., & Lorimer, D. R. 2012, ApJ, 755, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Meth., 17, 261 [Google Scholar]
- Worley, A., Krastev, P. G., & Li, B.-A. 2008, ApJ, 685, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Xi, S.-Q., Liu, R.-Y., Huang, Z.-Q., Fang, K., & Wang, X.-Y. 2019, ApJ, 878, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Zabalza, V. 2015, Int. Cosm. Ray Conf., 34, 922 [NASA ADS] [Google Scholar]
- Zhang, L., Chen, S. B., & Fang, J. 2008, ApJ, 676, 1210 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, H.-M., Xi, S.-Q., Liu, R.-Y., et al. 2020, ApJ, 889, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, X.-F. 2016, Chin. J. Phys., 54, 839 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Summary of baseline parameters used in modeling the halos around PSR J0633+1746 and PSR B0656+14.
All Figures
 |
Fig. 1. Model fits to HAWC+LAT observations of J0633+1746, and the corresponding predicted local positron fluxes, for different sizes of the suppressed diffusion region RSDR, and different high-energy injection indexes α2. All other parameters have their baseline values, in particular the diffusion coefficient DSDR(100 TeV)=4 × 1027 cm2 s−1. The set of dashed blue curves corresponds to the baseline model setup. The legend indicates the injection efficiency η and the χ2 of the fit. |
| In the text | |
 |
Fig. 2. Model fits to HAWC observations of B0656+14, and the corresponding predicted local positron fluxes, for different sizes of the suppressed diffusion region RSDR. All other parameters have their baseline values, in particular the diffusion coefficient DSDR(100 TeV)=1028 cm2 s−1. The set of dashed blue curves corresponds to the baseline model setup. The legend indicates the injection efficiency η and the χ2 of the fit. |
| In the text | |
 |
Fig. 3. Diffusion scale length in three different model setups for J0633+1746: the baseline setup (in blue), an alternative setup with a lower pulsar age (150 kyr instead of 342 kyr, in red), and a setup with a higher radiation field (eight times stronger than baseline, in green). Overlaid are the typical particle energy ranges probed directly or indirectly by the different observables considered in this work. The AMS-02 experiment is sensitive to positrons with energies from below 1 GeV to above 1 TeV, but only the range above 50 GeV is relevant to this work (at lower energies the flux is dominated by cosmic-ray secondaries). |
| In the text | |
 |
Fig. 4. Confidence interval in the diffusion normalization and injection index space, for model fits to HAWC+LAT data in the case of J0633+1746 (top panel), and to HAWC data only in the case of B0656+14 (bottom panel). The model setups feature a suppressed diffusion region extent of 50 pc. The color-coding indicates increasing χ2 variations from the optimum of up to 1 and 4 in the orange and yellow regions, respectively. The black vertical hatches indicate the model fits yielding positron fluxes in excess of the AMS-02 measurement in the 0.1−1 TeV range, while the gray slanting hatches indicate model fits implying injection efficiencies in excess of 100% of the spin-down power. |
| In the text | |
 |
Fig. 5. Confidence interval in the diffusion normalization and magnetic field strength space (top panel), and diffusion normalization and radiation field intensity space (bottom panel), for model fits to HAWC+LAT data in the case of J0633+1746, assuming a suppressed diffusion region extent of 50 pc. The meaning of graphical elements is the same as in Fig. 4. |
| In the text | |
 |
Fig. 6. Predicted local positron fluxes for different increases in the infrared and optical photon field densities UIR, Opt (top panel) and different ages for the pulsar tage (bottom panel), assuming a suppressed diffusion region extent of RSDR = 50 pc. The predicted gamma-ray emission is fitted to HAWC+LAT observations of Geminga and the corresponding injection efficiencies η and χ2 of the fits are given in the legend. |
| In the text | |
 |
Fig. 7. Confidence interval in the diffusion normalization and pulsar distance space (top panel) and diffusion normalization and pulsar age space (bottom panel), for model fits to HAWC+LAT data in the case of J0633+1746, assuming a suppressed diffusion region extent of 50 pc and injection index of 2.6. The meaning of graphical elements is the same as in Fig. 4. |
| In the text | |
 |
Fig. 8. Predicted local positron fluxes for variations in the injection index α2, assuming a suppressed diffusion region extent RSDR = 30 pc. The predicted gamma-ray emission is fitted to HAWC observations of Geminga only and the corresponding injection efficiencies η and χ2 of the fits are given in the legend. The χ2 includes the deviation from the LAT spectral points to illustrate the effect of neglecting that constraint. |
| In the text | |
 |
Fig. 9. Total local positron flux from known middle-aged pulsars within 1 kpc, except J0633+1746 and B0656+14, under the assumption that they develop a halo like J0633+1746 (top panel) or B0656+14 (bottom panel) past an age of 60 kyr, with different possible sizes for the suppressed diffusion region. For comparison, both plots also display the expected flux if all nearby pulsars develop no halo and particles released in the ISM diffuse out without experiencing any kind of strong and extended confinement around the source. By default, injection efficiencies of 100% are assumed, and several possibilities were tested for the injection index in the case of plain interstellar diffusion. |
| In the text | |
 |
Fig. 10. Total positron flux from the halos around J0633+1746 and B0656+14, and the population of known nearby middle-aged pulsars under two hypotheses for the latter: all pulsars develop a halo (top panel) or none develops a halo and particles are released without confinement around the source (bottom panel). Suppressed diffusion regions of 30 pc for both and an injection index of 2.4 were assumed for all halos. The injection efficiencies in J0633+1746 and B0656+14 were obtained by a fit to HAWC data, while the average value for other nearby pulsars was approximately set so that the sum of all contributions match the AMS-02 measurement in the ∼0.1−1 TeV range. |
| In the text | |
 |
Fig. 11. Same as Fig. 10, but for halos with a suppressed diffusion region of 80 pc for Geminga and 50 pc for others. |
| In the text | |
 |
Fig. 12. Individual contributions to the total positron flux from known middle-aged pulsars within 1 kpc, except J0633+1746 and B0656+14, assuming they develop a Geminga-like halo with a size of 50 pc past an age of 60 kyr. A default injection efficiency of 100% is assumed for all pulsars, and only those contributing at the ≳1% level or more are labeled. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



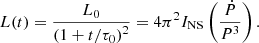
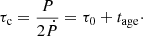
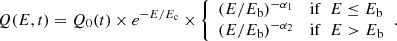
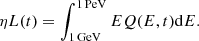
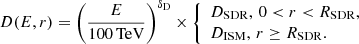
![$$ \begin{aligned}&N(r,E) = \int _{\mathrm{max}[t_{\rm exit},\,t_{\rm exit}-t_{\rm cool}(E_{\rm c}, E)]}^{t_{\rm age}} \frac{\dot{E}(E_0)}{\dot{E}(E)}Q(E_0,t_0) H(r,E) \mathrm{d}t_0,\end{aligned} $$](/articles/aa/full_html/2022/09/aa43481-22/aa43481-22-eq6.gif)
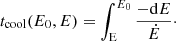
![$$ \begin{aligned} \dot{E} = \dot{E}_{\rm IC} +\dot{E}_{\rm syn} = -\frac{4}{3}c\sigma _{\rm T} \gamma ^2 \left[\sum _i\frac{U_{i}}{(1+4\pi \gamma \epsilon _i)^{3/2}} + \frac{B^2}{8\pi }\right]\cdot \end{aligned} $$](/articles/aa/full_html/2022/09/aa43481-22/aa43481-22-eq8.gif)