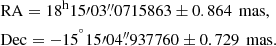EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 664 (August 2022) A&A, 664 (2022) L15 Full HTML
Open Access
Issue
A&A
Volume 664, August 2022
Article Number L15
Number of page(s) 9
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202244221
Published online 29 August 2022

© B. Morgado et al. 2022

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.

1. Introduction

Stellar occultations happen when a body passes in front of a star as viewed by an observer. The detection of these events allow the determination of 2D apparent sizes and shapes with kilometre uncertainties (Sicardy et al. 2011). Also, with these events, we can probe the vicinity of the occulting object in search for material, such as rings (Braga-Ribas et al. 2014; Ortiz et al. 2017), and even detect, characterise, or determine limits to atmospheres (Marques Oliveira et al. 2022; Meza et al. 2019; Arimatsu et al. 2019; Ortiz et al. 2012). From an astrometric point of view, these events can provide highly accurate positions of the occulting object, with uncertainties of the order of a few milliarcseconds (mas, Rommel et al. 2020).

This Letter details the analysis of the stellar occultation by the large transneptunian object (TNO; 50000) Quaoar on 2020 June 11. Quaoar belongs to the dynamical class of Cubewanos. It has a semi-major axis of 43.51 au, an orbital eccentricity of 0.035, and an inclination of 7.98 deg. Quaoar was discovered in 2002 by Brown & Trujillo (2004). These authors estimated Quaoar’s diameter to be about 1260 ± 190 km based on Hubble Space Telescope (HST) images. From previous stellar occultations, Braga-Ribas et al. (2013) obtained an area equivalent diameter of 1110 ± 5.0 km under the assumption that Quaoar is a Maclaurin spheroid. Also, thermal models based on Herschel data obtained an area equivalent diameter of 1074 ± 38 km (Fornasier et al. 2013).

In 2007, a small moon orbiting Quaoar was discovered (Brown & Suer 2007), and was later named Weywot. This satellite orbits Quaoar with a semi-major axis of 1.45 × 104 km and a period of 12.047 days. From its orbital motion, the mass of Quaoar was estimated as 1.65 × 1021 kg (Fraser & Brown 2010; Fraser et al. 2013; Vachier et al. 2012).

The occultation reported in the present Letter was observable from Australia and was detected by ESA’s CHaracterising ExOPlanet Satellite (CHEOPS, Benz et al. 2020) space telescope1. CHEOPS is a mission dedicated to studying exoplanets using the transit technique. This satellite was launched in December 2019, and is in a Sun-synchronous orbit, about 700 km above Earth. It has a 32 cm diameter Ritchey-Chrétien telescope (f/8) with a single, frame-transfer, back-illuminated CCD detector in its focal plane. Its focal plane is defocussed to deliver a large point spread function (PSF), where 90% of the stellar flux spreads within a radial aperture of 16 pixels. The CCD detector has 1024 × 1024 pixels and a pixel pitch of 13 μm. There is no filter in the optical path, resulting in a bandpass between 0.33 and 1.10 microns. This system was designed to deliver photometric measurements with high accuracy.

For the first time, we predicted and detected a stellar occultation by a TNO as observed by a space telescope orbiting Earth. This achievement was made possible thanks to the collaborative effort of the European Research Council (ERC) Lucky Star project2 and the ESA CHEOPS mission. Through this observation we are able to probe the object’s vicinity, avoiding interference from Earth’s atmosphere, detect a limit of a methane atmosphere around Quaoar, and determine the astrometric position of this large TNO with an uncertainty at the sub-mas level (less than 5 km at Quaoar’s distance).

Section 2 contains details about the prediction and observation of the occultation event. In Sect. 3, we describe the analysis of the images, determination of the light curve, and fitting the immersion (disappearance) and emersion (reappearance) times. Sect. 4 details the geometric reconstruction of the event and a determination of Quaoar’s astrometric position. Finally, our discussion and final remarks can be found in Sect. 5.

2. Prediction and observation

The event presented here was predicted in the framework of the ERC Lucky Star project. It uses the star’s position available in the Gaia catalogue (Gaia Collaboration 2016b,a; Brown 2018). Quaoar’s ephemeris was pinned down to the 5 mas accuracy level (∼150 km at Quaoar’s distance), using the Numerical Integration of the Motion of an Asteroid (NIMA, Desmars et al. 2015) integrator fed by observations in the Minor Planet Center3 (MPC) database and astrometrical positions derived from previous stellar occultations (Braga-Ribas et al. 2019, 2013).

Table 1 contains some general information about the June 2020 occultation, such as the Gaia Source ID of the occulted star, its G magnitude, and its position at the occultation epoch considering the robust propagation as suggested by Butkevich & Lindegren (2014), also considering the correct proper motion as discussed by Cantat-Gaudin & Brandt (2021). In this table we also added information about the occulting object, such as its positions in the occultation instant and visual magnitude.

Table 1.

Information about the occultation by Quaoar on 2020 June 11.

Figure 1 shows the prediction map for the occultation event. The red line on the right side of the map shows the position of CHEOPS from 16:22 to 16:33 UTC, and the green segment shows when and where CHEOPS observed the occultation (positive chord). The red dot represents the position of the ground-based observer J. Broughton, in Mount Carbine, Australia (144°52′29.4′′ E, 16°27′58.7′′ S), who observed the star under a clear sky with a 25-cm telescope, but did not see the expected occultation, thus it is a negative chord.

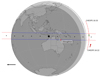thumbnail Fig. 1.

Prediction map of the Quaoar event on 2020 June 11, the black arrow on the lower left corner shows the direction of the shadow’s movement. The blue lines stand for the shadow limits, and the black dots are the centre of the shadow, separated by one minute, with the biggest one representing the geocentric closest approach time. The red dot on the map represents the position of the ground-based observer who participated in this campaign. The red line on the right side of the map shows the projected position of CHEOPS from 16:22 to 16:33 UTC, two consecutive red dots are separated by one minute in time, and the red arrow emphasises the direction of motion. The green line shows when and where CHEOPS obtained the positive chord.

The restituted CHEOPS ephemeris that was used contains its state vectors (X, Y, Z, Ẋ, Ẏ, and 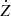Z ˙ $ \dot{Z} $) relative to the geocentre, with axes in the ICRS, between 2020 June 11 06:51 UTC and 2020 June 12 23:56 UTC. The observation was done between 15:47:55.069 and 16:46:05.024 UTC with an exposure time of 3.0 s and a mean cycle of 3.024 s. It resulted in 1148 frames where the target star and the TNO were measured in the same aperture. CHEOPS ephemeris and the observed data are available in its archive4.

3. Light curve analysis and times

CHEOPS was designed for exoplanet transit events, and the typical time resolution is 30–60 s, and a 200-pixel diameter sub-image was downloaded for the photometry. However, to avoid saturation for brighter stars, shorter exposure times can be chosen, and the images were stacked on board before being downloaded. In addition, smaller images – called imagettes – with a size of only 50 pixels in diameter, are provided for each exposure. Because of the (deliberately) de-focussed image, this is just enough to allow for photometry to enable high time resolution photometry. In the present case, the time resolution is 3 s, and the reduction steps are the following: bias subtraction, flat-fielding, non-linearity correction, pointing jitter calculation, and photometry.

First, the bias was determined from the overscan data provided with each sub-image. The bias is stable, and no uncertainty was introduced by interpolation to the 14 times more frequent imagettes. Then, we applied flat-fielding, which depends on the wavelength due to CHEOPS’s broad spectral response. Therefore, the applied flat field was weighted to match the spectral energy distribution of the star (in the present case, the effective temperature was 5040 K).

The needed non-linearity correction is a minor correction based on pre-launch measurements (Deline 2019; Deline et al. 2020; Futyan et al. 2020). For the background subtraction, we need to consider that the imagettes are too small to determine the background (basically the zodiacal light, but also the PSF wings of field stars). For this reason, sub-images were used for background calculation, and the background for each imagette was interpolated. The pointing jitter was evaluated by tracking the position of one of the three bright peaks in the PSF. The jitter amplitude was typically less than ±0.5 pixels.

Finally, the photometry was done considering that the Field of View (FoV) around the target star is crowded. So, to minimise the contamination from field stars, we used an aperture mimicking the PSF of the star rather than using a standard circular aperture. The total number of pixels in this mask was 852.

Observations made on ground by J. Broughton’s were analysed using the Platform for Reduction of Astronomical Images Automatically (PRAIA, Assafin et al. 2011). The occulted star was measured with a circular aperture and nearby stars were used as photometric calibrators to correct for sky fluctuations.

After normalising the light curve, we obtained the immersion and emersion times using Stellar Occultation Reduction and Analysis (SORA, Gomes-Júnior et al. 2022)5. This software fits an occultation model that considers a sharp-edge box model convolved with Fresnel diffraction, the stellar diameter (projected at the body’s distance), CCD bandwidth, and finite integration time. The light curves and the fitted models are available in CDS.

Figure 2 contains the normalised light curves and the fitted models. The obtained immersion and emersion times were 16:27:08.199 ± 0.020 and 16:27:43.556 ± 0.020, resulting in a chord duration of 35.357 ± 0.040 s. The minimum χ2 per degree of freedom obtained was 0.945. CHEOPS light curve standard deviation outside the event was 0.76%. Usually, only space telescopes can acquire such high photometric precision. Broughton’s negative observation was separated into two blocks. The first was obtained between 16:29:36.64 and 16:32:02.08 UTC, and the second between 16:32:16.77 and 16:33:02.05 UTC, both with exposures of 0.16 s. Broughton’s light curve has a standard deviation of 14.74%. A fairer comparison can be made if we stack Broughton’s light curve to have a similar exposure time as CHEOPS’ light curve (e.g., 3 s); for that, we stacked 19 data points (19 × 0.16 s = 3.04 s) and achieved a standard deviation of 4.2%.

thumbnail Fig. 2.

Normalised light curves on 2020 June 11 during the Quaoar’s stellar occultation relative to the closest approach (CA) time for each observer. The upper panel contains the CHEOPS light curve (black dots) and the fitted model (red line), and the middle panel contains CHEOPS residuals, in the sense of the observed flux minus the model. The bottom panel contains Broughton’s negative light curve, where the grey line stands for the single images, and the black line stands for the stack of 19 images, resulting in a better signal-to-noise ratio.

The photometric accuracy obtained with CHEOPS for the occultation presented here makes this light curve an interesting case study in searching for an atmosphere around Quaoar. We determined an upper limit of a pure methane (CH4) atmosphere using the ray-tracing method (Dias-Oliveira et al. 2015), the obtained upper limit was 85 nbar. This large value is caused by the large exposure time (3 s) and the fact that all the disappearance and reappearance information happen during a single data point. Simulations where the star disappearance happens in the limit between two data points shows that we would have a detection limit of about 3 nbar in that scenario. The detailed analysis can be found in Appendix A.

4. Geometric reconstruction of the event

The instants of disappearance and reappearance of the star behind the occulting body are the moments where the line-of-sight observer star matches the projected limb of the body. Therefore, the relative position between star and body at these moments gives the bi-dimensional position (f, g) of the limb relative to the body’s centre in a plane perpendicular to the line of sight, the tangent plane. This projection was made with the SORA package, and it results in a chord’s size of 871.61 ± 0.99 km.

The obtained chord is compatible with the area equivalent diameter obtained by stellar occultations (1110 km, Braga-Ribas et al. 2013) and with the diameter derived from thermal data (1074 km, Fornasier et al. 2013). Each chord extremity is a point at which we can fit the apparent shape of the occulting object. As only one chord was recorded, we fitted the centre of the figure (f0, g0), allowing the shape to vary within the Maclaurin spheroid solution proposed by Braga-Ribas et al. (2013), with an equatorial radius of 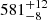581 − 8 + 12 $ 581^{+12}_{-8} $ km, apparent oblateness varying between 0 and 0.114, and a pole position angle between 0 and 180 deg. This fit was done using SORA, with a method that is fully described in Gomes-Júnior et al. (2022). The negative chord was used to eliminate solutions that would result in a positive detection of the occultation by J. Broughton.

Figure 3 shows the best-fitted ellipses and their respective 1σ region as representatives of Quaoar’s limb. Two solutions can be obtained, one with the centre north of the chord (at f0 = −252 km and g0 = −716 km, in red), and the second with the centre to the south (at f0 = −48 km and g0 = +81 km, in black). As can be seen in Table 1, the NIMA software obtained an uncertainty of ∼212 km in RA and ∼90 km in December for Quaoar ephemeris. Moreover, it is unlikely that the north solution is the correct one as it is not consistent with the knowledge we have about Quaoar’s orbit. Finally, we can shift the reference frame to the geocentre and determine Quaoar’s astrometric geocentric position on 2020 June 11 at 16:27:25.500 UTC as

RA = 18 h 15 ′ 03 . ″ 0715863 ± 0.864 mas , Dec = − 15 ° 15 ′ 04 . ″ 937760 ± 0.729 mas . $$ \begin{aligned}&\mathrm{RA} = 18^\mathrm{h}15\prime 03\overset{\prime \prime }{.}0715863 \pm 0.864\,\text{ mas}, \\&\mathrm{Dec} = -15^{^\circ }15\prime 04\overset{\prime \prime }{.}937760 \pm 0.729\,\text{ mas}. \end{aligned} $$

thumbnail Fig. 3.

Best fitted limb to the CHEOPS chord (in blue) and ellipses within their respective 1-σ region. Two solutions can be obtained, one with the centre north of the chord (in red), and another to the south (in black). The black line stands for the preferred resulted central position of Quaoar (f0,  g0) considering the centre to the south of the chord. The red line is the unlikely northern solution. The solution in black is the preferred solution as it agrees more with the expected orbit of Quaoar based on the NIMA ephemeris and its uncertainty (yellow dashed region). The green dashed line corresponds to the negative observation used to eliminate some of the solutions that cross it (light grey ellipses).

This position can be used to improve Quaoar’s ephemeris, which in turn helps us to predict future, accurate stellar occultations for this object.

As this was a single chord event, no further constraint on Quaoar’s shape was obtained. However, the resulting pole position angle for Quaoar was restrained to values between 14.2 ± 39.8 deg due to J. Broughton’s negative chord. This orientation is in agreement with Weywot’s orbital pole position for the occultation date of −5.2 deg, using the pole orientation published by Vachier et al. (2012).

5. Discussion

Stellar occultations are transient events that allow us to obtain physical parameters of the bodies in our Solar System. Networks of ground-based telescopes have been used to observe such events and derive many relevant results. Stellar occultations have also been observed by spacecrafts, such as the Cassini mission (Li et al. 2014). However, these were mostly in loco observations with events involving the objects the spacecrafts were visiting.

From space telescopes orbiting Earth, HST observed a stellar occultation by Saturn and its rings in 1991, as shown in Elliot et al. (1993). Furthermore, analysing HST Fine Guidance Sensors, two serendipitous occultations by small Oort cloud objects were reported by Schlichting et al. (2009); Schlichting et al. (2012).

For the first time, we report on the detection of a stellar occultation by a minor body as the primary target of the observation of a space telescope orbiting Earth. We obtained a non-diametrical chord of 871.61 ± 0.99 km for the TNO Quaoar, consistent with its previously published size. As a result, we detected limits of a global methane atmosphere around Quaoar. Finally, we obtained an astrometric position with an uncertainty better than 1 mas.

It is important to highlight that more ground-based stations could observe this occultation. Combining space- and ground-based observation can provide more constraints for the limb fitting and improve the result. Also, ground-based observations will detect chords that are usually parallel to each other, while the orientation of a space telescope will differ, which can be useful in the limb fitting as shown in Fig. 3. Finally, functions in the SORA package can be used to prepare automatic prediction pipelines based on the ephemeris of the space telescope and occulting objects, as presented in Appendix B.

The space observation of the Quaoar occultation presented in this paper is the first of its kind, and it serves as a proof of concept for future campaigns. Space telescopes and CubeSat telescopes can be used in conjunction with ground-based stations to detect stellar occultations. Space telescopes are not affected by weather and they extend the range of the Earth where an occultation can be observed. They can also help overcome the circumstances where the shadow would mostly cross the ocean and limited ground-based observations can be made, thus increasing the number of events observed. It is important to highlight that CHEOPS’s diameter is modest, but it allows for a photometric accuracy equivalent to what ground-based telescopes with much larger apertures would obtain.

Moreover, as discussed by Santos-Sanz et al. (2016), the prospect for the James Webb Space Telescope (JWST6) is impressive. JWST’s large primary mirror (6.5 m in diameter) with a temporal sampling of 20 frames per second will allow for the precise characterisation of material around the small bodies in our Solar System using stellar occultations, which would include detecting faint rings and thin atmospheres within the occulting bodies.

Acknowledgments

This work was carried out within the “Lucky Star” umbrella that agglomerates the efforts of the Paris, Granada and Rio teams, which is funded by the European Research Council under the European Community’s H2020 (ERC Grant Agreement No. 669416). CHEOPS is an ESA mission in partnership with Switzerland with important contributions to the payload and the ground segment from Austria, Belgium, France, Germany, Hungary, Italy, Portugal, Spain, Sweden, and the United Kingdom. The CHEOPS Consortium would like to gratefully acknowledge the support received by all the agencies, offices, universities, and industries involved. Their flexibility and willingness to explore new approaches were essential to the success of this mission. This research made use of SORA, a python package for stellar occultations reduction and analysis, developed with the support of ERC Lucky Star and LIneA/Brazil, within the collaboration of Rio-Paris-Granada teams. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). This study was financed in part by the National Institute of Science and Technology of the e-Universe project (INCT do e-Universo, CNPq grant 465376/2014-2). The following authors acknowledge the respective (i) CNPq grants: BEM 150612/2020-6; FB-R 314772/2020-0; (ii) CAPES/Cofecub grant: BEM 394/2016-05. (iii) FAPESP grants: ARGJr 2018/11239-8; GBr, VNa, IPa, GPi, RRa, and GSc acknowledge support from CHEOPS ASI-INAF agreement n. 2019-29-HH.0. ABr was supported by the SNSA. ACC acknowledges support from STFC consolidated grant numbers ST/R000824/1 and ST/V000861/1, and UKSA grant number ST/R003203/1. KGI is the ESA CHEOPS Project Scientist and is responsible for the ESA CHEOPS Guest Observers Programme. She does not participate in, or contribute to, the definition of the Guaranteed Time Programme of the CHEOPS mission through which observations described in this paper have been taken, nor to any aspect of target selection for the programme. ACC and TW acknowledge support from STFC consolidated grant numbers ST/R000824/1 and ST/V000861/1, and UKSA grant number ST/R003203/1. YA and MJH acknowledge the support of the Swiss National Fund under grant 200020_172746. We acknowledge support from the Spanish Ministry of Science and Innovation and the European Regional Development Fund through grants ESP2016-80435-C2-1-R, ESP2016-80435-C2-2-R, PGC2018-098153-B-C33, PGC2018-098153-B-C31, ESP2017-87676-C5-1-R, MDM-2017-0737 Unidad de Excelencia Maria de Maeztu-Centro de Astrobiologíca (INTA-CSIC), as well as the support of the Generalitat de Catalunya/CERCA programme. The MOC activities have been supported by the ESA contract No. 4000124370. SCCB acknowledges support from FCT through FCT contracts nr. IF/01312/2014/CP1215/CT0004. XB, SC, DG, MF and JL acknowledge their role as ESA-appointed CHEOPS science team members. This project was supported by the CNES. The Belgian participation to CHEOPS has been supported by the Belgian Federal Science Policy Office (BELSPO) in the framework of the PRODEX Program, and by the University of Liège through an ARC grant for Concerted Research Actions financed by the Wallonia-Brussels Federation. LD is an F.R.S.-FNRS Postdoctoral Researcher. This work was supported by FCT – Fundação para a Ciência e a Tecnologia through national funds and by FEDER through COMPETE2020 – Programa Operacional Competitividade e Internacionalizacão by these grants: UID/FIS/04434/2019, UIDB/04434/2020, UIDP/04434/2020, PTDC/FIS-AST/32113/2017 and POCI-01-0145-FEDER- 032113, PTDC/FIS-AST/28953/2017 and POCI-01-0145-FEDER-028953, PTDC/FIS-AST/28987/2017 and POCI-01-0145-FEDER-028987, ODSD is supported in the form of work contract (DL 57/2016/CP1364/CT0004) funded by national funds through FCT. PSS acknowledges financial support by the Spanish grant AYA-RTI2018-098657-J-I00 “LEO-SBNAF” (MCIU/AEI/FEDER, UE). PSS and JLO acknowledge financial support from the State Agency for Research of the Spanish MCIU through the “Center of Excellence Severo Ochoa” award for the Instituto de Astrofísica de Andalucía (SEV-2017-0709), they also acknowledge the financial support by the Spanish grants AYA-2017-84637-R and PID2020-112789GB-I00, and the Proyectos de Excelencia de la Junta de Andalucía 2012-FQM1776 and PY20-01309. BOD acknowledges support from the Swiss National Science Foundation (PP00P2-190080). This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (project FOUR ACES. grant agreement No 724427). It has also been carried out in the frame of the National Centre for Competence in Research PlanetS supported by the Swiss National Science Foundation (SNSF). DE acknowledges financial support from the Swiss National Science Foundation for project 200021_200726. MF and CMP gratefully acknowledge the support of the Swedish National Space Agency (DNR 65/19, 174/18). DG gratefully acknowledges financial support from the CRT foundation under Grant No. 2018.2323 “Gaseous or rocky? Unveiling the nature of small worlds”. MG is an F.R.S.-FNRS Senior Research Associate. SH gratefully acknowledges CNES funding through the grant 837319. This work was granted access to the HPC resources of MesoPSL financed by the Region Ile de France and the project Equip at Meso (reference ANR-10-EQPX-29-01) of the programme Investissements d’Avenir supervised by the Agence Nationale pour la Recherche. ML acknowledges support of the Swiss National Science Foundation under grant number PCEFP2_194576. PM acknowledges support from STFC research grant number ST/M001040/1. This work was also partially supported by a grant from the Simons Foundation (PI Queloz, grant number 327127). IRI acknowledges support from the Spanish Ministry of Science and Innovation and the European Regional Development Fund through grant PGC2018-098153-B- C33, as well as the support of the Generalitat de Catalunya/CERCA programme. SGS acknowledges support from FCT through FCT contract nr. CEECIND/00826/2018 and POPH/FSE (EC). GyMSz acknowledges the support of the Hungarian National Research, Development and Innovation Office (NKFIH) grant K-125015, a a PRODEX Experiment Agreement No. 4000137122, the Lendület LP2018-7/2021 grant of the Hungarian Academy of Science and the support of the city of Szombathely. VVG is an F.R.S-FNRS Research Associate. NAW acknowledges UKSA grant ST/R004838/1.

References

  1. Arimatsu, K., Ohsawa, R., Hashimoto, G. L., et al. 2019, AJ, 158, 236 [NASA ADS] [CrossRef] [Google Scholar]
  2. Assafin, M., Vieira Martins, R., Camargo, J. I. B., et al. 2011, Gaia follow-up Network for the Solar System Objects: Gaia FUN-SSO Workshop Proceedings, 85 [Google Scholar]
  3. Benz, W., Broeg, C., Fortier, A., et al. 2020, Exp. Astron., 51, 109 [Google Scholar]
  4. Braga-Ribas, F., Sicardy, B., Ortiz, J. L., et al. 2013, ApJ, 773, 26 [NASA ADS] [CrossRef] [Google Scholar]
  5. Braga-Ribas, F., Sicardy, B., Ortiz, J. L., et al. 2014, Nature, 508, 72 [NASA ADS] [CrossRef] [Google Scholar]
  6. Braga-Ribas, F., Crispim, A., Vieira-Martins, R., et al. 2019, J. Phys. Conf. Ser., 1365, 012024 [NASA ADS] [CrossRef] [Google Scholar]
  7. Brown, M. E., & Suer, T. A. 2007, IAU Circ., 8812, 1 [NASA ADS] [Google Scholar]
  8. Brown, M. E., & Trujillo, C. A. 2004, AJ, 127, 2413 [NASA ADS] [CrossRef] [Google Scholar]
  9. Butkevich, A. G., & Lindegren, L. 2014, A&A, 570, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Cantat-Gaudin, T., & Brandt, T. D. 2021, A&A, 649, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Deline, A. 2019, PhD Thesis, University of Geneva, Switzerland [Google Scholar]
  12. Deline, A., Queloz, D., Chazelas, B., et al. 2020, A&A, 635, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Desmars, J., Camargo, J. I. B., Braga-Ribas, F., et al. 2015, A&A, 584, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Dias-Oliveira, A., Sicardy, B., Lellouch, E., et al. 2015, ApJ, 811, 53 [NASA ADS] [CrossRef] [Google Scholar]
  15. Elliot, J. L., Bosh, A. S., Cooke, M. L., et al. 1993, AJ, 106, 2544 [NASA ADS] [CrossRef] [Google Scholar]
  16. Fornasier, S., Lellouch, E., Müller, T., et al. 2013, A&A, 555, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Fraser, W. C., & Brown, M. E. 2010, ApJ, 714, 1547 [NASA ADS] [CrossRef] [Google Scholar]
  18. Fraser, W. C., Batygin, K., Brown, M. E., & Bouchez, A. 2013, Icarus, 222, 357 [NASA ADS] [CrossRef] [Google Scholar]
  19. Futyan, D., Fortier, A., Beck, M., et al. 2020, A&A, 635, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Gaia Collaboration (Brown, A. G. A., et al.) 2016a, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Gaia Collaboration (Prusti, T., et al.) 2016b, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Gomes-Júnior, A. R., Morgado, B. E., Benedetti-Rossi, G., et al. 2022, MNRAS, 511, 1167 [CrossRef] [Google Scholar]
  24. Li, C., Zhang, X., Kammer, J. A., et al. 2014, Planet Space Sci., 104, 48 [NASA ADS] [CrossRef] [Google Scholar]
  25. Marques Oliveira, J., Sicardy, B., Gomes-Júnior, A. R., et al. 2022, A&A, 659, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Meza, E., Sicardy, B., Assafin, M., et al. 2019, A&A, 625, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Ortiz, J. L., Sicardy, B., Braga-Ribas, F., et al. 2012, Nature, 491, 566 [NASA ADS] [CrossRef] [Google Scholar]
  28. Ortiz, J. L., Santos-Sanz, P., Sicardy, B., et al. 2017, Nature, 550, 219 [NASA ADS] [CrossRef] [Google Scholar]
  29. Rommel, F. L., Braga-Ribas, F., Desmars, J., et al. 2020, A&A, 644, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Santos-Sanz, P., French, R. G., Pinilla-Alonso, N., et al. 2016, PASP, 128 [Google Scholar]
  31. Schlichting, H. E., Ofek, E. O., Wenz, M., et al. 2009, Nature, 462, 895 [NASA ADS] [CrossRef] [Google Scholar]
  32. Schlichting, H. E., Ofek, E. O., Sari, R., et al. 2012, ApJ, 761, 150 [NASA ADS] [CrossRef] [Google Scholar]
  33. Sicardy, B., Ortiz, J. L., Assafin, M., et al. 2011, Nature, 478, 493 [NASA ADS] [CrossRef] [Google Scholar]
  34. Vachier, F., Berthier, J., & Marchis, F. 2012, A&A, 543, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

Quaoar’s atmospheric limit based on CHEOPS data

Using CHEOPS data for the 11 June 2020 occultation, we determined an upper limit of Quaoar’s atmosphere. The model assumed was a pure methane (CH4) atmosphere with a temperature gradient at the surface of (dT/dz)surface  =  5.7 K km−1, and an isothermal upper branch at 102 K which is reached in about 10 km, see Figure A.1. The tested model is consistent with the ones used in Braga-Ribas et al. (2013) and Arimatsu et al. (2019). Quaoar was considered to be a sphere with a radius of 555 km; any departure from that should be negligible at this level of estimation.

thumbnail Fig. A.1.

Assumed temperature profile in Kelvin over radial distance in kilometres of a pure methane (CH4) atmosphere.

A ray-tracing method (See Dias-Oliveira et al. (2015) and references therein) was used to compute synthetic light curves convoluted with the instrumental response (exposure time of 3 seconds). We varied the surface pressure (Psurface, in nbar) and the closest approach (CA, in kilometres) between the star’s and Quaoar’s central position, and we performed Chi-squared (χ2) statistical tests to check the detection limit of a potential methane atmosphere.

This analysis resulted in a surface pressure between 15 and 85 nbars for the 1σ confidence level, and values between 0 and 95 nbars for 3σ. So no significant value was obtained and only the 85 nbar as an upper limit should be considered. Nonetheless, this limit is larger than the upper limits determined by Braga-Ribas et al. (2013) of 20 nbar, and by Arimatsu et al. (2019) of 6 nbar. This is caused by the large exposure time (3 seconds, about 75 km in radial distance in the sky plane) and the fact that all the disappearance and reappearance information occurred within one exposure, so the various models (with different pressure) are all contained in that exposure. That makes the discrimination between pressures ineffective.

As a test, we simulated data where the star disappearance and reappearance happens just at the limit between two exposures (the best case). This simulation resulted in an upper limit of only 3 nbar, assuming the same model. Is important to highlight that a smaller spatial resolution (e.g. smaller temporal resolution, smaller event velocity, or grazing occultations) would imply an even better result due to the photometric accuracy.

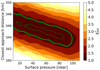thumbnail Fig. A.2.

Chi-squared per degree of freedom (χpdf2) map vs. surface pressure and CA distance. The inner dashed (resp. outer solid) green level curve is the 1σ (resp. 3σ) domain.

Prediction of stellar occultations for CHEOPS

With the success achieved in observing the stellar occultation by Quaoar, we predicted events to be observed by CHEOPS in the next months. We were granted time to observe five stellar occultations by objects in the outer Solar System. That was done in the context of the third Announcement of Opportunity. The occultation prediction maps are shown in Figure B.1-B.5. The path of CHEOPS on space is given as the circle around Earth. Given the uncertainty as to the exact position of CHEOPS at the occultation epoch, the predictions were made by computing the probability of CHEOPS to observe the event, considering its orbit is kept in a polar orbit with a movement just above the terminator of the Earth, and fixing its orbital velocity. Ground-based campaigns are being organised, and observations are planned to be made from Earth to complement CHEOPS’ observation.

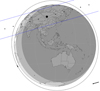thumbnail Fig. B.1.

Prediction map of a stellar occultation by Triton on 2022 October 06. The path of CHEOPS is shown as the circle just above the Earth, with an arrow indicating its sense of motion.

thumbnail Fig. B.2.

Similar to Figure B.1, but for the occultation by Quaoar on 2023 May 10.

thumbnail Fig. B.3.

Similar to Figure B.1, but for the occultation by Quaoar on 2023 May 26.

thumbnail Fig. B.4.

Similar to Figure B.1, but for the occultation by 2002 MS4 on 2023 July 03.

thumbnail Fig. B.5.

Similar to Figure B.1, but for the occultation by Chiron on 2023 September 10.

All Tables

Table 1.

Information about the occultation by Quaoar on 2020 June 11.

In the text

All Figures

thumbnail Fig. 1.

Prediction map of the Quaoar event on 2020 June 11, the black arrow on the lower left corner shows the direction of the shadow’s movement. The blue lines stand for the shadow limits, and the black dots are the centre of the shadow, separated by one minute, with the biggest one representing the geocentric closest approach time. The red dot on the map represents the position of the ground-based observer who participated in this campaign. The red line on the right side of the map shows the projected position of CHEOPS from 16:22 to 16:33 UTC, two consecutive red dots are separated by one minute in time, and the red arrow emphasises the direction of motion. The green line shows when and where CHEOPS obtained the positive chord.
In the text
thumbnail Fig. 2.

Normalised light curves on 2020 June 11 during the Quaoar’s stellar occultation relative to the closest approach (CA) time for each observer. The upper panel contains the CHEOPS light curve (black dots) and the fitted model (red line), and the middle panel contains CHEOPS residuals, in the sense of the observed flux minus the model. The bottom panel contains Broughton’s negative light curve, where the grey line stands for the single images, and the black line stands for the stack of 19 images, resulting in a better signal-to-noise ratio.
In the text
thumbnail Fig. 3.

Best fitted limb to the CHEOPS chord (in blue) and ellipses within their respective 1-σ region. Two solutions can be obtained, one with the centre north of the chord (in red), and another to the south (in black). The black line stands for the preferred resulted central position of Quaoar (f0,  g0) considering the centre to the south of the chord. The red line is the unlikely northern solution. The solution in black is the preferred solution as it agrees more with the expected orbit of Quaoar based on the NIMA ephemeris and its uncertainty (yellow dashed region). The green dashed line corresponds to the negative observation used to eliminate some of the solutions that cross it (light grey ellipses).
In the text
thumbnail Fig. A.1.

Assumed temperature profile in Kelvin over radial distance in kilometres of a pure methane (CH4) atmosphere.
In the text
thumbnail Fig. A.2.

Chi-squared per degree of freedom (χpdf2) map vs. surface pressure and CA distance. The inner dashed (resp. outer solid) green level curve is the 1σ (resp. 3σ) domain.
In the text
thumbnail Fig. B.1.

Prediction map of a stellar occultation by Triton on 2022 October 06. The path of CHEOPS is shown as the circle just above the Earth, with an arrow indicating its sense of motion.
In the text
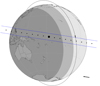thumbnail Fig. B.2.

Similar to Figure B.1, but for the occultation by Quaoar on 2023 May 10.
In the text
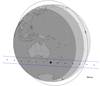thumbnail Fig. B.3.

Similar to Figure B.1, but for the occultation by Quaoar on 2023 May 26.
In the text
thumbnail Fig. B.4.

Similar to Figure B.1, but for the occultation by 2002 MS4 on 2023 July 03.
In the text
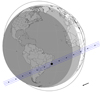thumbnail Fig. B.5.

Similar to Figure B.1, but for the occultation by Chiron on 2023 September 10.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.