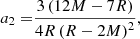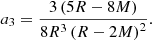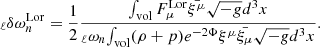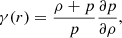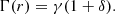| Issue |
A&A
Volume 664, August 2022
|
|
|---|---|---|
| Article Number | A177 | |
| Number of page(s) | 7 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202244082 | |
| Published online | 26 August 2022 | |
Quasi-periodic oscillations in precursor flares via seismic aftershocks from resonant shattering
1
Theoretical Astrophysics, IAAT, University of Tübingen, Tübingen 72076, Germany
e-mail: arthur.suvorov@tat.uni-tuebingen.de
2
Manly Astrophysics, 15/41-42 East Esplanade, Manly, NSW 2095, Australia
3
Department of Physics, National Tsing Hua University, Hsinchu 300, Taiwan
Received:
22
May
2022
Accepted:
30
June
2022
Context. GRB 211211A was accompanied by a kilonova, implying a merger origin for the event. A precursor flare, modulated by quasi-periodic oscillations at ≈22 Hz, was also seen ≈1 s prior to the main emission.
Aims. It is suggested here that the precursor resulted from the resonant shattering of one star’s crust prior to coalescence. Seismic aftershocks and low-frequency torsional modes may emanate from the rupture site in this case, explaining the underlying oscillations. This interpretation is directly analogous to proposals for giant flares from soft gamma repeaters, where oscillations at similar frequencies have been observed, involving starquakes followed by crustal vibrations.
Methods. Torsional mode properties were computed for sequences of slowly rotating, magnetised neutron stars in general relativity.
Results. The ≈22 Hz modulations in the precursor matches that of nodeless, ℓ = 2 torsional modes for a wide variety of stellar parameters. Global or discrete Alfvén modes are also viable candidates.
Key words: stars: magnetars / stars: oscillations / gamma-ray burst: individual: 211211A
© A. G. Suvorov et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
Gamma-ray bursts (GRBs) are observationally classified as being either long or short depending on their duration, T90. Long GRBs are typically associated with supernovae, and in most cases are well-explained by a ‘collapsar’ model where a relativistic jet, which formed at the heart of a core collapse, comes to drill through the stellar envelope, eventually producing the observed gamma rays (e.g., Bloom et al. 2002; Bromberg et al. 2012). Short GRBs instead arise from binary merger events involving at least one neutron star, and they are often associated with kilonovae (e.g., Ciolfi 2018). GRB 211211A, however, challenges this simple dichotomy (see also Zhang et al. 2007, for the case of GRB 060614), as the event was not accompanied by a supernova but rather a kilonova, despite its long duration (T90 ∼ 35 s; Gompertz et al. 2022; Rastinejad et al. 2022; Yang et al. 2022). This suggests that GRB 211211A originated from a merger.
GRB 211211A was preceded by a non-thermal, soft gamma-ray flash (‘precursor flare’) 1.08 ± 0.20 s prior to the main event (Xiao et al. 2022). This precursor flare, which is spectrally similar to those observed in short GRBs (Wang et al. 2020), may have launched prior to coalescence at an orbital separation that depends on a sub-second jet-formation timescale, τjet (Zhang 2019). For the first time, however, quasi-periodic oscillations (QPOs) at 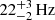 were detected within the precursor flare at the > 5σ level (Xiao et al. 2022). Although less significant, a second Fourier peak is also visible at 51 ± 2 Hz in the Fermi data (see extended data Fig. 7 in Xiao et al. 2022).
were detected within the precursor flare at the > 5σ level (Xiao et al. 2022). Although less significant, a second Fourier peak is also visible at 51 ± 2 Hz in the Fermi data (see extended data Fig. 7 in Xiao et al. 2022).
Tidal resonances may be responsible for precursor flares from binary mergers (Tsang et al. 2012; Tsang 2013). The basic mechanism involves the excitation, via orbital resonances, of stellar quasi-normal modes (QNMs) within one of the inspiralling constituents. If polar-parity QNM amplitudes reach a sufficiently high peak during the resonance window, the crust may strain enough so that it fractures, releasing copious gamma rays. Depending on the orbital frequency at the time of the precursor, different modes may be favoured, such as f (Suvorov & Kokkotas 2020b), i (Neill et al. 2021), or g modes (Kuan et al. 2021b).
Crustquakes are also popular models for giant flares in soft gamma repeaters (SGRs; Thompson & Duncan 1995). As first argued by Duncan (1998; see also Blaes et al. 1989), global seismic oscillations are likely to accompany a fracture; torsional modes, which are restored by the weak Coulomb forces of crustal ions, are especially easy to excite in such a scenario. Torsional mode properties have been calculated by many authors at various levels of sophistication. General-relativistic (Schumaker & Thorne 1983), rotational (Lee & Strohmayer 1996; Vavoulidis et al. 2007), and especially magnetic (Messios et al. 2001; Sotani et al. 2007; Colaiuda & Kokkotas 2011; Link & van Eysden 2016) effects, which are most relevant for magnetars, have been studied. The torsional eigenfunctions primarily depend on the shear modulus of the crust, μ (e.g., Tews 2017). Studies agree, however, that the nodeless, ℓ = 2 modes (2t0) for slowly rotating and modestly magnetised stars have frequencies in the range of 20≲2t0/Hz ≲ 30; ℓ = 4 mode frequencies instead have 40≲2t0f/Hz ≲ 60. If quakes are responsible for precursor flares, it is therefore natural that damped oscillations (i.e., QPOs) at these frequencies manifest within the spectrum.
Although the mechanism instigating the fracture differs, the excitation of torsional modes in GRB 211211A’s precursor may be exactly analogous to that in SGRs, such as SGR 1900+14, where QPOs at frequencies of 28 ± 2 Hz, 53 ± 5 Hz, ∼84 Hz, and 155 ± 6 Hz were detected in the tail of the 1998 giant flare (Hurley et al. 1999; Strohmayer & Watts 2005). We explore this scenario in this short paper. We complement our study with an analysis of the X-ray afterglow of the main event (Appendix A), which we find is well fitted by a magnetar wind model (Rowlinson et al. 2013). While tangential to the main goals of the paper, this allows us to infer additional information about the event as a whole.
2. Precursor flare in GRB 211211A
The precursor in GRB 211211A was observed by Fermi/GBM, Swift/BAT, and Insight-HXMT/HE (Xiao et al. 2022). The waiting time of the precursor relative to the main event is found to be ∼0.93 s for Fermi, ∼0.88 s for Swift, and ∼1.28 s from Insight data. Overall, therefore, we consider the waiting time to be 1.08 ± 0.20 s, which is not unusual for precursors in other merger-driven GRBs (e.g., GRBs 140209A and 181126413; Wang et al. 2020). With a binary-based kilonova model, Rastinejad et al. (2022) find best-fit masses (see their Fig. 7) for the progenitors to be M1 = 1.43 ± 0.05 M⊙ (primary) and M2 = 1.25 ± 0.03 M⊙ (companion). The timing delay therefore corresponds to an orbital frequency of 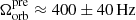 , though it could be higher if the jet-formation timescale τjet ≫ 0 (Zhang 2019).
, though it could be higher if the jet-formation timescale τjet ≫ 0 (Zhang 2019).
2.1. Resonant shattering
A neutron star, spiralling around a companion, experiences a tidal field that perturbs its crustal matter. If the frequency of the perturbing force matches the frequency of a given QNM, said mode becomes resonantly excited by efficiently depleting energy from the orbit. The amount of energy that can be transferred into the mode depends on its frequency and the degree of ‘tidal overlap’, which defines the coupling strength to the external tidal field (see, e.g., Alexander 1987; Kokkotas & Schafer 1995). If the overlap integral is large enough, the induced strain on the crust may exceed the elastic maximum, resulting in a failure (Tsang et al. 2012; Suvorov & Kokkotas 2020b; Kuan et al. 2021b; Neill et al. 2021). In brief, a resonant shattering is a feasible explanation for a given precursor if the following conditions are met. (i) The mode eigenfrequency should be approximately twice that of  since the m = 2 harmonic of the tidal field couples most strongly to stellar perturbations (Alexander 1987). (ii) The tidal overlap integral must be large enough, such that the mode is able to reach a saturation amplitude that can break the crust. (iii) Enough energy must be able to be relieved from the crust, so as to match the precursor luminosity. These criteria are referred to in subsequent sections. The spectrum of the precursor is also important to consider, as described in the next section.
since the m = 2 harmonic of the tidal field couples most strongly to stellar perturbations (Alexander 1987). (ii) The tidal overlap integral must be large enough, such that the mode is able to reach a saturation amplitude that can break the crust. (iii) Enough energy must be able to be relieved from the crust, so as to match the precursor luminosity. These criteria are referred to in subsequent sections. The spectrum of the precursor is also important to consider, as described in the next section.
2.2. A magnetar in the merger?
The precursor showed no evidence for a thermal component (Xiao et al. 2022). As discussed by Tsang et al. (2012), this suggests that a magnetar participated in the merger. Essentially, energy is able to propagate as Alfvén waves along open field lines if B is large enough (≫1013 G), and the spectrum will be predominantly non-thermal. Xiao et al. (2022) also find that the peak isotropic luminosity of the precursor is 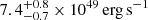 , which is rather high relative to other precursors (Wang et al. 2020). Tsang (2013) shows that the maximum luminosity, which is extractable from the crust of a star with radius R via the magnetic field, is given by the surface integral
, which is rather high relative to other precursors (Wang et al. 2020). Tsang (2013) shows that the maximum luminosity, which is extractable from the crust of a star with radius R via the magnetic field, is given by the surface integral
where v is the velocity of the mode-related perturbation. Demanding that Lmax ≳ 7 × 1049 erg s−1 implies a magnetic field of at least a few times 1014 G. The non-thermal character of the precursor and the lumsinosity budget Eq. (1) thus both seem to demand magnetar-level fields for the flaring component in GRB 211211A. As fields sof this strength can non-trivially shift the QNM spectrum, as can rotation, the timing of the precursor relative to the main event (criterion i) may favour certain mode scenarios over others (Suvorov & Kokkotas 2020b).
2.3. g-mode resonances
Fluid elements in a neutron star experience buoyancy whenever away from equilibrium if there are compositional or thermal gradients, or state changes (involving, e.g., superfluidity or superconductivity; Passamonti et al. 2016). These effects give rise to a rich spectrum of g modes, with Brunt–Väisälä frequencies that depend on the Fermi energies of the various particle species and the internal temperature. In principle, g-mode resonances can accommodate a wide range of precursor timings. In this work, these frequencies are calculated by assuming the adiabatic indices of the perturbed star and (normal fluid) equilibrium have a fixed ratio, which we take to be a ‘canonical’ value appropriate for a mature star (see Appendix B for details). Kuan et al. (2021b) show that 2g2 modes in this case can become resonant ∼1 s prior to coalescence, exerting crust-breaking levels of strain if the stellar parameters lie in a particular range. For a wide library of equations of state (EOS), however, 2g2 modes for stars with M ≈ 1.4 M⊙ tend to be ‘tidally-neutral’, in the sense that the overlap integrals are comparatively small (see Appendix A of Kuan et al. 2022). It is therefore more difficult, at least within a g-mode resonance scenario (cf. Sect. 2.4), to accept a crust breaking for the primary (criterion ii violated).
Assuming B ≳ 1014 G, the magnetic geometry (e.g., toroidal fields and multipoles) is an important ingredient for determining mode properties. For simplicity, we adopted a dipole field, the specifics of which are given in Appendix B. An additional input we required is the hydrostatic background, described by the Tolman–Oppenheimer–Volkoff equations for some EOS, with a separate model for the crust applied at low densities. We used the Akmal et al. (1998; APR4) EOS for the core, together with a Douchin & Haensel (2001) fit for the crust. This is supplemented with the shear modulus, 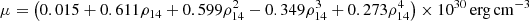 , with ρ14 being the mass density in units of 1014 g cm−3, which was found by fitting the high charge-number (Z) profile calculated by Tews (2017; see Fig. 6 therein).
, with ρ14 being the mass density in units of 1014 g cm−3, which was found by fitting the high charge-number (Z) profile calculated by Tews (2017; see Fig. 6 therein).
Following Kuan et al. (2021b, 2022), we find that a 2g2-mode resonance can fracture (criterion ii) a static companion at the right time (criterion i; assuming τjet ≈ 0) for polar field strength 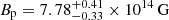 (criterion iii), where the uncertainties account for the ∼0.2 s timing window (Xiao et al. 2022); readers can refer to Fig. B.1 for more details. The formation of a binary with such a component is unlikely (Popov & Prokhorov 2006), though it cannot be ruled out a priori, and it is consistent with the luminoisty and non-thermality considerations detailed in Sect. 2.2.
(criterion iii), where the uncertainties account for the ∼0.2 s timing window (Xiao et al. 2022); readers can refer to Fig. B.1 for more details. The formation of a binary with such a component is unlikely (Popov & Prokhorov 2006), though it cannot be ruled out a priori, and it is consistent with the luminoisty and non-thermality considerations detailed in Sect. 2.2.
2.4. Other resonance scenarios
Our main goal in this work is to demonstrate that a tidal resonance, followed by aftershocks, can explain the observations leading up to GRB 211211A. The former can be accomplished with a 2g2 mode for a normal fluid star, of mass equal to that of the merger companion (M = 1.25 M⊙) with a dipole field of strength Bp ∼ 8 × 1014 G. This is not, however, the only viable scenario. For example, Neill et al. (2021) show that, depending on the nuclear symmetry energy and other properties of the star, the frequency of crustal i modes span a large range between 50 and 450 (2π Hz), which could easily match  . In non g-mode interpretations, one also cannot exclude the possibility of the primary being the flarer. Detailed, ab initio simulations of excitation and fracture are needed to tell resonance scenarios apart since the basic criteria outlined in Sect. 2.1 can be met with several models. We defer such considerations to future work (though see also Sects. 3 and 4.1).
. In non g-mode interpretations, one also cannot exclude the possibility of the primary being the flarer. Detailed, ab initio simulations of excitation and fracture are needed to tell resonance scenarios apart since the basic criteria outlined in Sect. 2.1 can be met with several models. We defer such considerations to future work (though see also Sects. 3 and 4.1).
3. Seismic excitations
Xiao et al. (2022) identified, with > 5σ significance, QPOs with frequency 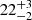 Hz in the GRB 211211A precursor. Secondary Fourier peaks are also visible at 51 ± 2 Hz in the Fermi spectrum (see extended data Figs. 7 and 8 in Xiao et al. 2022). If QNMs do indeed soak up enough orbital energy, such that the resulting crustal strain exceeds the threshold of the lattice structure in the crust ∼1 s prior to merger, aftershocks may excite torsional modes. Such a scenario is qualitatively similar to that put forth by Duncan (1998) for SGR flares, where similar frequencies have been observed (Hurley et al. 1999; Israel et al. 2005).
Hz in the GRB 211211A precursor. Secondary Fourier peaks are also visible at 51 ± 2 Hz in the Fermi spectrum (see extended data Figs. 7 and 8 in Xiao et al. 2022). If QNMs do indeed soak up enough orbital energy, such that the resulting crustal strain exceeds the threshold of the lattice structure in the crust ∼1 s prior to merger, aftershocks may excite torsional modes. Such a scenario is qualitatively similar to that put forth by Duncan (1998) for SGR flares, where similar frequencies have been observed (Hurley et al. 1999; Israel et al. 2005).
Magnetar QPOs are now understood to be more complicated, as crust and core oscillations are strongly coupled by the magnetic field. Similar considerations likely apply to the flaring component in GRB 211211A, as argued in Sect. 2.2. The total spectrum for axisymmetric stars with poloidal fields contains multiple (Alfvén) continua, separated by ‘gaps’ where discrete crustal and global modes reside (e.g., van Hoven & Levin 2011). If the field is tangled (Link & van Eysden 2016), polar-axial couplings are allowed (Colaiuda & Kokkotas 2012), or if axisymmetry is broken (Sotani & Kokkotas 2011), the continua dissolve into discrete modes. Either way, it is this richness that allows for the multiple, close QPO frequencies observed in the giant flare from SGR 1806–20 (∼16, 18, 22, 26,..., Hz; Hambaryan et al. 2011), for instance, to be modelled through QNMs. Colaiuda & Kokkotas (2011) found that ∼22 Hz oscillations are most easily explained with a crustal mode, residing on the edge of the Alfvén spectrum (see Fig. 1 therein). As this frequency coincidentally matches that reported by Xiao et al. (2022) for GRB 211211A, we focus on torsional modes here. It should be stressed though that the detection of only one or two frequencies makes it difficult to ascertain the mode character(s) (cf. Sect. 4.1). For example, Gabler et al. (2016) find that coherent, global magnetoelastic modes in a superfluid star with B ∼ 5 × 1014 G also share a frequency of 22 Hz. Superfluidity, however, increases g-mode frequencies (Passamonti et al. 2016), and thus a 2g2 mode is no longer a viable candidate for precursor ignition in this case. Though a magnetar likely contributed to GRB 211211A, resonant shattering events do not necessitate magnetar involvement in general, especially for thermal or dim precursors (see Sect. 2.2). Pure crustal modes would be the most natural explanation in such cases.
The strain tensor associated with the Lagrangian displacement of the resonant mode(s) can be used to deduce the fracture geometry, given a chemical model of the crust (Suvorov & Kokkotas 2020b; Kuan et al. 2021b). The resulting spatial profile can be projected into spheroidal harmonics, which serve as initial data for a QNM problem. In this way, predictions for seismic or magnetoelastic modes can be matched to fracture geometries.
3.1. Quasi-periodic oscillations from aftershocks
As a first step to solving the full problem described above, we made some quantitative predictions by computing the properties for free (i.e., without fracture seeding) torsional modes, assuming they are excited immediately after a tidal resonance. If the yielding is caused by a 2g2 mode (see Sect. 2.3), the cracking area1 is confined near the equator, with colatitudes 0.25 ≲ θ/π ≲ 0.75 (see Fig. 3 in Kuan et al. 2021b). The angular distribution is similar to that of ℓ = m = 2 harmonics. Modes with azimuth numbers m ≠ 2 are largely decoupled from the perturbation due to mode orthogonality. Similarly, odd-order harmonics with ℓ = 3, 5, … are dormant because the 2g2 mode seeding the fracture is reflection symmetric about the equator. For GRB 211211A then, the modes of most interest are 2t0 and 4t0 (both with m = 2; though cf. the caveats noted in Sect. 3).
3.2. Torsional mode spectrum
To calculate the torsional modes, we closely followed the formalism described by Sotani et al. (2007); in particular, their Eqs. (69) and (70) together with boundary conditions (71) and (72) completely describe the eigenproblem, including magnetic corrections, for torsional modes in the Cowling approximation. We solved these equations in this work using the EOS, shear modulus, and magnetic field specifications given in Sect. 2.3.
We find 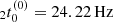 and
and 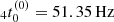 for a static, unmagnetised star with M = 1.25 M⊙. These already agree well with the Fourier peaks observed by Xiao et al. (2022), though they shift slightly if rotational and magnetic corrections are applied. For m = 2, we find a hybrid fitting to the frequency shift in the form
for a static, unmagnetised star with M = 1.25 M⊙. These already agree well with the Fourier peaks observed by Xiao et al. (2022), though they shift slightly if rotational and magnetic corrections are applied. For m = 2, we find a hybrid fitting to the frequency shift in the form
for fitting coefficients 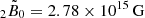 and
and 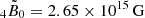 , where ℓtn is the inertial-frame frequency when ν > 0. Equation (2) is similar to Eq. (79) of Sotani et al. (2007) when ν = 0, and Eq. (26) of Vavoulidis et al. (2007) when Bp = 0.
, where ℓtn is the inertial-frame frequency when ν > 0. Equation (2) is similar to Eq. (79) of Sotani et al. (2007) when ν = 0, and Eq. (26) of Vavoulidis et al. (2007) when Bp = 0.
3.3. QPOs in the precursor of GRB 211211A
A variety of ℓ = 2 and ℓ = 4 torsional mode frequencies are collated in Table 1. Although the ν = Bp = 0 mode frequencies match those of the QPOs in GRB 211211A, a 2g2-mode resonance is unable to explain the precursor in this case, as the spectrum would be thermal and criteria (i) and (iii) would be violated (see Sect. 2). In contrast, we find that there are many possible combinations of modest spins, 0 ≲ ν/Hz ≲ 3, and polar field strengths, 7 ≲ Bp/1014 G ≲ 8, that can allow for a 2g2-resonant shattering to meet all necessary criteria, and excite torsional modes with the observed frequencies. Three such combinations are shown in the last three rows of Table 1.
4. Discussion
If resonant shatterings are responsible for (at least some) precursor flares in merger-driven GRBs, seismic aftershocks may emanate from the rupture site shortly thereafter. We show that the ∼22 and ∼51 Hz Fourier peaks observed in the precursor of GRB 211211A match those of ℓ = 2 and ℓ = 4 torsional modes for a variety of spin and magnetic field strength combinations (Table 1). These modes are expected based on the fracture geometry of 2g2-mode resonances, as quantified in Sect. 3.1. Even if a different mode is responsible for the resonant shattering (e.g., i mode; Tsang et al. 2012), the same qualitative picture applies, though the specific fracture patterns and timings may differ (see Sect. 2.4). Overall, the observation of precursor QPOs may allow for detailed inferences regarding the flaring star’s properties.
4.1. Avenues to disprove the scenario
An important question to ask is how might one falsify the resonant aftershock picture. For the resonance itself, because g and i modes are so sensitive to the stellar composition, precursor timings from ≲1 s to even ≳10 s prior to the main event can be met with some choice of mass, EOS, spin, and magnetic field strength (Kuan et al. 2021a; Neill et al. 2021). It is only when several (or all) of these aspects are pinned down – the first and last of which are for GRB 211211A – can models be definitively ruled out. For example, because of the tidal neutrality phenomenon for 2g2 modes discussed in Sect. 2.3, if it were proven that the primary released the flare, the relevant overlap integral would not be large enough to fracture the crust (criterion ii violated), and a 2g2-mode scenario could be excluded.
Torsional mode frequencies do not match the QPOs if the star is spinning at even a few Hz (see the third row of Table 1). Galactic magnetars spin slowly, implying that torsional modes take on a relatively narrow range of properties in such stars, but high spins cannot be ruled out a priori for the components in a merger. If gravitational waves are observed coincidentally with a GRB and its precursor, it may be possible to measure the stellar spin(s) (Zhu et al. 2018), thereby offering an avenue to exclude torsional modes. Excluding all QNM models (e.g., global magnetoelastic modes) is difficult, as again a wide range of QPO frequencies can be accommodated for various magnetic geometries (Colaiuda & Kokkotas 2011), or if superfluidity is considered (Gabler et al. 2016). If only high-frequency (≳102 Hz) QPOs were observed in a precursor, however, this would exclude an aftershock picture since low-order modes are easiest to excite, and their absence would imply a non-fracture mechanism unless the star is ultra-magnetised (Bp ≳ 4 × 1016 G; see Fig. 4 of Sotani et al. 2007). Such a star would be very difficult to explain in a neutron star merger event as field decay would occur on ≪Myr timescales, long before coalescence.
4.2. Future prospects
Given that giant flare tails are visible for ≳102 s (Watts & Strohmayer 2006), while GRB precursor emissions last less than a second (∼0.1 s for GRB 211211A; Xiao et al. 2022), it is not surprising that fewer Fourier peaks are observed in the latter. With improved instruments and more observations of precursor QPOs, additional modes may be detected in the future. In general, one would expect many QNMs, provided they can activate within ≲0.1 s (cf. Fig. 10 in Strohmayer & Watts 2006), to be excited in a rupture event beyond just 2t0 and 4t0 in a magnetised star. With each peak comes a constraint on the multi-dimensional parameter space relating the mass, spin, magnetic field strength, shear modulus, and so on, to the QNM spectrum (Colaiuda & Kokkotas 2012). For GRB 211211A, we have only one confidently measured frequency, and thus many possibilities are defensible, even within the restricted context of torsional modes (Table 1). If many QPOs spanning ∼15–1500 Hz were detected in a precursor, such as in the tail SGR 1806–20’s giant flare, this would tightly constrain the active member of the coalescing binary.
The above can be combined with constraints coming from gravitational waves, the kilonova, and afterglows (Gompertz et al. 2022). We show in Appendix A that the X-ray afterglow for GRB 211211A indicates that the remnant is a rapidly rotating, (meta-)stable magnetar with Bp ≳ 1014 G. This and other (e.g., tidal deformability) properties can, at least in principle, be connected to those of the pre-merging objects (Radice et al. 2018). Such considerations are relevant for population studies and evolutionary modelling of neutron stars (Popov & Prokhorov 2006).
The crack geometry also depends on the failure type (e.g., von Mises or Tresca) and the (likely anisotropic) elastic maximum the crust can absorb, neither of which are certain for neutron star matter; see Baiko & Kozhberov (2017) for a discussion.
To avoid confusion, we note that the function f(r) is denoted by a1(r) in Sotani et al. (2007), which affects the spectrum of torsional modes via the associated terms in Eqs. (69) and (70) therein.
Acknowledgments
The research leading to these results has received funding from the European Union’s Horizon 2020 Programme under the AHEAD2020 project (grant n. 871158). This work made use of data supplied by the UK Swift Science Data Centre at the University of Leicester. KK gratefully acknowledges financial support by DFG research Grant No. 413873357. We are grateful to the anonymous referee for providing helpful and specific feedback, which improved the quality of this work.
References
- Akmal, A., Pandharipande, V. R., & Ravenhall, D. G. 1998, Phys. Rev. C, 58, 1804 [Google Scholar]
- Alexander, M. E. 1987, MNRAS, 227, 843 [NASA ADS] [CrossRef] [Google Scholar]
- Baiko, D. A., & Kozhberov, A. A. 2017, MNRAS, 470, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Blaes, O., Blandford, R., Goldreich, P., & Madau, P. 1989, ApJ, 343, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Bloom, J. S., Kulkarni, S. R., & Djorgovski, S. G. 2002, AJ, 123, 1111 [NASA ADS] [CrossRef] [Google Scholar]
- Bromberg, O., Nakar, E., Piran, T., & Sari, R. 2012, ApJ, 749, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Ciolfi, R. 2018, Int. J. Mod. Phys. D, 27, 1842004 [NASA ADS] [CrossRef] [Google Scholar]
- Colaiuda, A., & Kokkotas, K. D. 2011, MNRAS, 414, 3014 [NASA ADS] [CrossRef] [Google Scholar]
- Colaiuda, A., & Kokkotas, K. D. 2012, MNRAS, 423, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Douchin, F., & Haensel, P. 2001, A&A, 380, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duncan, R. C. 1998, ApJ, 498, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, P. A., Osborne, J. P., Beardmore, A. P., et al. 2014, ApJS, 210, 8 [Google Scholar]
- Fujibayashi, S., Kiuchi, K., Nishimura, N., Sekiguchi, Y., & Shibata, M. 2018, ApJ, 860, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Fujibayashi, S., Wanajo, S., Kiuchi, K., et al. 2020, ApJ, 901, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Gabler, M., Cerdá-Durán, P., Stergioulas, N., Font, J. A., & Müller, E. 2016, MNRAS, 460, 4242 [NASA ADS] [CrossRef] [Google Scholar]
- Gompertz, B. P., Ravasio, M. E., Nicholl, M., et al. 2022, arXiv e-prints [arXiv:2205.05008] [Google Scholar]
- Hambaryan, V., Neuhäuser, R., & Kokkotas, K. D. 2011, A&A, 528, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hurley, K., Cline, T., Mazets, E., et al. 1999, Nature, 397, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Israel, G. L., Belloni, T., Stella, L., et al. 2005, ApJ, 628, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Kokkotas, K. D., & Schafer, G. 1995, MNRAS, 275, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Kuan, H.-J., Suvorov, A. G., & Kokkotas, K. D. 2021a, MNRAS, 506, 2985 [NASA ADS] [CrossRef] [Google Scholar]
- Kuan, H.-J., Suvorov, A. G., & Kokkotas, K. D. 2021b, MNRAS, 508, 1732 [NASA ADS] [CrossRef] [Google Scholar]
- Kuan, H.-J., Krüger, C. J., Suvorov, A. G., & Kokkotas, K. D. 2022, MNRAS, 513, 4045 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, U., & Strohmayer, T. E. 1996, A&A, 311, 155 [NASA ADS] [Google Scholar]
- Link, B., & van Eysden, C. A. 2016, ApJ, 823, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Messios, N., Papadopoulos, D. B., & Stergioulas, N. 2001, MNRAS, 328, 1161 [NASA ADS] [CrossRef] [Google Scholar]
- Neill, D., Newton, W. G., & Tsang, D. 2021, MNRAS, 504, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Passamonti, A., Andersson, N., & Ho, W. C. G. 2016, MNRAS, 455, 1489 [NASA ADS] [CrossRef] [Google Scholar]
- Popov, S. B., & Prokhorov, M. E. 2006, MNRAS, 367, 732 [NASA ADS] [CrossRef] [Google Scholar]
- Radice, D., Perego, A., Bernuzzi, S., & Zhang, B. 2018, MNRAS, 481, 3670 [NASA ADS] [CrossRef] [Google Scholar]
- Rastinejad, J. C., Gompertz, B. P., Levan, A. J., et al. 2022, ArXiv e-prints [arXiv:2204.10864] [Google Scholar]
- Ravi, V., & Lasky, P. D. 2014, MNRAS, 441, 2433 [NASA ADS] [CrossRef] [Google Scholar]
- Rowlinson, A., O’Brien, P. T., Metzger, B. D., Tanvir, N. R., & Levan, A. J. 2013, MNRAS, 430, 1061 [NASA ADS] [CrossRef] [Google Scholar]
- Schumaker, B. L., & Thorne, K. S. 1983, MNRAS, 203, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Sotani, H., & Kokkotas, K. D. 2011, J. Phys. Conf. Ser., 314, 012081 [NASA ADS] [CrossRef] [Google Scholar]
- Sotani, H., Kokkotas, K. D., & Stergioulas, N. 2007, MNRAS, 375, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Strohmayer, T. E., & Watts, A. L. 2005, ApJ, 632, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Strohmayer, T. E., & Watts, A. L. 2006, ApJ, 653, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Suvorov, A. G., & Glampedakis, K. 2022, Phys. Rev. D, 105, L061302 [NASA ADS] [CrossRef] [Google Scholar]
- Suvorov, A. G., & Kokkotas, K. D. 2020a, ApJ, 892, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Suvorov, A. G., & Kokkotas, K. D. 2020b, Phys. Rev. D, 101, 083002 [NASA ADS] [CrossRef] [Google Scholar]
- Suvorov, A. G., & Kokkotas, K. D. 2021, MNRAS, 502, 2482 [NASA ADS] [CrossRef] [Google Scholar]
- Tews, I. 2017, Phys. Rev. C, 95, 015803 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, C., & Duncan, R. C. 1995, MNRAS, 275, 255 [Google Scholar]
- Tsang, D. 2013, ApJ, 777, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Tsang, D., Read, J. S., Hinderer, T., Piro, A. L., & Bondarescu, R. 2012, Phys. Rev. Lett., 108, 011102 [NASA ADS] [CrossRef] [Google Scholar]
- van Hoven, M., & Levin, Y. 2011, MNRAS, 410, 1036 [NASA ADS] [CrossRef] [Google Scholar]
- Vavoulidis, M., Stavridis, A., Kokkotas, K. D., & Beyer, H. 2007, MNRAS, 377, 1553 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J.-S., Peng, Z.-K., Zou, J.-H., Zhang, B.-B., & Zhang, B. 2020, ApJ, 902, L42 [NASA ADS] [CrossRef] [Google Scholar]
- Watts, A. L., & Strohmayer, T. E. 2006, ApJ, 637, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Xiao, D., & Dai, Z.-G. 2019, ApJ, 878, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Xiao, S., Zhang, Y. Q., Zhu, Z. P., et al. 2022, ArXiv e-prints [arXiv:2205.02186] [Google Scholar]
- Yang, J., Zhang, B. B., Ai, S. K., et al. 2022, ArXiv e-prints [arXiv:2204.12771] [Google Scholar]
- Zhang, B. 2019, Front. Phys., 14, 64402 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B., Zhang, B.-B., Liang, E.-W., et al. 2007, ApJ, 655, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, X., Thrane, E., Osłowski, S., Levin, Y., & Lasky, P. D. 2018, Phys. Rev. D, 98, 043002 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Afterglow
The components in GRB 211211A are relatively light (M1 + M2 ≈ 2.68 ± 0.08 M⊙), suggesting the possibility of a neutron star merger remnant, rather than a black hole. From a three-component kilonova model, Rastinejad et al. (2022) estimate that 0.04 ± 0.02 M⊙ worth of r-process material was dynamically ejected via tidal torques and shock heating during a merger. After coalescence, additional mass may be lost as material in the temporary accretion disc surrounding the merger site unbinds through viscous heating. Fujibayashi et al. (2018, 2020) show that, for a long-lived remnant, the post-merger ejecta mass can reach ≈30−40% of the total disc mass, amounting to ≳0.1 M⊙. These considerations suggest a remnant mass of Mrem ≈ 2.5 ± 0.1 M⊙. A star at the lower end could stave off collapse for a number of spindown timescales if born with high angular momentum (e.g. Ravi & Lasky 2014), or even indefinitely, depending on the nuclear EOS.
GRB 211211A displayed an X-ray afterglow, part of which could be supplied by a magnetar wind (Rowlinson et al. 2013; Ciolfi 2018). The photon index for X-ray emissions and source redshift were determined as Γγ = 2.08 and z = 0.0763, respectively, the latter implying a distance of d ≈ 350 Mpc (Evans et al. 2014; Gompertz et al. 2022). Assuming uncollimated emissions, we translated the observed flux into an isotropic luminosity, namely LX = 4πd2K(z)F for K(z)≈(1 + z)Γγ − 2 (Bloom et al. 2002). The electromagnetic spindown luminosity of an oblique rotator braking via magnetic dipole torques is given by
where 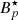 denotes the polar field strength, R⋆ the radius, Ω = 2πν⋆ the angular velocity, c the speed of light, I⋆ the moment of inertia, and λ is a magnetospheric factor that depends on the inclination angle, α. Assuming the source is surrounded by a vacuum and that α ≈ π/2, we have λ ≈ 1; similar values are expected if α ≈ 0, but the star is surrounded by plasma (see, e.g. Rowlinson et al. 2013; Ciolfi 2018). The dimensionless prefactor, η, is an efficiency term, which controls how easily spindown power is converted into X-rays. Though theoretically uncertain, Xiao & Dai (2019) analysed several GRB lightcurves to find that 10−7 ≲ η ≲ 10−1, depending on the saturated Lorentz factor of the emissions (see their Fig. 2). We consider an intermediate value here, η ≈ 10−4. Fitting expression (A.1) to LX, we find
denotes the polar field strength, R⋆ the radius, Ω = 2πν⋆ the angular velocity, c the speed of light, I⋆ the moment of inertia, and λ is a magnetospheric factor that depends on the inclination angle, α. Assuming the source is surrounded by a vacuum and that α ≈ π/2, we have λ ≈ 1; similar values are expected if α ≈ 0, but the star is surrounded by plasma (see, e.g. Rowlinson et al. 2013; Ciolfi 2018). The dimensionless prefactor, η, is an efficiency term, which controls how easily spindown power is converted into X-rays. Though theoretically uncertain, Xiao & Dai (2019) analysed several GRB lightcurves to find that 10−7 ≲ η ≲ 10−1, depending on the saturated Lorentz factor of the emissions (see their Fig. 2). We consider an intermediate value here, η ≈ 10−4. Fitting expression (A.1) to LX, we find
and
for the remnant’s polar field strength and spin frequency, respectively, at a 95% confidence level (χ2/dof = 53.9/49, weighting for uncertainties).
From numerical merger simulations with the APR4 EOS, Radice et al. (2018) find that the spin period for a newborn remnant is well fitted by P⋆ ≈ [−0.21(Mrem/M⊙−2.5)+0.67] ms, which agrees with expression (A.3). However, the APR4 EOS, for example, can only sustain maximum masses up to ≈2.21 M⊙ if the star is static. This limit increases by ≳20% if the star is rotating near the break-up limit (e.g. Suvorov & Glampedakis 2022). Assuming a remnant of mass Mrem ≈ 2.4 M⊙, this implies that the star would collapse after ∼10 ks for magnetic field strength (A.2) and spin (A.3) – when centrifugal support is depleted by the magnetar wind (see Eq. (2) in Ravi & Lasky 2014) – unless Bp or η are on their respective low ends, spindown is delayed (through fallback-induced spinup, for instance), or the excess mass is magnetically supported by a strong core field (Suvorov & Glampedakis 2022). This is potentially at odds with the fact that the flux persisted for ≳50 ks post-trigger (see Figure A.1), as black hole formation is expected to truncate the signal. Ravi & Lasky (2014) show that this could, in principle, allow us to rule out EOS candidates that have low (static) maximum masses. We emphasise, however, that the remnant mass estimate is itself model dependent, and thus strong conclusions cannot be drawn from this event alone (Fujibayashi et al. 2018, 2020; Rastinejad et al. 2022).
 |
Fig. A.1. Afterglow light-curve fittings for GRB 211211A. Blue data are attributable to the decaying tail of the prompt emission (Evans et al. 2014), while red data may be contributed by a newborn magnetar. The grey band shows the 95% confidence interval for an orthogonal-rotator fit, while the green curve shows a best-fit precessing model. |
In addition to an orthogonal-rotator fit, we consider the possibility of a precessing remnant for completeness. Although the model specifics are complicated in this case (see Suvorov & Kokkotas 2020a, 2021, for details), such a fit predicts similar parameters to the orthogonal case; we find Bp ≈ 4.4 × 1014 G, ν ≈ 1.55 kHz, and a quadrupolar ellipticity of ϵ ≈ 1.6 × 10−7 for the same efficiency and moment of inertia. Orthogonal (black) and precessing (green) fits to the afterglow light curve of GRB 211211A are shown in Fig. A.1. Overall, a magnetar wind model fits the data well, as they exhibit a plateau followed by a power-law fall-off with slope −2, as predicted by dipole braking.
Appendix B: Magnetic field and spin inferences from precursor timing
As discussed in Secs. 2 and 3, mode frequencies are shifted by Coriolis and Lorentz forces. Quantifying these effects requires a particular model; the one used in the main text is detailed here. The relative shifts also depend on the mode eigenfunction. For torsional modes, the shifts are given by expression (2) in the main text, while for g modes the patterns are different. In either case, specifying the nuclear EOS – assumed APR4 in this work because Colaiuda & Kokkotas (2011) found that torsional modes in a M ≈ 1.4 M⊙ star with this EOS match the QPO frequencies in the giant flare tails of SGR 1806–20 and SGR 1900+14 (Israel et al. 2005) – uniquely determines the former if the star is uniformly rotating. Relative to a static-star mode, we find that the leading-order, rotational corrections to m = 2 modes, ℓωn, in geometrised units with G = c = 1, read [see Eqs. (17) and (18) in Kuan et al. (2021b)]
with
for mode eigenfunction ξ, decomposed into radial (ξr) and poloidal (ξh) harmonics, stellar pressure p and density ρ, related to the metric functions Φ and λ, defining the (logarithms of the) gtt and grr components, respectively, via the Tolman-Oppenheimer-Volkoff relations. In the Newtonian limit, the above agrees with the classic Unno formula.
Although the presence of multipoles or a toroidal field can lead to sizeable adjustments in the Lorentz-related frequency shift (see, e.g. Colaiuda & Kokkotas 2011; Suvorov & Kokkotas 2020b; Kuan et al. 2021a), a purely dipole configuration for the magnetic field is considered here for simplicity. Following Kuan et al. (2021a), it can be shown that relations of the Faraday tensor imply that a general, stationary, and axisymmetric magnetic field has contravariant components
in Schwarzschild-like coordinates, where ζ is a toroidal function, which we set to zero. For a dipole field, the streamfunction ψ can be expressed as
for some radial function f. We picked2f(r) = a1r2 + a2r4 + a3r6, where the ai are constrained by assuming (I) that the B field smoothly extends to a force-free dipole outside of the star (where the geometry is Schwarzschild), and (II) that there are no surface currents. Enforcing these conditions leads to
and
Given this field, the Lorentz force 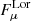 can be defined, which leads to a frequency shift in the unmagnetised value, in other words
can be defined, which leads to a frequency shift in the unmagnetised value, in other words
The matching of the 2g2 mode to the precursor time implies a relationship between Bp and ν for a given mass and stratification, that is we solved 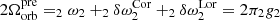 in the inertial frame, implicity assuming spin-orbit alignment (Alexander 1987; Kokkotas & Schafer 1995). We assumed M = 1.25 M⊙, as identified by Rastinejad et al. (2022), for the companion in GRB 211211A (see Sec. 2.1). The stratification is encoded by a phenomenological parameter that incorporates the particle Fermi energies and internal temperature, called δ in Kuan et al. (2021b, 2022). In general, the equilibrium adiabatic index reads
in the inertial frame, implicity assuming spin-orbit alignment (Alexander 1987; Kokkotas & Schafer 1995). We assumed M = 1.25 M⊙, as identified by Rastinejad et al. (2022), for the companion in GRB 211211A (see Sec. 2.1). The stratification is encoded by a phenomenological parameter that incorporates the particle Fermi energies and internal temperature, called δ in Kuan et al. (2021b, 2022). In general, the equilibrium adiabatic index reads
which we relate to the index of the perturbed star, Γ, through
The frequencies of thermal g modes are however much more sensitive to the surface temperature (see Sec. 2.1 of Kuan et al. 2022, for quantifications). We assumed δ is a constant that is set by the value in the crust; a ‘canonical’ value, appropriate for a mature neutron star, was adopted, in other words δ = 0.005 (justified in Kuan et al. 2022). This eventually yields values for 2ω2, and the 2g2-mode frequency can now be written as a function of Bp and ν.
Figure B.1 shows simultaneous estimates on Bp and ν, based on the above procedure, with the shaded area representing the uncertainty (i.e. Twait = 1.08 ± 0.20 s). For all spin frequencies, we find that magnetar-level fields of Bp ≳ 7 × 1014 G are required. Fields of this strength are consistent with the precursor energetics and non-thermality, discussed in Sec. 4. Though not shown, non-zero values for τjet imply even higher field strengths.
 |
Fig. B.1. Polar magnetic field strengths Bp, as a function of spin ν, such that the resonance of a 2g2 mode is able to instigate a crust yielding at the observed preceding time, Twait = 1.08 ± 0.20 s, assuming a negligible jet-formation time, τjet = 0, in GRB 211211A. The shaded region reflects the uncertainty in the waiting time. |
We emphasise that, although Fig. B.1 pertains to 2g2 modes, similar graphs may be drawn for other resonant shattering scenarios (involving, for example, i or s modes; Tsang et al. 2012; Neill et al. 2021). Furthermore, g modes, with the simple one-parameter characterisation (B.8), are only considered here for concreteness.
All Tables
All Figures
 |
Fig. A.1. Afterglow light-curve fittings for GRB 211211A. Blue data are attributable to the decaying tail of the prompt emission (Evans et al. 2014), while red data may be contributed by a newborn magnetar. The grey band shows the 95% confidence interval for an orthogonal-rotator fit, while the green curve shows a best-fit precessing model. |
| In the text | |
 |
Fig. B.1. Polar magnetic field strengths Bp, as a function of spin ν, such that the resonance of a 2g2 mode is able to instigate a crust yielding at the observed preceding time, Twait = 1.08 ± 0.20 s, assuming a negligible jet-formation time, τjet = 0, in GRB 211211A. The shaded region reflects the uncertainty in the waiting time. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



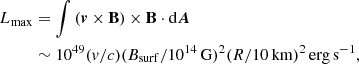
![$$ \begin{aligned} \frac{_{\ell }t_{n}}{_{\ell }t^{(0)}_{n}} = \sqrt{1+\left( \frac{B_{\rm p}}{{_{\ell }\tilde{B}_{n}}} \right)^{2}}- \frac{2 \nu (\ell ^2+\ell -1)}{_{\ell }t^{(0)}_{n} \ell (\ell +1)} + \mathcal{O} \left[ \left( \frac{B_{\rm p}}{{_{\ell }\tilde{B}_{n}}}\right)^2, \left(\frac{\nu }{_{\ell }t^{(0)}_{n}} \right)^2 \right] , \end{aligned} $$](/articles/aa/full_html/2022/08/aa44082-22/aa44082-22-eq12.gif)
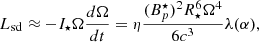
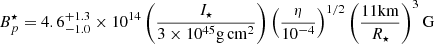
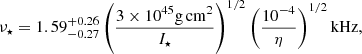
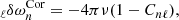
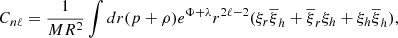
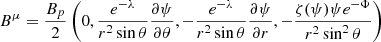
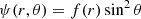
![$$ \begin{aligned} a_{1} =&- \frac{3 R^3}{8 M^3} \Bigg [ \log \left( 1 - \frac{ 2 M}{R} \right) \nonumber \\&+ \frac{M \left( 24 M^3 - 9 M^2 R - 6 M R^2 + 2 R^3 \right)}{R^2 \left( R - 2 M \right)^2} \Bigg ], \end{aligned} $$](/articles/aa/full_html/2022/08/aa44082-22/aa44082-22-eq23.gif)