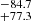| Issue |
A&A
Volume 676, August 2023
|
|
|---|---|---|
| Article Number | A65 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202346360 | |
| Published online | 08 August 2023 | |
Neutron star mass–radius constraints using the high-frequency quasi-periodic oscillations of GRB 200415A
1
Theoretical Astrophysics, IAAT, University of Tübingen, 72076 Tübingen, Germany
e-mail: sotani@yukawa.kyoto-u.ac.jp
2
Astrophysical Big Bang Laboratory, RIKEN, Saitama 351-0198, Japan
3
Interdisciplinary Theoretical & Mathematical Science Program (iTHEMS), RIKEN, Saitama 351-0198, Japan
4
Department of Physics, Aristotle University of Thessaloniki, Thessaloniki 54124, Greece
Received:
9
March
2023
Accepted:
19
June
2023
Context. Quasi-periodic oscillations (QPOs) observed in a giant flare of a strongly magnetized neutron star (magnetar) carry crucial information for extracting the properties od neutron stars.
Aims. The aim of this study is to constrain the mass and radius of the neutron star model for GRB 200415A by identifying the observed QPOs with crustal torsional oscillations and comparing these with experimental constraints on the nuclear matter properties.
The frequencies of the crustal torsional oscillations are determined by solving the eigenvalue problem with the Cowling approximation, assuming a magnetic field of about 1015 G.
Methods. We find that the observed QPOs can be identified with several overtones of crustal oscillations for carefully selected combinations of the nuclear saturation parameters. Thus, we can inversely constrain the neutron star mass and radius for GRB 200415A by comparing them to the values of nuclear saturation parameters obtained from terrestrial experiments.
Results. We impose further constraints on the neutron star mass and radius while the candidate neutron star models examined here are consistent with the constraints obtained from other available astronomical and experimental observations.
Key words: stars: neutron / asteroseismology / equation of state / stars: oscillations
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Neutron stars are remnants of core-collapse supernovae, in which extreme states of matter are realized. The density inside these stars easily exceeds the standard nuclear density (ρ0), while the gravitational and magnetic fields inside and around the neutron star are among the strongest observed anywhere in the Universe (Haensel et al. 2006). These extreme matter conditions cannot be reproduced on Earth, and therefore observations of neutron stars and the associated phenomena remain the only sources from which we can extract information about the state of matter at the most extreme densities. An example of this “indirect” study of nuclear matter under extreme conditions is the discovery of 2 M⊙ neutron stars (Demorest et al. 2010; Antoniadis et al. 2013; Cromartie et al. 2020). Based on these observations, the possibility of so-called soft equations of state (EOSs) for neutron star matter has mostly been abandoned (at least within the framework of Einstein’s general relativity theory). In particular, many of the EOSs containing hyperons, which generally have a soft core, have been excluded, leading to the so-called hyperon puzzle (but see also e.g., Sun et al. 2023). The detection and analysis of the gravitational wave signal during the binary neutron star merger GW170817 (Abbott et al. 2017, 2018) provided information on the tidal deformability of the merging neutron stars, which can be translated to constraints on the neutron star radius; see Chatziioannou (2020), Dietrich et al. (2021) for recent reviews.
Furthermore, pulsar observations provide useful constraints on the neutron star properties. For example, the light bending due to the strong gravitational field induced by the compact object, a purely relativistic effect, has proven extremely useful in constraining neutron star properties. More specifically, as the pulsar light curve depends on stellar compactness, one can constrain the neutron star mass and radius by carefully analyzing the observed light curve (e.g., Pechenick et al. 1983; Leahy & Li 1995; Poutanen & Gierlinski 2003; Psaltis & Özel 2014; Sotani & Miyamoto 2018). Recently, the Neutron star Interior Composition Explorer (NICER) on the International Space Station – which makes X-ray observations of neutron stars – provided constraints on the parameters of two neutron stars, PSR J0030+0451 (Riley et al. 2019; Miller et al. 2019) and PSR J0740+6620 (Riley et al. 2021; Miller et al. 2021). Moreover, for the first time, at the pre-merger stage preceding the GRB211211, quasi-periodic oscillations (QPOs) at 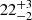 Hz and
Hz and 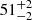 Hz were detected (Xiao et al. 2022), suggesting that these features of the precursor signal may have resulted from the resonant shattering (due to tidal interactions) of the crust of one of the stars prior to coalescence, leading to the excitation of crustal oscillations (Tsang et al. 2012; Tsang 2011; Suvorov et al. 2022)1.
Hz were detected (Xiao et al. 2022), suggesting that these features of the precursor signal may have resulted from the resonant shattering (due to tidal interactions) of the crust of one of the stars prior to coalescence, leading to the excitation of crustal oscillations (Tsang et al. 2012; Tsang 2011; Suvorov et al. 2022)1.
Modeling of the stellar oscillation spectrum provides a unique way to study the internal structure of stars. Especially for neutron stars, the oscillations can be associated with the spectrum of the emitted gravitational waves, and in this way, one can reveal details of their internal structure (gravitational wave asteroseismology), (Andersson & Kokkotas 1996, 1998; Sotani et al. 2004, 2011; Passamonti & Andersson 2012; Doneva et al. 2013; Krüger et al. 2021). Moreover, gravitational wave asteroseismology has been used to analyze the gravitational signals in numerical simulations of the formation of proto-neutron stars in core-collapse supernovae; see for example Morozova et al. (2018), Torres-Forné et al. (2019), Sotani et al. (2021).
In addition, the analysis of the afterglow spectra in magnetar giant flares (SGR 1900+14 and SGR 1806-20) revealed a rich spectrum, the so-called QPOs (Strohmayer & Watts 2005, 2006; Israel et al. 2005). The analysis suggested that the QPOs were due to magnetoelastic oscillation modes (Levin 2007; Sotani et al. 2007, 2012, 2013; Steiner & Watts 2009; Gabler et al. 2011, 2012, 2013, 2016, 2018; Gearheart et al. 2011; Colaiuda & Kokkotas 2012), which provided another opportunity to constrain the parameters of neutron stars.
Recently, another giant flare, GRB 200415A, was detected in the direction of the NGC 253 galaxy by the Atmosphere-Space Interactions Monitor (ASIM) on the International Space Station on 15 April 2020, where several high-frequency QPOs with varying significance were found at 836, 1444, 2132, and 4250 Hz (Castro-Tirado et al. 2021). Unlike the QPOs observed in the previous giant flares, the QPOs in GRB 200415A were confined to high frequencies, mainly due to the shortness of the observational interval. We note that, although GRB 200415A was originally classified as a type I (short) gamma-ray burst, it should be classified as a giant flare of a magnetar, considering the significant restrictions on the energetics and the position of the burst on the Ep, i − Eiso and T90, i − EH diagrams, where Ep, i, Eiso, T90, i, and EH are the position of the maximum in the energy spectrum νFν in the source frame, the isotropic equivalent of the total energy emitted in the gamma-ray range, the duration in the source frame, and EH ≡ (Ep, i/100 keV)/(Eiso/1051 erg)0.4; see Minaev & Pozanenko (2020).
Castro-Tirado et al. (2021) discuss two alternative explanations – previously proposed in the literature – for the occurrence of the high-frequency QPOs in GRB 200415A. One possible explanation is that the high-frequency QPOs are due to Alfvén waves traveling back and forth between the footpoints of magnetic field lines relatively close to the magnetar surface. This may be the result of a reconnection event, following the development of instability in the magnetosphere (Mahlmann et al. 2019). The second possible explanation is the excitation of crustal oscillation, which is a viable scenario for the QPOs reported for SGR 1900+14 and SGR 1806-20, as discussed above. Due to the very short lifetime of the observed QPOs, Castro-Tirado et al. (2021) slightly favor the first explanation, without excluding the second.
Here, without attempting to favor either of the two explanations, we examine the consequences of the second. That is, we try to decipher the constraints that can be placed on the neutron star EOS if we assume that the high-frequency QPOs in GRB 200415A are due to crustal oscillation.
Regarding the nature of the oscillations, one may attempt to associate some of the observed high-frequency QPOs with polar-type oscillations of neutron stars, such as the fundamental (f-) and pressure (p-) modes. Still, the excitation of such global modes during giant flares is questionable, as they require large density variations. It is therefore more natural to associate these oscillations with magnetoelastic or pure crustal torsional oscillations, depending on the magnetic field strength.
We note that the field strength estimated from the rotational period and its time derivative seems to be less than 1015 G for most of the observed magnetars (e.g., Turolla et al. 2015). Here, we work under the assumption that the strength of the magnetic field in GRB 200415A is in the second region, that is, ≲1015 G, so that it has a short damping time but the frequencies are still close to the values of pure crustal oscillations.
This assumption is discussed in more detail in Appendix A, where we show that for high-frequency torsional oscillations, the shift of the crustal mode frequency caused by a magnetic field with strength ≲1015G is less than the observational uncertainty of the QPOs in GRB 200415A, namely ∼10%, as reported in Castro-Tirado et al. (2021). In the remainder of the paper, we therefore use frequencies of pure crustal torsional oscillations (in the limit of no magnetic field).
In Sect. 2, we discuss the properties of the crust and their relation to torsional oscillations. In Sect. 3, we try to identify the observed QPOs with the higher overtones of torsional oscillations to arrive at EOS constraints. A discussion of the results is presented in Sect. 4.
2. Crust equilibrium and torsional oscillations
Matter in the neutron star crust forms a Coulomb lattice, which behaves as a solid (or liquid crystal). As a result, under perturbations, the torsional oscillations are favored. As the core (inner or outer) behaves as a fluid, the torsional oscillations are confined to the crust in the absence of rotation. Therefore, for a given EOS describing the core and the crust and for a given central density, one can construct a neutron star model by integrating the Tolman-Oppenheimer-Volkoff (TOV) equations starting with appropriate initial conditions at the center. Here, we take a different approach, specifying only the crust EOS and integrating the TOV equations inwards (starting at the surface of the star) for various sets of mass M and radius R (see Sotani et al. 2013 for details). With this approach, one has to select two boundary conditions (M and R), but one can avoid the uncertainty in the core EOS.
For the present study, we adopt the same phenomenological family of crust EOS constructed by Oyamatsu & Iida (2003, 2007), the so-called OI-EOSs. For this family of EOSs, the bulk energy per nucleon for zero-temperature uniform nuclear matter is expressed in the vicinity of the saturation density for the symmetric nuclear matter, n0, as a function of the baryon number density, nb, and the asymmetry parameter, α, as
where nb and α are defined as nb = nn + np and α = (nn − np)/nb. Here, nn and np are the neutron and the proton number density, respectively.
The five coefficients w0, n0, S0, K0, and L are the nuclear saturation parameters defining only the EOS of the crust. The first three parameters (w0, n0, and S0) are well constrained from terrestrial experiments (Oertel et al. 2017; Li et al. 2019), while the remaining two parameters (K0 and L) cannot be accurately constrained experimentally. Still, there is progress in this direction and certain constraints can be set, predicting the following values: K0 = 240 ± 20 MeV (Shlomo et al. 2006) and L = 60 ± 20 MeV (Li et al. 2019). Moreover, the magnetar QPOs in SGR 1806-20 and SGR 1900+14, if identified as crustal torsional oscillations, provide some more stringent constraints on L, that is LQPO = 58 − 73 MeV (Sotani et al. 2018). The OI-EOSs are directly characterized by the saturation parameters, but they describe the whole crust region.
The OI-EOSs (Oyamatsu & Iida 2007) adopted in this study are constructed in such a way that w0, n0, and S0 are optimized for given values of K0 and L to reproduce the experimental data for masses and charge radii of stable nuclei based on the extended Thomas-Fermi theory. The EOS parameters adopted here are listed in Table 1. Therefore, for constructing the crust equilibrium model, one needs to select two parameters for the EOS, that is, K0 and L, in addition to the global parameters defining the star, that is, the mass (M) and radius (R).
The EOS parameters adopted in this study, where η and ς are the combination of K0 and L given by η = (K0L2)1/3 and 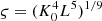 .
.
Torsional oscillations are characterized by the shear modulus, μ, as their frequency scales roughly as f ∝ (μ/ρ)1/2 where ρ is the local value of the density.
For the phase composed of spherical nuclei, the shear modulus is formulated as a function of the ion number density, the charge number of nuclei, and the Wigner-Seitz cell radius (Ogata & Ichimaru 1990; Strohmayer et al. 1991). When the phase is composed of nonspherical (cylindrical and slab-like) nuclei, as proposed by Pethick & Potekhin (1998), it behaves more like a liquid crystal. The shear modulus in the phase of slab-like nuclei then ceases to exist and at this part of the crust torsional oscillations are not excited, at least at a linear level. Therefore, torsional oscillations can be excited in two distinct areas of the crust: (a) in the parts where the phase is composed of spherical and cylindrical nuclei, and (b) in the part where the phase is composed of cylindrical holes (tubes) and spherical holes (bubbles) nuclei. This leads to double-layer torsional oscillations in the crust, which can be visualized as a “lasagna sandwich”. With such a structure, all QPOs observed in SGR 1806-20 and SGR 1900+14 can be identified; see Sotani et al. (2019).
In this study, we focus on the newly observed QPOs in GRB 200415A. These QPOs are of relatively higher frequency, and we suggest that they correspond to overtones of crustal torsional oscillations. Therefore, we systematically examine the overtones of the torsional oscillations excited in a phase composed of spherical and cylindrical nuclei. In addition, as some of the neutrons are not bound in the nuclei inside the inner crust, the effect of such unbound neutrons on the torsional oscillations can be taken into account. In practice, the ratio of the superfluid to the dripped neutron, Ns/Nd, in the phase composed of spherical nuclei, is calculated by the band theory (Chamel 2012). The corresponding ratio in the phase composed of cylindrical nuclei is still unclear. Therefore, in this study, we adopt the approach of Chamel (2012) for spherical nuclei and Ns/Nd as a parameter for cylindrical nuclei, as in Sotani et al. (2018).
The governing equation for torsional oscillations is derived from the linearized equations of motion (Schumaker & Thorne 1983), where we adopt the relativistic Cowling approximation as in Sotani et al. (2007). With the Cowling approximation, one neglects the metric perturbations, and therefore no gravitational waves are emitted. In the limit of slow rotation, axial oscillations do not induce density perturbations and only emit gravitational waves through very weak current multipoles. The Cowling approximation is therefore a good approximation for computing axial modes in the nonrotating limit. Then, the appropriate boundary conditions are imposed at the stellar surface and the bottom of the crust (composed of cylindrical nuclei). In this way, a well-defined eigenvalue problem is set for the frequency, f, of torsional oscillations. For further details, we refer to Sotani et al. (2012, 2018).
The fundamental frequencies of crustal torsional oscillations scale roughly as f ∼ vs/R, whereas the overtones scale as f ∼ vs/ΔR, where 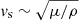 is the shear velocity, and ΔR the crust thickness (Hansen & Cioffi 1980). As the crust thickness depends on both the stellar compactness (ΔR/R ∼ R/M) and on the EOS parameters, as shown in Sotani et al. (2017), the overtones generally depend on K0 and L. Moreover, in Sotani et al. (2018) it was shown that the first overtone of crustal torsional oscillations can be described as a function of the parameter
is the shear velocity, and ΔR the crust thickness (Hansen & Cioffi 1980). As the crust thickness depends on both the stellar compactness (ΔR/R ∼ R/M) and on the EOS parameters, as shown in Sotani et al. (2017), the overtones generally depend on K0 and L. Moreover, in Sotani et al. (2018) it was shown that the first overtone of crustal torsional oscillations can be described as a function of the parameter
As shown in Fig. 1, the first overtone of a neutron star model with M = 1.6 M⊙, R = 12 km, and Ns/Nd = 0 can be expressed as a function of ς. The colored marks correspond to the eigenfrequencies for some typical values of K0, while the thick solid line represents the following quadratic fitting:
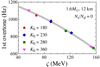 |
Fig. 1. First overtone of the ℓ = 2 crustal torsional oscillations for a neutron star model with M = 1.6 M⊙, R = 12 km, and Ns/Nd = 0. The marks denote the torsional oscillation frequencies estimated for the neutron star models constructed based on the crustal EOSs listed in Table 1, as a function of ς. The thick solid line is the quadratic fitting given by Eq. (3). |
Here, ς100 ≡ ς/(100 MeV), while the fitting coefficients dℓn depend on the values of the azimuthal quantum number ℓ, the nodal number in the corresponding eigenfunction n, the stellar mass M, the radius R, and the ratio Ns/Nd. Moreover, in this study, we further confirm that not only the first overtone but also the n-th overtones can be fitted by an equation of the form of Eq. (3). For instance, the relative deviation of the frequencies estimated with Eq. (3) from the eigenfrequencies for the stellar model shown in Fig. 1 is listed in the rightmost column of Table 1. That is, the fit given by Eq. (3) can predict the frequency with an accuracy of less than a few percent. For the stellar model with 1.4 M⊙, the coefficients in Eq. (3) with (ℓ,n) = (2, 1), (2, 4), and (2, 10) modes are listed in Table 2. Therefore, hereafter, we discuss the EOS dependence of the overtones using the fitting formula given by Eq. (3) as a function of ς. As discussed above, the overtone frequencies generally increase with the stellar compactness, M/R (because ΔR/R ∼ R/M) and f ∼ vs/ΔR for the overtones (Hansen & Cioffi 1980).
3. Comparison of the overtones with the observed QPOs
In this section, we attempt to identify the overtones of crustal torsional oscillations that match the QPO frequencies observed in GRB 200415A, keeping in mind that not all of the four QPOs were of the same significance.
The second QPO is the most prominent, while the first and fourth are less significant, and the third one has a significantly lower probability of occurring by chance. The lower significance of some of the QPOs is probably associated with the short duration of the signal (∼3 ms).
As a first step, we consider the correspondence between the first overtone and the lowest QPO frequency extracted from GRB 200415A, of namely 835.9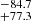 Hz (Castro-Tirado et al. 2021). In Fig. 2, we show the first overtones for three characteristic neutron star models with (M, R) = (1.4 M⊙, 14 km), (1.6 M⊙, 12 km), and (1.8 M⊙, 10 km). The solid and dotted lines denote the frequencies with ℓ = 2 and ℓ = 10, while the top and bottom panels correspond to the results with Ns/Nd = 0 and Ns/Nd = 1, respectively. From this figure, it is obvious that the dependencies of the overtones on ℓ and Ns/Nd are very weak, as mentioned in Hansen & Cioffi (1980), Sotani et al. (2018). Therefore, hereafter, we only consider the ℓ = 2 overtones for the neutron star model with Ns/Nd = 0. In addition, we see that the first overtones increase with compactness as mentioned in the previous section. More precisely, for the three models considered here, (M, R) = (1.4 M⊙, 14 km), (1.6 M⊙, 12 km), and (1.8 M⊙, 10 km), the compactness is M/R = 0.148, 0.197, and 0.266, respectively. As a result, for identifying the 836 Hz QPO as the first overtone, the suitable values of ς should increase as the neutron star compactness becomes higher.
Hz (Castro-Tirado et al. 2021). In Fig. 2, we show the first overtones for three characteristic neutron star models with (M, R) = (1.4 M⊙, 14 km), (1.6 M⊙, 12 km), and (1.8 M⊙, 10 km). The solid and dotted lines denote the frequencies with ℓ = 2 and ℓ = 10, while the top and bottom panels correspond to the results with Ns/Nd = 0 and Ns/Nd = 1, respectively. From this figure, it is obvious that the dependencies of the overtones on ℓ and Ns/Nd are very weak, as mentioned in Hansen & Cioffi (1980), Sotani et al. (2018). Therefore, hereafter, we only consider the ℓ = 2 overtones for the neutron star model with Ns/Nd = 0. In addition, we see that the first overtones increase with compactness as mentioned in the previous section. More precisely, for the three models considered here, (M, R) = (1.4 M⊙, 14 km), (1.6 M⊙, 12 km), and (1.8 M⊙, 10 km), the compactness is M/R = 0.148, 0.197, and 0.266, respectively. As a result, for identifying the 836 Hz QPO as the first overtone, the suitable values of ς should increase as the neutron star compactness becomes higher.
 |
Fig. 2. First overtones of the crustal torsional oscillations with ℓ = 2 (solid line) and ℓ = 10 (dashed line) are shown as functions of ς given by Eq. (2) for three neutron star models with (M, R, M/R) = (1.4 M⊙, 14 km, 0.146), (1.6 M⊙, 12 km, 0.197), and (1.8 M⊙, 10 km, 0.266). The top panel corresponds to Ns/Nd = 0, while the bottom panel to Ns/Nd = 1. In both panels, for reference, we draw (with a shaded thick line) the lowest QPO frequency found in GRB 200415A; i.e., 835.9 |
In Fig. 3, we show the suitable value of ς for identifying the 836 Hz QPO as the first overtone of crustal torsional oscillations for some typical neutron star models.
 |
Fig. 3. Suitable values of ς for identifying the 835 Hz QPO as the first overtone for various stellar masses and radii with Ns/Nd = 0. The shaded region corresponds to the range of ς = 85.3 − 135.1 MeV, estimated for the fiducial values L = 60 ± 20 and K0 = 240 ± 20 MeV. The dashed lines define the range of ςQPO = 104.9 − 128.4 MeV, corresponding to LQPO = 58 − 73 MeV. |
More specifically, the shaded region corresponds to neutron star models for ς = 85.3 − 135.1 MeV, corresponding to K0 = 240 ± 20 MeV and L = 60 ± 20 MeV. In addition, we draw the dashed lines at ς = 104.9 and ς = 128.4 MeV, defining the estimated range for the tighter range LQPO = 58 − 73 MeV. The latter bounds were set once the magnetar QPOs in SGR 1806-20 and 1900+14 were identified as crustal torsional oscillations (Sotani et al. 2018).
In this figure, we see that the suitable value of ς for identifying the 836 Hz QPO as the first overtone increases with M for fixed neutron star radius, and that some characteristic neutron star models, for example with masses M = 1.4 M⊙, 1.6 M⊙, 1.8 M⊙, and R = 10 km, do not fit with the observational data.
The next step is to associate all four QPO frequencies observed in GRB 200415A with overtones of the crustal torsional oscillations. We find that it is feasible to identify all four observed QPOs as the first, second, fourth, and tenth overtones for neutron star models with certain values of mass and radius. In Fig. 4, we show the suggested identification for one of the three neutron star models considered above, namely the one with M = 1.6 M⊙ and R = 12 km. In this figure, the correspondence for ς = 121.7 MeV for the aforementioned neutron star model is apparent. As the overtones vary – as they depend on the neutron star mass and radius –, the suitable value of ς for identifying the observed QPO frequencies varies accordingly. In principle, one could identify all observed QPOs with other combinations of the overtones, but it would not be consistent with the saturation parameters constrained via experiments (see Appendix B for details).
 |
Fig. 4. Correspondence of the observed QPOs to the overtones for the neutron star model with M = 1.6 M⊙ and 12 km. The QPOs observed in GRB 200415A can be identified with the first, second, fourth, and tenth overtones of crustal torsional oscillations, which leads to a suitable value of ς for the adopted stellar model of ς = 121.7 MeV. |
Figure 5 shows the extracted values of ς for a wider range of neutron star models. In all of them, we identified the observed QPO frequencies as the first, second, fourth, and tenth overtones. As in Fig. 3, in this figure we draw the fiducial range of ς (shaded region) and the range for ςQPO (dashed lines) as constrained by QPO observations.
 |
Fig. 5. Suitable value of ς (colored marks) for simultaneous identification of the four QPOs observed in GRB 200415A as the first, second, fourth, and tenth overtones of the crustal torsional oscillations for various neutron star models. The meaning of the shaded region and dashed lines is the same as in Fig. 3. The arrow denotes the particular model discussed in Fig. 4, where the extracted value is ς = 121.7 MeV. |
We note that for the stellar models not considered in Fig. 5, such as that for a neutron star model with M = 1.8 M⊙ and 10 km, the QPO frequencies cannot be identified with the same set of overtones.
Figure 6 shows a mass versus radius diagram from which we extract the constraints set in Fig. 5 for the mass, radius, and ς. The shaded region (the region enclosed with the solid lines) corresponds to the mass versus radius constraints obtained for ς = 85.3 − 135.1 MeV (ςQPO = 104.9 − 128.4 MeV).
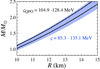 |
Fig. 6. Constraints on neutron star mass and radius set by the simultaneous identification of all four observed QPOs in GRB 200415A as the first, second, fourth, and tenth overtones of the crustal torsional oscillations. Here we accepted only the models meeting the constraints ς = 85.3 − 135.1 MeV (shaded region) and ςQPO = 104.9 − 128.4 MeV (bounded by solid lines). |
Sotani et al. (2014, 2022) showed that the mass and radius of low-mass neutron stars can be estimated using another combination of L and K0, that is, η = (K0L2)1/32. According to this approach, for neutron star models with a central density of ρc ≤ 2ρ0, its mass and gravitational redshift can be expressed as a function of η and the normalized ρc. This leads to a relation between the neutron star mass and radius, once η is fixed. Then we adopt a range for η = 70.6 − 118.5 MeV, corresponding to ς = 85.3 − 135.1 MeV, and ηQPO = 90.5 − 111.5 MeV, corresponding to ςQPO = 104.9 − 128.4 MeV. The expected region of the neutron star mass and radius with ρc ≤ 2ρ0 is given by the shaded region and the region enclosed by the solid lines on the bottom right side of Fig. 7. If the resultant region intersects with the region shown in Fig. 6, further constraints can be set on the parameters of the neutron star model corresponding to GRB 200415A. Unfortunately, the shaded area corresponding to neutron star models with ρc ≤ 2ρ0 does not intersect with the region shown in Fig. 6. Therefore, to constrain the allowed region for the neutron star models corresponding to GRB 200415A, we make a further assumption so that the expected mass and radius can somehow intersect with the region shown in Fig. 6.
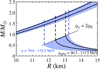 |
Fig. 7. Allowed range for the neutron star mass and radius obtained from the QPOs observed in GRB 200415A and shown in Fig. 6 compared to the mass and radius range derived via the empirical formula given in Sotani et al. (2014), (bottom right region). For defining the low-mass models, we used η = 70.6 − 118.5 MeV (shaded region) and ηQPO = 90.5 − 111.5 MeV (the region enclosed by the solid lines). Here we make the assumption that ρc ≤ 2ρ0. The black and blue dashed lines denote the neutron star radii expected from the empirical relation for η = 70.6, 90.5, 111.5, and 118.5 MeV with ρc = 2ρ0. |
As seen in Fig. 7, the masses of the neutron star models with ρc ≤ 2ρ0 are quite small and do not overlap with the constraint of the mass versus radius area found in Fig. 6. Still, the neutron star radius barely changes in the domain of M ≃ 0.5 − 1.5 M⊙ for any EOS. Based on this observation, we can extrapolate our mass versus radius domain as constrained by the vertical dashed lines corresponding to R = 11.73, 12.41, 13.03, and 13.23 km for η = 70.6, 90.5, 111.5, and 118.5 MeV. In this way, we obtain an overlap between the constrained region based on the information extracted from GRB 200415A, as shown in Fig. 6, and the neutron star models based on the allowed values of η (ηQPO).
Finally, the allowed mass versus radius area for the neutron star models constrained by the observed QPOs in GRB 200415A is compared to the other constraints on the neutron star mass and radius obtained from the astronomical and experimental observations. In Fig. 8, we use the two parallelograms to define the allowed region for the neutron star model that matches the information extracted from GRB 200415A. The outer (inner) parallelogram corresponds to the expected region assuming η = 70.6 − 118.5 MeV (ηQPO = 90.5 − 111.5 MeV). Meanwhile, in the same figure, we plot the constraints on the neutron star mass and radius set by (i) NICER observations for PSR J0030+0451 and MSP J0740+6620 (Riley et al. 2019, 2021; Miller et al. 2019, 2021; (ii) observations of x-ray bursts (Steiner et al. 2013); and (iii) gravitational wave observations and constraints set by GW170817. For GW170817 in particular, we draw the conservative constraint set by the tidal deformability, predicting that the radius of a neutron star with M = 1.4 M⊙ should be R1.4 ≤ 13.6 km (Annala et al. 2018) and that with M = 1.6 M⊙ should be R1.6 ≥ 10.7 km (Bauswein et al. 2017), as well as more stringent constraints obtained from the combination of multimessenger observations and nuclear theory, that is, 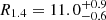 km (Capano et al. 2020) and
km (Capano et al. 2020) and 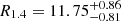 km (Dietrich et al. 2020).
km (Dietrich et al. 2020).
 |
Fig. 8. Neutron star mass and radius constraints in this study from GRB 200415A (double-parallelogram) are shown together with other observational and experimental constraints (see the text for details). For reference, we also plot the neutron star mass and radius theoretically constructed with several realistic EOSs. |
Recently, a new upper neutron star mass limit was set by PSR J0952-0607, the so-called “black widow”, of namely M = 2.35 ± 0.17 M⊙ (Romani et al. 2022), which is also shown in Fig. 8. In the high-mass region, we also draw the limits set by causality (Lattimer 2012). Finally, the low-mass region enclosed by the purple solid line is based on the constraints set for L = 60 ± 20 and K0 = 240 ± 20 MeV, as in Fig. 7. For reference, in Fig. 8, we also show the neutron star models constructed using realistic EOSs. Among the EOSs adopted here, the Shen EOS has already been excluded from the gravitational wave observation in GW170817; we keep it here as a reference because it is one of the standard EOSs in astrophysics.
4. Conclusion
Quasi-periodic oscillations observed in the magnetar giant flares can be an extremely useful tool for extracting neutron star properties. In this study, we examine the possibility of identifying the QPOs of the recently observed GRB 200415A as overtones of crustal torsional oscillations. As a result, we find that the observed QPO frequencies can be identified as the first, second, fourth, and tenth overtones with specific values of 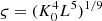 .
.
Then, by comparing the resultant value of ς for a variety of neutron star models to the appropriate range of ς restricted by the values of L and K0 determined by terrestrial experiments (or even the value of L constrained from the previous giant flare observations), we show the possible range of values for the mass and radius of GRB 200415A. Furthermore, assuming that the neutron star radius is almost the same as that of the neutron star model, whose central density is twice the saturation density, we derived a more stringent constraint for the neutron star mass and radius of GRB 200415A. The outcome of our analysis is in good agreement with the constraints set by other observations in the gravitational and electromagnetic spectrum (Fig. 8).
As only high frequencies have been observed in GRB 200415A, we only consider the identification of them with the overtones of crustal torsional oscillations. However, if lower frequencies are observed in the future from a similar object (or in the case of a repeated burst from the same object), it would be interesting to try to identify them with the fundamental oscillations in the same framework. In this way, one could verify whether or not the origin of the QPOs is the crustal torsional oscillations.
In this study, we worked under the assumption that the strength of the magnetic field in GRB 200415A is ≲1015 G, so that torsional oscillations have a short damping time but the frequencies are still close to the values of pure crustal oscillations. If it turns out that the magnetic field strength in GRB 200415A is higher than ∼1015 G, a revised analysis will be necessary because of the significant effect on the frequency spectrum of torsional oscillations. We emphasize that the alternative model discussed in Castro-Tirado et al. (2021) is also a viable solution.
A similar discussion is also possible using another combination of the nuclear saturation parameter given by ητ = ( − KτL5)1/6, where Kτ is the isospin dependence of incompressibility for asymmetric nuclear matter (Sotani & Ota 2022), or directly using the experimental observables, such as neutron skin thickness or dipole polarizability for neutron-rich nuclei (Sotani & Naito 2023).
Acknowledgments
This work is supported in part by Japan Society for the Promotion of Science (JSPS) KAKENHI Grant Numbers JP19KK0354 and Sotani JP21H01088, Sotani and by Pioneering Program of RIKEN for Evolution of Matter in the Universe (r-EMU).
References
- Abbott, B. P., Abbott, R., & Abbott, T. D. 2017, Phys. Rev. Lett., 119, 161101 [CrossRef] [Google Scholar]
- Abbott, B. P., et al. (LIGO Scientific Collaboration and Virgo Collaboration) 2018, Phys. Rev. X, 9, 011001 [Google Scholar]
- Andersson, N., & Kokkotas, K. D. 1996, Phys. Rev. Lett., 677, 4134 [NASA ADS] [CrossRef] [Google Scholar]
- Andersson, N., & Kokkotas, K. D. 1998, MNRAS, 299, 1059 [NASA ADS] [CrossRef] [Google Scholar]
- Annala, E., Gorda, T., Kurkela, A., & Vuorinen, A. 2018, Phys. Rev. Lett., 120, 172703 [Google Scholar]
- Antoniadis, J., Freire, P. C. C., Wex, N., et al. 2013, Science, 340, 6131 [Google Scholar]
- Bauswein, A., Just, O., Janka, H.-T., & Stergioulas, N. 2017, ApJ, 850, L34 [Google Scholar]
- Capano, C. D., Tews, I., Brown, S. M., et al. 2020, Nat. Astron., 4, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Castro-Tirado, A. J., Østgaard, N., Göğüş, E., et al. 2021, Nature, 600, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N. 2012, Phys. Rev. C, 85, 035801 [NASA ADS] [CrossRef] [Google Scholar]
- Chatziioannou, K. 2020, Gen. Rel. Grav., 52, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Dietrich, T., Hinderer, T., & Samajdar, A. 2021, Gen. Rel. Grav., 53, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Colaiuda, A., & Kokkotas, K. D. 2011, MNRAS, 414, 3014 [NASA ADS] [CrossRef] [Google Scholar]
- Colaiuda, A., & Kokkotas, K. D. 2012, MNRAS, 423, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Colaiuda, A., Beyer, H., & Kokkotas, K. D. 2009, MNRAS, 396, 1441 [NASA ADS] [CrossRef] [Google Scholar]
- Cromartie, H. T., Fonseca, E., Ransom, S. M., et al. 2020, Nat. Astron., 4, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Demorest, P., Pennucci, T., Ransom, S., et al. 2010, Nature, 467, 1081 [CrossRef] [PubMed] [Google Scholar]
- Dietrich, T., Coughlin, M. W., Pang, P. T. H., et al. 2020, Science, 370, 1450 [Google Scholar]
- Doneva, D. D., Gaertig, E., Kokkotas, K. D., & Krüger, C. 2013, Phys. Rev. D, 88, 044052 [NASA ADS] [CrossRef] [Google Scholar]
- Douchin, F., & Haensel, P. 2001, A&A, 380, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gabler, M., Cerdá, Durán P., Font, J. A., et al. 2011, MNRAS, 410, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Gabler, M., Cerdá, Durán P., Stergioulas, N., et al. 2012, MNRAS, 421, 2054 [NASA ADS] [CrossRef] [Google Scholar]
- Gabler, M., Cerdá, Durán P., Stergioulas, N., et al. 2013, Phys. Rev. Let., 111, 211102 [NASA ADS] [CrossRef] [Google Scholar]
- Gabler, M., Cerdá, Durán P., Stergioulas, N., et al. 2016, MNRAS, 460, 4242 [NASA ADS] [CrossRef] [Google Scholar]
- Gabler, M., Cerdá, Durán P., Stergioulas, N., et al. 2018, MNRAS, 476, 4199 [NASA ADS] [CrossRef] [Google Scholar]
- Gearheart, M., Newton, W. G., Hooker, J., & Li, B. A. 2011, MNRAS, 418, 2343 [NASA ADS] [CrossRef] [Google Scholar]
- Haensel, P., Potekhin, A. Y., & Yakovlev, D. G. 2006, Neutron Stars 1: Equation of 484 State and Structure (Springer) [Google Scholar]
- Hansen, C., & Cioffi, D. F. 1980, ApJ, 238, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Israel, G., Belloni, T., Stella, L., et al. 2005, ApJ, 628, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Krüger, C. J., Kokkotas, K. D., Manoharan, P., & Völkel, S. H. 2021, Front. Astron. Space Sci., 8, 736918 [CrossRef] [Google Scholar]
- Lattimer, J. M. 2012, Ann. Rev. Nucl. Part. Sci., 62, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Leahy, D. A., & Li, L. 1995, MNRAS, 277, 1177 [NASA ADS] [Google Scholar]
- Levin, Y. 2007, MNRAS, 377, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Li, B. A., Krastev, P. G., Wen, D. H., & Zhang, N. B. 2019, Euro. Phys. J. A, 55, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Mahlmann, J. F., Akgün, T., Pons, J. A., Aloy, M. A., & Cerdá-Durán, P. 2019, MNRAS, 490, 4858 [Google Scholar]
- Miller, M. C., Lamb, F. K., Dittmann, A. J., et al. 2019, ApJ, 887, L24 [Google Scholar]
- Miller, M. C., Lamb, F. K., Dittmann, A. J., et al. 2021, ApJ, 918, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Minaev, P. Y., & Pozanenko, A. S. 2020, Astron. Lett., 46, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Morozova, V., Radice, D., Burrows, A., & Vartanyan, D. 2018, ApJ, 861, 10 [CrossRef] [Google Scholar]
- Negele, J. W., & Vautherin, D. 1973, Nucl. Phys. A, 207, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Oertel, M., Hempel, M., Klähn, T., & Typel, S. 2017, Rev. Mod. Phys., 89, 015007 [Google Scholar]
- Ogata, S., & Ichimaru, S. 1990, Phys. Rev. A, 42, 4867 [NASA ADS] [CrossRef] [Google Scholar]
- Oyamatsu, K., & Iida, K. 2003, Prog. Theor. Phys., 109, 631 [CrossRef] [Google Scholar]
- Oyamatsu, K., & Iida, K. 2007, Phys. Rev. C, 75, 015801 [NASA ADS] [CrossRef] [Google Scholar]
- Passamonti, A., & Andersson, N. 2012, MNRAS, 419, 638 [NASA ADS] [CrossRef] [Google Scholar]
- Passamonti, A., & Lander, S. K. 2014, MNRAS, 438, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Pechenick, K. R., Ftaclas, C., & Cohen, J. M. 1983, ApJ, 274, 846 [Google Scholar]
- Pethick, C. J., & Potekhin, A. Y. 1998, Phys. Lett. B, 427, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Poutanen, J., & Gierlinski, M. 2003, MNRAS, 343, 1301 [NASA ADS] [CrossRef] [Google Scholar]
- Psaltis, D., & Özel, F. 2014, ApJ, 792, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Riley, T. E., Watts, A. L., Bogdanov, S., et al. 2019, ApJ, 887, L21 [Google Scholar]
- Riley, T. E., Watts, A. L., Ray, P. S., et al. 2021, ApJ, 918, L27 [CrossRef] [Google Scholar]
- Romani, R. W., Kandel, D., Filippenko, A. V., et al. 2022, ApJ, 934, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Schumaker, B. L., & Thorne, K. S. 1983, MNRAS, 203, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Shlomo, S., Kolomietz, V. M., & Colò, G. 2006, Eur. Phys. J. A, 30, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Sotani, H., & Miyamoto, U. 2018, Phys. Rev. D, 98, 044017 [NASA ADS] [CrossRef] [Google Scholar]
- Sotani, H., & Naito, T. 2023, Phys. Rev. C, in press [Google Scholar]
- Sotani, H., & Ota, S. 2022, Phys. Rev. D, 106, 103005 [NASA ADS] [CrossRef] [Google Scholar]
- Sotani, H., Kohri, K., & Harada, T. 2004, Phys. Rev. D, 69, 084008 [NASA ADS] [CrossRef] [Google Scholar]
- Sotani, H., Kokkotas, K. D., & Stergioulas, N. 2007, MNRAS, 375, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Sotani, H., Yasutake, N., Maruyama, T., & Tatsumi, T. 2011, Phys. Rev. D, 83, 024014 [NASA ADS] [CrossRef] [Google Scholar]
- Sotani, H., Nakazato, K., Iida, K., & Oyamatsu, K. 2012, Phys. Rev. Lett., 108, 201101 [NASA ADS] [CrossRef] [Google Scholar]
- Sotani, H., Nakazato, K., Iida, K., & Oyamatsu, K. 2013, MNRAS, 428, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Sotani, H., Iida, K., Oyamatsu, K., & Ohnishi, A. 2014, Prog. Theor. Exp. Phys., 2014, 051E01 [CrossRef] [Google Scholar]
- Sotani, H., Iida, K., & Oyamatsu, K. 2017, MNRAS, 470, 4397 [NASA ADS] [CrossRef] [Google Scholar]
- Sotani, H., Iida, K., & Oyamatsu, K. 2018, MNRAS, 479, 4735 [NASA ADS] [CrossRef] [Google Scholar]
- Sotani, H., Iida, K., & Oyamatsu, K. 2019, MNRAS, 489, 3022 [NASA ADS] [Google Scholar]
- Sotani, H., Takiwaki, T., & Togashi, H. 2021, Phys. Rev. D, 104, 123009 [NASA ADS] [CrossRef] [Google Scholar]
- Sotani, H., Nishimura, N., & Naito, T. 2022, Prog. Theor. Exp. Phys., 2022, 041D01 [CrossRef] [Google Scholar]
- Steiner, A. W., & Watts, A. L. 2009, Phys. Rev. Lett., 103, 181101 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, A. W., Lattimer, J. M., & Brown, E. F. 2013, ApJ, 765, L5 [Google Scholar]
- Strohmayer, T. E., & Watts, A. L. 2005, ApJ, 632, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Strohmayer, T. E., & Watts, A. L. 2006, ApJ, 653, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Strohmayer, T., van Horn, H. M., Ogata, S., et al. 1991, ApJ, 375, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, X., Miao, Z., Sun, B., & Li, A. 2023, ApJ, 942, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Suvorov, A. G., Kuan, H. J., & Kokkotas, K. D. 2022, A&A, 664, A177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Torres-Forné, A., Cerdá-Durán, P., Passamonti, A., et al. 2019, MNRAS, 482, 3967 [CrossRef] [Google Scholar]
- Tsang, D. 2011, ApJ, 777, 103 [Google Scholar]
- Tsang, D., Read, J. S., Hinderer, T., Piro, A. L., & Bondaresc, R. 2012, Phys. Rev. Lett., 108, 011102 [NASA ADS] [CrossRef] [Google Scholar]
- Turolla, R., Zane, S., & Watts, A. 2015, Rep. Prog. Phys., 78, 116901 [NASA ADS] [CrossRef] [Google Scholar]
- van Hoven, M., & Levin, Y. 2011, MNRAS, 410, 1036 [NASA ADS] [CrossRef] [Google Scholar]
- Xiao, S., Zhang, Y.-Q., Zhu, Z.-P., et al. 2022, arXiv eprints [arXiv:2205.02186] [Google Scholar]
Appendix A: Magnetic effects on the crustal torsional oscillations
In this study, we worked under the assumption that the strength of the magnetic field in GRB 200415A is ≲1015G, so that torsional oscillations have a short damping time but the frequencies are still close to the values of pure crustal oscillations. For B ≥ 1015 G, there is a strong shift in the torsional oscillation frequencies, and the damping due to the “continuous” spectrum is even stronger if one considers particular geometries for the magnetic field (Levin 2007; Colaiuda et al. 2009; van Hoven & Levin 2011; Colaiuda & Kokkotas 2011; Gabler et al. 2012, 2018). For mixed poloidal-toroidal fields, the magnetoelastic oscillation spectrum becomes discrete (Colaiuda & Kokkotas 2012).
The effect of the magnetic field on pure torsional oscillations was studied in Sotani et al. (2007). There, it was shown for a variety of neutron star models and EOS that the shift in the torsional oscillation frequencies due to magnetic field obeys the following formula:
where 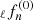 is the torsional mode frequency of the n-th overtone of a nonmagnetized neutron star, while ℓfn is the frequency of the equivalent magnetized one with the same parameters (M, R, EOS). B is the strength of the surface magnetic field normalized by Bμ = 4 × 1015 G. This was the case also in the 2D linear simulations in Colaiuda & Kokkotas (2011, 2012) and was almost confirmed in the most recent 2D nonlinear studies with a poloidal magnetic field (Gabler et al. 2018), where the oscillation frequencies are named as magnetically modified torsional modes.
is the torsional mode frequency of the n-th overtone of a nonmagnetized neutron star, while ℓfn is the frequency of the equivalent magnetized one with the same parameters (M, R, EOS). B is the strength of the surface magnetic field normalized by Bμ = 4 × 1015 G. This was the case also in the 2D linear simulations in Colaiuda & Kokkotas (2011, 2012) and was almost confirmed in the most recent 2D nonlinear studies with a poloidal magnetic field (Gabler et al. 2018), where the oscillation frequencies are named as magnetically modified torsional modes.
In previous studies (Sotani et al. 2007), the coefficients ℓαn were calculated only for n = 0, 1 and their values vary from 0.3 to 0.5 for EOS NV (Negele & Vautherin 1973) and 0.4 to 1.5 for EOS DH (Douchin & Haensel 2001). Here we calculated 2αn for larger values of n, as shown in Figure A.1. The values seem to reach a maximum value of about 2αn ≈ 2 − 2.5 for EOS DH and 2αn ≈ 0.8 − 1.1 for EOS NV.
 |
Fig. A.1. Coefficients of 2an in Eq. (A.1) for the neutron star models constructed with two different crust EOSs, NV (Negele & Vautherin 1973) and DH (Douchin & Haensel 2001). For the interior (core), we use the APR and WFF3 EOS. The open and filled marks correspond to results with NV and DH EOS, while the solid, dashed, and dotted lines correspond to the results for the 1.4M⊙, 2.0M⊙ neutron star models for the APR EOS, and 1.4M⊙ neutron star models for the WFF3 EOS. |
Therefore, the deviation of the magnetized neutron star frequencies from those of the nonmagnetized ones are ≲3.4% for the EOS NV and ≲7.5% for the EOS DH, if we assume B ∼ 1015 G. These values are still within the limits of uncertainty (∼10%) estimated in Castro-Tirado et al. (2021). For values of the magnetic field significantly higher than B ∼ 1015 G, our approach would need to be modified.
Regarding the damping of crustal oscillations due to the Alfvén continuum in the core, we recall that the 3.5ms duration of the high-frequency QPOs observed in GRB 200415A is consistent with the example of a timescale of ∼5ms for the damping of a crustal n = 1 shear mode in a model with a magnetic field strength of ∼1015G shown in Gabler et al. (2018), which justifies our assumptions.
Appendix B: Can the 836 Hz QPO be the second overtone?
In the main part of the article, we identified the lowest QPO frequency at 836 Hz as the first overtone. In this Appendix, we examine the possibility of identifying the lowest QPO as the second overtone. In Fig. B.1, we plot the first and second overtone of crustal torsional oscillations for a neutron star model with 1.4M⊙ and 14 km as a function of ς. In the same figure, we draw the observed QPO frequency and the aforementioned values for ς and ςQPO. It is apparent that the 836 Hz QPO frequency can be identified as the second overtone. As shown in Fig. B.2, indeed all four QPOs observed in GRB 200415A can be identified as the second, fifth, eighth, and sixteenth overtones if ς = 142.1 MeV. However, as mentioned above, the overtone frequencies increase with compactness, which implies that the suitable ς values for identifying the observed QPOs should be larger, beyond the accepted values for ς. Therefore, in order to remain in agreement with the range ς = 85.3 − 135.1 MeV, we would need to consider neutron star models with very small and somehow unphysical compactness.
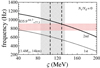 |
Fig. B.1. First (dotted line) and second (solid line) overtones of the ℓ = 2 crustal torsional oscillations for a neutron star model with (M, R) = (1.4M⊙, 14km) and Ns/Nd = 0 as functions of ς. For reference, we plot the lowest observed QPO frequency (red shaded area) in GRB 200415A, i.e., 835.9 |
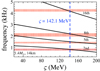 |
Fig. B.2. Identification of the QPOs observed in GRB 200415A as crustal torsional oscillation overtones for a neutron star model with M = 1.4M⊙ and R = 14 km, assuming that the lowest QPO in GRB 200415A corresponds to the second overtone. |
All Tables
The EOS parameters adopted in this study, where η and ς are the combination of K0 and L given by η = (K0L2)1/3 and 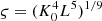 .
.
All Figures
 |
Fig. 1. First overtone of the ℓ = 2 crustal torsional oscillations for a neutron star model with M = 1.6 M⊙, R = 12 km, and Ns/Nd = 0. The marks denote the torsional oscillation frequencies estimated for the neutron star models constructed based on the crustal EOSs listed in Table 1, as a function of ς. The thick solid line is the quadratic fitting given by Eq. (3). |
| In the text | |
 |
Fig. 2. First overtones of the crustal torsional oscillations with ℓ = 2 (solid line) and ℓ = 10 (dashed line) are shown as functions of ς given by Eq. (2) for three neutron star models with (M, R, M/R) = (1.4 M⊙, 14 km, 0.146), (1.6 M⊙, 12 km, 0.197), and (1.8 M⊙, 10 km, 0.266). The top panel corresponds to Ns/Nd = 0, while the bottom panel to Ns/Nd = 1. In both panels, for reference, we draw (with a shaded thick line) the lowest QPO frequency found in GRB 200415A; i.e., 835.9 |
| In the text | |
 |
Fig. 3. Suitable values of ς for identifying the 835 Hz QPO as the first overtone for various stellar masses and radii with Ns/Nd = 0. The shaded region corresponds to the range of ς = 85.3 − 135.1 MeV, estimated for the fiducial values L = 60 ± 20 and K0 = 240 ± 20 MeV. The dashed lines define the range of ςQPO = 104.9 − 128.4 MeV, corresponding to LQPO = 58 − 73 MeV. |
| In the text | |
 |
Fig. 4. Correspondence of the observed QPOs to the overtones for the neutron star model with M = 1.6 M⊙ and 12 km. The QPOs observed in GRB 200415A can be identified with the first, second, fourth, and tenth overtones of crustal torsional oscillations, which leads to a suitable value of ς for the adopted stellar model of ς = 121.7 MeV. |
| In the text | |
 |
Fig. 5. Suitable value of ς (colored marks) for simultaneous identification of the four QPOs observed in GRB 200415A as the first, second, fourth, and tenth overtones of the crustal torsional oscillations for various neutron star models. The meaning of the shaded region and dashed lines is the same as in Fig. 3. The arrow denotes the particular model discussed in Fig. 4, where the extracted value is ς = 121.7 MeV. |
| In the text | |
 |
Fig. 6. Constraints on neutron star mass and radius set by the simultaneous identification of all four observed QPOs in GRB 200415A as the first, second, fourth, and tenth overtones of the crustal torsional oscillations. Here we accepted only the models meeting the constraints ς = 85.3 − 135.1 MeV (shaded region) and ςQPO = 104.9 − 128.4 MeV (bounded by solid lines). |
| In the text | |
 |
Fig. 7. Allowed range for the neutron star mass and radius obtained from the QPOs observed in GRB 200415A and shown in Fig. 6 compared to the mass and radius range derived via the empirical formula given in Sotani et al. (2014), (bottom right region). For defining the low-mass models, we used η = 70.6 − 118.5 MeV (shaded region) and ηQPO = 90.5 − 111.5 MeV (the region enclosed by the solid lines). Here we make the assumption that ρc ≤ 2ρ0. The black and blue dashed lines denote the neutron star radii expected from the empirical relation for η = 70.6, 90.5, 111.5, and 118.5 MeV with ρc = 2ρ0. |
| In the text | |
 |
Fig. 8. Neutron star mass and radius constraints in this study from GRB 200415A (double-parallelogram) are shown together with other observational and experimental constraints (see the text for details). For reference, we also plot the neutron star mass and radius theoretically constructed with several realistic EOSs. |
| In the text | |
 |
Fig. A.1. Coefficients of 2an in Eq. (A.1) for the neutron star models constructed with two different crust EOSs, NV (Negele & Vautherin 1973) and DH (Douchin & Haensel 2001). For the interior (core), we use the APR and WFF3 EOS. The open and filled marks correspond to results with NV and DH EOS, while the solid, dashed, and dotted lines correspond to the results for the 1.4M⊙, 2.0M⊙ neutron star models for the APR EOS, and 1.4M⊙ neutron star models for the WFF3 EOS. |
| In the text | |
 |
Fig. B.1. First (dotted line) and second (solid line) overtones of the ℓ = 2 crustal torsional oscillations for a neutron star model with (M, R) = (1.4M⊙, 14km) and Ns/Nd = 0 as functions of ς. For reference, we plot the lowest observed QPO frequency (red shaded area) in GRB 200415A, i.e., 835.9 |
| In the text | |
 |
Fig. B.2. Identification of the QPOs observed in GRB 200415A as crustal torsional oscillation overtones for a neutron star model with M = 1.4M⊙ and R = 14 km, assuming that the lowest QPO in GRB 200415A corresponds to the second overtone. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} { w} = { w}_0 + \frac{K_0}{18n_0^2}(n_{\rm b}-n_0)^2 + \left[S_0 + \frac{L}{3n_0}(n_{\rm b}-n_0)\right]\alpha ^2, \end{aligned} $$](/articles/aa/full_html/2023/08/aa46360-23/aa46360-23-eq3.gif)
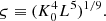
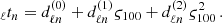
![$$ \begin{aligned} \frac{_\ell f_n}{_\ell f^{(0)}_n}\approx \left[1 + _\ell \alpha _n \left(\frac{B}{B_\mu }\right)^2\right]^{1/2}, \end{aligned} $$](/articles/aa/full_html/2023/08/aa46360-23/aa46360-23-eq13.gif)