| Issue |
A&A
Volume 663, July 2022
|
|
|---|---|---|
| Article Number | A25 | |
| Number of page(s) | 8 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202243274 | |
| Published online | 07 July 2022 | |
Desorption of polycyclic aromatic hydrocarbons by cosmic rays
Implications for PAH inventories under TMC-1 dense cloud conditions
1
Institut des Sciences Moléculaires d’Orsay, UMR8214, CNRS, Université Paris-Saclay,
91405
Orsay, France
e-mail: emmanuel.dartois@universite-paris-saclay.fr
2
Laboratoire de physique des deux infinis Irène Joliot-Curie, CNRS-IN2P3, Université Paris-Saclay,
91405
Orsay, France
3
GSI Helmholtzzentrum für Schwerionenforschung,
64291
Darmstadt, Germany
4
Hochschule RheinMain,
Am Brückweg 26,
65428
Rüsselsheim, Germany
5
Institut de Minéralogie, de Physique des Matériaux et de Cosmochimie, CNRS, MNHN, Sorbonne Univ.,
75005
Paris, France
6
TU Darmstadt,
64287
Darmstadt, Germany
Received:
6
February
2022
Accepted:
15
March
2022
Context. The rate of sputtering and release of condensed species is an important aspect of interstellar chemistry, as is photodesorption for the most volatile species, because in the absence of such mechanisms the whole gas phase would have to condense in times often shorter than the lifetime of the considered medium, in particular for dense clouds. The recent detection of cyclic aromatic molecules by radioastronomy requires an understanding of the potential mechanisms supporting the rather high abundances observed.
Aims. We perform experiments to advance our understanding of the sputtering yield due to cosmic rays for very large carbonaceous species in the solid phase.
Methods. Thin films of perylene and coronene were deposited on a quartz cell microbalance and exposed to a 1.5 MeV N+ ion beam at the Laboratoire de Physique des 2 Infinis Irène Joliot-Curie (IJCLab, Orsay, France) and a 230 MeV 48Ca10+ ion beam at the GSI Helmholtzzentrum für Schwerionenforschung (GSI, Darmstadt, Germany). The mass loss was recorded as a function of the fluence for the N+ beam. The microbalance response was calibrated using Fourier transform infrared (FTIR) reflectance measurements of the produced films. In addition, the destruction cross-section of the same species was measured with the 48Ca10+ ion beam by in situ monitoring of the evolution of the infrared spectra of the bombarded films.
Results. We deduced the sputtering yield for perylene and coronene and their radiolysis destruction cross-sections. Combining these results with a cosmic ray astrophysical spectrum, we discuss the impact on the possible abundance that may originate from the sputtering of dust grains with these molecules as well as from polycyclic aromatic molecules when they are trapped in ice mantles.
Key words: methods: laboratory: solid state / cosmic rays / molecular processes / ISM: abundances / ISM: molecules / solid state: volatile
© E. Dartois et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The relative contributions of the different desorption mechanisms are of paramount importance for constraining the chemical evolution of interstellar regions using astrophysical models, particularly in dense clouds (e.g. Wakelam et al. 2021, and reference therein).
The recently observed high abundances of cyclic aromatics such as cyanonaphthalene (10-10 n(H2); McGuire et al. 2021) and indene (~1.6 x 10-9 n(H2); Cernicharo et al. 2021) are not only difficult to explain using the current astrochemical models, but maintaining these species in the gas phase in relatively dense media also represents a challenge, as they should rapidly condense on the cold dust grains. This should be even more important for larger species.
Interstellar solids are exposed to cosmic radiation consisting of many ion species, mainly from protons to iron, in the energy range from the MeV to TeV. Irradiation of laboratory analogs with ions in the 1–500 MeV range provides important information for experimental simulations of the effects of cosmic rays and can be used to quantify the sputtering rates for astrophysical models.
In this article, we describe irradiation experiments at ion accelerators exposing small polycyclic aromatic hydrocarbon (PAH) species (perylene and coronene) in order to determine the desorption efficiencies of PAH species condensed on dust grains. We deduce their survival timescale and their abundance in the solid phase in a scenario of describing their solid–gas partition.
The experimental setup and the measurement process to determine and analyse the sputtering yields and destruction cross-sections for perylene and coronene are described. In the last section, we detail the astrophysical implications after calculating the effective sputtering rate by a distribution of cosmic rays, the survival timescale in the solid phase in astrophysical environments, and the sputtering-induced injection rate in the gas phase and how it is related to abundance constraints. We then summarise our findings and give an outlook for future observations.
2 Experiments
The irradiation experiments with ions in the electronic energy loss regime are combined with in situ microbalance measurements that provide the weight loss of the PAH films due to sputtering.
 |
Fig. 1 Experimental setups: (a) thin film holder showing interference fringes after deposition. The quartz is placed at the center of the holder. (b) Load lock system with manipulator for changing coated quartz crystals. (c) View of the setup mounted on the ARAMIS beam line. (d) View of the samples in the irradiation chamber at M3-beamline of the GSI M-branch including the microbalance and movable IR window. |
2.1 Microbalance setup
We used an Inficon Cool Drawer quartz cell microbalance (QCM) loaded with a quartz piezoelectric crystal operating at 6 MHz. When a thin film of material is deposited on top of the crystal, the piezoelectric resonance frequency varies according to the deposited film weight. The balance was operated in the opposite way to the conventional mode, starting with quartz crystals 'pre-coated' with a PAH thin film and following the resonance frequency changes upon mass loss, that is, measuring the mass loss induced by the sputtering. The sensitivity of the QCM was calibrated with the same molecular films as reference. In the following, we assume a constant density and shear modulus for each deposited film material during the ion irradiation and measurements, that is, a constant z-ratio for the QCM. This z-ratio evolves as the square root of the product of the density and shear modulus of the film. We estimate that this assumption may affect the absolute sensitivity during irradiation by up to a few tens of percent. The setup is mounted on a manipulator in a special chamber which allows the exchange of the sample in a load-lock system permitting sample (coated quartz) exchange without breaking the irradiation chamber vacuum (Fig. 1b). The chamber is pre-evacuated and the microbalance is transferred via the manipulator into the high-vacuum (≲10−7 mbar) main chamber, where it is exposed to the ion beams of the accelerator (Figs. 1c, d) while monitoring the QCM response. During the tests of the QCM, we forced a 10 K temperature increase to record the frequency-induced drift. We monitored a maximum drift of 3 Hz/K. Although no significant temperature variations were observed during the irradiation experiments that would compromise the microbalance sensitivity, to ensure the highest sensitivity, the microbalance was kept at a fixed temperature of 20 °C with circulating water using a Huber 300 H OLE Chiller achieving a ±0.2 °C regulation, which is about ±0.6 Hz maximum drift.
2.2 Film preparation and infrared measurements
Thin films were prepared by sublimation using a tantalum crucible heated with a tungsten filament in an evacuated chamber at base pressure below about 10−6 mbar. PAHs were purchased from Merck: coronene (C24H12 purified by sublimation) and perylene (C20H12). They were loaded into the crucible facing a QCM quartz holder, and were then heated until sublimation while rotating the holder to homogenise the film formation. The approximate desired thickness of the film is controlled visually during the deposition (Fabry-Perot interference fringes are observed, as can be seen in Fig. 1a). After deposition, the thickness of the film is measured using a Continuum 2 Fourier transform infrared (FTIR) microscope. To do so, a background reference spectrum is taken on the pristine gold-coated quartz crystal electrode, and spectra are measured in reflectance on the deposited film against this reference spectrum, with a microscope aperture of 75 × 75 microns using a ×32 objective. The thin film reflectance spectra (Figs. A.1 and A.2) display bands corresponding to the vibrational modes of the deposited PAH molecular film as well as interference fringes whose period is directly related to the thickness of the film.
2.3 Ion irradiation
JANNuS-SCALP. Ion irradiation with 1.5 MeV N+ ions was performed on the Joint Accelerators for Nano-science and Nuclear Simulation-Synthesis and Characterisation using ion Accelerators for Pluridisciplinary research (JANNuS-SCALP) platform (Bacri et al. 2017) at the ARAMIS Van de Graaff/Tandem accelerator. Ions were produced with a Penning source located at the high-voltage terminal of the accelerator. Dosimetry was performed by monitoring current on guard rings around the target. The beam was swept to ensure a homogeneity on the target of better than 10%.
GSI. The ion irradiations with swift heavy ions (SHIs) were performed at the M3 branch of the Universal Linear Accelerator (UNILAC) of GSI (Darmstadt, Germany). Dosimetry was performed by monitoring the current on slits upstream of the vacuum chamber, previously calibrated using a Faraday cup, while homogeneity was obtained using beam line optics visualised on a luminescent alumina screen. During the experiments, we used a 48Ca10+ beam of 4.8 MeV u−1 (230.2 MeV) energy with an ion flux of about 5 × 108 ions s−1 cm−2.
The ion properties for both ARAMIS and GSI irradiations are summarised in Table 1. The electronic stopping powers were calculated using the SRIM-2013 code (Ziegler et al. 2010).
3 Results
3.1 Calibrations
The calibration of the quartz microbalance response was performed using the PAH-coated quartz crystals combined with IR measurements. The thickness of the film was measured based on the interference fringes recorded in reflectance in the IR:
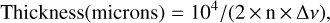 (1)
(1)
where Δν is the interference fringe period in cm−1 and n denotes the refractive index of the film. We assume a refractive index of n = 1.7 ± 0.15 for perylene (Buckman & Bomberger 1973) and coronene (Cherchneff et al. 1991) films. The measured quartz cell frequency shift as a function of the measured film thickness is reported in Fig. A.3. From the slope of this curve (−1.12 ± 0.22 × 104 Hz μm−1), we can estimate the sensitivity of the measurements. The 8 mm exposed diameter of the quartz cell corresponds to a surface of 0.50 cm2. Assuming a density of 1.35 g cm−3 for perylene (Haynes et al. 2016) yields a sensitivity of 6.1 ± 1.2 ng Hz−1. With a molar mass of 252.3 g mol−1 for perylene, this translates to 1.45 ± 0.32 χ 1013 molecules Hz−1. For coronene, with a density of 1.37 g cm−3 and a molar mass of 300.35 g mol−1, this gives 1.23 ± 0.24 χ 1013 molecules Hz−1.
 |
Fig. 2 Frequency shifts Δν recorded as a function of fluence in the various QCM experiments. The irradiation was performed with 1.5 MeV N+ ions using quartz coated with thin and thick films with respect to the ion range as well as bare quartz as a blank reference. Left: perylene, right: coronene. Solid lines are fits to the data using Eq. (2). |
Summary of ion properties including the total kinetic energy, the electronic energy loss (Se), the ion range assuming a film density of 1.35 g cm−3 for perylene and 1.37 g cm−3 for coronene (Haynes et al. 2016), and nuclear-to-electronic energy loss ratio (Sn/Se).
3.2 Irradiation monitoring with the quartz cell
Breuer et al. (2016) showed that under SHI bombardment of a thin, pure coronene film, the sputtering is largely dominated by nearly fragment-free desorption of intact neutral coronene molecules. The mass loss we monitor with the quartz cell frequency change is therefore ascribed to mainly intact molecules. However, upon irradiation of the bare quartz crystal, ion-induced damages modify the frequency of the crystal. To perform the experiments we therefore irradiated bare quartz crystal to monitor the effect of the damage on the response. As can be seen in Fig. 2, this effect results in a frequency drift, giving rise to an apparent mass increase of about −2.15 χ 10−12 Hz/(ion1 cm−2), or approximately 30 molecules (ion−1 cm−2). With the quartz cell surface of 0.50 cm2, this yields a frequency drift of about −4.30 × 10−12 Hz ion−1, giving rise to an apparent mass increase of approximately 60 molecules ion−1.
Sputtering yield measurements were performed at room temperature because this is far enough from the sublimation threshold for the considered perylene and coronene species, as checked by the constancy of the QCM frequency over the experiment durations when loaded with the PAH-coated quartz crystal. In addition, room temperatures mean that we do not have to deal with possible residual condensation affecting QCM measurements, which occurs at much lower temperatures if not under good UHV conditions. The sputtering yield for molecular solid has been shown to be temperature dependent, and the yield can to first order be described by 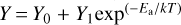 , where Ea is an activation energy related to the binding energy of the molecular solid under consideration and thermal diffusion of its radiolytic products. For water ice, Ea is of the order of 0.06 eV or about 700 K (Johnson et al. 2013). The binding energy on dust grains or multilayer perylene and coronene films is far higher, typically around 1 eV or above (e.g. Thrower et al. 2013, and references therein), and the measured sputtering yields are therefore expected to be fairly constant between 10 K and our room temperature measurements.
, where Ea is an activation energy related to the binding energy of the molecular solid under consideration and thermal diffusion of its radiolytic products. For water ice, Ea is of the order of 0.06 eV or about 700 K (Johnson et al. 2013). The binding energy on dust grains or multilayer perylene and coronene films is far higher, typically around 1 eV or above (e.g. Thrower et al. 2013, and references therein), and the measured sputtering yields are therefore expected to be fairly constant between 10 K and our room temperature measurements.
When a PAH-coated quartz film is exposed to the beam, the behaviour will depend on whether the ions are stopped in the film or in the quartz, as seen in Fig. 2. In the case of the 1.5 MeV N+ irradiations, for perylene, the range is of the order of 2.3 μm If the film is thinner than the range, at the beginning of the irradiation the quartz drift first appears less important than the drift of the bare quartz crystal because it is compensated by mass loss from the film (increase in frequency) due to the electronic sputtering. At large fluences, the remaining film on the substrate that evolved due to the bulk radiolysis is highly cross-linked and thus the sputtering efficiency drops significantly. It is no longer high enough to compete with the drift. Therefore, the frequency drift becomes parallel to the one measured for the blank quartz exposed to the same ion beam. In the case of a film thicker than the ion range, the behaviour is dominated by the film under ion beam modifications, as ions are now implanted in the PAH film, and do not reach the quartz cell. The mass loss is significant at low fluences (Fig. 2), as it is dominated by the original small PAH deposited. The PAH and thus the thin film cross-link upon irradiation. The sputtering yield decreases with fluence and should – asymptotically – reach a parallel to the fluence axis for thick films and parallel to the blank quartz evolution for thin films. We therefore describe the observed quartz microbalance signal evolution with a functional dependence given by
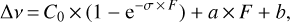 (2)
(2)
where σ represents a cross-section leading to cross-linking of the film, which will lead to a decrease in sputtering efficiency with fluence F. The linear contribution arises from radiation damages of the quartz, as discussed above. The solid lines in Fig. 2 are fits of this function to the data from irradiations with 1.5 MeV N+ ions. The tangent to the curve at low fluence, that is, the slope at the beginning of the irradiation is C0 × σ + a. The value of Δfmass loss ≈ C0 × σ gives the expected mass-loss frequency shift per ion for the virgin film converted to sputtering yield YS, reported in Table 2.
The irradiations with SHI were all conducted in the thin-film regime. The damage to the quartz cell was much greater because of the much longer ion range in the quartz. Ion tracks produced in quartz result in severe damage, and in macroscopic swelling at high fluences (Trautmann et al. 2002). After a fluence of ~1012 ion−1 cm−2, the quartz crystal resonance failed and/or even broke. The frequency shift of the blank quartz varied around −(0.8−1.1) × 10−8 Hz ion−1, which is equivalent to an ‘apparent’ sputtering rate of about 0.8−2 × 105 molecules ion−1. Based on the N+ measurements and assuming a quadratic dependence of the sputtering yield on electronic energy loss, as found for molecular solids (e.g. Boduch et al. 2015; Rothard et al. 2017), the expected sputtering yield at the electronic energy loss of the 230 MeV Ca ion beam is about 5−9 × 102 molecules ion−1 for perylene, or ≈4 × 10−11 Hz ion−1. This slope is more than two orders of magnitude lower than the slope induced by Ca ion damage. Uncertainties on the measurements prevented us from reaching the minimum required 1% stability in the blank and PAH-coated quartz to measure a sputtering rate in such an expected range.
Sputtering yields based on the quartz microbalance experiments.
 |
Fig. 3 Infrared spectra of a thin film of perylene irradiated with 48Ca+ ions recorded before irradiation (in blue) and after a fluence of 2.8 × 1012 ion cm−2 (in red). Insert: evolution of the integrated optical depth of the C=C IR band at ~1495 cm−1, normalised to the initial film prior to irradiation. The solid line is an exponential fit of the destruction cross-section (Eq. (6)) to the data, the dashed lines represent ±3σ with respect to the best fit. |
 |
Fig. 4 Infrared spectra of a thin film of coronene (in blue) irradiated with a 48Ca beam recorded at different fluences. Insert: evolution of the integrated optical depth of the C=C IR band at ~1315 cm−1, normalised to the initial film prior to irradiation. The solid line is an exponential fit of the destruction cross-section (Eq. (6)) to the data and the dashed lines represent ±3σ with respect to the best fit. |
3.3 Irradiation monitoring with infrared spectroscopy
In the experiment at GSI, we determined the destruction cross-section at room temperature for 230 MeV Ca ions by recording IR spectra of perylene and coronene films deposited on IR transparent ZnSe substrates (Figs. 3–4). These films were produced in the same setup as the one used for the quartz microbalance. The radiolytic cross-section at 10 K is expected to be very close to the 290 K measured one, especially with the low fluence used here; the main expected difference is that radiolytic products diffuse out more efficiently than at lower temperature, which would affect the chemistry after longer irradiation exposures. The integrated optical depth of the most intense perylene and coronene C = C stretching mode bands around 1495 cm−1 and 1315 cm−1, respectively, were used to monitor their destruction cross-section. We followed the usual approach where the column density Ν (in molecules cm−2) evolution of the film molecules exposed to ion irradiation is described by
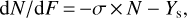 (3)
(3)
where Ys is the sputtering yield (in molecules ion−1) and σ the radiolysis destruction rate (in cm2 ion−1). The evolution of the column density is
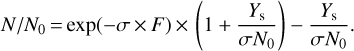 (4)
(4)
If the film is thick, then at the beginning of the irradiation, Ys ≪ σ × N0 and
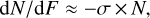 (5)
(5)
and the evolution of the column density follows an exponential
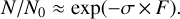 (6)
(6)
Fits of this equation to the data (Figs. 3–4) show that the measurements were conducted in the almost linear part of the exponential, with a destruction cross-section of σ = 1.9 ± 0.6 × 10−13 cm2 ion−1 and σ = 8.3 ± 1.2 × 10−14 cm2 ion−1 for perylene and coronene, respectively (Table 3). The column density of coronene molecules can be evaluated from the interference fringe period (Fig. 4) and the estimated density of 1.37 g cm−3. The initial column density at the beginning of the irradiation is of the order of N0 ≈ 5.3 × 1017 molecules cm−2 for coronene and N0 ≈ 1.1 × 1018 molecules cm−2 for perylene, and thus 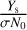 is of the order of 10−3 for the samples irradiated with the GSI 230 MeV Ca beam, thus validating a posteriori that σ × N0 ≫ Ys.
is of the order of 10−3 for the samples irradiated with the GSI 230 MeV Ca beam, thus validating a posteriori that σ × N0 ≫ Ys.
Destruction cross-section deduced from the IR experiments.
4 Astrophysical implications
Sputtering rate by cosmic rays. The effective sputtering yield 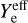 [molecules cm−2 s−1] by cosmic rays (CRs) can be calculated by integrating over their distribution in abundance and energy:
[molecules cm−2 s−1] by cosmic rays (CRs) can be calculated by integrating over their distribution in abundance and energy:
![$Y_{\rm{e}}^{{\rm{eff}}} = 2 \times 4\pi \sum\limits_{\rm{z}} {\int_{{E_{\min }}}^\infty {{Y_{\rm{s}}}\left[ {{S_{\rm{e}}}\left( {E,Z} \right)} \right]{{{\rm{d}}{N_{{\rm{CR}}}}} \over {{\rm{d}}E}}\left( {E,Z} \right){\rm{d}}E.} } $](/articles/aa/full_html/2022/07/aa43274-22/aa43274-22-eq12.png) (7)
(7)
The prefactor of two takes into account the sputtering at the entrance and exit of the dust grains. Ys(Se) [molecules ion−1 ] is determined experimentally. 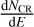 (E, Z)[ionscm−2 s−1 sr−1/(MeV u−1)] is the differential flux of the cosmic-ray element of atomic number Z, with a cut-off in energy Emin set at 1 keV. Moving the cut-off from 1 keV to 100 keV does not change the results significantly. The differential flux for different Z follows observed relative abundances of GCR from Wang et al. (2002; H, He), de Nolfo et al. (2006; Li, Be), and George et al. (2009; >Be), as explained in more detail in Dartois et al. (2013). The integration is performed from Z = 1 up to Z = 28 corresponding to Ni; a significant drop in the cosmic abundance and thus also in contribution is observed above Ni. The electronic stopping power Se is calculated using the SRIM-2013 code (Ziegler et al. 2010) as a function of atomic number Z and specific energy E (in MeV per nucleon). For the differential Galactic cosmic-ray flux, we adopted the functional form given by Webber & Yushak (1983) for primary cosmic-ray spectra using the leaky box model, which is also described in Shen et al. (2004):
(E, Z)[ionscm−2 s−1 sr−1/(MeV u−1)] is the differential flux of the cosmic-ray element of atomic number Z, with a cut-off in energy Emin set at 1 keV. Moving the cut-off from 1 keV to 100 keV does not change the results significantly. The differential flux for different Z follows observed relative abundances of GCR from Wang et al. (2002; H, He), de Nolfo et al. (2006; Li, Be), and George et al. (2009; >Be), as explained in more detail in Dartois et al. (2013). The integration is performed from Z = 1 up to Z = 28 corresponding to Ni; a significant drop in the cosmic abundance and thus also in contribution is observed above Ni. The electronic stopping power Se is calculated using the SRIM-2013 code (Ziegler et al. 2010) as a function of atomic number Z and specific energy E (in MeV per nucleon). For the differential Galactic cosmic-ray flux, we adopted the functional form given by Webber & Yushak (1983) for primary cosmic-ray spectra using the leaky box model, which is also described in Shen et al. (2004):
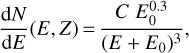 (8)
(8)
where C is a normalisation constant ( = 9.42 × 104, Shen et al. 2004) and E0 a parameter influencing the low-energy component of the distribution. Under such parametrisation, the high-energy differential flux dependence goes asymptotically to a −2.7 slope. The ionisation rate (ζ2) corresponding to the same distribution can be calculated, and gives an observable comparison with astrophysical observations in various environments. The ionisation rates for E0 = 200, 400, and 600 MeV u−1 correspond to ζ2 = 3.34 × 10−16 s−1, 5.89 × 10−17 s−1, and 2.12 × 10−17 s−1, respectively. Spectral density dNCR/dE is then close to the one obtained by propagation of CR to matter (Padovani et al. 2009; Chabot 2016).
In most molecular solids, the yield depends on the stopping power as
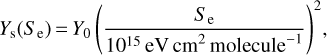 (9)
(9)
(e.g. Boduch et al. 2015; Rothard et al. 2017). Using the measured sputtering efficiency in this work (with 1.5 MeV N+ beam) as an anchor point, we obtain Y0 = 7.9 ± 3.8 × 10−6 molecules ion−1 for perylene, and Y0 = 1.65 ± 7.0 × 10−6 molecules ion−1 for coronene. The calculated sputtering rates corresponding to different ionisation rates are shown in Fig. 5.
Survival timescale in the solid phase. The destruction cross-section depends on the stopping power and is usually described by the following power law:
![${\sigma _{\rm{C}}} = {\rm{C}}\left[ {{\rm{c}}{{\rm{m}}^2}{\rm{io}}{{\rm{n}}^{ - 1}}} \right] = {\sigma _0}{\left( {{{{S_e}} \over {{{10}^{ - 15}}{\rm{eV c}}{{\rm{m}}^2}{\rm{ molecul}}{{\rm{e}}^{ - 1}}}}} \right)^\beta },$](/articles/aa/full_html/2022/07/aa43274-22/aa43274-22-eq16.png) (10)
(10)
where σC=C is the destruction cross-section measured for the C=C bonds in the considered molecules, interpreted as tracing the modification of the PAH molecule backbone, Se is the stopping power, and β the order of the dependency. The dependency of the radiolytic destruction cross-section on the stopping power has been shown to vary with a power generally lying in the range of 1–1.5 (e.g. Godard et al. 2011; Dartois et al. 2018). Using the measured cross-section as anchor points, we obtain:
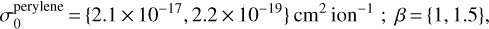 (11)
(11)
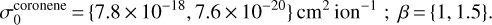 (12)
(12)
The destruction rate (in s−1) is inferred using the same formulation as described in Eq. (7) by replacing Ys[Se(E, Z)] with the radiolytic cross-section σC=C(Se(E, Z)) and withdrawing the prefactor 2. If one adopts a mean exponent of β = 1.25 ± 0.25, our measured destruction cross-sections yield a range of destruction timescales (i.e. the inverse of the destruction rate) as shown in Fig. 6. When exposed to cosmic rays, the inferred radiolytic survival timescale in the solid phase lies above 106 yr. The survival in the solid phase is therefore long enough to validate our neglect, to first order, of its destruction in the solid phase. We can therefore estimate the injection from the solid phase by CR sputtering processes in the electronic stopping regime from our experimental measurements.
Reinjection rate and abundance constraints. The rate of replenishment by sputtering of condensed PAH is given by:
![${R_{\rm{r}}}\left[ {{\rm{c}}{{\rm{m}}^{ - {\rm{3}}}}{{\rm{s}}^{ - 1}}} \right] = Y_{\rm{e}}^{{\rm{eff}}} \times {\sum _{{\rm{grains }}}} \times {\rm{ }}n\left( {\rm{H}} \right){\rm{ }} \times {\rm{ }}{f_{{\rm{solid}}}}(X),$](/articles/aa/full_html/2022/07/aa43274-22/aa43274-22-eq19.png) (13)
(13)
where 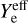 is the effective sputtering rate, Σgrains the effective grain surface per hydrogen atom adopting a given grain size distribution, n(H) the hydrogen number density, and fsolid(X) is the fraction of the solid phase that is dominated by PAHs (the fraction in the case where they are embedded in interstellar ice mantles is discussed later).
is the effective sputtering rate, Σgrains the effective grain surface per hydrogen atom adopting a given grain size distribution, n(H) the hydrogen number density, and fsolid(X) is the fraction of the solid phase that is dominated by PAHs (the fraction in the case where they are embedded in interstellar ice mantles is discussed later).
Assuming a classical interstellar dust grain size distribution as in Mathis et al. (1977, MRN), with a minimum and maximum grain radius of amin = 0.005 μm and amax = 0.25 μm, a gas to dust mass ratio of 100, and a density of 3 g cm−3 corresponding to silicate cores, the surface density of grains is about 1.2 × 10−21 cm2 per hydrogen atom. This value can be scaled if another density is assumed for the grains. The model by Jones et al. (2017) predicts a carbonaceous nanoparticle surface density of about 1.7 × 10−20 cm2 per hydrogen atom in the diffuse interstellar medium (ISM). In the following estimation, we use a large range of 1.2–17 × 10−21 cm2 H−1 for the possible surface density of grains.
Processes acting against the PAH gas phase abundance include their sequestration (freeze-out or accretion) on dust grains and their photolytic destruction. The accretion rate can be calculated from:
![${R_{\rm{a}}}\left[ {{\rm{c}}{{\rm{m}}^{ - 3}}{{\rm{s}}^{ - 1}}} \right] = {f_{{\rm{gas}}}}\left( X \right) \times n\left( {\rm{H}} \right) \times \sum\nolimits_{{\rm{grains}}} { \times n\left( {\rm{H}} \right)} \times \bar \upsilon ,$](/articles/aa/full_html/2022/07/aa43274-22/aa43274-22-eq22.png) (15)
(15)
with the mean gas velocity 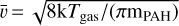 and fgas(X) the fraction of the considered PAH species in the gas phase with respect to hydrogen.
and fgas(X) the fraction of the considered PAH species in the gas phase with respect to hydrogen.
The photolytic destruction rate of the considered species is given by
![${R_{\rm{d}}}\left[ {{\rm{c}}{{\rm{m}}^{ - 3}}{{\rm{s}}^{ - 1}}} \right] = R_{\rm{d}}^{{\rm{VUV}}} + R_{\rm{d}}^{\sec {\rm{ondaryVUV}}},$](/articles/aa/full_html/2022/07/aa43274-22/aa43274-22-eq24.png) (16)
(16)
where 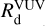 is the photolytic destruction rate by the VUV photon ambient field, which dominates the outer parts of dense clouds and the diffuse medium. It is given by:
is the photolytic destruction rate by the VUV photon ambient field, which dominates the outer parts of dense clouds and the diffuse medium. It is given by:
![$R_{\rm{d}}^{{\rm{VUV}}}\left[ {{\rm{c}}{{\rm{m}}^{ - 3}}{{\rm{s}}^{ - 1}}} \right] = R\left( 0 \right)\left[ {{{\rm{s}}^{ - 1}}} \right] \times \chi {{\rm{e}}^{ - {{\rm{\tau }}_{\rm{d}}}}}{\rm{ }}{f_{{\rm{gas}}}}\left( X \right){\rm{ }}n\left( {\rm{H}} \right)\left[ {{\rm{H c}}{{\rm{m}}^{ - 3}}} \right],$](/articles/aa/full_html/2022/07/aa43274-22/aa43274-22-eq26.png) (17)
(17)
where R(0) is the photodissociation rate per molecule for a standard interstellar radiation field (ISRF), i.e. for χ = 1; here χ is a factor to follow local radiation field enhancements. R(0) is attenuated by the dust absorption in the VUV 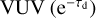 when penetrating into dense clouds, and can be approximated by
when penetrating into dense clouds, and can be approximated by 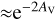 , with AV being the visual extinction.
, with AV being the visual extinction.
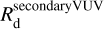 is the cosmic-ray-induced secondary VUV field photolytic rate, which will overcome the attenuated external field at high visual extinctions. The intensity of this secondary (cosmic ray induced) UV field is FUVCR = 103 photons cm−2 s−1 for an ionisation rate of 10−17 s−1. This value is the adopted value considering the ~3100 photons cm−2 s−1 for an ionisation rate of 3 × 10−17 s−1 from Shen et al. (2004), whereas Prasad & Tarafdar (1983) gave about 2380 photons cm−2 s−1 for an ionisation rate of 3 × 10−17 s−1. For simplicity in our calculations, the secondary VUV field induced by cosmic rays is related to the external VUV ISRF. This implies that we assume that the photodissociation rate integrated over the ISRF spectral shape and over the cosmic-ray-induced VUV field are of the same order of magnitude. The external integrated VUV photon flux from the ISRF would be of the order of 1.55 × 108 photons cm−2 s−1 using the ISRF field of Mathis et al. (1983). The ratio with the above-mentioned intensity of the CR secondary UV field leads to a value of FUVCR ≈ 6.5 × 10−6 × (ζext/10−17 s−1), and so
is the cosmic-ray-induced secondary VUV field photolytic rate, which will overcome the attenuated external field at high visual extinctions. The intensity of this secondary (cosmic ray induced) UV field is FUVCR = 103 photons cm−2 s−1 for an ionisation rate of 10−17 s−1. This value is the adopted value considering the ~3100 photons cm−2 s−1 for an ionisation rate of 3 × 10−17 s−1 from Shen et al. (2004), whereas Prasad & Tarafdar (1983) gave about 2380 photons cm−2 s−1 for an ionisation rate of 3 × 10−17 s−1. For simplicity in our calculations, the secondary VUV field induced by cosmic rays is related to the external VUV ISRF. This implies that we assume that the photodissociation rate integrated over the ISRF spectral shape and over the cosmic-ray-induced VUV field are of the same order of magnitude. The external integrated VUV photon flux from the ISRF would be of the order of 1.55 × 108 photons cm−2 s−1 using the ISRF field of Mathis et al. (1983). The ratio with the above-mentioned intensity of the CR secondary UV field leads to a value of FUVCR ≈ 6.5 × 10−6 × (ζext/10−17 s−1), and so
![$\matrix{ {R_{\rm{d}}^{{\rm{secondaryVUV}}}\left[ {{\rm{c}}{{\rm{m}}^{ - 3}}{{\rm{s}}^{ - 1}}} \right] \approx R\left( 0 \right)\left[ {{{\rm{s}}^{ - 1}}} \right] \times {{6.5 \times {{10}^{ - 6}}{\xi ^{{\rm{ext}}}}} \over {{{10}^{ - 17}}{{\rm{s}}^{ - 1}}}}} \cr { \times {f_{{\rm{gas}}}}\left( X \right)n\left( {\rm{H}} \right).} \cr } $](/articles/aa/full_html/2022/07/aa43274-22/aa43274-22-eq30.png) (18)
(18)
At steady state, Rr = Rd + Ra and so
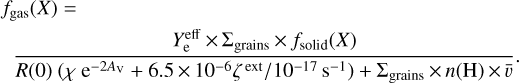 (19)
(19)
The pyrene and coronene photodissociation rates (loss of C2H2) were given by Allain et al. (1996): 7.13 × 10−11 s−1 and 4.55 × 10−11 s−1, respectively. We assume that perylene has a photodissociation rate intermediate between the pyrene and coronene rates relative to the proportion of the carbon of the PAH, i.e. about 5.8 × 10−11 s−1.
To calculate orders of magnitude corresponding to the external parts of dense clouds, we assume a typical density n(H) ≈ 104 cm−3, and a 10 K gas phase temperature, leading to a perylene mean gas velocity 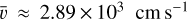 . At intermediate visual extinction, AV ≈ 2, with ζ ≈ 10−16 s−1, for perylene,
. At intermediate visual extinction, AV ≈ 2, with ζ ≈ 10−16 s−1, for perylene, 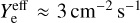 , and we derive a steady state value of fgas (perylene) = 3.2−32.6 × 10−9 fsolid (perylene).
, and we derive a steady state value of fgas (perylene) = 3.2−32.6 × 10−9 fsolid (perylene).
At AV ≈ 5, that is, ζ ≈ 4 × 10−17 s−1, for perylene, 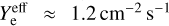 , we derive a steady state value of fgas (perylene) = 3.0−4.0 × 10−8 fsolid (perylene). In the latter case, the extinction is sufficiently high that most of the dust grains are covered by ice mantles. In this case, if the fractional abundance of PAH is low enough within the mantle, we can consider the effective sputtering yield of the ice matrix. Therefore,
, we derive a steady state value of fgas (perylene) = 3.0−4.0 × 10−8 fsolid (perylene). In the latter case, the extinction is sufficiently high that most of the dust grains are covered by ice mantles. In this case, if the fractional abundance of PAH is low enough within the mantle, we can consider the effective sputtering yield of the ice matrix. Therefore, 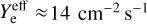 (evaluated from Dartois et al. 2015, including the prefactor of two for the cosmic-ray entrance and exit from the grain), and we derive a steady state value of fgas (perylene) = 3.4− 4.7 × 10−7 fsolid (perylene).
(evaluated from Dartois et al. 2015, including the prefactor of two for the cosmic-ray entrance and exit from the grain), and we derive a steady state value of fgas (perylene) = 3.4− 4.7 × 10−7 fsolid (perylene).
If we now extend the calculation to a parent molecule such as naphthalene, and assume it to be embedded in water ice, assuming a photodissociation rate of 1.7 × 10−10 s−1 based on Allain et al. (1996) yields fgas (naphthalene) = 1.9− 3.2 × 10−7 fsolid (naphthalene).
An observed abundance of fgas (naphthalene) ≈ 2 × 10−10 as recently detected by McGuire et al. (2021) implies that the minimum required fraction of napthalene in the ice mantle would be of the order of 6.1 × 10−4−1.1 × 10−3.
 |
Fig. 5 Calculated sputtering rate versus ionisation rate from Eq. (7) using the prescription presented in this work for perylene (C20H12, in red) and coronene (C24H12, in yellow). The filled region delimited by dashed lines shows the expected range of variations based on the uncertainties in the measurements. The upper x-axis gives the approximate visual extinction in a dense cloud corresponding to the ionisation rate of the lower x-axis, assuming an ionisation rate of 3 × 10−16 s−1 outside the cloud and based on observed cosmic-ray ionization rate attenuation with the visual extinction (e.g. Wakelam et al. 2021; Neufeld & Wolfire 2017; Indriolo & McCall 2012). |
 |
Fig. 6 Destruction timescale for solid perylene, using our measurement as an anchor point and assuming a dependency of the cross-section on the function of the stopping power evolving with a power law with an exponent β comprised between 1 and 1.5. |
5 Summary and outlooks
Irradiation experiments at different ion facilities allowed us to simulate cosmic-ray effects of energetic particles in the electronic stopping power regime for the PAHs perylene and coronene. The sputtering yields were measured experimentally and applied to a Galactic cosmic ray model propagated to dense cloud interfaces.
For perylene or coronene, eventually substituted by a chemical group acting as an antenna leading to a much lower astrophysical detection limit, such as a nitrile group, observable column densities in the radio domain are not expected to be below fgas ~ 10−10nH. The cosmic-ray-induced thermal spike sputtering from dust grains would require very high fractional abundances in the solid phase to explain such high gas phase abundances.
Very high naphthalene gas phase abundances are suggested as an initial condition at early evolutionary times based on an astrochemical model from the gas phase to back the observation of cyanonaphthalene species abundances. In such models, naphthalene gas phase abundance must be several orders of magnitude higher (fgas (naphthalene) ≈ 10−7). This would imply a very challenging, high fraction of such species locked in the solid phase if cosmic-ray sputtering in the electronic regime is responsible for their reinjection.
At steady state, we estimate that if the abundance of naphthalene were of the same order of magnitude as that of the recently observed cyanonaphthalene (≈2 × 10−10nH), it could be explained by the sputtering from naphthalene embedded in water ice mantle with an ice fractional abundance in the range of 10−3−10−4. An order of magnitude lower may still be viable, but to reach such abundances from much lower fractions in the solid phase would require extremely efficient reinjection mechanisms or more volatile ice mantles.
Acknowledgements
Part of the equipment used in this work has been financed by the French INSU-CNRS program “Physique et Chimie du Milieu Interstellaire” (PCMI). The results presented here are partly based on a UMAT experiment, which was performed at the M-branch of the UNILAC at the GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt (Germany) in the frame of FAIR Phase-0.
Appendix A Calibration
This Appendix displays the calibration of the quartz microbalance response performed using PAH-coated quartz crystals combined with IR measurements. Figures A.1 and A.2 show the reflectance spectra of several perylene and coronene coated gold quartz crystals. The thickness of the films was measured based on the interference fringes recorded in reflectance in the IR:
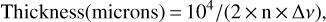 (A.1)
(A.1)
where Δv is the interference fringe period in cm−1 and n denotes the refractive index of the film. We assume a refractive index of n = 1.7 ± 0.15 for perylene (Buckman & Bomberger 1973) and coronene (Cherchneff et al. 1991) films. The measured quartz cell frequency shift as a function of the measured film thickness is reported in Fig.A.3. From the slope of this curve (−1.12 ± 0.22 × 104 Hz/μm) we can estimate the sensitivity of the measurements, as explained in the core of the article.
 |
Fig. A.1 Reflectance spectra of perylene films, recorded on the gold-coated quartz crystal. The spectra are shifted for clarity by increasing thickness. The interference fringe frequencies increase with thickness. |
 |
Fig. A.2 Reflectance spectrum of coronene film recorded on the gold-coated quartz crystal. |
 |
Fig. A.3 Quartz cell frequency calibration against perylene (red hexagons) and coronene (yellow squares) film thicknesses. The bare quartz frequency is set to zero. The range for the uncertainty, shown in light red, includes an estimate of the error bar on the linear fit plus an error on the true thickness. |
References
- Allain, T., Leach, S., & Sedlmayr, E. 1996, A&A, 305, 602 [NASA ADS] [Google Scholar]
- Bacri, C.-O., Bachelet, C., Baumier, C., et al. 2017, Nucl. Instrum. Methods Phys. Res. B, 406, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Boduch, P., Dartois, E., de Barros, A. L. F., et al. 2015, J. Phys. Conf. Ser., 629, 012008 [Google Scholar]
- Breuer, L., Meinerzhagen, F., Herder, M., et al. 2016, J. Vac. Sci. Technol. B, 34, 03H130 [CrossRef] [Google Scholar]
- Buckman, A. B., & Bomberger, W. D., 1973, JOSA, 63, 1432 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., Agúndez, M., Cabezas, C., et al. 2021, A&A, 649, L15 [EDP Sciences] [Google Scholar]
- Chabot, M. 2016, A&A, 585, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cherchneff, I., Barker, J. R., & Tielens, A. G. G. M. 1991, ApJ, 377, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Dartois, E., Ding, J. J., de Barros, A. L. F., et al. 2013, A&A, 557, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dartois, E., Augé, B., Boduch, P., et al. 2015, A&A, 576, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dartois, E., Chabot, M.I.D., Barkach, T., et al. 2018, A&A, 618, A173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Nolfo, G. A., Moskalenko, I. V., Binns, W. R., et al. 2006, Adv. Space Res., 38, 1558 [Google Scholar]
- George, J. S., Lave, K. A., Wiedenbeck, M. E., et al. 2009, ApJ, 698, 1666 [Google Scholar]
- Godard, M., Féraud, G., Chabot, M., et al. 2011, A&A, 529, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haynes, W. M., Lide, D.R., & Brunoet, T.J. 2016, CRC Handbook of Chemistry and Physics, 97th edn. (CRC Press) [Google Scholar]
- Indriolo, N., & McCall, B. J. 2012, ApJ, 745, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, R. E., Carlson, R. W., Cassidy, T. A., & Fama, M. 2013. The Science of Solar System Ices (New York, NY: Springer), 551. [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. P., Köhler, M., Ysard, N., et al. 2017, A&A, 602, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [Google Scholar]
- Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 500, 259 [NASA ADS] [Google Scholar]
- McGuire, B. A., Loomis, R. A., Burkhardt, A. M., et al. 2021, Science, 371, 1265 [Google Scholar]
- Neufeld, D. A., & Wolfire, M. G. 2017, ApJ, 845, 163 [Google Scholar]
- Padovani, M., Galli, D., & Glassgold, A. E. 2009, A&A, 501, 619 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prasad, S. S., & Tarafdar, S. P. 1983, ApJ, 267, 603 [Google Scholar]
- Rothard, H., Domaracka, A., Boduch, P., et al. 2017, J. Phys. B At. Mol. Phys., 50, 062001 [Google Scholar]
- Shen, C. J., Greenberg, J. M., Schutte, W. A., & van Dishoeck, E. F. 2004, A&A, 415, 203 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thrower, J. D., Friis, E. E., Skov, A. L., et al. 2013, J. Phys. Chem. C 117, 13520 [NASA ADS] [CrossRef] [Google Scholar]
- Trautmann, C., Boccanfuso, M., Benyagoub, A., et al. 2002, Nucl. Instrum. Methods Phys. Res. B, 191, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., Dartois, E., Chabot, M., et al. 2021, A&A, 652, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, J. Z., Seo, E. S., Anraku, K., et al. 2002, ApJ, 564, 244 [Google Scholar]
- Webber, W. R., & Yushak, S. M. 1983, ApJ, 275, 391 [Google Scholar]
- Ziegler, J. F., Ziegler, M. D., & Biersack, J. P. 2010, Nucl. Instrum. Methods Phys. Res. B, 268, 1818 [Google Scholar]
All Tables
Summary of ion properties including the total kinetic energy, the electronic energy loss (Se), the ion range assuming a film density of 1.35 g cm−3 for perylene and 1.37 g cm−3 for coronene (Haynes et al. 2016), and nuclear-to-electronic energy loss ratio (Sn/Se).
All Figures
 |
Fig. 1 Experimental setups: (a) thin film holder showing interference fringes after deposition. The quartz is placed at the center of the holder. (b) Load lock system with manipulator for changing coated quartz crystals. (c) View of the setup mounted on the ARAMIS beam line. (d) View of the samples in the irradiation chamber at M3-beamline of the GSI M-branch including the microbalance and movable IR window. |
| In the text | |
 |
Fig. 2 Frequency shifts Δν recorded as a function of fluence in the various QCM experiments. The irradiation was performed with 1.5 MeV N+ ions using quartz coated with thin and thick films with respect to the ion range as well as bare quartz as a blank reference. Left: perylene, right: coronene. Solid lines are fits to the data using Eq. (2). |
| In the text | |
 |
Fig. 3 Infrared spectra of a thin film of perylene irradiated with 48Ca+ ions recorded before irradiation (in blue) and after a fluence of 2.8 × 1012 ion cm−2 (in red). Insert: evolution of the integrated optical depth of the C=C IR band at ~1495 cm−1, normalised to the initial film prior to irradiation. The solid line is an exponential fit of the destruction cross-section (Eq. (6)) to the data, the dashed lines represent ±3σ with respect to the best fit. |
| In the text | |
 |
Fig. 4 Infrared spectra of a thin film of coronene (in blue) irradiated with a 48Ca beam recorded at different fluences. Insert: evolution of the integrated optical depth of the C=C IR band at ~1315 cm−1, normalised to the initial film prior to irradiation. The solid line is an exponential fit of the destruction cross-section (Eq. (6)) to the data and the dashed lines represent ±3σ with respect to the best fit. |
| In the text | |
 |
Fig. 5 Calculated sputtering rate versus ionisation rate from Eq. (7) using the prescription presented in this work for perylene (C20H12, in red) and coronene (C24H12, in yellow). The filled region delimited by dashed lines shows the expected range of variations based on the uncertainties in the measurements. The upper x-axis gives the approximate visual extinction in a dense cloud corresponding to the ionisation rate of the lower x-axis, assuming an ionisation rate of 3 × 10−16 s−1 outside the cloud and based on observed cosmic-ray ionization rate attenuation with the visual extinction (e.g. Wakelam et al. 2021; Neufeld & Wolfire 2017; Indriolo & McCall 2012). |
| In the text | |
 |
Fig. 6 Destruction timescale for solid perylene, using our measurement as an anchor point and assuming a dependency of the cross-section on the function of the stopping power evolving with a power law with an exponent β comprised between 1 and 1.5. |
| In the text | |
 |
Fig. A.1 Reflectance spectra of perylene films, recorded on the gold-coated quartz crystal. The spectra are shifted for clarity by increasing thickness. The interference fringe frequencies increase with thickness. |
| In the text | |
 |
Fig. A.2 Reflectance spectrum of coronene film recorded on the gold-coated quartz crystal. |
| In the text | |
 |
Fig. A.3 Quartz cell frequency calibration against perylene (red hexagons) and coronene (yellow squares) film thicknesses. The bare quartz frequency is set to zero. The range for the uncertainty, shown in light red, includes an estimate of the error bar on the linear fit plus an error on the true thickness. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![${\sum _{{\rm{grains}}}}\left[ {{\rm{c}}{{\rm{m}}^2}{{\rm{H}}^{ - 1}}} \right] = {1 \over {{n_{\rm{H}}}}}{\rm{ }}\smallint {\rm{ d}}a{\rm{ }}\pi {a^2}{\rm{ }}{{{\rm{d}}n} \over {{\rm{d}}a}}.$](/articles/aa/full_html/2022/07/aa43274-22/aa43274-22-eq21.png)