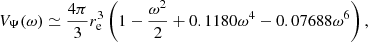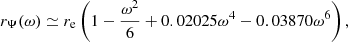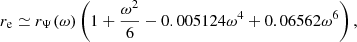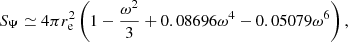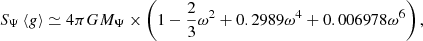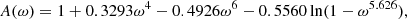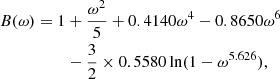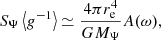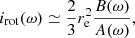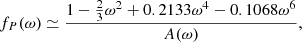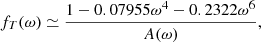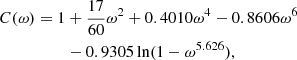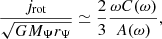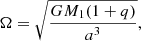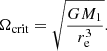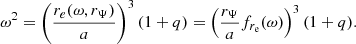| Issue |
A&A
Volume 661, May 2022
|
|
|---|---|---|
| Article Number | A123 | |
| Number of page(s) | 12 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202243094 | |
| Published online | 16 May 2022 | |
Modeling overcontact binaries
I. The effect of tidal deformation
Institute of Astronomy (IvS), KU Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
e-mail: matthias.fabry@kuleuven.be
Received:
12
January
2022
Accepted:
14
February
2022
Context. In the realm of massive stars, strong binary interactions are commonplace. One extreme case is that of overcontact systems, which are expected to be part of the evolution of all stars evolving towards a merger and hypothesized as playing a role in the formation of binary black holes. However, important simplifications are made to model the evolution of overcontact binaries. The deformation from tidal forces is almost always put aside, and even rotation is frequently ignored in such models. Yet, both observations and theory have shown that overcontact stars are tidally deformed to a great extent, leaving a potentially important effect on the outer layers unaccounted for in models. Furthermore, in eclipsing binaries where radii can be determined to high precision, the question of how large the effect of tidal deformation is on the inferred properties of stellar models is still uncertain.
Aims. We aim to consistently model overcontact binary stars in a one-dimensional (1D) stellar evolution code. To that end, we developed the required methodology to represent tidally distorted stars in 1D evolution codes.
Methods. Using numerical methods, we computed the structure correction factors to the 1D spherical stellar structure equations of hydrostatic equilibrium and radiative energy transfer due to the binary Roche potential. We then compared them to existing results and the structure corrections of single, rotating stars. We implemented the new structure correction factors in the stellar evolution code MESA and explored several case studies. We compared the differences between our simulations: when no rotation is included, when we treat rotation using single star corrections (only accounting for centrifugal deformation), or when we use tidal deformation.
Results. We find that ignoring rotation in deformed detached eclipsing binaries can produce a radius discrepancy of up to 5%. The difference between tidal and single star centrifugal distortion models is more benign at 1%, showing that single rotating star models are a suitable approximation of tidally deformed stars in a binary system. In overcontact configurations, we find a similar 5% variation in surface properties as a result of tidal distortion with respect to non-rotating models, showing that it is inappropriate to model binary stars filling their Roche lobe significantly as non-rotating.
Key words: binaries: close / stars: evolution
© ESO 2022
1. Introduction
Massive stars (Minitial ≳ 8 M⊙) give rise to a multitude of astrophysical phenomena on the stellar to the galactic scale. Binarity is responsible for several of these and it is expected that the vast majority of massive stars are in binary systems that interact during their lifetime (Vanbeveren et al. 1998; Sana et al. 2012), these effects cannot be ignored. Furthermore, population synthesis calculations predict that about a quarter of all O-type stars will merge with its companion (Sana et al. 2012). Stellar mergers are thought to be responsible for strong magnetism in massive stars (Ferrario et al. 2009; Wickramasinghe et al. 2014; Schneider et al. 2016, 2019) and are a potential source of the high rotation needed in models of long-duration gamma-ray bursts (Yoon & Langer 2005; Yoon et al. 2006; Aguilera-Dena et al. 2018) and superluminous supernovae (Justham et al. 2014; Aguilera-Dena et al. 2020). As mergers are preceded by an overcontact phase, understanding the properties of an overcontact model can give crucial insights into the merger process itself and the transients associated with them, or, in a broader sense, into the question of whether the merger happens at all.
In the past, a significant effort has been undertaken to observe and model the low-mass overcontact binaries known as W Ursae Majoris (W UMa) binaries. These systems have short periods of less than a day and total masses on the order of 1 M⊙. From the observational side, surveys from Eggen (1967) and Binnendijk (1970) characterized the masses and mass ratio of the first identified W UMa systems and, most notably, they found that the majority of them have unequal mass components. Later, over a thousand low-mass, near-contact or overcontact binaries were found based on the light curve analysis of OGLE-I survey data (Szymanski et al. 2001). Extensive studies have aimed to characterize the population of W UMa binaries and identify systems that are expected to merge (Gazeas et al. 2021). Recently, more and more massive overcontact binaries have been identified, the most massive of which, VFTS 352 (Almeida et al. 2015), has components over 30 M⊙.
The fact that a large number of unequal overcontact binaries were observed challenged the argument from Kuiper (1941), who stated that overcontact stars cannot be stable; however, it was shown by Lucy (1968) that for the convective envelopes of W UMa binaries, this argument does not apply and they constructed an approximate model of a low-mass overcontact binary. Shu et al. (1976) expanded on these models and argued there must be significant energy transport in the innermost overcontact layers between both components. However, the theory of overcontact models of massive stars with radiative envelopes has not yet been well developed.
In the context of gravitational wave astrophysics, massive overcontact binaries have been proposed as progenitors of merging binary black holes (BBH) (Marchant et al. 2016; Mandel & de Mink 2016), as tidal synchronization leads to rapid rotation and enhanced rotational mixing (de Mink et al. 2009). Recently, new analysis techniques of observations have allowed for an improved characterization of the components of a massive overcontact binary (Palate et al. 2013; Abdul-Masih et al. 2020, 2021). Such observations give critical constraints to evolutionary models that try to explain the evolution of overcontact systems on their way to BBH mergers. However, to model these strongly interactive systems, important approximations need to be made (Marchant et al. 2016; Menon et al. 2021). Even though orbital evolution, tidal torques and mass transfer by Roche lobe (RL) overflow is usually taken care of, whereas the tidal deformation of the stellar structure from a binary companion or energy transfer in overcontact layers are ignored.
Since centrifugal forces introduce a latitudinal dependence and tidal forces an additional azimuthal one, in order to properly compute stellar models for single rotating or binary stars, the stellar structure equations would need to be recast and solved in 2D or 3D, respectively. From a computational standpoint, doing full 3D stellar evolution is not feasible with current resources, so simplifying assumptions need to be made in order to remain in 1D. Kippenhahn & Thomas (1970) introduced a methodology to correct the spherical stellar structure equations to account for deformation from the spherical geometry by rotation, which was later extended by Endal & Sofia (1976). This method is built on the premise that hydrostatic layers of stars fall on equipotential surfaces of the system. For single star rotation, this method has been implemented in the stellar evolution code Methods for Experiments in Stellar Astrophysics (MESA, Paxton et al. 2011, 2013, 2015, 2018, 2019). Currently, these single star corrections are also called upon when using the code to evolve binary stars. This means that while the centrifugal deformation from stellar rotation is accounted for, tidal deformation as a result of a nearby companion is not.
In this first paper of a three-part series, we apply the method of Kippenhahn & Thomas (1970) and Endal & Sofia (1976) to synchronized binary stars, as a first step in consistently modeling tidally deformed stars. The problem of energy transfer in overcontact layers will be studied in the next paper of this series. Still, the methods developed here are applicable to model twin overcontact binaries (binaries of mass ratio unity), where no energy is transferred between components, as well as for very close detached and semi-detached systems that are tidally synchronized. In Sect. 2, we calculate the modified 1D stellar structure equations in a conservative potential and compute the structure correction factors fP and fT for a Roche binary. In Sects. 3 and 4, we consider the Eddington limit and boundary conditions as appropriate to the modified equations, respectively. Section 5 shows stellar models computed using the MESA code comparing currently implemented physics with the new methods in representative case studies. Lastly, Sect. 6 presents our final remarks. All the input files needed to reproduce the results and associated data products in this paper can be downloaded from the Zenodo data repository1.
2. Methods
2.1. Modifications to the spherical stellar structure equations
In non-rotating stars, the equations of stellar structure and evolution are solved in a 1D space of the radius, r, or mass coordinate, M, and assume spherically symmetric stellar shells. As such, the equation of mass continuity takes the following form:
with ρ as the density at radius, r, and M = M(r) as the total mass interior to r. The equation of hydrostatic equilibrium is written as follows:
where P is the total pressure and G the gravitational constant. Finally, in radiative regions of a star, the energy transport is described by:
with L as the luminosity, T the gas temperature, κ the local opacity, a the radiation constant, and c the speed of light. However, several physical effects can break the spherical symmetry that is assumed when calculating 1D stellar evolution models. Centrifugal forces introduce a latitudinal dependence and a binary companion introduces an additional azimuthal dependence. Yet, if the total potential Ψ, which is the sum of all gravitational and rotational contributions, is conservative, Kippenhahn & Thomas (1970) showed that such effects can be accounted for in 1D equations. The only assumption that remains is the one of shellularity: We assume that stellar isobars exactly coincide with equipotential surfaces of the given geometry, therefore, the total pressure, P, is constant at constant Ψ. von Zeipel (1924) showed that in hydrostatic equilibrium, a solidly rotating stellar shell has all its thermodynamical quantities, including T and ρ, remaining constant along isobars. However, he also showed that in this case, the stellar shell cannot be in radiative thermal equilibrium. Therefore one expects a deviation from shellularity coupled with large scale meridionial flows (Eddington 1925; Sweet 1950). Still, large horizontal flows are also present, keeping the rotation of isobars near to solid (Zahn 1992), so that the star is kept approximately shellular.
Instead of spherically symmetric stellar shells, we write the equations of stellar structure in terms of these equipotentials surfaces, which can be characterized by a single independent variable and thus be appropriate for 1D stellar evolution. Here, we summarize the model of Endal & Sofia (1976, henceforth ES) that cast the equations of stellar structure in 1D given a conservative potential Ψ. This potential can, for example, be the Roche potential of a single rotating star (Sect. 2.2) or of a binary star (Sect. 2.3).
We start by defining rΨ as the equivalent radius of a sphere enclosing the same volume VΨ enclosed by an equipotential surface:
Hence, as the spherical relation from radius to volume is retained and the mass density, ρ, is assumed constant over an equipotential, the equation of continuity is unaffected:
where MΨ is the total mass enclosed by the equipotential. The variable rΨ (or MΨ in a Lagrangian prescription) goes on to act as the new independent variable to describe stellar models.
Next, we denote with g the magnitude of the effective gravity at each point in space:
with dn being the distance between potential surfaces Ψ and Ψ + dΨ. Considering then a change in equipotential volume, we have:
where SΨ is the surface area of the equipotential, and we defined for convenience, the average of a quantity f over an equipotential as:
Continuing from Eq. (8), we have
which, along with the statement of hydrostatic equilibrium ∇P = −ρ∇Ψ gives the modified momentum equation:
with the correction to the standard spherical equation contained in the factor
This factor thus measures the strength of the pressure gradient acting on a deformed shell (as a result of the non-spherical potential) with respect to a spherical shell enclosing the same volume and mass.
Similarly to the mass continuity equation, the equation of energy conservation retains its spherical form as mass, radius, and volume relate to each other spherically, hence,
where LΨ is the energy flowing through the equipotential per unit time, ϵ is the (specific) nuclear energy generation rate, U the specific internal energy, and t is time.
Considering lastly the equation of energy transport through radiative layers of the star, we have for the radiative flux:
by the chain rule. Equation (14) is to the von Zeipel theorem (von Zeipel 1924), stating that the radiative flux ℱ is proportional to the local effective gravity g = |∇Ψ|. Taking then the integral over an equipotential surface:
using the previous results, namely, Eqs. (6), (9), and (10). Rewriting this using (11) and (12) transforms this into the usual spherical-like form of radiative energy transport:
with the second correction factor to the spherical equations being
Similarly to fP (Eq. (12)), the correction fT/fP measures the strength of the radiative gradient of a deformed stellar shell relative to that of a spherical shell of the same volume and enclosed mass.
2.2. Single star rotation
A stellar shell rotating with angular velocity Ω exterior to a mass M has a total potential defined by
where θ is the polar angle and Φ is the gravitational potential due to the mass interior to the shell. Since stars, especially massive ones with radiative envelopes, are heavily condensed toward their centers, significant deformation from spherical symmetry is only expected in the outermost layers, justifying that the gravitational potential Φ of the star is taken as 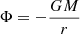 of a point mass, with M as the total mass of the star.
of a point mass, with M as the total mass of the star.
Paxton et al. (2019) calculated analytical approximations to the corrections, fP and fT, and provided polynomial fits for these as a function of the variable 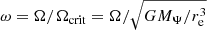 , with re the equatorial radius of the shell. In Appendix A, we provide new, more accurate fits without increasing the degree of the polynomial expansions.
, with re the equatorial radius of the shell. In Appendix A, we provide new, more accurate fits without increasing the degree of the polynomial expansions.
2.3. Synchronized Roche binaries
We expect that tidal torques in binary systems are very sensitive to the separation of components (Zahn 1975), causing stars that significantly fill their RL to be synchronized with their orbits. Therefore, the total potential of these systems is the well-known Roche potential and may be written in the corotating frame as follows:
where Φ is the gravitational contribution due to the two component stars, a their separation, while the second term represents the centrifugal contribution of the synchronous rotation around the center of mass. We employ the same reasoning as in Sect. 2.2 to approximate the gravitational potential Φ by point mass potentials of mass M1 and M2, that is, the total masses of the component stars. Finally, defining the mass-ratio q = M2/M1, normalizing all distances r → r/a and shifting 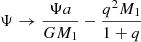 , we arrive at the dimensionless form of the potential in spherical coordinates:
, we arrive at the dimensionless form of the potential in spherical coordinates:
where r2 = x2 + y2 + z2, r sin θ cos ϕ = x, r sin θ sin ϕ = y and r cos θ = z relate to the Cartesian frame, and  . In Fig. 1, we show an illustration of the Roche geometry in the equatorial plane and highlight the colinear Lagrangian point equipotentials.
. In Fig. 1, we show an illustration of the Roche geometry in the equatorial plane and highlight the colinear Lagrangian point equipotentials.
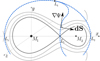 |
Fig. 1. Illustration of the Roche geometry in the equatorial plane. It shows the L1, L2, and L3 equipotentials (gray), as well as the splitting surfaces (blue dashed). The splitting surfaces have their normals always perpendicular to the potential gradient. |
2.4. Overcontact shells
In the context of 1D evolution models, we have to distinguish the two stellar components within the geometry of a Roche binary. For equipotential shells lying within their respective RLs, this is trivial, as such layers are physically separated, but shells in overcontact are shared between the two stars. We therefore construct three “splitting surfaces”, one through each of the colinear Lagrangian points L1, L2, and L3, separating the Roche geometry in three main parts. This will ensure distinction between the two components, as well as either from regions beyond the outer Lagrangian points L2 and L3, from which outflows are expected if any component overflows them. We construct them in such a way that the condition:
holds on all points of these splitting surfaces (see Fig. 1, in blue dashed lines), such that the surface normal is always perpendicular to the gradient of the potential (20). We note that by our construction of the splitting surfaces, the scalar product dn ⋅ dS is zero. This ensures that Eq. (7) still holds, and if the overcontact layers are shellular, there is no net flux of radiative energy between the components following Eq. (14) However, since the condition of shellularity cannot be held exactly, there will exist a flow LΨ, trans = ∫dΨ[BOLD]ℱ ⋅ dSsplit across equipotentials, representing energy transfer from one component to the other. In this work, we assume this contribution is zero and defer the modeling of energy transfer to later work. We note also that in the case q ≠ 1, the L1 splitting surface is not a vertical plane through L1, which differentiates our results of equipotential volumes and surface areas from those of Mochnacki (1984) and Marchant et al. (2021).
2.5. Numerical calculations
In order to use the modified stellar structure equations in a stellar evolution code, we require for each shell in the geometry the quantities VΨ, SΨ, ⟨g⟩ and ⟨g−1⟩ which specify rΨ, fP and fT of Eqs. (4), (12), and (17). Additionally, the specific moment of inertia, irot, is needed to calculate the rotational velocity of the equipotential shell from the angular momentum: ΩΨ = jrot/irot. We approach this problem using numerical methods. First of all we note that the problem is symmetric under y → −y and z → −z, so we need only explicitly do calculations in the quadrant of positive y and z.
Given a set of mass ratios, q, and target equipotential values, Ψ0, we calculate, in a spherical coordinate system on rays of constant (θ, ϕ), the points r = r(θ, ϕ) that lie on the corresponding equipotential surface, such that:
When solving Eq. (22), care has to be taken in order to avoid roots beyond the splitting surfaces (Sect. 2.4), as these belong to a part the geometry not associated to the considered component star, and would instead belong to the other component or to the region beyond the outer Lagrangian points. We therefore restrict the solver to values r smaller than the value rsplit(θ, ϕ) on the splitting surface that the ray (θ, ϕ) crosses. If it finds no roots in the interval (0, rsplit), rsplit is recorded instead as the splitting surfaces mark the maximal extent of the components.
Next, for these points r(θ, ϕ), we numerically integrate the following quantities:
where the 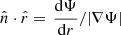 and we used the notation dmΨ = ρdndS to signify a small mass element within the equipotential shell, such that dMΨ = ∫ΨdmΨ. From these, fP and fT can be computed for each equipotential shell with Eqs. (12) and (17).
and we used the notation dmΨ = ρdndS to signify a small mass element within the equipotential shell, such that dMΨ = ∫ΨdmΨ. From these, fP and fT can be computed for each equipotential shell with Eqs. (12) and (17).
2.6. Integration results
We consider the component of a Roche binary at the origin with mass M1 and a companion with mass M2, and we computed all the necessary integrals of Eqs. (23)–(27) in the two-dimensional parameter space of mass ratio q ≡ M2/M1 and Roche equipotentials, Ψ0. We emphasize here that we calculate solely the properties of the component with mass M1 and that the properties of the companion M2 can be obtained by inverting the mass ratio. We sampled 280 equally spaced mass ratios in logarithmic space in the interval log q ∈ [ − 7, 7], as well as the equal mass ratio log q = 0 case while in potential space, we sampled 158 values in several logarithmic ranges from Ψ0 = 50ΨL1 to 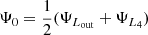 of different densities. With Lout we denote the outer Lagrangian point of the considered component of the binary (always having xLout < 0, which is L3 if q ≤ 1 and L2 if q ≥ 1). As quantities exhibit important variations around the overflow potentials ΨL1 and ΨLout, those will be the regions we sample more densely. We note that ΨL1 < ΨL2 ≤ ΨL3 < ΨL4 = ΨL5 as in our convention Ψ is strictly negative.
of different densities. With Lout we denote the outer Lagrangian point of the considered component of the binary (always having xLout < 0, which is L3 if q ≤ 1 and L2 if q ≥ 1). As quantities exhibit important variations around the overflow potentials ΨL1 and ΨLout, those will be the regions we sample more densely. We note that ΨL1 < ΨL2 ≤ ΨL3 < ΨL4 = ΨL5 as in our convention Ψ is strictly negative.
Figure 2 shows the integration results of fP for various mass ratios as a function of their radius relative to the RL radius rΨ/rRL, where we defined rΨL1 ≡ rRL. We observe discontinuities at the Lagrangian overflow points, which is a result of the splitting surfaces limiting the considered volume to one component (Fig. 1). For a comparison with the single rotating star deformation model, we overplot the equivalent fP values as if the binary star was interpreted as a single rotating star with the same volume and rotational velocity (see Appendix B for details).
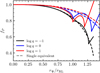 |
Fig. 2. Structure correction factor fP as a function of fractional RL radius rΨ/rRL for various mass ratios. The discontinuities in all graphs correspond to the crossing of the Lagrangian points L1 (at rΨ/rRL = 1, by construction) and Lout at larger radii. For reference, the equivalent single rotating star inferred fP is overplotted in dashed lines. |
2.7. Comparison to literature
As verification of our integrations, we compare our results to calculations performed by Mochnacki (1984). As this study considered vertical splitting surfaces through L1 at all mass ratio’s, for overcontact layers we are limited to comparing the mass ratio unity case. Figure 3 shows excellent agreement between our fP values and those computed via Eq. (12) using the results from Mochnacki (1984), with the relative difference being less than about 1 part in 103. A resolution convergence test of our integrations show our calculations converge to the 10−5 level at eight times our original default resolution. The final computations of all integrals for use in stellar evolution instruments are done with this eight-fold resolution increase, and corresponds to dividing the interval ϕ = [0, π] in nϕ = 5280 parts and cos θ = [0, 1] in nθ = nϕ/2 parts so that Δϕ = π/nϕ and Δ cos θ = 2/nϕ.
 |
Fig. 3. Comparison of the calculations of the structure correction factor fP from Mochnacki (1984) and those in this work, as a function of the fractional RL radius rΨ/rRL. We performed a resolution convergence test with double, quadruple and octuple the default spacial resolution, and conclude our integrations have well converged at an eight-fold resolution increase. |
3. The ΩΓ limit
Thanks to the radiation pressure of the photon flux generated in the core, a star gains radiative support against its self-gravity. In the situation where these effects are canceled out exactly, the star has reached the Eddington limit, which is given as (for a single, non-rotating and thus spherical star):
Defining then the Eddington factor Γ as:
with Lrad the radiative luminosity, equal to L in a radiative envelope, Γ = 1 is then an equivalent statement of the Eddington limit. If Γ > 1, the sum of radiative and gravitational acceleration is directed outward. In the interior of the star this can in principle be compensated by an inversion of the gas pressure (Joss et al. 1973), but if a star approaches Γ = 1 at the surface, strong outflows are expected to develop (Gräfener et al. 2011).
After adding a centrifugal contribution to the force balance, we have:
where we write g = ∇Ψ as the effective gravity. Langer (1997) then considered the Eddington limit on the equator of a rotating (but non-deformed) star, and, assuming that the radiation field is isotropic, the radiative flux is ℱ = L/4πR2, so that the force balance reduces to
where we have defined ω = Ω/Ωcrit, class as the fractional classical critical rotation rate 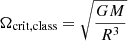 . It is important to make the distinction here as the formal critical velocity is lowered to:
. It is important to make the distinction here as the formal critical velocity is lowered to:
Therefore, the closer a star is to the Eddington limit, the lower the critical velocity will be.
Maeder & Meynet (2000) later noted that this treatment does not take von Zeipel’s theorem into account, namely that the radiative flux is dependent on local effective gravity, Eq. (14). Expressing this for a rotating star to lowest order in rotational velocity Ω gives
where ϑ signifies a polar dependence and ΓΩ ≡ Γ × f(Ω, ϑ) is now a rotation-dependent Eddington factor. Since the strength of the radiative flux is a function of the effective gravity through the von Zeipel effect, Maeder & Meynet (2000) showed that, neglecting the ϑ dependence, Eq. (33) bifurcates when Γ = 0.639. Below this, g = 0 is the only solution, so that, independent of luminosity, the break up velocity is the classical velocity 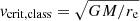 , with re the equatorial radius of the rotating star. Above the bifurcation point, both g = 0 and, importantly,
, with re the equatorial radius of the rotating star. Above the bifurcation point, both g = 0 and, importantly,
determine the critical velocities, the second of which is lower than the classical critical velocity. The lowest of these two velocities then determines the physical break-up velocity of a rotating star.
We further expand on the notion of break-up limits by considering the case of deformed stars due to a conservative potential. As a starting point, we consider the same criterion of zero net acceleration, gtot = 0, as the stability boundary. The contributions to this acceleration are the effective gravity, g, as a result of the potential, and the radiative acceleration. Using von Zeipel’s expression for radiative flux (Eq. (14)), and combining with the equation of hydrostatic equilibrium results in:
which, upon using Eq. (16) as the radiative gradient in the non-spherical geometry, gives the stability criterion:
We recognize however that von Zeipel’s law of radiation can break down close to critical velocity due to significant baroclinicity, that is, departure from shellularity (see for example Espinosa Lara & Rieutord 2011). Continuing on our assumption of shellularity, Eq. (36) is of a very similar form as that of Maeder & Meynet (2000), namely, g(1 − ΓΨ) = 0, where ΓΨ = Γ × f is again a product of the classical Eddington factor with a function dependent on the geometry. For the single rotating star deformation, f = f(ω), dependent on the fractional critical rotation rate, while in the tidal deformation case of f = f(rψ/rRL, q), dependent on the mass ratio and degree of Roche filling. In Eq. (36), the classical solution g = 0 is present of course, where the effective gravity vanishes as a result of rotational support only. As above, in this case there is no corresponding Eddington luminosity as it is independent of any radiative acceleration due to the Von Zeipel effect. The other solution is given by:
which translates to a modified expression of the Eddington luminosity:
or the Eddington factor (see also Sanyal et al. 2015):
These expressions, as in the case of the equations derived in Sect. 2.1, are applicable in any conservative potential Ψ.
As the criteria for instability, Eqs. (31), (34), and (37) all express a departure of the Eddington limit of a star from the classical Eddington limit of Γ = 1. In the model developed here, it amounts to a reduction of the maximal Eddington factor by the ratio fP/fT, which is smaller than one in both the single rotating star or synchronized binary case. In Fig. 4, we show the comparison of this reduction from the results of Langer (1997) to this work in the case of a single rotating star. Moreover, consistent to Maeder & Meynet (2000), we find a bifurcation in the critical rotation velocity at at Γ = 0.639. Below this number, only the classical critical velocity ω = 1 will make the star unstable, while above it, this velocity is reduced. The case of a synchronized Roche binary is shown in Fig. 5. For example, an equal mass ratio binary overflowing to its outer Lagrangian point has its Eddington limit reduced to about 84% its classical value.
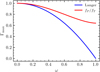 |
Fig. 4. Maximal Eddington factor Γmax that a rotating star can have as a function of fractional classical critical rotation rate of ω = Ω/Ωcrit, class. Our model of shellular stars has a maximal reduction to Γmax = 0.639. |
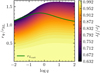 |
Fig. 5. Reduction, fP/fT, of the maximal Eddington factor as a function of mass ratio, q, and fractional overflow radius, rΨ/rRL. The equivalent radius of a star filling up to its outer Lagrangian point in marked with the green line. |
4. Atmospheric boundary conditions
The equations of stellar structure must be supplied with appropriate boundary conditions (BCs) at the center and atmosphere of the star. In the center, the conditions are such that r = M = L = 0, which transform to rΨ = MΨ = LΨ = 0 in our equipotential shell model. At the surface, an atmosphere model is integrated to supply the pressure Psurf and temperature Tsurf. A common choice is the so called gray Eddington atmosphere, which is a plane parallel model integrated from τ = 0 to some predetermined atmospheric optical depth τsurf, and is presented in, for example, Cox & Giuli (1968, henceforth CG).
In spherical stars, the surface optical depth τsurf is reached at the same physical perpendicular depth, z, at all points in the star. For deformed shellular stars, however, the optical depth τ across an equipotential depends on local effective gravity, as follows:
with κ and ρ as the opacity and density of the equipotential, respectively. Consequently, equipotential surfaces do not coincide with surfaces of constant optical depth. For example, in single rotating stars, a fixed τsurf is reached at a deeper equipotential on the poles compared to on the equator, resulting in a different observed effective temperature between those regions. The same is true for highly deformed binary stars like overcontact systems. The atmosphere properties output by stellar evolution codes should therefore also take into account this effect of position dependent atmospheric depth.
Within the treatment of deformed stars in a conservative potential, we proceeded as follows. We start by defining the global effective temperature Teff, Ψ of an equipotential by the law of Stefan-Boltzmann:
that is, the global effective temperature of an equipotential shell is that of a black body radiating a luminosity LΨ over an area SΨ, which need not be spherical. Next, using the equation of radiative flux Eq. (14), we can define a local effective temperature Teff, l that varies across the equipotential:
We now consider a gray, plane parallel, Eddington-approximated atmosphere to construct appropriate BCs. At each point on the surface equipotential, the temperature profile can be written as (CG):
This expression is derived using two standard assumptions that can be similarly applied to the case of deformed stars. First, it is assumed that the radiation pressure at all optical depths can be written as 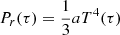 . Second, the intensity of radiation on top of the atmosphere is assumed to be isotropic in the outward directions, meaning that we ignore limb darkening, so that the pressure at the τ = 0 surface is computed to be (CG):
. Second, the intensity of radiation on top of the atmosphere is assumed to be isotropic in the outward directions, meaning that we ignore limb darkening, so that the pressure at the τ = 0 surface is computed to be (CG):
The first BC we consider constrains the temperature Tsurf of the outermost boundary by requiring that Tsurf = Teff, Ψ. To find the second BC on the surface pressure Psurf, we consider the equation of hydrostatic equilibrium:
Taking a point on the surface equipotential where Teff, l = Teff, Ψ, then by Eq. (42), we have that g = ⟨g⟩. As we also require that Tsurf = Teff, Ψ, Eq. (43) implies that the surface optical depth is τsurf = 2/3. The surface pressure can then be integrated at this point of the equipotential surface by assuming a thin atmosphere such that g and κ are constants.
where we substituted ⟨g⟩ with the definitions of fP and fT in Eqs. (12) and (17), respectively.
In summary, the atmospheric BCs are represented by the following system of equations:
Tsurf = [4]LS We emphasize that this surface temperature Tsurf of the stellar models is not the local effective temperature across the whole surface equipotential, the variations of which can be observed. However, it is possible to relate the surface temperature output by stellar models using these BCs to an observed local effective temperature at any point on the surface equipotential by applying Eq. (42). Finally, we mention that going forward, whenever the effective temperature is referenced, we mean the global effective temperature as defined by Eq. (41).
5. Stellar model comparison
We assess the effect of including tidal distortion on the structure of the star as well as the modified boundary conditions by computing stellar evolution models using the 1D MESA code, version 15140, with the mesasdk-x86_64-macos-21.2.1 SDK. Starting at the zero age main sequence (ZAMS), we compare the evolution of stars in three cases: (1) a 5 M⊙ single rotating star, (2) a 5 M⊙ detached star in orbit with a compact object, and (3) a 32 M⊙ twin binary in overcontact.
The next subsection lists the physical assumptions made when computing stellar models. The following subsections detail and discuss the results of the respective case studies.
5.1. Physical ingredients
5.1.1. Mixing, microphysics, and stellar winds
In all stellar models, we used the Ledoux criterion (Ledoux 1947) for determining convective regions. Within such regions, convection itself is modeled via the mixing length theory of Böhm-Vitense (1958) as described by CG, with the mixing length parameter α = 2. We used efficient semiconvective mixing (Langer et al. 1983), with αsc = 100 as proposed by Schootemeijer et al. (2019). Thermohaline mixing is applied as prescribed in Kippenhahn et al. (1980), with an efficiency of αth = 1. During the main sequence, the convective core is allowed to overshoot into the radiative envelope. We use a step overshoot as calibrated by Brott et al. (2011) with f = 0.345, f0 = 0.01, meaning that the diffusion coefficient is taken as constant from f0 pressure scale heights into the convective boundary up to f − f0 pressure scale heights out of the boundary. All other extra mixing processes, including rotational mixing from, for example, Eddington-Sweet type circulations are ignored in these sample models so as to isolate the effects of including the different forms of rotational deformation.
In terms of microphysics, we use the basic nuclear network consisting of 1H, 3He, 4He, 12C, 14N, 16O, 20Ne and 24Mg, which is sufficient to follow the main sequence evolution (Paxton et al. 2011) and the reaction rates are taken from the JINA library (Cyburt et al. 2010). MESA uses a blend of different equation of states (EOS) from Saumon et al. (1995), Timmes & Swesty (2000), Rogers & Nayfonov (2002) and Potekhin & Chabrier (2010), as described in Paxton et al. (2019). Radiative opacities are similarly determined from a blend of opacity tables from Iglesias & Rogers (1996) and Ferguson et al. (2005). The solar metallicity Z⊙ = 0.0142 as well as the relative metal fractions from are taken from Asplund et al. (2009).
Wind mass loss of individual stars is included following the prescription of Brott et al. (2011). As we focus on main sequence evolution, where the surface hydrogen fraction is X > 0.7, this method takes rates from Vink et al. (2001) when the effective temperature is higher than the iron bi-stability jump (as calibrated by Vink et al. 2001). For effective temperatures below the bi-stability, the mass loss rate is computed as the maximum of the rates of Vink et al. (2001) and Nieuwenhuijzen & de Jager (1995), where the latter is scaled with the same metallicity factor (Z/Z⊙)0.85 as with the rates of Vink et al. (2001).
5.1.2. Rotation and binary physics
At all times during the evolution of all models, angular momentum is continuously diffused throughout the whole star so as to enforce rigid rotation during the evolution. This, as with the omission of rotational mixing, is a way to reduce differences between the different rotational distortion models. When modeling single star rotation, the structure correction factors fP and fT that we use are the ones presented in Appendix A. In binary models, the angular velocity is always synchronized to the orbital period, so that the Roche potential (20) describes the geometry of the system, and the timescale of this synchronization is the orbital period itself. The structure corrections fP and fT are determined by interpolating the results of Sect. 2.6 on a grid of mass ratio and fractional RL radius (q = M2/M1, rΨ/rRL), where the RL sizes are determined according to the Eggleton approximation (Eggleton 1983)2. We do not model mass nor energy transfer in these models, as this is not needed for detached or equal mass binaries.
5.2. Main sequence evolution of a single rotating star
We compare the main sequence evolution of a 5 M⊙ star rotating initially at around 70% critical velocity at Solar metallicity with and without the modified atmospheric BCs developed in Sect. 4. In MESA, the default BCs are integrated from a standard spherically symmetric, plane parallel, gray Eddington atmosphere (Eddington 1926). Our new BCs, however, take into account the modified pressure and area of the outer surface of the star, as represented by the correction factors, fP, fT, and the non-spherical area, SΨ, in Eqs. (47) and (48).
Figure 6 shows the evolutionary track of the single rotating stars in a Hertzsprung-Russell diagram. We see that the change in BC has little impact on the overall evolution, with the largest difference of the surface properties occurring near hydrogen depletion (Xc = 0.001), where at constant L, the corresponding Teff varies by about 0.7%. Since the spherical BC calculates Teff from 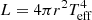 , in comparing with Eq. (48) at constant luminosity and radius results in the temperatures differing by a factor
, in comparing with Eq. (48) at constant luminosity and radius results in the temperatures differing by a factor ![$ \sqrt[4]{4\pi r_\Psi^2/S_\Psi} $](/articles/aa/full_html/2022/05/aa43094-22/aa43094-22-eq58.gif) . We plot the quantity
. We plot the quantity 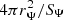 as a function of stellar age in Fig. 7. As the star loses thermodynamic equilibrium nearing hydrogen exhaustion, it contracts and tends toward critical rotation at the surface (recall we are enforcing solid body rotation). At this limit, the area ratio reaches its minimum of about 0.945, which, per Eq. (41) and at constant luminosity, leads to an effective temperature ratio of 0.986, meaning a 2.4% difference. In the bulk of the main sequence, however, we have an area ratio of around 0.99, which corresponds to just a 0.25% difference in effective temperature.
as a function of stellar age in Fig. 7. As the star loses thermodynamic equilibrium nearing hydrogen exhaustion, it contracts and tends toward critical rotation at the surface (recall we are enforcing solid body rotation). At this limit, the area ratio reaches its minimum of about 0.945, which, per Eq. (41) and at constant luminosity, leads to an effective temperature ratio of 0.986, meaning a 2.4% difference. In the bulk of the main sequence, however, we have an area ratio of around 0.99, which corresponds to just a 0.25% difference in effective temperature.
 |
Fig. 6. Hertzsprung-Russell diagram of the main sequence evolution of 5 M⊙ rotating stars in MESA using the default and new BCs. The inset zooms in on the blue hook near the terminal age main sequence. |
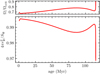 |
Fig. 7. Fraction of equivalent spherical area to true area at the surface as a function of age of the single rotating 5 M⊙ model. A lower fraction indicates a further departure from spherical symmetry due to rotation. Top panel: fractional critical rotation rate for comparison. |
5.3. Evolution of a detached B-type star
We modeled the evolution of a 5 M⊙ solar metallicity B-type star in a binary with a point mass companion of 3 M⊙ (q = 0.6) and with an initial period of three days until the star reaches its RL. With this setup we mimic the situation of intermediate mass stars found in short-period eclipsing binaries. We varied the rotation distortion model between (1) no rotation, (2) single star rotation where only centrifugal forces are taken into account, and (3) tidal deformation that account for both centrifugal and tidal forces. For the latter two, we also varied the atmospheric BCs between the new atmospheric BCs (Sect. 4) and the default spherical ones. For the non-rotating model, the new BCs reduce to the default ones, as there is no departure from spherical symmetry.
Figure 8 shows the radius evolution of the stars as a function of the central hydrogen fraction, Xc. At the onset of evolution, where the star is well within its RL, we see negligible difference between the various assumptions on BCs or rotation. However, as the star approaches its RL size, at constant Xc, the family of rotating tracks differ from the non-rotating model by up to 5%. This is a significant difference, and is resolvable by very precise observations of eclipsing binaries, whose errors on measured radii can be better than 3% (Torres et al. 2010; Graczyk et al. 2018; Pavlovski et al. 2018; Tkachenko et al. 2020, and references therein). Therefore, modeling stars in eclipsing binaries as non-rotating in evolution codes could induce a systematic mismatch when fitting measured radii to inferred radii from such models. Finally, we note that the difference in radii between the tidal and single rotating star models, which is at most 1%, is only resolvable by the most accurate of observations, if at all. Furthermore, the difference in radii between considered BC is on the order of 0.1% and is not perceivable on the figure.
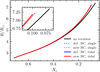 |
Fig. 8. Radius evolution of a 5 M⊙ star starting on a 3-day orbit around a 3 M⊙ point mass, as a function of central hydrogen fraction Xc. The difference between the rotation models is small while the one resulting from the different BCs is imperceivable. |
5.4. Evolution of a twin overcontact binary
We evolved a 32 M⊙ star with a metallicity of Z = Z⊙/2 in a binary system with its twin, meaning all properties of the stars are identical. In particular, this means that the mass ratio is unity, and we can ignore binary interaction effects like mass or energy transfer. We start the evolution at the ZAMS with a 1.5 day orbit and stop the simulation once the stars reach the outer Lagrangian points. This setup is the closest we can currently and consistently model massive overcontact binaries such as VFTS 352 in the Large Magellanic Cloud (Almeida et al. 2015).
In Fig. 9, we show the effective temperature evolution of the 32 M⊙ model under the various rotation model and BC assumptions. We notice again, like in the detached case, that the observable stellar parameter (in this plot Teff) can vary up to 5% in the late stages of the overcontact configuration. The difference between the rotation models are minor, on the order of 1%, and the tidally distorted model with the new BCs of Sect. 4 shows a rather complex evolution. It kinks at the RL filling point and subsequently crosses the other rotating tracks as the degree of overcontact increases. This behavior may be related to the crossing of the structure correction factors, fP and fT, as rΨ keeps rising (see Fig. 2). Moreover, there is a ∼25% age discrepancy between the rotating and non-rotating models. This difference can be understood in the context of spin orbit coupling. In the non-rotating model, the star can store no angular momentum, so that tidal synchronization has no effect (at least with the current implementation in MESA) and the RL size slowly increases due to wind mass loss (see top panel Fig. 9). However, when the star is modeled with angular momentum, wind mass loss causes an efficient spindown of the star. Tidal synchronization then keeps the star rotating close to the orbital velocity at the cost of decreasing the orbital separation, thus reducing the RL size and accelerating the points of contact and L2 overflow. This effect is also visible in the detached binary of Sect. 5.3.
 |
Fig. 9. Effective temperature evolution of the 32 M⊙ contact model with the different assumptions on BC and rotation model. We notice that the models including rotation are up to 5% cooler during overcontact. Between the different rotation models and BCs, we find only minor differences. Top panel: RL evolution, which explains the difference in age at onset of overflow of the Lagrangian points through spin orbit coupling. |
6. Discussion and conclusions
We developed the methodology needed to account for tidal deformation in binary stars in 1D stellar evolution codes. They are represented in the structure-correction factors of fP and fT that multiply the equations of hydrostatic equilibrium and radiative energy transport, respectively. Additionally, modified expressions of the Eddington limit and atmospheric boundary conditions as a result of the deformation have been calculated.
We show that the radii predicted by stellar evolution models can shift by ∼5% if centrifugal deformation is included, while also including tidal deformation leads to a smaller ∼1% effect. This means comparing observed stellar parameters to non-rotating models could result in a mismatch and this could have implications for high-precision astrophysics. In a study where observed surface properties with uncertainties on the order of 5% are used, centrifugal deformation has to be included in the stellar models. In binaries, if the precision of measurement is better than 1%, then the tidal deformation has to be taken into account. We note that the effect observed here is only due to geometrical considerations, that is, the equator bulges out due to rapid rotation or the presence of a companion. Mixing as a result of rapid rotation was not included and will further affect the radius evolution. Generally, the effect of rotational mixing is to keep the stars compact as fresh fuel is introduced into the core, so this may somewhat cancel the geometrical effect. However, the exact interplay and outcome of these competing effects is far from established.
The methods developed here have a wide range of applicability as they can be used for any (semi-)detached binary of arbitrary mass ratio. This can be applied, for instance, in studying the effect of tidal forces in mass transfer stability, which can have a potential impact on the formation of gravitational wave sources through stable mass transfer (van den Heuvel et al. 2017; Marchant et al. 2021). There are, however, limitations to our model, most notably that the structure correction factors computed from the binary Roche potential only apply to fully tidally locked systems. The general case, where the rotation of the components is free, cannot be described with a conservative potential, and is thus not suitable to the treatment of Kippenhahn & Thomas (1970) and Endal & Sofia (1976) used here. Developing a global model of free rotation including tides is a complex problem, but a potential workaround would be to consider free rotation for stars well within their RLs and use the centrifugal deformation corrections of single stars, and then implementing a switch to the synchronized binary corrections once a star fills an appreciable amount of its RL.
For contact configurations, currently only the mass ratio of unity can be considered consistently, as the energy transfer in the overcontact layers, is zero. When we include the processes of mass and energy transfer in overcontact layers, which is the subject of the following paper in this series, the methods we developed in this work enable the consistent modeling of all overcontact binary systems.
Acknowledgments
M.F. thanks the Flemish research foundation (FWO, Fonds voor Wetenshappelijk Onderzoek) PhD fellowship No. 11H2421N for its support. P.M. acknowledges support from the FWO junior postdoctoral fellowship No. 12ZY520N. The research leading to these results has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement numbers 772225: MULTIPLES).
References
- Abdul-Masih, M., Sana, H., Conroy, K. E., et al. 2020, A&A, 636, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abdul-Masih, M., Sana, H., Hawcroft, C., et al. 2021, A&A, 651, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aguilera-Dena, D. R., Langer, N., Moriya, T. J., & Schootemeijer, A. 2018, ApJ, 858, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Aguilera-Dena, D. R., Langer, N., Antoniadis, J., & Müller, B. 2020, ApJ, 901, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Almeida, L. A., Sana, H., de Mink, S. E., et al. 2015, ApJ, 812, 102 [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Binnendijk, L. 1970, Vist. Astron., 12, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm-Vitense, E. 1958, ZAp, 46, 108 [NASA ADS] [Google Scholar]
- Brott, I., de Mink, S. E., Cantiello, M., et al. 2011, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, J. P., & Giuli, R. T. 1968, Principles of Stellar Structure (New York: Gordon and Breach) [Google Scholar]
- Cyburt, R. H., Amthor, A. M., Ferguson, R., et al. 2010, ApJS, 189, 240 [NASA ADS] [CrossRef] [Google Scholar]
- de Mink, S. E., Cantiello, M., Langer, N., et al. 2009, A&A, 497, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eddington, A. S. 1925, The Observatory, 48, 73 [NASA ADS] [Google Scholar]
- Eddington, A. S. 1926, The Internal Constitution of the Stars (Cambridge: Cambridge University Press) [Google Scholar]
- Eggen, O. J. 1967, Mem. R. Astron. Soc., 70, 111 [NASA ADS] [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [Google Scholar]
- Endal, A. S., & Sofia, S. 1976, ApJ, 210, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Espinosa Lara, F., & Rieutord, M. 2011, A&A, 533, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [Google Scholar]
- Ferrario, L., Pringle, J. E., Tout, C. A., & Wickramasinghe, D. T. 2009, MNRAS, 400, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Gazeas, K. D., Loukaidou, G. A., Niarchos, P. G., et al. 2021, MNRAS, 502, 2879 [NASA ADS] [CrossRef] [Google Scholar]
- Graczyk, D., Pietrzyński, G., Thompson, I. B., et al. 2018, ApJ, 860, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Gräfener, G., Vink, J. S., de Koter, A., & Langer, N. 2011, A&A, 535, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Joss, P. C., Salpeter, E. E., & Ostriker, J. P. 1973, ApJ, 181, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Justham, S., Podsiadlowski, P., & Vink, J. S. 2014, ApJ, 796, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., & Thomas, H. C. 1970, Stellar Rotation (Columbus, Ohio: Gordon and Breach Science Publishers) [Google Scholar]
- Kippenhahn, R., Ruschenplatt, G., & Thomas, H.-C. 1980, A&A, 91, 175 [NASA ADS] [Google Scholar]
- Kopal, Z. 1959, Close Binary Systems (London: Chapman & Hall) [Google Scholar]
- Kuiper, G. P. 1941, ApJ, 93, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N. 1997, ASP Conf. Ser., 120, 83 [Google Scholar]
- Langer, N., Fricke, K. J., & Sugimoto, D. 1983, A&A, 126, 207 [NASA ADS] [Google Scholar]
- Ledoux, P. 1947, ApJ, 105, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1968, ApJ, 151, 1123 [Google Scholar]
- Maeder, A., & Meynet, G. 2000, A&A, 361, 159 [NASA ADS] [Google Scholar]
- Mandel, I., & de Mink, S. E. 2016, MNRAS, 458, 2634 [NASA ADS] [CrossRef] [Google Scholar]
- Marchant, P., Langer, N., Podsiadlowski, P., Tauris, T. M., & Moriya, T. J. 2016, A&A, 588, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marchant, P., Pappas, K. M. W., Gallegos-Garcia, M., et al. 2021, A&A, 650, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Menon, A., Langer, N., de Mink, S. E., et al. 2021, MNRAS, 507, 5013 [NASA ADS] [CrossRef] [Google Scholar]
- Mochnacki, S. W. 1984, ApJS, 55, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Nieuwenhuijzen, H., & de Jager, C. 1995, A&A, 302, 811 [NASA ADS] [Google Scholar]
- Palate, M., Rauw, G., Koenigsberger, G., & Moreno, E. 2013, A&A, 552, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pavlovski, K., Southworth, J., & Tamajo, E. 2018, MNRAS, 481, 3129 [NASA ADS] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
- Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
- Potekhin, A. Y., & Chabrier, G. 2010, Contrib. Plasma Phys., 50, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, F. J., & Nayfonov, A. 2002, ApJ, 576, 1064 [Google Scholar]
- Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
- Sanyal, D., Grassitelli, L., Langer, N., & Bestenlehner, J. M. 2015, A&A, 580, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saumon, D., Chabrier, G., & van Horn, H. M. 1995, ApJS, 99, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, F. R. N., Podsiadlowski, P., Langer, N., Castro, N., & Fossati, L. 2016, MNRAS, 457, 2355 [Google Scholar]
- Schneider, F. R. N., Ohlmann, S. T., Podsiadlowski, P., et al. 2019, Nature, 574, 211 [Google Scholar]
- Schootemeijer, A., Langer, N., Grin, N. J., & Wang, C. 2019, A&A, 625, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shu, F. H., Lubow, S. H., & Anderson, L. 1976, ApJ, 209, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Sweet, P. A. 1950, MNRAS, 110, 548 [Google Scholar]
- Szymanski, M., Kubiak, M., & Udalski, A. 2001, Acta Astron., 51, 259 [NASA ADS] [Google Scholar]
- Timmes, F. X., & Swesty, F. D. 2000, ApJS, 126, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Tkachenko, A., Pavlovski, K., Johnston, C., et al. 2020, A&A, 637, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
- Vanbeveren, D., De Donder, E., Van Bever, J., Van Rensbergen, W., & De Loore, C. 1998, New Astron., 3, 443 [CrossRef] [Google Scholar]
- van den Heuvel, E. P. J., Portegies Zwart, S. F., & de Mink, S. E. 2017, MNRAS, 471, 4256 [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Meth., 17, 261 [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Wickramasinghe, D. T., Tout, C. A., & Ferrario, L. 2014, MNRAS, 437, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S.-C., & Langer, N. 2005, A&A, 443, 643 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S.-C., Langer, N., & Norman, C. 2006, A&A, 460, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zahn, J.-P. 1975, A&A, 41, 329 [Google Scholar]
- Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
Appendix A: Polynomial fits in the rotating shell potential
In the case of the rotating star potential (18), integral expressions can be written down to compute all relevant quantities required to use the modified stellar structure equations presented in Sect. 2.1. Paxton et al. (2019) numerically integrated these and provided polynomial fits in the variable ω = Ω/Ωcrit, where 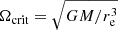 is the classical critical velocity of equatorial radius re.
is the classical critical velocity of equatorial radius re.
To improve on the errors introduced by such fits, we recalculated the integrals and used the Levenberg-Marquardt non-linear least squares algorithm from scipy (Virtanen et al. 2020) to find more accurate polynomial fits.
First, for the equipotential volumes VΨ, we have the fit:
with a maximal error of 0.20% in ω ∈ [0, 1]. We note that since VΨ(1) is an analytical result (Kopal 1959) and the leading order term in the expansion is set by requiring that a slow rotating shell is ellipsoidal, this fit has only one free parameter. For the volume equivalent radius, rΨ, and equatorial radius, re, have the following fits:
with a maximal error of 0.11% in ω ∈ [0, 1], and,
with a maximal error of 0.15% in ω ∈ [0, 1]. Next, the surface area SΨ and average effective gravity ⟨g⟩ are approximated by:
with a maximal error of 0.07% and 0.25% in ω ∈ [0, 1], respectively. Since the inverse gravity diverges when ω → 1, we require a non-polynomial term to represent it appropriately in that limit. Therefore, constructing the auxiliary functions:
we have then for the average inverse effective gravity ⟨g−1⟩, and the specific moment of inertia irot, the following fits:
with a maximal error of 0.85% and 0.68% in ω ∈ [0, 0.9999], respectively.
For the correction factors, fP and fT, we construct the following fits:
with a maximal error of 0.56% and 0.58% in ω ∈ [0, 0.9999], respectively.
Finally, with the auxiliary function:
the implicit equation from which ω can be obtained from jrot is:
with a maximal error of 0.54% in ω ∈ [0, 0.9999].
With these fits, we improve all the fits of Paxton et al. (2019), especially the maximal error of fT, namely, taking it from 1.6% to 0.58%.
Appendix B: Matching the tidal and single rotating star distortion models
In Fig. 2, we make the comparison of the structure correction factor, fP, of the tidal model as well as the single rotating star model in one plot. This is meant to illustrate the corrections that would be used in a simulation with the MESA code if rotation is included in a model for a binary system without including tidal deformation. In practice, a tidally distorted star does not have a well defined equatorial radius with which to define ω, but nevertheless the current implementation of MESA makes use of the equipotential radius rΨ, the mass contained within the shell MΨ and the angular frequency of the shell ΩΨ to derive the corrections as if these properties corresponded to a single rotating star with cylindrical symmetry.
For a tidally synchronized binary, the angular velocity is derived from Kepler’s third law:
with q = M2/M1 as the mass ratio and a as the separation of the binary. Next, we consider the equivalent single rotating star. Given the mass M1 and equatorial radius re, it has a critical rotation rate:
Dividing these equations, and setting ω = Ω/Ωcrit as the dimensionless rotation rate, we arrive at an implicit equation for ω:
where fre relates the volume equivalent radius to the equatorial radius as a function of the dimensionless rotation rate in a single rotating star. For a given value of rΨ/a and q, this implicit equation gives the value of ω that a MESA simulation would determine to compute the corrections to the stellar structure equations, despite there not being a well defined equatorial radius. The values shown in Fig. 2 for the single star equivalent correspond to evaluating the results of Appendix A for fP(ω), with ω derived from rΨ/a and q with the implicit Eq. (B.3).
All Figures
 |
Fig. 1. Illustration of the Roche geometry in the equatorial plane. It shows the L1, L2, and L3 equipotentials (gray), as well as the splitting surfaces (blue dashed). The splitting surfaces have their normals always perpendicular to the potential gradient. |
| In the text | |
 |
Fig. 2. Structure correction factor fP as a function of fractional RL radius rΨ/rRL for various mass ratios. The discontinuities in all graphs correspond to the crossing of the Lagrangian points L1 (at rΨ/rRL = 1, by construction) and Lout at larger radii. For reference, the equivalent single rotating star inferred fP is overplotted in dashed lines. |
| In the text | |
 |
Fig. 3. Comparison of the calculations of the structure correction factor fP from Mochnacki (1984) and those in this work, as a function of the fractional RL radius rΨ/rRL. We performed a resolution convergence test with double, quadruple and octuple the default spacial resolution, and conclude our integrations have well converged at an eight-fold resolution increase. |
| In the text | |
 |
Fig. 4. Maximal Eddington factor Γmax that a rotating star can have as a function of fractional classical critical rotation rate of ω = Ω/Ωcrit, class. Our model of shellular stars has a maximal reduction to Γmax = 0.639. |
| In the text | |
 |
Fig. 5. Reduction, fP/fT, of the maximal Eddington factor as a function of mass ratio, q, and fractional overflow radius, rΨ/rRL. The equivalent radius of a star filling up to its outer Lagrangian point in marked with the green line. |
| In the text | |
 |
Fig. 6. Hertzsprung-Russell diagram of the main sequence evolution of 5 M⊙ rotating stars in MESA using the default and new BCs. The inset zooms in on the blue hook near the terminal age main sequence. |
| In the text | |
 |
Fig. 7. Fraction of equivalent spherical area to true area at the surface as a function of age of the single rotating 5 M⊙ model. A lower fraction indicates a further departure from spherical symmetry due to rotation. Top panel: fractional critical rotation rate for comparison. |
| In the text | |
 |
Fig. 8. Radius evolution of a 5 M⊙ star starting on a 3-day orbit around a 3 M⊙ point mass, as a function of central hydrogen fraction Xc. The difference between the rotation models is small while the one resulting from the different BCs is imperceivable. |
| In the text | |
 |
Fig. 9. Effective temperature evolution of the 32 M⊙ contact model with the different assumptions on BC and rotation model. We notice that the models including rotation are up to 5% cooler during overcontact. Between the different rotation models and BCs, we find only minor differences. Top panel: RL evolution, which explains the difference in age at onset of overflow of the Lagrangian points through spin orbit coupling. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



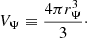
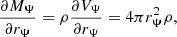
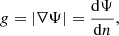
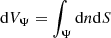
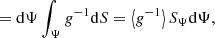
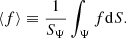
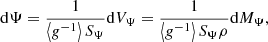
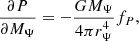
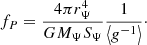
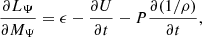
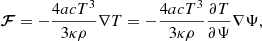
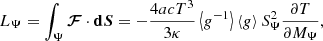
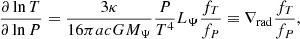
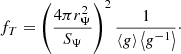
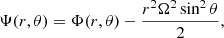
![$$ \begin{aligned} \Psi (x, y, z) =&\Phi (x, y, z) - \frac{G (M_1 + M_2)}{2a^3}\nonumber \\&\times \left[\left(x-\frac{M_2}{M_1+M_2}a\right)^2+y^2\right], \end{aligned} $$](/articles/aa/full_html/2022/05/aa43094-22/aa43094-22-eq21.gif)
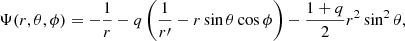
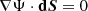
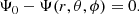
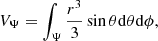
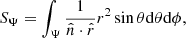
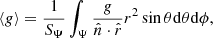
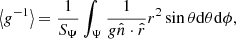
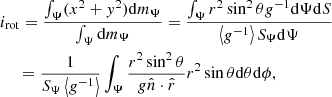
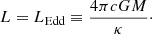
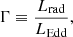
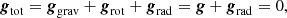
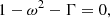
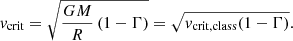

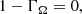
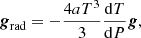
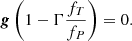
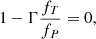
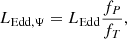
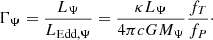
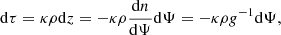
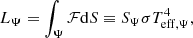
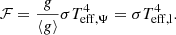
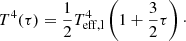
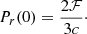
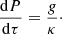
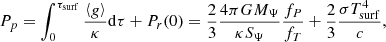
![$$ \begin{cases} P_{\rm surf} = \frac{2}{3}\frac{4\pi GM_\Psi}{\kappa(T_{\rm surf}, P_{\rm surf})S_\Psi}\frac{f_P}{f_T} + \frac{2}{3}\frac{\sigma T_{\rm surf}^4}{c}, &(47)\\ T_{\rm surf} = \sqrt[4]{\frac{L_\Psi}{\sigma S_\Psi}}\cdot &(48)\end{cases} $$](/articles/aa/full_html/2022/05/aa43094-22/aa43094-22-eq56.gif)