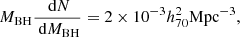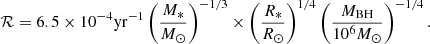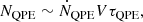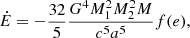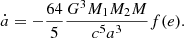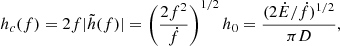| Issue |
A&A
Volume 661, May 2022
|
|
|---|---|---|
| Article Number | A55 | |
| Number of page(s) | 8 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202142519 | |
| Published online | 02 May 2022 | |
Quasi-periodic eruptions from the helium envelope of hydrogen-deficient stars stripped by supermassive black holes
1
School of Astronomy and Space Science, Nanjing University, Nanjing, 210093, PR China
e-mail: fayinwang@nju.edu.cn
2
Anton Pannekoek Institute for Astronomy, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands
3
School of Physics, Huazhong University of Science and Technology, Wuhan 430074, PR China
4
Key Laboratory of Modern Astronomy and Astrophysics (Nanjing University), Ministry of Education, Nanjing 210093, PR China
5
Department of Astronomy, School of Physical Sciences, University of Science and Technology of China, Hefei, 230026 Anhui, PR China
Received:
25
October
2021
Accepted:
18
March
2022
Quasi-periodic eruptions (QPEs), a new kind of X-ray burst with a recurrence time of several hours, have been detected from supermassive black holes (SMBHs) in galactic nuclei. Recently, the two QPEs discovered by the eROSITA showed asymmetric light curves with a fast rise and a slow decline. Current models cannot explain the observational characteristics of QPEs. In this work, we show that QPEs can be generated from the Roche lobe overflows at each periapsis passage of an evolved star orbiting a SMBH. The properties of the companion stars are constrained via analytic estimations. We find that hydrogen-deficient post-AGB stars are promising candidates for exhibiting this phenomenon. We used the Modules for Experiments in Stellar Astrophysics (MESA) stellar evolution code to construct the hydrogen-deficient stars that can fulfill the requirements, as obtained through analytical estimates, to produce the properties of QPEs, including the fast-rise and slow-decay light curves, periods, energetics, and rates. Furthermore, the extreme mass ratio ∼105 between the SMBH and the donor leads to a phenomenon called extreme mass-ratio inspiral (EMRI), producing millihertz gravitational waves. These QPEs would be detected as EMRI sources with electromagnetic counterparts for space-based GW detectors, such as Laser Interferometer Space Antenna (LISA) and Tianqin. These instruments would provide a new way to measure the Hubble constant and further test the Hubble constant tension.
Key words: X-rays: bursts / stars: evolution / black hole physics / accretion, accretion disks
© ESO 2022
1. Introduction
Quasi-periodic eruptions (QPEs) are a new kind of sudden X-ray brightening originating in the region near the supermassive black holes (SMBHs) of galactic nuclei, both active (Miniutti et al. 2019; Giustini et al. 2020) and quiescent (Arcodia et al. 2021). The peak luminosities of the X-ray bursts are ∼1041 − 1043 erg in 0.5–2 keV energy band. The average recurrence time of QPEs is ∼2.4−18 h with the duty cycle ∼6%−41%. No optical/UV counterpart has been reported for them.
The first QPE was discovered with XMM-Newton in the central region of Seyfert 2 galaxy GSN 069 (Miniutti et al. 2019). The decay of X-ray emission of GSN 069 could be a tidal disruption event (TDE) source according to the long-term evolution of X-ray flux and spectrum (Shu et al. 2018) and the carbon and nitrogen ratio [C/N] abundance (Sheng et al. 2021). A second QPE system was discovered in RX J1301.9+2747 (Giustini et al. 2020). More recently, two more QPEs, eRO-QPE1 and eRO-QPE2, were discovered with the eROSITA instrument on the Spectrum-Roentgen-Gamma (SRG) space observatory (Arcodia et al. 2021). Follow-up observations by the XMM-Newton X-ray telescope and NICER confirmed the bursting nature of the two sources. The eRO-QPE1 and eRO-QPE2 expand QPE durations and recurrence times towards longer and shorter timescales, respectively. The light curves of them are asymmetric, with a fast rise and a slow decay (Arcodia et al. 2021). The first QPE in GSN 069 also shows asymmetric behavior from its phase-folded light curve.
The QPEs associated with SMBHs have typically low masses. For GSN 069, the mass of SMBH is 4 × 105 M⊙ (Miniutti et al. 2019). From the X-ray and UV analysis, the centeral SMBH mass of RXJ1301.9+2747 is found to be 0.8−2.8 × 106 M⊙ (Shu et al. 2017). The total stellar masses are estimated to be 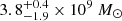 and
and 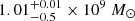 from the optical spectra for eRO-QPE1 and eRO-QPE2 (Arcodia et al. 2021), indicating that the masses of central SMBHs are in the range of 105 − 106 M⊙ based on the scaling relation between central SMBH mass and total galaxy stellar mass (Reines & Volonteri 2015). The properties of the four QPEs are listed in Table 1.
from the optical spectra for eRO-QPE1 and eRO-QPE2 (Arcodia et al. 2021), indicating that the masses of central SMBHs are in the range of 105 − 106 M⊙ based on the scaling relation between central SMBH mass and total galaxy stellar mass (Reines & Volonteri 2015). The properties of the four QPEs are listed in Table 1.
Observed properties of quasi-periodic eruptions events.
There have been some theoretical models to explain the unusual characteristics of QPEs. For the first QPE, the radiation-pressure accretion disk instability (Janiuk et al. 2002; Merloni & Nayakshin 2006; Janiuk & Czerny 2011; Grzedzielski et al. 2017) was proposed as a way of interpreting this aspect (Miniutti et al. 2019). However, the quiescent galactic nuclei origin of eRO-QPE1 and eRO-QPE2, together with the fast-rise and slow-decay light curves, would challenge this explanation because the stable rise and rapid decay light curves are predicted (Czerny et al. 2009; Wu et al. 2016). The gravitational self-lensing binary SMBH model can generate the flare spacings (Ingram et al. 2021), but cannot reproduce the observed flare profile. Periodic variability is also often associated with a binary orbital period. If the orbital evolution is dominated by gravitational wave emission, the observed properties of eRO-QPE1 and eRO-QPE2 require the mass of the companion to be much smaller than that of the main body (Arcodia et al. 2021), called extreme mass-ratio inspirals (EMRIs). A low-mass white dwarf (WD) EMRI on a highly eccentric orbit has been proposed to explain the QPEs in GSN 069 (King 2020), which was first proposed by Zalamea et al. (2010). However, we find that the model of WD companion cannot explain other three QPEs (RXJ1301.9+2747, eRO-QPE1, and eRO-QPE2, see Sect. 2). More recently, a complex model with a large degree of uncertainty (both observational and theoretical) was built, in which the QPEs are due to periodic close interactions between two coplanar stellar EMRIs (Metzger et al. 2022).
The fast rise and slow decay of the light curves, combined with the repetition property and the spatial consistency with SMBHs, imply that the profile of QPEs resembles that of a tidal stripping event (Shen 2019). Although the nature of the rise and decay of the light curves is complex, the dynamical timescale of the companion is the key parameter. The more compact the objects, the faster the flux that is found (Guillochon & Ramirez-Ruiz 2013; Law-Smith et al. 2017). For CO WDs, the rise time of flux is about one minute, and for sun-like stars or red giants, the rise time of flux is a few days. The rise time of QPEs is ∼0.2−3 h, indicating that they cannot produce QPEs. We find that hydrogen-deficient post-asymptotic giant branch (post-AGB) stars which remove H envelopes after very late thermal pulse (VLTP) phase (Herwig et al. 1999) can satisfy the conditions for QPEs.
Our model is shown as follows. For a low- or intermediate-mass star (initial mass 1 M⊙ < M < 10 M⊙) following the MS, it goes on to evolve into the red giant, AGB, post-AGB, the central star of planetary nebulae (CSPNe), and finally WD, successively. It is captured by the SMBH at the post-AGB stage, leading to the formation of an eccentric binary. It can undergo Roche lobe overflow (RLOF) at periapsis, resulting in QPEs. Our model is built on the work by Wang et al. (2019), who studied the electromagnetic counterpart of EMRIs produced by the tidal stripping of the He envelope of a massive star by an SMBH. Motivated by eruption recurrence of cataclysmic variable binaries (CV, e.g., V803 Centauri, Patterson et al. 2000), we consider that the mass transfer is driven by angular momentum loss caused by gravitational radiation (Paczynski & Sienkiewicz 1981). This scenario can quantitatively account for the fast rise and slow decay light curves, periods, energetics, and rates of the QPE phenomenon. Moreover, these four QPE systems are detectable sources of gravitational waves (GW) by the Laser Interferometer Space Antenna (LISA; Danzmann 2000; Amaro-Seoane et al. 2017; Amaro-Seoane 2018) and Tianqin (Luo et al. 2016).
This paper is organized as follows. The constraints on the properties of the companion star are given in Sect. 2. The Modules for Experiments in Stellar Astrophysics (MESA) stellar evolution code is used to construct the hydrogen-deficient post-AGB stars, and the results are shown in Sect. 3. We estimate the event rate of QPEs in Sect. 4. A discussion of QPEs as the promising GW sources for LISA and Tianqin is given in Sect. 5 and a summary is presented in Sect. 6.
2. Constraints on the properties of the companion star
The tidal interaction between the SMBH and the companion can be described via the penetration factor β = RT/Rp, where RT is the tidal radius and Rp is periapsis. For β ≳ 1, the star becomes fully disrupted. The conditions for full tidal disruption can be found in Rosswog et al. (2009) and Gezari (2021). For 0.6 ≲ β < 1, partial disruptions are expected to occur (Guillochon & Ramirez-Ruiz 2013). If β < 0.6, the mass loss of the companion is slow, which is so called tidal disruption near miss (King 2020). The onset of mass-loss can be assumed when the star just fills the Roche lobe at periapsis.
We consider an SMBH with hydrogen-deficient post-AGB star orbiting around it on an eccentric orbit, as is illustrated in Fig. 1. It has a compact core surrounded by He envelope. When the star approaches periapsis, it marginally fills its Roche lobe, namely, the star’s radius R2 equals its Roche lobe size. The He envelope with low density becomes tidally stripped by the SMBH, while the compact core survives the encounter. The stripped matter loses the orbital energy during the circularization stage. Finally, in the case of highly eccentric orbit, about half of the stripped material falls back to the SMBH, which produces X-ray eruptions. At each periapsis passage, mass-transfer onto the SMBH generates QPEs. Mass transfer from the companion onto the SMBH is driven by angular momentum loss caused by gravitational radiation. The system can be analogous to an eccentric version of short-period cataclysmic variable evolution (Paczynski & Sienkiewicz 1981).
 |
Fig. 1. Schematic diagram of the mechanism for QPEs. A hydrogen-deficient post-AGB star with He envelope orbits around an SMBH on an eccentric orbit. When the star approaches periapsis, it just fills its Roche lobe. The He envelope with low density ends up partially tidally stripped by the SMBH, while the compact core survives the encounter. Finally, the stripped material falls back to the SMBH, resulting in QPEs. |
The observed recurrence time of QPEs is the orbital period, P, in our model, and the orbital semimajor axis is:
In this section, strict constraints of our model are given. In order to produce luminous QPEs with fast rise times, at least three requirements should be satisfied. First, the star’s radius equals its Roche lobe size at periapsis. Second, the stars need to be dense enough to make the fast rise timescale of QPEs. Third, the mass-transfer rate driven by gravitational radiation loss should be large enough to generate the luminosities of QPEs.
2.1. The stable radius for mass-loss
The star should fill the Roche lobe at periapsis Rp. The radius of the Roche lobe Rlobe is taken from Sepinsky et al. (2007). We can get:
In this case, β ≃ 0.46. We discuss the orbital stability of the onset of mass-loss. For a Schwarzschild BH, the radius of innermost stable circular orbit (ISCO) is:
where M1, 5 = M1/105 M⊙. For Kerr BHs, the corresponding radius of ISCO are:
for the co-rotating and counter-rotating case, respectively, where as is the dimensionless spin (Bardeen et al. 1972; Jefremov et al. 2015). For as = 1 and as = −1, the RISCO is 1Rg and 9Rg respectively, where Rg = GM1/c2 is the gravitational radius. The realistic upper limit for as is 0.998 (Thorne 1974), and the radius of ISCO is RISCO ≃ 1.237Rg. The mass–radius relation of WDs can be well approximated by (Zalamea et al. 2010)
for 0.2 M⊙ < M2 < 1.4 M⊙, where MCh is the Chandrasekhar mass and R⋆ = 0.013 R⊙. From Eqs. (2) and (5), we can get periapsis radius where is the onset of mass-loss for four QPEs (see Fig. 2). The mass of SMHB of GSN 069 is M1 ∼ 4 × 105 M⊙ (Miniutti et al. 2019), and for RXJ1301.9+2747 is M1 ∼ (0.8−2.8) × 106 M⊙ (Giustini et al. 2020). Although, the masses of the SMBHs for eRO-QPE1 and eRO-QPE2 are unknown, we can use the BH-to-total stellar mass fraction M1/Mstellar ∼ 0.025% (Reines & Volonteri 2015) to estimate the mass of the central SMBH. The total stellar masses of the host galaxies for eRO-QPE1 and eRO-QPE2 are found to be 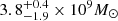 and
and 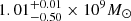 (Arcodia et al. 2021), respectively. Thus, the mass of the SMBH of eRO-QPE1 and eRO-QPE2 is ∼105 − 106 M⊙. The result of King (2020) associated with a low-mass WD companion are shown in black circle. For high-mass SMHBs, the mass of the WD companion should be extreme low (see Sect. 2.4). Therefore, the companion cannot be a WD.
(Arcodia et al. 2021), respectively. Thus, the mass of the SMBH of eRO-QPE1 and eRO-QPE2 is ∼105 − 106 M⊙. The result of King (2020) associated with a low-mass WD companion are shown in black circle. For high-mass SMHBs, the mass of the WD companion should be extreme low (see Sect. 2.4). Therefore, the companion cannot be a WD.
 |
Fig. 2. Periapsis Rp in units of the gravitational radius from the mass–radius relation of WDs (shown in panel a) and orbital eccentricity (shown in panel b). The results of King (2020) are shown in black circles for GSN 069. For eRO-QPE1 and eRO-QPE2, M1 is estimated by 0.025%Mstellar (Reines & Volonteri 2015). The radii of ISCO for Schwarzschild BHs (a = 0) and extreme-rotating BHs (a = 0.998) are also illustrated in black lines. Panel a: Mass–radius relation of WDs is taken from Zalamea et al. (2010). The case of WDs companion for RXJ1301.9+2747 and eRO-QPE2 is only possible for extreme low-mass WDs or Kerr BHs. Panel b: unless the eccentricity is very high, the mass transfer can be carried out stably. |
2.2. The mean density of the companion
The light curves of the QPEs have a fast rise and a slow decay (Miniutti et al. 2019; Arcodia et al. 2021). The decay timescale is determined by the viscous timescale of accretion disk, and the rise timescale relates to the radiation region or the interaction between the stripped material and the disk (Shen 2019). The rise time is comparable to the local circularly orbital timescale at periapsis:
where 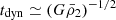 is the dynamical timescale of the companion star (Shen 2019). The local circularly orbital timescale at periapsis is used to estimate the rise timescale.
is the dynamical timescale of the companion star (Shen 2019). The local circularly orbital timescale at periapsis is used to estimate the rise timescale.
For CO WDs (tdyn ≃ 3 s), the rise time of the flux is estimated as trise ∼ 1 min. For He WDs with a mass of 0.2 M⊙(tdyn ≃ 12 s), the rise timescale is trise ∼ 0.06 h. Law-Smith et al. (2017) constructed a He WD with a hydrogen envelope via the MESA stellar evolution code, and they found the dynamical timescale is tdyn ≃ 535 s. From the phase-folded light curve of QPEs, the rise timescale is ∼0.2−3 h. The rise timescale of QPEs is much longer than that of WDs. For short-duration QPEs (e.g., GSN 069, RXJ1301.9+2747, and eRO-QPE2), the rise timescale is much shorter than He WDs with hydrogen envelopes. From Eq. (6), we can derive 52 g cm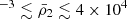 g cm−3 from 12 s ≲ tdyn ≲ 535 s. To sum up, the fast rise timescale requires that the stripped material is much denser than Sun-like stars (
g cm−3 from 12 s ≲ tdyn ≲ 535 s. To sum up, the fast rise timescale requires that the stripped material is much denser than Sun-like stars (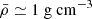 ) or red giants (
) or red giants (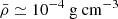 ).
).
The MS stars, red giants, and WDs cannot meet the mean density discussed above. The evolved or stripped stars that lost their H envelopes eventually become dense enough. In this work, we focus on the evolved stars. There are two main evolving channels of the hydrogen-deficient stars. For low- or intermediate-mass stars (initial mass 1 M⊙ < M < 10 M⊙), the H envelope was removed in the VLTP phase (Herwig et al. 1999) (see Sect. 3). The other case is the product of the evolution of massive stars (e.g., Wolf-Rayet stars). We did not consider massive stars for the following reasons. First, the massive stars have more obvious optical/UV variability during the circularization stage, however, all the detected QPEs lack the optical/UV counterpart (Miniutti et al. 2019; Giustini et al. 2020; Arcodia et al. 2021). Second, the strong emission bands of helium were found for Wolf-Rayet stars (Hiltner & Schild 1966; Sander et al. 2012), which is inconsistent with the optical observations of eRO-QPE1 and eRO-QPE2 (Arcodia et al. 2021). Third, these kinds of massive stars are rare.
2.3. Orbital eccentricity
The tidal stripping process is stable for an EMRI binary system lasting for ∼10 000–100 000 years when the star fills the Roche lobe (Hameury et al. 1994; Dai & Blandford 2013). The star should fill the Roche lobe at periapsis. From Eqs. (1) and (2), we can get the relation between the star parameters and the eccentricity:
or in terms of the average density:
Obviously, the orbital eccentricity must be positive (e > 0), thus
From the Rp > RISCO for a Schwarzschild BH, the eccentricity needs to meet the following terms:
The periapsis radii, Rp, as a function of eccentricity for four QPEs are shown in Fig. 2. For GSN 069, e = 0.94 is taken from King (2020), which is shown as black circle. For eRO-QPE1 and eRO-QPE2, M1 is estimated by 0.025%Mstellar (Reines & Volonteri 2015). For high eccentricity orbits, the mass transfer is not stable, namely, the WD companion are to be swallowed by the SMBH (Rp < RISCO).
2.4. Mass-transfer rate
The accretion luminosity of the stripped material falling back to the SMBH is L = ϵṀc2, where ϵ is the radiative efficiency. We take a typical value ϵ = 0.1 which has been widely used, such as King (2020). In order to generate luminous QPEs, the cycle-average mass-accretion rate is:
where η = ΔP/P is the average duty cycle.
Similar to the process of CV binary evolution (Paczynski & Sienkiewicz 1981), the mass transfer is driven by angular-momentum loss caused by gravitational radiation. The gravitational wave radiation is efficient due to the short period and it goes on to drive the mass transfer near periapsis. The orbital angular momentum lost caused by gravitational radiation is (Paczynski & Sienkiewicz 1981):
where M = M1 + M2 is the total mass, and
In the case of extreme eccentricity, e → 1, f(e)≃2−7/2(1 + 73/24 + 37/96)(1 − e)−7/2. As discussed by King (2020), periapsis separation is almost constant. Therefore, the variation of the orbital angular momentum is mainly resulted from the mass transfer of the secondary star 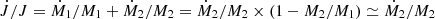 (King 2020). Therefore, we can get the mass transfer rate due to gravitational wave radiation as:
(King 2020). Therefore, we can get the mass transfer rate due to gravitational wave radiation as:
The mass-transfer timescale is tGW = −M2/Ṁ2 ∼ 105 yr. If the post-AGB stars which still have burning He shells are captured by the SMBHs, the onset of RLOF would also be caused by nuclear evolution. The nuclear timescale of He shell burning is 105 − 106 yr, which is similar to tGW. The ongoing RLOF process caused by thermodynamical conditions of the convective envelope is also discussed in Sect. 3, and we find the mass transfer rate is mainly determined by gravitational wave radiation.
From Eqs. (8) and (14), we find that the mass-transfer rate is:
and the luminosity is
For a MS star (e.g., the Sun) and a red giant (e.g., M2 = 1 M⊙, R2 = 25 R⊙), the characteristic accretion luminosities are 3.6 × 1038 erg s−1 and 6.3 × 1033 erg s−1, respectively. Thus, they are much lower than those of observed QPEs.
From Eqs. (8), (11), and (14), we derived the relation between star parameters (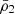 and M2) and BH mass for four QPEs (see Fig. 3). The white solid lines refer to constraints from the rise time. The infeasible range is in blue. The yellow vertical solid line (for GSN 069 shown in panel (a)) and shading regions – for the other three shown in panels (b), (c), and (d) – represent the mass of the SMBH. The allowed parameter space is shown in yellow. It is obvious that MS stars and red giants with higher mass and lower density are located in the infeasible range. Only low and intermediate mass stars whose H envelopes have been removed in the post-AGB phase can fulfill them. The mass of hydrogen-deficient post-AGB stars are almost the same as the final stellar evolution product WDs (0.5−1.4 M⊙), but the density is lower because of the existence of He envelopes. In Sect. 3, we show the evolved low- and intermediate-mass stars (1 M⊙ < M < 10 M⊙) that have lost their H envelopes in the post-AGB phase, which can explain all the observation properties. Taking the hydrogen-deficient post-AGB stars constructed in Sect. 3 as examples, the required averaged density is depicted in Fig. 3. For GSN 069, the stars with masses of 0.6 M⊙ and 1.1 M⊙ are shown as a red circle and square in panel (a), respectively. For the other QPEs shown in panels (b–d), the stars with masses of 0.6 M⊙ and 1.1 M⊙ are shown in red solid and dashed lines, respectively. The average density of stars required to explain the properties of QPEs is listed in Table 2, which is between 52 g cm−3 and 3642 g cm−3.
and M2) and BH mass for four QPEs (see Fig. 3). The white solid lines refer to constraints from the rise time. The infeasible range is in blue. The yellow vertical solid line (for GSN 069 shown in panel (a)) and shading regions – for the other three shown in panels (b), (c), and (d) – represent the mass of the SMBH. The allowed parameter space is shown in yellow. It is obvious that MS stars and red giants with higher mass and lower density are located in the infeasible range. Only low and intermediate mass stars whose H envelopes have been removed in the post-AGB phase can fulfill them. The mass of hydrogen-deficient post-AGB stars are almost the same as the final stellar evolution product WDs (0.5−1.4 M⊙), but the density is lower because of the existence of He envelopes. In Sect. 3, we show the evolved low- and intermediate-mass stars (1 M⊙ < M < 10 M⊙) that have lost their H envelopes in the post-AGB phase, which can explain all the observation properties. Taking the hydrogen-deficient post-AGB stars constructed in Sect. 3 as examples, the required averaged density is depicted in Fig. 3. For GSN 069, the stars with masses of 0.6 M⊙ and 1.1 M⊙ are shown as a red circle and square in panel (a), respectively. For the other QPEs shown in panels (b–d), the stars with masses of 0.6 M⊙ and 1.1 M⊙ are shown in red solid and dashed lines, respectively. The average density of stars required to explain the properties of QPEs is listed in Table 2, which is between 52 g cm−3 and 3642 g cm−3.
 |
Fig. 3. Contours of allowed average density for different values of the SMBH mass, M1, and the companion star mass, M2. The white solid lines refer to constraints from the rise time. The excluded region is shown in blue. The gray region shows different densities of the companion star. The yellow vertical solid line (for panel a) and shading regions (for panel b–d) represent the mass of SMBHs. The allowed parameter space is shown in yellow. For GSN 069, the star with mass of 0.6 M⊙ and 1.1 M⊙ are shown in red circle and square in panel a, respectively. For the other three shown in panel b–d, the stars with a mass of 0.6 M⊙ and 1.1 M⊙ are shown in red solid and dashed lines, respectively. The average density of stars to explain the properties of QPEs is listed in Table 2, which is between 52.34 g cm−3 and 3642.22 g cm−3. Only low- and intermediate-mass stars whose H envelopes are lost in the VLTP phase (Herwig et al. 1999) can fulfill these requirements. The mass of hydrogen-deficient post-AGB stars are almost the same as the final stellar evolution product WDs, but the density is lower because the existence of He envelopes. |
Required average density of post-AGB stars to produce QPEs.
3. Hydrogen-deficient post-AGB stars
For a low- or intermediate-mass star (initial mass of 1 M⊙ < M < 10 M⊙), the mass loss becomes important in the AGB phase (Bloecker 1995). After hydrogen envelopes are lost in the VLTP phase (Herwig et al. 1999), a hydrogen-deficient star forms. The hydrogen-deficient post-AGB stars have a compact core with He envelopes of several times 10−2 M⊙. The mass of hydrogen-deficient post-AGB stars is almost the same as the final stellar evolution product WDs (0.5−1.4 M⊙), but the density is lower because of the existence of He envelopes. When it evolves to the phase that average density satisfying the range given above, it is captured by the SMBH. It fills the Roche-lobe and donates to the SMBH, generating QPEs.
For the stars with the initial mass 1 M⊙ < M < 8 M⊙, the degenerate CO cores form after core He burning, and the remnants are CO WDs after the residual burning. If the initial stellar mass is higher (8 M⊙ < M < 10 M⊙), the core carbon will be ignited. In this work, we take the evolution of the CO WD with ∼0.6 M⊙ and ONe WD ∼1.1 M⊙ as examples. The initial mass is 3.1 M⊙ and 10 M⊙, respectively. The MESA stellar evolution code (Paxton et al. 2011, 2013, 2015; Paxton et al. 2018) is used to construct the hydrogen-deficient post-AGB stars.
In Fig. 4, the evolution of the average density of hydrogen-deficient post-AGB stars is shown. For the star with an initial mass of 3.1 M⊙, the degenerate CO core (preformed CO WD) is formed in the final phase of AGB evolution. The black line in panel (a) represents the evolution of the post-AGB phase after the H shell extinct in VLTPs. The star has a burning He envelope and finally cools down as a CO WD with the mass of ∼0.6 M⊙. However, for the star with an initial mass of 10 M⊙, it becomes a super-AGB star that is massive enough to ignite C after the giant branch. The black line in panel (b) represents the evolution in C burning phase after the H envelope was removed due to the strong stellar wind. Finally, the star becomes a ONe WD with the mass of ∼1.1 M⊙. The shading regions represent the conditions to produce QPEs given in Table 2, which can last for several 103 years and 104 years for M2 = 0.6 and M2 = 1.1, respectively. When the stars evolve onto the post-AGB phase, the stars are captured by the SMBHs. Due to nuclear evolution or gravitational wave radiation, the star marginally fills its Roche lobe at periapsis and donates material to SMBHs, producing QPEs. The density profile of the hydrogen-deficient post-AGB stars is depicted in Fig. 5. The corresponding age and average density are represented by red stars in Fig. 4, and the stellar properties are listed in Table 3. The regions of degenerate CO core and He envelope are shown in blue and orange, respectively.
 |
Fig. 4. Average density evolution of the post-AGB stars for the initial mass of 3.1 M⊙ (shown in panel a) and 10 M⊙ (shown in panel b). The shading regions represent the conditions to produce QPEs given in Table 2, which can last for several times 103 years and 104 years for M2 = 0.6 and M2 = 1.1, respectively. The age and average density corresponding to Fig. 5 are represented by red stars, and the stellar properties are listed in Table 3. |
 |
Fig. 5. Density (blue lines) and mass (red lines) profiles of the hydrogen-deficient post-AGB stars for the initial mass of 3.1 M⊙ (panel a) and 10 M⊙ (panel b). The stellar properties are listed in Table 3. The regions of degenerate CO core and He envelope are shown in blue and orange, respectively. |
Because the hydrogen-deficient post-AGB stars we got still have a convective envelope, the mass-transfer caused by thermodynamical conditions is also important (Ritter 1988; Kolb & Ritter 1990). It can be expressed as
where ℛ is the gas constant, T2 is the effective temperature, μ is the mean molecular weight, ρph is the photosphere density, and F(q)≪1 for our interest (e.g., the mass ratio q = M1/M2 ∼ 105). The characteristic stellar parameters of hydrogen depleted post-AGB stars are given in Table 3. This mass-transfer rate is negligible compared with that caused by gravitational radiation.
Properties of hydrogen-deficient post-AGB stars with initial masses 3.1 M⊙ and 10 M⊙.
The star can possibly be captured before the post-AGB phase, such as in the formation channel of King (2020). The SMBH captures a red giant and strips the H envelope, then the left He core (low-mass WD) donates material to the SMBH and generates QPEs, which was proposed to explain GSN 069. However, the WD companion quickly loses all its material after a few thousand orbits (Zalamea et al. 2010), which cannot explain the long-standing QPE (Giustini et al. 2020). From the mass-radius relation of WDs (King 2020), we find that the WDs mass is ∼0.05 M⊙ for RXJ1301.9+2747 and eRO-QPE2. However, the extreme low-mass WDs are rare in the Montreal White Dwarf Database1 (Dufour et al. 2017; Kuerban et al. 2020). In addition, eRO-QPE1 and eRO-QPE2 were discovered in quiescent galactic nuclei, which implies the companion will not fill the Roche-lobe before the post-AGB phase.
If the star fills its Roche lobe at periapsis, the stripped matter falls back to the black hole and generate QPEs. From Eq. (15), the life span of QPEs can be estimated by
For M1 = 105 M⊙ and P = 1 h, the life span of QPEs for the post-ABG star donor is ∼2721.57 yr and ∼768.40 yr for M2 = 0.6 M⊙ and M2 = 1.1 M⊙, respectively. The star properties are the same as those in Table 3. The subsequent evolution of the hydrogen-deficient post-AGB stars can be ignored because the life span of QPEs are quite short. Finally, the He enevlopes are all stripped, the compact objects are swallowed by the SMBHs.
4. Event rate
The standard formation channel of EMRIs is the capture of a compact object (WD, NS, or BH) by an SMBH (Sigurdsson & Rees 1997; Amaro-Seoane et al. 2007; Amaro-Seoane 2018). Its rate is about a few percent of the TDE rate. Some other processes include the tidal separation of compact binaries or the formation or capture of massive stars in accretion disks (Amaro-Seoane et al. 2007; Maggiore 2018). In addition, “fake plunges” can serve as high-eccentric EMRIs with a rate about 30 times larger than the typical rate of EMRIs (Amaro-Seoane et al. 2013). Considering the stars injected on high-eccentric orbits in the vicinity of the SMBH due to the Hills binary disruption, the EMRI rate can approach the TDE rate if the binary fraction at the SMBH affecting radius is close to unity (Sari & Fragione 2019). Interestingly, the fraction of binaries is larger than 50% based on the observations. Therefore, we safely assume that the total EMRI rate is on the same order as the TDE rate. Below, we follow the method proposed by our previous work (Wang et al. 2019) to estimate the QPE rate. The mass of SMBHs can be approximated by the MBH − σ relation:
where σ is the spheroid velocity dispersion. The MBH − σ relation also applies for low-mass SMBH (<106 M⊙), considering the uncertainties (Xiao et al. 2011). Hence, this is the relation used in this work. Combined with the constraints from galaxy luminosity functions and the L–σ correlation (Aller & Richstone 2002), the BH mass function is (Gair et al. 2004):
where σ = 3.08/λ, ϕ* is the total number density of galaxies, and Γ(z) is the gamma function. The spatial density of BHs can be estimated from the parameters of low-mass SMBHs (<106 M⊙) (Aller & Richstone 2002)
where h70 ≡ H0/70 km s−1 Mpc−1 is the dimensionless Hubble constant. Then, for solar-type stars, the disruption rate per galaxy is (Wang & Merritt 2004):
The number ratio of 1–10 M⊙ stars to solar-type stars is about 0.48 using the Salpeter initial mass function, while the lifetime ratio is estimated to be 10−2 on average. Since the density of the He envelope in our scenario is 102 to 103 times larger than that of solar-type stars, this results in a smaller tidal radius. We reduce the rate by a factor of 1 × 10−2. Last but not least, our model requires the star to be located in the He main sequence, whose duration is roughly 0.1 times that of the H main sequence. Integrating Eq. (22) over 1 M⊙ < M* < 10 M⊙ and 20 R⊙ < R* < 60 R⊙ and then combining all the aforementioned factors gives the event rate of ṄQPE = 1.5 Gpc−3 yr−1 for MBH = 5 × 105 M⊙. Therefore, the observed number of QPEs can be calculated as
where V is the searching volume, and τQPE is the active lifttime of QPEs. The co-moving volume within the redshift z = 0.0505 of the most distant QPE event (eRO-QPE1) is V ∼ 0.04Gpc3. In our model, the range of τdest is 100 ∼ 1000yr (Eq. (18)). Hence, NQPE is between 6−60. It has been estimated that eROSITA would discover up to about 10 or 15 QPEs by the end of 2023 (Arcodia et al. 2021), which is fully consistent with our estimation.
5. Gravitational wave signal detection
The mass-loss systems involving MS and SMBH can be the GW sources (Linial & Sari 2017). In our model, these QPEs are also promising GW sources for space-based GW detectors, such as LISA (Amaro-Seoane et al. 2017; Amaro-Seoane 2018) and TianQin (Luo et al. 2016). The Keplerian orbital frequency of QPEs is about forb ∼ 10−4 Hz. The compact core with helium envelopes inspiral into the SMBH produces EMRI signals at a frequency of f = 2forb, which can be detected by LISA and Tianqin. The current LISA mission, planned to be launched in 2030s, has an arm-length of 2.5 × 109 m and is sensitive to low frequency bands (10−4 ∼ 10−1 Hz). The Tianqin has a similar scientific goal, but uses the Earth orbit instead of the heliocentric orbit. Generally, it takes several years for the compact core to plunge into the SMBH after entering the GW detection bands. Therefore, 104 to 105 circles can be recorded by detectors to build up the signal-to-noise ratio (S/N) with a hierarchical matched filtering method, which divides data into short segments and adds their power incoherently.
The GW emission power evolution is (Peters 1964):
and the Keplerian orbital evolution is:
The characteristic strain of the GW emission from the proper distance D away from the detector is (Amaro-Seoane 2018; Maggiore 2018):
where h0 is an instantaneous root-mean-square amplitude. Unlike Chen et al. (2021), GW radiation in harmonic frequencies is not considered. The characteristic strains of different BH masses are shown in Fig. 6, where we set z = 0.02, M2 = 0.6 M⊙, a = 5 × 1012 cm, and e = 0.9. These GW signal of these QPEs is well above the sensitivity curves of LISA (blue line) and Tianqin (purple line). These sources with EMRI signals and electromagnetic counterparts are important for cosmological purposes, such as measuring the Hubble constant (Abbott et al. 2017; Chen et al. 2018; Yu et al. 2018) and the peculiar velocity (Wang et al. 2018; Palmese & Kim 2021).
 |
Fig. 6. Diagram of the characteristic strains of EMRIs for different BH masses. We set z = 0.02, M2 = 0.6 M⊙ , a = 5 × 1012 cm, and e = 0.9. The sensitivity curves of LISA (blue line) and Tianqin (purple line) are also plotted for comparison. These QPEs are promising EMRI sources for LISA and Tianqin. |
6. Summary
In this paper, we propose a hydrogen-deficient post-AGB star orbiting the SMBH as the generation mechanism of QPEs. The whole picture of this scenario is as follows: a star with an initial mass between 1–10 M⊙ evolves into a post-AGB phase, then it is captured by a SMBH to form an elliptic orbit. When it passes the periapsis, the star fills its Roche lobe, leading to a mass transfer to the SMBH. The accretion of the mass by the SMBH leads to the production of QPEs.
According to the rise time, the orbit stability, and the luminosity of QPEs, we find the average density of the companion ranges from tens to thousands of g cm−3. The average density of the donor of GSN 069, RXJ1301.9+2747, eRO-QPE1and eRO-QPE2 is expected to be 899.26 g cm−3, 91.81−187.85 g cm−3, 2314.79−3642.22 g cm−3, and 538.98−800.92 g cm−3 for M2 = 0.6 M⊙, respectively. For M2 = 1.1 M⊙, the required average density is 318.13 g cm−3, 52−66.46 g cm−3, 818.92−1288.53 g cm−3, and 190.68−283.35 g cm−3, respectively. The properties of hydrogen-deficient post-AGB stars are consistent with these constraints.
The MESA stellar evolution code is used to construct the evolutions of low and intermediate-mass stars. We find that when they lost the H envelopes in the VLTP phase and evolve to hydrogen-deficient post-AGB stars can meet the constraints on the average density. The rate of QPEs is estimated to be 1.5 Gpc−3 yr−1. In our model, QPEs are promising candidates for the electromagnetic counterparts of EMRIs. The GWs from these QPEs can be detected by LISA and Tianqin.
Acknowledgments
We thank the anonymous referee for helpful comments, Rong-Feng Shen, Xin-Wen Shu, Ting-Gui Wang, Abudushataer Kuerban and Ying Qin for discussions. This work was supported by the National Natural Science Foundation of China (grant Nos. U1831207 and 11833003), the Fundamental Research Funds for the Central Universities (No. 0201-14380045), and the National Key Research and Development Program of China (grant No. 2017YFA0402600 and 2020YFC2201400), the National SKA Program of China (No. 2020SKA0120300) and NWO, the Dutch Research Council, under Vici research programme ‘ARGO’ with project number 639.043.815.
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017, Nature, 551, 85 [Google Scholar]
- Aller, M. C., & Richstone, D. 2002, AJ, 124, 3035 [NASA ADS] [CrossRef] [Google Scholar]
- Amaro-Seoane, P. 2018, Liv. Rev. Relativ., 21, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Amaro-Seoane, P., Gair, J. R., Freitag, M., et al. 2007, Classical Quantum Gravity, 24, R113 [NASA ADS] [CrossRef] [Google Scholar]
- Amaro-Seoane, P., Sopuerta, C. F., & Freitag, M. D. 2013, MNRAS, 429, 3155 [NASA ADS] [CrossRef] [Google Scholar]
- Amaro-Seoane, P., Audley, H., Babak, S., et al. 2017, ArXiv e-prints [arXiv:1702.00786] [Google Scholar]
- Arcodia, R., Merloni, A., Nandra, K., et al. 2021, Nature, 592, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Bardeen, J. M., Press, W. H., & Teukolsky, S. A. 1972, ApJ, 178, 347 [Google Scholar]
- Bloecker, T. 1995, A&A, 297, 727 [Google Scholar]
- Chen, H.-Y., Fishbach, M., & Holz, D. E. 2018, Nature, 562, 545 [Google Scholar]
- Chen, X., Qiu, Y., Li, S., & Liu, F. K. 2021, ArXiv e-prints [arXiv:2112.03408] [Google Scholar]
- Czerny, B., Siemiginowska, A., Janiuk, A., Nikiel-Wroczyński, B., & Stawarz, Ł. 2009, ApJ, 698, 840 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, L., & Blandford, R. 2013, MNRAS, 434, 2948 [NASA ADS] [CrossRef] [Google Scholar]
- Danzmann, K. 2000, Adv. Space Res., 25, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Dufour, P., Blouin, S., Coutu, S., et al. 2017, ASP Conf. Ser., 509, 3 [Google Scholar]
- Gair, J. R., Barack, L., Creighton, T., et al. 2004, Classical Quantum Gravity, 21, S1595 [NASA ADS] [CrossRef] [Google Scholar]
- Gezari, S. 2021, ARA&A, 59, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Giustini, M., Miniutti, G., & Saxton, R. D. 2020, A&A, 636, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grzedzielski, M., Janiuk, A., Czerny, B., & Wu, Q. 2017, A&A, 603, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillochon, J., & Ramirez-Ruiz, E. 2013, ApJ, 767, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Hameury, J. M., King, A. R., Lasota, J. P., & Auvergne, M. 1994, A&A, 292, 404 [NASA ADS] [Google Scholar]
- Herwig, F., Blöcker, T., Langer, N., & Driebe, T. 1999, A&A, 349, L5 [NASA ADS] [Google Scholar]
- Hiltner, W. A., & Schild, R. E. 1966, ApJ, 143, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Ingram, A., Motta, S. E., Aigrain, S., & Karastergiou, A. 2021, MNRAS, 503, 1703 [NASA ADS] [CrossRef] [Google Scholar]
- Janiuk, A., & Czerny, B. 2011, MNRAS, 414, 2186 [NASA ADS] [CrossRef] [Google Scholar]
- Janiuk, A., Czerny, B., & Siemiginowska, A. 2002, ApJ, 576, 908 [NASA ADS] [CrossRef] [Google Scholar]
- Jefremov, P. I., Tsupko, O. Y., & Bisnovatyi-Kogan, G. S. 2015, Phys. Rev. D, 91, 124030 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. 2020, MNRAS, 493, L120 [Google Scholar]
- Kolb, U., & Ritter, H. 1990, A&A, 236, 385 [NASA ADS] [Google Scholar]
- Kuerban, A., Huang, Y. F., Geng, J. J., & Zong, H. S. 2020, ArXiv e-prints [arXiv:2012.05748] [Google Scholar]
- Law-Smith, J., MacLeod, M., Guillochon, J., Macias, P., & Ramirez-Ruiz, E. 2017, ApJ, 841, 132 [CrossRef] [Google Scholar]
- Linial, I., & Sari, R. 2017, MNRAS, 469, 2441 [CrossRef] [Google Scholar]
- Luo, J., Chen, L.-S., Duan, H.-Z., et al. 2016, Classical Quantum Gravity, 33, 035010 [NASA ADS] [CrossRef] [Google Scholar]
- Maggiore, M. 2018, Gravitational Waves, Vol. 2 (Oxford University Press) [CrossRef] [Google Scholar]
- Merloni, A., & Nayakshin, S. 2006, MNRAS, 372, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Metzger, B. D., Stone, N. C., & Gilbaum, S. 2022, ApJ, 926, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Miniutti, G., Saxton, R. D., Giustini, M., et al. 2019, Nature, 573, 381 [Google Scholar]
- Paczynski, B., & Sienkiewicz, R. 1981, ApJ, 248, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Palmese, A., & Kim, A. G. 2021, Phys. Rev. D, 103, 103507 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, J., Walker, S., Kemp, J., et al. 2000, PASP, 112, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
- Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, P. C. 1964, Phys. Rev., 136, 1224 [Google Scholar]
- Reines, A. E., & Volonteri, M. 2015, ApJ, 813, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Ritter, H. 1988, A&A, 202, 93 [NASA ADS] [Google Scholar]
- Rosswog, S., Ramirez-Ruiz, E., & Hix, W. R. 2009, ApJ, 695, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Sander, A., Hamann, W. R., & Todt, H. 2012, A&A, 540, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sari, R., & Fragione, G. 2019, ApJ, 885, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Sepinsky, J. F., Willems, B., & Kalogera, V. 2007, ApJ, 660, 1624 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, R.-F. 2019, ApJ, 871, L17 [CrossRef] [Google Scholar]
- Sheng, Z., Wang, T., Ferland, G., et al. 2021, ApJ, 920, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, X. W., Wang, T. G., Jiang, N., et al. 2017, ApJ, 837, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, X. W., Wang, S. S., Dou, L. M., et al. 2018, ApJ, 857, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Sigurdsson, S., & Rees, M. J. 1997, MNRAS, 284, 318 [NASA ADS] [Google Scholar]
- Thorne, K. S. 1974, ApJ, 191, 507 [Google Scholar]
- Wang, J., & Merritt, D. 2004, ApJ, 600, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y. Y., Wang, F. Y., & Zou, Y. C. 2018, Phys. Rev. D, 98, 063503 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y. Y., Wang, F. Y., Zou, Y. C., & Dai, Z. G. 2019, ApJ, 886, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Q., Czerny, B., Grzedzielski, M., et al. 2016, ApJ, 833, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Xiao, T., Barth, A. J., Greene, J. E., et al. 2011, ApJ, 739, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, H., Ratra, B., & Wang, F.-Y. 2018, ApJ, 856, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Zalamea, I., Menou, K., & Beloborodov, A. M. 2010, MNRAS, 409, L25 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Properties of hydrogen-deficient post-AGB stars with initial masses 3.1 M⊙ and 10 M⊙.
All Figures
 |
Fig. 1. Schematic diagram of the mechanism for QPEs. A hydrogen-deficient post-AGB star with He envelope orbits around an SMBH on an eccentric orbit. When the star approaches periapsis, it just fills its Roche lobe. The He envelope with low density ends up partially tidally stripped by the SMBH, while the compact core survives the encounter. Finally, the stripped material falls back to the SMBH, resulting in QPEs. |
| In the text | |
 |
Fig. 2. Periapsis Rp in units of the gravitational radius from the mass–radius relation of WDs (shown in panel a) and orbital eccentricity (shown in panel b). The results of King (2020) are shown in black circles for GSN 069. For eRO-QPE1 and eRO-QPE2, M1 is estimated by 0.025%Mstellar (Reines & Volonteri 2015). The radii of ISCO for Schwarzschild BHs (a = 0) and extreme-rotating BHs (a = 0.998) are also illustrated in black lines. Panel a: Mass–radius relation of WDs is taken from Zalamea et al. (2010). The case of WDs companion for RXJ1301.9+2747 and eRO-QPE2 is only possible for extreme low-mass WDs or Kerr BHs. Panel b: unless the eccentricity is very high, the mass transfer can be carried out stably. |
| In the text | |
 |
Fig. 3. Contours of allowed average density for different values of the SMBH mass, M1, and the companion star mass, M2. The white solid lines refer to constraints from the rise time. The excluded region is shown in blue. The gray region shows different densities of the companion star. The yellow vertical solid line (for panel a) and shading regions (for panel b–d) represent the mass of SMBHs. The allowed parameter space is shown in yellow. For GSN 069, the star with mass of 0.6 M⊙ and 1.1 M⊙ are shown in red circle and square in panel a, respectively. For the other three shown in panel b–d, the stars with a mass of 0.6 M⊙ and 1.1 M⊙ are shown in red solid and dashed lines, respectively. The average density of stars to explain the properties of QPEs is listed in Table 2, which is between 52.34 g cm−3 and 3642.22 g cm−3. Only low- and intermediate-mass stars whose H envelopes are lost in the VLTP phase (Herwig et al. 1999) can fulfill these requirements. The mass of hydrogen-deficient post-AGB stars are almost the same as the final stellar evolution product WDs, but the density is lower because the existence of He envelopes. |
| In the text | |
 |
Fig. 4. Average density evolution of the post-AGB stars for the initial mass of 3.1 M⊙ (shown in panel a) and 10 M⊙ (shown in panel b). The shading regions represent the conditions to produce QPEs given in Table 2, which can last for several times 103 years and 104 years for M2 = 0.6 and M2 = 1.1, respectively. The age and average density corresponding to Fig. 5 are represented by red stars, and the stellar properties are listed in Table 3. |
| In the text | |
 |
Fig. 5. Density (blue lines) and mass (red lines) profiles of the hydrogen-deficient post-AGB stars for the initial mass of 3.1 M⊙ (panel a) and 10 M⊙ (panel b). The stellar properties are listed in Table 3. The regions of degenerate CO core and He envelope are shown in blue and orange, respectively. |
| In the text | |
 |
Fig. 6. Diagram of the characteristic strains of EMRIs for different BH masses. We set z = 0.02, M2 = 0.6 M⊙ , a = 5 × 1012 cm, and e = 0.9. The sensitivity curves of LISA (blue line) and Tianqin (purple line) are also plotted for comparison. These QPEs are promising EMRI sources for LISA and Tianqin. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



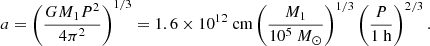
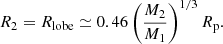
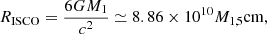
![$$ \begin{aligned} \begin{aligned}&R_{\mathrm{ISCO} }=\frac{G M_{\mathrm{1} }}{c^{2}}\left\{ 3+Z_{2} \mp \left[\left(3-Z_{1}\right)\left(3+Z_{1}+2 Z_{2}\right)\right]^{1 / 2}\right\} , \\&Z_{1} \equiv \left(1-3 a_{\text{s}}^{2} / M_{\mathrm{1} }^{2}\right)^{1 / 3}\left[\left(1+a_{\text{s}} / M_{1}\right)^{1 / 3}+\left(1-a_{\text{s}} / M_{1}\right)^{1 / 3}\right], \\&Z_{2} \equiv \left(3 a_{\text{s}}^{2} / M_1^{2}+Z_{1}^{2}\right)^{1 / 2}, \end{aligned} \end{aligned} $$](/articles/aa/full_html/2022/05/aa42519-21/aa42519-21-eq6.gif)
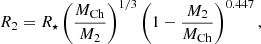
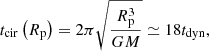
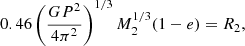
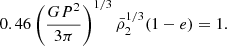
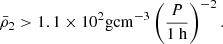
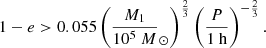
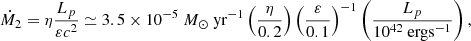
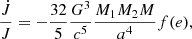
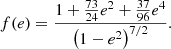
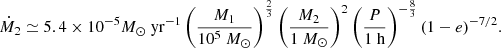
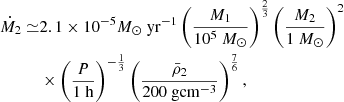
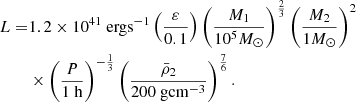
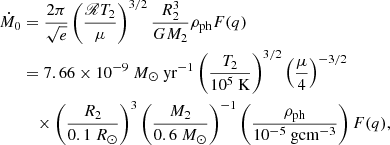
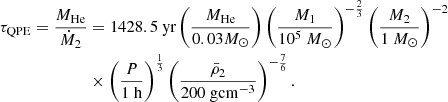
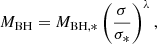
![$$ \begin{aligned} M_{\mathrm{BH} } \frac{\text{ d} N}{\text{ d} M_{\mathrm{BH} }}=\phi _{*} \frac{\epsilon }{\Gamma \left(\frac{\gamma }{\epsilon }\right)}\left(\frac{M_{\mathrm{BH} }}{M_{\mathrm{BH} , *}}\right)^{\gamma } \times \exp \left[-\left(\frac{M_{\mathrm{BH} }}{M_{\mathrm{BH} , *}}\right)^{\epsilon }\right] ,\end{aligned} $$](/articles/aa/full_html/2022/05/aa42519-21/aa42519-21-eq32.gif)