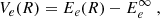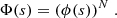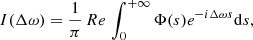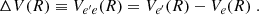EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 659 (March 2022) A&A, 659 (2022) A157 Full HTML
Open Access
Issue
A&A
Volume 659, March 2022
Article Number A157
Number of page(s) 7
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/202142717
Published online 22 March 2022

© F. Spiegelman et al. 2022

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1. Introduction

In the spectra of white dwarf stars exhibiting strong heliums lines with weaker hydrogen lines, that is to say DBA white dwarfs, there is a discrepancy between the values of the hydrogen abundances determined from Balmer-α in the visible and those from Lyman-α in the ultraviolet (see Xu et al. 2017, and references therein). The existence of close line satellites in the blue wing of these lines was found in detailed collisional broadening profiles computed for both H-He and H-H (Spiegelman et al. 2021; Allard et al. 2022). These features are responsible for the asymmetrical shape and the decreasing strength of the core of the lines in those cases. In this paper we extend our study to the Balmer-β line by considering the H(n = 4) perturbed by He.

In recent previous works, we used new multi-reference configuration interaction (MRCI) calculations of the excited state potential energy curves dissociating into H(n = 1,2,3)+He, as well as the relevant electric dipole transition moments contributing to the Lyman-α and Balmer-α spectra. We illustrated how tiny relativistic effects affect the asymptotic correlation of the H-He adiabatic states and change the related transition dipole moments.

In the present work, we determine potential energy curves dissociating into H(n = 4)+He and transition dipole moments of H-He involving initial and final states correlated with H(n = 2)+He and H(n = 4)+He, respectively. Between these states, there are 23 H-He transitions which generate the complete Balmer-β line profile. The Σ − Σ transitions provide the essential contribution to the blue wing of the Balmer series lines, explain their asymmetrical behavior, and are relevant to the cool DBA white dwarf analyses. The potential energy curves and transition dipole moments are discussed in Sect. 2. Unified profile calculations are presented in Sect. 3. They show that in He-rich white dwarf stars, the non-Lorentzian shape of Balmer-β increases with He density and it will affect abundance analyses if not included in stellar atmosphere models. Consequently the strength and shape of the Balmer line series are also diagnostics of the atmospheric conditions of cool DZA white dwarf stars.

In Sect. 4 we consider the general trend of the repulsive Σ state of the excited states of H-He. They contribute through the Lyman and Balmer lines and lead to a non-Lorentzian shape that is increasingly significant in higher series members that affect the visible spectrum of helium-rich white dwarfs.

2. Diatomic H-He potentials and electronic transition dipole moments

The calculation scheme for the potentials dissociating into H(n = 2,3,4)+He is the same as described in our previous publications concerned with the Lyman-α (Spiegelman et al. 2021) and the Balmer-α (Allard et al. 2022) broadenings. Briefly, a MRCI (Knowles & Werner 1992; Werner et al. 2015) calculation was run within an extensive Gaussian-type orbital (GTO) basis set. Scalar relativistic corrections (namely the Darwin and mass-velocity terms) according to the Douglas-Kroll-Hess (DKH) scheme (Reiher 2006; Nakajima & Hirao 2011), breaking the specific degeneracy of the atomic hydrogen levels determined with the Coulomb Hamiltonian only, were added. In order to improve the description of the adiabatic molecular states of H-He toward the n = 4 atomic limit, we refined the basis set used in our previous works (Spiegelman et al. 2021; Allard et al. 2022), consisting of an aug-cc-pv6z quality description complemented by diffuse exponents for all s, p, d, f, g, and h functions for H and He, reoptimizing the exponents of the external d and f GTO functions of hydrogen (see Table A.1). Table A.2 compares the calculated transitions from 1s to n = 4 with the j-averaged experimental ones. The calculated 4s − 4f splitting is 0.14 cm−1 larger, but of the same order of magnitude as the experimental value 0.061 cm−1.

In the following, we use the spectroscopist’s notations X, A, B, and C to label the lower adiabatic molecular states of H-He, namely the ground state 1 2Σ+, the lowest excited states 2 2Σ+, 1 2Π, and 3 2Σ+ correlated with H(n = 2)+He, while we label the upper states correlated with H(n = 4)+He according to their adiabatic ranking in their respective symmetries. For a detailed characterization of states n = 2, 3, we refer readers to our previous papers (Spiegelman et al. 2021; Allard et al. 2022) and to earlier literature (Theodorakopoulos et al. 1987; Ketterle et al. 1985, 1988; Ketterle 1989; Sarpal et al. 1991; Lo et al. 2006; van Hemert & Peyerimhoff 1991; Ketterle 1990a,b; Allard et al. 2020). The molecular states dissociating into 4s, 4p, 4d, and 4f are (7–10) 2Σ+, (4–6) 2Π, (2,3) 2Δ, and 1 2Φ. Figure 1 shows the potential energy curves of the states dissociating into H(n = 2)+He and H(n = 4)+He. All states are bound with equilibrium distances close to 0.77 Å, most of them have similar dissociation energies around 16 500 cm−1 and vibrational constants ωexe, and they can hardly be individually identified at the scale of the figure. Those dissociation energies are also quite similar to those of the HeH+ ion (Re = 0.7742 Å, De = 16 455.64 cm−1, and ωe = 3220 cm−1) calculated by Koos & Peek (1976), which are consistent with the Rydberg nature of those states (Ketterle 1990c,d). The detailed spectroscopic constants are given in the Table A.3. The most stable state is 7 2Σ+ with a dissociation energy of De = 16 882 cm−1. Conversely, state 10 2Σ+ is the least stable (De = 15 157 cm−1), and it has a barrier to dissociation. This feature is analog to those observed for the respective highest states dissociating into the n = 2 and n = 3 configurations, namely C2Σ+ and 6 2Σ+. To our knowledge, no previous theoretical data exist for the molecular states of HHe correlated with n = 4. A detailed experimental investigation was published by Ketterle (1990c) who could characterize states 4 2Π, 5 2Π, and 2 2Δ. The present calculated v′ = 0 to v″ = 0 vibrational transitions (T00 values) are in agreement with Ketterle’s data with a rms deviation of 16 cm−1 (see Table A.3). At long distance in the range 17–28 Å, the states undergo multiple avoided crossings, which determine their correlation with the atomic asymptotes, as illustrated in Fig. 2.

thumbnail Fig. 1.

MRCI adiabatic potential energy curves of molecular states dissociating into H(n = 2,4)+He. The R scale is a logarithmic graduation. The dashed lines correspond to potential energy curves dissociating into H(n = 3)+He.

thumbnail Fig. 2.

Long range zoom on the adiabatic potential energy curves of H(n = 4)+He.

All transition dipole moments D(R) between the n = 2 and n = 4 adiabatic states were calculated using the MRCI wavefunctions, namely transitions from A2Σ+, C2Σ+ to 7,8,9,10 2Σ+ and to 4,5,6 2Π, from B2Π to 7,8,9,10 2Σ+, 4,5,6 2Π and 2,3 2Δ. The A2Σ+, C2Σ+, B2Π − 102Σ+ asymptotically forbidden transitions are involved in the blue wing contribution, as discussed below. The A2Σ+, C2Σ+ − 7,8,9,10 2Σ+ transition moments display a rather complex picture shown in Fig. 3. Their evolution can be rationalized considering the following three key features: (i) the avoided crossing between the lower states A2Σ+ and C2Σ+ around R = 8.1 Å (Spiegelman et al. 2021), (ii) the multiple avoided crossing between the upper states (7 − 10)2Σ+ in the range R = 17–28 Å illustrated in Fig. 2, and (iii) other avoided crossings between the upper states at short distance of R ≤ 5 Å.

thumbnail Fig. 3.

Transition dipole moments D(R) of H-He between 2Σ+ states n = 2 and n = 4.

The situation is thus similar to what was observed for the Lyman-α and Balmer-α molecular transitions: while relativistic effects, partly taken into account here, obviously play a negligible role in the energies of the H(4f)+He states (less than ≈0.1 cm−1) and in the transition dipole moments at short distance, they break the Coulomb asymptotic degeneracy and induce cascade avoided crossings which determine the asymptotic correlation of the adiabatic states and the variation of the dipole transition moments at medium and long distance.

3. Analysis of the Balmer-β profile perturbed by He atoms

The highest molecular states correlated to n = 2 and n = 3 have a prominent role in the appearance of blue satellite features in Lyman-α (Spiegelman et al. 2021) and Balmer-α (Allard et al. 2022) line profiles. If we define the potential energy V(R) for a state e as

(1)

the prediction of a line satellite in the blue wing is related to the maximum of V(R) of these repulsive states. The upper box of Fig. 4 shows a comparison of the short-range part of the potential curve V(R) of the following repulsive states: C2Σ+, 6 2Σ+, and 10 2Σ+, corresponding to the highest states correlated to the n = 2, n = 3, and n = 4 levels, respectively. With increasing n, the barrier height decreases (5386 cm−1, 1390 cm−1, and 574 cm−1 for n = 2, 3, and 4, respectively) and the repulsion of the state above the asymptote rises at greater distances, namely R = 8, 15, and 25 Å for n = 2, 3, and 4, as can be seen in Figs. 1 and 2.

thumbnail Fig. 4.

Repulsive potentials and their difference. Top: potential energy V of the repulsive states of Lyman-α (dashed black curve), Balmer-α (dashed red curve), and Balmer-β (blue curve). Bottom: difference potential ΔV(R) for the Lyman-α transition X → C (dashed black curve), for the Balmer-α transition C → 62Σ+ (dashed red curve), and for the Balmer-β transitions C → 102Σ+ (blue curve).

It is essential to use a general unified theory in which the electric dipole moment varies during a collision because all transitions of Balmer-β from the 2s and 2p states to the 4f state are asymptotically forbidden. Most of the problems in collision-induced radiative transitions have been solved within the one-perturber approximation. At low densities, the binary model for an optically active atom in collision with one perturber is valid for the whole profile, except for the central part of the line. In dense plasmas, as in very cool DZ white dwarfs (Allard et al. 2016; Kawka et al. 2021) and liquid helium clusters (Allard et al. 2013), the possibility of several atoms interacting strongly is high, and the effects play a role in the wavelength of the line center, for example in the shift of the line as well as the general shape of the line profile. For such a high perturber density, the collisional effects should be treated by using the autocorrelation formalism in order to take simultaneous collisions with more than one perturbing atom into account. A pairwise additive assumption allows us to calculate the total profile I(Δω), when all the perturbers interact through the Fourier transform (FT) of the Nth power of the autocorrelation function ϕ(s) of a unique atom-perturber pair. Therefore

(2)

That is to say, we neglect the interperturber correlations. The radiator can interact with several perturbers simultaneously, but the perturbers do not interact with each other. It is what Royer (1980) calls the "totally uncorrelated perturbers approximation”. The fundamental result expressing the autocorrelation function for many perturbers in terms of a single perturber quantity g(s) was first obtained by Anderson (1952) and Baranger (1958b) in the classical and quantum cases, respectively. From the point of view of a general classical theory, the solution to the Anderson (1952) model corresponds to the first order approximation in the gas density obtained by the cumulant expansion method (Royer 1972). The higher order terms representing correlations between the perturbers are neglected since they are extremely complicated (Royer 1972; Kubo 1962a,b; Kampen 1974). In Allard et al. (1999), we derived a classical path expression for a pressure-broadened atomic spectral line shape that allows for an electric dipole moment that is dependent on the position of perturbers, which is not included in the approximations of Anderson (1952) and Baranger (1958a,b).

The spectrum I(Δω) can be written as the FT of the dipole autocorrelation function Φ(s) ,

(3)

where s is time. The FT in Eq. (3) is taken such that I(Δω) is normalized to unity when integrated over all frequencies, and Δω is measured relative to the unperturbed line. We have provided an overview of the unified theory in Sect. 3 of Spiegelman et al. (2021).

The unified theory predicts that line satellites will be centered periodically at frequencies corresponding to integer multiples of the extrema of ΔV(R), the difference between the energies of the quasi-molecular transition, defined as follows:

(4)

The bottom of Fig. 4 shows ΔV(R) for the transitions X → C related to Lyman-α, C → 6 2Σ+ related to Balmer-α compared to ΔV(R) for the transition C → 10 2Σ+ related to Balmer-β. The main contribution to the blue wing is due to the forbidden C 2p2Σ+ →4f 102Σ+ transition. The transition dipole moment D(R) between the C 2p electronic state and the 4f state asymptotically vanishes as the radiative transition between the corresponding atomic states is forbidden (Fig. 3). Although this transition should not contribute to the unperturbed line profile, radiative transitions can be induced by close collisions because D(R) differs from zero when a He atom passes close to the H atom. To point out the importance of the variation of the dipole moment on the formation of collision-induced (CI) satellite, we have displayed D(R) together with the corresponding ΔV(R) for the C 2p − 4f transition in Fig. 5. The satellite amplitude depends on the value of D(R) through the region of the potential maximum responsible for the satellite and on the position of this extremum (Allard et al. 1998). The presence of quasi-molecular satellites due to collision effects is unimportant when the He density is low; however, in the physical conditions found in the cool atmospheres of He-rich white dwarfs, their presence leads to an asymmetrical shape of the Balmer profiles which is a signature of a high helium density. Figure 6 shows a very broad blue wing with a close CI line satellite at about 200 cm−1 from the line center corresponding to the maximum of ΔV(R). The line profile obtained when taking only the allowed transitions into account is overplotted. The main objective of this figure is to illustrate the contribution of the forbidden transitions to the Balmer-β profile. Figure 7 shows that the presence of a line satellite in the near line wing leads to a complex behavior of the dependence of the line shape on He density. As in the case of the DZA white dwarf L745-46A obtained at the ESO La Silla 3.6m telescope, the observed spectrum of Ross 640 obtained at Calar Alto (Fig. 7 in Koester & Wolff 2000) shows an observed Balmer-β line with a very broad blue wing due to high He densities which can reach 1021 cm−3 in the Balmer-α and β formation region (Vennes, priv. comm.). Figure 8 shows a very broad line profile at this He density for both Balmer lines. In particular, we have found that the Balmer-β line profile is totally asymmetric in this range of He density. This effect is already present at the lower density, 2 × 1020 cm−3, and it has an increasing importance with He density (Fig. 7). The development of the blue wing leads to the center of the main line being overwhelmed by the blend of line satellites. As a result, the full treatment of the Balmer-β line reveals strong effects on its opacity outside the impact approximation. The Lorentzian approximation is overplotted in Figs. 6 and 7. Consequently, we conclude that these collision-induced effects are not always negligible when models of stellar spectra are compared with observations to determine abundances, structural properties, or ages.

thumbnail Fig. 5.

Difference potential energy ΔV(R) in cm−1 (black line) and dipole moment D(R) (black dashed line) for the forbidden C 2p → 4f 102Σ+ transition.

thumbnail Fig. 6.

Comparison of the total profile (blue line) to the profile restrictly obtained with the allowed transitions (red dashed line). The Balmer-β line profile is also compared to the Lorentzian approximation (black dashed curve). The He density is 5 × 1020 cm−3, and the temperature is 8000 K.

thumbnail Fig. 7.

Variation with the He density of the Balmer-β line profile for 2 × 1020 (black line), 3 × 1020 (blue line), and 5 × 1020 cm−3 (red line); the temperature is 8000 K. The Balmer-β line profiles are also compared to the Lorentzian approximation for the He densities 2 × 1020 cm−3 (dashed black line) and 3 × 1020 cm−3 (dashed blue line).

4. Consequences on the Balmer series

Figure 1 illustrates the potential energies involved in Lyman-α, Balmer-α, and Balmer-β. Due to the more diffuse character of the 4s, 4p, 4d, and 4f orbitals with respect to those with smaller n, the barrier height of the highest state extends to a wider distance range and is lower than that of states C2Σ+ and 62Σ+. The characteristics of the highest states must be stressed in view of the study of the asymmetrical shape dependence on the order of the Balmer series. The top of Fig. 4 summarizes the potential energies of the highest states involved in Lyman-α, Balmer-α, and Balmer-β, and the bottom of it shows the corresponding ΔV(R). The essential characteristics to note are that the maximum in ΔV occurs at larger internuclear distances (Rmax ∼ 10 Å) for Balmer-β than for Balmer-α (Rmax ∼ 5.4 Å) and Lyman-α (Rmax ∼ 2 Å). ΔV(R) presents a flat maximum at a larger distance for Balmer-β. The average number of perturbers in the interaction volume at Rmax is the most determining parameter for the amplitude of the satellites in the spectral line (Allard 1978; Royer 1978; Allard & Kielkopf 1982). This dependence on the average number of perturbers in the collision volume is expected on the basis of the Poisson distribution, which indicates the probability of finding a given number of uncorrelated perturbers in the collision volume. It was decisively identified in the theoretical analysis of experimental Cs spectra by Kielkopf & Allard (1979). The other crucial point is that the maximum ΔVmax is smaller with 350 cm−1 for Balmer-β, versus 1000 cm−1 for the Balmer-α line and 5000 cm−1 for the Lyman-α line. The Balmer-β line satellite gets closer to the main line than the Balmer-α and Lyman satellites, as shown in Fig. 8, Fig. 6 of Allard et al. (2022), and Fig. 11 of Spiegelman et al. (2021). Its effect on the asymmetrical shape of the Balmer profile and on its amplitude becomes more important and appears at a lower density.

thumbnail Fig. 8.

Comparison of the Balmer-α (black curves) and Balmer-β (red curves) line profiles. The He densities are 1021 cm−3 (full curves) and 6 × 1020 cm−3 (dashed curves); the temperature is 8000 K.

Because of this general trend characterizing the repulsive Σ states, the average number of perturbers in the interaction volume will get larger for higher series of Balmer lines, leading to a higher probability of multiple-pertuber effects. The core of the main line due to allowed transitions will disappear, being replaced by the blend of multiple satellites (Kielkopf 1983, 1985). This is what is already happening in the Balmer-β line when the He density gets as large as 1021 cm−3. Figure 8 shows a broad line profile with a decreasing asymmetry and a change in the sign of its shift resulting from the disappearance of the main line due to the allowed transitions replaced by the blend of multiple line satellites. Increasing the He density has the same effect as considering a higher member of the Balmer series as it increases the probability of multiple pertuber effects. This behavior is well known in line broadening theory and has been thoroughly studied in the 1950s by the Ch’en group (Allard & Kielkopf 1982). The spectra of members of the Balmer series corresponding to a transition to upper level n are then progressively more blueshifted and shallower as n increases. The observed spectra of PG 1157+004 (Fig. 17, 11598+007 of Limoges et al. 2015) or of WDJ0103-0522 (Fig. 2 of Tremblay et al. 2020), which are both massive white dwarfs with a very high log g, exhibit a strong asymmetry and a blue shift, providing further evidence that we are dealing with an unresolved blend of quasi-molecular line satellites due to high He densities. For PG 1157+004, the helium density is 3 × 1020 cm−3 in the region of the formation of the Balmer-α and β lines (Vennes, priv. comm.). Figure 7 shows that even at this rather low density, the Balmer-β line profile shows an asymmetrical shape. For cooler atmospheres, as in the case of WDJ0103-0522, the He density is as high as 1021 (Vennes, priv. comm.). Many explanations have tried to solve that puzzle of such white dwarf spectra, such as two sources contributing to the Balmer features (Limoges et al. 2015) or magnetic fields (Tremblay et al. 2020).

The resonance broadening of H perturbed by collisions with H atoms produces asymmetry in the Balmer-α line profiles similar to that due to H-He (Allard et al. 2022), but the H density in DA white dwarfs is not as large as the He density in cool He-rich DBA to have such an effect in their observed spectra. This a major difference between Balmer spectra of a DA or of a cool DBA white dwarf. More generally, the important sensitivity of the Balmer line shapes to the nature of the perturber and its density suggests that they could be used as a diagnostic tool given precision low-noise observed spectra and appropriate line shape theory based on the high accuracy now provided by first-principles theoretical atomic and molecular physics.

In conclusion, an accurate determination of neutral-collision-broadened lines is required to interpret the strength, broadening, and shift of the resulting Balmer line profiles correctly. Calculations reported in Allard et al. (2022) for Balmer-α and in this paper for Balmer-β, especially for H-H collisions, involve a huge number of transitions, and they are dependent on very accurate molecular data. The past laboratory experimental work and analysis of observations of multiple-perturber effects on the broadening of atomic spectral lines such as by Kielkopf (1983, 1985) is also fundamental, as we have pointed out because it confirms that the higher the excitation of the atomic state, the larger the effects of multiple perturbers are at a lower density in the laboratory (Kielkopf & Allard 1979), as shown in Fig. 8 for stellar atmospheres.

Acknowledgments

We would like to thank Adela Kawka and Stephane Vennes who initiated this study. We also acknowledge with appreciation Stephane Vennes, for his determinations of He density in the Balmer-α and β formation regions of the DZ white dwarfs which are cited in the paper. We thank the anonymous referee for helpful comments that improved the manuscript.

References

  1. Allard, N. F. 1978, J. Phys. B: At. Mol. Opt. Phys., 11, 1383 [NASA ADS] [CrossRef] [Google Scholar]
  2. Allard, N. F., & Kielkopf, J. F. 1982, Rev. Mod. Phys., 54, 1103 [Google Scholar]
  3. Allard, N. F., Drira, I., Gerbaldi, M., Kielkopf, J. F., & Spielfiedel, A. 1998, A&A, 335, 1124 [NASA ADS] [Google Scholar]
  4. Allard, N. F., Royer, A., Kielkopf, J. F., & Feautrier, N. 1999, Phys. Rev. A, 60, 1021 [Google Scholar]
  5. Allard, N. F., Nakayama, A., Spiegelman, F., Kielkopf, J. F., & Stienkemeier, F. 2013, Eur. Phys. J. D, 67, 52 [NASA ADS] [CrossRef] [Google Scholar]
  6. Allard, N. F., Leininger, T., Gadéa, F. X., Brousseau-Couture, V., & Dufour, P. 2016, A&A, 588, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Allard, N. F., Kielkopf, J. F., Xu, S., et al. 2020, MNRAS, 494, 868 [Google Scholar]
  8. Allard, N. F., Spiegelman, F., Kielkopf, J. F., & Bourdreux, S. 2022, A&A, 657, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Anderson, P. W. 1952, Phys. Rev., 86, 809 [Google Scholar]
  10. Baranger, M. 1958a, Phys. Rev., 111, 481 [NASA ADS] [CrossRef] [Google Scholar]
  11. Baranger, M. 1958b, Phys. Rev., 111, 494 [NASA ADS] [CrossRef] [Google Scholar]
  12. Kampen, N. G. V. 1974, Physica, 74, 215 [NASA ADS] [CrossRef] [Google Scholar]
  13. Kawka, A., Vennes, S., Allard, N. F., Leininger, T., & Gadéa, F. X. 2021, MNRAS, 500, 2732 [Google Scholar]
  14. Ketterle, W. 1989, Phys. Rev. Lett., 62, 1480 [CrossRef] [Google Scholar]
  15. Ketterle, W. 1990a, J. Chem. Phys., 93, 3752 [NASA ADS] [CrossRef] [Google Scholar]
  16. Ketterle, W. 1990b, J. Chem. Phys., 93, 3760 [NASA ADS] [CrossRef] [Google Scholar]
  17. Ketterle, W. 1990c, J. Chem. Phys., 93, 6929 [NASA ADS] [CrossRef] [Google Scholar]
  18. Ketterle, W. 1990d, J. Chem. Phys., 93, 6935 [NASA ADS] [CrossRef] [Google Scholar]
  19. Ketterle, W., Figger, H., & Walther, H. 1985, Phys. Rev. Lett., 55, 2941 [Google Scholar]
  20. Ketterle, W., Dodhy, A., & Walther, H. 1988, J. Chem. Phys., 89, 3442 [Google Scholar]
  21. Kielkopf, J. 1983, J. Phys. B At. Mol. Phys., 16, 3149 [NASA ADS] [CrossRef] [Google Scholar]
  22. Kielkopf, J. 1985, J. Quant. Spectr. Rad. Transf., 33, 267 [NASA ADS] [CrossRef] [Google Scholar]
  23. Kielkopf, J. F., & Allard, N. F. 1979, Phys. Rev. Lett., 43, 196 [NASA ADS] [CrossRef] [Google Scholar]
  24. Knowles, P. J., & Werner, H.-J. 1992, Theor. Chim. Acta, 84, 95 [CrossRef] [Google Scholar]
  25. Koester, D., & Wolff, B. 2000, A&A, 357, 587 [NASA ADS] [Google Scholar]
  26. Koos, W., & Peek, J. M. 1976, Chem. Phys., 12, 381 [NASA ADS] [CrossRef] [Google Scholar]
  27. Kramida, A., Ralchenko, Yu., Reader, J., & NIST ASD Team 2020, NIST Atomic Spectra Database (ver. 5.8) (Gaithersburg, MD: National Institute of Standards and Technology), https://physics.nist.gov/asd [Google Scholar]
  28. Kubo, R. 1962a, J. Phys. Soc. Jpn., 17, 1100 [NASA ADS] [CrossRef] [Google Scholar]
  29. Kubo, R. 1962b, J. Math. Phys., 4, 174 [Google Scholar]
  30. Limoges, M. M., Bergeron, P., & Lépine, S. 2015, ApJS, 219, 19 [NASA ADS] [CrossRef] [Google Scholar]
  31. Lo, J. M. H., Klobukowski, M., Bielińska-Waz, D., Schreiner, E. W. S., & Diercksen, G. H. F. 2006, J. Phys. B: At. Mol. Opt. Phys., 39, 2385 [NASA ADS] [CrossRef] [Google Scholar]
  32. Nakajima, T., & Hirao, K. 2011, Chem. Rev., 112, 385 [Google Scholar]
  33. Reiher, M. 2006, Theor. Chem. Acc., 116, 241 [Google Scholar]
  34. Royer, A. 1972, Phys. Rev. A, 6, 1741 [NASA ADS] [CrossRef] [Google Scholar]
  35. Royer, A. 1978, Acta Phys. Pol. A, 54, 805 [Google Scholar]
  36. Royer, A. 1980, Phys. Rev. A, 22, 1625 [NASA ADS] [CrossRef] [Google Scholar]
  37. Sarpal, B. K., Branchett, S. E., Tennyson, J., & Morgan, L. A. 1991, J. Phys. B: At. Mol. Opt. Phys., 24, 3685 [NASA ADS] [CrossRef] [Google Scholar]
  38. Spiegelman, F., Allard, N., & Kielkopf, J. 2021, A&A, 651, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Theodorakopoulos, G., Petsalakis, I. D., Nicolaides, C. A., & Buenker, R. J. 1987, J. Phys. B, 20, 2339 [Google Scholar]
  40. Tremblay, P. E., Hollands, M. A., Gentile Fusillo, N. P., et al. 2020, MNRAS, 497, 130 [NASA ADS] [CrossRef] [Google Scholar]
  41. van Hemert, M. C., & Peyerimhoff, S. D. 1991, J. Chem. Phys., 94, 4369 [NASA ADS] [CrossRef] [Google Scholar]
  42. Werner, H. J., Knowles, P. J., Knizia, G., et al. 2015, MOLPRO, version 2015.1, a package of ab initio programs [Google Scholar]
  43. Xu, S., Zuckerman, B., Dufour, P., et al. 2017, ApJ, 836, L7 [Google Scholar]

Appendix A: Complementary H-He molecular data

Table A.1.

Complementary basis set information

Table A.2.

Calculated atomic energy levels of Hydrogen (n = 4) vs experiment

Table A.3.

Spectroscopic constants of HHe molecular states correlated with H(n = 4)+He

All Tables

Table A.1.

Complementary basis set information

In the text
Table A.2.

Calculated atomic energy levels of Hydrogen (n = 4) vs experiment

In the text
Table A.3.

Spectroscopic constants of HHe molecular states correlated with H(n = 4)+He

In the text

All Figures

thumbnail Fig. 1.

MRCI adiabatic potential energy curves of molecular states dissociating into H(n = 2,4)+He. The R scale is a logarithmic graduation. The dashed lines correspond to potential energy curves dissociating into H(n = 3)+He.
In the text
thumbnail Fig. 2.

Long range zoom on the adiabatic potential energy curves of H(n = 4)+He.
In the text
thumbnail Fig. 3.

Transition dipole moments D(R) of H-He between 2Σ+ states n = 2 and n = 4.
In the text
thumbnail Fig. 4.

Repulsive potentials and their difference. Top: potential energy V of the repulsive states of Lyman-α (dashed black curve), Balmer-α (dashed red curve), and Balmer-β (blue curve). Bottom: difference potential ΔV(R) for the Lyman-α transition X → C (dashed black curve), for the Balmer-α transition C → 62Σ+ (dashed red curve), and for the Balmer-β transitions C → 102Σ+ (blue curve).
In the text
thumbnail Fig. 5.

Difference potential energy ΔV(R) in cm−1 (black line) and dipole moment D(R) (black dashed line) for the forbidden C 2p → 4f 102Σ+ transition.
In the text
thumbnail Fig. 6.

Comparison of the total profile (blue line) to the profile restrictly obtained with the allowed transitions (red dashed line). The Balmer-β line profile is also compared to the Lorentzian approximation (black dashed curve). The He density is 5 × 1020 cm−3, and the temperature is 8000 K.
In the text
thumbnail Fig. 7.

Variation with the He density of the Balmer-β line profile for 2 × 1020 (black line), 3 × 1020 (blue line), and 5 × 1020 cm−3 (red line); the temperature is 8000 K. The Balmer-β line profiles are also compared to the Lorentzian approximation for the He densities 2 × 1020 cm−3 (dashed black line) and 3 × 1020 cm−3 (dashed blue line).
In the text
thumbnail Fig. 8.

Comparison of the Balmer-α (black curves) and Balmer-β (red curves) line profiles. The He densities are 1021 cm−3 (full curves) and 6 × 1020 cm−3 (dashed curves); the temperature is 8000 K.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.