EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 659 (March 2022) A&A, 659 (2022) A11 Full HTML
Free Access
Issue
A&A
Volume 659, March 2022
Article Number A11
Number of page(s) 6
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/202141801
Published online 25 February 2022

© ESO 2022

1 Introduction

The abundances of elements in astrophysical objects is determined from details of stellar nucleosynthesis and the chemical evolution of galaxies, stars, and planets. Nitrogen is one of the most abundant elements in the Universe. Emission spectra of nitrogen have been studied in astrophysical objects (Kewley & Dopita 2002; Denicoló et al. 2002; Shapley et al. 2015; Faisst et al. 2018; Martens et al. 2019) and laser-produced plasmas (Rongwei et al. 2013). Furthermore, nitrogen ions can be found among impurities that have to be monitored in fusion devices (Neu et al. 2013). The chemical evolution of the nitrogen in the Universe is poorly understood because the origin of this element has a complex dependence on the metallicity of the environment.

Emission spectra from distant celestial objects provide information about the abundances of elements in these objects. Spectral line intensities depend on the population of charge states. Electron-impact ionization plays a crucial role in defining ionization balance in the collisionally ionized plasmas. The electron-impact ionization cross-sections for the nitrogen atom were observed using a modulated molecular beam technique (Smith et al. 1962). Measurements were compared to theoretical values computed from the Bethe approximation (Seaton 1959). Later, the crossed beams method was employed by Brook et al. (1978) to measure the single-ionization cross-sections. The experimental data below the single ionization threshold clearly demonstrate a small contribution from the long-lived levels. The theoretical cross-sections (Seaton 1959; Peach 1970, 1971; McGuire 1971; Omidvar et al. 1972) overestimated the measurements by ~30–60% for the peak values. Born-Ochkur (Peach 1970, 1971) and Born (McGuire 1971; Omidvar et al. 1972) approximations were used to calculate the cross-sections.

The binary-encounter-Bethe (BEB) model (Kim & Rudd 1994) was applied to calculate collisional ionization (CI) cross-sections for the N atom (Kim & Desclaux 2002). The excitation-autoionization (EA) contribution was determined using the scaled plane-wave Born (SPWB) cross-sections (Kim 2001). However, theoretical data showed values below those of the measurements (Brook et al. 1978) by ~10% at the peak of the cross-sections. The difference was attributed to a contribution from the long-lived levels. The study of the ionization process in the N atom was extended using the B-spline R-matrix-with-pseudostates (BSR) method (Wang et al. 2014). The close-coupling expansion included 690 states of atomic nitrogen. Ionization cross-sections were presented from the ionization threshold up to 150 eV. The total ionization cross-sections from the BSR calculations (Wang et al. 2014) were in good agreement with the measurements (Brook et al. 1978) and data provided by Kim & Desclaux (2002). On the other hand, a large difference between the BSR (Wang et al. 2014) and BEB+SPWB (Kim & Desclaux 2002) calculations was determined for the excitation-autoionization (EA) contribution to the ionization process. This was explained by the overestimated oscillator strengths used for scaling of the plane-wave Born approximation (Wang et al. 2014).

Later, the R-matrix with pseudostates (RMPS; Bartschat et al. 1996) and time-dependent close-coupling methods (Pindzola et al. 2007; Colgan & Pindzola 2012) were applied to analyze electron-impact ionization cross-sections for the ground and excited levels of the N atom (Abdel-Naby et al. 2014). It should be noted that the RMPS calculation uses an approach developed by Gorczyca & Badnell (1997). Furthermore, the configuration average distorted wave (CADW) method was compared with non-perturbative approaches. It was demonstrated that the CADW results overestimated measurements (Brook et al. 1978) by ~80%. On the other hand, the RMPS data showed relatively good agreement with the measurements and the BSR calculations.

The aim of the current work is to study electron-impact single ionization for the N atom using the scaled distorted-wave (DW) approximation (Jonauskas 2018). It is well known that the DW approximation often overestimates experimental data for neutral atoms and near neutral ions. Previously, it was demonstrated that scaling of the DW cross-sections provided a good agreement with experimental cross-sections for the C atom and C+ ion (Jonauskas 2018), Fe3+ ion (Kynienė et al. 2019), and Si atom (Jonauskas 2020). Therefore, the same approach is used here to study single-ionization cross-sections in the nitrogen atom. We analyze the contributions of the direct and indirect ionization processes using the scaled cross-sections, and tabulate the cross-sections for the EA and CI processes. We also present the Maxwellian rate coefficients (MRCs) for all levels of the ground configuration.

The rest of the paper is structured as follows. In Sect. 2, give an overview of the theoretical approach; in Sect. 3, we discuss the obtained results. Finally, a brief summary with some final conclusions are provided in Sect. 4.

2 Theoretical approach

We used theflexible atomic code (FAC; Gu 2008) to study energy levels, radiative and Auger probabilities, electron-impact excitation, and ionization cross-sections of the N atom, and implemented the Dirac-Fock-Slater (DFS) approximation in the code. Calculations were performed in the jj-coupling scheme. We calculated the electron-impact excitation and ionization cross-sections in the DW approximation.

Direct and indirect processes are studied to obtain the total ionization cross-section for transition from level i of the N atom to level f of the N+ ion: 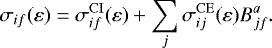σif(ε)=σifCI(ε)+∑jσijCE(ε)Bjfa.\begin{equation*} \sigma_{if}(\varepsilon)=\sigma^{\mathrm{CI}}_{if}(\varepsilon)+\sum_j\sigma_{ij}^{\mathrm{CE}}(\varepsilon)B^{a}_{jf}.\end{equation*}(1)

Here, ε is an energy of the incident electron, 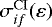\(σifCI(ε)\)\(\sigma^{\mathrm{CI}}_{if}(\varepsilon)\) is the CI cross-section, 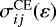\(σijCE(ε)\)\(\sigma_{ij}^{\mathrm{CE}}(\varepsilon)\) is the collisional excitation (CE) cross-section to level j of the N atom, 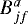\(Bjfa\)\(B^{a}_{jf}\) is a branching ratio for the autoionization process from level j to the final level f. The second term in Eq. (1) determines the indirect process initiated by electron-impact excitation with subsequent autoionization. The autoionization branching ratio is defined using the following equation: 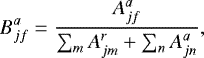Bjfa=Ajfa∑mAjmr+∑nAjna,\begin{equation*} B^{a}_{jf}=\frac{A_{jf}^a}{{\sum_m{A_{jm}^r}}+{\sum_n{A_{jn}^a}}},\end{equation*}(2)

where Ar and Aa are the radiative and Auger transition probabilities, respectively. Summation in the denominator goes through all levels that can be reached by the radiative and Auger decays from level j. Therefore, the denominator determines the total decay probability for level j. The autoionization branching ratio diminishes the cross-sections of the EA process because the autoionizing levels can decay through the radiative transitions to the energetically lower levels of the N atom below the single ionization threshold. The branching ratio defines a part of the population transferred from level j to level f. The branching ratio is equal to zero for the levels below the single ionization threshold. The decay of the autoionizing intermediate states reached by the radiative transitions is not investigated in this work because its contribution is negligible.

It is well known that the DW approximation often overestimates excitation and ionization cross-sections for the neutral and near neutral ions. Previously, corrections were suggested for the PWB calculations to improve height and position for the peak of the cross-sections (Cowan 1981). The BEB+SPWB cross-sections were used to explain measurements (Kim 2001; Kim & Desclaux 2002; Kwon et al. 2005, 2006). The scaled DW cross-sections were suggested for study of the electron impact excitation and ionization processes in the C atom and the C+ ion (Jonauskas 2018), and the Fe3+ (Kynienė et al. 2019) and Si atom (Jonauskas 2020). The scaled DW cross-sections for the excitation are obtained using 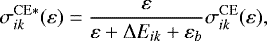σikCE*(ε)=εε+ΔEik+εbσikCE(ε),\begin{equation*}\sigma_{ik}^{\mathrm{CE*}}(\varepsilon) = \frac{\varepsilon}{\varepsilon+\Delta{E_{ik}}+\varepsilon_{b}}\sigma_{ik}^{\mathrm{CE}}(\varepsilon), \end{equation*}(3)

where εb is a binding energy of the electron, and ΔEik is a transition energy. The scaled DW cross-sections for CI are determined using the following equation: 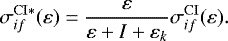σifCI*(ε)=εε+I+εkσifCI(ε).\begin{equation*}\sigma_{if}^{\mathrm{CI*}}(\varepsilon) = \frac{\varepsilon}{\varepsilon + I + \varepsilon_{k}} \sigma_{if}^{\mathrm{CI}}(\varepsilon). \end{equation*}(4)

Here, I is the ionization energy, and εk is the kinetic energy of the bound electron.

Electron-impact ionization cross-sections are used to calculate MRC: 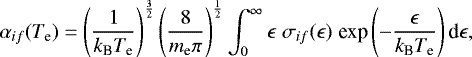αif(Te)=(1kBTe)32(8meπ)12∫0∞ϵ  σif(ϵ) exp(−ϵkBTe)dϵ,\begin{equation*}\alpha_{if}(T_{\textrm{e}}) = \left(\frac{1}{k_{\textrm{B}}T_{\textrm{e}}}\right)^{\frac{3}{2}}\left(\frac{8}{m_{\textrm{e}}\pi}\right)^{\frac{1}{2}} \int_0^{\infty}\epsilon\; \sigma_{if}(\epsilon)\; \textrm{exp} \left(-\frac{\epsilon}{k_{\textrm{B}}T_{\textrm{e}}}\right)\textrm{d}\epsilon, \end{equation*}(5)

where kB is the Boltzmann constant, me is the electron mass, and σif(ϵ) is the cross-section for transition from level i to level f.

The studied direct process for the nitrogen atom includes CI from the 2 s and 2 p subshells: [He]2s22p3 +e−→[He]{2s22p22s12p3 +2e− ​.\begin{equation*} [\mathrm{He}] 2\textrm{s}^{2}2\textrm{p}^{3} \; + \textrm{e}^{-} \rightarrow [\mathrm{He}] \left\{ \begin{array}{ll} 2\textrm{s}^{2} 2\textrm{p}^{2} \\ 2\textrm{s}^{1} 2\textrm{p}^{3} \\ \end{array} + 2e^{-} \right.\!.\end{equation*}(6)

Collisional ionization from the 1 s subshell produces states above the double ionization threshold of the nitrogen atom. The decay of these states leads mainly to double ionization. Excitations from the 2 s and 2 p subshells produce ions in the autoionizing levels: [He]2s22p3+e−→[He]{2s22p2 nl2s12p42s12p3 n′l+e− ​,\begin{equation*} [\mathrm{He}] 2\textrm{s}^{2}2\textrm{p}^{3} + \textrm{e}^{-} \rightarrow [\mathrm{He}] \left\{ \begin{array}{l} 2\textrm{s}^{2}2\textrm{p}^{2}\; \textrm{nl} \\ 2\textrm{s}^{1}2\textrm{p}^{4} \\ 2\textrm{s}^{1}2\textrm{p}^{3} \; \textrm{n\prime l} \\ \end{array} + e^{-} \right.\!, \end{equation*}(7)

where 3 ≤ n ≤ 30, 3 ≤ n′≤ 10, l < n, and l ≤ 6. Previous studies demonstrated that the EA channels corresponding to the excitations from the valence subshell can be important in providing good agreement with measurements close to the ionization threshold (Kwon & Savin 2012). We therefore investigated these EA channels for the electron-impact ionization in the N atom.

3 Results

The energy levels of the main configurations contributing to the single ionization process in the N atom ion are presented in Fig. 1. The excited 2s12p4 configuration has some energy levels above the ionization threshold. Excitation to these levels with subsequent autoionization leads to single ionization. Furthermore, there are many configurations produced by promotion of an electron from the 2 p subshell of the ground configuration that have energy levels that straddle the single ionization threshold. Even the first excited 2p2 3s configuration has energy levels above the single ionization threshold. However, these configurations have not yet been studied using the SPWB approximation (Kim & Desclaux 2002). The theoretical single ionization threshold for the N atom amounts to 13.57 eV. This is slightly lower than the value of 14.53 eV recommended by the National Institute of Standards and Technology (NIST; Kramida et al. 2021). A similar trend between the single-ionization thresholds calculated using the DFS approximation and those derived from the NIST data was obtained for other ions: Se2+ (Konceviciūtė et al. 2018), Se3+ (Pakalka et al. 2018; Koncevičiutė et al. 2019), Fe3+ (Kynienė et al. 2019), W25+ (Kynienė et al. 2016), W26+ (Kynienė et al. 2015, 2018), and W27+ (Jonauskas et al. 2015). The energy levels for the ground configuration of the N atom are compared to the NIST values in Table 1. Splitting for the energy levels of the ground configuration is higher by ~0.92 eV as compared to the NIST data. The difference can be related to the correlation effects that are missing in this study.

Theoretical cross-sections obtained in the potential of the ionized ion are compared to measurements (Brook et al. 1978) in Fig. 2. The cross-sections corresponding to ionization from the 2D5∕2 and 2D3∕2 levels and the 2P1∕2 and 2P3∕2 levels are in close agreement and therefore only values for the lowest levels 2D5∕2 and 2P1∕2 of the corresponding terms are presented. Peaks of the theoretical cross-sections appear on the lower energy side from experimental cross-sections (Fig. 2). The theoretical peaks shift to lower energies by ~40 eV for the lowest level and ~60 eV for the highest one of the ground configuration. It should be noted that a similar situation was previously determined for the DW cross-sections compared to the measurements from the carbon atom and C+ ion (Jonauskas 2018), Fe3+ (Kynienė et al. 2019), and Si atom (Jonauskas 2020). The scaled DW cross-sections were used to explain the measurements in these studies. Furthermore, the experimental values for the N atom are lower than those predicted by theoretical calculations at low energies (Fig. 2). However, relatively good agreement with the measurements is obtained at the high-energy side for the levels belonging to the 2D and 2P terms. The theoretical cross-sections are below the measurements for the ground level at the high-energy side.

Cross-sections calculated in the potential of the ionizing ion for three levels of the ground configuration of the N atom are compared to measurements (Brook et al. 1978) in Fig. 3. All theoretical cross-sections are higher than those derived from experimental data except for the ground level at the high-energy side. Good agreement with the measurements is obtained forthe ground level at the higher energies of the impacting electron. Furthermore, peaks of the theoretical cross-sections shift to the lower energy side from the peak of the experimental values. However, the peaks in this case are lower by ~10 eV, except for the peak of the ground level, which is ~20 eV lower than that seen in the theoretical data obtained in the potential of the ionized ion (Fig. 2).

The peak of the scaled DW cross-sections (not presented here) obtained in the potential of the ionized ion for the ground level of the N atom shifts to lower energies by ~10 eV compared to the experimental one (Brook et al. 1978). Larger shifts are obtained for the higher levels of the ground configuration. Therefore, these theoretical data are not suitable for explaining the measurements.

The scaled DW cross-sections for energy levels of the ground configuration are presented in Fig. 4. The theoretical cross-sections for the direct ionization process are studied in the potential of the ionizing ion. The cross-sections obtained for the ground level show good agreement with measurements (Brook et al. 1978). All peak positions of the scaled theoretical cross-sections are in better agreement with the measurements than the unscaled ones (Fig. 3). The theoretical cross-sections obtained for the 2D and 2P terms are higher than experimental ones by ~40 and ~60%, respectively,at the peak values.

The convergence of the cross-sections for the indirect process must be evaluated in order to provide reliable data (Jonauskas et al. 2015; Kynienė et al. 2015, 2016, 2018). The EA channels corresponding to excitations from the 2 s subshell up to shells with the principal quantum number n ≤ 10 are shown in Fig. 5 for the ground level. It is interesting that the 2 s → 2 p transition provides ~35% of the total EA cross-sections from the ground level. However, a small contribution from this EA channel was expected (Wang et al. 2014). The excitations to the n = 3 shell dominate for the ground level. It should be noted that the EA contribution is smaller than the total ionization cross-sections from the ground level by two orders of magnitude (Fig. 4). The situation drastically changes for the excited 2D3∕2 level where the excitation to the n = 2 shell consists of ~90% of the total EA cross-sections (Fig. 6). A similar situation is obtained for other excited levels of the ground configuration. It can be seen that the studied excitations up to the n = 10 shell ensure convergence of the EA cross-sections. The EA channels corresponding to the excitations to the higher shells (n > 10) would not contribute more than 2% to the total EA cross-sections.

We investigate excitations from the 2 p subshell to the shells up to n = 30 for the indirect process of single ionization in the N atom. For the ground level, the excitations to the shells with 11 ≤ n ≤ 20 provide cross-sections that are larger by a factor of 1.5 than the excitations up to n = 10. The excitations to the shells with 21 ≤ n ≤ 30 contribute ~10% of those to shells with n ≤ 20. It should benoted that the EA cross-sections corresponding to the excitations from the 2 p subshell provide ~25% to the total cross-sections of the indirect process for the ground level. Furthermore, the excitations to 11 ≤ n ≤ 20 add ~10% of those to n ≤ 10 for the 2D5∕2 level. The 20 ≤ n ≤ 30 excitations contribute ~2% for the EA cross-sections from the 2 p subshell. A similar situation to that seen for 2D5∕2 is obtained for the 2P1∕2 level.

Contributions of the direct and indirect processes to the total electron-impact ionization cross-sections for the ground level of the N atom are compared in Fig. 7. The CI channel corresponding to the ionization from the 2 p subshell produces ~80% of the total cross-sections for the ground level. The EA contribution to the total ionization cross-sections is ~5%. The dominant part of the EA cross-sections comes from the excitations of the 2 s subshell. The EA channels corresponding to the excitations from the 2 p subshell produce ~2% for the total indirect process. It should be noted that the excitations from the 2 p subshell lead to autoionizing states starting from the 2s22p23s configuration (Fig. 1). There is only one level above the single ionization threshold for the 2s22p23s configuration.

The contribution of the indirect process is up to ~30% of the total single ionization cross-sections from the 2D3∕2 level (Fig. 8). A similar contribution of the EA cross-sections compared to the CI ones is obtained for the 2P1∕2 level of the ground configuration. Excitations from the outer 2 p subshell produce ~9% and ~12% of the total ionization cross-sections for the 2D3∕2 and 2P1∕2 levels, respectively. However, as mentioned above, the EA channels corresponding to the excitations from the 2 p subshell provide 2% of the excitations to the ground level (Fig. 7).

Modeling of the contribution for the ground 4S3∕2 and excited 2D5∕2 levels is compared to experimental data (Brook et al. 1978) in Fig. 9. The single ionization threshold is taken to be equal to 14.53 eV, which corresponds to the NIST recommended value. Because of this, the cross-sections are diminished by ~5% for the total ionization from the ground level. The contribution from the 2D5∕2 level was predicted in the measurements, but the fraction of metastable atoms in the beam was not estimated (Brook et al. 1978). The modeling shows that about 80% of atoms in the beam reside in the ground level. This prediction corresponds to the lowest limit of the fraction for the ground level. The modeling of the contribution from the higher long-lived levels with the higher cross-sections than those currently used would lead to a lower fraction of the atoms in the ground level. A slightly higher value (85%) for the ground level population was found from the BSR data (Ciccarino & Savin 2019). It should be noted that some uncertainties in the presented cross-sections may arise from correlation effects that are missing in the current study. For example, it was demonstrated that the correlation effects diminish the cross-sections for the W5+ ion by ~20% (Jonauskas et al. 2019). The current modeling (Fig. 7) does not provide information about the relative populations of the atoms in the excited states of the ground configuration because the population mechanisms of the levels in the experiment are not determined. For this, collisional-radiative modeling with the subsequent radiative cascade (Jonauskas et al. 2013)may be needed to determine the population of the levels.

A previous theoretical study of single ionization cross-sections using the BSR method (Wang et al. 2014) demonstrated good agreement with measurements (Brook et al. 1978) at peak for the ground level of the N atom (Fig. 10). However, the experimental data were slightly underestimated by the BSR calculations at the lower energies (Wang et al. 2014). Surprisingly, the scaled DW cross-sections are in a good agreement with the BSR calculations for the ground level. However, the scaled DW data produced for the ground level are below the measurements by ~5% at peak. The single ionization cross-sections calculated for the two highest terms of the ground configuration using the BSR method are in close agreement for the peak values (Fig. 10). On the other hand, the scaled DW cross-sections obtained for the 2P1∕2 level are ~10% above the data corresponding to the 2D5∕2 level. The cause of this difference is not clear. However, the RMPS calculations (Abdel-Naby et al. 2014) show similar differences for the 4S, 2D, and 2P terms as provided by the scaled DW cross-sections (Fig. 11). The higher RMPS values compared to the BSR calculations were explained by inclusion of more excitation-autoionization contributions (Abdel-Naby et al. 2014).

thumbnail Fig. 1

Energy levels of the N atom and N+ ion. The single ionization threshold is shown by the horizontal line. Even-parity configurations are presented by red lines and odd-parity configurations are shown by blue lines.
Table 1

Comparison of theoretical (DFS) and NIST (Kramida et al. 2021) energy levels for the ground configuration.

thumbnail Fig. 2

Electron-impact single ionization cross-sections for levels of the ground configuration of the N atom. The CI data obtained in the potential of the ionized ion. Experiment: open circles with error bars (Brook et al. 1978).
thumbnail Fig. 3

Electron-impact single ionization cross-sections for levels of the ground configuration of the N atom. The CI data were obtained in the potential of the ionizing ion. Experiment: open circles with error bars (Brook et al. 1978).
thumbnail Fig. 4

Same as Fig. 3 but for the scaled DW cross-sections.
thumbnail Fig. 5

Comparison of the contribution from the different EA channels (n ≤ 10) corresponding to excitations for the 2s subshell for the ground level of the N atom.
thumbnail Fig. 6

Comparison of the contribution from the different EA channels (n ≤ 10) corresponding to excitations for the 2 s subshell for the 2D3∕2 level of the N atom.
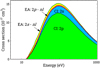thumbnail Fig. 7

Comparison of the contributions from CI and EA channels for the ground level of the N atom.
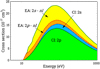thumbnail Fig. 8

Comparison of the contributions from CI and EA channels for the 2D3∕2 level of the N atom.
thumbnail Fig. 9

Modeled contribution of the metastable fraction in the atom beam. Experiment: open circles with error bars (Brook et al. 1978).
thumbnail Fig. 10

Comparison of the scaled DW cross-sections to the BSR (Wang et al. 2014) calculations. Experiment: open circles with error bars (Brook et al. 1978).
thumbnail Fig. 11

Comparison of the scaled DW cross-sections to the RMPS (Abdel-Naby et al. 2014) calculations. Experiment: open circles with error bars (Brook et al. 1978).

4 Summary and conclusions

We studied the electron-impact ionization cross-sections for the N atom from all levels of the ground configuration using the DW approximation. Specifically, we analyzed the direct and indirect processes for the electron-impact ionization. We found good agreement with the experimental data and BSR calculations for the scaled DW cross-sections.

We studied excitations from the 2 s and 2 p subshells of the ground configuration. Convergence of the EA channels was determined by analyzing the excitations up to shells with the principal quantum number n = 10 for the 2 s subshell. However, the EA cross-sections corresponding to the excitations from the 2 p subshell are calculated up to n = 30 to reach the convergence. The contribution of the direct process to the total ionization cross-sections dominates for all levels of the ground configuration. However, the CI contribution amounts to ~95% for the ground level while the EA contribution reaches ~30% for the higher levels of the ground configuration. Modeling of the contribution of the levels of the ground configuration predicts that the fraction of atoms in the excited levels is less than ~20%.

Finally, we present cross-sections for the direct, indirect, and total ionization by electron impact as supplementary data, and tabulate the Maxwellian rate coefficients for all levels of the ground configuration of the N atom. We present the contributions from the different subshells in order that the data may be used not only for equilibrium plasmas but also for nonequilibrium modeling.

Acknowledgements

Part of the computations were performed on the High Performance Computing (HPC) cluster at the Institute of Theoretical Physics and Astronomy, Faculty of Physics, Vilnius University.

References

  1. Abdel-Naby, S. A., Pindzola, M. S., Pearce, A. J., Ballance, C. P., & Loch, S. D. 2014, J. Phys. B Atom. Mol. Opt. Phys., 48, 025203 [Google Scholar]
  2. Bartschat, K., Bray, I., Burke, P. G., & Scott, M. P. 1996, J. Phys. B Atom. Mol. Opt. Phys., 29, 5493 [NASA ADS] [CrossRef] [Google Scholar]
  3. Brook, E., Harrison, M. F. A., & Smith, A. C. H. 1978, J. Phys. B Atom. Mol. Opt. Phys., 11, 3115 [NASA ADS] [CrossRef] [Google Scholar]
  4. Ciccarino, C. J., & Savin, D. W. 2019, J. Thermophys. Heat Transfer, 33, 154 [Google Scholar]
  5. Colgan, J., & Pindzola, M. 2012, Eur. Phys. J. D, 66, 284 [NASA ADS] [CrossRef] [Google Scholar]
  6. Cowan, R. D. 1981, The Theory of Atomic Structure and Spectra (Berkeley, CA: University of California Press) [Google Scholar]
  7. Denicoló, G., Terlevich, R., & Terlevich, E. 2002, MNRAS, 330, 69 [CrossRef] [Google Scholar]
  8. Faisst, A. L., Masters, D., Wang, Y., et al. 2018, ApJ, 855, 132 [NASA ADS] [CrossRef] [Google Scholar]
  9. Gu, M. F. 2008, Can. J. Phys., 86, 675 [NASA ADS] [CrossRef] [Google Scholar]
  10. Gorczyca, T. W., & Badnell, N. R. 1997, J. Phys. B Atom. Mol. Opt. Phys., 30, 3897 [NASA ADS] [CrossRef] [Google Scholar]
  11. Jonauskas, V. 2018, A&A, 620, A188 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Jonauskas, V. 2020, Atom. Data Nucl. Data Tables, 135–136, 101363 [Google Scholar]
  13. Jonauskas, V., Masys, S., Kynienė, A., & Gaigalas, G. 2013, J. Quant. Spectr. Rad. Transf., 127, 64 [NASA ADS] [CrossRef] [Google Scholar]
  14. Jonauskas, V., Kynienė, A., Merkelis, G., et al. 2015, Phys. Rev. A, 91, 012715 [NASA ADS] [CrossRef] [Google Scholar]
  15. Jonauskas, V., Kynienė, A., Kučas, S., et al. 2019, Phys. Rev. A, 100, 062701 [NASA ADS] [CrossRef] [Google Scholar]
  16. Kewley, L. J., & Dopita, M. A. 2002, ApJS, 142, 35 [Google Scholar]
  17. Kim, Y.-K. 2001, Phys. Rev. A, 64, 032713 [NASA ADS] [CrossRef] [Google Scholar]
  18. Kim, Y.-K., & Desclaux, J.-P. 2002, Phys. Rev. A, 66, 012708 [NASA ADS] [CrossRef] [Google Scholar]
  19. Kim, Y.-K., & Rudd, M. E. 1994, Phys. Rev. A, 50, 3954 [NASA ADS] [CrossRef] [Google Scholar]
  20. Konceviciūtė, J., Kucas, S., Masys, Š., Kynienė, A., & Jonauskas, V. 2018, Phys. Rev. A, 97, 012705 [CrossRef] [Google Scholar]
  21. Koncevičiutė, J., Kučas, S., Kynienė, A., Š Masys, & Jonauskas, V. 2019, J. Phys. B Atom. Mol. Opt. Phys., 52, 025203 [CrossRef] [Google Scholar]
  22. Kramida, A., Ralchenko, Yu., Reader, J., & NIST ASD Team (2021). NIST Atomic Spectra Database (ver. 5.7.1), [Online]. Available: https://physics.nist.gov/asd [2021, January 10]. National Institute of Standards and Technology, Gaithersburg, MD [Google Scholar]
  23. Kwon, D.-H., & Savin, D. W. 2012, Phys. Rev. A, 86, 022701 [NASA ADS] [CrossRef] [Google Scholar]
  24. Kwon, D.-H., Rhee, Y.-J., & Kim, Y.-K. 2005, Int. J. Mass Spectrom., 245, 26 [NASA ADS] [CrossRef] [Google Scholar]
  25. Kwon, D.-H., Rhee, Y.-J., & Kim, Y.-K. 2006, Int. J. Mass Spectrom., 252, 213 [NASA ADS] [CrossRef] [Google Scholar]
  26. Kynienė, A., Masys, Š., & Jonauskas, V. 2015, Phys. Rev. A, 91, 062707 [CrossRef] [Google Scholar]
  27. Kynienė, A., Pakalka, S., Masys, Š., & Jonauskas, V. 2016, J. Phys. B Atom. Mol. Opt. Phys., 49, 185001 [CrossRef] [Google Scholar]
  28. Kynienė, A., Merkelis, G., Šukys, A., et al. 2018, J. Phys. B Atom. Mol. Opt. Phys., 51, 155202 [CrossRef] [Google Scholar]
  29. Kynienė, A., Kučas, S., Pakalka, S., Masys, Š., & Jonauskas, V. 2019, Phys. Rev. A, 100, 052705 [CrossRef] [Google Scholar]
  30. Martens, D., Fang, X., Troxel, M. A., et al. 2019, MNRAS, 485, 211 [NASA ADS] [CrossRef] [Google Scholar]
  31. McGuire, E. J. 1971, Phys. Rev. A, 3, 267 [NASA ADS] [CrossRef] [Google Scholar]
  32. Neu, R., Kallenbach, A., Balden, M., et al. 2013, J. Nucl. Mater., 438, S34 [NASA ADS] [CrossRef] [Google Scholar]
  33. Omidvar, K., Kyle, H. L., & Sullivan, E. C. 1972, Phys. Rev. A, 5, 1174 [NASA ADS] [CrossRef] [Google Scholar]
  34. Pakalka, S., Kučas, S., Masys, v., et al. 2018, Phys. Rev. A, 97, 012708 [NASA ADS] [CrossRef] [Google Scholar]
  35. Peach, G. 1970, J. Phys. B Atom. Mol. Opt. Phys., 3, 328 [NASA ADS] [CrossRef] [Google Scholar]
  36. Peach, G. 1971, J. Phys. B Atom. Mol. Opt. Phys., 4, 1670 [NASA ADS] [CrossRef] [Google Scholar]
  37. Pindzola, M. S., Robicheaux, F., Loch, S. D., et al. 2007, J. Phys. B Atom. Mol. Opt. Phys., 40, R39 [Google Scholar]
  38. Rongwei, F., Hai, Z., Xiaohui, L., et al. 2013, J. Russ. Laser Res., 34, 369 [Google Scholar]
  39. Seaton, M. J. 1959, Phys. Rev., 113, 814 [NASA ADS] [CrossRef] [Google Scholar]
  40. Shapley, A. E., Reddy, N. A., Kriek, M., et al. 2015, ApJ, 801, 88 [NASA ADS] [CrossRef] [Google Scholar]
  41. Smith, A. C. H., Caplinger, E., Neynaber, R. H., Rothe, E. W., & Trujillo, S. M. 1962, Phys. Rev., 127, 1647 [CrossRef] [Google Scholar]
  42. Wang, Y., Zatsarinny, O., & Bartschat, K. 2014, Phys. Rev. A, 89, 062714 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Comparison of theoretical (DFS) and NIST (Kramida et al. 2021) energy levels for the ground configuration.

In the text

All Figures

thumbnail Fig. 1

Energy levels of the N atom and N+ ion. The single ionization threshold is shown by the horizontal line. Even-parity configurations are presented by red lines and odd-parity configurations are shown by blue lines.
In the text
thumbnail Fig. 2

Electron-impact single ionization cross-sections for levels of the ground configuration of the N atom. The CI data obtained in the potential of the ionized ion. Experiment: open circles with error bars (Brook et al. 1978).
In the text
thumbnail Fig. 3

Electron-impact single ionization cross-sections for levels of the ground configuration of the N atom. The CI data were obtained in the potential of the ionizing ion. Experiment: open circles with error bars (Brook et al. 1978).
In the text
thumbnail Fig. 4

Same as Fig. 3 but for the scaled DW cross-sections.
In the text
thumbnail Fig. 5

Comparison of the contribution from the different EA channels (n ≤ 10) corresponding to excitations for the 2s subshell for the ground level of the N atom.
In the text
thumbnail Fig. 6

Comparison of the contribution from the different EA channels (n ≤ 10) corresponding to excitations for the 2 s subshell for the 2D3∕2 level of the N atom.
In the text
thumbnail Fig. 7

Comparison of the contributions from CI and EA channels for the ground level of the N atom.
In the text
thumbnail Fig. 8

Comparison of the contributions from CI and EA channels for the 2D3∕2 level of the N atom.
In the text
thumbnail Fig. 9

Modeled contribution of the metastable fraction in the atom beam. Experiment: open circles with error bars (Brook et al. 1978).
In the text
thumbnail Fig. 10

Comparison of the scaled DW cross-sections to the BSR (Wang et al. 2014) calculations. Experiment: open circles with error bars (Brook et al. 1978).
In the text
thumbnail Fig. 11

Comparison of the scaled DW cross-sections to the RMPS (Abdel-Naby et al. 2014) calculations. Experiment: open circles with error bars (Brook et al. 1978).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.