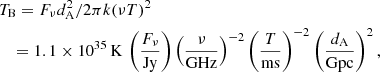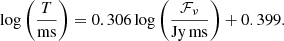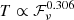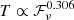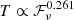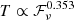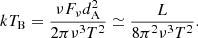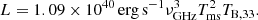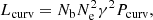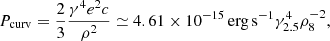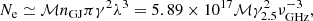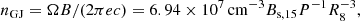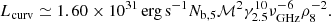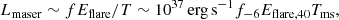| Issue |
A&A
Volume 657, January 2022
|
|
|---|---|---|
| Article Number | L7 | |
| Number of page(s) | 5 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202142268 | |
| Published online | 10 January 2022 | |
Letter to the Editor
New insights into the criterion of fast radio burst in the light of FRB 20121102A
1
School of Astronomy and Space Science, Nanjing University, Nanjing 210023, PR China
e-mail: dxiao@nju.edu.cn
2
Key Laboratory of Modern Astronomy and Astrophysics (Nanjing University), Ministry of Education, PR China
3
Department of Astronomy, University of Science and Technology of China, Hefei 230026, PR China
Received:
21
September
2021
Accepted:
22
December
2021
The total number of observed fast radio burst (FRB) events is rising rapidly thanks to the improvement of existing radio telescopes and the delivery of new facilities. In particular, the Five-hundred-meter Aperture Spherical radio Telescope Collaboration recently reported more than one thousand bursts in a short observing period of 47 days. The striking bimodal distribution in their work motivated us to revisit the definition of FRBs. In this work, we ascribe the bimodal distribution to two physical kinds of radio bursts that may exhibit different radiation mechanisms. We propose using brightness temperature to separate two subtypes. For FRB 20121102A, the critical brightness temperature is TB, cri ≃ 1033 K. Bursts with TB ≥ TB, cri are denoted as “classical” FRBs and we find a tight pulse width-fluence relation (T ∝ ℱν0.306) for them. On the contrary, the other bursts are considered as “atypical” bursts that may have originated from a different type of physical process. We suggest that for each FRB event, a similar dividing line should exist but that the TB, cri is not necessarily the same in such cases. Its exact value depends on the FRB radiation mechanism and the properties of the source.
Key words: methods: statistical / radiation mechanisms: non-thermal
© ESO 2022
1. Introduction
Fast radio bursts (FRBs) are new, bright millisecond radio pulses that were first discovered more than a decade ago (Lorimer et al. 2007). Early on, there were doubts as to whether FRBs were truly astrophysical until a new sample was identified in 2013 (Thornton et al. 2013). Ever since then, this mysterious phenomenon has started to attract intense attention from the community, with breakthroughs announced consistently (for reviews, see Katz 2018; Popov et al. 2018; Petroff et al. 2019; Cordes & Chatterjee 2019; Zhang 2020; Xiao et al. 2021; Petroff et al. 2021). One striking achievement to note is the discovery of the first repeating event FRB 20121102A in 2016 (Spitler et al. 2016; Scholz et al. 2016) and later the identification of its host galaxy (Chatterjee et al. 2017; Marcote et al. 2017; Tendulkar et al. 2017). Up to now, there have been more than 20 repeaters and 600 apparently non-repeating FRBs listed in the catalog (Petroff et al. 2016; The CHIME/FRB Collaboration 2021). However, it is still under hot debate whether genuinely non-repeating FRBs exist (Caleb et al. 2018, 2019; Palaniswamy et al. 2018; Xiao et al. 2021). A few works have discussed the possibility to judge this question using the number fraction of repeaters (Caleb et al. 2019; Lu et al. 2020; Ai et al. 2021; Gardenier et al. 2021). With the accumulation of observing time, this fraction will increase to 100% if all FRBs turn out to be repeating. Otherwise, it will peak at a value less than 100% at a certain time (Ai et al. 2021).
Apart for the repetitive behavior, there is no good criterion established for the classification of FRBs yet. In fact, the definition for FRBs is not very strict at present. Generally, an FRB is characterized by duration (T∼ millisecond) and extremely high brightness temperature (typically TB > 1030 K). A large dispersion measure is often needed to distinguish FRBs from rotating radio transients (RRATs). Among all the observational properties, brightness temperature seems the most promising criterion for the classification because it relates to the radiation mechanism directly. Different coherent radio emission mechanisms should have their own “extremes”, resulting in various transient phenomena such as pulsar radio emission, RRATs, giant pulses, nanoshots, and so on. They cluster in different regions of the spectral luminosity-duration phase space for radio transients and the most prominent difference between them is TB (e.g., Fig. 3 of Nimmo et al. 2021). However, the critical value TB, cri to define an FRB is not well known. Very recently, the large sample of FRB 20121102A bursts released by the Five-hundred-meter Aperture Spherical radio Telescope (FAST) Collaboration makes it possible to explore this issue (Li et al. 2021).
In particular, FRB 20121102A has been well studied and observed by different radio telescopes (Spitler et al. 2016; Gourdji et al. 2019; Hessels et al. 2019; Rajwade et al. 2020; Cruces et al. 2021; Hewitt et al. 2021). Its burst rate is very high, thus, it could be a appropriate event for the study of FRB classification. Previous works showed that the energy distribution can usually be approximated by a power-law form, but the index varies while using different samples from different telescopes (Wang & Yu 2017; Law et al. 2017; Gourdji et al. 2019; Wang & Zhang 2019; Zhang et al. 2021). Similar distributions have been found for solar type III radio bursts (Wang et al. 2021), as well as magnetar bursts (Göǧüş et al. 1999; Prieskorn & Kaaret 2012; Wang & Yu 2017; Cheng et al. 2020), which are considered close relatives to FRBs. However, as the largest single-dish radio telescope presently available, FAST has a very high sensitivity and the energy threshold for detection is lower than ever. The new sample of FRB 20121102A consists of 1652 bursts and the rate is as high as ∼ 122 hr−1. Intriguingly, a bimodal burst energy distribution has been found (Li et al. 2021), indicating that there are two subtypes of FRBs. This has motivated us to consider the criterion for FRBs and we expect to find some empirical relation in the classified subtype sample.
This letter is organized as follows. We introduce the method of classification by brightness temperature and apply it to the FAST sample in Sect. 2. An evident two-parameter empirical relation is found in Sect. 3 and we discuss the reasonability of choosing the value of TB,cri ≃ 1033 K for FRB 20121102A. Finally, we present our discussion and conclusions in Sect. 4.
2. FRB classification by brightness temperature
The brightness temperature of an FRB is determined by equaling the observed intensity with blackbody luminosity, which gives
where Fν is flux density, ν is the emission frequency, and T is the pulse width. We note that it should be angular diameter distance, dA, here instead of luminosity distance dL (Zhang 2020; Xiao et al. 2021), therefore the brightness temperatures of FRBs have been overestimated in previous works. Adopting the redshift of z = 0.19273 (Tendulkar et al. 2017), we get dA = 0.682 Gpc for FRB 20121102A using the cosmological parameters, H0 = 67.7 km s−1 Mpc−1, Ωm = 0.31, ΩΛ = 0.69 (Planck Collaboration XIII 2016). With the burst properties given in Supplementary Table 1 of Li et al. (2021), we can easily obtain TB for each of the 1652 bursts and its distribution is shown in Fig. 1. It is obvious that this distribution centers around ∼a few × 1031 K, lower than the typical TB of other FRB events. This can be attributed to the ability of detecting low-energy bursts by FAST.
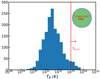 |
Fig. 1. Distribution of TB for FAST 1652 bursts. Red vertical line represents the critical brightness temperature of defining “classical” FRBs. |
However, the main point we argue here is that there is a critical line, namely TB, cri, and, thus, the majority of these low energy bursts may be “atypical.” Bursts with TB ≥ TB, cri are considered to be “classical” FRBs. Since this critical value is unknown, tentatively we chose TB,cri = 1033 K, indicated by the plot of spectral luminosity-duration phase space (Keane 2018; Nimmo et al. 2021; Petroff et al. 2021). The impact of choosing different TB, cri is discussed later on in this paper (in Sect. 3). After drawing this dividing line, we find 76 out of 1652 bursts are “classical.” Furthermore, the energy distribution for this subtype is shown in Fig. 2. The red dashed line represents the probability density function of Gaussian distribution, which has the form of ![$ f(x)=\frac{1}{\sigma\sqrt{2\pi}}\exp\left[-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2\right]\!, $](/articles/aa/full_html/2022/01/aa42268-21/aa42268-21-eq3.gif) where μ is the mean value and σ is standard deviation. We can see the energy distribution is consistent with a single Gaussian profile now. Our result is different from an another latest analysis of 1652 FAST bursts that suggested a power-law energy distribution for high-energy bursts (Zhang et al. 2021). This may arise from the different method of classification and they used burst energy instead. Until now it might still not have been enough to classify FRBs by TBwith full certitude, however, further evidence can be obtained if we go on to find some similarity within these subtype bursts.
where μ is the mean value and σ is standard deviation. We can see the energy distribution is consistent with a single Gaussian profile now. Our result is different from an another latest analysis of 1652 FAST bursts that suggested a power-law energy distribution for high-energy bursts (Zhang et al. 2021). This may arise from the different method of classification and they used burst energy instead. Until now it might still not have been enough to classify FRBs by TBwith full certitude, however, further evidence can be obtained if we go on to find some similarity within these subtype bursts.
 |
Fig. 2. Energy distribution of “classical” subtype of the FAST bursts. Red dashed line shows the probability density function of the Gaussian distribution. |
3. Two-parameter relation for “classical” bursts of FRB 20121102A
As we point out above, if the subtype of “classical” bursts is genuine, all of them should all originate from one particular physical mechanism and share some properties in common. Here, we examine whether a correlation exists between burst width T and fluence ℱν. Intriguingly, while the full FAST sample looks rather scattered on the T − ℱν plane, we find a tight relation for these 76 “classical” bursts, which is shown in the upper panel of Fig. 3. The best-fitting blue line is expressed as:
 |
Fig. 3. Scatter plot of pulse width versus fluence for the full FAST sample, in which 76 “classical” bursts are marked with colored dots (upper panel). The blue solid line represents the best-fitting of |
We calculated the correlation coefficient commonly used in linear regression analysis by 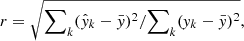 where
where 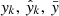 are the observed value, regressed value and mean of observed value respectively. The correlation coefficient is r = 0.936, very close to unity. Furthermore, an F-test is implemented, where the method of calculating Fvalue can be found in Tu & Wang (2018). We obtain that Fvalue = 527.63 for these 76 bursts, much larger than the critical Fα, 1, 76 − 2 = 3.97 where α = 5% is adopted. Therefore, the null hypothesis is rejected and the relation
are the observed value, regressed value and mean of observed value respectively. The correlation coefficient is r = 0.936, very close to unity. Furthermore, an F-test is implemented, where the method of calculating Fvalue can be found in Tu & Wang (2018). We obtain that Fvalue = 527.63 for these 76 bursts, much larger than the critical Fα, 1, 76 − 2 = 3.97 where α = 5% is adopted. Therefore, the null hypothesis is rejected and the relation 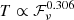 can be well established. Since the faint bursts generally have low brightness temperatures (see subsequent Fig. 6) and seem to show complex time-frequency structures (Li et al. 2021), we plot the dependence of variance on TB in the lower panel of Fig. 3; however, we find no clear correlation. Therefore, the morphological changes of the bursts do not have a prominent effect on the T − ℱν relation.
can be well established. Since the faint bursts generally have low brightness temperatures (see subsequent Fig. 6) and seem to show complex time-frequency structures (Li et al. 2021), we plot the dependence of variance on TB in the lower panel of Fig. 3; however, we find no clear correlation. Therefore, the morphological changes of the bursts do not have a prominent effect on the T − ℱν relation.
In order to verify this relation, we randomly analyzed two other samples of FRB 20121102A, namely, 19 bursts detected by Arecibo and GBT (Hessels et al. 2019) and 36 bursts by Effelsberg (Cruces et al. 2021). Different telescopes have different central frequencies and we repeat the above procedure. The results are shown in Fig. 4. Red symbols represent bursts with TB ≥ 1033 K within these two samples and it is obvious that all these red ones lie fairly close to the best-fitting line. As a comparison, grey dots are those with TB < 1033 K that lie farther away from the line. This greatly increases the confidence of our classification by TB, cri.
 |
Fig. 4. Scatter plot of pulse width versus fluence for two other samples of FRB 20121102A. Blue dots and line are the same as in Fig. 3. Upper panel: 19 bursts from Hessels et al. (2019), marked by stars. Lower panel: 36 bursts from Cruces et al. (2021), marked by squares. In both panels the red ones are “classical” bursts, while the grey ones are “atypical”. Clearly, the red ones are consistent with the |
However, one issue remains with regard to these findings; namely, we chose TB,cri ≃ 1033 K somewhat subjectively. Other values of TB, cri should also be tested for completeness. We thus adopt different values and check whether the T − ℱν relation still holds. We plotted other two cases of TB,cri = 1032.5,1033.5 K in panels a and b of Fig. 5, respectively. For relatively low TB, cri, the scatter is very large and the correlation is loose. Generally, the correlation coefficient, r, gets larger for stronger correlation between two quantities. We plotted its evolution with TB, cri in panel c. The red solid line represents the calculated r and the black dashed line represents the critical value of rejection regions. The fact that the red line is above the black one means that the T − ℱν correlation is always expected. We can clearly see that r increases with TB, cri, indicating that the relation becomes tighter for higher TB, cri. Moreover, we also plotted the dependence of root mean square (rms) of the fitting residuals on TB, cri in panel d. The rms decreases as TB, cri increases. This makes sense since it is easier to pick out real “classical” bursts with a higher criterion on TB. Around 1033 K, this relation is prominent enough and it is reasonable for us to take this value for FRB 20121102A. Numerical estimation gives the similar value later in Sect. 4. We note that TB, cri could differ significantly for other FRB events, which will be discussed later.
 |
Fig. 5. Impact of adopting different TB, cri. Panel a: case of TB,cri = 1032.5 K. Total 181 bursts with TB ≥ TB, cri indicate |
4. Discussion and conclusions
In this paper, we resent a data-oriented study and we discuss a promising criterion for classifying FRBs, namely: the brightness temperature. We analyzed the FAST sample of FRB 20121102A and we find that TB,cri ≃ 1033 K is a reasonable dividing line. Bursts with TB ≥ TB, cri are “classical” FRBs. For this subtype, we found a tight relation of 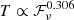 . This relation has been further verified using different samples.
. This relation has been further verified using different samples.
According to Eq. (1), TB is roughly in proportion to ℱν/T3, then we can get a relation 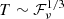 directly for a fixed brightness temperature. However, this simple scaling could not be extended to a sample of bursts with a wide range of TB, as we can clearly see in the upper panel of Fig. 3, in which no clear relation exists for the total 1652 FAST bursts. The positive power-law relation is hidden because the full sample is a mixture of two types of bursts and it finally emerges if we separate them by TB, cri. The width-fluence relation we found is actually for bursts with a value of TB that is higher than some critical value, namely,
directly for a fixed brightness temperature. However, this simple scaling could not be extended to a sample of bursts with a wide range of TB, as we can clearly see in the upper panel of Fig. 3, in which no clear relation exists for the total 1652 FAST bursts. The positive power-law relation is hidden because the full sample is a mixture of two types of bursts and it finally emerges if we separate them by TB, cri. The width-fluence relation we found is actually for bursts with a value of TB that is higher than some critical value, namely, 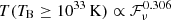 .
.
A temporal energy distribution is clear in Fig. 1 of Li et al. (2021), favoring the argument that two types of bursts exist. As we can infer from Eq. (1), TB ∝ EFRB/T3. For bursts with greater energy, their brightness temperature is generally higher, as we can see in the trend of Fig. 6. The temporal energy distribution actually reflects the rate of two burst types. There are 1576 “atypical” bursts in the FAST sample after our classification. The majority of these bursts should have a different radiation mechanism from “classical” FRBs, for which the brightness temperature could hardly reach TB, cri. These bursts could be pulsar radio emission, giant pulses or some other kind of radio emission that have a much higher burst rate than “classical” FRBs. In fact, if we plot 1576 bursts on the radio transient phase space, they fill the gap between pulsar radio emission and FRBs. We note that the Galactic FRB 20200428A also lies in this range (Bochenek et al. 2020; CHIME/FRB Collaboration 2020; Kirsten et al. 2021); thus, it could also be regarded as an “atypical” burst. Alternatively, it is possible that these “atypical” bursts may not belong to a single subtype and consist of different types of radio transient; therefore, the correlation between T and ℱν is very loose.
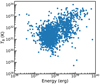 |
Fig. 6. Brightness temperature versus burst energy for the full FAST sample. |
The existence of the dividing line should be related to FRB radiation mechanism directly. In principle, the emission frequency, instead of the central frequency of the receiver, should be used to obtain a more physical TB value. The reason is that some bursts are narrow-banded, for instance, a sample of low-energy bursts from FRB 20121102A are generally detected in less than one-third of the observing bandwidth (Gourdji et al. 2019). Moreover, the pulse width in Eq. (1) should be intrinsic width. Because a physical dividing line, if exist, should be totally intrinsic to the source and unaffected by propagation effect and observation bias. This dividing line is naturally expected, since different types of coherent radio emission have been found to be separated by their brightness temperature in radio transient phase space (Nimmo et al. 2021).
The radiation mechanism of FRBs is largely unknown. Currently, two leading theories are coherent curvature emission by bunched particles in the magnetosphere of a neutron star, and synchrotron maser emission from magnetized shocks outside the magnetosphere (for reviews, see Zhang 2020; Xiao et al. 2021). Constraints can be made using the critical value of brightness temperature. We can rewrite Eq. (1) as:
Therefore, the FRB luminosity can be estimated as:
For the coherent curvature emission mechanism, its luminosity can be expressed as (Zhang 2021),
where Nb is the number of bunches, Ne is the number of electrons in one bunch, and γ is the Lorentz factor of radiating electrons. The radiation power of a single electron is
where ρ is the curvature radius. The length of the bunch should be smaller than emission wavelength λ in order to be coherent, and the transverse size of causally connection can be approximated as ∼γλ (Kumar et al. 2017). Therefore:
where ℳ is the multiplicity factor and the Goldreich-Julian number density is (Goldreich & Julian 1969):
where we assume a magnetar engine with surface magnetic field Bs ∼ 1015 Gauss, rotation period P ∼ 1 s and emission radius R ∼ 108 cm. Substituting Eqs. (6) and (7) into Eq. (5), we have
Basically, the Lorentz factor γ can not exceed 103 due to the drag force exerted by resonant scattering with the soft X-ray radiation field of the magnetar (Beloborodov 2013a). The multiplicity ℳ ∼ 102 from resonant scattering is expected (Beloborodov 2013b). Comparing Eqs. (4) and (9), we find that in the most optimistic case, the brightness temperature of coherent curvature emission can merely reach 1033 K. For TB > 1033 K, this model requires unrealistic large value of 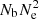 , for which the formation and maintenance of the bunches can be problematic (Saggion 1975; Cheng & Ruderman 1977; Kaganovich & Lyubarsky 2010). A more stringent constraint on TB is given based on a similar method (Lyutikov 2021a). However, this mechanism can still responsible for “atypical” bursts.
, for which the formation and maintenance of the bunches can be problematic (Saggion 1975; Cheng & Ruderman 1977; Kaganovich & Lyubarsky 2010). A more stringent constraint on TB is given based on a similar method (Lyutikov 2021a). However, this mechanism can still responsible for “atypical” bursts.
For the maser mechanism from magnetized shocks, a very small fraction of shock energy is released in the form of radio precursor (Hoshino & Arons 1991). A particle-in-cell simulation suggests that this fraction is 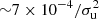 , where σu ≥ 1 is the upstream magnetization (Plotnikov & Sironi 2019). Moreover, only a fraction of bolometric maser power can turns into FRB emission due to strong induced Compton scattering (Metzger et al. 2019). These two effects give a combined fraction f ∼ 10−6 − 10−5 (Xiao & Dai 2020), such that
, where σu ≥ 1 is the upstream magnetization (Plotnikov & Sironi 2019). Moreover, only a fraction of bolometric maser power can turns into FRB emission due to strong induced Compton scattering (Metzger et al. 2019). These two effects give a combined fraction f ∼ 10−6 − 10−5 (Xiao & Dai 2020), such that
where the flare energy Eflare is assumed to be comparable to magnetar X-ray bursts energy, EX. Observations of hundreds of X-ray bursts from SGR 1806-20 and SGR 1900+14 gives that EX ∼ 1038 − 1041 erg (Göǧüş et al. 1999, 2000). Comparing Eqs. (4) and (10), we find maser emission from shocks by normal flares cannot produce high brightness temperature FRBs. Magnetar giant flares with Eflare > 1043 erg is need to reach TB > 1033 K. However, giant flares can not happen as frequently as FRB 20121102A bursts. Also, the synchrotron maser mechanism has difficulty in explaining polarization swing (Luo et al. 2020) and nano-second variability in the light curve (Lu et al. 2022).
To conclude, both these two mechanisms have their own limitations. Conservatively speaking, both of them seem unlikely to produce FRBs with TB > 1033 K. So it remains unclear what mechanism makes the “classical” FRBs. There have been tens of possible mechanisms for pulsar radio emission, and it has been proposed that some of them (e.g., free electron laser mechanism) can be applied to FRBs and reach high brightness temperature (Lyutikov 2021b). Interestingly, Zhang (2021) recently suggested that the coherent inverse Compton scattering could be a promising mechanism, in which the bunch formation problem can be largely relieved due to the enhanced emission power of a single electron. Plenty of works ought to be carried out to better understand the FRB radiation mechanism and the T − ℱν relation could provide some hints for future studies. Lastly, while we expect a critical brightness temperature for every FRB event, the difference in source property and environment could result in different TB, cri values. A subsequent analysis based on other FRBs using similar methods is now in progress.
Acknowledgments
We would like to thank an anonymous referee for helpful comments. This work is supported by the National Key Research and Development Program of China (Grant No. 2017YFA0402600), the National SKA Program of China (grant No. 2020SKA0120300), and the National Natural Science Foundation of China (Grant No. 11833003, 11903018). DX is also supported by the Natural Science Foundation for the Youth of Jiangsu Province (Grant NO. BK20180324).
References
- Ai, S., Gao, H., & Zhang, B. 2021, ApJ, 906, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Beloborodov, A. M. 2013a, ApJ, 777, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Beloborodov, A. M. 2013b, ApJ, 762, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Bochenek, C. D., Ravi, V., Belov, K. V., et al. 2020, Nature, 587, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Caleb, M., Spitler, L. G., & Stappers, B. W. 2018, Nat. Astron., 2, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Caleb, M., Stappers, B. W., Rajwade, K., & Flynn, C. 2019, MNRAS, 484, 5500 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, S., Law, C. J., Wharton, R. S., et al. 2017, Nature, 541, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, A. F., & Ruderman, M. A. 1977, ApJ, 212, 800 [Google Scholar]
- Cheng, Y., Zhang, G. Q., & Wang, F. Y. 2020, MNRAS, 491, 1498 [NASA ADS] [CrossRef] [Google Scholar]
- CHIME/FRB Collaboration (Andersen, B. Â. C., et al.) 2020, Nature, 587, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Cordes, J. M., & Chatterjee, S. 2019, ARA&A, 57, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Cruces, M., Spitler, L. G., Scholz, P., et al. 2021, MNRAS, 500, 448 [Google Scholar]
- Gardenier, D. W., Connor, L., van Leeuwen, J., Oostrum, L. C., & Petroff, E. 2021, A&A, 647, A30 [EDP Sciences] [Google Scholar]
- Göǧüş, E., Woods, P. M., Kouveliotou, C., et al. 1999, ApJ, 526, L93 [CrossRef] [Google Scholar]
- Göǧüş, E., Woods, P. M., Kouveliotou, C., et al. 2000, ApJ, 532, L121 [CrossRef] [Google Scholar]
- Goldreich, P., & Julian, W. H. 1969, ApJ, 157, 869 [Google Scholar]
- Gourdji, K., Michilli, D., Spitler, L. G., et al. 2019, ApJ, 877, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Hessels, J. W. T., Spitler, L. G., Seymour, A. D., et al. 2019, ApJ, 876, L23 [Google Scholar]
- Hewitt, D. M., Snelders, M. P., Hessels, J. W. T., et al. 2021, MNRAS, submitted [arXiv:2111.11282] [Google Scholar]
- Hoshino, M., & Arons, J. 1991, Phys. Fluids B, 3, 818 [NASA ADS] [CrossRef] [Google Scholar]
- Kaganovich, A., & Lyubarsky, Y. 2010, ApJ, 721, 1164 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, J. I. 2018, Prog. Part. Nucl. Phys., 103, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Keane, E. F. 2018, Nat. Astron., 2, 865 [Google Scholar]
- Kirsten, F., Snelders, M. P., Jenkins, M., et al. 2021, Nat. Astron., 5, 414 [Google Scholar]
- Kumar, P., Lu, W., & Bhattacharya, M. 2017, MNRAS, 468, 2726 [NASA ADS] [CrossRef] [Google Scholar]
- Law, C. J., Abruzzo, M. W., Bassa, C. G., et al. 2017, ApJ, 850, 76 [Google Scholar]
- Li, D., Wang, P., Zhu, W. W., et al. 2021, Nature, 598, 267 [CrossRef] [Google Scholar]
- Lorimer, D. R., Bailes, M., McLaughlin, M. A., Narkevic, D. J., & Crawford, F. 2007, Science, 318, 777 [Google Scholar]
- Lu, W., Piro, A. L., & Waxman, E. 2020, MNRAS, 498, 1973 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, W., Beniamini, P., & Kumar, P. 2022, MNRAS, 510, 1867 [Google Scholar]
- Luo, R., Men, Y., Lee, K., et al. 2020, MNRAS, 494, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Lyutikov, M. 2021a, ApJ, 918, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Lyutikov, M. 2021b, ApJ, 922, 166 [CrossRef] [Google Scholar]
- Marcote, B., Paragi, Z., Hessels, J. W. T., et al. 2017, ApJ, 834, L8 [CrossRef] [Google Scholar]
- Metzger, B. D., Margalit, B., & Sironi, L. 2019, MNRAS, 485, 4091 [NASA ADS] [CrossRef] [Google Scholar]
- Nimmo, K., Hessels, J. W. T., Kirsten, F., et al. 2021, ArXiv e-prints [arXiv:2105.11446] [Google Scholar]
- Palaniswamy, D., Li, Y., & Zhang, B. 2018, ApJ, 854, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Petroff, E., Barr, E. D., Jameson, A., et al. 2016, PASA, 33 [Google Scholar]
- Petroff, E., Hessels, J. W. T., & Lorimer, D. R. 2019, A&ARv, 27, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Petroff, E., Hessels, J. W. T., & Lorimer, D. R. 2021, ArXiv e-prints [arXiv:2107.10113] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plotnikov, I., & Sironi, L. 2019, MNRAS, 485, 3816 [NASA ADS] [CrossRef] [Google Scholar]
- Popov, S. B., Postnov, K. A., & Pshirkov, M. S. 2018, Phys. Usp., 61, 965 [CrossRef] [Google Scholar]
- Prieskorn, Z., & Kaaret, P. 2012, ApJ, 755, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Rajwade, K. M., Mickaliger, M. B., Stappers, B. W., et al. 2020, MNRAS, 495, 3551 [NASA ADS] [CrossRef] [Google Scholar]
- Saggion, A. 1975, A&A, 44, 285 [NASA ADS] [Google Scholar]
- Scholz, P., Spitler, L. G., Hessels, J. W. T., et al. 2016, ApJ, 833, 177 [CrossRef] [Google Scholar]
- Spitler, L. G., Scholz, P., Hessels, J. W. T., et al. 2016, Nature, 531, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Tendulkar, S. P., Bassa, C. G., Cordes, J. M., et al. 2017, ApJ, 834, L7 [NASA ADS] [CrossRef] [Google Scholar]
- The CHIME/FRB Collaboration (Amiri, M., et al.) 2021, ApJS, submitted [arXiv:2106.04352] [Google Scholar]
- Thornton, D., Stappers, B., Bailes, M., et al. 2013, Science, 341, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Tu, Z. L., & Wang, F. Y. 2018, ApJ, 869, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, F. Y., & Yu, H. 2017, JCAP, 2017, 023 [CrossRef] [Google Scholar]
- Wang, F. Y., & Zhang, G. Q. 2019, ApJ, 882, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, F. Y., Zhang, G. Q., & Dai, Z. G. 2021, MNRAS, 501, 3155 [CrossRef] [Google Scholar]
- Xiao, D., & Dai, Z.-G. 2020, ApJ, 904, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Xiao, D., Wang, F., & Dai, Z. 2021, Sci. China Phys. Mech. Astron., 64, 249501 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B. 2020, Nature, 587, 45 [CrossRef] [Google Scholar]
- Zhang, B. 2021, ApJ, submitted [arXiv:2111.06571] [Google Scholar]
- Zhang, G. Q., Wang, P., Wu, Q., et al. 2021, ApJ, 920, L23 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Distribution of TB for FAST 1652 bursts. Red vertical line represents the critical brightness temperature of defining “classical” FRBs. |
| In the text | |
 |
Fig. 2. Energy distribution of “classical” subtype of the FAST bursts. Red dashed line shows the probability density function of the Gaussian distribution. |
| In the text | |
 |
Fig. 3. Scatter plot of pulse width versus fluence for the full FAST sample, in which 76 “classical” bursts are marked with colored dots (upper panel). The blue solid line represents the best-fitting of |
| In the text | |
 |
Fig. 4. Scatter plot of pulse width versus fluence for two other samples of FRB 20121102A. Blue dots and line are the same as in Fig. 3. Upper panel: 19 bursts from Hessels et al. (2019), marked by stars. Lower panel: 36 bursts from Cruces et al. (2021), marked by squares. In both panels the red ones are “classical” bursts, while the grey ones are “atypical”. Clearly, the red ones are consistent with the |
| In the text | |
 |
Fig. 5. Impact of adopting different TB, cri. Panel a: case of TB,cri = 1032.5 K. Total 181 bursts with TB ≥ TB, cri indicate |
| In the text | |
 |
Fig. 6. Brightness temperature versus burst energy for the full FAST sample. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.