| Issue |
A&A
Volume 657, January 2022
|
|
|---|---|---|
| Article Number | A135 | |
| Number of page(s) | 13 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202141719 | |
| Published online | 21 January 2022 | |
A survey on Hungaria asteroids involved in mean motion resonances with Mars
1
Department of Astronomy, Institute of Geography and Earth Sciences, Eötvös Loránd University,
Pázmány Péter sétány 1/A,
1117
Budapest,
Hungary
e-mail: e.forgacs-dajka@astro.elte.hu; zs.sandor@astro.elte.hu
2
Centre for Astrophysics and Space Science, Eötvös Loránd University,
Pázmány Péter sétány 1/A,
1117
Budapest,
Hungary
3
Wigner Research Centre for Physics,
PO Box 49,
1525
Budapest,
Hungary
4
Konkoly Observatory, Research Centre for Astronomy and Earth Sciences,
Budapest,
Hungary
5
Eszterházy Károly Catholic University, Faculty of Natural Sciences, Institute of Chemistry and Physics, Department of Physics,
Leányka utca 6–8,
3300
Eger,
Hungary
e-mail: sztakovics.jan@uni-eszterhazy.hu
Received:
6
July
2021
Accepted:
19
October
2021
Context. A region at the inner edge of the main asteroid belt is populated by the Hungaria asteroids. Among these objects, the Hungaria family formed as the result of a catastrophic disruption of the (434) Hungaria asteroid a few hundred million years ago. Due to the Yarkovsky effect, the fragments depending on their direction of rotation are slowly drifting inwards or outwards from the actual place of collision. Due to this slow drift, these bodies could approach the locations of the various outer-type mean-motion resonances (MMRs) with Mars.
Aims. We aim to study the actual dynamical structure of Hungaria asteroids, which is primarily shaped by various outer-type MMRs with Mars. Moreover, we also seek connections between the orbital characteristics of Hungaria asteroids and their absolute magnitude.
Methods. To map the resonant structure and dynamics of asteroids belonging to the Hungaria group, we used the FAst Identification of mean motion Resonances method, which can detect MMRs without the a priori knowledge of the critical argument. We also compiled stability maps of the regions around the MMRs by using the maximal variations in the asteroids’ eccentricities, semi-major axes, and inclinations. We numerically integrated the orbits of all asteroids belonging to the Hungaria group available in the JPL Horizon database together with the Solar System planets for one and ten million years.
Results. Having studied the resonant structure of the Hungaria group, we find that several asteroids are involved in various MMRs with Mars. We identify both short- and long-term MMRs. Besides this, we also find a relationship between the absolute magnitude of asteroids and the MMR in which they are involved.
Key words: celestial mechanics / methods: numerical / minor planets, asteroids: general
© ESO 2022
1 Introduction
Asteroids located in the main belt (orbiting between Mars and Jupiter) show highly complex dynamical behaviour. The most spectacular manifestation of this complex dynamics is the existence of the Kirkwood gaps that are minima in the number distribution of asteroids with respect to their semi-major axes at the locations of the 3:1, 5:2, 7:3, and 2:1 mean motion resonances (MMRs) with Jupiter.
In the innermost region of the main belt, there is a group of asteroids that occupies a dynamically protected region that is practically affected neither by the MMRs with Jupiter, nor the most important secular resonances. This is the group of Hungaria asteroids (named after (434) Hungaria), whose members orbit within a narrow range of semi-major axes (1.78–2.06 au), being separated from the majority of the main asteroid belt by the 4:1 inner-type MMR with Jupiter. This region is dynamically bounded by the ν6, ν16 secular resonances on the (a, i) plane (Milani et al. 2010). Hungaria asteroids revolve in highly inclined orbits (i = 16°–30°), while their eccentricities range between low and moderate values (e < 0.18). The higher limit in their eccentricity is close to the value necessary for asteroids to cross the orbit of Mars (Gradie et al. 1979; Milani et al. 2010).
The present Hungaria asteroids could be survivors of the much more extended asteroid belt, the hypothetical ‘E-belt’, which has been destabilised by the late migration of giant planets (see Bottke et al. (2012). Members of the Hungaria group are also unique in the sense that they are the closest asteroids to the Earth on dynamically stable orbits. Due to their peculiar position in the inner Solar System and relative proximity to the orbit of Earth, the dynamics of Hungaria asteroids is of great interest. Investigations revealed that the members of Hungaria population are slowly escaping by crossing the orbit of Mars, therefore they are thought to be unstable over the age of the Solar System (Milani et al. 2010; McEachern et al. 2010). It was recently found that the eccentricity of Mars, which has changed chaotically over a very long timescale, plays an important role in affecting the stability of Hungaria asteroids (Ćuk & Nesvorný 2018). The higher eccentricity of Mars enhances the probability of close encounters of the asteroids, and therefore the destabilisation of Hungaria asteroids is not due to secular effects. This latter result may render the conclusions of the previous studies on the determination of the half life time and decline rate of Hungaria asteroids less certain. Moreover, there is another escape mechanism through the chaotic diffusion of Hungaria asteroids. This is when, due the Yarkovsky effect (Farinella & Vokrouhlicky 1999) asteroids drifting towards the locations of MMRs with Mars, where due to the combined effects of the resonant and non-conservative perturbations, their eccentricities are gradually increased. By numerical integration, McEachern et al. (2010) found that the eccentricities of Hungaria asteroids involved in MMRs can increase until reaching the Mars orbit crossing limit. As a consequence, the chaotic variation of the eccentricity of Mars could also have a strong impact on the destabilisation of the Hungaria asteroids that are involved in various MMRs with Mars. Here, we note that the Yarkovsky effect is a non-conservative force that is due to the solar irradiation and thermal emission of a rotating small asteroid. This effect manifests as a slow orbital drift that depends on the direction of the asteroid’s rotation.
According to dynamical studies, the boundaries of Hungaria asteroids can further be refined: they are clustered between the4:3 and 3:2 outer-type MMRs with Mars, while the inclinations of these objects are bounded by ν5, ν4 linear, and ν56 non-linear secular resonances (see for instance Correa-Otto & Cañada-Assandri 2018). A region of strong chaotic behaviour and instability already developed inthe (a, e) parameter plane at lower values of eccentricities; this is the result of overlapping of various outer-type MMRs with Mars Correa-Otto& Cañada-Assandri (2018). Thus, in that work further evidence is given of the importance of dynamical effects of Mars through MMRs that seem to be essential when the stability boundaries of Hungaria asteroids are investigated. Regarding the investigations related to the MMRs between Hungaria asteroids and Mars, it is noteworthy to mention the pioneering work of Connors et al. (2008), in which asteroids were identified in the 3:2 MMR. In a preliminary work, Sztakovics et al. (2019) investigated the MMRs between all known Hungaria asteroids and Mars with the FAst Identification of mean motion Resonances (FAIR) method (Forgács-Dajka et al. 2018). Finally, we mention the work of Correa-Otto et al. (2021), in which the authors compiled a catalogue of Hungaria asteroids involved in the 3:2 MMR with Mars. It is also noteworthy to mention the work of Michel & Froeschlé (1997) on the secular resonances in the inner Solar System whose locations mark the boundaries for Hungaria asteroids.
Another important result related to Hungaria asteroids is the identification of the Hungaria collisional family among the background population (Lemaitre 1994). This finding was further confirmed by Warner et al. (2009) and Milani et al. (2010), assuming that the Hungaria collisional family was formed by a catastrophic disruption of (434) Hungaria approximately 300–500 Myr ago. A collisional family is usually spreading out, because besides the gravitational perturbations, fragments formed at the disruption event are also subject to the Yarkovsky effect. As the result of the orbital drift of asteroids occurred due to the Yarkovsky effect, family members are gradually departing from the location of the disruption event. Smaller fragments that are more sensitive to the Yarkovsky effect drift further fromthe location of the disruption than larger fragments. The zone that can host family members can thus be determined by plotting the V-shaped curved lines characteristic of a collisional-born family, as seen in the work of Warner et al. (2009) for Hungaria asteroids. A reliable description on the formation of the above-mentioned asteroids, this V-shape distribution can be found in Paolicchi et al. (2019). Interestingly, the Yarkovsky effect may not work when an asteroid is captured in an MMR (Vokrouhlický et al. 2015).
A more accurate distinction between family members and background asteroids can be done by calculating their proper elements. In the case of Hungaria asteroids, proper elements were first calculated by Lemaitre (1994), and later on the ‘synthetic’ proper elements in large number of them were determined by Milani et al. (2010). More recently, Vinogradova (2019) determined the proper elements of more than 650 000 asteroids also including the Hungaria asteroids. The proper elements in this work were determined with an empirical method, in which the calculation of the secular perturbations is based on the distribution of the orbital elements. This method enables one to distinguish between the two most important effects, namely the classical perturbation and the Lidov-Kozai effect. According to the author, in the case of Hungaria asteroids neither the method based on the classic secular theory nor the empirical method give reliable results. This is due to the MMRs that can be found in this region.
According to the investigations of Lucas et al. (2019), one can also make a distinction between Hungaria family members and background asteroids. Based on the relative taxonomic distribution, it has been found that 71% of the background population belong to the S type, while 24% of them belong to the X type. On the contrary, 88% of the Hungaria family members are classified as X type, while the remaining asteroids belong to the C and B types. We should note, however, that in this case according to Vinogradova (2019) the taxonomical composition for the Hungaria family has not been changed. The C- and X-type asteroids in the Hungaria family are of the E type that is the consequence of the very high albedos of the asteroids. Moreover, the C, X, and E types are spectrally very similar to each other, and therefore they might be confused.
Based on the above considerations, in our survey we do not distinguish between the Hungaria collisional family members and background asteroids, instead of that we globally study all asteroids that share the orbital elements that are characteristic to the Hungaria group. We also note that we investigated the dynamical behaviour of the Hungaria group members, which is mainly governed by various outer-type MMRs with Mars, as it is reflected in the structure of our paper.
In the second section, we describe the asteroid data and their source. We used two data sets originating from two different epochs, which enabled us to compare the effects of the observations to the results obtained in our dynamical survey. In this section, we briefly describe the methods applied, namely the FAIR method (Forgács-Dajka et al. 2018), which is our main tool for identifying the different MMRs, and also its automatisation, which makes it possible to detect MMRs in the large sample of asteroids included in our survey. In the third section, we analyse our numerical results. We compare the asteroids exhibiting resonant behaviour in both data sets.
Similarly to previous works (Wisdom 1985; Correa-Otto et al. 2021), we introduce the concepts of the short-term and long-term resonances based on the length of the time interval during which an asteroid is involved in a certain MMR. Using the numerical results obtained, we compiled dynamical maps of certain parts of the whole region filled with Hungaria group members to better understand the dynamical effects of the various MMRs. Aside from the well-known, classical method of the maximum variation of asteroids’ eccentricities, we also used the maximum variation of other orbital elements (as the asteroids’ semi-major axes and inclinations), which helped us obtain a comprehensive picture regarding the variety of MMRs in this region. Finally, we statistically investigated a possible relationship between the location of Hungaria asteroids involved in MMRs and their absolute magnitude using observational data. The most plausible reason for this size segregation effect could be the Yarkovsky effect; however, other dynamical effects could also play an important role here.
 |
Fig. 1 Hungaria-population asteroids projected onto the plane of absolute magnitude H versus semi-major axis of nearly 24 000 objects. The lines correspond to the four most populated MMRs with Mars. Asteroid (434) Hungaria ismarked by a red point. The curved lines show Hungaria-family zone, where we used a canonical form 0.2H = log((a − ac)∕C), where ac = 1.94au and C = [3 × 10−5, 2.5 × 10−5, 2 × 10−5]au, denotes by [blue, black, and orange] and discussed by Vokrouhlický et al. (2006) and Warner et al. (2009). |
2 Data and methods
Due to the recent sky surveys, the number of objects with orbit type of Hungaria asteroids is rapidly growing. In 2019, the number of such asteroids was 19 529, while in 2020 this number changed to 23 860, which is a significant increase of 22%. In our work, we considered the objects classified as Hungaria orbit types by the IAU Minor Planet Center1, while the heliocentric coordinates and velocities of all identified bodies are taken from the NASA JPL Horizon2 database.
As a first step of our data analysis, we display all members of the Hungaria group (found in the above database) in the (a, H) plane, where a is the semi-major axis and H is the absolute magnitude of asteroids. As expected, most of the asteroids are located within the curved V-shaped lines on the (a, H) plane (Fig. 1), whose canonical forms are given by Vokrouhlický et al. (2006), indicating that they are in the Hungaria family zone. The parent asteroid of the family, (434) Hungaria is denoted by a red dot. We note that Fig. 1 is similar to the corresponding figure in Warner et al. (2009), however, we also display all asteroids involved in MMRs of outer-type with Mars with thick black dots. The automatised procedure of identifying asteroids involved in MMRs is described later in this section. From Fig. 1, one can immediately conclude that the 4:3, 7:5, 10:7, and 3:2 outer-type MMRs with Mars are the most populated ones. An interesting feature of Fig. 1 is the sharp limit of Hungaria asteroids at the 3:2 MMR with Mars, where a relatively large number of asteroids are affected by the resonance. At the 4:3 MMR, a considerable number of Hungaria asteroids are also involved; however, the inner boundary of the Hungaria population seems to be located at the 9:7 MMR, where only a few asteroids are identified. While the sign of the Yarkovsky effect is clearly seen in the figure, another interesting feature is the asymmetry in the distribution of asteroids: a significant number of fainter objects are orbiting at lower semi-major axes, moreover, their orbital distance is larger from the orbit of (434) Hungaria, which is the progenitor of the collisional family, than the orbital distance of asteroids at the outer boundary of the whole Hungaria population. One possible explanation of the asymmetrical distribution that is compatible with the Yarkovsky effect is given in Sect. 4 with the help of a detailed statistical analysis.
As already mentioned, stability studies have proposed so far natural boundaries of the stability region hosting Hungaria asteroids (for example Milani et al. 2010; Correa-Otto & Cañada-Assandri 2018). Moreover, there are several MMRs with Mars that may govern the dynamics of Hungarias inside their stability region (see McEachern et al. 2010, for details). In order to reveal the role of these MMRs, we numerically integrate the orbits of all members of the Hungaria group found in database, together with all major planets of the Solar System. The numerical integrations have been calculated by using a self-developed adaptive step size Runge-Kutta-Nystrom 6/7 N-body integrator (Dormand & Prince 1978). We note that our work is the first comprehensive dynamical survey of Hungaria asteroids so far aimed at identifying each object in MMR with Mars.
Having integrated the orbits numerically, we applied the FAIR method to quickly detect all asteroids involved in MMRs with Mars. In what follows, we briefly describe the FAIR method. A detailed description and application can be found in Forgács-Dajka et al. (2018). Let us denote by n the mean motion, λ the mean longitude, and ϖ the longitude of perihelion of the asteroid, while the same primed quantities (n′, λ′, and ϖ′) refer to the perturber (in our case to Mars). Considering an outer-type MMR, the ratio of the mean motions satisfies
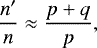 (1)
(1)
with p and q being positive integers. According to FAIR, when displaying λ − λ′ versus M, stripes appear that intersect thehorizontal axis in p nodes and the vertical axis in p + q nodes. The critical argument for this MMR,
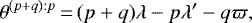 (2)
(2)
librates around the centre of the resonance. Thus, the FAIR method can be ideally applied to a large sample of bodies that members might be involved in various MMRs with an external perturber without the a priori knowledge of the librating critical argument. The above-described application of FAIR can be seen in Fig. 2, where the left panel displays the stripes on the λ − λ′ versus M plane, while in the middle panel the critical argument librates as a function of time. The colours indicate the time evolution in order to reveal the dynamics on the semi-major axis versus eccentricity (a, e) plane shown in the right panel. In this panel, we denote the resonant semi-major axis with a dashed vertical line, and it is clearly visible that the a, e values cover quite a large region.
To detect whether a Hungaria asteroid is in an MMR with Mars, we automatised the use of the FAIR method. We recall that the number of nodes along the x and y axes that should be detected are the crossings of the stripes with the horizontal and vertical axes. To do so, we created a two-dimensional distribution of all points on the λ − λ′ versus M plane by covering it by a bi-dimensional grid, and counting the number of points falling in each cell. The bin size we used is 5 degrees in both directions. We note that although this choice seems to be arbitrary, according to visual checks it gives reliable results in identifying MMRs. After calculating the average of the points on this plane, we determined the variance in each cell. If the variance is larger than a pre-defined threshold, then the examined body might be in an MMR. In the next step, one should determine the crossing of the stripes with axes, as we already mentioned. We cut two not too narrow rectangular regions (we used 20 degrees) along both x and y directions and created two histograms in both directions. We applied a fast Fourier transform (FFT) on these histograms that gives the number of nodes, which are the values of p and q in Eq. (2). In the last step of this method, we check whether the MMR detected is around the nominal position of the resonance. To test this method, we check the results by eye. The above method finds fewer cases (approximately 10%) than were detected by eye. This apparent error in this method is due to the fact that there are two temporal types of MMR, i.e. long-term and short-term resonances (see Sect. 3.2 for a more detailed explanation), and in the case of very short-term resonances the variance is very small. It is important to note that in the case of the short-term resonances the sampling frequency affects the detection of an MMR because rarely sampling makes it difficult to identify the stripes on the λ − λ′ versus M plane.
 |
Fig. 2 Dynamics of the asteroid 2016AX8 in 3:2 MMR of outer type with Mars. In the left panel, the FAIR method indicates the 3:2 MMR. In the middle panel, one can see the variation of the critical argument showing libration for ten million years. In the right panel, the excursion of the orbit on the (a, e) is shown. The colour-coding is explained in the text. |
3 The resonant structure of the Hungaria asteroids
In this section, we summarise our findings obtained by a dynamical and statistical survey of nearly 24 000 asteroids belonging to the Hungaria group.
In the first phase of our research, we compare the differences that occur by using the databases from the years 2019 and 2020. As wementioned before, the number of asteroids increased, and on the other hand the orbital elements of the asteroids might be more accurate as the result of new and continuous observations. We investigated how the population and lifetime of an MMR are modified by the possible changes of the orbital elements due to the two different sets of orbital data. In some cases, the formerly librating critical argument does not librate according to the new database from the year 2020, or the long-term libration becomes temporary or in other words short-term libration.
In the second phase, we investigate how the integration time affects the population of asteroids involved in various MMRs, and also thetime length that an asteroid spends in an MMR. By using the orbital elements in the database from 2020, we numerically integrated the orbits of asteroids together with the Solar System planets for 1 and 10 million years. Some of the asteroids that are involved in an MMR for 1 million years showing only libration may lose their resonant character in the 10-million-year integration. This is a clear signature of the chaotic behaviour that is the result of the resonant perturbations from Mars, and non-resonant ones from Jupiter and other planets. To explore the dynamical character of asteroids, we also compiled various stability maps of some of the most populated MMRs.
Abundance of the various MMRs taken from the 2019 and 2020 databases.
3.1 Comparison of dynamics of asteroids from databases of years 2019 and 2020
In Table 1, we show how the abundance of resonant Hungaria asteroids changes by using the orbital elements in the two databases of years 2019 and 2020. We can state that in the database from year 2020, the increase in the number of resonant asteroids is approximately 20% that corresponds to the change in the whole population of Hungaria asteroids. In the database from 2019, we find 301 resonant asteroids, while in the database from 2020 this number is increased to 363 resonant asteroids. Based on the above fact, both databases can be considered for statistical purposes. On the other hand, by comparing the two databases we can also discover interesting differences.
We expect that since the number of known asteroids is increased by 20%, the number of resonant asteroids also increases by the same amount, that is confirmed by the results obtained. On the other hand, if we carefully investigate the distribution of asteroids captured in MMRs, we can conclude that in the 4:3, 7:5, and 10:7 cases the number of asteroids increases, while fewer are captured in the 3:2 MMR. If we consider the ratios of librating objects in a certain MMR to the whole resonant population, the distribution of asteriods in certain MMRs is also changing (see Table 1). The reason for this fact might be the consequence of observations. Additionally, in the last column of the table the numbers of those resonant asteroids are shown that librate in both databases. Curiously, in the 3 : 2 MMR the number of librating objects is proportionally larger than in the other MMRs. The reason for this difference could be that the orbital elements are known to be more accurate in this case.
Similar to the previous cases, where we examined the differences due to the initial conditions, we also examined how the integration time affects the population of a given MMR and the distribution of resonant asteroids in different resonances. The results are shown in Table 2, where the number of asteroids caught in each resonance is given by the two integration times, and the last column shows the number of celestial bodies that were resonant in both runs. Here, we note that in this case, we started from the 2020 data as an initial condition. Comparing the two integration times, we can see that the total number of resonant celestial bodies decreased (for one million years 363 asteroids, for ten million years 330 asteroids), and small fluctuations can also be observed in the distributions. We note here that each asteroid showing libration in some interval of the whole integration time is already considered a resonant celestial body. This results in an interesting phenomenon, for example, where in the case of 4:3 MMR, the number of resonant asteroids increased during the longer integration time, because those that did not show resonant behaviour on a short timescale could be captured on a longer timescale (after the first one million years). In almost all of the main MMRs (except the 3:2 one), the number of asteroids does not decrease significantly after the ten-million-year long integration. Interestingly, the number of asteroids involved in the 3:2 MMR decreased a lot. The role of this MMR as a natural outer boundary of the Hungaria group, and the chaotic diffusion that may be acting here is discussed further in Sect. 5.
If we examine those asteroids that show libration on both integration time scales, we see that the number of these asteroids is less than the number obtained during one million years of integration. The reason for this is to be found in the sampling frequency and the length of the libration period. This is because those asteroids that were only librating for a short timeinterval during the one-million-year integration may not have shown a detectable variation in the λ − λ′ versus M plane at thesampling frequency of the ten-million-year integration (cf. Sect. 2).
3.2 Long-term and short-term MMRs between Hungaria asteroids and Mars
In the following, we present the two types of resonant behaviour that we detected in the case of the Hungaria asteroids. The difference between these two cases is the length of the time interval on which the critical argument shows libration. Although the semi-major axis of Mars does not change significantly, perturbations, mainly from the giant planets, can cause the capture of asteroids by MMRs to become episodic, which is why we observe that in many cases the critical argument librates for a shorter time than the whole length of numerical integration. In some cases, the resonance turns out to be long-lasting, as the critical argument shows libration during the ten-million-year integration time. These cases are classified as long-term MMRs. We note, however, that even the long-term libration of the critical argument can be changed into circulation if we integrate the orbit for a longer time. As already mentioned, the FAIR method is suitable for the detection of both types of resonance (short-term and long-term), taking into account the sampling time. We note that episodic libration of the critical argument in the case of the 3:1 MMR was first observed by Wisdom (1985), and very recently in the case of Hungaria asteroids involved in the 3:2 MMR of outer type with Mars by Correa-Otto et al. (2021).
Since the above cited paper deals with Hungaria asteroids involved in the 3:2 MMR of outer type with Mars, we could compare our results with those of Correa-Otto et al. (2021). The authors identified 22 asteroids whose critical arguments librate during the two-million-year numerical integration (see Table 1 in Correa-Otto et al. 2021). The majority of these bodies can also be found in our database; all have librating critical arguments, except one asteroid (referred to as 458 733 in Correa-Otto et al. 2021 and 2011NN2 in our database). In Table 3 of Correa-Otto et al. (2021), there are asteroids referred to as ‘quasi-resonant’. Among these bodies, we find some of them with librating critical arguments for the whole length of numerical integration. We have to note, however, that there are a few discrepancies between our work and that of Correa-Otto et al. (2021): (i) we used a different numerical integrator; (ii) there could be differences in the initial conditions used; (iii) asteroids are selected from the databases used in both studies by using different criteria.
In Fig. 2, we show the case in which the asteroid 2016AX8 is involved into the 3:2 long-term MMR with Mars. In the left panel, the stripes clearly indicate the character of the resonance, while in the middle panel we show the libration of the corresponding critical argument, which is calculated based on the left panel. Finally, in the right panel the corresponding values of the semi-major axis and eccentricity are shown around the nominal value of the resonant semi-major axis, ar. In the middle and right panels, a colour-coding is applied: the black dots indicate the onset, the red dots indicate epochs close to the end of the numerical integration, and the intermediate colours are for intermediate epochs. With this coding, the scattering of the a, e values around the nominal value of the MMR can be followed. In this particular case, the corresponding values are changing in time; for example, it is clearly seen that a larger libration amplitude of the critical argument implies larger variations in a.
In both Figs. 3 and 4, the time behaviour of the critical argument of asteroid 2007RX4 is shown in the case of the 4:3 outer-type MMR with Mars for one-million-year and ten-million-year long numerical integrations, respectively. During the one-million-year integration, the critical argument only librates, showing slightly irregular behaviour, but without any sign that this libration would stop later on. In the case of the ten-million-year numerical integration, the libration of the critical argument changes to circulation around 7 × 106 years. Interestingly, libration occurs for relatively larger eccentricity values, in this particular case between 0.1 and 0.2, while when the critical argument circulates the eccentricity is confined between 0.01 and 0.1. Moreover, the libration of the critical argument is accompanied by smaller variations in the asteroid’s semi-major axis than its variation when the critical argument circulates.
An interesting example of short-term resonance can be seen in Fig. 5, where the asteroid 2016UY4 is in 7:5 MMR with Mars. In the beginning of the numerical integration, the critical argument circulates, and around 5 × 106 years it turns to libration, while close to the end of integration it circulates again. Similarly to the case of the asteroid 2007RX4 (see Fig. 4), when the critical argument librates, the corresponding a, e points (green and orange) are confined between larger eccentricity values, while the variations of the semi-major axis are closer to the exact value of the MMR. We emphasise that if the semi-major axis of an asteroid is near to a certain resonant semi-major axis would not automatically mean that the body is captured in that MMR. The asteroid is only captured in an MMR if the corresponding critical argument librates.
 |
Fig. 3 Same as in Fig. 2, but for the asteroid 2007RX4 in 4:3 MMR, and the integration time is one million years. |
 |
Fig. 6 Dynamical maps of the four most populated MMRs using the maximum eccentricity variation as indicator. In the figures, the dots show all asteroids with librating critical argument (involved in short- and long-term libration) in the vicinity of the exact resonance. The diamond represents the asteroid whose clones are used to compile the dynamical map of the corresponding MMR. The vertical dashed line shows the semi-major axis of the exact resonance. In order to visualise thefine structure of the dynamical map, the colour scale is logarithmic, but the eccentricity values in the colour bar are transformed back to linear values. When compiling the dynamical maps for the four MMRs investigated, we use the same colour scale, which guarantees the comparability of these figures. |
3.3 Dynamical maps
In the cases presented in the previous section, one can see that the asteroids belonging to the Hungaria group exhibit very interesting dynamical behaviour. In order to study the dynamical behaviour of asteroids, we compiled dynamical maps of the corresponding main MMRs. First, we applied the widely used method of the maximum variation of the asteroid’s eccentricity. In the semi-major axis versus eccentricity plane, we assigned the maximum of the eccentricity variation of the asteroid’s orbit throughout the duration of numerical integration to each a, e pair. In Fig. 6, one can see the dynamical map of the four most populated MMRs. This figure was compiled by numerically integrating the clones of four chosen asteroids, each of them representing one MMR, in which the corresponding asteroid shows long-term libration. The initial conditions of the clones were calculated by varying the semi-major axis and eccentricity values of the given asteroid on a uniform grid (with 200 grid points in the horizontal direction and 100 grid points in the vertical direction) of the computational domain in the a − e plane. The remaining orbital elements (i, ω, Ω, M) were kept fixed to the nominal values of the original asteroid being in the MMR under study. The maximum eccentricity variation is calculated as Δemax = emax − emin, where emin and emax are the minimum and maximum values of the eccentricities during the one-million-year numerical integration. The representative asteroids of the four most populated MMRs are the following: (i) in the 4:3 MMR 2004RG84; (ii) in the 7:5 MMR 2005QS200; (iii) in the 10:7 MMR 1981EE17; and finally (iv) in the 3:2 MMR 2016AX18. In Fig. 6, one can observe the fine structure of the 4:3, 7:5, and 3:2 MMRs, while the eccentricity variation does not indicate a complex dynamical behaviour in the 10:7 MMR.
In each case of the four most populated MMRs, we also display the semi-major axis and eccentricity values of asteroids yielding either short-term or long-term libration. In each figure, the vertical dashed curve shows the location of the exact resonance, while the position of the representative asteroid is marked by a diamond. In order to see the resonant structure of the given MMR shown by the variation of eccentricity, we used a logarithmic colour scale. The black and dark blue regions correspond to small changes in eccentricity, while the green are for the moderate ones, and the red regions show large eccentricity variations. Based on these figures, one can see that in the neighbourhood of resonances the variation of eccentricity increases. Moreover, all asteroids yielding even episodically librating critical arguments are falling to this widened (V-shaped) region, although their inclination i, and angular orbital elements (ω, Ω, M) differ from the corresponding orbital elements of the representative asteroid. Although the semi-major axis and eccentricity values of these asteroids are marked in these dynamical maps for illustrative purposes only, their positions fit well to the region affected by the corresponding MMR. On the other hand, to reveal the dynamics of a selected asteroid, a separate dynamical map of its neighbourhood should be calculated following the method described above.
As we already mentioned, the dynamical structure of the 10:7 MMR is not as visible as it is in the cases of the other three MMRs. Thereason of this less detailed dynamical map could be that we use the same colour scale for all four MMRs. The same colour scale is useful for a better comparison between the dynamical maps, on the other hand it could also be possible that an individual colour scale for the 10:7 MMR would better reveal the fine structure of the resonance, such as the V-shape pattern.
To obtain a more complete structure of the neighbourhood of a given MMR, we investigated not only the variation of the maximum eccentricity but also variations in the semi-major axis of asteroids. Using the variations in the semi-major axis as an indicator is also motivated by the fact that in Figs. 2–5 the semi-major axis shows larger oscillations around the exact position of the MMR when the critical argument circulates than when it librates. In this way, both the variations of eccentricities and the variations of semi-major axes can be used to compile the dynamical map of an MMR. The variation of the semi-major axis is calculated similarly to the variation of the eccentricity: Δamax = amax − amin, where amax is the maximum value and amin is the minimum value of the semi-major axis during the numerical integration. In Fig. 7, we also display the a and e values of asteroids with librating critical arguments and the position of the exact MMR. On the contrary to the cases when Δemax is the tool used to map the dynamical structure of resonances, in these figures the variation of the semi-major decreases in size when approaching the location of the exact resonance. Another interesting feature that can be observed in these figures is the sharp horizontal boundary at certain values of eccentricities that separates regions characterised by small and quite large semi-major axis variations. The boundary that separates small and large semi-major variations is quite sharp in the cases of the 4:3, 7:5, and 10:7 MMR being located at e ~ 0.1, while it is less sharp in the case of the 3:2 MMR, and it is located at e ~ 0.2.
The dynamical maps of a certain MMR show different structures when using different indicators (Δamax versus Δemax). For instance, in the previous dynamical map we find that around the MMR the values of Δemax increase, while the values ofΔamax decrease. For lower eccentricity values of the asteroids, the V-shape pattern is also recognisable, while for larger eccentricities the region affected by the resonance shrinks. The overall resonant pattern takes the form of a deltoid. The shrinking of the domain affected by the resonance cannot be observed in the dynamical maps that are compiled using Δemax as an indicator. An additional feature of the dynamical map around the 4:3 MMR is that the upper part of the deltoid is bending towards smaller semi-major axis values. In dynamical maps obtained by Δemax, it can be observed that the 3:2 MMR is extended in a wider region than the other three resonances; this difference is even more stringent when using Δamax. Moreover, by using Δamax as an indicator, one can conclude that the 3:2 MMR is not as stable as the three other MMRs regarding the semi-major axis variations. We note that the bending deltoid structure we observe in this case was already found in another study (see Érdi et al. 2012) when the dynamical maps of some higher order MMRs of outer type were computed using the relative Lyapunov indicator (RLI), which is a chaos indicator (Sándor et al. 2004), and the librating critical argument.
Motivated by the introduction of Δamax as an indicator, we also applied the maximum inclination variation Δimax = imax − imin. The results obtained are displayed in Fig. 8, where we find further interesting dynamical features around the MMRs. One of the most stringent features is the sudden change in inclination variation at certain values of the eccentricities of asteroids. A deeper study, which is planned in a forthcoming paper, is needed to decide whether these structures are due to secular resonances or close encounters with Mars. Regarding their structures, the four main MMRs show similarities; however, for the 3:2 MMR, the maximum variation of the inclination is larger than in the three other cases. When comparing the dynamical maps obtained by Δamax and Δimax, one can conclude that the 3:2 MMR might be less stable than the three other main MMRs.
3.4 Overall dynamical state of Hungaria asteroids using real data as initial conditions
In our investigations so far, we have mapped the structure of the four main MMRs by cloning the representative asteroids of the given MMR, obtaining large swarms of test particles. Our next question is the following: how would the dynamical map be modified if instead of test particles we numerically integrated the orbits of real asteroids belonging to the group of Hungaria asteroids and used the previously introduced indicators of dynamical behaviour? A mapping of the dynamical state of the Hungaria asteroids at a given epoch can be done because the number of the known Hungaria asteroids increased a lot due to the recent sky surveys, enabling the use of their orbital data as initial conditions of numerical integrations. To do so, we divided the computational domain of the semi-major axis (a = 1.75−2.05 au) into 200 cells, the computation domain of the eccentricity (e = 0–0.4) into 100 cells, and the computational domain of the absolute magnitude (H = 10−27) into 100 cells. In the following, we count all asteroids whose semi-major axis and eccentricity or absolute magnitude values fall in the given cell, and the median value of their Δamax, Δemax, and Δimax are determined, respectively. The cell is then coloured according to these median values in the corresponding panels of Fig. 9. Our approach is definitely a novel one when comparing it to the usual dynamical maps where the action-like initial orbital elements are taken from a regular grid, either from the (a, e) and the (a, i) planes, while the angular elements are kept fixed to certain values. We should also note that our approach is only applicable when in the investigated region of the parameter space asteroids are present in large numbers and are not emptied due to strong destabilisation mechanisms such as strongly chaotic behaviour caused by close encounters.
Our results are shown in the six panels of Fig. 9, in which Δemax, Δamax, and Δimax are displayed both in the (a, e) and (a, H) parameter planes. The dynamical structures shown in these panels were obtained after a one-million-year numerical integration. In those panels that have been compiled by using Δemax and Δamax, the MMRs are clearly visible. It is noteworthy that in the upper left panel of Fig. 9, in which the (a, e) plane is mapped, the eccentricities of the asteroids already begin to show larger variations when e ~ 0.12, which is clearly less than the maximum eccentricity limit of Hungaria asteroids. The mechanism that is responsible for the larger eccentricity variations of asteroids is the overlapping of the MMRs with Mars, a phenomenon among Hungaria asteroids recently identified and described by Correa-Otto & Cañada-Assandri (2018).
In the middle panels, we use Δamax as an indicator, and one can see that even the weaker MMRs can be identified, because the overall variation of the semi-major axes around the MMRs is larger than the surrounding regions of the a − e plane. As a general conclusion, by investigating Fig. 9 carefully, one can conclude that the MMRs of outer type with Mars result in larger variations in the eccentricities and semi-major axes of the majority of real asteroids involved in those resonances.
When Δimax is applied as an indicator, an interesting phenomenon can be observed: at smaller semi-major axes, the variation of the inclinations of the real asteroids are also smaller than at larger values of semi-major axes. Although a few of theMMRs can also be identified in this case, there is a general trend of increasing inclinations towards larger semi-major axes; therefore, the variations of the inclinations are suppressed in the figure. Thus, Δimax, among the real Hungaria asteroids is not strongly influenced by the different MMRs with Mars (see the lower panels of Fig. 9).
Summarising our findings from Fig. 9, we can conclude that the most visible dynamical features on these panels are due to the various MMRs with Mars. This does not mean that other effects do not shape the dynamics of Hungaria asteroids, but the most visible ones are certainly due to the MMRs.
The presented dynamical investigations reveal the very complex and interesting dynamics of asteroids in the Hungaria group due to the MMRs with Mars. Besides this, we find that for the calculation of dynamical maps around various MMRs, the application of the maximum variation of semi-major axes is also a suitable tool that in certain cases could reveal the fine structure of the MMRs investigated. The applicability of Δamax as a dynamical indicator is based on the fact that the larger the variation of the semi-major axis, the larger the libration amplitude of the critical argument.
 |
Fig. 9 Dynamical state of the whole Hungaria group at a given epoch. We used the maximum variations of eccentricity, semi-major axis, and inclination as dynamical indicators. We show the dynamical state of the whole Hungaria group on the a − e and a − H parameter planes in the right and left panels, respectively. Instead of test particles taken from a regular grid, the orbital elements and absolute magnitudes of real asteroids were used. |
4 Comparison of the absolute magnitudes and dynamical properties of asteroids
As a last step of our survey, we investigated possible relationships between dynamical and physical properties of the asteroids belonging to the Hungaria group. There has been a series of measurements (Lucas et al. 2017, 2019) aimed at revealing various physical properties of Hungaria asteroids, such as the absolute magnitude, size, shape, and albedo. These measurements are thought to help unveil the variety of asteroids, in a broader sense even the properties of the building blocks of the ancient Solar System. In our work, we studied the absolute magnitude of the Hungaria asteroids in the context of their dynamics. Our choice is motivated by the fact that the absolute magnitude can be determined for all asteroids, while their other physical parameters are hardly known. On the other hand, the absolute magnitude of an asteroid also depends on many other physical properties. We may know the spectral properties of an asteroid and therefore its surface composition, however the surface-forming processes can affect the asteroid’s albedo and therefore its absolute magnitude (see details in Gaffey 2010). For instance, one can consider different kinds of space weathering effects that result in different albedo and spectral properties for objects originally with a similar surface composition. Thus, space weathering is a significant source of uncertainty when performing a taxonomic classification.
In Fig. 10, we show the empirical cumulative distribution function (CDF) of the absolute magnitudes calculated for Hungaria asteroids. The thick grey line is calculated for asteroids that are not affected by any MMR. The coloured lines are calculated for asteroids influenced by the four most populated MMRs. There are two significant differences with respect to the grey line: (i) asteroids found at the 10:7 MMR are brighter than the average value of Hungarias, (ii) while asteroids around the 4:3 MMR are fainter. Besides these two very stringent features, in the case of asteroids at the 3:2 MMR one can also see a small deviation from the average magnitude values in the case of fainter bodies.
To better visualise the properties described above in the distribution of the absolute magnitudes, we also show a box and whiskers plot in Fig. 11. We remind the reader that a box plot is a way to graphically depict different groups of numerical data using their quartiles. Whiskers are lines that extend outside of boxes, indicating the variability of data outside the lower and upper quartiles. Outlying data are plotted as separate points. Box plots are used to display variation in the given samples without any a priori assumption or knowledge on their statistical distribution. The spacings between the different parts of the box show the degree of dispersion and the possible skewness in the data.
Studying Fig. 11, one can also see that asteroids in the 4:3 MMR are fainter than asteroids in the 10:7 MMR. Moreover, the distribution of asteroids in the 4:3 MMR is symmetric, while the distribution of asteroids in 10:7 MMR is elongated towards the brighter bodies. In other words, the distribution has a negative skew. In the case of the asteroids in the 3:2 MMR, the distribution of asteroids had a positive skew, which is the reason of the deformity in the empirical CDF figure (see Fig. 10), meaning that in the sample a considerable number of fainter objects can be found.
The results described above can be explained, however, with strong assumptions. In the following, we describe a possible scenario butemphasise its uncertainty due to the lack of direct measurements concerning the surface of these bodies.
By assuming a similar albedo for these asteroids, based on Figs. 10 and 11, asteroids in the 10:7 MMR might be larger, while asteroids in the 4:3 MMR might be smaller in size than the other ones. This assumption is also supported by Fig. 1, where the sign of the Yarkovsky effect is clearly seen. Since the Yarkovsky effect is weaker for larger bodies, an MMR can block the radial drift of the affected bodies (see Vokrouhlický et al. 2015). One can conclude that the 10:7 MMR indeed contains larger bodies. On the contrary, the Yarkovsky effect is stronger for smaller asteroids, resulting in a longer range of radial drift from the original location of the catastrophic collision. This might be the reason why smaller asteroids can be found in the 4:3 MMR.
We would like to emphasise that the aim of our investigation is not the determination of the physical characteristics of Hungariaasteroids, we are seeking eventual connections between their physical and dynamical properties. Our results show that a given MMR becomes significant when a large number of bodies are drifting to the nominal locations of the MMRs. The reason for such an orbital drift might be a scattering effect due to the collision event itself, and later the Yarkovsky effect.
We are aware of the fact that the scenario described above might only be valid for the members of the collisional family, as they show the V-shape pattern on the a − H plane. On the other hand, it is not uncommon in the literature for the whole Hungaria group to be considered in dynamical studies (e.g. Warner et al. 2009), since the identification of the family members can be cumbersome and uncertain. However, our speculative scenario might not be restricted to the members of the collisional family, because the Yarkovsky effect acts on the whole groupof asteroids. Depending on their spin, some of the group members are drifting inwards and some of them are drifting outwards, which in turn would result the observed distribution of asteroids. During their drift, as has been found by McEachern et al. (2010), asteroids can be captured by various MMRs and escape from the swarm of Hungaria asteroids due to the increase of their eccentricities up to the Mars-crossing limit. Moreover, according to McEachern et al. (2010), a repopulation of the Hungaria asteroid region is also possible through this escape mechanism, as Hungaria asteroids escaping from the MMRs can undergo close encounters with Mars and could be injected back into the region of Hungaria asteroids. It is therefore clear that Hungaria asteroids are not only moving under the Yarkovsky effect, but they may undergo drastic orbital changes due to the very complex gravitational perturbations acting on them. On the other hand, the observed distribution of asteroids requires a certain size segregation process thatmight be most easily explained by the Yarkovsky effect. A more careful analysis aimed at revealing the size differentiation process of asteroids is out of the scope of this work and will be the subject of a forthcoming study.
 |
Fig. 10 Empirical cumulative distribution function for absolute magnitude of the asteroids captured in the four main MMRs and not captured in MMRs. |
 |
Fig. 11 Box and whiskers plot from absolute magnitude of the asteroids captured in the four main MMRs and not captured in MMRs. The box encloses the interquartile range (IQR), defined as IQR75–IQR25. The whiskers extend out to the maximum or minimum value of the data, or to 1.5 times either the IQR75 or IQR25, if there is data beyond this range. Outliers are identified by small circles. |
5 Conclusion
Asteroids in the Hungaria group are of high interest in both dynamical studies. This is because chaotic diffusion and non-conservative effects play an important role in shaping their long-term dynamics and in investigating their physical properties to obtain more knowledge on the ancient planetesimal population that might have contributed to the formation of terrestrial planets. These two very important research areas can be observed in several studies in which the dynamical stability of the region occupied by Hungaria asteroids has been addressed (e.g. Milani et al. 2010; Correa-Otto & Cañada-Assandri 2018); moreover, due to the recent observations, there is also growing knowledge of the physical properties of Hungaria asteroids (e.g. Lucas et al. 2017, 2019).
In this paper, we performed a comprehensive survey on the Hungaria group of asteroids. By using the method FAIR (Forgács-Dajka et al. 2018), considering all known asteroids belonging to the Hungaria group, we identified several MMRs between these bodies and the planet Mars. According to our results, the four most populated MMRs in this region are the 4:3, 7:5, 10:7, and 3:2 ones. In the cases of these MMRs, we performed detailed dynamical investigations, in which, besides the classical maximum eccentricity variation method, we calculated the maximum variation of other action-like orbital elements such as the asteroids’ semi-major axes and inclinations. Our results reveal the complex dynamical properties of the regions around the above-mentioned MMRs, also indicating the usefulness of simultaneous and complementary application of the maximum variations of a, e, and i.
According to our dynamical investigations, there are two types of resonant behaviour of asteroids; namely, when the critical argument (resonance variable) shows short-term or long-term libration, a behaviour that was also found among Hungaria asteroids by Correa-Otto et al. (2021). There may also be a time interval of circulation between two short-term librations. The short-term libration of the critical argument being more frequent than the long-term one is a clear sign of chaotic behaviour. We observed that during the libration of the critical argument the eccentricity of an asteroid changes between higher limits in the case of almost all MMRs, while in the case of circulation the eccentricity becomes lower (cf. Figs. 2–5, right panels). Dynamical maps of the four most populated MMRs, and the map of the dynamical state calculated by using the orbital data of real Hungaria asteroids for the initial conditions, reveal the high importance of the MMRs with Mars. These MMRs dynamically excite the involved asteroids, their overlapping determines the eccentricity limit for the asteroids, moreover MMRs can act as leaking chanels for the members of the Hungaria population that are affected.
According to the above-mentioned results, the members of the Hungaria groups are ideal targets for studying chaotic diffusion, which is a very important feature of the dynamics of asteroids (Tsiganis 2007), and the effects of non-conservative dynamics such as the Yarkovsky and YORP effects. Another very interesting question is the existence of the outer sharp boundary of the Hungaria group at the 3:2 MMR, while the inner boundary of the population cannot be related to the 4:3 MMR, because asteroids seem to be drifting inwards through this MMR and their number is gradually decreasing towards smaller semi-major axes. A thorough investigation of the long-term dynamics of asteroids at the outer boundary of the Hungaria population would be necessary to reveal the possible role of the 3:2 MMR in the destabilisation of Hungaria asteroids.
During our statistical investigations, we found an interesting relationship between Hungaria asteroids that might be certainly the results of the Yarkovsky effect. Near to the semi-major axis of (434) Hungaria is the location of the 10:7 MMR. Asteroids involved in this MMR are brighter than the average group members, while asteroids affected by the 4:3 MMR are fainter than the average value. This latter aspect is very interesting, since the nominal position of the 4:3 MMR is farther from the semi-major axis of the (434) Hungaria asteroid, which is supposed to be the parent body of the Hungaria collisional family. Assuming that the members of the collisional family have similar albedo (that is an acceptable assumption, because the surface albedo reflects the mineralogical composition of the progenitor body), asteroids involved in the 10:7 MMR should be bigger in size, and therefore the Yarkovsky effect is weaker on them, while the smaller family members involved in the 4:3 MMR could have driftedquite far away from the position of the catastrophic collision due to the stronger Yarkovsky effect acting on them. Due to this latter effect, smaller asteroids drift through longer radial ranges and are involved in the 4:3 MMR later. This finding is also supported by Fig. 1. On the other hand, one should be careful when making the above assumptions, because Hungaria asteroids are also the subject of a complex dynamical behaviour due to the MMRs with Mars and secular resonances. Moreover, space weathering can alter the surface properties of asteroids. We do not yet have very much information concerning the relationship between the albedo, spectral properties, and absolute magnitude of asteroids. To better understand the various space weathering processes in situ measurements of the surface of asteroids or even sample return missions is of high importance (Gaffey 2010).
As we already mentioned, the Hungaria family is formed presumably as the result of a catastrophic collision, of which one of the involvedbodies is the (434) Hungaria asteroid. The resulting family members therefore inherit the physical and dynamical properties of the parent bodies; thus, it is of utmost importance to know the properties of the parent bodies. Such a collision event might be modelled by smooth particle hydrodynamic simulations (e.g. Maindl et al. 2013; Jutzi et al. 2019) combined with a simple numerical treatment of the Yarkovsky effect. Although these simulations are very time consuming, and there could be many uncertainties even in the physical models applied, they could be useful for better understanding the formation and origin of the Hungaria collisional family. As a future work, we intend to study the formation and evolution of Hungaria asteroids numerically, including their collisional formation and also the effects of non-conservative forces, as well as the chaotic diffusion shaping their dynamical properties.
Acknowledgements
We thank the reviewer Dr. J. Correa-Otto for the useful comments and suggestions that helped us improve the manuscript. E.F.-D. and Zs.S. thank the support of the Hungarian National Research, Development and Innovation Office (NKFIH), under the grant K-119993. We acknowledge the computational resources for the Wigner GPU Laboratory of the Wigner Research Centre for Physics.
References
- Bottke, W. F., Vokrouhlický, D., Minton, D., et al. 2012, Nature, 485, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Connors, M., Stacey, R. G., Wiegert, P., & Brasser, R. 2008, Icarus, 194, 789 [NASA ADS] [CrossRef] [Google Scholar]
- Correa-Otto, J. A., & Cañada-Assandri, M. 2018, MNRAS, 479, 1694 [NASA ADS] [CrossRef] [Google Scholar]
- Correa-Otto, J. A., Cañada-Assandri, M., García, R. S., et al. 2021, Icarus, 367, 114564 [CrossRef] [Google Scholar]
- Ćuk, M., & Nesvorný, D. 2018, Icarus, 304, 9 [CrossRef] [Google Scholar]
- Dormand, J. R., & Prince, P. J. 1978, Celest. Mech., 18, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Érdi, B., Rajnai, R., Sándor, Z., & Forgács-Dajka, E. 2012, Celest. Mech. Dyn. Astron., 113, 95 [CrossRef] [Google Scholar]
- Farinella, P., & Vokrouhlicky, D. 1999, Science, 283, 1507 [CrossRef] [Google Scholar]
- Forgács-Dajka, E., Sándor, Z., & Érdi, B. 2018, MNRAS, 477, 3383 [Google Scholar]
- Gaffey, M. J. 2010, Icarus, 209, 564 [NASA ADS] [CrossRef] [Google Scholar]
- Gradie, J. C., Chapman, C. R., & Williams, J. G. 1979, Families of minor planets., eds. T. Gehrels, & M. S. Matthews, 359 [Google Scholar]
- Jutzi, M., Michel, P., & Richardson, D. C. 2019, Icarus, 317, 215 [CrossRef] [Google Scholar]
- Lemaitre, A. 1994, in ASP Conf. Ser., 63, 75 Years of Hirayama Asteroid Families: The Role of Collisions in the Solar System History, eds. Y. Kozai, R. P. Binzel, & T. Hirayama, 140 [NASA ADS] [Google Scholar]
- Lucas, M. P., Emery, J. P., Pinilla-Alonso, N., Lindsay, S. S., & Lorenzi, V. 2017, Icarus, 291, 268 [CrossRef] [Google Scholar]
- Lucas, M. P., Emery, J. P., MacLennan, E. M., et al. 2019, Icarus, 322, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Maindl, T. I., Schäfer, C., Speith, R., et al. 2013, Astron. Nachr., 334, 996 [NASA ADS] [CrossRef] [Google Scholar]
- McEachern, F. M., Ćuk, M., & Stewart, S. T. 2010, Icarus, 210, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Michel, P., & Froeschlé, C. 1997, Icarus, 128, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Milani, A., Knežević, Z., Novaković, B., & Cellino, A. 2010, Icarus, 207, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Paolicchi, P., Spoto, F., Knežević, Z., & Milani, A. 2019, MNRAS, 484, 1815 [NASA ADS] [CrossRef] [Google Scholar]
- Sándor, Z., Érdi, B., Széll, A., & Funk, B. 2004, Celest. Mech. Dyn. Astron., 90, 127 [CrossRef] [Google Scholar]
- Sztakovics, J., Forgács-Dajka, E., Sándor, Z., Vanyó, J., & Gucsik, A. 2019, Lunar Planet. Sci. Conf. [Google Scholar]
- Tsiganis, K. 2007, Chaotic Diffusion of Asteroids, eds. D. Benest, C. Froeschle, & E. Lega, 729, 111 [NASA ADS] [Google Scholar]
- Vinogradova, T. A. 2019, MNRAS, 484, 3755 [NASA ADS] [Google Scholar]
- Vokrouhlický, D., Brož, M., Bottke, W. F., Nesvorný, D., & Morbidelli, A. 2006, Icarus, 182, 118 [Google Scholar]
- Vokrouhlický, D., Bottke, W. F., Chesley, S. R., Scheeres, D. J., & Statler, T. S. 2015, The Yarkovsky and YORP Effects, 509 [Google Scholar]
- Warner, B. D., Harris, A. W., Vokrouhlický, D., Nesvorný, D., & Bottke, W. F. 2009, Icarus, 204, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Wisdom, J. 1985, Icarus, 63, 272 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Hungaria-population asteroids projected onto the plane of absolute magnitude H versus semi-major axis of nearly 24 000 objects. The lines correspond to the four most populated MMRs with Mars. Asteroid (434) Hungaria ismarked by a red point. The curved lines show Hungaria-family zone, where we used a canonical form 0.2H = log((a − ac)∕C), where ac = 1.94au and C = [3 × 10−5, 2.5 × 10−5, 2 × 10−5]au, denotes by [blue, black, and orange] and discussed by Vokrouhlický et al. (2006) and Warner et al. (2009). |
| In the text | |
 |
Fig. 2 Dynamics of the asteroid 2016AX8 in 3:2 MMR of outer type with Mars. In the left panel, the FAIR method indicates the 3:2 MMR. In the middle panel, one can see the variation of the critical argument showing libration for ten million years. In the right panel, the excursion of the orbit on the (a, e) is shown. The colour-coding is explained in the text. |
| In the text | |
 |
Fig. 3 Same as in Fig. 2, but for the asteroid 2007RX4 in 4:3 MMR, and the integration time is one million years. |
| In the text | |
 |
Fig. 4 Same as in Fig. 3, but the integration time is ten million years. |
| In the text | |
 |
Fig. 5 Same as in Fig. 2, but for the asteroid 2016UY4 in 7:5 MMR. |
| In the text | |
 |
Fig. 6 Dynamical maps of the four most populated MMRs using the maximum eccentricity variation as indicator. In the figures, the dots show all asteroids with librating critical argument (involved in short- and long-term libration) in the vicinity of the exact resonance. The diamond represents the asteroid whose clones are used to compile the dynamical map of the corresponding MMR. The vertical dashed line shows the semi-major axis of the exact resonance. In order to visualise thefine structure of the dynamical map, the colour scale is logarithmic, but the eccentricity values in the colour bar are transformed back to linear values. When compiling the dynamical maps for the four MMRs investigated, we use the same colour scale, which guarantees the comparability of these figures. |
| In the text | |
 |
Fig. 7 Same as in Fig. 6, except that the dynamical maps are calculated using Δamax as an indicator. |
| In the text | |
 |
Fig. 8 Same as in Fig. 6, except that the dynamical maps are calculated by using Δimax as indicator. |
| In the text | |
 |
Fig. 9 Dynamical state of the whole Hungaria group at a given epoch. We used the maximum variations of eccentricity, semi-major axis, and inclination as dynamical indicators. We show the dynamical state of the whole Hungaria group on the a − e and a − H parameter planes in the right and left panels, respectively. Instead of test particles taken from a regular grid, the orbital elements and absolute magnitudes of real asteroids were used. |
| In the text | |
 |
Fig. 10 Empirical cumulative distribution function for absolute magnitude of the asteroids captured in the four main MMRs and not captured in MMRs. |
| In the text | |
 |
Fig. 11 Box and whiskers plot from absolute magnitude of the asteroids captured in the four main MMRs and not captured in MMRs. The box encloses the interquartile range (IQR), defined as IQR75–IQR25. The whiskers extend out to the maximum or minimum value of the data, or to 1.5 times either the IQR75 or IQR25, if there is data beyond this range. Outliers are identified by small circles. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


