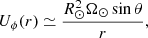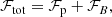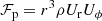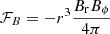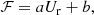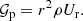| Issue |
A&A
Volume 656, December 2021
Solar Orbiter First Results (Cruise Phase)
|
|
|---|---|---|
| Article Number | A28 | |
| Number of page(s) | 10 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202140956 | |
| Published online | 14 December 2021 | |
The angular-momentum flux in the solar wind observed during Solar Orbiter’s first orbit
1
Mullard Space Science Laboratory, University College London, Holmbury House, Holmbury St. Mary, Dorking RH5 6NT, UK
e-mail: d.verscharen@ucl.ac.uk
2
Space Science Center, University of New Hampshire, Durham, NH 03824, UK
3
Department of Astrophysics-AIM, University of Paris-Saclay and University of Paris, CEA, CNRS, 91191 Gif-sur-Yvette Cedex, France
4
Department of Physics, The Blackett Laboratory, Imperial College London, London SW7 2AZ, UK
5
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Université de Paris, 5 place Jules Janssen, 92195 Meudon, France
6
Department of Earth, Planetary, and Space Sciences, University of California Los Angeles, Los Angeles, CA 90095, USA
7
Physics Department, University of California, Berkeley, CA 94720, USA
8
Space Sciences Laboratory, University of California, Berkeley, CA 94720, USA
9
School of Physics and Astronomy, Queen Mary University of London, London E1 4NS, UK
10
Institut de Recherche en Astrophysique et Planétologie, 31028 Toulouse Cedex 4, France
11
INAF-Istituto di Astrofisica e Planetologia Spaziali, 00133 Roma, Italy
12
Southwest Research Institute, San Antonio, TX 78238, USA
13
Swedish Institute of Space Physics (IRF), Box 537 751 21 Uppsala, Sweden
14
Radboud Radio Lab., Department of Astrophysics/IMAPP-Radboud University, PO Box 9010, 6500 GL Nijmegen, The Netherlands
Received:
31
March
2021
Accepted:
31
May
2021
Aims. We present the first measurements of the angular-momentum flux in the solar wind recorded by the Solar Orbiter spacecraft. Our aim is to validate these measurements to support future studies of the Sun’s angular-momentum loss.
Methods. We combined 60-min averages of the proton bulk moments and the magnetic field measured by the Solar Wind Analyser and the magnetometer onboard Solar Orbiter. We calculated the angular-momentum flux per solid-angle element using data from the first orbit of the mission’s cruise phase in 2020. We separated the contributions from protons and from magnetic stresses to the total angular-momentum flux.
Results. The angular-momentum flux varies significantly over time. The particle contribution typically dominates over the magnetic-field contribution during our measurement interval. The total angular-momentum flux shows the largest variation and is typically anti-correlated with the radial solar-wind speed. We identify a compression region, potentially associated with a co-rotating interaction region or a coronal mass ejection, which leads to a significant localised increase in the angular-momentum flux, albeit without a significant increase in the angular momentum per unit mass. We repeated our analysis using the density estimate from the Radio and Plasma Waves instrument. Using this independent method, we find a decrease in the peaks of positive angular-momentum flux, but otherwise, our results remain consistent.
Conclusions. Our results largely agree with previous measurements of the solar wind’s angular-momentum flux in terms of amplitude, variability, and dependence on radial solar-wind bulk speed. Our analysis highlights the potential for more detailed future studies of the solar wind’s angular momentum and its other large-scale properties with data from Solar Orbiter. We emphasise the need for studying the radial evolution and latitudinal dependence of the angular-momentum flux in combination with data from Parker Solar Probe and other assets at heliocentric distances of 1 au and beyond.
Key words: magnetohydrodynamics (MHD) / plasmas / Sun: magnetic fields / solar wind / stars: rotation
© ESO 2021
1. Introduction
The solar corona expands into interplanetary space in the form of the solar wind (Parker 1958; Neugebauer & Snyder 1962; Verscharen et al. 2019). In this process, the solar wind plasma removes mass, momentum, energy, and angular momentum from the Sun. In the lower corona, the Sun’s magnetic field forces the plasma into a quasi-rigid co-rotation with the photosphere, following the co-rotation of the field’s photospheric footpoints. With increasing distance from the photosphere, the torque exerted by the coronal magnetic field on the plasma decreases (Weber & Davis 1967). In this way, the large-scale magnetic field mediates a smooth transition from co-rotation to quasi-radial expansion. Therefore, the solar wind is not “flung” from the photosphere on a ballistic trajectory, which would lead to a torque-free azimuthal velocity profile taking the following form:
where R⊙ is the solar radius, Ω⊙ is the Sun’s angular rotation frequency, θ is the co-latitude, and r is the heliocentric distance. Instead, the solar wind experiences a significant torque in its acceleration region at even larger distances from the photosphere, leading to greater azimuthal speeds than predicted by Eq. (1). In turn, the torque applied to the Sun by the magnetic field in this process slows down the Sun’s rotation on long time scales (Mestel 1968; Reiners & Mohanty 2012). Local measurements of the solar-wind angular-momentum flux provide an estimate for the global angular-momentum loss rate, which ultimately causes the rotation period of the Sun and, by extrapolation, of Sun-like stars on the main sequence to increase with age (Barnes 2003; Gallet & Bouvier 2013; Matt et al. 2015; Pantolmos & Matt 2017).
Measurements of the solar-wind angular-momentum flux are particularly challenging from an instrumental point of view. They require an accurate determination of the azimuthal component Uϕ of the particle bulk velocity, which is typically more than one order of magnitude less than its radial component Ur. Nevertheless, early measurements of the solar wind already estimated its angular momentum (Hundhausen et al. 1970; Lazarus & Goldstein 1971; Pizzo et al. 1983; Marsch & Richter 1984). Modern space instrumentation provides us with higher spacecraft-pointing accuracy and, thus, a more accurate determination of Uϕ. Moreover, as the average ratio Uϕ/Ur increases with decreasing heliocentric distance, the error in the quantification of the angular-momentum flux is generally smaller when measured at smaller distances from the Sun (Finley et al. 2020, 2021). In addition, co-rotating interaction regions have not yet formed (Richter & Luttrell 1986; Allen et al. 2020) and interplanetary coronal mass ejections have not expanded enough to disturb nearby wind streams (Möstl et al. 2020) at small distances from the Sun. Therefore, near-Sun measurements enable the sampling of more pristine and less processed solar wind. Solar Orbiter and Parker Solar Probe share the advantages of both modern space instrumentation and an orbit that leads them close to the Sun (Fox et al. 2016; Müller et al. 2020). We present the first observations of the solar wind’s angular-momentum flux observed by Solar Orbiter during the first orbit of its cruise phase in 2020.
2. Data analysis
We analyse a combined set of data from the Proton-Alpha Sensor (PAS) of Solar Orbiter’s Solar Wind Analyser (SWA, Owen et al. 2020) suite and from Solar Orbiter’s fluxgate magnetometer (MAG, Horbury et al. 2020). Our dataset includes all time intervals from 2020-07-07 until 2020-10-27, for which both SWA/PAS and MAG data are available. We ignore all other intervals and those in which the quality flags for either dataset indicate poor data quality (we only include data with a quality flag of 3). After this selection, we thus retain about 38.9% of the total time interval in our dataset (for time coverage, see also Fig. 1). During this time, Solar Orbiter recorded data at heliocentric distances between 0.591 and 0.989 au. The time average of the spacecraft’s heliocentric distance in our dataset is 0.851 au.
 |
Fig. 1. Time series of the angular-momentum flux per solid-angle element measured during Solar Orbiter’s first orbit of the cruise phase. The diagram shows the proton contribution ℱp, the magnetic-field contribution ℱB, and the sum of both, ℱtot. In order to increase the visibility, we multiply ℱB with a factor 10. The magenta squares represent the measurements of ℱtot during the time of the compression region (CR) on 2020-09-06. The axis at the top indicates the heliocentric distance of the spacecraft at the time of the measurement. The scale of this axis is not linear. The grey-shaded areas indicate times for which our merged SWA/PAS-MAG data product is unavailable or the data flags for either dataset indicate poor data quality. |
The calculation of the angular-momentum flux is very sensitive to uncertainties in the direction of the bulk velocity and in the direction of the magnetic field. The finite angular resolution of PAS introduces an uncertainty in the knowledge of the bulk-speed direction. The calibration accuracy of PAS is ≲1°. The pointing knowledge of the MAG sensor is largely determined by the uncertainty of the spacecraft’s boom deployment angle. It introduces an angular uncertainty of the magnetic-field measurement of ≲1°. Planned inter-instrument alignment reconstructions of the boom orientation will become feasible in the future once the instruments have recorded sufficient amounts of data for a large statistical analysis (Walsh et al. 2020). For solar wind speeds above 300 km s−1, the relative uncertainty of the SWA/PAS speed measurement due to counting statistics is less than 1%. The relative uncertainty of the density measurement is energy-dependent with a maximum of 20%, which we apply as a conservative estimate to our entire dataset. At very low energies (corresponding to solar-wind speeds below ∼300 km s−1), the sensitivity decreases further so that additional correction factors are required, which have not yet been conclusively determined. The expected MAG offset is ∼ ± 0.1 nT, which we take as the absolute uncertainty of our individual magnetic-field component measurements. The requirement of the absolute knowledge error of the spacecraft pointing is ≤3 arcmin (García Marirrodriga et al. 2021), which is mostly driven by the instrument requirements of the remote-sensing suite and a minor contributor to the pointing knowledge uncertainties for our study.
We base our analysis on the PAS normal-mode ground moments integrated from the proton part (core and beam) of the full three-dimensional measured ion distributions and the MAG normal-mode vectors of the magnetic field. In normal mode, the PAS ground moments are available every four seconds, while the MAG vectors are available with a cadence of 8 vectors per second. We merge and average both data products over intervals of 60 min to reduce any natural fluctuations in the data due to, for example, waves and turbulence, as we are interested in the angular-momentum flux of the bulk solar wind. Our selection and averaging procedure leaves us with 1036 individual data points.
The angular momentum is contained in the mechanical flux of the solar-wind particles. In addition, there is transport of angular momentum due to magnetic-field stresses. Ignoring anisotropies in the particle distributions and contributions from particles other than protons1, the total angular-momentum flux is thus the sum of the proton and magnetic-field terms (see Marsch & Richter 1984). We define the total angular-momentum flux per solid-angle element in spherical heliocentric coordinates as:
where
is the proton contribution to the angular-momentum flux, and
is the contribution from magnetic stresses (in cgs units) to the angular-momentum flux, ρ is the proton mass density, U is the proton bulk velocity, and B is the magnetic field. The subscript r indicates the radial vector component, and the subscript ϕ indicates the azimuthal component in spherical heliocentric coordinates. We use our 60-min averages of the measured solar-wind parameters as the input for our calculations of ℱp and ℱB according to Eqs. (3) and (4). We recognise that our analysis represents only a first validation of methods to study angular-momentum flux with Solar Orbiter. Therefore, it ignores other contributions to the total angular-momentum flux (see Sect. 4), which must be investigated in future detailed studies.
3. Results
3.1. Timeseries and overview
Figure 1 shows the timeseries of ℱp, ℱB, and ℱtot over the analysed data interval. Gaps in this plot represent data gaps or those intervals that we exclude according to our selection criteria. Figure 1 illustrates the natural variation of the angular-momentum flux over time, which is typically greater than its mean magnitude. Across all data points, the mean value of ℱp is 2.29 × 10−11 au3 g cm−1 s−2 sr−1, while the mean value of ℱB is 1.72 × 10−11 au3 g cm−1 s−2 sr−1. In general, ℱp exhibits significantly more variation than ℱB. As expected for a conserved quantity, ℱtot shows no secular dependence on heliocentric distance.
On 2020-09-06, we recorded a time interval of significantly increased ℱp and ℱtot. Upon closer inspection, this interval corresponds to a time of increased ρ, probably associated with the compression in front of a co-rotating interaction region or a coronal mass ejection seen as a flux rope in the magnetic field. Due to this enhancement in ρ, the associated plasma carries more angular-momentum flux than the solar wind before or after the compression region. The compression region does not exhibit enhancements in Ur or Uϕ (not shown here), suggesting that the compression region facilitates a similar angular-momentum flux per unit mass as the solar wind. Our results in Sect. 3.4 support this suggestion. We highlight the measurements taken during the time interval associated with this compression region in our figures as magenta squares.
3.2. Variability of the angular-momentum flux
In Figs. 2 and 3, we show histograms of the measured values of ℱp and ℱB for our dataset in terms of their probability distributions. We colour-code the contributions from fast, intermediate, and slow solar wind in our histograms. Due to the dominance of ℱp, the histogram of the probability distribution for ℱtot (not shown) is almost identical to the histogram for ℱp. Both histograms reflect the broad variation in the angular-momentum flux and the range of observed values. According to Fig. 2, the majority of the distribution is centred around negative values of ℱp, while the outliers at large ℱp shift the mean of our measurements to ℱp > 0. These outliers are mostly associated with the compression region on 2020-09-06.
 |
Fig. 2. Histogram of the proton contribution ℱp to the solar wind’s angular-momentum flux per solid-angle element. The vertical axis indicates the probability density of ℱp. We stack the histograms for fast (Ur > 500 km s−1), intermediate (400 km s−1 ≤ Ur ≤ 500 km s−1), and slow (Ur < 400 km s−1) wind. The magenta areas represent the measurements of ℱp during the time of the compression region (CR) on 2020-09-06. |
 |
Fig. 3. Histogram of the magnetic-field contribution ℱB to the solar wind’s angular-momentum flux per solid-angle element. Details are the same as in Fig. 2. |
For a more quantitative statistical analysis, we list the mean values, the standard deviations, as well as the maximum and minimum values of ℱp, ℱB, and ℱtot in Table 1. In addition, Table 1 provides these statistical markers separated by time intervals with Ur < 400 km s−1 and Ur > 500 km s−1 as a means to distinguish characteristic slow wind from fast wind, respectively. We find that ℱp > 0 and ℱtot > 0 in the observed slow-wind intervals (Ur < 400 km s−1), while ℱp < 0 and ℱtot < 0 in the observed fast-wind intervals (Ur > 500 km s−1). A similar behaviour has been seen in Parker Solar Probe measurements (Finley et al. 2021). In the separated data subsets for slow wind and fast wind, the mean values of |ℱp| are greater than the mean value of |ℱp| in our full dataset of all measurements. The means of ℱB are positive, independent of our categorisation by wind speed, and the mean value of ℱB in our slow-wind and fast-wind intervals is less than the mean value of ℱB in all measurement intervals. We note, however, that the mean value of ℱB is very small for the separated slow-wind and fast-wind intervals, so that this result is potentially not significant (see also Fig. 5).
Statistical properties of ℱp, ℱB, and ℱtot in our full dataset and split by radial solar-wind speed.
3.3. Speed dependence of the angular-momentum flux
Figure 4 shows our measurements of ℱp as a function of Ur. This visualisation confirms the significant Ur-dependence of the angular-momentum flux, which has been noted in previous studies and is discussed further in Sect. 4. The particle contribution to the angular-momentum flux shows a stronger relative variation in slow wind compared to fast wind. We also observe a trend towards negative values of ℱp (and thus ℱtot) at larger Ur. Figure 5 shows the same but for ℱB. The magnetic-field contribution does not follow the same clear trend in its Ur-dependence as ℱp. Figures 4 and 5 include horizontal and vertical error bars to represent ΔUr, Δℱp, and ΔℱB. The error bars follow from error propagation of the individual measurement uncertainties quoted in Sect. 2, which corresponds to the application of the standard error of the mean based on the individual uncertainties. We find that, in our hourly averages, the relative errors ΔUr, Δℱp, and ΔℱB are negligible.
 |
Fig. 4. Dependence of the proton contribution ℱp to the angular-momentum flux on the radial proton bulk speed Ur. We show the measurements of ℱp as points and overplot the linear fit to Eq. (5) as a black line. All measurement points have horizontal and vertical error bars, which are small due to the time-averaging. The fit parameters are given in Table 2. The magenta squares represent the measurements of ℱp during the time of the compression region (CR) on 2020-09-06. |
A comparison of the magenta points in Figs. 4 and 5 reveals that ℱB is not enhanced in the compression region compared to the time intervals outside the compression region. We note that the unit on the vertical axis in Fig. 5 is one order of magnitude smaller than the unit on the vertical axis in Fig. 4. This reflects again that ℱp is on average the dominant contribution to ℱtot. In order to quantify the Ur-dependence, we apply least-squares Marquardt–Levenberg fits to our measurements according to the linear equation:
 |
Fig. 5. Dependence of the magnetic-field contribution ℱB to the angular-momentum flux on the radial proton bulk speed Ur. We show the measurements of ℱB as points and overplot the linear fit to Eq. (5) as a black line. All measurement points have horizontal and vertical error bars, which are small due to the time-averaging. The fit parameters are given in Table 2. The magenta squares represent the measurements of ℱB during the time of the compression region (CR) on 2020-09-06. |
with the fit parameters a and b, where ℱ represents either ℱp, ℱB, or ℱtot. We show the resulting fit parameters including their errors in Table 2.
3.4. Mass-flux dependence of the angular-momentum flux
We define the proton mass flux per solid-angle element as:
As ℱp is carried by the proton flow, we combine ℱp and 𝒢p in Fig. 6 and analyse their dependence. We colour-code each measurement point with its associated value of Ur, which allows us to link Fig. 6 with Fig. 4. All time intervals with 𝒢p ≳ 2 × 10−15 au2 g cm−2 s−1 sr−1 in our dataset exhibit ℱp > 0. The majority of these points correspond to the compression region on 2020-09-06. We highlight them as magenta squares in Fig. 6, illustrating that the mass-flux dependence is a useful method to separate transient and atypical plasma intervals from the regular background solar wind (see also Stansby et al. 2019).
 |
Fig. 6. Dependence of the proton contribution ℱp to the angular-momentum flux on the radial proton mass flux 𝒢p. The point colour represents the value of Ur for each measurement. The magenta squares represent measurements during the time of the compression region (CR) on 2020-09-06. The grey dashed curves indicate contours of constant rUϕ. |
The value of rUϕ is a measure of the local specific angular momentum per proton. Since ℱp = rUϕ𝒢p, isocontours of constant rUϕ correspond to bent curves when using a logarithmic 𝒢p-axis in Fig. 6. We show these isocontours as grey dashed curves for a range of rUϕ values from ±10 to ±40 au km s−1. At the low-𝒢p end, the distribution scatters almost symmetrically around a value of ℱp = 0. The envelope of the distribution in this 𝒢p range follows isocontours of constant ±|rUϕ|, meaning that the scatter in ℱp is well defined by a fixed range of constant magnitudes of the angular momentum per proton. At intermediate 𝒢p, the symmetry around ℱp = 0 breaks, and more data points occur at ℱp > 0. At ℱp > 0, the envelope of the data distribution in terms of rUϕ decreases as 𝒢p increases in the intermediate-𝒢p range. The points representing the compression region largely lie on the same isocontours of rUϕ as the bulk of the slow solar wind. This behaviour suggests that the increase in ℱp associated with the compression region is mostly due to an increase in ρ rather than to an increase in the specific angular momentum per proton compared to the regular slow wind.
3.5. Spectral analysis of the angular-momentum flux
Solar Orbiter’s high temporal resolution in the measurement of both the particles and the magnetic field enables the analysis of the power spectrum of the variable angular-momentum flux over a wide range of frequencies. In order to demonstrate the suitability of Solar Orbiter data for future studies of this type, we present such a spectral analysis of the angular-momentum flux based on our dataset. We applied a non-uniform fast Fourier transform (Barnett et al. 2019; Barnett 2021) to the timeseries data of ℱp and ℱB throughout our entire dataset. For this calculation, we use 1-min averages of the data instead of the 60-min averages used in our study otherwise. This choice allows us to explore the variability of ℱp and ℱB over a wider range of frequencies. Figure 7 shows the resulting power spectral densities (PSDs) of ℱp and ℱB as functions of frequency ν.
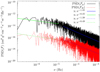 |
Fig. 7. Power spectral densities (PSDs) of ℱp and ℱB. The straight lines show power-law fits of the partial spectra of ℱp and ℱB. |
We observe a spectral break in the PSDs of both contributions to the angular-momentum flux near a frequency of ν ≈ 10−5 Hz. We perform separate power-law fits to PSD(ℱp) and PSD(ℱB) on both sides of their spectral breakpoints. We find PSD(ℱp) ∝ ν−0.45 ± 0.12 in the low-ν regime and PSD(ℱp) ∝ ν−1.448 ± 0.012 in the high-ν regime. Likewise, PSD(ℱB) ∝ ν−0.49 ± 0.14 in the low-ν regime and PSD(ℱB) ∝ ν−1.377 ± 0.012 in the high-ν regime. We overplot the fit results in Fig. 7.
4. Discussion
Our measurements of |ℱp| are largely in agreement with previous measurements in the solar wind, which reveal values of about 4.4…5.9 × 10−11 au3 g cm−1 s−2 sr−1 (Pizzo et al. 1983), 4.4…11.2 × 10−11 au3 g cm−1 s−2 sr−1 (Finley et al. 2020), and 1.09…2.43 × 10−10 au3 g cm−1 s−2 sr−1 (Liu et al. 2021) as averages over their whole datasets.
As shown in Sect. 3.3, we find a general trend of decreasing ℱp with increasing Ur, consistent with previous findings in data from Wind and Parker Solar Probe (Finley et al. 2019, 2020, 2021) and with estimates based on the observation of the Earth’s magnetotail deflection (Němeček et al. 2020). The observation of this trend in near-Sun data suggests that the trend is generated close to the Sun and not by local deflections at large distances. On average, ℱp > 0 for Ur ≲ 376 km s−1 and ℱp < 0 for Ur ≳ 376 km s−1 according to our fit result applied to the data shown in Fig. 4. The magnetic-field contribution ℱB shows only a small dependence on Ur, which is consistent with recent measurements from Parker Solar Probe (Liu et al. 2021).
Averaged over very long timescales, we expect both the particle contribution and the magnetic-field contribution to the angular-momentum flux to be positive due to the Sun’s sense of rotation and the direction of the average Parker (1958) field. In addition, we anticipate an overall loss of the Sun’s angular momentum based on observed trends in the rotation periods of Sun-like stars, which decrease with age along the main sequence. This finding is generally interpreted as a consequence of magnetised stellar winds (Lorenzo-Oliveira et al. 2019; do Nascimento et al. 2020). In the Sun’s specific case, a positive net ℱtot corresponds to a net loss of the Sun’s rotational angular momentum.
Moreover, we expect the average relative contribution of ℱB to the total angular-momentum flux to decrease slightly with increasing heliocentric distance as magnetic stress is converted into particle angular momentum (Weber & Davis 1967), although Marsch & Richter (1984) do not find clear evidence for this behaviour within 1 au. Previous measurements of ℱB reveal values of about 4.1…4.7 × 10−11 au3 g cm−1 s−2 sr−1 (Pizzo et al. 1983), 3.6…4.7 × 10−11 au3 g cm−1 s−2 sr−1 (Finley et al. 2020), and 2.1…3.8 × 10−11 au3 g cm−1 s−2 sr−1 (Liu et al. 2021) as the averages over their whole datasets at small heliocentric distances. These values are indeed greater than our mean values measured at Solar Orbiter’s distances from the Sun, consistent with an average transfer of angular momentum from the field to the particles taking place between 0.3 and 0.7 au. Averaged over two solar cycles, Finley et al. (2019) find ℱB ≈ 3.58 × 10−11 au3 g cm−1 s−2 sr−1 in data from the Wind spacecraft at 1 au. Comparing to the averages at small heliocentric distances, this 1 au long-term average is also consistent with an overall decreasing trend of ℱB with increasing r. We note, however, that our average ℱB at intermediate distances is even smaller than the 1 au long-term average from Wind. This discrepancy is probably the result of the limited statistics in our dataset and the specific solar wind streams encountered by Solar Orbiter during its first orbit at this particular phase of the solar cycle. Radial alignments between Solar Orbiter, Parker Solar Probe, and potentially other assets with suitable pointing accuracy and instrumentation will help us to understand the partition of the contributions to the angular-momentum flux over longer time intervals in the future. In general, we expect a significant dependence of the angular-momentum flux on the Sun’s 11-year activity cycle based on changes to the global magnetic field strength and changing solar-wind source regions (Finley et al. 2018).
Notwithstanding these expectations regarding large-scale behaviour, our measurements reveal the large variation of the angular-momentum flux over many timescales, from a few hours to months. Taking our full measurement time interval into account, the relative variations in ℱp are greater than the relative variations in ℱB. When separating fast and slow wind, however, the relative variations in ℱB are greater than those in ℱp both in the intervals with slow (Ur < 400 km s−1) and in the intervals with fast (Ur > 500 km s−1) solar wind. A potential reason for this behaviour lies in the fact that ℱB does not directly depend on Ur, while ℱp changes significantly with Ur (see Figs. 4 and 5). We attribute the natural variations in the angular-momentum flux to changes in the solar-wind source regions (Schwenn 2006; Tindale & Chapman 2017), deflections during the expansion (Egidi et al. 1969; Siscoe et al. 1969), or large-scale fluctuations as part of the turbulent spectrum (Tu & Marsch 1995; Bruno & Carbone 2013). Furthermore, the complex field and flow geometries in the low corona and latitudinal variations of the source regions create variations in ℱtot (Finley & Matt 2017; Réville & Brun 2017; Boe et al. 2020; Finley et al. 2020).
Figure 6 confirms that the scatter of data points around ℱp = 0 is more symmetric in the tenuous, low-𝒢p wind than in the denser, high-𝒢p wind. Assuming that all wind is ejected from the Sun with positive ℱp due to the Sun’s sense of rotation2, negative ℱp can only be created by local stream interactions, which in turn must increase ℱp of neighbouring plasma in order to fulfil angular-momentum conservation. Our observation of a more symmetric distribution around ℱp = 0 at low 𝒢p is then consistent with a scenario in which these local stream interactions occur more effectively in low-𝒢p wind. In this scenario, the mixing of ℱp in low-𝒢p wind leaves the high-𝒢p wind as the main carrier of net angular-momentum flux. Figure 6 then suggests that most of the net angular-momentum flux in the solar wind is carried by dense slow wind with ℱp > 0 in the intermediate-to-high-𝒢p range.
Our spectral analysis of ℱp and ℱB in Sect. 3.5 quantifies the variations of the angular-momentum flux depending on the frequency, ν. The averaging time (60 min) for our analysis of the angular-momentum flux outside of Sect. 3.5 corresponds to ν = 2.78 × 10−4 Hz, which lies well inside the accessible frequency range of the high-ν regime. Figure 7 does not exhibit a clear peak at the frequency associated with the Sun’s equatorial rotation frequency, ν = Ω⊙/2π ≈ 4.7 × 10−7 Hz. The lack of such a feature suggests that the variability of the angular-momentum flux induced by repeated passes of source regions due to the Sun’s rotation is negligible in our dataset. However, a spectral analysis of variations on these long timescales is not fully reliable at this stage of the mission due to the short overall duration of the dataset and its patchiness. The smallest gaps in our dataset are on order a few minutes, while the longest gap is 18 days long. We note in this context that large-scale interplanetary structures such as co-rotating interaction regions, which could be responsible for variations on these timescales, typically decay after a few revolutions. The breakpoint at ν ∼ 10−5 Hz corresponds to a timescale of ∼28 h. Assuming that this variation is frozen into the solar wind flow, this timescale corresponds to a convected length scale of ∼0.27 au according to Taylor’s hypothesis (Taylor 1938) based on an average Ur ≈ 400 km s−1. This scale is greater than the typical correlation length in solar wind turbulence in the inner heliosphere (Matthaeus & Goldstein 1982; Bruno & Dobrowolny 1986; Bruno & Carbone 2013; Bourouaine et al. 2020). We note, however, that the uncertainty in the visual determination of the breakpoint frequency permits values between ∼6 × 10−6 Hz and ∼4 × 10−5 Hz due to the noise in our Fourier spectrum. Length scales within the corresponding range of breakpoint scales are still greater than the typical correlation length. In addition, the determination of the correlation length itself is to a certain degree method-dependent. Some estimates for the correlation length of velocity fluctuations provide the same order of magnitude as the length scale associated with our breakpoint in PSD(ℱp) (Podesta et al. 2008), supporting the link between fluctuations in angular-momentum flux with the turbulent fluctuations in the solar wind. It is worthwhile to perform a scale-dependent study of the angular-momentum flux in the future, in particular, by separating the variations in the low-ν regime and in the high-ν regime.
Sporadic events, such as the compression on 2020-09-06, contribute to the natural variations of the angular-momentum flux. We do not remove events like these from our statistical analysis even though they introduce a bias, as seen in Figs. 1 and 2. The on-average greater variations in slow solar wind are reflected by the greater variation of the proton contribution ℱp to the angular-momentum flux at small Ur in Fig. 4. The mass-flux dependence of ℱp during the time interval associated with the compression region in Fig. 6 reveals a way to separate dense intermittent structures for future analyses. Using this method, it will be interesting to investigate the contribution of co-rotating interaction regions, coronal mass ejections, and other transient mass-flux enhancements to the Sun’s long-term angular-momentum loss. In fact, the amount of angular momentum carried by coronal mass ejections is still not well known. Since angular momentum is conserved, however, local angular-momentum enhancements by the deflection of background solar wind must be balanced via flows with opposite angular momentum elsewhere in space. Figure 6 shows that the compression region in our dataset carries approximately the same specific angular momentum per proton, rUϕ, as the regular slow wind, yet with a higher density. This observation suggests that the compression region represents “scooped-up” solar wind mass, which has not undergone a significant alteration in terms of the particles’ individual angular momentum. As shown in Fig. 5, the value of ℱB in the compression region is comparable to the average value of ℱB across our dataset. This observation supports our interpretation of the compression region as a density increase of otherwise unaltered background solar wind. Composition measurements of solar wind transients have the potential to confirm this interpretation in the future.
Our measurements neglect the contribution of α-particles to the angular-momentum flux. Given that their contribution to the local momentum flux is on the order of 20% (even greater near the Sun), α-particles can make a significant contribution to the total angular-momentum flux (Pizzo et al. 1983; Marsch & Richter 1984; Verscharen et al. 2015; Finley et al. 2021). Both Finley et al. (2021) and Liu et al. (2021) suggest a reconstruction of the α-particle component based on the field-alignment of the differential flow between protons and α-particles. It is still an open question, however, whether the α-particles generally serve as a net source of positive or negative angular-momentum flux. In addition, the proton beam component can carry a significant angular momentum flux (Finley et al. 2021), which we directly subsume through our using of total proton moments for ρ and U. Our analysis also neglects stresses due to pressure anisotropies in the particle populations (Hundhausen 1970; Marsch et al. 1982; Verscharen et al. 2019). This contribution to the angular-momentum flux is not significant for most of the solar wind plasma, however.
At this early stage of the mission, it is difficult to quantify the measurement uncertainties of the instruments accurately. These estimates will become more reliable as the mission progresses. At Ur ≲ 300 km s−1, the sensitivity of SWA/PAS decreases, so that the uncertainty in the proton moments increases. Therefore, we urge caution regarding the interpretation of the proton data (especially, the proton density) in this velocity range, which includes the compression region. Solar Orbiter’s Radio and Plasma Waves (RPW, Maksimovic et al. 2020) instrument provides an estimate of the local electron density based on the probe-to-spacecraft potential and quasi-thermal noise measurements (Khotyaintsev et al. 2021), which is independent of the SWA/PAS density measurement. We find that, especially during intervals with low Ur, SWA/PAS provides a greater density value than RPW. In Appendix A, we repeat part of our analysis using the independent RPW density estimate. Although we find a reduction in the peaks of ℱp when using the RPW density, our conclusions hold in spite of the density measurement that is applied. RPW is also able to provide an independent measurement of |U| from the bias DC electric field combined with the measurement of |B| from MAG. A careful cross-calibration between SWA/PAS and RPW both in terms of density and bulk-speed measurements will improve further studies in the future (Owen et al. 2020; Maksimovic et al. 2020; Walsh et al. 2020).
Early results from Parker Solar Probe report an increased azimuthal flow of the protons compared to the expectation of the Weber & Davis (1967) model at heliocentric distances up to about 0.23 au (Kasper et al. 2019). Possible explanations for this observed “angular-momentum paradox” (Réville et al. 2020) include the partitioning of angular-momentum flux between the different particle species, non-axisymmetric flows and pressure gradients, and pressure anisotropies. In our data, however, we do not find evidence for such a persistent positive azimuthal flow. Admittedly, our data were recorded at distances greater than 0.59 au and show a different distribution of solar wind speeds compared to the study by Kasper et al. (2019). In the future, when Solar Orbiter’s perihelion distance is reduced, it will be important to monitor the azimuthal flow of the protons more closely to compare with Parker Solar Probe’s findings of super-rotational flows in the near-Sun solar wind.
5. Concluding remarks
A reliable quantification of the Sun’s global angular-momentum loss requires measurements of the angular-momentum flux over long time intervals. In addition, we require distinctive measurements of typical equatorial and polar solar wind (McComas et al. 2000; Verscharen et al. 2021) to complete the understanding of the global angular-momentum loss. At this early point in the mission, we cannot confidently ascertain our measurement interval as a representative sample of the solar wind’s angular-momentum flux. Further long-term studies will become available during Solar Orbiter’s mission lifetime. At later stages of the mission, the spacecraft will leave the plane of the ecliptic making observations of the angular-momentum flux of polar solar wind feasible. Nevertheless, our study already confirms the potential for future detailed studies of the large-scale properties of the solar wind with the data from Solar Orbiter.
Acknowledgments
Solar Orbiter is a space mission of international collaboration between ESA and NASA, operated by ESA. The Solar Orbiter Solar Wind Analyser (SWA) PAS was designed, created, and is operated under funding provided in numerous contracts from the UK Space Agency (UKSA), the UK Science and Technology Facilities Council (STFC), the Centre National d’Études Spatiales (CNES, France), the Centre National de la Recherche Scientifique (CNRS, France), and the Czech contribution to the ESA PRODEX programme. In particular, operations at UCL/MSSL are currently funded under STFC grant ST/T001356/1. The Solar Orbiter Magnetometer was funded by the UK Space Agency (grant ST/T001062/1). The RPW instrument has been designed and funded by CNES, CNRS, the Paris Observatory, the Swedish National Space Agency, ESA-PRODEX, and all the participating institutes. D.V. is supported by STFC Ernest Rutherford Fellowship ST/P003826/1. D.V. and D.S. are supported by STFC Consolidated Grant ST/S000240/1. A.J.F. is supported by the ERC Synergy grant “Whole Sun”, #810218. T.H. is supported by STFC grant ST/S000364/1. Y.V.K. is supported by the Swedish National Space Agency grant 20/136. We appreciate helpful discussions at the ISSI Team “Exploring The Solar Wind In Regions Closer Than Ever Observed Before”. We appreciate helpful discussions with Silvia Perri, Christian Möstl, and the members of the Solar Orbiter in-situ science working group “CMEs, CIRs, HCS and large-scale structures”.
References
- Allen, R. C., Lario, D., Odstrcil, D., et al. 2020, ApJS, 246, 36 [Google Scholar]
- Barnes, S. A. 2003, ApJ, 586, 464 [Google Scholar]
- Barnett, A. H. 2021, Appl. Comput. Harmon. Anal., 51, 1 [Google Scholar]
- Barnett, A. H., Magland, J. F., & Klinteberg, L. A. 2019, SIAM J. Sci. Comput., 41, C479 [Google Scholar]
- Boe, B., Habbal, S., & Druckmüller, M. 2020, ApJ, 895, 123 [Google Scholar]
- Bourouaine, S., Perez, J. C., Klein, K. G., et al. 2020, ApJ, 904, L30 [Google Scholar]
- Bruno, R., & Carbone, V. 2013, Liv. Rev. Sol. Phys., 10, 2 [Google Scholar]
- Bruno, R., & Dobrowolny, M. 1986, Annal. Geophys., 4, 17 [NASA ADS] [Google Scholar]
- do Nascimento, J. D., Jr., de Almeida, L., Velloso, E. N., et al. 2020, ApJ, 898, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Egidi, A., Pizzella, G., & Signorini, C. 1969, J. Geophys. Res., 74, 2807 [NASA ADS] [CrossRef] [Google Scholar]
- Finley, A. J., & Matt, S. P. 2017, ApJ, 845, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Finley, A. J., Matt, S. P., & See, V. 2018, ApJ, 864, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Finley, A. J., Hewitt, A. L., Matt, S. P., et al. 2019, ApJ, 885, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Finley, A. J., Matt, S. P., Réville, V., et al. 2020, ApJ, 902, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Finley, A. J., McManus, M. D., Matt, S. P., et al. 2021, A&A, 650, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fox, N. J., Velli, M. C., Bale, S. D., et al. 2016, Space Sci. Rev., 204, 7 [Google Scholar]
- Gallet, F., & Bouvier, J. 2013, A&A, 556, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García Marirrodriga, C., Pacros, A., Strandmoe, S., et al. 2021, A&A, 646, A121 [CrossRef] [EDP Sciences] [Google Scholar]
- Horbury, T. S., O’Brien, H., Carrasco Blazquez, I., et al. 2020, A&A, 642, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hundhausen, A. J. 1970, Rev. Geophys. Space Phys., 8, 729 [CrossRef] [Google Scholar]
- Hundhausen, A. J., Bame, S. J., Asbridge, J. R., & Sydoriak, S. J. 1970, J. Geophys. Res., 75, 4643 [NASA ADS] [CrossRef] [Google Scholar]
- Kasper, J. C., Bale, S. D., Belcher, J. W., et al. 2019, Nature, 576, 228 [Google Scholar]
- Khotyaintsev, Yu. V., Graham, D. B., Vaivads, A., et al. 2021, A&A, 656, A19 (SO Cruise Phase SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lazarus, A. J., & Goldstein, B. E. 1971, ApJ, 168, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y. D., Chen, C., Stevens, M. L., & Liu, M. 2021, ApJ, 908, L41 [CrossRef] [Google Scholar]
- Lorenzo-Oliveira, D., Meléndez, J., Yana Galarza, J., et al. 2019, MNRAS, 485, L68 [Google Scholar]
- Maksimovic, M., Bale, S. D., Chust, T., et al. 2020, A&A, 642, A12 [EDP Sciences] [Google Scholar]
- Marsch, E., & Richter, A. K. 1984, J. Geophys. Res., 89, 5386 [NASA ADS] [CrossRef] [Google Scholar]
- Marsch, E., Schwenn, R., Rosenbauer, H., et al. 1982, J. Geophys. Res., 87, 52 [Google Scholar]
- Matt, S. P., Brun, A. S., Baraffe, I., Bouvier, J., & Chabrier, G. 2015, ApJ, 799, L23 [Google Scholar]
- Matthaeus, W. H., & Goldstein, M. L. 1982, J. Geophys. Res., 87, 6011 [Google Scholar]
- McComas, D. J., Barraclough, B. L., Funsten, H. O., et al. 2000, J. Geophys. Res., 105, 10419 [Google Scholar]
- Mestel, L. 1968, MNRAS, 138, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Möstl, C., Weiss, A. J., Bailey, R. L., et al. 2020, ApJ, 903, 92 [Google Scholar]
- Müller, D., St. Cyr, O. C., Zouganelis, I., et al. 2020, A&A, 642, A1 [Google Scholar]
- Neugebauer, M., & Snyder, C. W. 1962, Science, 138, 1095 [Google Scholar]
- Němeček, Z., Ďurovcová, T., Šafránková, J., et al. 2020, ApJ, 897, L39 [Google Scholar]
- Owen, C. J., Bruno, R., Livi, S., et al. 2020, A&A, 642, A16 [EDP Sciences] [Google Scholar]
- Pantolmos, G., & Matt, S. P. 2017, ApJ, 849, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1958, ApJ, 128, 664 [Google Scholar]
- Pizzo, V., Schwenn, R., Marsch, E., et al. 1983, ApJ, 271, 335 [Google Scholar]
- Podesta, J. J., Galvin, A. B., & Farrugia, C. J. 2008, J. Geophys. Res.: Space Phys., 113, A09104 [Google Scholar]
- Reiners, A., & Mohanty, S. 2012, ApJ, 746, 43 [Google Scholar]
- Réville, V., & Brun, A. S. 2017, ApJ, 850, 45 [Google Scholar]
- Réville, V., Velli, M., Panasenco, O., et al. 2020, ApJS, 246, 24 [Google Scholar]
- Richter, A. K., & Luttrell, A. H. 1986, J. Geophys. Res., 91, 5873 [NASA ADS] [CrossRef] [Google Scholar]
- Schwenn, R. 2006, Space Sci. Rev., 124, 51 [Google Scholar]
- Siscoe, G. L., Goldstein, B., & Lazarus, A. J. 1969, J. Geophys. Res., 74, 1759 [NASA ADS] [CrossRef] [Google Scholar]
- Stansby, D., Horbury, T. S., & Matteini, L. 2019, MNRAS, 482, 1706 [Google Scholar]
- Taylor, G. I. 1938, Proc. R. Soc. London Ser. A, 164, 476 [Google Scholar]
- Tindale, E., & Chapman, S. C. 2017, J. Geophys. Res.: Space Phys., 122, 9824 [NASA ADS] [CrossRef] [Google Scholar]
- Tu, C. Y., & Marsch, E. 1995, Space Sci. Rev., 73, 1 [Google Scholar]
- Verscharen, D., Chandran, B. D. G., Bourouaine, S., & Hollweg, J. V. 2015, ApJ, 806, 157 [Google Scholar]
- Verscharen, D., Klein, K. G., & Maruca, B. A. 2019, Liv. Rev. Sol. Phys., 16, 5 [Google Scholar]
- Verscharen, D., Bale, S. D., & Velli, M. 2021, MNRAS, 506, 4993 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, A. P., Horbury, T. S., Maksimovic, M., et al. 2020, A&A, 642, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weber, E. J., & Davis, L., Jr. 1967, ApJ, 148, 217 [Google Scholar]
Appendix A: The angular-momentum and mass flux based on the RPW density
RPW measures the local total electron density ne based on a combination of both the peak-tracking of the plasma frequency and the spacecraft potential (Khotyaintsev et al. 2021). Due to quasi-neutrality, ne serves as an independent measure of the total charge-weighted ion density. For comparison with our SWA/PAS-MAG measurements, we create a new dataset using U from SWA/PAS, B from MAG, and ρ = mpne from RPW, where mp is the proton mass. We apply the same selection, averaging, and analysis methods as in the main part of this work. This leaves us with 913 data points for our combined SWA/PAS-MAG-RPW dataset in total.
We show the timeseries of our combined SWA/PAS-MAG-RPW dataset in Fig. A.1. Qualitatively, the timeseries agrees with Fig. 1. However, the peaks with ℱp > 0 are less pronounced in the SWA/PAS-MAG-RPW dataset than in the SWA/PAS-MAG dataset. These peaks, including our compression region on 2020-09-06, correspond to intervals of slow and dense solar wind, for which the SWA/PAS and RPW densities diverge most.
 |
Fig. A.1. Same as Fig. 1, but using ρ from RPW in the calculation of ℱp and ℱtot. The grey-shaded areas indicate times for which our merged SWA/PAS-MAG-RPW data product is unavailable or the data flags for either dataset indicate poor data quality. |
We present the statistical properties of our combined SWA/PAS-MAG-RPW dataset in Table A.1. Due to the lower peaks in ℱp, the signs of the mean values for ℱp and ℱtot across our full dataset are now different from the signs of the same quantities in the SWA/PAS-MAG dataset shown in Table 1. The maxima of ℱp and ℱtot in Table A.1 are lower than those given in Table 1, reflecting the lower peaks seen in Fig. A.1. All other statistical markers in Table A.1 agree with our results shown in Table 1.
Same as Table 1, but using ρ from RPW in the calculation of ℱp and ℱtot.
We show the dependence of ℱp on 𝒢p for our combined SWA/PAS-MAG-RPW dataset in Fig. A.2. The comparison between Figs. 6 and A.2 shows that most high-𝒢p measurements, including the compression region, shift towards smaller values of 𝒢p when using the RPW density estimate. In addition, the compression region shifts towards smaller values of ℱp. Notwithstanding these differences, our conclusions drawn based on Fig. 6 are still valid.
All Tables
Statistical properties of ℱp, ℱB, and ℱtot in our full dataset and split by radial solar-wind speed.
All Figures
 |
Fig. 1. Time series of the angular-momentum flux per solid-angle element measured during Solar Orbiter’s first orbit of the cruise phase. The diagram shows the proton contribution ℱp, the magnetic-field contribution ℱB, and the sum of both, ℱtot. In order to increase the visibility, we multiply ℱB with a factor 10. The magenta squares represent the measurements of ℱtot during the time of the compression region (CR) on 2020-09-06. The axis at the top indicates the heliocentric distance of the spacecraft at the time of the measurement. The scale of this axis is not linear. The grey-shaded areas indicate times for which our merged SWA/PAS-MAG data product is unavailable or the data flags for either dataset indicate poor data quality. |
| In the text | |
 |
Fig. 2. Histogram of the proton contribution ℱp to the solar wind’s angular-momentum flux per solid-angle element. The vertical axis indicates the probability density of ℱp. We stack the histograms for fast (Ur > 500 km s−1), intermediate (400 km s−1 ≤ Ur ≤ 500 km s−1), and slow (Ur < 400 km s−1) wind. The magenta areas represent the measurements of ℱp during the time of the compression region (CR) on 2020-09-06. |
| In the text | |
 |
Fig. 3. Histogram of the magnetic-field contribution ℱB to the solar wind’s angular-momentum flux per solid-angle element. Details are the same as in Fig. 2. |
| In the text | |
 |
Fig. 4. Dependence of the proton contribution ℱp to the angular-momentum flux on the radial proton bulk speed Ur. We show the measurements of ℱp as points and overplot the linear fit to Eq. (5) as a black line. All measurement points have horizontal and vertical error bars, which are small due to the time-averaging. The fit parameters are given in Table 2. The magenta squares represent the measurements of ℱp during the time of the compression region (CR) on 2020-09-06. |
| In the text | |
 |
Fig. 5. Dependence of the magnetic-field contribution ℱB to the angular-momentum flux on the radial proton bulk speed Ur. We show the measurements of ℱB as points and overplot the linear fit to Eq. (5) as a black line. All measurement points have horizontal and vertical error bars, which are small due to the time-averaging. The fit parameters are given in Table 2. The magenta squares represent the measurements of ℱB during the time of the compression region (CR) on 2020-09-06. |
| In the text | |
 |
Fig. 6. Dependence of the proton contribution ℱp to the angular-momentum flux on the radial proton mass flux 𝒢p. The point colour represents the value of Ur for each measurement. The magenta squares represent measurements during the time of the compression region (CR) on 2020-09-06. The grey dashed curves indicate contours of constant rUϕ. |
| In the text | |
 |
Fig. 7. Power spectral densities (PSDs) of ℱp and ℱB. The straight lines show power-law fits of the partial spectra of ℱp and ℱB. |
| In the text | |
 |
Fig. A.1. Same as Fig. 1, but using ρ from RPW in the calculation of ℱp and ℱtot. The grey-shaded areas indicate times for which our merged SWA/PAS-MAG-RPW data product is unavailable or the data flags for either dataset indicate poor data quality. |
| In the text | |
 |
Fig. A.2. Same as Fig. 6, but using ρ from RPW in the calculation of ℱp and 𝒢p. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.