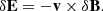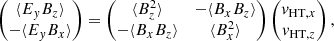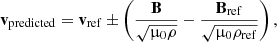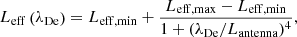| Issue |
A&A
Volume 656, December 2021
Solar Orbiter First Results (Cruise Phase)
|
|
|---|---|---|
| Article Number | A9 | |
| Number of page(s) | 7 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202140855 | |
| Published online | 14 December 2021 | |
Solar wind current sheets and deHoffmann-Teller analysis
First results from Solar Orbiter’s DC electric field measurements
1
Swedish Institute of Space Physics (IRF), Uppsala 75121, Sweden
e-mail: konrad.steinvall@irfu.se
2
Space and Plasma Physics, Department of Physics and Astronomy, Uppsala University, Uppsala 75120, Sweden
3
Division of Space and Plasma Physics, School of Electrical Engineering and Computer Science, KTH Royal Institute of Technology, Stockholm 11428, Sweden
4
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Univ. Paris Diderot, Sorbonne Paris Cité, 5 place Jules Janssen, 92195 Meudon, France
5
Space Sciences Laboratory, University of California, Berkeley, CA, USA
6
Physics Department, University of California, Berkeley, CA, USA
7
LPP, CNRS, Ecole Polytechnique, Sorbonne Université, Observatoire de Paris, Université Paris-Saclay, Palaiseau, Paris, France
8
LPC2E, CNRS, 3A avenue de la Recherche Scientifique, Orléans, France
9
Université d’Orléans, Orléans, France
10
CNES, 18 avenue Edouard Belin, 31400 Toulouse, France
11
Technische Universität Dresden, Helmholtz Str. 10, 01187 Dresden, Germany
12
Institute of Atmospheric Physics of the Czech Academy of Sciences, Prague, Czech Republic
13
Space Research Institute, Austrian Academy of Sciences, Graz, Austria
14
Astronomical Institute of the Czech Academy of Sciences, Prague, Czech Republic
15
Radboud Radio Lab, Department of Astrophysics, Radboud University, Nijmegen, The Netherlands
16
Imperial College London, South Kensington Campus, London SW7 2AZ, UK
17
Institut de Recherche en Astrophysique et Planétologie, 9 avenue du Colonel Roche, BP 4346, 31028 Toulouse Cedex 4, France
18
Laboratoire d’astrophysique de Bordeaux, Univ. Bordeaux, CNRS, Pessac, France
19
Mullard Space Science Laboratory, University College London, Holmbury St. Mary, Dorking, Surrey RH5 6NT, UK
Received:
22
March
2021
Accepted:
26
April
2021
Context. Solar Orbiter was launched on 10 February 2020 with the purpose of investigating solar and heliospheric physics using a payload of instruments designed for both remote and in situ studies. Similar to the recently launched Parker Solar Probe, and unlike earlier missions, Solar Orbiter carries instruments designed to measure low-frequency DC electric fields.
Aims. In this paper, we assess the quality of the low-frequency DC electric field measured by the Radio and Plasma Waves instrument (RPW) on Solar Orbiter. In particular, we investigate the possibility of using Solar Orbiter’s DC electric and magnetic field data to estimate the solar wind speed.
Methods. We used a deHoffmann-Teller (HT) analysis, based on measurements of the electric and magnetic fields, to find the velocity of solar wind current sheets, which minimises a single component of the electric field. By comparing the HT velocity to the proton velocity measured by the Proton and Alpha particle Sensor (PAS), we have developed a simple model for the effective antenna length, Leff of the E-field probes. We then used the HT method to estimate the speed of the solar wind.
Results. Using the HT method, we find that the observed variations in Ey are often in excellent agreement with the variations in the magnetic field. The magnitude of Ey, however, is uncertain due to the fact that the Leff depends on the plasma environment. Here, we derive an empirical model relating Leff to the Debye length, which we can use to improve the estimate of Ey and, consequently, the estimated solar wind speed.
Conclusions. The low-frequency electric field provided by RPW is of high quality. Using the deHoffmann-Teller analysis, Solar Orbiter’s magnetic and electric field measurements can be used to estimate the solar wind speed when plasma data are unavailable.
Key words: solar wind / plasmas / magnetic reconnection / methods: data analysis
© ESO 2021
1. Introduction
With the recent launch of NASA’s Parker Solar Probe (Fox & McComas 2016) and ESA’s Solar Orbiter (Müller et al. 2020), the low-frequency ‘DC’ electric field, E, associated with the solar wind, can be measured for the first time at heliocentric distances below 1 AU. The electric field is one of the most challenging quantities to measure. One significant complication is that the spacecraft and its solar panels are charged to some variable potential and will generate an electrostatic field, which is not of physical interest (Cully et al. 2007; Johansson et al. 2020). Another difficulty is that the E-field probes must be adequately separated to provide the sensitivity necessary to measure weak electric fields in plasma. To investigate the quality of the E-field measurement, it can often be useful to analyse large-scale fluctuations in the magnetic field, B. Since the solar wind plasma is, on large scales, in the ideal MHD state, E is related to B via the simple formula E = −v × B, where v is the plasma bulk velocity. Thus, if a magnetic structure, such as a current sheet, crosses the spacecraft at a constant v, then the E fluctuations linearly related to the fluctuations in B will be observed. Moreover, if the plasma velocity is measured independently, it is possible to calculate the electric field as E = −v × B and compare the results directly to the measured E-field as a method of quality control (Mozer et al. 2020a).
When analysing magnetic structures such as current sheets, Alfvén waves, or shocks, it is often necessary to find the proper frame of the structure. This is commonly done using deHoffmann-Teller analysis (De Hoffmann & Teller 1950; Sonnerup et al. 1987). The proper frame of a magnetic structure is a deHoffmann-Teller (HT) frame if E = 0 in it. Thus, if the HT frame exists, the electric field in the spacecraft frame is given by E = −vHT × B, where the HT velocity vHT, is the velocity of the HT frame with respect to the spacecraft frame. We note that we cannot transform away any component of E parallel to B (E∥). However, on the large scales we are interested in, E∥ is typically zero. Historically, HT analysis has been used extensively to analyse shocks (e.g., Schwartz et al. 1988; Lefebvre et al. 2007) and magnetic reconnection at Earth’s magnetopause (e.g., Fuselier et al. 1991; Phan et al. 2004) and in the solar wind (e.g., Gosling et al. 2005). More recently, Horbury et al. (2020a) used HT analysis to find the proper frame of large-scale solar wind spikes (Horbury et al. 2018), also known as ‘switchbacks’ (e.g., Bale et al. 2019; Mozer et al. 2020b), observed by Parker Solar Probe. Also, Němeček et al. (2020a) applied a HT analysis to particle velocity data in the solar wind, concluding that the HT frame can be considered a proper solar wind frame.
Another important application of the HT analysis, which to the best of our knowledge has not been previously reported, is to estimate the solar wind speed in the absence of particle data. Fluctuations in the solar wind magnetic field are primarily either frozen-in current sheets or MHD turbulence (Borovsky 2010). The HT frame of a current sheet is the frame in which E = 0 on both sides of the discontinuity. In other words, it is the frame in which the plasma flow is field aligned on both sides. In the solar wind, the plasma flow is usually approximately constant across the discontinuity, while B is arbitrarily rotated in the plane of the discontinuity, implying v cannot be field-aligned simultaneously on both sides (unless the fields are exactly parallel or anti-parallel, in which case vHT is not unique, as discussed by Khrabrov & Sonnerup 1998). It thus follows that if a HT frame exists, v must be zero in it, implying vHT = v. Therefore, by applying the HT analysis to solar wind current sheets, which are often tangential discontinuities (Knetter et al. 2004), we obtain a measure of the solar wind velocity. For completeness we note that while rotational discontinuities always have a HT frame, there is a specific theoretical configuration in which tangential discontinuities do not have a HT frame. In this special configuration, the magnetic fields on the two sides of the discontinuity are perfectly parallel or anti-parallel, while the plasma flow has a different perpendicular (to B) component on the two sides of the discontinuity (Khrabrov & Sonnerup 1998). However, due to the strict criteria on the magnetic fields, this situation does not occur in practice, and the discontinuities we observe in the solar wind should always have a HT frame.
If we instead apply the HT analysis on an Alfvénic structure, Faraday’s law implies that vHT is the phase velocity of the structure. In the spacecraft frame, this gives vHT = v + vϕ, where vϕ is the phase velocity in the plasma frame, which depends on the wave-mode and propagation direction, and typically is on the order of the Alfvén speed vA. Far from the Sun, vA is small compared to v, and we can treat it as a small correction to the solar wind speed. However, closer to the Sun, this extra contribution might become non-negligible when analysing Alfvénic structures such as switchbacks, as discussed by Horbury et al. (2020a).
To avoid potential confusion, we want to emphasise that while the HT velocity is derived from E = −v × B, vHT is not necessarily perpendicular to the ambient magnetic field. One way to understand this is to realise that we are applying the analysis to magnetic structures which have associated magnetic fluctuations, δB, such that B = B0 + δB, where B0 is the background magnetic field. For simplicity, if v is constant, the corresponding electric fluctuation is given by
So even if B0 and v are parallel, as long as δB has a component perpendicular to B0, it can be used together with δE to estimate v.
In this study, we apply a HT analysis based on electric and magnetic field measurements to solar wind current sheets to investigate the quality of Solar Orbiter’s DC electric field. Once we establish that the quality is sufficient, we apply the HT analysis to estimate the solar wind speed. We find that our method can be used to distinguish between fast and slow solar wind, providing a measure of the solar wind velocity even when particle data are unavailable.
2. Instrumentation and DC E calibration
The data used in this study come from the Solar Orbiter mission. We use magnetic field data from the magnetometer (MAG; Horbury et al. 2020b) sampled at 8 vectors per second, plasma measurements from the Solar Wind Analyser suite (SWA; Owen et al. 2020), in particular, from the Proton and Alpha particle Sensor (PAS) at 0.25 samples per second, and electric fields from the Radio and Plasma Waves instrument (RPW; Maksimovic et al. 2020) sampled at 16 vectors per second. Throughout this paper, we primarily present vector quantities in the spacecraft coordinate system (SRF) defined in such a way that 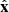 is pointing away from Solar Orbiter toward the Sun,
is pointing away from Solar Orbiter toward the Sun, 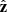 is along RPW antenna 1 (approximately normal to the ecliptic plane for the data used in this study, see Fig. 1), and
is along RPW antenna 1 (approximately normal to the ecliptic plane for the data used in this study, see Fig. 1), and 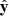 completes the right-handed coordinate system.
completes the right-handed coordinate system.
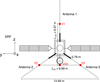 |
Fig. 1. Qualitative sketch of Solar Orbiter as seen from behind, showing the RPW antennas (i.e. the probes) and the nominal effective antenna lengths L23 and L123. |
Since the main focus of this study is on the DC electric field E, we briefly summarise the method used to calculate and calibrate E, while referring to Maksimovic et al. (2020) for more details about the RPW instrument. The electric field is measured using three cylindrical probes lying in the YZ plane as shown in Fig. 1. RPW measures the probe-to-spacecraft potential for the three probes, V1, V2, and V3, respectively. Since probes 2 and 3 are symmetrically positioned along y with respect to both spacecraft and solar panels, spacecraft effects are mostly cancelled out when computing Ey = (V3 − V2)/L23, where L23 is the nominal effective antenna length (6.99 m), that is, the spatial distance between the measurements of V2 and V3. This, however, is not the case when we compute Ez = (V23 − V1)/L123, where V23 = (V2 + V3)/2 is the mean potential of probes 2 and 3, and L123 is the nominal effective antenna length (6.97 m) in the z-direction, since probe 1 is placed in a different potential environment compared to probes 2 and 3. As a result, Ez does not behave as well as Ey, and tends to be more noisy. Consequently, throughout this investigation, we only use Ey, which is sufficient for the purposes of this study.
In the ideal case Ey can be directly computed as Ey=(V3 − V2)/L23. In reality however, the probe signals may have instrumental offsets which we need to compensate for. The source of the offsets can for example be a difference in characteristics of the individual probes, asymmetries in the electrostatic potential of the spacecraft and solar panels, and plasma wakes. We account for these by taking a large window (several hours) of data and fitting V2 against V3 linearly to find a slope k23, and offset d23. Typically, k23 is steady and very close to 1, and we set it to be identically 1 throughout this study. The offset is more variable with a typical value of ∼d23 = 0.1 V. We therefore correct V2 for the offset 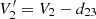 . This correction implicitly assumes that Ey = 0 on the time-scale of the window. One additional complication we occasionally need to account for is that we sometimes find an unphysical correlation between
. This correction implicitly assumes that Ey = 0 on the time-scale of the window. One additional complication we occasionally need to account for is that we sometimes find an unphysical correlation between 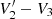 and
and 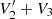 , that is, a correlation between Ey and the spacecraft potential. When this correlation is strong and the absolute value of the correlation coefficient between the two terms exceeds 0.7, we add an additional step to the calibration to remove this common mode signal. This step is to fit
, that is, a correlation between Ey and the spacecraft potential. When this correlation is strong and the absolute value of the correlation coefficient between the two terms exceeds 0.7, we add an additional step to the calibration to remove this common mode signal. This step is to fit 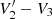 linearly against
linearly against 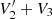 yielding an offset Γ0 and a slope Γ1, which we adjust for symmetrically as
yielding an offset Γ0 and a slope Γ1, which we adjust for symmetrically as ![$ V_2^*=V_2^\prime-[\Gamma_0+\Gamma_1(V_2^\prime+V_3)]/2 $](/articles/aa/full_html/2021/12/aa40855-21/aa40855-21-eq10.gif) ,
, ![$ V_3^*=V_3+[\Gamma_0+\Gamma_1(V_2^\prime+V_3)]/2 $](/articles/aa/full_html/2021/12/aa40855-21/aa40855-21-eq11.gif) . We can then finally compute Ey as
. We can then finally compute Ey as 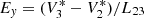 .
.
3. Current sheets and the deHoffmann-Teller analysis
To validate Ey, we make use of fact that the plasma is in the ideal MHD state, meaning E = −v × B. Since the solar wind velocity is relatively steady if compared to the magnetic field, which changes significantly in both magnitude and direction, variations in E correspond primarily to variations in B. Because of this, current sheet crossings serve as an excellent opportunity to test the DC E measurements using the HT analysis. In this study, we calculate vHT in two ways. Firstly, following the theory discussed by Khrabrov & Sonnerup (1998) and Paschmann & Sonnerup (2008), dropping the contribution of Ex, Ez, By and vy results in
where ⟨ ⋅ ⟩ denotes averaging. Solving for vHT, we find the velocity of the frame in which Ey = 0. What is evident from Eq. (2) is the fact that we are unable to determine vHT, y, and vHT is not unique in that respect. However, the solar wind is mainly expanding radially from the Sun, so that |vx|≫|vy| (Němeček et al. 2020b), and the observed vy is mainly due to orbital motion of the spacecraft, which is rarely of practical importance. Secondly, when PAS data are available, we use the 3D ion velocity vectors and Eq. (9.10) from Khrabrov & Sonnerup (1998) to obtain an estimate of vHT that does not involve E, which can be compared to the results of Eq. (2).
In Fig. 2, we present two examples of current sheets identified as sharp rotations in at least one component of B, where we apply the HT analysis. For the first current sheet (observed at 0.75 AU), there are PAS data available and we use both methods to calculate vHT. We show the results in Fig. 2b, where we plot Ey (black) together with −(vHT × B)y, where vHT was obtained using RPW data with Eq. (2) (red), as well as PAS data using Eq. (9.10) from Khrabrov & Sonnerup (1998) (blue). The two vHT estimates are in good agreement, ![$ \mathbf{v}^{(\mathrm{RPW})}_{\mathrm{HT}}=[-400,\mathrm{N/A},-1] $](/articles/aa/full_html/2021/12/aa40855-21/aa40855-21-eq14.gif) ,
, ![$ \mathbf{v}^{(\mathrm{PAS})}_{\mathrm{HT}}=[-380,68,-24] $](/articles/aa/full_html/2021/12/aa40855-21/aa40855-21-eq15.gif) . There is an excellent agreement between Ey and −vHT × B, indicating that the HT frame exists, and that Ey is accurately measured on both large and small scales. The obtained HT velocities are close to the solar wind velocity measured by PAS, v = [ − 370, 64, −18] km s−1, which shows that the HT method indeed can be used to estimate the solar wind speed. For reference, the average Alfvén speed in this interval is 35 km s−1. The second current sheet (Figs. 2d−f) was observed closer to the Sun, at 0.54 AU, and there was no particle data from PAS for a comparison. Using the spacecraft potential and plasma frequency measured by RPW we estimate the plasma density (Khotyaintsev et al. 2021) shown in Fig. 2f, and find an average Alfvén speed of 34 km s−1. The results of the HT analysis in Fig. 2e shows a good agreement between Ey and −(vHT × B)y, suggesting again that the HT frame exists and that Ey accurately follows the changes in B. However, we note the low value of
. There is an excellent agreement between Ey and −vHT × B, indicating that the HT frame exists, and that Ey is accurately measured on both large and small scales. The obtained HT velocities are close to the solar wind velocity measured by PAS, v = [ − 370, 64, −18] km s−1, which shows that the HT method indeed can be used to estimate the solar wind speed. For reference, the average Alfvén speed in this interval is 35 km s−1. The second current sheet (Figs. 2d−f) was observed closer to the Sun, at 0.54 AU, and there was no particle data from PAS for a comparison. Using the spacecraft potential and plasma frequency measured by RPW we estimate the plasma density (Khotyaintsev et al. 2021) shown in Fig. 2f, and find an average Alfvén speed of 34 km s−1. The results of the HT analysis in Fig. 2e shows a good agreement between Ey and −(vHT × B)y, suggesting again that the HT frame exists and that Ey accurately follows the changes in B. However, we note the low value of ![$ \mathbf{v}^{(\mathrm{RPW})}_{\mathrm{HT}}=[-174,\mathrm{N/A},-20] $](/articles/aa/full_html/2021/12/aa40855-21/aa40855-21-eq16.gif) km s−1 compared to the typical solar wind velocity, which suggests that the magnitude of Ey is underestimated. This is likely related to the effective antenna length Leff, being shorter than the nominal length L23 = 6.99 m used in the calibration leading to both Ey and vHT being underestimated.
km s−1 compared to the typical solar wind velocity, which suggests that the magnitude of Ey is underestimated. This is likely related to the effective antenna length Leff, being shorter than the nominal length L23 = 6.99 m used in the calibration leading to both Ey and vHT being underestimated.
 |
Fig. 2. Current sheet crossings at different heliocentric distances (left column 0.75 AU, right column 0.54 AU). Panel a: magnetic field in SRF coordinates. Panel b: Ey (black) and −(vHT × B)y with vHT from PAS (blue) and RPW (red). Panel c: plasma density from PAS. Panels d–f: same format as a-c for a different current sheet where PAS data are unavailable. Plasma density was estimated from the spacecraft potential (Khotyaintsev et al. 2021). |
The first current sheet (Figs. 2a–c) had a small magnetic field component that was normal to the current sheet Bn ≈ 0.2 nT, Bn/|B|≈0.04, obtained using minimum variance analysis (Sonnerup & Cahill 1967), and the plasma data showed no signatures of reconnection. The second current sheet (Figs. 2d–f) had a much larger normal component Bn ≈ 1.5 nT, Bn/|B|≈0.15, but no plasma data were available to compare with. Next, we investigate a current sheet with an intermediate normal magnetic field component Bn ≈ −0.3 nT, Bn/|B|≈0.09, where plasma data, which shows several signatures of magnetic reconnection, were available.
On 20 August 2020, Solar Orbiter observed several sharp B changes during which Bx changed its sign (i.e. radial polarity changes), often concurrently to significant reductions in magnetic field magnitude, which occasionally reached values as low as 0.1 nT. The Magnetic Connectivity Tool (Rouillard et al. 2020) shows that Solar Orbiter was very close to the heliospheric current sheet (HCS) during this time, suggesting that these observations were likely multiple crossings of the HCS. In Fig. 3, we present an overview of two such crossings that show signatures of ongoing magnetic reconnection. By applying our HT analysis on the whole interval (Fig. 3c), we are again able to find a good agreement between Ey and −(vHT × B)y, and we conclude that a HT frame exists. The difference between ![$ \mathbf{v}^{(\mathrm{RPW})}_{\mathrm{HT}}=[-246,\mathrm{N/A},48] $](/articles/aa/full_html/2021/12/aa40855-21/aa40855-21-eq17.gif) km s−1 and,
km s−1 and, ![$ \mathbf{v}^{(\mathrm{PAS})}_{\mathrm{HT}}=[-320,36,-18] $](/articles/aa/full_html/2021/12/aa40855-21/aa40855-21-eq18.gif) km s−1, indicates that |Ey| is underestimated by about 20%. We again find that the average Alfvén speed of 22 km s−1 is much slower than the solar wind speed, and the effect of Alfvénic fluctuations are negligible. During the first crossing at 13:57 UT (yellow highlight), there is a clear peak in the plasma velocity (Fig. 3b), which is concurrent with an increase in density (Fig. 3d) and ion temperature (Fig. 3e). These are signatures of a reconnection outflow. In order to investigate whether this observation is consistent with ongoing magnetic reconnection, we use a minimum variance analysis on B to determine the local current sheet coordinate system (Sonnerup & Cahill 1967). We limit the minimum variance analysis to the first small-scale current sheet highlighted in yellow, and find L = [0.75, 0.17, 0.64], M = [0.31, −0.94, −0.11], N = [0.58, 0.27, −0.76], where N is normal to the current sheet, L is in the direction of the reconnecting B component, and M points out of the reconnection plane. In Figs. 3f,g we show a zoom-in on the jet, and present B and v in LMN coordinates. One important feature in the data is the changing correlation between BL and vL, highlighted by the green and magenta dashed lines. During the leading part of the crossing, BL and vL are correlated (green dashes), while in the trailing part they are anti-correlated (magenta dashes), consistent with the sketch in Fig. 3h. This signature corresponds to the two Alfvén waves propagating away from the reconnection site, parallel and anti-parallel to B (e.g., Gosling et al. 2005; Lavraud et al. 2009; Phan et al. 2020; Froment et al. 2021), and distinguishes it from Alfvénic structures such as switchbacks, characterised by a single correlation. We show the results from a more quantitative test of the magnetic reconnection hypothesis, a Walén test, in Fig. 3g, where the overplotted grey, cyan, and orange curves are the predicted velocity components when crossing a rotational discontinuity in an isotropic plasma (Hudson 1970):
km s−1, indicates that |Ey| is underestimated by about 20%. We again find that the average Alfvén speed of 22 km s−1 is much slower than the solar wind speed, and the effect of Alfvénic fluctuations are negligible. During the first crossing at 13:57 UT (yellow highlight), there is a clear peak in the plasma velocity (Fig. 3b), which is concurrent with an increase in density (Fig. 3d) and ion temperature (Fig. 3e). These are signatures of a reconnection outflow. In order to investigate whether this observation is consistent with ongoing magnetic reconnection, we use a minimum variance analysis on B to determine the local current sheet coordinate system (Sonnerup & Cahill 1967). We limit the minimum variance analysis to the first small-scale current sheet highlighted in yellow, and find L = [0.75, 0.17, 0.64], M = [0.31, −0.94, −0.11], N = [0.58, 0.27, −0.76], where N is normal to the current sheet, L is in the direction of the reconnecting B component, and M points out of the reconnection plane. In Figs. 3f,g we show a zoom-in on the jet, and present B and v in LMN coordinates. One important feature in the data is the changing correlation between BL and vL, highlighted by the green and magenta dashed lines. During the leading part of the crossing, BL and vL are correlated (green dashes), while in the trailing part they are anti-correlated (magenta dashes), consistent with the sketch in Fig. 3h. This signature corresponds to the two Alfvén waves propagating away from the reconnection site, parallel and anti-parallel to B (e.g., Gosling et al. 2005; Lavraud et al. 2009; Phan et al. 2020; Froment et al. 2021), and distinguishes it from Alfvénic structures such as switchbacks, characterised by a single correlation. We show the results from a more quantitative test of the magnetic reconnection hypothesis, a Walén test, in Fig. 3g, where the overplotted grey, cyan, and orange curves are the predicted velocity components when crossing a rotational discontinuity in an isotropic plasma (Hudson 1970):
 |
Fig. 3. Observations of a reconnecting current sheet. Panels a,b: magnetic field and ion velocity in SRF. Panel c: Ey and −(vHT × B)y with vHT from PAS (blue) and RPW (red). Panels d,e: ion density and temperature from PAS. Panel f: magnetic field in LMN coordinates at the reconnection jet. Panel g: observed (black, blue, red) and predicted (green, cyan, orange) plasma velocities in LMN coordinates. The green and magenta dashed horizontal bars highlight where BL and VL are correlated and anti-correlated, respectively. Panel h: simplified sketch of the reconnection event illustrating the expected correlation and anti-correlation between BL and VL. |
where ρ is the ion mass density, and the subscript ‘ref’ denotes reference values selected on either side of the jet. The + solution is taken for the leading edge, and − is taken for the trailing edge, while the corresponding time for the reference values are 13:56:10 and 13:57:55 UT. The good agreement between the prediction and observation indicates that Solar Orbiter crossed a rotational discontinuity. Performing the same analysis on similar crossings later in the day (e.g., 16:44:00 UT) yields similar results.
In summary, by applying our HT method on Solar Orbiter data from crossings of current sheets, some of which are undergoing magnetic reconnection, we find that the HT frames exist, and Ey well captures changes in B. However, due to variations in the effective antenna length, the magnitude of Ey, and consequently also |vHT|, is not always accurate. We address this issue in the following section.
4. Solar wind velocity and the effective antenna length
As shown in Sect. 3, the shape of Ey is often well represented by −(vHT × B)y, while the magnitude |Ey|, and subsequently also vHT, can be off by a scaling factor, which is likely related to the effective antenna length, Leff. Understanding how Leff varies with plasma conditions is therefore essential for our method to give as good velocity estimates as possible. In the following, we compare plasma velocities from PAS with the estimates from Eq. (2) to model Leff.
Our procedure is as follows. When PAS, MAG, and RPW data are all available (discrete intervals between the end of May through October 2020), we take a ±4 hour interval around a given time t0. In this interval we compute Ey according to the calibration method discussed in Sect. 2, and band-pass filter both Ey and B between 0.139 mHz (2 hour period) and 0.3 Hz to get rid of potential problems associated with possible drifts of the probe offsets and any high-frequency noise. Applying Eq. (2) on the data within ±30 min from t0, we finally obtain vHT. We then take a step of ten minutes, t0 → t0 + 10[minutes], and repeat this process for all data to obtain a dataset of estimated solar wind velocities.
There are a few ways to quantify the quality of the obtained vHT. The most straightforward ones are the correlation coefficient and the inclination of the linear slope between Ey and −(vHT × B)y. For the data to be considered of good quality, we require that the correlation coefficient is larger than 0.9, and that the inclination of the linear slope is between 0.95 and 1.05. In Fig. 4, we show an example of a failed HT analysis where clearly Ey ≠ −(vHT × B)y. If the Ey data were good, the measured Ey (black) should have been in good agreement with 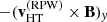 (red), and similar in shape (but potentially have a different magnitude due to Leff) to
(red), and similar in shape (but potentially have a different magnitude due to Leff) to 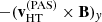 (blue). The cause of this behaviour has yet to be identified, but by using the above-mentioned quality measures we can discard intervals such as this one, for which the absolute value of the correlation coefficient is well below 0.9.
(blue). The cause of this behaviour has yet to be identified, but by using the above-mentioned quality measures we can discard intervals such as this one, for which the absolute value of the correlation coefficient is well below 0.9.
To estimate Leff, we assume that vx measured by PAS is exact, so that 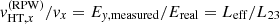 , where Ey, measured is calculated using the nominal L23 = 6.99 m, and Ereal is the physical electric field we would obtain by calculating Ey using Leff. In Fig. 5a, using the data fulfilling our criteria for good quality, we plot Leff against
, where Ey, measured is calculated using the nominal L23 = 6.99 m, and Ereal is the physical electric field we would obtain by calculating Ey using Leff. In Fig. 5a, using the data fulfilling our criteria for good quality, we plot Leff against 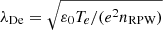 , where e is the elementary charge, and we assume a constant electron temperature Te = 10 eV, representative at 1 AU (Wilson et al. 2018), and nRPW is the plasma density measured by RPW (Khotyaintsev et al. 2021). We see that Leff can vary by several meters, which is in stark contrast to other missions such as Cluster, where Leff was found to be close to constant (Khotyaintsev et al. 2014). This difference is likely due to the different probe and spacecraft geometries, and importantly, the relative length of the Debye length with respect to the probe-to-spacecraft separation. In particular, Solar Orbiter’s E-field probes are cylindrical, close to the spacecraft, and in a plasma where the Debye length is comparable to the antenna length. In contrast, Cluster has spherical probes located around 40 meters away from the spacecraft and it samples the magnetosphere, where the Debye length is typically much larger than the probe-to-spacecraft separation. We also note that the effective antenna length of Parker Solar Probe, which has probes comparable to Solar Orbiter, has been found to be highly variable (Mozer et al. 2020a). While the observed range of Leff is quite large, the results are reasonable in that Leff < 14 m, which is the tip-to-tip distance of the probes as shown in Fig. 1. In addition, we see that for increasing Debye lengths Leff tends to decrease and appears to converge to a steady value. Similarly, for Debye lengths approaching zero, we expect Leff to reach a constant value, since the antennas will eventually be completely unaffected by the spacecraft potential, due to Debye shielding. However, there is not enough data at short λDe to give a conclusive picture of the asymptotic behaviour. We note that the data from the beginning of June (dark-blue dots) are clustered at a significantly shorter Leff compared to later data with similar Debye length. We believe this difference can be attributed to changes in the probe surface and photo-electron yield observed during the first perihelion.
, where e is the elementary charge, and we assume a constant electron temperature Te = 10 eV, representative at 1 AU (Wilson et al. 2018), and nRPW is the plasma density measured by RPW (Khotyaintsev et al. 2021). We see that Leff can vary by several meters, which is in stark contrast to other missions such as Cluster, where Leff was found to be close to constant (Khotyaintsev et al. 2014). This difference is likely due to the different probe and spacecraft geometries, and importantly, the relative length of the Debye length with respect to the probe-to-spacecraft separation. In particular, Solar Orbiter’s E-field probes are cylindrical, close to the spacecraft, and in a plasma where the Debye length is comparable to the antenna length. In contrast, Cluster has spherical probes located around 40 meters away from the spacecraft and it samples the magnetosphere, where the Debye length is typically much larger than the probe-to-spacecraft separation. We also note that the effective antenna length of Parker Solar Probe, which has probes comparable to Solar Orbiter, has been found to be highly variable (Mozer et al. 2020a). While the observed range of Leff is quite large, the results are reasonable in that Leff < 14 m, which is the tip-to-tip distance of the probes as shown in Fig. 1. In addition, we see that for increasing Debye lengths Leff tends to decrease and appears to converge to a steady value. Similarly, for Debye lengths approaching zero, we expect Leff to reach a constant value, since the antennas will eventually be completely unaffected by the spacecraft potential, due to Debye shielding. However, there is not enough data at short λDe to give a conclusive picture of the asymptotic behaviour. We note that the data from the beginning of June (dark-blue dots) are clustered at a significantly shorter Leff compared to later data with similar Debye length. We believe this difference can be attributed to changes in the probe surface and photo-electron yield observed during the first perihelion.
 |
Fig. 5. Modelling the effective antenna length. Panel a: effective antenna length as a function of λDe using densities from RPW from solar wind analysis. The time of each observation in units of days since 2020-06-01 are colour-coded. The solid red curve shows a fit to the data (see text for details), and the dashed curve shows the extrapolation. Panel b: relative error of solar wind speed before (white) and after (red) correcting for Leff. |
We construct a simple semi-empirical model for Leff of the form
where Lantenna = 6.5 m is the length of each individual RPW antenna, and optimisation gives Leff, min = 4.1 m Leff, max = 9.5 m, which are the asymptotic values for long and short λDe, respectively. This is of course just one of many possible equations to fit the data to, but we favor it due to its relative simplicity and the fact that Leff, min and Leff, max are within the limiting values expected by Fig. 1 (3.76 and 13.99 m respectively). We plot Eq. (4) in Fig. 5a in red. This model can serve as a first order approximation of Leff. We use the model to correct the velocities in our dataset which satisfy the criteria for good quality described above, as vcorrected = vHT, xL23/Leff. We plot the relative error between vHT, x and vx before and after correction as histograms in Fig. 5b. The correction leads to a clear improvement, with the corrected data being centred around 0, and 71% of the corrected data has a relative error within ±20%, and 90% of data within ±30%. For the original data, these numbers are 58% and 81%, respectively.
5. Discussion
Our results open the door to the possibility of using magnetic and electric field data to estimate the solar wind speed in the absence of plasma measurements. For the method to give reliable results for a set of data, variations in the magnetic field due to current sheets or MHD turbulence as well as an estimate of the effective antenna length are crucial.
The need for magnetic fluctuations of substantial amplitude limits the time resolution of the computed solar wind velocity. In addition, by applying the HT method on sequential intervals, we often find vHT to vary more than we expect the solar wind velocity to do. It is therefore often appropriate to average our velocities on the scale of a few hours. For these reasons we believe our method should primarily be used to estimate the solar wind speed and distinguish between fast and slow solar wind on a large scale. However, the method is very flexible, and could in principle be used to determine the phase speed of structures on a shorter time scale as well.
Our simple model of Leff in Eq. (4) enables us to estimate Leff using density measurements, which can be provided by the spacecraft potential and plasma frequency measured by RPW (Khotyaintsev et al. 2021). We note that the current model does not account for any variations in Te or other effects depending on heliocentric distance. Kretzschmar et al. (2021) used E and B measurements of electromagnetic whistler waves to compute Leff. Their results are in good agreement with our model. Their method could thus be important in the future to obtain local values of Leff even if no plasma data are available.
6. Conclusions
In summary, we investigate the quality of the Ey-component of Solar Orbiter’s low frequency ‘DC’ electric field by applying a deHoffmann-Teller analysis to solar wind current sheets, one of which (likely to be the heliospheric current sheet) shows several signatures of ongoing magnetic reconnection. We conclude that Ey is often accurate but can vary by a certain scaling factor which is likely related to the effective antenna length. By applying the deHoffmann-Teller analysis to estimate the solar wind velocity and comparing the results to measured plasma velocities, we are able to model how the effective antenna length depends on the Debye length. By applying this model, we can significantly improve our estimate of the solar wind speed, with 90% of measurements having relative errors below 30%.
Since we can use the RPW measurements of the spacecraft potential and plasma frequency to estimate the plasma density (Khotyaintsev et al. 2021), our results can be used in the future to measure the solar wind speed with sufficient accuracy to distinguish fast and slow solar wind, even in the absence of plasma measurements.
Acknowledgments
Solar Orbiter is a mission of international cooperation between ESA and NASA, operated by ESA. We thank the entire Solar Orbiter team and instrument PIs for data access and support. Solar Orbiter data are available at http://soar.esac.esa.int/soar/#home. This work is supported by the Swedish Research Council, grant 2016-05507, and the Swedish National Space Agency grant 20/136. G.C. is supported by Swedish National Space Agency contract SNSA 144/18, and Swedish Research Council contract VR 2018-03569. E.Y. is supported by the Swedish Civil Contingencies Agency, grant 2016-2102. The Solar Orbiter magnetometer was funded by the UK Space Agency (grant ST/T001062/1). T.H. is supported by STFC grant ST/S000364/1. The RPW instrument has been designed and funded by CNES, CNRS, the Paris Observatory, The Swedish National Space Agency, ESA-PRODEX and all the participating institutes. The Solar Orbiter Solar Wind Analyser (SWA) PAS were designed, created, and are operated under funding provided in numerous contracts from the UK Space Agency (UKSA), the UK Science and Technology Facilities Council (STFC), the Centre National d’Etudes Spatiales (CNES, France), the Centre National de la Recherche Scientifique (CNRS, France), and the Czech contribution to the ESA PRODEX programme. Data analysis was partly performed with the AMDA science analysis system provided by the Centre de Données de la Physique des Plasmas (CDPP) supported by CNRS, CNES, Observatoire de Paris and Université Paul Sabatier, Toulouse.
References
- Bale, S. D., Badman, S. T., Bonnell, J. W., et al. 2019, Nature, 576, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Borovsky, J. E. 2010, Phys. Rev. Lett., 105, 111102 [Google Scholar]
- Cully, C. M., Ergun, R. E., & Eriksson, A. I. 2007, J. Geophys. Res.: Space Phys., 112 [Google Scholar]
- De Hoffmann, F., & Teller, E. 1950, Phys. Rev., 80, 692 [NASA ADS] [CrossRef] [Google Scholar]
- Fox, N. J., & McComas, D. J. 2016, Space Sci. Rev., 204, 1 [Google Scholar]
- Froment, C., Krasnoselskikh, V., de Wit, T. D., et al. 2021, A&A, 650, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuselier, S. A., Klumpar, D. M., & Shelley, E. G. 1991, Geophys. Res. Lett., 18, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Gosling, J. T., Skoug, R. M., McComas, D. J., & Smith, C. W. 2005, J. Geophys. Res.: Space Phys., 110 [CrossRef] [Google Scholar]
- Horbury, T. S., Matteini, L., & Stansby, D. 2018, MNRAS, 478, 1980 [Google Scholar]
- Horbury, T. S., Woolley, T., Laker, R., et al. 2020a, ApJS, 246, 45 [Google Scholar]
- Horbury, T. S., OBrien, H., Carrasco Blazquez, I., et al. 2020b, A&A, 642, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hudson, P. 1970, Planet. Space Sci., 18, 1611 [Google Scholar]
- Johansson, F. L., Eriksson, A. I., Gilet, N., et al. 2020, A&A, 642, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khotyaintsev, Y. V., Lindqvist, P.-A., Cully, C. M., Eriksson, A. I., & André, M. 2014, Geosci. Instrum. Methods Data Syst., 3, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Khotyaintsev, Yu. V., Graham, D. B., Vaivads, A., et al. 2021, A&A, 656, A19 (SO Cruise Phase SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khrabrov, A. V., & Sonnerup, B. U. 1998, Analysis Methods for Multi-Spacecraft Data, 1, 221 [Google Scholar]
- Knetter, T., Neubauer, F. M., Horbury, T., & Balogh, A. 2004, J. Geophys. Res.: Space Phys., 109 [CrossRef] [Google Scholar]
- Kretzschmar, M., Chust, T., Krasnoselskikh, V., Graham, D. B., et al. 2021, A&A, 656, A24 (SO Cruise Phase SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lavraud, B., Gosling, J. T., Rouillard, A. P., et al. 2009, Sol. Phys., 256, 379 [Google Scholar]
- Lefebvre, B., Schwartz, S. J., Fazakerley, A. F., & Décréau, P. 2007, J. Geophys. Res.: Space Phys., 112 [Google Scholar]
- Maksimovic, M., Bale, S. D., Chust, T., et al. 2020, A&A, 642, A12 [EDP Sciences] [Google Scholar]
- Mozer, F. S., Agapitov, O. V., Bale, S. D., et al. 2020a, J. Geophys. Res.: Space Phys., 125, e2020JA027980 [CrossRef] [Google Scholar]
- Mozer, F. S., Agapitov, O. V., Bale, S. D., et al. 2020b, ApJS, 246, 68 [Google Scholar]
- Müller, D., St Cyr, O. C., Zouganelis, I., et al. 2020, A&A, 642, A1 [Google Scholar]
- Němeček, Z., Ďurovcová, T., Šafránková, J., et al. 2020a, ApJ, 889, 163 [CrossRef] [Google Scholar]
- Němeček, Z., Ďurovcová, T., Šafránková, J., et al. 2020b, ApJ, 897, L39 [Google Scholar]
- Owen, C. J., Bruno, R., Livi, S., et al. 2020, A&A, 642, A16 [EDP Sciences] [Google Scholar]
- Paschmann, G., & Sonnerup, B. U. 2008, ISSI Sci. Rep. Ser., 8, 65 [NASA ADS] [Google Scholar]
- Phan, T. D., Dunlop, M. W., Paschmann, G., et al. 2004, Ann. Geophys., 22, 2355 [NASA ADS] [CrossRef] [Google Scholar]
- Phan, T. D., Bale, S. D., Eastwood, J. P., et al. 2020, ApJS, 246, 34 [Google Scholar]
- Rouillard, A. P., Pinto, R. F., Vourlidas, A., et al. 2020, A&A, 642, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwartz, S. J., Thomsen, M. F., Bame, S. J., & Stansberry, J. 1988, J. Geophys. Res.: Space Phys., 93, 12923 [NASA ADS] [CrossRef] [Google Scholar]
- Sonnerup, B. U., & Cahill, L. J. Jr. 1967, J. Geophys. Res. (1896-1977), 72, 171 [CrossRef] [Google Scholar]
- Sonnerup, B. U. Ö., Papamastorakis, I., Paschmann, G., & Lühr, H. 1987, J. Geophys. Res.: Space Phys., 92, 12137 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, L. B., III, Stevens, M. L., Kasper, J. C., et al. 2018, ApJS, 236, 41 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Qualitative sketch of Solar Orbiter as seen from behind, showing the RPW antennas (i.e. the probes) and the nominal effective antenna lengths L23 and L123. |
| In the text | |
 |
Fig. 2. Current sheet crossings at different heliocentric distances (left column 0.75 AU, right column 0.54 AU). Panel a: magnetic field in SRF coordinates. Panel b: Ey (black) and −(vHT × B)y with vHT from PAS (blue) and RPW (red). Panel c: plasma density from PAS. Panels d–f: same format as a-c for a different current sheet where PAS data are unavailable. Plasma density was estimated from the spacecraft potential (Khotyaintsev et al. 2021). |
| In the text | |
 |
Fig. 3. Observations of a reconnecting current sheet. Panels a,b: magnetic field and ion velocity in SRF. Panel c: Ey and −(vHT × B)y with vHT from PAS (blue) and RPW (red). Panels d,e: ion density and temperature from PAS. Panel f: magnetic field in LMN coordinates at the reconnection jet. Panel g: observed (black, blue, red) and predicted (green, cyan, orange) plasma velocities in LMN coordinates. The green and magenta dashed horizontal bars highlight where BL and VL are correlated and anti-correlated, respectively. Panel h: simplified sketch of the reconnection event illustrating the expected correlation and anti-correlation between BL and VL. |
| In the text | |
 |
Fig. 4. Example of a failed HT analysis due to bad Ey data. Same format as Figs. 2a,b. |
| In the text | |
 |
Fig. 5. Modelling the effective antenna length. Panel a: effective antenna length as a function of λDe using densities from RPW from solar wind analysis. The time of each observation in units of days since 2020-06-01 are colour-coded. The solid red curve shows a fit to the data (see text for details), and the dashed curve shows the extrapolation. Panel b: relative error of solar wind speed before (white) and after (red) correcting for Leff. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.