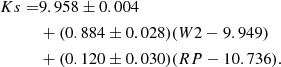| Issue |
A&A
Volume 654, October 2021
|
|
|---|---|---|
| Article Number | L4 | |
| Number of page(s) | 5 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202142189 | |
| Published online | 08 October 2021 | |
Letter to the Editor
Bright single-mode RR Lyrae stars: Matching Gaia EDR3 with pulsation and evolutionary models
Konkoly Observatory, Research Center for Astronomy and Earth Sciences, Eötvös Loránd Research Network, Konkoly Thege ut. 15-17, Budapest 1121, Hungary
e-mail: kovacs@konkoly.hu
Received:
9
September
2021
Accepted:
28
September
2021
We combine observed metallicity, optical, and infrared magnitudes with evolutionary and pulsation models to derive average luminosities for 156 single-mode RR Lyrae stars. These luminosities are compared with those obtained from the Gaia EDR3 parallaxes and are found to be in excellent agreement with the high accuracy subsample (62 stars, with relative parallax errors of less than 2%). With the temperature and metallicity scale used, no parallax shift seems to be necessary when α-enhanced evolutionary models are employed. Some 10% of the sample shows curious “distance keeping” between the evolutionary and pulsation models. The cause of this behavior is not clear at this moment but can be cured by an excessive increase in the reddening.
Key words: stars: fundamental parameters / stars: distances / stars: variables: RR Lyrae / stars: horizontal-branch / stars: oscillations
© ESO 2021
1. Introduction
In a former paper (Kovacs & Karamiqucham 2021, hereafter K21) we used pulsational and evolutionary models to close the relations governing the basic physical parameters of double-mode RR Lyrae (RRd) stars. The so-derived luminosities of 30 galactic RRd stars were compared with the direct estimates from the Gaia Early Data Release 3 (EDR3; Lindegren et al. 2021). The agreement between these independent sets was satisfactory, considering the overall low brightness of the available objects and the consequentially low accuracy of their parallaxes.
One of the issues in the case of RRd stars is the lack of chemical composition measurements. In K21 we determined the overall metal abundance, [M/H], as a by-product of the matching procedure of the pulsation and the evolutionary models. Opposite to the RRd stars, single-mode RR Lyrae (RRabc) stars have very abundant chemical analyses, many of which are based on high-dispersion spectra and multiple visits by different studies. The work presented in this Letter relies heavily on past and current spectral analyses that fixed [M/H], thereby letting us use RRabc stars when matching the pulsation and evolutionary models.
The ultimate goal of this work is to check the consistency of the nearly directly derived Gaia luminosities with the model values using basic observables only. Because of the significantly higher accuracy of the input data and the weaker dependence on the more intricate details of the pulsation models, we consider this study to be more stringent for the compatibility of the Gaia and theoretical luminosities than the one presented in K21 (though the two studies are consonant within the error limits).
2. Method
Our method of deriving the basic physical parameters (mass, luminosity, and temperature – M, L, and Teff, respectively) is similar to those used in our earlier papers (Kovacs & Walker 1999; Kovacs 2000; K21). A simple flowchart of the analysis is shown in Fig. 1. Some additional details are as follows.
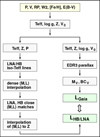 |
Fig. 1. Main steps of the star-by-star procedure to obtain estimates of the RR Lyrae luminosities. Boxes on the left exhibit the steps for computing the theoretical luminosity, LHB/LNA, whereas those on the right show the steps leading to the empirical luminosity, LGaia. We follow standard notation (i.e., RP for the Gaia red and W2 for the WISE W2 magnitudes). |
For any given star, we have the following input parameters: period (P), intensity-averaged Johnson V and K magnitudes, and iron abundance, [Fe/H] (see Sect. 3 for the derivation of these quantities). From these parameters, we calculated Teff (the weak gravity (log g) dependence can be handled via the pulsation equation as given in K21). We used the Teff zero point (ZP) of González Hernández & Bonifacio (2009) as detailed in K21.
Once Teff has been estimated, for its fixed value we can compute the corresponding (M, L) values for the evolutionary and pulsation models. To avoid the somewhat cumbersome procedure of directly interpolating the model values to the observed metallicity, we opted to compute the iso-Teff lines for three metallicity values that bracket the observed metallicity. The following metric is used to measure the distance between the pulsation and evolution models for any matching metallicity, Z,
where the superscripts HB and LNA denote, respectively, the horizontal branch evolution and linear non-adiabatic pulsation models. Once the minima of 𝒟(M, L, Z) for the three metallicities were found, we used quadratic interpolation in log(Z) to derive the closest matching (M, L) values for the HB and LNA models.
We used the recently updated HB models from the Bag of Stellar Tracks and Isochrones (BaSTI) project, as described by Hidalgo et al. (2018). The models have fixed metallicity values that span the full range of galactic field RR Lyrae stars (i.e., −3.0 < [Fe/H] < 0.1). All models are without convective overshooting. We used two sets of models: those with scaled solar composition and those with enhanced α elements (i.e., O, Ca, Mg, etc.). For the latter models, the degree of enhancement is [α/Fe] = +0.4, and all have a diffusion and mass loss of η = 0.3; none of the solar-scaled models we used have either of these properties. In searching for the best HB − LNA matches, we considered all evolutionary stages, not only those close to the zero-age HB.
The pulsation models are linear non-adiabatic models without α enhancement – the effect of enhancement on the period is around a few times 10−3 days, too small to have an influence on the derived stellar parameters. All models have a hydrogen abundance of 0.76, very close to those of the HB models, and Z values that match those of the HB metallicity grid (altogether, 18 discrete metallicities). For any fixed Z, there are 4095 models on the (M, L, Teff) grid given in Table 2 of K21.
Since we used observed [Fe/H], we needed to convert this to the corresponding overall metallicity, Z, for the enhanced models. We did this conversion by using the table available at the BaSTI home page. The +0.4 dex increase in the α elements results in a factor of two overall increase in Z throughout the full range of [Fe/H].
3. Data sets
Most of the RR Lyrae stars we deal with in this Letter are bright, (8 < V < 13), and therefore have abundant observational material. Nevertheless, various observational settings and details in the analyses may introduce differences into the derived parameters. Consequently, in gathering the essential data, we tried to rely on homogeneous data sets. For [Fe/H], such data sets are apparently not available; therefore, we rescaled the data from the same source and adjusted the ZP to some chosen level.
Our basic data set contains 67 stars with EDR3 parallax errors of less than 2%. For assessing error dependence, we also used a larger data set that contained an additional 94 stars with larger relative parallax errors, up to 10%. Both sets are based on the combination of the target lists of Dambis et al. (2013), Monson et al. (2017), and several recent spectroscopic studies, as detailed in Sect. 3.1. The basic set is complete with respect to the above source lists with the parallax constraint. The extended set is incomplete and mostly satisfies the constraints of “relatively low parallax error”, “easy data access”, and [Fe/H] availability.
3.1. Iron abundance
In recent years, several high-dispersion spectroscopic (HDS) works have been devoted to deep chemical analysis of RR Lyrae stars. Here, we used the combined lists of Magurno et al. (2018) and Crestani et al. (2021), which are based on the works of Clementini et al. (1995), Fernley & Barnes (1996), Lambert et al. (1996), For et al. (2011), Hansen et al. (2011), Liu et al. (2013), Nemec et al. (2013), Govea et al. (2014), Pancino et al. (2015), Chadid et al. (2017), Sneden et al. (2017), and Andrievsky et al. (2018). The individual [Fe/H] values in these compilations can differ by as much as ∼0.4 dex due to, for example, differences in the reduction methods or the turbulent velocity used. Therefore, simple averaging, in general, does not seem to be justified. Consequently, we followed the procedure below to put all [Fe/H] values on the same scale.
To establish a common base of comparison, we used the metallicities compiled by Jurcsik & Kovacs (1996, hereafter J96). This list is based on the low-dispersion spectroscopic (LDS) measurements carried out primarily by Blanco (1992), Layden (1994), and Suntzeff et al. (1994). We found that the J96 metallicities correlate well with the values of the individual HDS studies; however, there are systematic differences in the ZPs, and the HDS values are lower toward lower [Fe/H]. In particular, for Chadid et al. (2017, hereafter C17) we find that
with an rms scatter of 0.12 dex1. This excellent agreement (see Fig. 2) between the two independent sets of abundances led us to convert all the HDS and LDS data sets of Layden (1994) and Layden et al. (1996) to the scale of C17 and then average them out for each target. For the HDS sets, we employed only ZP shifts. Several data sets did not have overlap with C17. In those cases, we used the overlaps with those that had overlaps with the set in question and with C17 to convert the published [Fe/H] for that data set. Altogether, we ended up with 177 objects, most of which had HDS metallicities, often with independent measurements from multiple (up to six) sources per target.
 |
Fig. 2. Published iron abundances: Jurcsik & Kovacs (1996) vs. HDS [Fe/H] for the data sources given in the upper-left corner of each panel (C17, A18, and L13 from, respectively, Chadid et al. 2017; Andrievsky et al. 2018; Liu et al. 2013). In the lower-right panel we plot the transformed values for all [Fe/H] values, matching the list of Jurcsik & Kovacs (1996). The HDS identity line is shown by the red line. |
3.2. Reddening
One of the sensitive parameters that enter into the estimation of the luminosity is interstellar reddening. Because the commonly used all-sky maps give the total reddening in a certain direction, the exact amount of the extinction between the object and the observer remains hidden. In the case of excessive reddening, this might lead to a serious overestimation of the reddening. For instance, based on the map of Schlafly & Finkbeiner (2011), we got over 104 K for Teff in the cases of RZ Cep, AR Per, BN Vul, SW Cru, and BI Cen, with E(B − V) > 0.7 for all of them.
For fundamental-mode (RRab) stars, one can use some of the formulae available to estimate their intrinsic colors (Sturch 1966; Blanco 1992; Kovacs & Jurcsik 1997). We found this approach unsatisfactory, mainly because of the need of additional color and light curve information and the relative low accuracy of the derived reddenings. The ideal approach would be to use spectroscopic Teff and employ the related intrinsic color index to estimate E(B − V) from the observed colors. Although HDS [Fe/H] values are often derived from multiple-epoch data, the phase coverage is usually rather limited, and it is beyond the scope of this Letter to derive reliable average Teff values from those sparsely sampled sets.
We also tested the recent 3D map of Green et al. (2019) derived from 2MASS and Pan-STARRS1 colors, aided by the Gaia parallaxes. Except for the targets with large reddenings, we found no improvement in the correlation between the HB − LNA and Gaia luminosities. Consequently, we stayed with the map of Schlafly & Finkbeiner (2011), which is accessible at the NASA/IPAC Infrared Science Archive2.
3.3. Johnson V, K photometry
The intensity-averaged V magnitudes were gathered from three sources. In order of priority, they came from Monson et al. (2017) and Dambis et al. (2013) or, whenever the given target was not available in the first two sources3, from ASAS (Pojmanski 1997).
For the intensity-averaged 2MASS K (Ks) magnitudes, we were able to use the recently compiled set of Layden et al. (2019). However, despite being the biggest homogenized sample of direct Ks measurements available today, it misses some Gaia objects with high-precision parallaxes (e.g., CS Eri, EL Aps, etc.). In addition, several Ks values had been derived via template fitting due to the low number of data points available. As a result, we decided to use the unWISE catalog of Schlafly et al. (2019) and sought a transformation from the WISE and Gaia simple average magnitudes to approximate the Ks values of Layden et al. (2019). With the 145 stars used, we found that by leaving out eight 2.5σ outliers the following formula fits the Layden et al. data with an rms scatter of 0.028 mag:
Here, RP denotes the Gaia EDR3 red magnitude. The unWISE W2 magnitude is calculated from the published FW2 fluxes from W2 = 22.5 − 2.5log10(FW2). Unlike the transformation presented in K21, Eq. (3) is also applicable to RRab stars due to the correction introduced by the Gaia red magnitude.
4. Luminosities
To investigate the data quality dependence of the level of agreement between the Gaia and model (HB − LNA) luminosities, we divided the total sample into three groups. The division is based on the relative parallax errors (see Table 1). Set A, the basic data set without the five stars with overestimated reddenings (see Sect. 3.2), is the most populated and of the highest accuracy. Figure 3 shows the correlation between the Gaia and model luminosities following the division mentioned; it is completed by a similar plot for the RRd stars from K21.
 |
Fig. 3. Gaia EDR3 vs. evolutionary and pulsation model luminosities for RRabc stars (panels A, B, and C). The single-letter labels denote independent data sets in order of increasing parallax error (see Table 1). We used α-enhanced evolutionary models. For comparison, we also plotted the parallax-shifted RRd models of K21. The Gaia identity lines are shown by the red lines. |
Gaia and model luminosities.
We recall that (except for the RRd stars) no adjustments were made for any of the parameters used. The dependence on the data quality is clearly visible. However, the Gaia luminosities seem to be systematically overestimated for higher luminosities. The difference depends on the quality of the data, and it increases for poorer data. We suspect that most of the effect comes from the increasing errors of the Gaia luminosities that are, on average, twice as large as the HB − LNA errors. This difference leads to a flattening of the log L − log L relation, with the Gaia luminosities plotted on the abscissa (see, in particular, data set B in Fig. 3). Then, the finite sample size and nonuniform sampling lead to a further distortion of the ridge, causing apparent systematic deviations for certain groups of stars.
For set A, with accurate parallaxes, the α-enhanced models show a preference against the solar-scaled models with respect to the Gaia luminosities. For sets B and C, this preference diminishes, primarily because of the higher parallax errors. For set A, no parallax shift (with a sufficient significance) is needed. In K21 we found a shift of +0.02 mas to be appropriate for the RRd stars with low overall parallax accuracy. However, the significance of this shift is only a few sigma, even if we omit the stars with apparent outlier status. The α-enhanced models also perform better in terms of the HB − LNA solution (see Sect. 5), lending further support for the use of these models.
5. The distance keepers
Our model luminosities are based on the solutions provided by the intersections of the iso-TeffHB and LNA lines. Unfortunately, as in K21, this solution may not exist for some observed parameter sets, even if we consider the errors associated with the given objects. We refer to these “stubborn” objects as “distance keepers” (DKs).
As a part of the error estimate of the model luminosities, we calculated the solutions for each object by using the observed V, Ks, [Fe/H], E(B − V), and parallax values; we made the same calculations for 20 perturbed sets, which were obtained by adding perturbations computed from the observational errors and assuming a Gaussian distribution for these errors. We searched for the closest (M, L) pairs from the HB and LNA models and derived the metric given by Eq. (1) for each realization. These simulations not only yielded the errors of the theoretical luminosities but also informed us if the high 𝒟(M, L, Z) values could be explained by observational errors. Figure 4 shows the various scenarios found in our sample. The two upper panels show examples of when solutions were found for the observed parameters, albeit with slightly different statistical significance. The lower two panels are examples of DKs. Both DK stars, albeit at various degrees, “keep the distance” between the nearest HB and LNA points in the (M, L) space.
 |
Fig. 4. Examples of the solution types from the HB and LNA models. Filled circles show the closest (M, L) pairs of the two types of models from 20 random realizations with the errors of V, Ks, [Fe/H], E(B − V), and parallax, centered around their observed values. Gray and blue coloring is used for the HB and LNA models, respectively. The closest values at the observed parameters are shown by yellow squares for the HB models and by red triangles for the LNA models. The odds of being a DK are shown under the variable names. |
By (somewhat arbitrarily) fixing the maximum 𝒟(M, L, Z) to 0.01, we counted the number of realizations for each object that exceeded this limit. The relative number of these cases for the 20 realizations (PDK) for each object yielded an approximation of the probability that a given object is a DK. We found that for the α-enhanced models 122 have a less than 50% chance of being a DK (and ∼100 have a 0% chance). However, there are some 15 stars without an HB − LNA solution (i.e., practically none of the simulated values yield lower than 0.01 for 𝒟(M, L, Z)).
The analysis of PDK is also useful in the comparison of the overall performance of α-enhanced models with the solar-scaled models. We checked set A (see Table 1) and found that, on average, PDK is smaller for the enhanced models by 0.2 for those with PDK > 0.5 for the solar-scaled models. The number of severe DKs (i.e., those with PDK > 0.9) shrank from seven to three when switching from the solar-scaled to the enhanced models. Some stars with a low 𝒟(M, L, Z) of 0.01 − 0.02 completely recovered from the DK status when enhanced models were used (e.g., SW And, AV Peg, and U Pic). We consider these figures as additional pieces of evidence for the likely higher relevance of the α-enhanced models.
We conducted a few tests to investigate the possibility of major parameter errors causing the DK classification of the more stubborn stars. We introduced large and separate changes to the period (±0.01), V magnitude (±0.03), [Fe/H] (±0.4), and in E(B − V) (as much as needed to go below the cutoff for 𝒟(M, L, Z)). We found that even with the above large changes in P, V, and [Fe/H], the more stubborn DKs are left in the same status. However, varying E(B − V) may help. We examined the top 21 DKs with PDK > 0.8 and found solutions for each of them by increasing E(B − V). The amount of increase varied between 0.01 and 0.04, which is well above the nominal errors of their reddenings. Two variables, ST Oph and TV Lib, required an even more excessive increase, 0.07 and 0.10, respectively. In the case of TV Lib, together with its short period and light curve shape, this might indicate a different variable classification (e.g., evolved high-amplitude δ Scuti status).
Although the all-out increase in E(B − V) might indicate the need to shift the ZP of the Teff scale, we found that an increase of 0.0045 in log Teff4 is insufficient to cure the notorious DKs. The increased temperature leads to more luminous theoretical models and thereby a difference of −0.015 in log L (Gaia minus models). Although this can be remedied for the enhanced models of set A with an overall parallax decrease of 0.02 mas, the final gain of these ZP shifts does not seem to be justified in seeking the root cause of the DK phenomenon.
One may also wonder if a slight change in the helium abundance (Y) alters the DK status. Although a deeper discussion of the effect of helium is beyond the scope of this study, we note the following. Increasing Y increases the HB luminosity (e.g., Sweigart & Gross 1976; Marconi et al. 2018), and, with the pulsation periods remaining basically the same, the DK status is exacerbated. Decreasing Y by 0.02 − 0.05 may match the evolutionary and pulsational luminosities; however, the smaller helium abundance may raise other questions concerning its currently accepted primordial value5 and the errors involved (e.g., Cooke & Fumagalli 2018).
6. Conclusions
With the aid of evolutionary and linear stellar pulsation models, we computed the luminosities of bright RR Lyrae stars by using basic observed parameters, such as period, average magnitudes (Johnson V, GaiaRP, WISE W2), iron abundance, and interstellar reddening. These luminosities have been compared with those derived from the latest release of the Gaia parallaxes. By using α-enhanced evolutionary models, for the bright part of the sample (62 stars, with relative parallax errors of less than 2%), we found a high level of agreement between the two sets, including both fundamental and first overtone pulsators. The log L values span a range of ∼0.5 with an rms of 0.029. Solar-scaled models for the same sample yield a similarly good correlation between the two (essentially independent) luminosity sets. However, the solar-scaled models seem to be brighter by 0.012 ± 0.004 in log L. For the remaining 94 stars with larger parallax errors, we observe a tendency for increasing Gaia luminosities (relative to the theoretical luminosities) for both the α-enhanced and solar-scaled models.
Based on these results, it seems that stars with accurate parallaxes yield luminosities that match the theoretical values well, without the need for parallax shifts. This assertion likely holds whenever the “theoretical values” are derived by using:
-
α-enhanced evolutionary models, such as BaSTI (Hidalgo et al. 2018) or similar;
-
standard radial pulsation models (e.g., Kovacs 2000);
-
Teff ZPs, based on the infrared flux method (e.g., González Hernández & Bonifacio 2009).
Our result is essentially in agreement with the conclusion of Marconi et al. (2021), which is based on theoretical period–Wesenheit relations and largely relies on nonlinear pulsation models and Gaia DR2 parallaxes. In our previous paper on 30 RRd stars (Kovacs & Karamiqucham 2021), we landed on a slightly different conclusion by accepting an overall shift of +0.02 mas for the EDR3 parallaxes. Because of the considerably lower accuracy of the data used in that study, this shift may seem to be justified, considering the similar trend observed in the present sample. However, due to the different method used in our double-mode study (because of the lack of metallicity measurements for those faint stars) and the size of the sample (together with the large errors involved), we are hesitant to give a strong weight to the conclusion concerning the parallax shift from that study.
Finally, it is important to note that ∼10% of the stars show curious “distance keeping” between the evolutionary and pulsation models. In other words, in a strict sense they do not yield theoretical solutions, with zero distance in the (L, M) space, and even stretch the errors of the observed parameters. We found that an object-dependent increase in the reddening well above the formal error limits solves the problem. This, however, is not very easy to understand, since the reddening maps are believed to be based on the total dust density, so any increase in the extinction is expected to be related to the star rather than to the interstellar matter.
That is, we used the Teff scale compatible with the Castelli et al. (1997) models rather than the recent scale of González Hernández & Bonifacio (2009), which is based on the infrared flux method.
Acknowledgments
We thank the referee for the quick and helpful report (in particular, suggesting the investigation of the effect of helium abundance). This research has made use of the VizieR catalogue access tool, CDS, Strasbourg, France (DOI: 10.26093/cds/vizier). This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This publication makes use of data products from the Wide-field Infrared Survey Explorer, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, funded by the National Aeronautics and Space Administration. This research has made use of the NASA/IPAC Infrared Science Archive, which is funded by the National Aeronautics and Space Administration and operated by the California Institute of Technology. This research has made use of the International Variable Star Index (VSX) database, operated at AAVSO, Cambridge, Massachusetts, USA. Supports from the National Research, Development and Innovation Office (grants K 129249 and NN 129075) are acknowledged.
References
- Andrievsky, S., Wallerstein, G., Korotin, S., et al. 2018, PASP, 130, 024201 [NASA ADS] [CrossRef] [Google Scholar]
- Blanco, V. M. 1992, AJ, 104, 734 [NASA ADS] [CrossRef] [Google Scholar]
- Castelli, F., Gratton, R. G., & Kurucz, R. L. 1997, A&A, 318, 841 [NASA ADS] [Google Scholar]
- Chadid, M., Sneden, C., & Preston, G. W. 2017, ApJ, 835, 187 [Google Scholar]
- Clementini, G., Carretta, E., Gratton, R., et al. 1995, AJ, 110, 2319 [NASA ADS] [CrossRef] [Google Scholar]
- Cooke, R. J., & Fumagalli, M. 2018, Nat. Astron., 2, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Crestani, J., Fabrizio, M., Braga, V. F., et al. 2021, ApJ, 908, 20 [Google Scholar]
- Dambis, A. K., Berdnikov, L. N., Kniazev, A. Y., et al. 2013, MNRAS, 435, 3206 [Google Scholar]
- Fernley, J., & Barnes, T. G. 1996, A&A, 312, 957 [NASA ADS] [Google Scholar]
- For, B.-Q., Sneden, C., & Preston, G. W. 2011, ApJS, 197, 29 [Google Scholar]
- González Hernández, J. I., & Bonifacio, P. J. I. 2009, A&A, 497, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Govea, J., Gomez, T., & Preston, G. W. 2014, ApJ, 782, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Green, G. M., Schlafly, E., Zucker, C., et al. 2019, ApJ, 887, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, C. J., Nordström, B., Bonifacio, P., et al. 2011, A&A, 527, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hidalgo, S. L., Pietrinferni, A., Cassisi, S., et al. 2018, ApJ, 856, 125 [Google Scholar]
- Jurcsik, J., & Kovacs, G. 1996, A&A, 312, 111 [Google Scholar]
- Kovacs, G. 2000, A&A, 363, L1 [NASA ADS] [Google Scholar]
- Kovacs, G., & Jurcsik, J. 1997, A&A, 322, 218 [NASA ADS] [Google Scholar]
- Kovacs, G., & Karamiqucham, B. 2021, A&A, 653, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kovacs, G., & Walker, A. R. 1999, ApJ, 512, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Lambert, D. L., Heath, J. E., Lemke, M., et al. 1996, ApJS, 103, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Layden, A. C. 1994, AJ, 108, 1016 [Google Scholar]
- Layden, A. C., Hanson, R. B., Hawley, S. L., et al. 1996, AJ, 112, 2110 [NASA ADS] [CrossRef] [Google Scholar]
- Layden, A. C., Tiede, G. P., Chaboyer, B., et al. 2019, AJ, 158, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021, A&A, 649, A2 [EDP Sciences] [Google Scholar]
- Liu, S., Zhao, G., Chen, Y.-Q., et al. 2013, Res. Astron. Astrophys., 13, 1307 [CrossRef] [Google Scholar]
- Magurno, D., Sneden, C., Braga, V. F., et al. 2018, ApJ, 864, 57 [CrossRef] [Google Scholar]
- Marconi, M., Bono, G., Pietrinferni, A., et al. 2018, ApJ, 864, L13 [Google Scholar]
- Marconi, M., Molinaro, R., Ripepi, V., et al. 2021, MNRAS, 500, 5009 [Google Scholar]
- Monson, A. J., Beaton, R. L., Scowcroft, V., et al. 2017, AJ, 153, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Nemec, J. M., Cohen, J. G., Ripepi, V., et al. 2013, ApJ, 773, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Pancino, E., Britavskiy, N., Romano, D., et al. 2015, MNRAS, 447, 2404 [Google Scholar]
- Pojmanski, G. 1997, Acta Astron., 47, 467 [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., Meisner, A. M., & Green, G. M. 2019, ApJS, 240, 30 [Google Scholar]
- Sneden, C., Preston, G. W., Chadid, M., et al. 2017, ApJ, 848, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Sturch, C. 1966, ApJ, 143, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Suntzeff, N. B., Kraft, R. P., & Kinman, T. D. 1994, ApJS, 93, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Sweigart, A. V., & Gross, P. G. 1976, ApJS, 32, 367 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Main steps of the star-by-star procedure to obtain estimates of the RR Lyrae luminosities. Boxes on the left exhibit the steps for computing the theoretical luminosity, LHB/LNA, whereas those on the right show the steps leading to the empirical luminosity, LGaia. We follow standard notation (i.e., RP for the Gaia red and W2 for the WISE W2 magnitudes). |
| In the text | |
 |
Fig. 2. Published iron abundances: Jurcsik & Kovacs (1996) vs. HDS [Fe/H] for the data sources given in the upper-left corner of each panel (C17, A18, and L13 from, respectively, Chadid et al. 2017; Andrievsky et al. 2018; Liu et al. 2013). In the lower-right panel we plot the transformed values for all [Fe/H] values, matching the list of Jurcsik & Kovacs (1996). The HDS identity line is shown by the red line. |
| In the text | |
 |
Fig. 3. Gaia EDR3 vs. evolutionary and pulsation model luminosities for RRabc stars (panels A, B, and C). The single-letter labels denote independent data sets in order of increasing parallax error (see Table 1). We used α-enhanced evolutionary models. For comparison, we also plotted the parallax-shifted RRd models of K21. The Gaia identity lines are shown by the red lines. |
| In the text | |
 |
Fig. 4. Examples of the solution types from the HB and LNA models. Filled circles show the closest (M, L) pairs of the two types of models from 20 random realizations with the errors of V, Ks, [Fe/H], E(B − V), and parallax, centered around their observed values. Gray and blue coloring is used for the HB and LNA models, respectively. The closest values at the observed parameters are shown by yellow squares for the HB models and by red triangles for the LNA models. The odds of being a DK are shown under the variable names. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



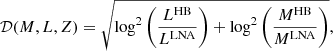
![$$ \begin{aligned} \mathrm{[Fe/H]}_{\rm C17} = 1.10\mathrm{[Fe/H]}_{\rm J96} - 0.22, \end{aligned} $$](/articles/aa/full_html/2021/10/aa42189-21/aa42189-21-eq2.gif)