EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 654 (October 2021) A&A, 654 (2021) A103 Full HTML
Free Access
Issue
A&A
Volume 654, October 2021
Article Number A103
Number of page(s) 10
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202141518
Published online 20 October 2021

© ESO 2021

1. Introduction

It is generally accepted that Type Ia supernovae (SNe Ia) result from thermonuclear explosions of white dwarfs (WDs) in interacting binary systems. SNe Ia have been used as accurate cosmic distance indicators, which led to the discovery of the accelerating expansion of the Universe (Riess et al. 1998; Schmidt et al. 1998; Perlmutter et al. 1999). The specific progenitor systems of SNe Ia and their explosion mechanism, however, remain an unsolved problem. Different progenitor scenarios have been proposed for explaining SNe Ia (Hillebrandt et al. 2013; Maoz et al. 2014).

The sub-Chandrasekhar-mass double-detonation (DDet) scenario is a promising model for explaining normal SNe Ia (e.g. Shen et al. 2018a; Townsley et al. 2019; Gronow et al. 2020, 2021). In this scenario, a WD accretes material from its He-rich companion star, which could be a He-burning star or a He WD, to accumulate a He layer on its surface. If the He shell reaches a critical mass, ≃0.02 − 0.2 M⊙ (Woosley & Kasen 2011; Neunteufel et al. 2016; Polin et al. 2019), it triggers an initial detonation that ignites a second detonation of the core material. The entire sub-Chandrasekhar-mass WD then undergoes a thermonuclear explosion (e.g. Taam 1980; Woosley et al. 1986; Livne & Arnett 1995; Fink et al. 2007, 2010; Sim et al. 2010; Moll & Woosley 2013; Gronow et al. 2020, 2021; Boos et al. 2021). The DDet scenario has recently gained attention thanks to its features that explain current observations for SNe Ia. For instance, the lack of H emission in SN Ia spectra (Leonard 2007) and the non-detection of a pre-explosion companion in Hubble Space Telescope imaging (Li et al. 2011) are inherent to DDet models. Early UV flash signatures of an ejecta interaction with a companion (Kasen 2010) should be very small in the DDet scenario because binary systems are generally very close at the moment of supernova (SN) explosions. In addition, population synthesis calculations show that the DDet scenario can explain a large fraction of SNe Ia as well as their delay time distribution (DTD; Ruiter et al. 2011, 2014).

Observations of several binary systems composed of a WD and a He-rich companion star (e.g. the KPD 1930+2752, V445 Pup, HD 49798, and CD-30° 11223 systems; Maxted et al. 2000; Geier et al. 2007, 2013; Kato & Hachisu 2003; Kudritzki & Simon 1978; Vennes et al. 2012) seem to support this scenario. For instance, CD-30° 11223 is a WD plus B-type subdwarf (sdB) star system with a WD mass of MWD = 0.76 M⊙, a companion mass of MsdB = 0.51 M⊙, and a short orbital period of Porb ≃ 1.2 h. Vennes et al. (2012) and Geier et al. (2013) suggest that CD-30° 11223 will likely explode as a SN Ia via the DDet scenario during its future evolution.

In the DDet scenario, the companion star is expected to be significantly shocked and heated as parts of its outer layers are removed during the ejecta-companion interaction. The binary system is disrupted, but the companion star survives the interaction with the SN blast wave and is ejected at a high speed, which is dominated by its pre-explosion orbital velocity (e.g. Wheeler et al. 1975; Fryxell & Arnett 1981; Livne et al. 1992; Marietta et al. 2000; Pakmor et al. 2008; Liu et al. 2012, 2013a,b,c; Pan et al. 2012a; Bauer et al. 2019; Zeng et al. 2020). Binary progenitor systems in the DDet scenario are relatively close when SN Ia explosions occur. In this scenario, the companion stars are expected to have a high orbital velocity of up to ≃900 km s−1 at the moment of explosion (e.g. Geier et al. 2015; Neunteufel 2020). The surviving companion stars from this scenario are therefore good candidates for hypervelocity stars (HVSs), such as US 708 (e.g. Geier et al. 2013, 2015; Neunteufel 2020; Neunteufel et al. 2021; Shen et al. 2018b). An unambiguous identification of a donor remnant of such an event would therefore support the DDet scenario of SNe Ia. Such an identification requires knowledge of the observable signatures of surviving companion stars of SNe Ia in the DDet scenario.

Hypervelocity stars are generally defined as stars that move sufficiently fast to escape the gravitational potential of our Galaxy, that is to say, they typically have velocities larger than ∼400 km s−1 in the Galactic rest frame (for a review, see Brown 2015). Hypervelocity stars are believed to be ejected by three-body interactions with the supermassive black hole at the Galactic centre (e.g. Hills 1988; Yu & Tremaine 2003; Brown et al. 2005), by exchange encounters in other dense stellar environments (e.g. Aarseth 1974) between hard binaries and massive stars (e.g. Leonard 1991; Gvaramadze et al. 2009), or by disruptions of close binaries via SN explosions (e.g. Blaauw 1961; Tauris & Takens 1998; Zubovas et al. 2013; Tauris 2015; Geier et al. 2015; Neunteufel et al. 2021).

The HVS US 708 has been classified as an O-type subdwarf and sdB star. Based on a spectroscopic and kinematic analysis, Geier et al. (2015) have reported that US 708 travels with a velocity of about 1200 km s−1, suggesting that it is one of the fastest unbound stars in our Galaxy that was ejected from the Galactic disc 14.0 ± 3.1 Myr ago. Considering the possibilities of different acceleration mechanisms of HVSs, Geier et al. (2015) further concluded that it is very unlikely that US 708 originated from the Galactic centre, and that it is instead likely the ejected donor remnant of a DDet SN Ia.

Geier et al. (2015), however, did not compare the long-term evolution and appearance of surviving companion stars of DDet SNe Ia with the observations of US 708. It is therefore still an open question whether the observations of this star match the expected properties of a surviving SN Ia donor star in the DDet scenario. The present paper predicts observable signatures of the surviving companion stars of sub-Chandrasekhar-mass DDet SNe Ia by combining the outcomes of 3D hydrodynamic simulations of ejecta-companion interactions with detailed 1D calculations of the long-term evolution of the donor remnant. The results of our models are then compared to the observations of US 708 to assess its proposed origin from a SN Ia ejection.

The methods, the companion models, and the SN Ia explosion model used in this study are described in Sect. 2. In Sect. 3 we present the results of 3D simulations of ejecta-donor interactions and 1D post-explosion evolution calculations of the surviving companion stars. A comparison with the observation of US 708 and some discussion of our models is given in Sect. 4. The main conclusions are summarised in Sect. 5.

2. Numerical methods and models

We constructed the initial He-star companion models at the moment of a SN Ia explosion based on a SN explosion model within the sub-Chandrasekhar-mass DDet scenario of Gronow et al. (2020). Here we describe in detail the initial conditions and setup for our 3D hydrodynamic impact simulation, the conversion between the 3D smooth particle hydrodynamics (SPH) models and the 1D model, and the 1D post-impact evolution of a surviving companion star.

2.1. Code for the ejecta-donor interaction

To obtain the detailed post-explosion properties of surviving companion stars of SNe Ia, we performed a 3D hydrodynamic simulation of a SN ejecta-companion interaction with the SPH code STELLAR GADGET (Springel 2005; Pakmor et al. 2012). The initial conditions and basic setup for the impact simulation of this work are similar to those in our previous impact studies (e.g. Liu et al. 2012, 2013a,b,c). The companion star at the moment of SN explosion and the SN ejecta model are the two fundamental inputs of our hydrodynamic impact simulation, and we discuss our setups for these two models below.

2.1.1. The He-star donor model

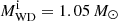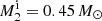Geier et al. (2015) proposed a DDet SN explosion resulting from a binary progenitor system composed of a WD with and a He-burning companion star with an initial orbital period of Pi ≃ 0.0182 days as a possible origin of US 708. In their model, the first detonation is assumed to be triggered when the mass of the accreted He shell reaches MHe = 0.15 M⊙. The surviving donor He star of 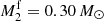is ejected from the system. In this model, the He donor has an orbital velocity of Vorb ≃ 920 km s−1 at the moment of the SN Ia explosion. This can explain the observed high velocity of US 708 (1200 km s−1; Geier et al. 2015). Woosley & Kasen (2011), Bildsten et al. (2007), Shen & Bildsten (2009), Shen & Moore (2014), and Shen et al. (2018a), for example, suggest that a massive WD could trigger a He detonation by accreting a rather thin He shell from its companion star. For this scenario, recent 2D-3D hydrodynamic models of SN Ia explosions have also shown that a core detonation is still possible despite the weaker He shell detonation (Fink et al. 2010; Sim et al. 2010; Townsley et al. 2019; Gronow et al. 2020, 2021). This seems to indicate that a massive initial WD of ∼1.05 M⊙ is likely to accumulate a thin He shell rather than the 0.15 M⊙ required otherwise to successfully trigger a thermonuclear explosion by undergoing a DDet.

We adopted the method of Geier et al. (2015) to construct the He-star donor model at the moment of explosion by performing binary evolution calculations using the 1D stellar evolution code MESA (Paxton et al. 2011, 2015, 2018)1. As detailed in Sect. 2.1.2, our goal is to directly connect to the DDet Model M2a2 of Gronow et al. (2020). We therefore diverged from the system parameters given by Geier et al. (2015) and started our consistent binary evolution calculation with a progenitor system consisting of an initial WD (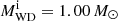) and a He-burning star (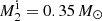) with an orbital period of Pi ≃ 0.0135 days (Table 1). Figure 1 shows the key parameters of the detailed binary evolution calculation of the He-star donor model used for our reference impact simulation. The initial He companion model is set up with a He abundance of Y = 0.98 and a metallicity of Z = 0.02, and the WD is treated as a point mass in our binary evolution calculation. This binary system starts mass transfer when the He donor star fills its Roche lobe. The orbital angular momentum loss due to gravitational wave radiation is included by following the standard formula given by Landau & Lifshitz (1971). According to previous works, at a mass transfer rate of Ṁtr < 4.0 × 10−8 M⊙ yr−1, the He shell builds up steadily, avoiding He burning (e.g. Woosley et al. 1986; Ruiter et al. 2014). Matching to the hydrodynamic explosion Model M2a of Gronow et al. (2020, see their Table 1), the DDet is assumed to trigger when the He-shell mass reaches a critical value of MHe = 0.05 M⊙ (see also Fink et al. 2010).

thumbnail Fig. 1.

Left panel: evolutionary tracks of the luminosity of the He-star companion (dash-dotted cyan line) and the orbital period of the binary system (solid orange line) during the whole mass-transfer process until the SN Ia explosion. Right panel: time evolution of the mass transfer rate (Ṁtr; dash-dotted cyan line) and the mass growth of a helium shell onto the WD (MHe; solid orange line). The vertical dotted lines give the moment of the SN explosion. The initial and final binary parameters (WD mass MWD, companion mass M2, and orbital period P) in our detailed binary calculations are shown in the plot and indicated with superscript letters ‘i’ and ‘f’, respectively.

Table 1.

Three He donor models studied in this work.

For our binary evolution simulation, we obtain a He donor model with a mass of 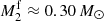(Fig. 1) at the moment of the SN Ia explosion. This model is used as input to our 3D SN explosion impact simulation. This is our reference model (Table 1). The properties of this companion model – its density profile, the orbital velocity of Vorb ≃ 901 km s−1, and the effective temperature of log10 Teff ≃ 4.1 – are quite similar to those suggested by Geier et al. (2015) for US 708.

2.1.2. The SN explosion model

Our binary progenitor models were constructed to match the hydrodynamic simulation Model M2a of Gronow et al. (2020) for a DDet sub-Chandrasekhar-mass SN Ia explosion. We directly adopted their Model M2a to represent a SN Ia explosion here. This model has masses of the exploding star, of the C/O core, and of the He shell of Mtot ≈ 1.05 M⊙, Mcore ≈ 1.00 M⊙, and Mshell ≈ 0.05 M⊙, respectively (Gronow et al. 2020, see their Table 1). The total explosion energy is about 1.25 × 1051 erg, and the average velocity of the ejecta is of the order of 104 km s−1. Gronow et al. (2020) and Fink et al. (2010) provide a detailed description of this explosion model. In addition, Gronow et al. (2020) present the results of time-dependent multi-wavelength radiative transfer calculations for this model.

2.1.3. Initial setup

As described in Pakmor et al. (2012), we used the HEALPix method (Górski et al. 2005) to map the 1D profiles of density and internal energy of our He-star donor model to a particle distribution suitable for the 3D SPH code (see also Liu et al. 2012, 2013a,b,c). Before we started the actual impact simulation, the SPH model of each donor star was relaxed for ten dynamical timescales, tdyn = 1/2 (Gρ)−1/2, to reduce numerical noise introduced by the mapping (e.g. Pakmor et al. 2012; Liu et al. 2012).

For our reference simulation, about 1.8 × 107 SPH particles were used in total to represent both the He companion star and the explosion model. All SPH particles were assigned the same mass of about 7.4 × 10−8 M⊙. Once the relaxation of the He-star donor was finished, the DDet sub-Chandrasekhar explosion model described above was placed at the distance to the donor star given by the binary separation at the moment of SN Ia initiation in our 1D binary evolution calculation. Based on the 1D-averaged radial profiles of Model M2a of Gronow et al. (2020), SPH particles were placed randomly in shells to reproduce the density profile. The chemical composition and radial velocity of each particle were set to the values of the initial 1D explosion model at a given radius. The ejecta-companion interaction was then simulated for several thousand seconds until it ceased and the total stripped mass and kick velocity received by the donor due to the interaction had saturated.

For our second set of impact simulations, which also take into account the orbital and stellar spin velocities of the companion star, we assumed that the companion star co-rotates with its orbit due to a strong tidal interaction during the pre-explosion mass-transfer phase. This leads to a locking of the spin period of the companion star with its orbital period. The companion star was assumed to rotate as a solid body. To isolate the impact of the binary model parameters, we used the same explosion model as described in Sect. 2.1.2 in all the simulations presented in this work.

2.2. Mapping from 3D to 1D

Predicting the observable properties of a surviving companion star in the SN remnant phase requires its post-impact evolution to be modelled over a few hundred years after the SN Ia explosion. Since the time step in our 3D SPH impact simulations is of the order of the dynamical timescale – hundreds of seconds – this is not possible in the framework of our 3D hydrodynamic simulation. To limit the computational cost of the simulation to a reasonable wall-clock time, the outcome of the 3D impact simulations was mapped into the 1D stellar evolution code MESA using the method of Liu & Zeng (2021, see their Sect. 2) to trace the subsequent long-term post-explosion evolution (see also Pan et al. 2013, 2014; Bauer et al. 2019). The three main steps of this method are briefly summarised as follows: First, the 3D post-impact companion models from our hydrodynamic impact simulations (Fig. 2f) are converted into 100−200 spherical shells; the physical properties of the SPH particles, such as the internal energy and composition, are averaged to give a value for that shell. Second, the 1D-averaged radial profiles of internal energy, chemical composition, and density are used as inputs for the MESA code to compute suitable starting models for the subsequent post-explosion calculations by directly adopting the relaxation routines provided in MESA (Paxton et al. 2018, see their Appendix B). Third, we follow the long-term evolution of a surviving companion model to predict its observable properties until it enters the WD cooling phase.

thumbnail Fig. 2.

Density distributions of all material (panels a–c) and of the bound companion material (panels d–f). The panels shows a slice in the orbital plane for three different times each. Colours indicate density as per the colour bar (right). The 3D hydrodynamical simulation of the SN ejecta-companion interaction shown here does not include binary orbital motion or stellar spin. All panels use the same length scales.

We used the MESA code in its hydrostatic mode and therefore artificially relaxed our hydrodynamic post-impact model to hydrostatic equilibrium. To test the effect of this approximation, we additionally performed a simulation of the post-impact evolution for our reference model with the 1D hydrodynamic stellar evolution code KEPLER (Weaver et al. 1978; Rauscher et al. 2002; Woosley et al. 2002; Heger & Woosley 2010). Similarly, we used the angle-averaged 1D radial profiles obtained from 3D post-impact companion models as inputs of the subsequent KEPLER calculations, but without performing any relaxation process. In addition, we included the radial velocity of each spherical shell at the end of our impact simulation in the KEPLER models. This way, the hydrodynamics was also followed from the beginning of the mapping in the KEPLER calculations. We find no significant difference between MESA and KEPLER results for our reference calculation for Model A (Sect. 3.2). For consistent analysis and discussion, all the other He-star donor models in Sect. 4.2 were only simulated using the MESA code.

3. Numerical results

In this section we present the results of the 3D hydrodynamic simulations of ejecta-companion interactions. The 1D post-explosion evolution calculations of the surviving companion stars with the MESA and KEPLER codes are also given.

3.1. Ejecta-donor interaction

Figure 2 shows the density distribution of all material (top row) and bound donor material (bottom row) as a function of time in our 3D impact simulation for our reference He-star donor model (Model A). The figure is oriented such that the SN explodes to the right of the donor star. After the explosion, the SN ejecta expand freely for a while (a few tens of seconds) and hit the surface of donor star, stripping some He-rich material from its surface and forming a bow shock. Subsequently, the bow shock propagates through the donor star (Fig. 2b), removing more He-rich material from its far side. The donor star is significantly shocked and heated during the interaction with the SN blast wave. It inflates dramatically but survives the interaction and starts to relax (Fig. 2f). The stripped He-rich donor material is largely embedded in the low-velocity SN debris behind the star. Quantitative details of the models and of the simulation results are summarised in Table 1.

At the end of our 3D simulation, we find that the total amount of stripped He material from the donor surface during the ejecta-donor interaction is about ΔM ≈ 0.02 M⊙ (i.e. about 6% of the total donor mass). The donor star receives a kick velocity of υkick ≈ 200 km s−1, which moves its remnant to the left by about 1010 cm at 500 s after the explosion (Fig. 2f). The impact simulations for our reference donor model were run with or without including binary orbital motion and stellar spin to test their effect on the results. Since the orbital and spin velocities of the donor star are much lower than the typical expansion velocity of SN ejecta of our explosion model (∼104 km s−1 according to Gronow et al. 2020), only small differences (less than 5%) in the total amount of stripped donor mass and in the kick velocity are observed when the binary orbital motion and stellar spin are included. This is consistent with previous works (e.g. Liu et al. 2013a,b; Pan et al. 2012a). The density distribution of the ejected donor remnant from our impact simulations that include binary orbital motion and stellar spin is shown in Fig. 3. More asymmetric features in the morphology are observed for this case compared with that shown in Fig. 2f.

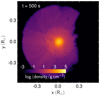thumbnail Fig. 3.

Similar to Fig. 2f, but for the 3D simulation that includes binary orbital motion and stellar spin.

3.2. 1D post-impact evolution

As described in Sect. 2.2 (see also Liu & Zeng 2021), the final outcomes of our 3D impact simulations (Fig. 3) were used to construct the initial inputs for the MESA and KEPLER codes to model the long-term post-impact evolution of the surviving donor stars. Figure 4 shows a comparison between the 1D-averaged internal energy and density profiles of our reference model (i.e. Model A in Table 1) at the end of impact simulation and of the corresponding post-relaxed profiles in MESA.

thumbnail Fig. 4.

Post-impact 1D angle-averaged profiles (thin lines) of specific internal energy, ℰint (top panel) and density, ρ (bottom panel) as functions of fractional mass coordinates at the end of the SPH impact simulation for our reference model, Model A. For a comparison, the relaxed starting models in MESA are shown as thick lines. The results for the impact simulation with or without binary orbital motion and stellar spin taken into account are shown as dash-dotted lines and solid lines, respectively.

Figure 5 shows the post-impact evolution of photospheric luminosity, L, the effective temperature, Teff, the radius, R, and the surface gravity, g, as functions of time for our reference model (Model A in Table 1). The donor star is significantly shocked by the SN impact during the ejecta-donor interaction. This leads to an energy deposition of 1.15 × 1049 erg. This value was calculated by tracing the increase in binding energy of the star after the SN Ia impact (see also Pan et al. 2012b; Liu & Zeng 2021). We find that ∼50% of the incident energy of the SN Ia ejecta, about 2.30 × 1049 erg3, is injected into the donor star during the ejecta-donor interaction. The donor star continues to expand dramatically for about 1000 years before it starts to contract (Fig. 5). This expansion timescale is determined by the local radiative diffusion timescale of the donor envelope at the shell where it contains the injected energy from the SN Ia ejecta (see their Eq. (49) Henyey & L’Ecuyer 1969). This expansion makes the post-impact donor star much more luminous (≳80 L⊙; Fig. 5) than it was pre-explosion. A few thousand years after the explosion, the radius and luminosity of the ejected donor star decrease again as it starts to contract, releasing gravitational energy while the deposited energy radiates away (Fig. 5; Kelvin-Helmholtz contraction). Figure 6 shows the post-impact evolution tracks of the ejected donor in the Hertzsprung-Russell (H-R) diagram and in the effective temperature-surface gravity (Teff − g) diagram.

thumbnail Fig. 5.

Post-impact evolution of the photosphere luminosity, L, effective temperature, Teff, radius, R, and surface gravity, g, of a surviving He-star companion as functions of time. The solid line and dash-dotted line respectively correspond to the results from 1D calculations using the KEPLER code and the MESA code. For comparison, the MESA results based on the impact simulations that do and do not include the binary orbital motion and stellar spin are given as thick solid lines and thin solid lines, respectively.

We find that including the binary orbital motion and stellar spin in 3D impact simulations has no significant effect on the post-impact evolution of the surviving donor stars (Figs. 5 and 6). For a comparison, the post-impact evolution of the ejected donor was calculated with the KEPLER code. As shown in Figs. 5 and 6, the KEPLER model has a lager radius and is thus more luminous than the MESA model. The difference between the KEPLER and the MESA results is attributed to the circumstance that the output models at the end of 3D impact simulations are still somewhat out of equilibrium. Nonetheless, the evolution trends in two approaches are very similar, and no significant difference is observed between these two models (Figs. 5 and 6). This indicates that, at the time of the mapping from 3D to 1D, the SPH models are already very close to hydrostatic equilibrium (Fig. 4).

thumbnail Fig. 6.

Post-impact evolutionary tracks of a surviving He-star companion model in the H-R diagram (left panel) and surface gravity vs. temperature diagram (right panel). The solid lines and dash-dotted lines respectively correspond to the results of KEPLER and MESA calculations. The filled circle, square, triangle, and star markers on the tracks represent post-impact evolutionary phases of 1 yr, 1 kyr, 100 kyr, and 10 Myr after the SN impact, respectively. The thin lines and thick lines have the same meaning as those in Fig. 5.

4. Discussion

4.1. Comparison with US 708

At the time when the SN explodes in our binary evolution calculation of Model A, the donor star has an orbital velocity of Vorb = 901 km s−1 and a surface rotational velocity of Vrot = 320 km s−1 (Table 1). We directly obtained from our impact simulation that this star receives a kick velocity of about Vkick ≈ 210 km s−1 due to the ejecta impact (Sect. 3.1). This kick velocity was simply assumed to be 200 km s−1 by Geier et al. (2015). Therefore, we expect the donor remnant to be ejected with a velocity of 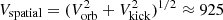km s−1. This velocity is dominated by the donor’s pre-explosion orbital velocity. This spatial velocity provides a good explanation for the observed high velocity of US 708, ∼1200 km s−1 (Table 1 of Geier et al. 2015).

Based on the effective temperature of Teff = 47 200 ± 400 K, and the surface gravity of log10 (g/cm s−2) = 5.69 ± 0.09 given by Geier et al. (2015), the luminosity of US 708 can simply be calculated using 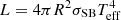under the assumption that the mass of US 708 is M = 0.3 M⊙ (see also Bauer et al. 2019). The constant σSB is the Stefan-Boltzmann constant, as usual. Figure 6 shows a comparison between the properties of the ejected He donor remnant, its luminosity, effective temperature, and surface gravity, as predicted by our simulations, and those observed for US 708. During its entire post-impact evolution, our Model A stays too cool to pass through the positions of US 708 in the H-R diagram and in the Teff − g diagram. This suggests that a low-mass donor remnant (≲0.3 M⊙) from a DDet SN Ia cannot easily reproduce the observational properties of US 708. In the next section we explore whether a more massive ejected donor remnant from a DDet SN Ia could match the observations of US 708, including its luminosity and effective temperature.

Geier et al. (2015) used the long-term evolution of a He star without any ejecta-donor interaction to fit the observational properties of US 708. As shown in Figs. 5 and 6, the SN impact and heating during the ejecta-donor interaction play an important role in the post-impact evolution of a surviving companion star from a DDet SN Ia before it re-establishes thermal equilibrium over the Kelvin-Helmholtz timescale. All energy deposited into the donor star by the SN blast wave has radiated away by about 106 yr after the explosion. The star relaxes back into thermal equilibrium and continues to evolve by following an evolutionary track very close to that of a He star with the same mass that has not been impacted and heated by an ejecta-donor interaction. As mentioned above, based on its kinematics, US 708 was ejected from the Galactic disc about 14 Myr ago (Geier et al. 2015). At these late epochs after the explosion, the thermal effects of an ejecta-donor interaction on the evolution of the surviving He star become negligible. This suggests that the ejecta-donor interaction does not play an important role in explaining the current observational properties of US 708 if it is indeed an ejected donor remnant from a DDet SN Ia.

4.2. More massive donor models

By neglecting the effect of ejecta-donor interactions, Geier et al. (2015) have suggested that the evolutionary track of a post extended horizontal branch (EHB) star with an original mass of 0.45 M⊙ passes the position of US 708 in the effective temperature-surface gravity diagram. Following their suggestion, we also generated two He-star donor models with larger initial masses to check whether the post-impact properties of a more massive ejected donor remnant in a DDet SN Ia would match the observations of US 708 better. Model B has an initial mass of 0.50 M⊙, and Model C has an initial mass of 0.55 M⊙ (Table 1). For both models we followed the method described in Sect. 2.1.1. The detailed binary evolution calculations are shown in Fig. 7. In Model B the donor star has a mass of 0.45 M⊙ at the moment of the SN explosion, and Model C reaches a mass of 0.50 M⊙ at the SN explosion of the accreting WD. The key properties of both models are summarised in Table 1. With these models, we repeated the 3D modelling of ejecta-donor interaction and 1D post-impact evolution calculations in the same fashion as for Model A and compared the results to the observational properties of US 708.

thumbnail Fig. 7.

Similar to the left panel of Fig. 1, but for two more massive He-star donor models with initial masses of 0.50 M⊙ (left panel) and 0.55 M⊙ (right panel).

Figures 8 and 9 show the detailed post-impact properties and evolution tracks of Models B and C. These more massive surviving He-star donors reach their peak luminosities of (1.5 − 2.1)×103 L⊙ at ≲60 yr, much faster than the ∼3000 yr needed in Model A. The energy deposition in the more massive models occurs at lower depths, leading to a shorter local radiative diffusion timescale of the donor envelope. Additionally, the total amounts of energy deposition from SN ejecta in these two models are smaller than that in Model A (Table 1). A fundamental and qualitative difference is that donor models with > 0.3 M⊙ show He burning as they contract. As the deposited energy is radiated away, their temperature increases significantly (about 107 yr after the explosion) with an almost fixed radius and luminosity before they enter the WD cooling stage (Figs. 8 and 9). Our most massive ejected donor remnant model (∼0.5 M⊙) becomes bright and hot enough to achieve the observed luminosity and temperature of US 708 (Geier et al. 2015). Unfortunately, with log10 (g/cm s−2)≈6.20, it has a higher surface gravity than that of US 708. This could indicate that an even more massive He-star donor model may be needed to match the observations of US 708. However, our detailed binary evolution calculations indicate that a binary progenitor system with such a massive He-star donor is unlikely to be close enough to reach a sufficiently high orbital velocity at the moment of the SN explosion (Table 1), and hence it would fail to explain the observed high spatial velocity of US 708.

thumbnail Fig. 8.

Similar to Fig. 5, but for the more massive He-star donor models with a post-impact mass of 0.45 M⊙ (i.e. Model B; see the solid black line) and 0.50 M⊙ (i.e. Model C; see the dash-dotted red line).

thumbnail Fig. 9.

Similar to Fig. 6, but for the more massive He-star donor models with a post-impact mass of 0.45 M⊙ (solid black line) and 0.50 M⊙ (dash-dotted red line). For a comparison, the results of the 0.30 M⊙ He donor model of Fig. 6 are shown as a double-dotted line. The observed properties of US 708 are indicated with a black plus sign.

Our results and conclusions are similar to those presented by Geier et al. (2015). Figures 8 and 9 show that our surviving companion stars re-established thermal equilibrium completely about 14 Myr after the explosion. At these late epochs, the observational properties of our surviving companion stars are not sensitive to the details of ejecta-donor interaction and are thus similar to those of EHB-star models with the same mass adopted by Geier et al. (2015) at similar epochs. This confirms that neglecting the effect of ejecta-donor interactions for the comparison with US 708 is a reasonable approximation.

Low-mass donors not becoming bright enough and high-mass donors not becoming fast enough pose problems for explaining US 708 as a He-star donor ejected from a DDet SNe Ia. An alternative explanation would be that the pre-explosion binary progenitor system has travelled at a speed of about 400 km s−1 in the direction of its current motion (see also Brown et al. 2015; Bauer et al. 2019).

4.3. Uncertainties and future work

In this work the He-star donor models are constructed based on a sub-Chandrasekhar-mass DDet explosion model given by Gronow et al. (2020). The exact critical He-shell mass required to successfully initiate a thermonuclear SN explosion by triggering DDets is still quite uncertain (e.g. Woosley & Kasen 2011; Bildsten et al. 2007; Shen & Moore 2014; Townsley et al. 2019; Gronow et al. 2021). Our investigation is inherently limited by the assumption of a critical He-shell mass of ∼0.05 M⊙. Different core and He-shell masses of exploding WDs could significantly affect the SN ejecta properties and thus the predicted observational features of the resulting SNe Ia (e.g. Gronow et al. 2021). This introduces some uncertainties into the firmness of our conclusions. Nevertheless, we do demonstrate that certain companion masses are promising for reproducing US 708, and therefore we think that such a model seems likely to explain the main features of this star.

The exact He-retention efficiency of the accreting WD in the progenitor system is still poorly constrained (e.g. Ruiter et al. 2014; Toonen et al. 2014). This is expected to add to the uncertainties of our 1D binary evolution calculation that provides the binary properties and donor structures at the time of the SN explosion. To comprehensively model the predictions on the observables of surviving donors of DDet SNe Ia and to improve the fit with US 708, more donor models need to be constructed and investigated. Our future work will include different DDet explosion models that cover a range of core and He-shell masses of exploding WDs.

In our impact simulations, we find that some SN ejecta material is captured by the donor star during the ejecta-donor interaction. The decay of the deposited radioactive elements (e.g. 56Ni) could reheat the donor star and thus affect its post-impact evolution (e.g. Shen & Schwab 2017). We leave a detailed study of the influence of captured ejecta elements on the post-impact evolution of a surviving companion star of a DDet SN Ia to future work.

5. Summary

For the first time, we have consistently performed 3D hydrodynamical simulations of ejecta-donor interactions within the DDet scenario of SNe Ia. We then followed the long-term post-impact evolution of surviving He-star companions of DDet SNe Ia by combining the outcomes of 3D hydrodynamic impact simulations into 1D post-impact evolution codes. We have provided the observable signatures of the surviving companion stars of DDet SNe Ia, which can guide the search for such companion stars in future observations. We have also compared our results to the observations of the HVS US 708 to assess the validity of explaining the origin of this star with an ejected He donor from a DDet SN Ia. The results and conclusions of this work are summarised as follows.

  • (1)

    We find that about 3%−6% of the initial donor mass is stripped off from the outer layers during the ejecta-donor interaction for our three He-star donor models. The donor stars receive impact kick velocities of 80 − 200 km s−1, resulting in ejected donor remnant spatial velocities of 619 − 923 km s−1. These velocities are dominated by the pre-explosion orbital velocities of 614 − 901 km s−1 (Table 1).

  • (2)

    We find that the donors are significantly shocked and heated during the ejecta-donor interaction. In addition, we find that an energy of about (1.07 − 1.15)×1049 erg is deposited into the donor stars, which corresponds to about 35%−48% of the total incident energy from SN ejecta being absorbed by the donor remnants (Table 1). The surviving donor stars inflate for about 100 − 1000 yr and reach peak luminosities of (0.08 − 2.2)×103 L⊙, exceeding their pre-explosion luminosities by up to a factor of about 800 (Figs. 5 and 8).

  • (3)

    We find that the ejecta-donor interaction plays an important role in determining the post-impact observable signatures of surviving companion stars of DDet SNe Ia during the thermal re-equilibration phase. This leads to the surviving companion stars becoming significantly overluminous for the Kelvin-Helmholtz timescale of about 106 yr. After the stars re-establish thermal equilibrium, they continue to evolve by following an evolutionary track very close to that of a He star with the same mass that has not been impacted and heated by an ejecta-donor interaction.

  • (4)

    Although our reference model (Model A) matches the high velocity of US 708 (about 1200 km s−1; Geier et al. 2015), it does not reproduce the observed temperature or luminosity of this star.

  • (5)

    The US 708 was ejected about 14 Myr ago, based on its kinematics (Geier et al. 2015). At these late epochs after the explosion, the observational properties of our surviving companions are not sensitive to the details of the ejecta-donor interaction. Therefore, the ejecta-donor interaction may not play an important role in determining the SN Ia origin of US 708.

  • (6)

    Based on the results (Fig. 9) of our more massive donor star models (Models B and C), we suggest that a He-star donor with an initial mass of ≳0.5 M⊙ is needed to reproduce the observed properties of US 708, such as its luminosity, effective temperature, and surface gravity (see also Geier et al. 2015). However, our detailed binary evolution calculations show that such massive donors might not reach sufficiently high orbital velocities at the moment of a SN explosion in the DDet scenario to explain the observed high spatial velocity of US 708.

  • (7)

    Explaining the high spatial velocity of US 708 with a massive ejected donor remnant (≳0.5 M⊙) from a DDet SN Ia event may require its binary progenitor system to have already travelled at a speed of about 400 km s−1 in the observed direction in the galactic halo prior to the SN explosion (see also Brown et al. 2015).

To determine whether or not US 708 is indeed an ejected donor remnant from a DDet SN Ia requires further improvements in the binary evolution calculations, in particular the accumulation efficiency of accreted He material onto the WD, and the hydrodynamic impact modelling with different DDet explosion models covering a range of core and He-shell masses of exploding WDs.

1

Geier et al. (2015) used the Cambridge stellar evolution code STARS (Eggleton 1971, 1972; Pols et al. 1995; Stancliffe 2010) for their binary evolution calculations. When a consistent setup is adopted, we find that the donor structures and binary parameters are identical between the MESA and the STARS models at the moment of the SN explosion.

2

Model M2a was constructed to be similar to Model 3 of Fink et al. (2010), and it was presented as the reference model in Gronow et al. (2020).

3

Here, the incident energy of SN ejecta is obtained for a ratio of binary separation to companion radius at the moment of the SN explosion of 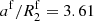(see Table 1).

Acknowledgments

We thank the anonymous referee for constructive comments that helped to improve this paper. ZWL would like to thank Robert G. Izzard for his fruitful discussions. ZWL is supported by the National Natural Science Foundation of China (NSFC, No. 11873016), the Chinese Academy of Sciences (CAS) and the Natural Science Foundation of Yunnan Province (No. 202001AW070007). The work of FR is supported by the Klaus Tschira Foundation and by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project-ID 138713538 – SFB 881 (“The Milky Way System”, Subproject A10). AH acknowledges support by the Australian Research Council (ARC) Centre of Excellence (CoE) for Gravitational Wave Discovery (OzGrave) project number CE170100004, by the ARC CoE for All Sky Astrophysics in 3 Dimensions (ASTRO 3D) project number CE170100013, and by the US National Science Foundation under Grant No. PHY-1430152 (JINA Center for the Evolution of the Elements). The authors gratefully acknowledge the ‘PHOENIX Supercomputing Platform’ jointly operated by the Binary Population Synthesis Group and the Stellar Astrophysics Group at Yunnan Observatories, CAS. This work made use of the Heidelberg Supernova Model Archive (HESMA, see https://hesma.h-its.org, Kromer et al. 2017).

References

  1. Aarseth, S. J. 1974, A&A, 35, 237 [NASA ADS] [Google Scholar]
  2. Bauer, E. B., White, C. J., & Bildsten, L. 2019, ApJ, 887, 68 [Google Scholar]
  3. Bildsten, L., Shen, K. J., Weinberg, N. N., & Nelemans, G. 2007, ApJ, 662, L95 [Google Scholar]
  4. Blaauw, A. 1961, Bull. Astron. Inst. Neth., 15, 265 [NASA ADS] [Google Scholar]
  5. Boos, S. J., Townsley, D. M., Shen, K. J., Caldwell, S., & Miles, B. J. 2021, ApJ, submitted [arXiv:2101.12330] [Google Scholar]
  6. Brown, W. R. 2015, ARA&A, 53, 15 [Google Scholar]
  7. Brown, W. R., Geller, M. J., Kenyon, S. J., & Kurtz, M. J. 2005, ApJ, 622, L33 [Google Scholar]
  8. Brown, W. R., Anderson, J., Gnedin, O. Y., et al. 2015, ApJ, 804, 49 [NASA ADS] [CrossRef] [Google Scholar]
  9. Eggleton, P. P. 1971, MNRAS, 151, 351 [CrossRef] [Google Scholar]
  10. Eggleton, P. P. 1972, MNRAS, 156, 361 [NASA ADS] [Google Scholar]
  11. Fink, M., Hillebrandt, W., & Röpke, F. K. 2007, A&A, 476, 1133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Fink, M., Röpke, F. K., Hillebrandt, W., et al. 2010, A&A, 514, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Fryxell, B. A., & Arnett, W. D. 1981, ApJ, 243, 994 [NASA ADS] [CrossRef] [Google Scholar]
  14. Geier, S., Nesslinger, S., Heber, U., et al. 2007, A&A, 464, 299 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Geier, S., Marsh, T. R., Wang, B., et al. 2013, A&A, 554, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Geier, S., Fürst, F., Ziegerer, E., et al. 2015, Science, 347, 1126 [Google Scholar]
  17. Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [Google Scholar]
  18. Gronow, S., Collins, C., Ohlmann, S. T., et al. 2020, A&A, 635, A169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Gronow, S., Collins, C. E., Sim, S. A., & Röpke, F. K. 2021, A&A, 649, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Gvaramadze, V. V., Gualandris, A., & Portegies Zwart, S. 2009, MNRAS, 396, 570 [Google Scholar]
  21. Heger, A., & Woosley, S. E. 2010, ApJ, 724, 341 [Google Scholar]
  22. Henyey, L., & L’Ecuyer, J. 1969, ApJ, 156, 549 [CrossRef] [Google Scholar]
  23. Hillebrandt, W., Kromer, M., Röpke, F. K., & Ruiter, A. J. 2013, Front. Phys., 8, 116 [Google Scholar]
  24. Hills, J. G. 1988, Nature, 331, 687 [Google Scholar]
  25. Kasen, D. 2010, ApJ, 708, 1025 [Google Scholar]
  26. Kato, M., & Hachisu, I. 2003, ApJ, 598, L107 [NASA ADS] [CrossRef] [Google Scholar]
  27. Kromer, M., Ohlmann, S., & Röpke, F. K. 2017, Mem. Soc. Astron. It., 88, 312 [NASA ADS] [Google Scholar]
  28. Kudritzki, R. P., & Simon, K. P. 1978, A&A, 70, 653 [NASA ADS] [Google Scholar]
  29. Landau, L. D., & Lifshitz, E. M. 1971, The Classical Theory of Fields (New York: Pergamon Press) [Google Scholar]
  30. Leonard, P. J. T. 1991, AJ, 101, 562 [NASA ADS] [CrossRef] [Google Scholar]
  31. Leonard, D. C. 2007, ApJ, 670, 1275 [NASA ADS] [CrossRef] [Google Scholar]
  32. Li, W., Bloom, J. S., Podsiadlowski, P., et al. 2011, Nature, 480, 348 [NASA ADS] [CrossRef] [Google Scholar]
  33. Liu, Z.-W., & Zeng, Y. 2021, MNRAS, 500, 301 [Google Scholar]
  34. Liu, Z. W., Pakmor, R., Röpke, F. K., et al. 2012, A&A, 548, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Liu, Z.-W., Pakmor, R., Röpke, F. K., et al. 2013a, A&A, 554, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Liu, Z.-W., Pakmor, R., Seitenzahl, I. R., et al. 2013b, ApJ, 774, 37 [NASA ADS] [CrossRef] [Google Scholar]
  37. Liu, Z.-W., Kromer, M., Fink, M., et al. 2013c, ApJ, 778, 121 [NASA ADS] [CrossRef] [Google Scholar]
  38. Livne, E., & Arnett, D. 1995, ApJ, 452, 62 [Google Scholar]
  39. Livne, E., Tuchman, Y., & Wheeler, J. C. 1992, ApJ, 399, 665 [NASA ADS] [CrossRef] [Google Scholar]
  40. Maoz, D., Mannucci, F., & Nelemans, G. 2014, ARA&A, 52, 107 [Google Scholar]
  41. Marietta, E., Burrows, A., & Fryxell, B. 2000, ApJS, 128, 615 [NASA ADS] [CrossRef] [Google Scholar]
  42. Maxted, P. F. L., Marsh, T. R., & North, R. C. 2000, MNRAS, 317, L41 [NASA ADS] [CrossRef] [Google Scholar]
  43. Moll, R., & Woosley, S. E. 2013, ApJ, 774, 137 [NASA ADS] [CrossRef] [Google Scholar]
  44. Neunteufel, P. 2020, A&A, 641, A52 [EDP Sciences] [Google Scholar]
  45. Neunteufel, P., Yoon, S. C., & Langer, N. 2016, A&A, 589, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Neunteufel, P., Kruckow, M., Geier, S., & Hamers, A. S. 2021, A&A, 646, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Pakmor, R., Röpke, F. K., Weiss, A., & Hillebrandt, W. 2008, A&A, 489, 943 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Pakmor, R., Edelmann, P., Röpke, F. K., & Hillebrandt, W. 2012, MNRAS, 424, 2222 [Google Scholar]
  49. Pan, K.-C., Ricker, P. M., & Taam, R. E. 2012a, ApJ, 750, 151 [NASA ADS] [CrossRef] [Google Scholar]
  50. Pan, K.-C., Ricker, P. M., & Taam, R. E. 2012b, ApJ, 760, 21 [NASA ADS] [CrossRef] [Google Scholar]
  51. Pan, K.-C., Ricker, P. M., & Taam, R. E. 2013, ApJ, 773, 49 [NASA ADS] [CrossRef] [Google Scholar]
  52. Pan, K.-C., Ricker, P. M., & Taam, R. E. 2014, ApJ, 792, 71 [NASA ADS] [CrossRef] [Google Scholar]
  53. Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
  54. Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
  55. Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]
  56. Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [Google Scholar]
  57. Polin, A., Nugent, P., & Kasen, D. 2019, ApJ, 873, 84 [Google Scholar]
  58. Pols, O. R., Tout, C. A., Eggleton, P. P., & Han, Z. 1995, MNRAS, 274, 964 [Google Scholar]
  59. Rauscher, T., Heger, A., Hoffman, R. D., & Woosley, S. E. 2002, ApJ, 576, 323 [Google Scholar]
  60. Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [Google Scholar]
  61. Ruiter, A. J., Belczynski, K., Sim, S. A., et al. 2011, MNRAS, 417, 408 [CrossRef] [Google Scholar]
  62. Ruiter, A. J., Belczynski, K., Sim, S. A., Seitenzahl, I. R., & Kwiatkowski, D. 2014, MNRAS, 440, L101 [NASA ADS] [CrossRef] [Google Scholar]
  63. Schmidt, B. P., Suntzeff, N. B., Phillips, M. M., et al. 1998, ApJ, 507, 46 [NASA ADS] [CrossRef] [Google Scholar]
  64. Shen, K. J., & Bildsten, L. 2009, ApJ, 699, 1365 [NASA ADS] [CrossRef] [Google Scholar]
  65. Shen, K. J., & Moore, K. 2014, ApJ, 797, 46 [Google Scholar]
  66. Shen, K. J., & Schwab, J. 2017, ApJ, 834, 180 [NASA ADS] [CrossRef] [Google Scholar]
  67. Shen, K. J., Kasen, D., Miles, B. J., & Townsley, D. M. 2018a, ApJ, 854, 52 [Google Scholar]
  68. Shen, K. J., Boubert, D., Gänsicke, B. T., et al. 2018b, ApJ, 865, 15 [Google Scholar]
  69. Sim, S. A., Röpke, F. K., Hillebrandt, W., et al. 2010, ApJ, 714, L52 [Google Scholar]
  70. Springel, V. 2005, MNRAS, 364, 1105 [Google Scholar]
  71. Stancliffe, R. J. 2010, MNRAS, 403, 505 [Google Scholar]
  72. Taam, R. E. 1980, ApJ, 242, 749 [NASA ADS] [CrossRef] [Google Scholar]
  73. Tauris, T. M. 2015, MNRAS, 448, L6 [Google Scholar]
  74. Tauris, T. M., & Takens, R. J. 1998, A&A, 330, 1047 [NASA ADS] [Google Scholar]
  75. Toonen, S., Claeys, J. S. W., Mennekens, N., & Ruiter, A. J. 2014, A&A, 562, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Townsley, D. M., Miles, B. J., Shen, K. J., & Kasen, D. 2019, ApJ, 878, L38 [Google Scholar]
  77. Vennes, S., Kawka, A., O’Toole, S. J., Németh, P., & Burton, D. 2012, ApJ, 759, L25 [Google Scholar]
  78. Weaver, T. A., Zimmerman, G. B., & Woosley, S. E. 1978, ApJ, 225, 1021 [NASA ADS] [CrossRef] [Google Scholar]
  79. Wheeler, J. C., Lecar, M., & McKee, C. F. 1975, ApJ, 200, 145 [NASA ADS] [CrossRef] [Google Scholar]
  80. Woosley, S. E., & Kasen, D. 2011, ApJ, 734, 38 [Google Scholar]
  81. Woosley, S. E., Taam, R. E., & Weaver, T. A. 1986, ApJ, 301, 601 [NASA ADS] [CrossRef] [Google Scholar]
  82. Woosley, S. E., Heger, A., & Weaver, T. A. 2002, Rev. Mod. Phys., 74, 1015 [NASA ADS] [CrossRef] [Google Scholar]
  83. Yu, Q., & Tremaine, S. 2003, ApJ, 599, 1129 [Google Scholar]
  84. Zeng, Y., Liu, Z.-W., & Han, Z. 2020, ApJ, 898, 12 [NASA ADS] [CrossRef] [Google Scholar]
  85. Zubovas, K., Wynn, G. A., & Gualandris, A. 2013, ApJ, 771, 118 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Three He donor models studied in this work.

In the text

All Figures

thumbnail Fig. 1.

Left panel: evolutionary tracks of the luminosity of the He-star companion (dash-dotted cyan line) and the orbital period of the binary system (solid orange line) during the whole mass-transfer process until the SN Ia explosion. Right panel: time evolution of the mass transfer rate (Ṁtr; dash-dotted cyan line) and the mass growth of a helium shell onto the WD (MHe; solid orange line). The vertical dotted lines give the moment of the SN explosion. The initial and final binary parameters (WD mass MWD, companion mass M2, and orbital period P) in our detailed binary calculations are shown in the plot and indicated with superscript letters ‘i’ and ‘f’, respectively.
In the text
thumbnail Fig. 2.

Density distributions of all material (panels a–c) and of the bound companion material (panels d–f). The panels shows a slice in the orbital plane for three different times each. Colours indicate density as per the colour bar (right). The 3D hydrodynamical simulation of the SN ejecta-companion interaction shown here does not include binary orbital motion or stellar spin. All panels use the same length scales.
In the text
thumbnail Fig. 3.

Similar to Fig. 2f, but for the 3D simulation that includes binary orbital motion and stellar spin.
In the text
thumbnail Fig. 4.

Post-impact 1D angle-averaged profiles (thin lines) of specific internal energy, ℰint (top panel) and density, ρ (bottom panel) as functions of fractional mass coordinates at the end of the SPH impact simulation for our reference model, Model A. For a comparison, the relaxed starting models in MESA are shown as thick lines. The results for the impact simulation with or without binary orbital motion and stellar spin taken into account are shown as dash-dotted lines and solid lines, respectively.
In the text
thumbnail Fig. 5.

Post-impact evolution of the photosphere luminosity, L, effective temperature, Teff, radius, R, and surface gravity, g, of a surviving He-star companion as functions of time. The solid line and dash-dotted line respectively correspond to the results from 1D calculations using the KEPLER code and the MESA code. For comparison, the MESA results based on the impact simulations that do and do not include the binary orbital motion and stellar spin are given as thick solid lines and thin solid lines, respectively.
In the text
thumbnail Fig. 6.

Post-impact evolutionary tracks of a surviving He-star companion model in the H-R diagram (left panel) and surface gravity vs. temperature diagram (right panel). The solid lines and dash-dotted lines respectively correspond to the results of KEPLER and MESA calculations. The filled circle, square, triangle, and star markers on the tracks represent post-impact evolutionary phases of 1 yr, 1 kyr, 100 kyr, and 10 Myr after the SN impact, respectively. The thin lines and thick lines have the same meaning as those in Fig. 5.
In the text
thumbnail Fig. 7.

Similar to the left panel of Fig. 1, but for two more massive He-star donor models with initial masses of 0.50 M⊙ (left panel) and 0.55 M⊙ (right panel).
In the text
thumbnail Fig. 8.

Similar to Fig. 5, but for the more massive He-star donor models with a post-impact mass of 0.45 M⊙ (i.e. Model B; see the solid black line) and 0.50 M⊙ (i.e. Model C; see the dash-dotted red line).
In the text
thumbnail Fig. 9.

Similar to Fig. 6, but for the more massive He-star donor models with a post-impact mass of 0.45 M⊙ (solid black line) and 0.50 M⊙ (dash-dotted red line). For a comparison, the results of the 0.30 M⊙ He donor model of Fig. 6 are shown as a double-dotted line. The observed properties of US 708 are indicated with a black plus sign.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.