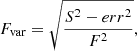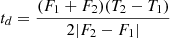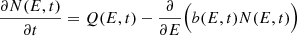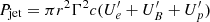EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 654 (October 2021) A&A, 654 (2021) A38 Full HTML
Free Access
Issue
A&A
Volume 654, October 2021
Article Number A38
Number of page(s) 14
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202140708
Published online 07 October 2021

© ESO 2021

1. Introduction

The BL Lac type active galactic nucleus OJ 287, located at a redshift of 0.306, was discovered in 1967 (Dickel et al. 1967). It was as an exceptionally active variable source even five decades ago (Andrew et al. 1971). A proper study of the variability of OJ 287 on different timescales can be found in Valtonen et al. (2006). Intraday variability in radio and optical data of OJ 287 was first detected by Valtaoja et al. (1985). Variability in blazars fits into three different categories as described below. Changes over a period of time ranging from minutes to less than a day (e.g., Wagner & Witzel 1995; Kinman 1975; Rector & Perlman 2003) are defined as intranight variability (INV) or intraday variability (IDV), which are known as microvariability; those on a timescale of days to a few months are commonly known as short-term variations (STVs); and variations over several months to years are defined as long-term variations (LTV, e.g., Andruchow et al. 2011; Raiteri et al. 2005; Agarwal et al. 2017).

Short timescale variability of this BL Lac object at near-infrared (NIR) frequencies was studied using standard JHK photometry, which showed a variability of amplitude of 0.7 mag over the observing period of 23 months (Lorenzetti et al. 1989). From the long-term optical light curve of OJ 287 it was inferred that it has binary supermassive black holes (Sillanpaa et al. 1988). They found that the light curve shows repeated outbursts at intervals of 11.65 years and minimum flux at intervals of 11 years. These results were verified by others (Kidger et al. 1992). Different models for the periodic outburst of OJ 287 at optical frequencies have been discussed earlier (Dey et al. 2019) involving the periodic motion of a binary supermassive black hole. One kind of model assumes that the orientation of the jet of the primary black hole changes in a regular manner due to precession. The optical flare would thus be the result of the enhancement in the Doppler factor of the jet. In another model, optical flaring in OJ 287 results from enhanced accretion during pericenter passage or collision between the secondary black hole and the accretion disk of the primary black hole.

A giant flare from OJ 287 was predicted to happen in 1994 according to the binary black hole model of Sillanpaa et al. (1988). This was observed by Sillanpaa et al. (1996a), and thus the prediction of 12 year cycle was confirmed. Lehto & Valtonen (1996) proposed that the reason for the flares is an impact of the secondary black hole on the accretion disk of the primary, which means that there has to be two such flares during each orbital cycle. This is a unique property of the model, not easily accounted for in other proposals. The model predicted the time of the second flare in November 1995 within a two week time window (Valtonen 1996), and subsequently Sillanpaa et al. (1996b) observed the flare and confirmed the prediction. Sundelius et al. (1996, 1997) calculated the flare arising from tides in this binary model, and predicted the next big impact flare in 2005, a year earlier than was expected from strict periodicity. It was reported by Valtonen et al. (2006). The flares come sooner than in the strictly periodic models due to precession, as is clearly stated in their paper. Finally, the observation of the 2015 flare confirmed this shift, which by then was 3 years (Valtonen et al. 2016). This paper also found the signature of disk impacts, the thermal nature of the flare. Valtonen et al. (2019) updated the model of Lehto & Valtonen (1996) and determined the disk parameters using time delays calculated in Dey et al. (2018).

During the 2008–2010 phase, tidal flares were expected according to the model by Sundelius et al. (1996, 1997). The γ-ray light curve of OJ 287 during 2008 August – 2010 January was studied by Neronov & Vovk (2011). They found that the variability timescale is shorter than 3.2 h. Therefore, they inferred that the observed γ-ray emission was from the smaller mass black hole jet. urthermore, detecting γ rays of energy higher than 10 GeV constrained the lower limit of the Doppler factor to 4.

The broadband spectrum of the major γ-ray flare in 2009 was studied by Kushwaha et al. (2013). They explained the multiwavelength spectral energy distribution (SED) by combining synchrotron, synchrotron self-Compton (SSC), and external Compton (EC) processes. They suggested that the emission region in the jet is surrounded by a bath of photons at 250 K. They also inferred that the location of this emission region is 9 pc away from the central engine. The high activity of OJ 287 during December 2015 – April 2016 was studied by Kushwaha et al. (2018a), and the authors inferred simultaneous multiwavelength emission. They explained the optical bump as accretion disk emission associated with the primary black hole. The smaller bump feature in the optical–UV appeared to be consistent with line emission. They explained the γ-ray emission with inverse Compton scattering of photons from the line emission.

The flux and polarisation variability at optical bands of OJ 287 during the December 2015 to February 2016 outburst was studied by Rakshit et al. (2017). The intranight optical variability data were analyzed, and the shortest variability timescale was estimated as 142 ± 38 min. This constrained the lower limit on the value of the Doppler factor to 1.17 and the upper limit on the value of the magnetic field to 3.8 Gauss. The size of the emission region was constrained to less than 2.28 × 1014 cm.

The multi-band optical variability from September 2015 to May 2016 was studied by Gupta et al. (2017) using nine ground-based optical telescopes. They detected a large optical outburst in December 2015 and a second comparably strong flare in March 2016. The long-term optical, ultraviolet and X-ray variability in different activity states of OJ 287 was studied using UVOT and XRT instruments of Swift (Siejkowski & Wierzcholska 2017). They did not find any clear relation between optical–UV and X-ray emission during quiescence states or outbursts.

The strong activity in optical to X-ray frequency from July 2016 to July 2017 was studied by Kushwaha et al. (2018b). The daily γ-ray fluxes during this time are consistent with no variability. They modeled the SEDs with a two-zone leptonic model. The first zone gives a low BL Lac (LBL) SED, and the second zone gives a high BL Lac(HBL) SED. In their model the second zone is located at a parsec-scale distance from the central engine.

A hadronic model to explain the X-ray and γ-ray November 2015 outburst of OJ 287 is given in Rodríguez-Ramírez et al. (2020). They use a binary supermassive black hole model where the initial trigger comes from the impact of the secondary black hole on the accretion disk of the primary black hole. An idealized spherical outflow is generated from this impact. A shock is formed when this spherical outflow, which contains cosmic rays and thermal ions, interacts with the AGN wind of the primary black hole. In their model the cosmic rays are shock accelerated due to the collision of the outflow with the AGN wind of the primary black hole. The cosmic ray protons interact with the thermal ions, and as a result secondary leptons, photons are produced in proton-proton interactions. The optical flare is explained by combining the jet emission from Kushwaha et al. (2013) and the thermal bremsstrahlung emission in the outflow. The photon field produced due to thermal bremsstrahlung acts as a target for inverse Compton emission by the secondary leptons. They explained the X-ray and γ-ray data as this inverse Compton emission of the secondary electrons.

Recently, Komossa et al. (2020b) reported the detection of a very bright outburst of OJ 287 covering X-ray, UV, and optical frequency from April to June of 2020. They concluded that the outburst is jet driven, and it is consistent with the binary supermassive black hole model. In this model the impact of the secondary black hole on the disk of the primary triggers an after-flare. This impact enhances the accretion activity of the primary black hole, which results in enhanced jet emission by the primary black hole.

In this paper we analyzed the multiwavelength data of OJ 287 for the period of 2017–2020, which includes the outburst discussed in the paper by Komossa et al. (2020b). The total period 2017–2020 considered in our work has been divided into five segments after analyzing the variability timescale in the optical and X-ray data. We performed the modeling of the SEDs with a time-dependent leptonic model, which includes synchrotron and SSC processes. The data analysis is discussed in Sect. 2. Our results of data analysis and the modelling of SEDs is discussed in Sect. 3. The discussions and conclusions of our study are given in Sect. 4.

2. Multiwavelength observations and data analysis

2.1. Fermi-LAT

Fermi-LAT is an excellent space-based telescope to explore the extragalactic and Galactic objects in the γ-ray sky. It uses the pair conversion method to detect γ-rays in the energy range of 20 MeV–500 GeV. It has a wide field of view (FoV) of about 2.4 sr (Atwood et al. 2009), which scans 20% of the sky at any time. The total scanning period of the entire sky with this telescope is around three hours. OJ 287 was observed in the brightest flaring state in X-rays when monitored by the Swift-telescope (Atel 10043) in 2017, and soon after flares in other frequency bands were also detected. Fermi-LAT has been continuously monitoring source OJ 287 since 2008. We collected the data from January 2017 to May 2020, and found that the source was in a moderate flux state within this period. We analyzed the γ-ray data following the standard data reduction and analysis procedure described by Science Tools1. The details of the method of this analysis are discussed in Prince et al. (2018).

2.2. X-ray observations

On February 3, 2017, an X-ray flare was observed by the Swift telescope, and the results were reported in Atel 10043. It is reported as the brightest flare ever detected since the monitoring started by the Swift telescope. After that, many multiple flares were observed in X-rays until May 2020, and this whole period is studied in this paper. Swift is a space-based telescope with three instruments on board, simultaneously observing all kinds of Galactic and extragalactic sources in soft and hard X-rays, optical, and UV. The working energy range of Swift-XRT is 0.3–10.0 keV. The BL Lac OJ 287 was observed by the Swift-XRT telescope during the multiple flaring episodes in X-ray frequencies in the period from January 2017 to May 2020. We analyzed all the observations done during this period. The raw data processing was done by using the task xrtpipeline2, and cleaned event files are produced for each observation. The CALDB version 20160609 was used while processing the raw data. Our analysis only focuses on the Photon Counting mode observations, and the task xselect was used for source and background selection. We selected a region of 12 arcseconds around the source and away from the source respectively for the source and background in our data analysis. The task xselect was also used to extract the spectrum and light curve, and the modeling of the spectrum was done in Xspec (Arnaud 1996). To model the spectra, we used a single power-law model. The Galactic absorption column density nH = 1.10 × 1020 cm−2 from Kalberla et al. (2005) was used. The modeling was done for an energy range of 0.3–10.0 keV.

2.3. Optical and UV observations

Having the Swift Ultraviolet/Optical Telescope (UVOT, Roming et al. 2005) on board with Swift-XRT has the advantage that it provides simultaneous observations in optical and UV bands. Swift-UVOT also observed the OJ 287 in all of the available six filters, U, V, B, W1, M2, and W2, simultaneously with the X-ray observations. The source instrumental magnitudes were extracted following the uvotsource procedure. We considered the region of 5 arcsec around the source and away from it as the source and the background region, respectively, in our data analysis. The magnitudes were corrected for galactic extinction by using the reddening E(B − V) = 0.0241 from Schlafly & Finkbeiner (2011) and zero points from Breeveld et al. (2011). Moreover, the magnitudes were converted into flux by multiplying by the conversion factor estimated by Poole et al. (2008) and the ratios of extinction to reddening from Giommi et al. (2006).

In the period between Feb. 2019 – Jan. 2020, we performed observations of OJ 287 using five different telescopes around the globe: the 2.15 m Jorge Sahade telescope (JS, telescope A) and the 60 cm Helen Sawyer Hogg telescope (HSH, telescope B), CASLEO, Argentina; the 1.3 m JC Bhattacharya Telescope (JCBT; telescope C) at the Vainu Bappu Observatory (VBO), India. The technical descriptions of the above telescopes are summarized in Table 1 of Agarwal et al. (2019) and Agarwal et al. (2021). The number of observations made in each band on a particular date during our monitoring campaign is provided in Table 1.

Table 1.

Log of photometric observations for the blazar OJ 287.

The preliminary data reduction includes bias correction, flat fielding, and cosmic-ray removal, which was performed with IRAF3 software. We then processed the cleaned CCD images using the Dominion Astronomical Observatory Photometry (DAOPHOT II) software (Stetson 1987, 1992) using the aperture photometry technique through which we obtained instrumental magnitudes for our target and four standard stars located in the same field. A more detailed and comprehensive description of data reduction methods used is given in Sect. 2 of Agarwal et al. (2019). Finally, to extract the instrumental differential light curves (LCs), we selected two non-variable standards having magnitude and color values very similar to those of the blazar. The calibrated LCs were obtained using star 10 in Fiorucci & Tosti (1996). After constructing the calibrated LCs of our source, we carefully inspected the LCs for any outliers. A handful of such suspicious data points were detected and corrected.

2.4. Radio data at 15 GHz

The Owens Valley Radio Observatory (OVRO; Richards et al. 2011) is one of the observatories that monitors the bright Fermi detected blazars. It is a 40-meter single-dish antenna working at a frequency of 15 GHz. A large number of Fermi blazars are continuously monitored by OVRO twice a week. Our candidate source, OJ 287, is also part of the OVRO monitoring program, and collected the data from September 2017 to July 2020.

3. Results

A detailed temporal and spectral study was performed using the multiwavelength data from the Fermi-LAT, Swift-XRT/UVOT telescope. The archival data from OVRO are used to perform the correlation study with the γ-ray.

3.1. Multiwaveband fractional and temporal variability

3.1.1. Multiwaveband variability

OJ 287 is mentioned as a γ-ray source in 3FGL (Acero et al. 2015) and in 4FGL (Abdollahi et al. 2020) catalog by Fermi-LAT. The blazar OJ 287 is one of the most active blazars with a binary black hole system, which makes it one of a kind and thus an interesting source in the Fermi-LAT catalog. It is monitored by various ground-based and space-based telescopes across the entire wavelength range. The recent flare seen by Swift-XRT and UVOT at the beginning of the year 2020 has been confirmed as the second brightest flare in X-ray and optical–UV (Komossa et al. 2020b).

The multiwavelength light curve, since January 2017 to May 2020, from radio (at 15 GHz) to γ-ray (0.1–300 GeV) is shown in Fig. 1. The whole light curve is divided into various activity states based on the variability and flux states seen in X-ray, optical, and UV. The states are defined as A, B, C, D, and E. Of these five states, A and E have higher mag and flux values in optical and X-ray and considered to be flaring states. The X-ray flare in state A was studied earlier by Kushwaha et al. (2018b), and Kapanadze et al. (2018). They found strong positive correlation between optical, UV and X-ray outbursts. Our results are consistent with theirs, which suggests that the same population of electrons is generating the optical, UV and X-ray outbursts. The flare in the optical and X-ray bands during state E is widely reported in many astronomer’s telegram (Zola et al. 2020, Komossa et al. 2020a, Reinhart et al. 2020, Hosokawa et al. 2020, Komossa & Grupe 2020) and studied by Komossa et al. (2020b) and Kushwaha et al. (2020). Here, we provide a broadband temporal and spectral analysis of these states and the broadband SED modeling was also done to compare the jet parameters between various high (A and E) and low (B, C, and D) states.

thumbnail Fig. 1.

Broadband light curve of OJ 287 from 2017–2020. Panel 1 (top) shows the weekly binned γ-ray light curve for 0.1–300 GeV. Panels 2, 3, and 4 are the Swift-XRT and UVOT light curves. Panel 5 is the radio light curve from OVRO at 15 GHz. The entire light curve is divided in five different states based on the flux and magnitude seen in Swift-XRT and UVOT. The various states are denoted A, B, C, D, and E and their time duration is represented by the color patches.

The upper panel shows the γ-ray light curve by Fermi-LAT. We found that the source is not very bright in γ-ray. The variation in flux is nearly a factor of 5 between its lowest and highest flux states. The average flux during this period is 2.65 × 10−8 ph cm−2 s−1. The average flux from the 4FGL catalog for 1–100 GeV is 0.6 × 10−8 ph cm−2 s−1 (horizontal dashed line in Fig. 1). In the last segment of the light curve for the period 2017–2020 the γ-ray data show the highest flux of approximately 1.0 × 10−7 ph cm−2 s−1.

The X-ray light curve is shown in the second panel. It is observed that the source is most variable in the states A and E, and the flux was at its maximum in early 2017. The highest flux state in X-ray coincides with the high flux state in radio and optical–UV. In γ-rays, the flux is not very high, but the variability can be seen in the light curve.

The light curves for various bands of optical and UV are shown in panels 3 and 4. The source seems to be variable across the whole light curve and achieving its maxima in early 2017 and mid 2020. These light curves are similar to the X-ray light curve, suggesting the link between their production site and physical processes. The multiwavelength SED modeling is presented later in this paper to discuss these possibilities.

Panel 5 shows the simultaneous observations in radio at 15 GHz. The light curve reveals that the source is variable in radio and the maximum variation is a strong decrease from 10 to 1 Jy.

The fractional variability estimated for various states is reported in Table 2. The fractional variability is used to characterize the long-term variability in various bands. It is formulated by Vaughan et al. (2003) as

(1)

where F denotes the mean flux, and S2 and err2 are the variance and the mean square error in the flux, respectively. The error in flux variability amplitude is given in Prince (2019). The fractional variability amplitude estimated for the various states in all wavebands is depicted in Table 2.

Table 2.

Fractional variability and variability time estimated for various states in different waveband as shown in Fig. 1, and explained in Sect. 3.1.1 in detail.

The flux doubling or halving time is also estimated for all the states in all bands. The values are further used to characterize the variability in OJ 287. The flux doubling time, also known as variability time, is defined as (Zhang et al. 1999)

(2)

where F1 and F2 are fluxes at time T1 and T2. The doubling time or the fastest (or shortest) variability time (tvar) is considered to be the smallest value among the available pairs in the light curve. The variability amplitude and the doubling time together characterize the variability of the source in various states. In segment E the source appeared to be more variable with the highest variability amplitude among all the states in all wavebands and have the shortest (fastest) variability time of the order of 1 day (Table 2). The values of variability amplitude vary from 50% to 60% among all the wavebands and the shortest variability time of OJ 287 during 2017–2020 in X-ray is nearly 1 day.

The radio data are very sparse during this entire period, and hence we did not include them in the variability study.

3.1.2. Intraday variability (IDV)

Considering the modest number of observations in each passband, the variability of the source is measured using the C-criterion, which compares the dispersion in the blazar-comparison star and control star – comparison star. We also used the F-test, which is the ratio of the variance of the blazar instrumental light curve (LC) to that of the standard star. The above tests are discussed in more detail in Agarwal et al. (2019). As claimed by Zibecchi et al. (2017), dispersion scaling by the Howell (ΓSF) factor (Howell et al. 1988) to match the control star and the target error distributions result in the most reliable results. We call a particular LC variable (Var) only when both tests reject the null hypothesis at the 99.5% confidence level, possibly variable (PV) if just one of the tests rejects the null hypothesis, and non-variable (NV) if both tests fail to reject the null hypothesis. Intraday variability results for our observation campaign are summarized in Table 3 where Cols. 1–8 are, respectively, observation date, the passband of observation, number of data points in the given passband, dispersion of blazar differential LC (DLC), dispersion of the control star DLC, Howell’s factor, results for C-test and F-test. The variability state of the source is given in Col. 9. Our total monitoring coverage contains 13 intraday LCs. The IDV behavior of OJ 287 over the entire duration is displayed in Fig. 2. We found only 1 LC (April 07, 2019) to be Var (variable) according to our conditions, while 5 LCs were PV. On the remaining seven nights, the source was found to be NV. Our intraday LCs span a duration of 2–4 h. Therefore, the relatively short span of observations reduces the chances of detecting genuine variability. The highest level recorded for OJ 287 was in 2015 December by Gupta et al. (2017). OJ 287 has been monitored for more than a century and has R-band data available since 1890. It is one of the extensively studied sources using both photometry and polarimetry observations on diverse timescales. During the 2015 flare the source attained a V mag of ∼13.4, R mag of ∼13.0, and I mag ∼12.4. From the current monitoring session we found that the brightest state reached by the source was on January 03, 2020, with R ∼ 14.38 mag, fainter than its brightest state in 2015 by ∼1.4 mag, while the faintest state attained by the source was on December 18, 2019, with R-band mag of 15.15, approximately 2.15 mag fainter than its brightest state during the 2015–2016 outburst. Significant optical LTV is also observed for the source with an R-band magnitude change of ∼2 (Fig. 1). The variability trends observed during our monitoring period are quite different from the previous ones (Gupta et al. 2017). The target did not display high IDV during the current phase, which could be due to the lesser data cadence.

Table 3.

Results of INV observations of OJ 287.

thumbnail Fig. 2.

Light curves for OJ 287; green denotes V band while red denotes R filter. In each plot the X-axis is JD and the Y axis is the source magnitude. Observation date and the telescope used are indicated in each plot. Telescope A, is JS (2.15 m Jorge Sahade telescope), telescope B is HSH (Helen Sawyer Hogg telescope), and telescope C is JCBT (Vainu Bappu Observatory, India).

3.2. Gamma-ray spectral analysis

We also produced the γ-ray spectra for all the various states of the source identified in Fig. 1. The γ-ray spectra are produced with the help of likeSED.py4 a python code provided by the Fermi Science Tools. First, the Likelihood analysis is done with the default spectral model power-law (PL) to model the spectral data points, in addition we changed the model to various other models, such as log parabola (LP) and broken power law (BPL), to get the best fit. The details of the models are discussed in Prince et al. (2018). The isotropic γ-ray luminosity corresponding to each spectral models are estimated during all the segments following the Eq. 5 in Prince et al. (2021), and the values are on the order of 1047–1048 erg s−1, which is lower than the Eddington luminosity (1050 erg s−1) of this source as estimated in Sect. 3.4. The estimated γ-ray luminosity values are given in Table 4. The γ-ray spectrum and model fitting are shown in Fig. 3, and corresponding model parameters are presented in Table 4. Considering the PL spectral model, the spectral state of the source changes from segment A to Segment B, C, and D from harder (ΓPL = 1.90 ± 0.06) to softer (ΓPL = 2.27 ± 0.08)), and it becomes harder again from segment D (ΓPL = 2.35 ± 0.10) to segment E (ΓPL = 2.21 ± 0.06).

Table 4.

Modeled parameters of γ-ray SEDs for all the segments identified in Fig. 1.

thumbnail Fig. 3.

Gamma-ray SED of all the segments identified during 2017–2020 in OJ 287 modeled with three different spectral models: PL, LP, and BPL (see Sect. 3.2 for more details). The down arrow represents the upper limit in that particular segment.

The Likelihood analysis returns the test statistics (TS ∼ 25, which corresponds to 5σ significance; Mattox et al. 1996) corresponding to each model and is generally used to decide which model gives the best fit to the spectral data points. Finally, we measure the TScurve = 2(log L(LP/BPL) − log L(PL)), where L represents the likelihood function (Nolan et al. 2012). The TScurve reveals the presence of curvature or a break in the spectrum, and which could be caused by the absorption of high energy photons (>20 GeV; Liu & Bai 2006) by the broad-line region (BLR), assuming the emitting region is located within the BLR. However, if the emitting region is located outside the BLR, a power-law spectral behavior is expected. The best spectral model favors a high positive value of TScurve over a low value of TScurve.

The various models and their corresponding parameters are exhibited in Table 4. The values of TScurve are close to each other for the different models. The TS values are nearly equal for the PL and LP models, but differ for BPL. However, there is no clear trend in the spectral model that can explain the γ-ray SED from all the segments, which shows that the source has a very complex behavior during 2017–2020.

3.3. Correlations studies

We collected multiwavelength data from 2017 to May 2020. Five different states are identified based on the flux and variability seen in X-rays and Optical–UV. During this period we did not observe any flare in γ-ray, but the source is variable in this low state, as can be seen in the top panel of Fig. 1. On the other hand, the source is flaring in X-ray and optical–UV and appears to be more variable in the X-rays, optical, UV, and radio (15 GHz) wavebands, as shown in Fig. 1 from top to bottom. Here we investigate the correlation between the X-ray and optical–UV emission for all the states since they have good coverage in all the wavebands. The observed time lags between light curves at different wavebands can be helpful to locate their emission regions along the jet axis.

To estimate the correlation, we followed the method developed by Edelson & Krolik (1988). Different bin sizes were chosen in different combinations to examine the discrete correlation function (DCF) peaks. The DCF estimated for all the possible combinations between X-rays and optical–UV are shown in Fig. 4. The top row of the figure shows the DCF for state A and is followed by B, C, D, and E at the bottom. The correlation coefficients, time lags, and the bin size for all the combinations are given in Table 5. Our results show that optical–X-ray and the UV–X-ray emissions for the states A, B, D, and E are highly correlated with values of correlation coefficient above 50% and with time lags within the bin size. This strong correlation with zero time lag suggests that these two emissions have a common emission region. However, for state C we do not observe any correlation between optical-UV and X-rays. We also estimated the significance of the DCF peaks by simulating the 1000 artificial optical and UV light curves by following the monte carlo procedure described in Emmanoulopoulos et al. (2013), for PSD slope 1.5. The simulated light curves are cross-correlated with the observed X-ray light curves. Furthermore, the 2σ and 3σ significance is estimated, shown in red and blue dashed lines in Fig. 4. Our results show that in most of the cases, emissions are correlated above 2σ significance.

thumbnail Fig. 4.

Cross-correlation of optical/UV vs X-ray. The five rows of the plot are the five states (A, B, C, D, E) defined in Fig. 1. Horizontal red and blue dashed lines are 2σ and 3σ significance respectively. We do not observe any significant time lag in any of the combinations. During state C, we see some time lags but the correlation coefficient are below 50% and below 2σ significance, and hence do not consider as an actual time lag.

Table 5.

DCF parameters for all the combinations.

As shown in Fig. 1, the radio data are very sparse so we did not include them in the correlation study.

3.4. Modeling the multiwavelength SEDs

Good coverage of OJ 287 in various wavebands provides an opportunity to obtain the multiwavelength spectral energy distribution (MWSED), used in our modeling. We produced the MWSED using Swift-XRT, UVOT and Fermi-LAT data for all the observations in different states. The modeling of OJ 287 was done previously in various ways. We assume that the emission region is in the jet of the primary black hole. The emission region is a spherical blob that is moving with Doppler factor δ down the jet. The shock accelerated leptons are lose energy inside this blob by synchrotron, and SSC processes.

We used a publicly available time-dependent code, GAMERA5 (Hahn 2015) to model the broadband SED. It is a python-based code and needs an initial injected electron spectrum as an input which further solves the transport equation (3) and estimates the propagated electron spectrum. Finally, the propagated electron spectrum is used to calculate the emission from the various processes, such as Synchrotron, SSC, and EC by external photons of various origin (BLR, DT, accretion disk). We use the following transport equation to find the electron spectrum after energy loss:

(3)

Here Q(E, t) is the input spectrum and N(E, t) is the propagated one-at-a time ‘t’. b(E, t) corresponds to the radiative loss by different physical processes (synchrotron, SSC, and EC scattering). We assume a LogParabola electron distribution as the injected electron spectrum in our modeling.

The MWSED could be modelled with the leptonic scenario, where SSC and EC emission are generating the high energy peak. The study by Kushwaha et al. (2013) on the 2009 flare suggests that the X-ray and γ-ray emission can be explained by SSC and EC processes respectively, where the seed photons for the external Compton are originated by a thermal bath of 250 K located at distance of ∼9 pc from the supermassive black hole (SMBH). In a more recent study by Kushwaha et al. (2018a) the December 2015 – May 2016 high state is modelled using both SSC and EC emissions. The December 2015 high activity has been predicted to occur from the impact of the second black hole on the accretion disk of the primary black hole. The non-thermal emission showed nearly co-spatial origin. They modelled the γ-ray flux by EC emission of relativistic electrons by optical–UV line emission, which shows the signature of a blue bump in the optical–UV flux. They fitted the X-ray data with SSC emission. In the present study we find that the source is variable in all wavebands including γ-rays, though we did not see any flaring behavior in this band. The observed day scale variability time in γ-ray flux suggests the location of the emission region close to the SMBH, within a few parsec from the base of the jet. The variability study across all the wavebands exhibits flux variability on timescales of approximately 1 day. For this reason we model the broadband SED with only synchrotron and SSC processes within a single emission zone. The correlation study also suggests that the emissions are produced at the same location.

The SSC emission is determined by the synchrotron emission and the size of the emission region. The synchrotron emission depends on the magnetic field in the emission region in the jet and the energy of the leptons. The variability timescale can constrain the size of the emission region. Considering 1 day variability time in the γ-ray data, we estimated the size of the emission region as r ∼ ctvarδ/(1 + z), where δ = 20, and it is found to be r ∼ 4.0 × 1016 cm. However, in our modeling the size of the emission region is a free parameter and we have found that a smaller size of the emission region is required to explain the broadband SED.

We also have many other parameters in our model, such as the magnetic field, injected electron spectrum, lower and higher energy cutoffs in the injected electron spectrum, normalization of the electron spectrum; these parameters are optimized to achieve the best SED fit. The MWSED modeling results are depicted in Fig. 5 for the various states, and their corresponding best-fit parameters are listed in Table 6. States C and D are very similar to each other in variability and flux states, and hence we only show the SED modeling of state C. The modeling confirms that the low and high energy peaks can be constrained with synchrotron and SSC processes, respectively. Figure 5 shows that the source has more emission in the optical–UV than in γ-rays. Hence a large value of magnetic field (∼4–7 Gauss) is used to fit the data.

thumbnail Fig. 5.

Multiwavelength spectral energy distribution for all the various segments observed during the year 2017–2020. The dot-dahsed and dahsed line in different colors in the synchrotron and SSC peaks are the time evolution of the model. The down arrow represents the γ-ray upper limits. The optical–UV, X-ray, and γ-ray data points are shown in red, blue, and magenta.

Table 6.

Multiwavelength SED modeling results with the best-fit parameters values.

The previous broadband SED modeling of OJ 287 at different occasions of low and bright state (Kushwaha et al. 2013, 2018a,b) was carried out with a range of values of the Doppler and Lorentz factors. In this study, we fixed the Doppler and Lorentz factor of the blob at 20 and 15.5 respectively, which are similar to the values reported in earlier papers.

We have also estimated the total jet power and the power in the individual component of the jet. The components are leptons, magnetic fields, and protons. We assume that the number ratio of leptons to protons is 20:1 in the jet, and we estimate the jet power in leptons and protons separately. The total jet power is generally defined as

(4)

where U′e, U′B, and U′p are the energy densities in leptons, magnetic field and protons in the jet or co-moving frame. The values of the size of the emission region (r) and the Lorentz factor (Γ) are already provided in the discussion above.

The total jet power calculated for all the states is shown in Table 6, and the value is much smaller than the Eddington luminosity of the source. The Eddington luminosity for the primary BH is estimated as LEdd = 4πGmmpc/σT, where m is the mass of the primary BH, mp is the proton mass, and σT is the Thompson scattering cross-section. The primary BH mass was estimated by Kushwaha et al. (2018a) by modeling the NIR–optical spectrum with an accretion disk, and the reported value is ∼1.8 × 1010 M⊙. The Eddington luminosity is estimated to be 2.30 × 1050 erg s−1, which is much higher than the total jet power estimated in this study by SED modeling. Modeling the high optical flux state with synchrotron emission requires a higher value of the magnetic field, and hence higher jet power in the magnetic field. During the flaring state A and E we found that the total jet power is 1.5 times higher than the total jet power estimated for low states B and C. The SED modeling also suggests that more luminosity in high energetic electrons is required to produce the broadband emission during flaring states A and E. The non-thermal flares during states A and E might have resulted from disk impact in November-December 2015 (Valtonen et al. 2016) and July-September 2019 (Laine et al. 2020), respectively, when thermal flares were observed. The injection of high energetic electrons in jet could be due to the time delayed increase in the accretion rate and jet activity triggered by disk impact of secondary black hole or by tidal disruption events Sundelius et al. (1997). The variable accretion rate causes internal shock in the jet, which accelerates the electrons and causes them to lose energy radiatively (Valtonen et al. 2006). The model of Sundelius et al. (1997) predicted a major increase in accretion rate at the beginning of January 2020. However, the non-thermal flares happened during April-June 2020, nearly 4 months after their predicted time. The physical explanation for this delay requires a better understanding of the disk–jet connection as discussed by Komossa et al. (2020b).

4. Discussions and conclusions

During the period between 2017 and 2020 the blazar OJ 287 did not show any bright flaring states in γ-ray. However, high flux states were reported across the optical–UV and X-ray wavebands in various Atels notifications during that period. Variability in flux was also observed at optical, UV, X-ray and γ-ray frequencies. Five states have been identified (A, B, C, D, and E) based on the flux and fractional variability seen in optical–UV and X-rays. States A and E appear to be the brightest (see Fig 1), which can also be verified by the total jet power (Table 6) found from the modeling of these states. The variability timescale found across the bands ranges from 12 h to ∼20 days across all states. The fastest variability time in X-rays is found to be on the order of 1 day. The optical bands U, B, and V have the shortest variability time of ∼14 h, 30 h, and 18 h, while in the UV bands they are on the order of 1 day, 4 days, and 1 day for the W1, M2, and W2 bands, respectively. Though the source was not bright in γ-rays, we produced the γ-ray spectrum for the different states to see if there is any variation in the spectrum. The γ-ray data shows day scale variability and the maximum variation in flux between high and low states is found to be five times. The γ-ray data can be well fitted with the PL or LP model. The values of the test statistics are similar for both the models. Furthermore, we estimated the correlations between various wavebands in order to understand whether they have a common emission region. The results show that emission is highly correlated (within the errorbars) between the different bands, which suggests their co-spatial origin. A single-zone emission model is applied to explain the multiwavelength emission by performing the MWSED modeling. The SED modeling confirms the presence of high magnetic field in the jet, and that the jet emission is powered by relativistic electrons.

In the binary black hole model the primary black hole is surrounded by an accretion disk. The orbit of the secondary black hole around the primary black hole is such that it intersects the accretion disk of the primary black hole two times. The major outbursts which occur at intervals of approximately 12 years, could be due to tidally induced mass flows. One such outburst is expected for every pericenter passage of the secondary (Sundelius et al. 1997). Pihajoki et al. (2013) theoretically predicted the timings of the precursor flares and compared with the observed flares in the light curve of OJ 287. Based on the model of Sundelius et al. (1997) a major after-flare is expected in January 2020, but it was observed in May 2020. The various physical conditions that affect this time delay are disk and/or corona properties and geometry, magnetic field geometry, and shock formation in the jet. They are not yet well understood (Komossa et al. 2020b), which makes it very hard to predict this time delay from first principle.

The disk impact model predicts thermal bremsstrahlung radiation as outbursts in optical–UV frequency due to the impact of the secondary black hole on the accretion disk of the primary black hole Lehto & Valtonen (1996). This model successfully predicted the impact flares in 2007, 2015, and 2019 (Dey et al. 2021). The disk impact triggers a time-delayed increase in accretion rate and jet activity, which leads to after-flare effects. The flares in states A and E in our work can be explained with this model. During states B, C, and D there was no flare, hence a lower jet power is needed to model these low states.

Microvariability studies of blazars are among the most relevant probes to understand the physical conditions very close to the central supermassive black hole. However, the exact phenomenon behind IDV in blazars is still under debate. Flux variations in blazars on intraday timescales almost certainly arise from intrinsic factors that are inherent to the blazar jets, such as shocks in the helical jets (Calafut & Wiita 2015), blobs of plasma traversing through the Doppler boosted magnetized jet, or the formation of ultra-relativistic mini jets in the helical jet itself. In the low state of blazars, an alternative source for optical IDV is the accretion disk (AD, e.g., Chakrabarti & Wiita 1993). According to the AD-based models, instabilities or hot spots or any other enhanced emission on the AD can yield optical IDV in blazars when the source is in a low state. The presence of confirmed IDV on only 1 out of 13 nights could most likely be due to a uniform jet emission, and any change in the direction of the relativistic shock with respect to our line of sight (LOS) if present at all, is very weak. LTV in blazars can be attributed to both intrinsic and extrinsic factors. Extrinsic mechanisms involve geometrical effects such as deviation of the emitting region with respect to LOS, thus causing variation in the Doppler factor (Villata et al. 2009) which in turn is observed as variation on a long-term basis. The launching of the new shocks can also cause long-term flux variations in blazar LCs. In general, optical IDV in blazars involve both intrinsic and extrinsic mechanisms (Pollack et al. 2016) and are usually difficult to disentangle.

Komossa et al. (2020b) studied the large X-ray data sample from 2015 to 2020, and their results pose a few fundamental questions. They observed the strong flare in X-ray, optical, and UV bands. The observation at the peak of the X-ray flare shows a steep power-law spectrum with index 2.8, which is very rare in blazars but consistent with the synchrotron origin of X-ray emission. They concluded that the emission is jet-driven, which is consistent with the binary black hole model. In another study by Kushwaha et al. (2020) the spectral change in X-ray emission was noted during 2017–2020, and they also suggested that it could be an emission from the jet. We modeled the various low and high states observed during 2017–2020 considering that the emissions are produced inside the jet.

It was reported earlier by Kushwaha et al. (2018a) that the source was active during December 2015 – April 2016 in the IR to γ-ray frequencies. However, another study by Kushwaha et al. (2018b) for the period of June 2016 – September 2017 found that the source was very bright in IR to X-rays, but no variability was seen in γ-rays. A similar behavior was seen during early 2017 and mid-2020 when the source was flaring in optical–UV and X-rays, but was not very active in γ-rays. The different behaviors at different frequencies and at different epochs of time make this source very complex in nature. Many more observational and theoretical studies are required to understand the complex nature of the blazar OJ 287.

3

IRAF is distributed by the National Optical Astronomy Observatories, which are operated by the Association of Universities for Research in Astronomy Inc., under a cooperative agreement with the National Science Foundation.

Acknowledgments

The project was partially supported by the Polish Funding Agency National Science Centre, project 2017/26/A/ST9/00756 (MAESTRO 9), and MNiSW grant DIR/WK/2018/12. Based on data obtained at Complejo Astronómico El Leoncito, operated under agreement between the Consejo Nacional de Investigaciones Científicas y Técnicas de la República Argentina and the National Universities of La Plata, Córdoba and San Juan.

References

  1. Abdollahi, S., Acero, F., Ackermann, M., et al. 2020, ApJS, 247, 33 [NASA ADS] [CrossRef] [Google Scholar]
  2. Acero, F., Ackermann, M., Ajello, M., et al. 2015, ApJS, 218, 23 [Google Scholar]
  3. Agarwal, A., Mohan, P., Gupta, A. C., et al. 2017, MNRAS, 469, 813 [NASA ADS] [CrossRef] [Google Scholar]
  4. Agarwal, A., Cellone, S. A., Andruchow, I., et al. 2019, MNRAS, 488, 4093 [CrossRef] [Google Scholar]
  5. Agarwal, A., Mihov, B., Andruchow, I., et al. 2021, A&A, 645, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Andrew, B. H., Harvey, G. A., & Medd, W. J. 1971, Astrophys. Lett., 9, 151 [NASA ADS] [Google Scholar]
  7. Andruchow, I., Combi, J. A., Muñoz-Arjonilla, A. J., et al. 2011, A&A, 531, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
  9. Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
  10. Breeveld, A. A., Landsman, W., Holland, S. T., et al. 2011, in American Institute of Physics Conference Series, eds. J. E. McEnery, J. L. Racusin, N. Gehrels, et al., AIP Conf. Ser., 1358, 373 [NASA ADS] [CrossRef] [Google Scholar]
  11. Calafut, V., & Wiita, P. J. 2015, JApA, 36, 255 [NASA ADS] [Google Scholar]
  12. Chakrabarti, S. K., & Wiita, P. J. 1993, A&A, 271, 216 [Google Scholar]
  13. Dey, L., Valtonen, M. J., Gopakumar, A., et al. 2018, ApJ, 866, 11 [CrossRef] [Google Scholar]
  14. Dey, L., Gopakumar, A., Valtonen, M., et al. 2019, Universe, 5, 108 [Google Scholar]
  15. Dey, L., Valtonen, M. J., Gopakumar, A., et al. 2021, MNRAS, 503, 4400 [NASA ADS] [CrossRef] [Google Scholar]
  16. Dickel, J. R., Yang, K. S., McVittie, G. C., & Swenson, G. W. 1967, AJ, 72, 757 [NASA ADS] [CrossRef] [Google Scholar]
  17. Edelson, R. A., & Krolik, J. H. 1988, ApJ, 333, 646 [NASA ADS] [CrossRef] [Google Scholar]
  18. Emmanoulopoulos, D., McHardy, I. M., & Papadakis, I. E. 2013, MNRAS, 433, 907 [NASA ADS] [CrossRef] [Google Scholar]
  19. Fiorucci, M., & Tosti, G. 1996, A&AS, 116, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Giommi, P., Blustin, A. J., Capalbi, M., et al. 2006, A&A, 456, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Gupta, A. C., Agarwal, A., Mishra, A., et al. 2017, MNRAS, 465, 4423 [NASA ADS] [CrossRef] [Google Scholar]
  22. Hahn, J. 2015, in 34th International Cosmic Ray Conference (ICRC2015), Int. Cosmic Ray Conf., 34, 917 [NASA ADS] [Google Scholar]
  23. Hosokawa, R., Adachi, R., Murata, K. L., et al. 2020, ATel, 13755, 1 [NASA ADS] [Google Scholar]
  24. Howell, S. B., Mitchell, K. J., & Warnock, A. I. 1988, AJ, 95, 247 [NASA ADS] [CrossRef] [Google Scholar]
  25. Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Kapanadze, B., Vercellone, S., Romano, P., et al. 2018, MNRAS, 480, 407 [NASA ADS] [CrossRef] [Google Scholar]
  27. Kidger, M., Takalo, L., & Sillanpaa, A. 1992, A&A, 264, 32 [NASA ADS] [Google Scholar]
  28. Kinman, T. D. 1975, in Variable Stars and Stellar Evolution, eds. V. E. Sherwood, & L. Plaut, IAU Symp., 67, 573 [NASA ADS] [CrossRef] [Google Scholar]
  29. Komossa, S., & Grupe, D. 2020, ATel, 13785, 1 [NASA ADS] [Google Scholar]
  30. Komossa, S., Grupe, D., Parker, M. L., et al. 2020a, MNRAS, 498, L35 [NASA ADS] [CrossRef] [Google Scholar]
  31. Komossa, S., Grupe, D., & Gomez, J. L. 2020b, ATel, 13658, 1 [NASA ADS] [Google Scholar]
  32. Kushwaha, P., Sahayanathan, S., & Singh, K. P. 2013, MNRAS, 433, 2380 [NASA ADS] [CrossRef] [Google Scholar]
  33. Kushwaha, P., Gupta, A. C., Wiita, P. J., et al. 2018a, MNRAS, 473, 1145 [NASA ADS] [CrossRef] [Google Scholar]
  34. Kushwaha, P., Gupta, A. C., Wiita, P. J., et al. 2018b, MNRAS, 479, 1672 [NASA ADS] [Google Scholar]
  35. Kushwaha, P., Pal, M., Kalita, N., et al. 2020, ApJ, submitted [arXiv:2010.14431] [Google Scholar]
  36. Laine, S., Dey, L., Valtonen, M., et al. 2020, ApJ, 894, L1 [CrossRef] [Google Scholar]
  37. Lehto, H. J., & Valtonen, M. J. 1996, ApJ, 460, 207 [NASA ADS] [CrossRef] [Google Scholar]
  38. Liu, H. T., & Bai, J. M. 2006, ApJ, 653, 1089 [NASA ADS] [CrossRef] [Google Scholar]
  39. Lorenzetti, D., Massaro, E., Perola, G. C., & Spinoglio, L. 1989, ApJS, 71, 175 [NASA ADS] [CrossRef] [Google Scholar]
  40. Mattox, J. R., Bertsch, D. L., Chiang, J., et al. 1996, ApJ, 461, 396 [NASA ADS] [CrossRef] [Google Scholar]
  41. Neronov, A., & Vovk, I. 2011, MNRAS, 412, 1389 [NASA ADS] [Google Scholar]
  42. Nolan, P. L., Abdo, A. A., Ackermann, M., et al. 2012, ApJS, 199, 31 [NASA ADS] [CrossRef] [Google Scholar]
  43. Pihajoki, P., Valtonen, M., Zola, S., et al. 2013, ApJ, 764, 5 [NASA ADS] [CrossRef] [Google Scholar]
  44. Pollack, M., Pauls, D., & Wiita, P. J. 2016, ApJ, 820, 12 [NASA ADS] [CrossRef] [Google Scholar]
  45. Poole, T. S., Breeveld, A. A., Page, M. J., et al. 2008, MNRAS, 383, 627 [Google Scholar]
  46. Prince, R. 2019, ApJ, 871, 101 [Google Scholar]
  47. Prince, R., Raman, G., Hahn, J., Gupta, N., & Majumdar, P. 2018, ApJ, 866, 16 [NASA ADS] [CrossRef] [Google Scholar]
  48. Prince, R., Khatoon, R., & Stalin, C. S. 2021, MNRAS, 502, 5245 [NASA ADS] [CrossRef] [Google Scholar]
  49. Raiteri, C. M., Villata, M., Ibrahimov, M. A., et al. 2005, A&A, 438, 39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Rakshit, S., Stalin, C. S., Muneer, S., Neha, S., & Paliya, V. S. 2017, ApJ, 835, 275 [NASA ADS] [CrossRef] [Google Scholar]
  51. Rector, T. A., & Perlman, E. S. 2003, AJ, 126, 47 [NASA ADS] [CrossRef] [Google Scholar]
  52. Reinhart, D., Steineke, R., Schoch, K., et al. 2020, ATel, 13677, 1 [NASA ADS] [Google Scholar]
  53. Richards, J. L., Max-Moerbeck, W., Pavlidou, V., et al. 2011, ApJS, 194, 29 [Google Scholar]
  54. Rodríguez-Ramírez, J. C., Kushwaha, P., de Gouveia Dal Pino, E. M., & Santos-Lima, R. 2020, MNRAS, 498, 5424 [Google Scholar]
  55. Roming, P. W. A., Kennedy, T. E., Mason, K. O., et al. 2005, Space Sci. Rev., 120, 95 [NASA ADS] [CrossRef] [Google Scholar]
  56. Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
  57. Siejkowski, H., & Wierzcholska, A. 2017, MNRAS, 468, 426 [NASA ADS] [CrossRef] [Google Scholar]
  58. Sillanpaa, A., Haarala, S., Valtonen, M. J., Sundelius, B., & Byrd, G. G. 1988, ApJ, 325, 628 [NASA ADS] [CrossRef] [Google Scholar]
  59. Sillanpaa, A., Takalo, L. O., Pursimo, T., & Lehto, H. J. 1996a, A&A, 305, L17 [Google Scholar]
  60. Sillanpaa, A., Takalo, L. O., Pursimo, T., et al. 1996b, A&A, 315, L13 [Google Scholar]
  61. Stetson, P. B. 1987, PASP, 99, 191 [Google Scholar]
  62. Stetson, P. B. 1992, in Astronomical Data Analysis Software and Systems I, eds. D. M. Worrall, C. Biemesderfer, & J. Barnes, ASP Conf. Ser., 25, 297 [Google Scholar]
  63. Sundelius, B., Wahde, M., Lehto, H. J., & Valtonen, M. J. 1996, in Blazar Continuum Variability, eds. H. R. Miller, J. R. Webb, & J. C. Noble, ASP Conf. Ser., 110, 99 [NASA ADS] [Google Scholar]
  64. Sundelius, B., Wahde, M., Lehto, H. J., & Valtonen, M. J. 1997, ApJ, 484, 180 [NASA ADS] [CrossRef] [Google Scholar]
  65. Valtaoja, E., Lehto, H., Teerikorpi, P., et al. 1985, Nature, 314, 148 [CrossRef] [Google Scholar]
  66. Valtonen, M. J. 1996, in Workshop on Two Years of Intensive Monitoring of OJ 287 and 3C66A, ed. L. O. Takalo, 64 [Google Scholar]
  67. Valtonen, M. J., Nilsson, K., Sillanpää, A., et al. 2006, ApJ, 643, L9 [NASA ADS] [CrossRef] [Google Scholar]
  68. Valtonen, M. J., Zola, S., Ciprini, S., et al. 2016, ApJ, 819, L37 [NASA ADS] [CrossRef] [Google Scholar]
  69. Valtonen, M. J., Zola, S., Pihajoki, P., et al. 2019, ApJ, 882, 88 [CrossRef] [Google Scholar]
  70. Vaughan, S., Edelson, R., Warwick, R. S., & Uttley, P. 2003, MNRAS, 345, 1271 [NASA ADS] [CrossRef] [Google Scholar]
  71. Villata, M., Raiteri, C. M., Gurwell, M. A., et al. 2009, A&A, 504, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Wagner, S. J., & Witzel, A. 1995, ARA&A, 33, 163 [NASA ADS] [CrossRef] [Google Scholar]
  73. Zhang, Y. H., Celotti, A., Treves, A., et al. 1999, ApJ, 527, 719 [NASA ADS] [CrossRef] [Google Scholar]
  74. Zibecchi, L., Andruchow, I., Cellone, S. A., et al. 2017, MNRAS, 467, 340 [NASA ADS] [Google Scholar]
  75. Zola, S., Reichart, D. E., Kouprianov, V., et al. 2020, ATel, 13637, 1 [NASA ADS] [Google Scholar]

All Tables

Table 1.

Log of photometric observations for the blazar OJ 287.

In the text
Table 2.

Fractional variability and variability time estimated for various states in different waveband as shown in Fig. 1, and explained in Sect. 3.1.1 in detail.

In the text
Table 3.

Results of INV observations of OJ 287.

In the text
Table 4.

Modeled parameters of γ-ray SEDs for all the segments identified in Fig. 1.

In the text
Table 5.

DCF parameters for all the combinations.

In the text
Table 6.

Multiwavelength SED modeling results with the best-fit parameters values.

In the text

All Figures

thumbnail Fig. 1.

Broadband light curve of OJ 287 from 2017–2020. Panel 1 (top) shows the weekly binned γ-ray light curve for 0.1–300 GeV. Panels 2, 3, and 4 are the Swift-XRT and UVOT light curves. Panel 5 is the radio light curve from OVRO at 15 GHz. The entire light curve is divided in five different states based on the flux and magnitude seen in Swift-XRT and UVOT. The various states are denoted A, B, C, D, and E and their time duration is represented by the color patches.
In the text
thumbnail Fig. 2.

Light curves for OJ 287; green denotes V band while red denotes R filter. In each plot the X-axis is JD and the Y axis is the source magnitude. Observation date and the telescope used are indicated in each plot. Telescope A, is JS (2.15 m Jorge Sahade telescope), telescope B is HSH (Helen Sawyer Hogg telescope), and telescope C is JCBT (Vainu Bappu Observatory, India).
In the text
thumbnail Fig. 3.

Gamma-ray SED of all the segments identified during 2017–2020 in OJ 287 modeled with three different spectral models: PL, LP, and BPL (see Sect. 3.2 for more details). The down arrow represents the upper limit in that particular segment.
In the text
thumbnail Fig. 4.

Cross-correlation of optical/UV vs X-ray. The five rows of the plot are the five states (A, B, C, D, E) defined in Fig. 1. Horizontal red and blue dashed lines are 2σ and 3σ significance respectively. We do not observe any significant time lag in any of the combinations. During state C, we see some time lags but the correlation coefficient are below 50% and below 2σ significance, and hence do not consider as an actual time lag.
In the text
thumbnail Fig. 5.

Multiwavelength spectral energy distribution for all the various segments observed during the year 2017–2020. The dot-dahsed and dahsed line in different colors in the synchrotron and SSC peaks are the time evolution of the model. The down arrow represents the γ-ray upper limits. The optical–UV, X-ray, and γ-ray data points are shown in red, blue, and magenta.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.