| Issue |
A&A
Volume 652, August 2021
|
|
|---|---|---|
| Article Number | A83 | |
| Number of page(s) | 12 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202140851 | |
| Published online | 13 August 2021 | |
Relation of internal attenuation, dust emission, and the size of spiral galaxies
Calibration at low-z and how to use it as a cosmological test at high-z
1
Instituto de Astrofísica de Canarias, 38205 La Laguna, Tenerife, Spain
e-mail: fuego.templado@gmail.com
2
Departamento de Astrofísica, Universidad de La Laguna, 38206 La Laguna, Tenerife, Spain
Received:
22
March
2021
Accepted:
25
May
2021
Aims. Dust in spiral galaxies produces emission in the far-infrared (FIR) and internal absorption in visible wavelengths. However, the relation of the two amounts is not trivial because optical absorption may saturate, but the FIR emission does not. Moreover, the volume concentration of dust plays a role in the relation of absorption and emission, which depends on the size of the galaxy. We explore the relation of these three quantities.
Methods. In order to understand the geometrical problem, we developed a model of dust distribution. We also investigated the relation of the three variables with real data of spiral galaxies at z < 0.2 using the spectroscopic Sloan Digital Sky Survey and FIR AKARI survey. Internal absorptions were derived with two different methods: the ratio of emission lines Hα and Hβ, and a previously calibrated relation based on the color variations as a function of absolute magnitude and concentration index.
Results. We find that in our low-z sample, the dependence of the average internal attenuation on galaxy size is negligible on average because of the relation of dust mass with size. It allows us to derive the internal attenuation of the galaxy, AV, even when we only know its FIR flux. This attenuation approximately depends on the inclination of the galaxy i as AV̄ = γV̄ log101cos i, where γV is a constant. We found that γV has a maximum value for galaxies of 1.45 ± 0.27 magnitudes. When similar properties of dust are assumed, a general expression can be used at any z: γV̄ = (1.45 ± 0.27)fMexp[−(1.0 ± 0.6)fM] and fM = 7.6 × 10−6 αhR−1.75 × (FFIR/700 Jy) 1.87 × fcosmol.(z); the dependence on the cosmological model is embedded in fcosmol.(z) = dL(z)(Mpc)2(1 + z)(1.75η − 1.87), where η = 2 for cosmologies following Etherington’s relation, dL is the luminosity distance, αhR is the angular size of the scalelength, and FFIR the flux at wavelength 100(1 + z) μm.
Conclusions. For cases of nonsaturation (f ≲ 3.6), this might be used as a cosmological test because the factor fcosmol. at high z varies strongly in different cosmologies. Although the present-day sensitivity of FIR or millimeter surveys does not allow us to carry out this cosmological test within the standard model, it may be used in the future, when we can observe galaxies at z = 3−5 with a sensitivity at ∼500 μm better than ∼10 μJy, for instance. For much lower z or different cosmological models, a test might be feasible at present.
Key words: dust, extinction / galaxies: spiral / galaxies: ISM / cosmology: observations
© ESO 2021
1. Introduction
The distribution of dust and its corresponding absorption are well known in the Milky Way (e.g., Unavane et al. 1998; Drimmel et al. 2003; Schlafly & Finkbeiner 2011) and in other nearby spiral galaxies (e.g., Peletier et al. 1995; Paleologou 1997; Cho & Park 2009; Pohlen et al. 2010; Devour & Bell 2016; Viaene et al. 2017; Bianchi et al. 2018; Salim et al. 2018; Salim & Narayanan 2020). Attenuation curves result from a combination of dust grain properties, dust content, and the spatial arrangement of dust and different populations of stars (e.g., Salim & Narayanan 2020). Maps of Galactic extinction and internal attenuation within a galaxy are important to correct the magnitudes of extragalactic objects, in order to derive the properties of the stellar distribution in that galaxy.
Although the terms extinction and attenuation are sometimes used interchangeably in the literature, the internal absorption we analyzed refers more to the usual meaning of the second term. Dust attenuation refers to the general effect on the spectrum of an extended object through dust; in this sense, all extinction curves are attenuation curves, but not all attenuation curves are extinction curves. In general, ‘attenuation’ is used here to indicate that the geometry of the sources and dust in a system is more complex than a single point-like object in the background of a dust layer. The measurement and/or theoretical calculation of attenuation is therefore significantly more complex than for extinction because it also includes the effects arising from the distribution of stars and dust in the galaxy (Salim & Narayanan 2020).
There are different methods to derive the internal attenuation in spiral galaxies that are different from the Milky Way. The simplest method is using the colors and concentration indexes (e.g., Cho & Park 2009), or, when many filters are available, the fitting of photometry in several bands, the spectral energy distribution (SED), using templates based on stellar population synthesis models (e.g., Bruzual & Charlot 2003; Maraston 2005; Vazdekis et al. 2010) to model the stellar emission, which is perhaps the most common method at either low z (e.g., Boquien et al. 2013; Decleir et al. 2019) or high z (e.g., Walcher et al. 2011; Conroy 2013; Lo Faro et al. 2017; Buat et al. 2018; Schreiber et al. 2018). The attenuation curve can also be derived by modeling the galaxy SEDs using radiative transfer calculations (e.g., De Looze et al. 2014; Nersesian et al. 2020). Another way, applicable to galaxies with high ratios of star formation or to active galaxies, would be using the ratio of some spectral lines with known intrinsic values, for instance, the ratio of Hα and Hβ (Calzetti 2001).
Dust also produces emission, and this is another way to investigate its distribution, by using far-infrared (FIR) surveys (e.g., Calanog et al. 2013; Lam et al. 2019). Because the dust that produces FIR emission and internal attenuation is the same, it is clear that the two quantities must be related. In principle, we would expect a linear proportionality, but it is not so simple because optical absorption may saturate, that is, over a given amount of dust, we cannot see the stars in the far part of the galaxy, and adding more dust will not add more extinction over these stars, but the FIR emission does not saturate because the FIR absorption is totally negligible and all the radiation of the dust in a galaxy comes to the observer, regardless of how much dust we put on it.
Another element that plays a role in the relation of absorption and emission is the volume concentration of dust, which depends on the size of the galaxy. A galaxy with a given amount of dust and a large diameter receives a low average density of dust that produces small absorption. The opposite is also true: When the same amount of dust that produces the same FIR luminosity is distributed within a galaxy with a very small diameter, the concentration of dust is much higher, and consequently, the average absorption is much larger.
Qualitatively, the relation among the three variables (internal attenuation, dust emission, and size of spiral galaxies) is clear, but the quantitative evaluation of this relation is not immediate and needs some analyses. This is precisely one of the purposes of this paper: modeling the dust distribution to understand the connection among the three variables, which will be later calibrated with real data from the local universe. For modeling the dust distribution that gives rise to the galactic attenuation, the literature is rich: either based on analytic prescriptions for the galactic structure (e.g., Witt & Gordon 2000; Inoue et al. 2006; Popescu et al. 2011; Seon & Draine 2016), or semianalytical prescriptions (Granato et al. 2000; Fontanot & Somerville 2011; Wilkins et al. 2012; González-Pérez et al. 2013; Popping et al. 2017), or complex hydrodynamic galaxy formation simulations (Jonsson et al. 2006; Rocha et al. 2008; Natale et al. 2015; Narayanan et al. 2018; Trayford et al. 2020), many of them including a cosmological context. We do not enter in the discussion of complex models, but use simple analytical expressions, and we mainly focus on the statistical relation among the three variables, with the purpose of obtaining some easy-to-use recipes that can be used with multiple purposes, such as obtaining the average expected value of one of the variables when we know the other two.
The dependence of the absorption on the galaxy size and the dust mass (obtained from FIR emission) is indeed interesting as a cosmological test of the galaxies at high z. For instance, it has been questioned whether the strong linear size evolution of spiral galaxies (Trujillo et al. 2006; Shibuya et al. 2015) is intrinsic or is an artifact due to the use of an incorrect cosmological model (López-Corredoira 2010; Lerner 2018; Balakrishna Subramani et al. 2019). A tool for these characteristics might therefore break the degeneracy and give an answer, provided that the dust characteristics do not change the temperature and emission and absorption properties with time.
In order to understand the geometrical problem, we develop a simple toy model in Sect. 2. The real relation for low-redshift (z < 0.2) galaxies is obtained for a sample derived from a cross-correlation of the optical Sloan Digital Sky Survey (SDSS) spectroscopic survey (York et al. 2000; Abazajian et al. 2009) and the FIR AKARI survey (Doi et al. 2015) in Sect. 3. In Sect. 4 we indicate how this relation among attenuation, FIR emission, and size can be extrapolated at high z as a possible cosmological test.
2. Toy model of internal dust absorption in spiral galaxies
2.1. Basic considerations
First, we give the basic equations that relate the average attenuation in magnitudes with the distribution of flux in the galaxy. Within a maximum angular radius α from the center of the galaxy, corresponding to a linear size R0, max = αdA, where dA is the angular distance of the galaxy, the average internal attenuation in V-band measured by an external observer is
where R0 and θ0 are polar coordinates of the linear projected area onto the sky; FV, obs(R0, θ0), AV(R0, θ0) are the corresponding observed flux after extinction absorption and cumulative extinction in those coordinates, respectively; and FV, obs, total is the total integrated flux in the area. The attenuation is related to the flux through
where FV, em is the emitted flux of the stars in V band (before attenuation correction).
Because the galaxies have different inclinations i and their internal absorption is proportional to  (Shao et al. 2007; Cho & Park 2009) (where in practice
(Shao et al. 2007; Cho & Park 2009) (where in practice  , with rmajor and rminor the major and minor axis of the projected disk galaxy), we would instead consider the amount γV independent of the inclination, which is defined as
, with rmajor and rminor the major and minor axis of the projected disk galaxy), we would instead consider the amount γV independent of the inclination, which is defined as
2.2. Disk model
Previous equations can be used to compute the attenuation for any flux and dust distribution of any galaxy. We applied them to the particular case of a spiral galaxy with an exponential disk in the stellar populations and dust. It does not include spiral arms, a stellar halo, or the central components (bulge, long bar, or stellar ring). Therefore this simple toy model may better represent disk-dominated galaxies, in which the ratio of bulge flux to the total is low. Nonetheless, for the relation of Petrosian radii and scalelength in Sect. 2.5, we show that the effect of the bulge is negligible, and for the distribution of stars and dust, the effect of the bulge changes the distribution of stars and dust in the central parts only slightly, as we show in Sect. 2.4. The relations derived in this section should be interpreted as a rough approximation of the expected behavior, not as an accurate predictive model, which is better derived in the calibration with real galaxies in Sect. 3.
For an axisymmetric star and dust distribution corresponding to a disk,
where R, z are the coordinates in the plane of the galaxy, r is the distance from the plane of the galaxy along the line of sight with positive values toward the observer, ρ*, V is the emitted flux per unit volume in V band by the stellar component, and ρd is the dust density.
For a simple exponential disk for stars and dust, with the same scalelength hR for both components,
where Md is the total mass of dust in the exponential disk. Hence, with Eq. (2),
With this model, γV is independent of the absolute magnitude of the galaxy because the amplitude FV, total, em cancels out in numerator and denominator of Eq. (2).
This simple model fails in representing the flux of spiral galaxies in the central part, where a bulge or bar may produce a high amount of light, and where the disk usually presents a deficit of stars with respect to a pure exponential disk (López-Corredoira et al. 2004). Nonetheless, the deficit of flux produced by a hole in the disk may roughly be compensated for with the excess produced by the other central components; and for the external part, the exponential disk is a quite accurate representation.
For low-attenuation cases (AV ≪ 1), AV ≈ 1.086 κVMd g(R, hR, hz, *,hz, d), that is, proportional to the total dust mass and a function g depending on the geometrical scales of the disk. For low attenuation, the ratio  is therefore independent of the dust mass and only depends on the geometrical distribution of stars and dust. However, as we show below, for high dust masses, the relation is not linear.
is therefore independent of the dust mass and only depends on the geometrical distribution of stars and dust. However, as we show below, for high dust masses, the relation is not linear.
2.3. Numerical example
We carried out a numerical calculation for some usual values of the parameters. We set κV = 1.33 × 103 m2 kg−1 (Loeb & Haiman 1997). We set the scalelength hR, and dust mass Md variable parameters around typical values of the Milky Way: hR = 3 kpc (McMillan 2011) and Md = Md, MW = 2.8 × 107 M⊙ (Gutiérrez & López-Corredoira 2014). We assumed the average value of cos i = 0.5.
First, we assumed an angular radius α = 1.5″ corresponding to the radius of fibers for spectroscopy in the SDSS survey (York et al. 2000) and a typical angular distance of 200 kpc (corresponding to z = 0.050 with the standard cosmology, h0 = 0.7, ΩΛ = 0.7), that is, R0, max = 1.5 kpc. We plot the average absorption γV (absorption normalized to cos i = 0.1) versus the scalelength hR for different combinations of scaleheights (typical values obtained in the Milky Way) in the left panel of Fig. 1. Second, we assumed R0, max = ∞, that is, the average attenuation of the whole galaxy. We plot in the left panel of Fig. 1γV versus scalelength, also for different combinations of scaleheights. For any value of R0, max, the mean absorption decreases with the size of the galaxy (proportional to hR), but it is almost independent of the variation in scaleheight. For low hR, the absorption saturates and goes asymptotically to a limit. With lowest R0, max, the mean absorption is higher because we averaged only in the central parts of the galaxy. In the central panel of Fig. 1 we plot this for a fixed hR and as a function of the dust mass, where the relation is linear for low masses, but slowly grows for high masses. The ratio of the average absorption up to R0, max = 1.5 kpc and the average total absorption remain more or less constant. Therefore we can apply a correcting factor  in the absorption that only depends on the size of the galaxy to take the limited size of the SDSS fiber into account,
in the absorption that only depends on the size of the galaxy to take the limited size of the SDSS fiber into account,
 |
Fig. 1. Theoretical value of γV for a model of a purely exponential disk in three cases. Left: constant dust mass. Middle: constant scaleheight. Right: dust mass proportional to the square of the scalelength. |
derived from a fit in the left panel of Fig. 1 (rms of the fit with respect to C equal to 0.052).
Although the dependence of the absorption and dust mass in the left and central panel of Fig. 1 is clear, these two numerical calculations are not realistic in practice because hR and Md are not independent variables. A more realistic case would be modeling the dependence of Md on hR as well. We assumed for a third experiment 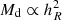 (this dependence is indeed observed in the data; see Sect. 3), that is, we made ρd(R = 0, z = 0) constant (see Eq. (7)). The dependence of γV on hR (proportional to the square root of Md) is illustrated in the right panel of Fig. 1. The net increase of the average absorption with scalelength for R0, max = 1.5 kpc and the constant average absorption when integrated in the whole galaxy (R0, max = ∞) are interesting results.
(this dependence is indeed observed in the data; see Sect. 3), that is, we made ρd(R = 0, z = 0) constant (see Eq. (7)). The dependence of γV on hR (proportional to the square root of Md) is illustrated in the right panel of Fig. 1. The net increase of the average absorption with scalelength for R0, max = 1.5 kpc and the constant average absorption when integrated in the whole galaxy (R0, max = ∞) are interesting results.
2.4. Adding a bulge
The previous toy model only includes an exponential disk of stars and dust. With the same method, a set of models might be created in which we can substitute Eqs. (6) and (7) for other more complex expressions, including a clumpy disk and/or a bulge. The results will change, but the trends of the variation in attenuation with size and dust mass will be similar. For instance, we substituted Eq. (6) for
that is, an exponential disk for R ≥ hR and a bulge (taking the expression by López-Corredoira et al. (2005) for the Milky Way ellipsoidal bulge, but not considering the triaxiality and setting an axisymmetry), and setting K1(hR) and K2(hR) such that the disk contributes 80% of the observed light, and the bulge contributes 20%. The result for the case of  is shown in the right panel of Fig. 1. We observe variations with respect to the disk alone, but with similar trends.
is shown in the right panel of Fig. 1. We observe variations with respect to the disk alone, but with similar trends.
2.5. Relation of scalelength and Petrosian radii
In the SDSS, Petrosian radii are used to measure the size of the galaxies instead of the scalelength, but both quantities can be easily related. The SDSS provides the Petrosian radius, defined as RP such that (Shimasaku et al. 2001)1
The Petrosian flux used in the SDSS is
The Petrosian half-light and 90% light radii are RP50 and RP90, respectively, such that
When we apply these definitions to our previous disk model, we obtain the results that we show in Fig. 2. In the same figure, we also show RP50 and RP90 of the cases with a different inclination of the galaxy (cos i = 0.2 instead of 0.5) and including a bulge component that is represented by a ratio of the total observed light coming from the center of the galaxy apart from the disk. The three different cases for RP50 and RP90 show slight differences. However, when we calculate RP90 − RP50, this last amount as a function of hR is almost independent of the inclination of the galaxy and the ratio of the bulge contamination. This is expected because the outer light between 50% and 90% only traces the disk. Therefore we took this amount to determine the correlation with hR independently of other parameters. A linear fit of RP90 − RP50 in Fig. 2 for cos i = 0.5 and a pure disk gives
 |
Fig. 2. Relation of Petrosian half-light and 90% light radii with the scalelength of a spiral galaxy, either with a purely exponential disk or with some bulge component with 20% of the light; we set hz, * = 0.3 kpc, hz, d = 0.1 kpc, and Md = 2.8 × 107 M⊙. |
The deviation from a perfect proportionality ([RP90 − RP50]∝hR) stems from the nonzero thickness of the disk. The term 0.35 kpc is almost negligible and does not affect our calculations strongly. We use this relation to derive hR from RP50 and RP90 given in the SDSS data, independently of the inclination and the bulge ratio.
3. Local calibration of absorption as a function of size and dust emission
The theoretical calculations in the previous section give us a clear relation of absorption, dust emission (correlated with the dust mass), and size of the galaxy. We assumed a simplistic model, however, and the reality may be more complex. Particularly, the dependence on the size of the galaxy depends on the geometrical distribution of gas and stars. In order to determine this relation in reality, we calibrated it with local (z < 0.2) galaxies using a cross-correlation of the surveys SDSS and AKARI for FIR fluxes.
3.1. Data
For our purpose, we need information of the galaxy sizes and colors and/or spectra, which we obtained from the SDSS. We also need FIR fluxes to calculate dust masses, which we obtained using the AKARI survey.
Photometric and morphological information in the optical range was obtained from the SDSS Data Release 7 (SDSS-DR7; York et al. 2000; Abazajian et al. 2009). The spectroscopic data were taken from SDSS-Data Release 14 (Abolfathi et al. 2018)2. Petrosian radii RP50 and RP90, magnitudes, fluxes in Hα and Hβ, and the galaxy classification were taken from the SDSS data as well. The scalelength hR was derived with Eq. (15). Data for the inclination i were obtained from the ellipticity ϵ of the projected galaxy, in which cos i = 1 − ϵ, and  , with U, Q the Stokes parameters given by the SDSS (we took them at r band). We selected only galaxies with significant emission lines of Hα and Hβ: > 3σ detection.
, with U, Q the Stokes parameters given by the SDSS (we took them at r band). We selected only galaxies with significant emission lines of Hα and Hβ: > 3σ detection.
AKARI (Murakami et al. 2007; Doi et al. 2015) is a FIR all-sky atlas from a sensitive all-sky survey using the Japanese AKARI satellite. The survey covers > 99% of the sky in four photometric bands centered at 65 μm, 90 μm, 140 μm, and 160 μm, with spatial resolutions ranging from 1.0 to 1.5 arcsec. It has a better spatial resolution and wider wavelength coverage than previous all-sky survey such as IRAS. AKARI was operated with a telescope with a 68.5 cm diameter, cooled down to 6 K and observed from a Sun-synchronous polar orbit at 700 km altitude. It was successfully launched on 21 February 2006 by an M–V rocket from the Uchinoura Space Center, Japan. AKARI ran out of its onboard supply of cryogen, liquid helium, on August 26, 2007, after successful operation and observations that began on May 8, 2006, achieving the expected lifetime of 550 days, including the performance verification phase and three observation phases. This survey was particularly useful for exploring the dusty Universe. We only used data of galaxies with flags GRADE and FQUAL90 of AKARI with a maximum quality equal to 3 and available fluxes in the four wavelengths.
First, we cross-correlated the AKARI data with those from the SDSS, matching objects of the AKARI and SDSS catalogs with separations < 10 arcsec. This resulted in a sample of 9059 galaxies. Then we completed the required information by selecting only galaxies with measured Hα and Hβ flux in the SDSS galspecline catalog. Finally, for morphology, we used the classification made by Meert et al. (2015), which provides 2D decompositions in the Sloan g, r, and i bands for several parametric models (de Vaucouleurs, Sérsic, de Vaucouleurs plus exponential disk, and Sérsic plus exponential disk). The final sample containing photometric, spectroscopic, and morphology information comprises 5386 galaxies. Examples of the selected galaxies are shown in Fig. 3. The use of nearby galaxies with z < 0.2 makes the angular and luminosity distance calculation almost independent of the cosmological model, that is, with a dependence on the cosmological model that is negligible. We calculated these distances from the redshift using the standard ΛCDM model with h0 = 0.7, ΩΛ = 0.7.
 |
Fig. 3. Examples of SDSS-selected galaxies with a counterpart in AKARI, that is, with a significant amount of dust. |
The selected galaxies have significant amounts of dust so that they can be detected in the FIR regime by AKARI. In addition, all galaxies have Hα and Hβ emission lines, which means that they should also be star forming. Therefore these are spiral or elliptical galaxies with a high amount of dust that might be produced by residual star formation (López-Corredoira et al. 2017b). About 1–2% of the whole set of galaxies were morphologically classified by the SDSS as ellipticals. However, all of them present significant emission lines, which means that they were either misclassified based on their apparent morphology, or they are elliptical galaxies with a high amount of residual star formation and/or nuclear activity.
3.2. Relation of dust mass to FIR at rest luminosities
In our model in Sect. 2 we used the dust mass instead of the FIR luminosities given by AKARI, but they can be approximately related to each other. We fit the observed fluxes Fν, obs in the four AKARI wavelengths λ to a dependence (e.g., López-Corredoira et al. 2017a, Sect. 4)
where Td is the dust temperature, βd is the emissivity, Ad is the amplitude, and B(ν, T) is the blackbody emission function. We obtain the parameters Td, βd, Ad with the four available frequencies, taking the error bars of the flux into account, in a χ2 fit. After we derived the three parameters of the dust emission, we obtained the bolometric luminosity through
where dL(z) is the luminosity distance. In the galaxies with an error in Lbol, dust lower than 20%, the average and rms of the two free parameters are ⟨β⟩ = 2.4, σβ = 2.1, ⟨Td⟩ = 23 K, and σTd = 10 K.
The calibration with mass can be made with the Milky Way dust, for which Lbol, MW = 2.6 × 1043 erg s−1 (Davies et al. 1997), and the dust mass is Md, MW = 2.8 × 107 M⊙. Therefore
3.3. Method 1 for calculating the internal absorption
A first method for calculating the absorption is using the ratio of the fluxes of the Hα and Hβ emission lines in the spectra of the galaxies: FHα and FHβ, respectively. The spectra are available in the SDSS, although with a fiber diameter of 3″, which assumes that the area in which we average the absorption is restricted. For an average z = 0.05 galaxy, we would be observing the innermost 1.5 kpc of the galaxy. The average attenuation is (Calzetti 2001)
where Rαβ = 2.86 in non-active galaxies, and Rαβ = 3.10 in active galactic nuclei (Osterbrock 1989).
We selected galaxies with z < 0.2, ΔHα/Hα < 1/3, ΔHβ/Hβ < 1/3,  , 0.1 < hR(kpc) < 10, and different ranges of absolute magnitude in r band (Mr; we did not correct for K–correction, which is small given the low redshift of the galaxies) between −23.0 and −18.0. Moreover, we required an error in the value of the dust mass Md obtained through Eq. (18) lower than 10%. In total, we have 3551 galaxies with these constraints.
, 0.1 < hR(kpc) < 10, and different ranges of absolute magnitude in r band (Mr; we did not correct for K–correction, which is small given the low redshift of the galaxies) between −23.0 and −18.0. Moreover, we required an error in the value of the dust mass Md obtained through Eq. (18) lower than 10%. In total, we have 3551 galaxies with these constraints.
The left panel of Fig. 4 shows that the dust mass is approximately proportional to the luminosity in r band. The central panel of Fig. 4 shows that  is approximately proportional to the luminosity in r band (we assumed Mr, MW = −20.5). This means through Eqs. (6) and (7) that when a single exponential disk is assumed, the luminosity and dust surface densities at R = 0 are approximately constant in the whole range of absolute magnitudes on average. The direct relation of the average dust mass with the scalelength is illustrated in the right panel of Fig. 4, giving a less clear trend. It forms a circle of points rather than an elongated structure, over which a linear trend is not clearly visible: a best linear fit in the log-log plot gives a slope 1.165, but as the green line shows, a slope of 2.00 is not excluded, therefore we can conclude nothing from this last plot. Hence we assumed a relation ⟨Md⟩∝⟨hR⟩2 derived from the combination of the plots in the right and central panels of Fig. 4.
is approximately proportional to the luminosity in r band (we assumed Mr, MW = −20.5). This means through Eqs. (6) and (7) that when a single exponential disk is assumed, the luminosity and dust surface densities at R = 0 are approximately constant in the whole range of absolute magnitudes on average. The direct relation of the average dust mass with the scalelength is illustrated in the right panel of Fig. 4, giving a less clear trend. It forms a circle of points rather than an elongated structure, over which a linear trend is not clearly visible: a best linear fit in the log-log plot gives a slope 1.165, but as the green line shows, a slope of 2.00 is not excluded, therefore we can conclude nothing from this last plot. Hence we assumed a relation ⟨Md⟩∝⟨hR⟩2 derived from the combination of the plots in the right and central panels of Fig. 4.
 |
Fig. 4. Correlation of dust mass and optical luminosity (left), scalelength and optical luminosity (middle), and dust mass and scalelenth (right). |
We carried out a double linear fit of the type
The reason for the choice of these variables is that (1) because the absorption is more or less proportional to the total dust mass within the linear regime of low attenuation, we set this variable y which reflects the excess or deficit of absorption with respect to the amount of dust on it; (2) because of the relation found previously of  on average (see Fig. 4), we set the independent variable x2 as stated in order to measure the effect of the variation in dust mass independently of the size of galaxy. Rearranging the terms, this equation can be rewritten as
on average (see Fig. 4), we set the independent variable x2 as stated in order to measure the effect of the variation in dust mass independently of the size of galaxy. Rearranging the terms, this equation can be rewritten as
where a′ = a, b′ = b − 2c, and c′ = 1 + c. However, Eq. (21) cannot be physically interpreted in a direct way because Md and hR are not independent variables, and an increase in hR should be associated with an increase in Md on average. Equation (20) physically represents the absorption per unit dust mass as a function of scalelength and excess or deficit of dust mass for an average galaxy of a given scalelength. We therefore relate the ratio of absorption to dust mass with two quantities that are almost independent.
The result of the best fit gives a = 0.46, b = −1.63, c = −0.89, with an rms of σ = 0.26, or equivalently, a′ = 0.46, b′ = 0.15, and c′ = 0.11. In Fig. 5 we show the data, this best fit of a′, b′, and c′, and the residuals. The dependence is dominated by the choice of variables, which with a constant absorption would by default result in a b′ = 0, c′ = 0 dependence.
 |
Fig. 5. Data (top panel; brown stands for an absence of data), best double-linear fit (middle), and residuals (bottom panel) of Eq. (21): |
In these double-linear fits, an average departure of γV ∝ Md is high, and the nonlinear regime is evident. Our toy-model predictions in Sect. 2 already foresaw this deviation for high values of Md, although it should be strictly linear for low values of Md (meaning c = 0, c′ = 1). In order to test that the rough estimates of the model can represent the data approximately, we analyzed the dependence on the double-linear fit as a function of Md. In Fig. 6 we plot the dependence on Md when instead of taking the whole sample, different subsamples in different ranges of dust mass in bins of 0.5 of log10 Md/Md, MW are used. c′ = 1 (absorption proportional to dust mass Md) is obtained for low Md, as expected, but the departure from linearity is conspicuous for Md > ∼Md, MW. For the remaining coefficients, a′ is more or less constant, and b′ presents a linear variation with dust mass, but within the rms of the fit (about 0.26). We therefore did not consider the variations of b′. The coefficient c′ follows the following dependence with Md from a fit of the data:
 |
Fig. 6. Dependence on Md of the fit coefficients log10γV = a′+b′log10hR(kpc)+c′log10(Md/Md, MW). |
The different samples have a different average redshift (see also Fig. 6), which means a different linear size aperture instead of the average 1.5 kpc. We assumed, as observed in the test with the toy model (Sect. 2; middle panel of Fig. 1), that the shape of the dependence on mass does not change with the average linear size aperture, however, only a constant would change, to be added to the factor a′.
The above expressions also give the absorption only within 1.5" from the center of the galaxy, and in order to estimate the average global absorption in the whole galaxy, we need to calculate  where C(1.5 kpc) is model dependent. When we apply the values of C given by Eq. (9) to a purely exponential disk model, average the redshift equal to 0.05, and take the average dependence of c′ on Md given in Eq. (22) into account, we obtain
where C(1.5 kpc) is model dependent. When we apply the values of C given by Eq. (9) to a purely exponential disk model, average the redshift equal to 0.05, and take the average dependence of c′ on Md given in Eq. (22) into account, we obtain
In Eq. (23), the last term is negative and monotonously increases with Md, except for a small fluctuation around Md ∼ 2.2Md, MW, but only with a negligible maximum amplitude of 0.09, which is due the approximation of c′ to an exponential function; asymptotically, it converges to a value zero for high dust masses. For hR > 0.1 kpc therefore  .
.
3.4. Method 2 for calculating internal absorption
Based on fitting of reddening in late-type galaxies, Cho & Park (2009) reported an average relation of internal attenuation in r band and concentration index  and the absolute magnitude
and the absolute magnitude
applicable within −21.95 ≤ Mr < ≤ − 18.65, 1.74 ≤ c ≤ 3.06. We assumed γV = 1.34γr (Rieke & Lebofsky 1985). This gives absorption values that are constrained within γV < 1.78.
Within the ranges of validity of Eq. (25), we have 3348 galaxies with −21.95 < Mr < −18.65. The dependences and considerations of Fig. 4 are the same as with method 1 because they do not depend on the absorption. Following the same type of analysis as with method 1, we arrive at the best double-linear fit of y = a + b * x1 + c * x2 with ![$ \mathit{y}=\log _{10}\left[\overline{\gamma _V}(R_{0,\mathrm{max}}=\infty)\left(\frac{M_{\mathrm{d}}}{M_{\mathrm{d,MW}}}\right)^{-1}\right] $](/articles/aa/full_html/2021/08/aa40851-21/aa40851-21-eq55.gif) and x1 = log10hR(kpc),
and x1 = log10hR(kpc), ![$ x_2=\log_{10}\left[\left(\frac{M_{\mathrm{d}}}{M_{\mathrm{d,MW}}}\right)\left(\frac{1}{h_R(\mathrm{kpc})^2}\right)\right] $](/articles/aa/full_html/2021/08/aa40851-21/aa40851-21-eq56.gif) : a = 0.10, b = −1.84, c = −0.96, and an rms of σ = 0.10; or equivalently, a′ = 0.10, b′ = 0.08, c′ = 0.04 for a fit of the type y = a′+b′*x1 + c′*x2 with
: a = 0.10, b = −1.84, c = −0.96, and an rms of σ = 0.10; or equivalently, a′ = 0.10, b′ = 0.08, c′ = 0.04 for a fit of the type y = a′+b′*x1 + c′*x2 with ![$ \mathit{y}=\log _{10}\overline{\gamma _V}(R_{0,\mathrm{max}}=\infty)] $](/articles/aa/full_html/2021/08/aa40851-21/aa40851-21-eq57.gif) x1 = log10hR(kpc), and
x1 = log10hR(kpc), and  .
.
When we compare these numbers with those of method 1, we see that they are similar. However, the data of absorption for individual galaxies calculated with both methods, although they presents an average correlation, do not agree well for individual galaxies: see Fig. 7 for 272 galaxies with 0.045 < z < 0.055 [this is in the redshift range in which the correction factor C of Eq. (9) is applied], with a best power-law fit of  .
.
 |
Fig. 7. Log-log plot of the correlation of the average absorption in the whole galaxy calculation with method 1 (and the model-dependent correction of aperture C) and method 2. |
The dependence of c′ on the dust mass is also similar to that of method 1: ![$ c^\prime=\exp\left[-(1.47^{+0.19}_{-0.16})\frac{M_{\mathrm{d}}}{M_{\mathrm{d,MW}}}\right] $](/articles/aa/full_html/2021/08/aa40851-21/aa40851-21-eq60.gif) . In spite of the small discrepancies, the average dependence of the absorption on size and dust mass is approximately the same as in method 1. The coefficients are summarized in Table 13, with the average of both methods. This average value of b′= − 0.05 ± 0.19 agrees with the value of zero deduced with the theoretical model (see the left panel of Fig. 1).
. In spite of the small discrepancies, the average dependence of the absorption on size and dust mass is approximately the same as in method 1. The coefficients are summarized in Table 13, with the average of both methods. This average value of b′= − 0.05 ± 0.19 agrees with the value of zero deduced with the theoretical model (see the left panel of Fig. 1).
Coefficients of the double linear fit log10γV(R0.max = ∞) = a′+b′*log10hR(kpc)+c′*log10(Md/Md, MW) for different ranges of dust mass Md, with γV calculated with two different methods.
3.5. Attenuation as a function of FIR flux
3.5.1. Dust mass as a function of 100 μm flux
We can express the attenuation as a function of the FIR flux through the corresponding relation of luminosity and flux, making use of the luminosity distance in a given cosmology. Bolometric luminosities are not always accessible in FIR. A total sampling in many frequencies would be required. However, it can be approximately obtained with only one filter at rest around 100 μm at rest: When a fixed temperature Tdust ∼ 20−25 K (Galametz et al. 2012) is assumed, in agreement with the 23 K we obtain from our fits, the maximum emission is precisely at λ ≈ 100 μm. We can also assume that
where Lbol is the bolometric luminosity of dust,  , λ = 100 μm. The parameter is usually set to f100 ≈ 1 because ν is approximately the width of the luminosity distribution (Δν). However, we can derive a better estimate of the parameter using our sample: 4379 galaxies from the AKARIxSDSS sample with errors of the two luminosities lower than 20%. Figure 8 shows the relation of the bollometric luminosity and the luminosity corresponding to 100 μm (with AKARI fluxes at 90 and 140 μm, we interpolated the value of the observed frequency 100(1 + z) μm flux). As a result of the best fit, we obtain f100 = 0.65 on average (χ2 fit assuming ΔLν/Lν constant).
, λ = 100 μm. The parameter is usually set to f100 ≈ 1 because ν is approximately the width of the luminosity distribution (Δν). However, we can derive a better estimate of the parameter using our sample: 4379 galaxies from the AKARIxSDSS sample with errors of the two luminosities lower than 20%. Figure 8 shows the relation of the bollometric luminosity and the luminosity corresponding to 100 μm (with AKARI fluxes at 90 and 140 μm, we interpolated the value of the observed frequency 100(1 + z) μm flux). As a result of the best fit, we obtain f100 = 0.65 on average (χ2 fit assuming ΔLν/Lν constant).
 |
Fig. 8. Log-log plot of the correlation of the luminosities at 100 μm (at rest) and bolometric luminosity for 4370 galaxies from the AKARIxSDSS sample with errors of the two luminosities lower than 20%. |
The FIR bolometric flux F100 μm(1 + z) is related to the luminosity νL100 μm(1 + z) by means of
where dL(z) is the luminosity distance.
When we relate the luminosity at 100 μm at rest with the dust mass through Eq. (18), with the bolometric luminosity related according to Eq. (26), f100 = 0.65, taking the average values of a′ and b′ from Table 1, and neglecting the dependence with hR (because b′= − 0.05 ± 0.19 is compatible with zero, which is the expected theoretical value), we obtain that the attenuation is
or equivalently, applying the definition of Eq. (3),
As discussed in Sect. 2, this negligible dependence on the galaxy size is kept while a relation  is given for most of the galaxies. The data indicate that this is a good approximation for low redshift. However, as we show in Sect. 4, the ratio of dust mass and size may not be the same.
is given for most of the galaxies. The data indicate that this is a good approximation for low redshift. However, as we show in Sect. 4, the ratio of dust mass and size may not be the same.
3.5.2. Regimes of low and high dust mass
Two special cases can be observed. For very high dust masses (Md ≳ 108 M⊙, f ≳ 3, 6), we may consider the term c′≈0 (saturation of absorption), so that the absorption is  . For very low dust masses (Md ≲ 107 M⊙, f ≲ 0.36), we may consider c′≈1 (linear relation of absorption and dust mass), so that we can consider the following dependence:
. For very low dust masses (Md ≲ 107 M⊙, f ≲ 0.36), we may consider c′≈1 (linear relation of absorption and dust mass), so that we can consider the following dependence:  (with f ≪ 1).
(with f ≪ 1).
4. Evolution of the ratio of dust absorption to emission
The dependence of the absorption on the galaxy size and FIR luminosity (implicit in the dependence on the dust mass) is interesting because this might be used as a cosmological test of the galaxies at high z. We did not carry out an analysis at high z given the lack of data at present, but we provide some indications how it might be used.
4.1. General law for any Md(hR)
The equation of the ratio of absorption to emission is interesting for studying high-redshift galaxies because it is not affected by evolution. It is independent of the stellar luminosity evolution and only depends on the dust properties (parameters β and Td), but we know that the evolution of dust properties with z in spiral galaxies is not significant (López-Corredoira et al. 2017a). Only the possible evolution in size is expected to affect this evolution.
The stellar mass and dust mass are roughly proportional in spiral galaxies (Calura et al. 2017; Davies et al. 2019), and spiral galaxies with the same stellar mass have sizes at high z that are much smaller than at low z (Trujillo et al. 2006). When we assume that this evolution of galaxy sizes is correct, we therefore have much smaller hR at high z than at low z for the same dust masses. The equations derived in Sect. 3 are not valid in the application to high z accordingly because the proportionality between dust mass and size changes. Nonetheless, from Sect. 3 we learned that our basic predictions of the toy model in Sect. 2 are roughly correct: in particular, that the dependence on the size is almost null when  because the decrease in absorption with increase in size is compensated for by the increase in dust mass. The question now is what happens in an hypothetical case in which the size increases or decreases, but the dust mass is kept constant. In this case, the dependence on size is not null because the dust mass does not vary in the way predicted in the left panel of Fig. 1.
because the decrease in absorption with increase in size is compensated for by the increase in dust mass. The question now is what happens in an hypothetical case in which the size increases or decreases, but the dust mass is kept constant. In this case, the dependence on size is not null because the dust mass does not vary in the way predicted in the left panel of Fig. 1.
At low z, we obtain
(see the right panel of Fig. 4). A null dependence on size can be understood as a factor f in Eq. (28),
When we use Md from Eq. (30), we recover  . However, when high z is compared with low z, Md is kept constant and hR changes at high z with respect to the low z cases, an inconstant f(hR) would result. In a general case, taking β = 1.75 as obtained in the right panel of Fig. 1 in the linear regime, Eq. (28) would be expressed as
. However, when high z is compared with low z, Md is kept constant and hR changes at high z with respect to the low z cases, an inconstant f(hR) would result. In a general case, taking β = 1.75 as obtained in the right panel of Fig. 1 in the linear regime, Eq. (28) would be expressed as
where αhR is the equivalent angular size of the scalelength hR, and dA is the angular distance. With fM we represent f for a fixed value of Md. Only the factor fcosmol.(z) depends on the cosmological model. For any cosmological model, dA = (1 + z)−ηdL(z) (in the case of a Friedmann-Lemaître-Robertson-Walker cosmology, η = 2, what is called Etherington’s distance-duality relation; Holanda et al. 2011), therefore
Figure 9 shows the dependence of fcosmol. on the cosmological models4, thus giving the possibility of using the above relation as a cosmological test. The differences are especially large for static cosmologies that do not follow Etherington’s relation, therefore the test would be very suitable for testing the value of η, even at z < 1.
 |
Fig. 9. Predictions of fcosmol.(z) for nine cosmological models. |
Equation (32) should not be interpreted as a direct dependence in the linear regime of the absorption proportional to  ; this is not the physical meaning because Md is not independent of hR. It is a simple rule to compare low- and high-redshift data, which means that when we fix the value of the dust mass, we can evaluate how a change in galaxy size with respect to the low z cases increases the absorption.
; this is not the physical meaning because Md is not independent of hR. It is a simple rule to compare low- and high-redshift data, which means that when we fix the value of the dust mass, we can evaluate how a change in galaxy size with respect to the low z cases increases the absorption.
4.2. Difficulties in applying Eq. (32) to data at high z
In order to use this expression in practical cases and show the variation of absorption with size for a given dust mass, we need to be in the regime of nonsaturation, that is, f ≲ 3.6. In Fig. 10 we plot the required sensitivity of the FIR photometer assuming the standard cosmological model. As observed, we would need a detector that reached well below 0.5 mJy at z > 1. At z = 3, we would need to detect sources with F400 μm below 10–100 μJy.
 |
Fig. 10. Minimum sensitivity of a significant detection of a photometer at a wavelength (1 + z)100 μm as a function of the redshift and the scalelength of the galaxy, derived making fM = 3.6 in Eq. (32) using standard cosmological ΩΛ = 0.7, H0 = 70 km s−1Mpc−1 to evaluate the luminosity distance. |
In Table 2 we list available FIR and millimeter surveys. No survey reaches the required limit of nonsaturation for high z. The only survey that approaches the limits is ALMA at 1 mm, which can reach 47.5 μJy, although we would only observe the peak of dust emission for sources at z ≈ 9 at these wavelengths, which requires still better sensitivity, and for lower z, we expect lower fluxes at 1 mm, which would again require better sensitivities. With current surveys, we therefore cannot analyze the separate dependence on radius and mass because we would be in the saturation regime. Nonetheless, it is only a matter of time that some FIR or millimeter survey with the required sensitivity become available, or some explicit very deep observations could be carried out in some few high z galaxies in order to reach the limits. Because of the strong dependence of fcosmol. on the cosmological model, current surveys might moreover obtain nonsaturated dust sources at high z for some exotic cosmological models (see Fig. 9 or Sect. 4.3).
FIR and millimetric wavelength ≤1.5 mm surveys and their sensitivity at 5σ detection.
A greater difficulty might be obtaining a good absorption measurement. The application of the method of the line ratios of Hα and Hβ (method 1) is possible and was already obtained for some high z galaxies (e.g., Masters et al. 2014; Schreiber et al. 2018) (note that these lines are observed in the near-infrared at high z). However, we obtain a dispersion of  equal to 0.28 (Eq. (23)), and at higher z, the dispersion might be higher because noisier spectra are used. Method 2 cannot be applied directly to high z because its calibration was only valid at low z and depends precisely on the size evolution that we wish to test. Another method, method 3, might be used to derive the absorptions. It uses photometry in many filters and fits the SED with galactic templates, where the mean absorption
equal to 0.28 (Eq. (23)), and at higher z, the dispersion might be higher because noisier spectra are used. Method 2 cannot be applied directly to high z because its calibration was only valid at low z and depends precisely on the size evolution that we wish to test. Another method, method 3, might be used to derive the absorptions. It uses photometry in many filters and fits the SED with galactic templates, where the mean absorption  is a free parameter, as was already obtained for z > 2 galaxies (e.g., Onodera et al. 2010; Glazebrook et al. 2017; Schreiber et al. 2018). The absorption can also be estimated using the reddening, that is, the excess of intrinsic colors: for instance, Cho & Park (2009) (the basis of our method 2) have used at low z the colors r − K, u − K or u − r to statistically estimate the absorption of galaxies. Regardless of the method used to derive the absorption, our guess is that the errors of individual sources will be large, and we will need too many galaxies at high z to explore the relation successfully.
is a free parameter, as was already obtained for z > 2 galaxies (e.g., Onodera et al. 2010; Glazebrook et al. 2017; Schreiber et al. 2018). The absorption can also be estimated using the reddening, that is, the excess of intrinsic colors: for instance, Cho & Park (2009) (the basis of our method 2) have used at low z the colors r − K, u − K or u − r to statistically estimate the absorption of galaxies. Regardless of the method used to derive the absorption, our guess is that the errors of individual sources will be large, and we will need too many galaxies at high z to explore the relation successfully.
The last quantity that is necessary to carry out a galaxy size test at high z is the galaxy size using different cosmological models Trujillo et al. (2006), Shibuya et al. (2015) for the standard cosmological model or López-Corredoira (2010) for different cosmological models). When we have the three amounts, absorption, dust mass derived from FIR emission, and galaxy size for a given cosmology, we can verify that they follow Eq. (32), corroborating or rejecting the cosmological model that was used.
4.3. Example of an application of Eq. (32)
We illustrate how Eq. (32) should be applied for the cases in the future when we have enough data, or for cases of alternative cosmologies that give a fcosmol. much lower than ΛCDM cosmology. We assumed that we have a spiral galaxy at z = 4 and inclination i = 60 ± 5 deg. We also assumed that we measured an angular scalelength (or the Petrosian angular size, which can later be converted into the scalelength through Eq. (15)) of αhR = 0.20 ± 0.02 arcsec, and we measured a flux F500 μm = (100 ± 20) μJy. Dust mass and sizes may be calculated depending on the cosmological model. For illustration, we give two very different examples (whether they are realistic or not is not the discussion here).
– Using the standard ΛCDM cosmological model with H0 = 69.6 km s−1 Mpc−1, Ωm = 0.286, at z = 4 the luminosity distance dL and the angular distance dA are dL = dA (1 + z)2 = 3.65 × 104 Mpc; fcosmol. = 1.81 × 1010. The linear size scalelentgh is hR = 1.41 ± 0.14 kpc. With the relation of flux and dust mass given in Eq. (28), this means Md = (10.5 ± 2.2)×108 M⊙. When we now apply Eq. (32), we obtain f = 113 ± 23, which is hypersaturated because f is much larger than 3.6:  , or using Eq. (3),
, or using Eq. (3),  magnitudes.
magnitudes.
– For a simple static Euclidean universe with redshift due to a simple tired light effect (López-Corredoira 2010; López-Corredoira et al. 2016), with H0 = 69.6 km s−1 Mpc−1, at z = 4 the luminosity distance dL and the angular distance dA are dL = dA (1 + z)1/2 = 1.55 × 104 Mpc; fcosmol. = 4.81 × 107. The linear size scalelength is hR = 6.7 ± 0.7 kpc. With the relation of flux and dust mass given in Eq. (28), this means Md = (1.88 ± 0.38)×108 M⊙. When we now apply Eq. (32), we obtain f = (0.31 ± 0.07), which in the linear regime is  , or using Eq. (3),
, or using Eq. (3),  magnitudes.
magnitudes.
We are probably unable to measure  with enough precision to distinguish between the two results, but when the analysis is performed with many galaxies, it will be possible to statistically distinguish the two cosmologies. We have used an example that saturates in the standard cosmological model at z = 4. If we were able to measure much lower FIR fluxes, below 10 μJy, the case would become even more interesting because the difference in absorption between the two models is distinguished by a factor larger than 100. At lower z, for instance, z ≲ 1, the distinction between the different cosmologies is small, but the sensitivity of FIR photometers might be enough with our present technology.
with enough precision to distinguish between the two results, but when the analysis is performed with many galaxies, it will be possible to statistically distinguish the two cosmologies. We have used an example that saturates in the standard cosmological model at z = 4. If we were able to measure much lower FIR fluxes, below 10 μJy, the case would become even more interesting because the difference in absorption between the two models is distinguished by a factor larger than 100. At lower z, for instance, z ≲ 1, the distinction between the different cosmologies is small, but the sensitivity of FIR photometers might be enough with our present technology.
5. Conclusions
We have derived an average relation of the internal mean absorption of galaxies in V filter (for another filter, we just need to multiply it by some factor (e.g., Rieke & Lebofsky 1985)) and the dust mass derived from FIR emission at low z: Eq. (29), finding that the dependence on galaxy size is negligible. A smaller galaxy for the same amount of dust would give larger absorption, but because  on average, this dependence on size cancels out. This equation allowed us to derive the internal attenuation of the galaxy only knowing its 100 μm flux.
on average, this dependence on size cancels out. This equation allowed us to derive the internal attenuation of the galaxy only knowing its 100 μm flux.
There is a maximum value of  of 1.45 ± 0.27 magnitudes because when a dust density is exceeded, the absorption saturates because we cannot see the stars in the background of a thick layer of dust and we only see the last scattering surface of the galaxy. This saturation limit is reached approximately for dust masses higher than 108 M⊙ for low z. For dust mass lower than 107 M⊙, we are in a linear regime, and the mean absorption is proportional to the dust mass.
of 1.45 ± 0.27 magnitudes because when a dust density is exceeded, the absorption saturates because we cannot see the stars in the background of a thick layer of dust and we only see the last scattering surface of the galaxy. This saturation limit is reached approximately for dust masses higher than 108 M⊙ for low z. For dust mass lower than 107 M⊙, we are in a linear regime, and the mean absorption is proportional to the dust mass.
When this law is extrapolated to high z galaxies, we must bear in mind that the relation of  observed at low z is not kept because for a constant dust mass, we have much smaller sizes due to the putative galaxy size evolution necessary to make the data compatible with standard cosmology. Considering the observational results of low z galaxies and the toy model we developed, we can derive a equation that relates the internal mean absorption of galaxies, the dust mass derived from FIR emission at low z, and the scalelength of the galactic disk (or the Petrosian radius). This is given in Eq. (32). This might be used as a cosmological test because the factor fcosmol. (to which the absorption is proportional in the linear regime) at high z varies strongly in different cosmologies. Although the capabilities of the present-day FIR and millimeter surveys do not allow us to carry out this cosmological test at present within the standard model, it may be used in the future, when, for instance, we can observe galaxies at z = 3−5 with a sensitivity better than ∼10 μJy. For alternative very different models such as a static Universe, the application of the Eq. (32) would predict very low absorptions in detectable FIR fluxes at high z.
observed at low z is not kept because for a constant dust mass, we have much smaller sizes due to the putative galaxy size evolution necessary to make the data compatible with standard cosmology. Considering the observational results of low z galaxies and the toy model we developed, we can derive a equation that relates the internal mean absorption of galaxies, the dust mass derived from FIR emission at low z, and the scalelength of the galactic disk (or the Petrosian radius). This is given in Eq. (32). This might be used as a cosmological test because the factor fcosmol. (to which the absorption is proportional in the linear regime) at high z varies strongly in different cosmologies. Although the capabilities of the present-day FIR and millimeter surveys do not allow us to carry out this cosmological test at present within the standard model, it may be used in the future, when, for instance, we can observe galaxies at z = 3−5 with a sensitivity better than ∼10 μJy. For alternative very different models such as a static Universe, the application of the Eq. (32) would predict very low absorptions in detectable FIR fluxes at high z.
File specObj-dr14.fits available at https://www.sdss.org/dr14/spectro/spectro_access/
The nine cosmological models are given by López-Corredoira et al. (2016, Sect. 2). Note that all of the cosmological models follow Etherington’s relation (η = 2) except the static models, which have η equal to 0.5, 0.5, 1.5 respectively for linear Hubble law, single tired light and plasma tired light.
Acknowledgments
Thanks are given to Helmut Dannerbauer for providing information of Table 2. Thanks are given to the anonymous referee for very useful comments and suggestions that helped to improve this paper. M.L.-C. was supported by the grant PGC-2018-102249-B-100 of the Spanish Ministry of Economy and Competitiveness (MINECO). Based on observations with AKARI, a JAXA project with the participation of ESA. Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the US Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [Google Scholar]
- Abolfathi, B., Aguado, D. S., Aguilar, G., et al. 2018, ApJS, 235, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Balakrishna Subramani, V., Kroupa, P., Shenavar, H., & Muralidhara, V. 2019, MNRAS, 488, 3876 [Google Scholar]
- Bianchi, S., De Vis, P., Viaene, S., et al. 2018, A&A, 620, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boquien, M., Boselli, A., Buat, V., et al. 2013, A&A, 554, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Buat, V., Boquien, M., Małek, K., et al. 2018, A&A, 619, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calanog, J. A., Wardlow, J., Fu, H., et al. 2013, ApJ, 775, 61 [Google Scholar]
- Calura, F., Pozzi, F., Cresci, G., et al. 2017, MNRAS, 465, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D. 2001, PASP, 113, 1449 [NASA ADS] [CrossRef] [Google Scholar]
- Cho, J., & Park, C. 2009, ApJ, 693, 1045 [Google Scholar]
- Conroy, C. 2013, ARA&A, 51, 393 [Google Scholar]
- Davies, J. I., Trewhella, M., Jones, H., et al. 1997, MNRAS, 288, 679 [Google Scholar]
- Davies, J. I., Nersesian, A., Baes, M., et al. 2019, A&A, 626, A63 [CrossRef] [EDP Sciences] [Google Scholar]
- Decleir, M., De Looze, I., & Boquien, M. 2019, MNRAS, 486, 743 [Google Scholar]
- De Looze, I., Fritz, J., Baes, M., et al. 2014, A&A, 571, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Devour, B. M., & Bell, E. F. 2016, MNRAS, 459, 2054 [Google Scholar]
- Doi, Y., Takita, S., Ootsubo, T., et al. 2015, PASJ, 67, 50 [NASA ADS] [Google Scholar]
- Drimmel, R., Cabrera-Lavers, A., & López-Corredoira, M. 2003, A&A, 409, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eales, S., Dunne, L., Clements, D., et al. 2010, PASP, 122, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Fontanot, F., & Somerville, R. S. 2011, MNRAS, 416, 2962 [Google Scholar]
- Franco, M., Elbaz, D., Béthermin, M., et al. 2018, A&A, 620, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galametz, M., Kennicutt, R. C., Albrecht, M., et al. 2012, MNRAS, 425, 763 [Google Scholar]
- Glazebrook, K., Schreiber, C., Labbé, I., et al. 2017, Nature, 544, 71 [NASA ADS] [CrossRef] [Google Scholar]
- González-Pérez, V., Lacey, C. G., Baugh, C. M., Frenk, C. S., & Wilkins, S. M. 2013, MNRAS, 429, 1609 [Google Scholar]
- Granato, G. L., Lacey, C. G., Silva, L., et al. 2000, ApJ, 542, 710 [Google Scholar]
- Gutiérrez, C. M., & López-Corredoira, M. 2014, A&A, 571, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hatsukade, B., Kohno, K., Yamaguchi, Y., et al. 2018, PASJ, 70, 105 [Google Scholar]
- Holanda, R. F. L., Lima, J. A. S., & Ribeiro, M. B. 2011, A&A, 528, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inoue, A. K., Buat, V., Burgarella, D., et al. 2006, MNRAS, 370, 380 [Google Scholar]
- Jonsson, P., Cox, T. J., Primack, J. R., et al. 2006, ApJ, 637, 255 [Google Scholar]
- Lam, A., Malkan, M., & Wright, E. 2019, PASJ, 71, 9 [Google Scholar]
- Lerner, E. J. 2018, MNRAS, 477, 3185 [Google Scholar]
- Loeb, A., & Haiman, Z. 1997, ApJ, 490, 571 [Google Scholar]
- Lo Faro, B., Buat, V., Roehlly, Y., et al. 2017, MNRAS, 472, 1372 [Google Scholar]
- López-Corredoira, M. 2010, IJMPD, 19, 245 [Google Scholar]
- López-Corredoira, M., Cabrera-Lavers, A., Gerhard, O. E., & Garzón, F. 2004, A&A, 421, 953 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Corredoira, M., Cabrera-Lavers, A., & Gerhard, O. E. 2005, A&A, 439, 107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Corredoira, M., Melia, F., Lusso, E., & Risaliti, G. 2016, IJMPD, 25, 1650060 [Google Scholar]
- López-Corredoira, M., Gutiérrez, C. M., & Genova-Santos, R. T. 2017a, ApJ, 840, 62 [Google Scholar]
- López-Corredoira, M., Vazdekis, A., Gutiérrez, C. M., & Castro-Rodríguez, N. 2017b, A&A, 600, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lutz, D., Poglitsch, A., Altieri, B., et al. 2011, A&A, 532, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magnelli, B., Elbaz, D., Chary, R. R., et al. 2009, A&A, 496, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Małek, K., Pollo, A., Takeuchi, T. T., et al. 2013, Earth Planets Space, 65, 1101 [Google Scholar]
- Maraston, C. 2005, MNRAS, 362, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Masters, D., McCarthy, P., Siana, B., et al. 2014, ApJ, 785, 153 [Google Scholar]
- McMillan, P. J. 2011, MNRAS, 414, 2446 [NASA ADS] [CrossRef] [Google Scholar]
- Meert, A., Vikram, V., & Bernardi, M. 2015, MNRAS, 446, 3493 [Google Scholar]
- Murakami, H., Baba, H., Barthel, P., et al. 2007, PASJ, 59, S369 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Narayanan, D., Conroy, C., Davé, R., Johnson, B. D., & Popping, G. 2018, ApJ, 869, 70 [Google Scholar]
- Natale, G., Popescu, C. C., Tuffs, R. J., et al. 2015, MNRAS, 449, 243 [Google Scholar]
- Nersesian, A., Verstocken, S., Viaene, S., et al. 2020, A&A, 637, A25 [CrossRef] [EDP Sciences] [Google Scholar]
- Oliver, S. J., Bock, J., Altieri, B., et al. 2012, MNRAS, 424, 1614 [Google Scholar]
- Onodera, M., Arimoto, N., Daddi, E., et al. 2010, ApJ, 715, 385 [Google Scholar]
- Osterbrock, D. E. 1989, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei (Mill Valley (CA): University Science Books) [Google Scholar]
- Paleologou, E. 1997, A&A, 325, 135 [Google Scholar]
- Peletier, R. F., Valentijn, E. A., Moorwood, A. F. M., et al. 1995, A&A, 300, L1 [NASA ADS] [Google Scholar]
- Pohlen, M., Cortese, L., Smith, M. W. L., et al. 2010, A&A, 518, L72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popescu, C. C., Tuffs, R. J., Dopita, M. A., et al. 2011, A&A, 527, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popping, G., Puglisi, A., & Norman, C. A. 2017, MNRAS, 472, 2315 [Google Scholar]
- Rieke, G. H., & Lebofsky, M. J. 1985, ApJ, 288, 618 [Google Scholar]
- Rocha, M., Jonsson, P., Primack, J. R., et al. 2008, MNRAS, 383, 1281 [Google Scholar]
- Salim, S., & Narayanan, D. 2020, ARA&A, 58, 529 [Google Scholar]
- Salim, S., Boquiem, M., & Lee, J. C. 2018, ApJ, 859, 11 [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schreiber, C., Glazebrook, K., Nanayakkara, T., et al. 2018, A&A, 618, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seon, K.-I., & Draine, B. T. 2016, ApJ, 833, 201 [Google Scholar]
- Shao, Z., Xiao, Q., Shen, S., et al. 2007, ApJ, 659, 1159 [Google Scholar]
- Shibuya, R., Ouchi, M., & Harikane, Y. 2015, ApJ, 219, 15 [Google Scholar]
- Shimasaku, K., Fukugita, M., Doi, M., et al. 2001, ApJ, 122, 1238 [Google Scholar]
- Trayford, J. W., del P Lagos, C., Robotham, A. S. G., & Obreschkow, D. 2020, MNRAS, 491, 3937 [Google Scholar]
- Trujillo, I., Förster Schreiber, N. M., Rudnick, G., et al. 2006, ApJ, 650, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Unavane, M., Gilmore, G., Epchtein, N., et al. 1998, MNRAS, 295, 119 [Google Scholar]
- Vazdekis, A., Sánchez-Blázquez, P., Falcón-Barroso, J., et al. 2010, MNRAS, 404, 1639 [NASA ADS] [Google Scholar]
- Viaene, S., Baes, M., Tamm, A., et al. 2017, A&A, 599, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walcher, J., Groves, B., Budavári, T., & Dale, D. 2011, ApSS, 331, 1 [Google Scholar]
- Walter, F., Decarli, R., Aravena, M., et al. 2016, ApJ, 833, 67 [Google Scholar]
- Wilkins, S. M., González-Pérez, V., Lacey, C. G., & Baugh, C. M. 2012, MNRAS, 424, 1522 [Google Scholar]
- Witt, A. N., & Gordon, K. D. 2000, ApJ, 528, 799 [Google Scholar]
- York, D. G., Adelman, J., Anderson, J. E., et al. 2000, AJ, 120, 1579 [CrossRef] [Google Scholar]
All Tables
Coefficients of the double linear fit log10γV(R0.max = ∞) = a′+b′*log10hR(kpc)+c′*log10(Md/Md, MW) for different ranges of dust mass Md, with γV calculated with two different methods.
FIR and millimetric wavelength ≤1.5 mm surveys and their sensitivity at 5σ detection.
All Figures
 |
Fig. 1. Theoretical value of γV for a model of a purely exponential disk in three cases. Left: constant dust mass. Middle: constant scaleheight. Right: dust mass proportional to the square of the scalelength. |
| In the text | |
 |
Fig. 2. Relation of Petrosian half-light and 90% light radii with the scalelength of a spiral galaxy, either with a purely exponential disk or with some bulge component with 20% of the light; we set hz, * = 0.3 kpc, hz, d = 0.1 kpc, and Md = 2.8 × 107 M⊙. |
| In the text | |
 |
Fig. 3. Examples of SDSS-selected galaxies with a counterpart in AKARI, that is, with a significant amount of dust. |
| In the text | |
 |
Fig. 4. Correlation of dust mass and optical luminosity (left), scalelength and optical luminosity (middle), and dust mass and scalelenth (right). |
| In the text | |
 |
Fig. 5. Data (top panel; brown stands for an absence of data), best double-linear fit (middle), and residuals (bottom panel) of Eq. (21): |
| In the text | |
 |
Fig. 6. Dependence on Md of the fit coefficients log10γV = a′+b′log10hR(kpc)+c′log10(Md/Md, MW). |
| In the text | |
 |
Fig. 7. Log-log plot of the correlation of the average absorption in the whole galaxy calculation with method 1 (and the model-dependent correction of aperture C) and method 2. |
| In the text | |
 |
Fig. 8. Log-log plot of the correlation of the luminosities at 100 μm (at rest) and bolometric luminosity for 4370 galaxies from the AKARIxSDSS sample with errors of the two luminosities lower than 20%. |
| In the text | |
 |
Fig. 9. Predictions of fcosmol.(z) for nine cosmological models. |
| In the text | |
 |
Fig. 10. Minimum sensitivity of a significant detection of a photometer at a wavelength (1 + z)100 μm as a function of the redshift and the scalelength of the galaxy, derived making fM = 3.6 in Eq. (32) using standard cosmological ΩΛ = 0.7, H0 = 70 km s−1Mpc−1 to evaluate the luminosity distance. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.









![$$ \begin{aligned} F_{V,\mathrm{obs}}=\int _{-\infty }^\infty \mathrm{d}r\, \rho _{*,V}(R,z)\, \exp {\left[-\kappa _V\int _r^\infty \mathrm{d}r^\prime \rho _{\rm d}(R,z=r^\prime \cos i )\right]}, \end{aligned} $$](/articles/aa/full_html/2021/08/aa40851-21/aa40851-21-eq12.gif)
![$$ \begin{aligned} \rho _{*,V}=\frac{F_{V,\mathrm{total,em}}}{4\pi h_R^2h_{z,*}}\exp {\left[-\frac{R}{h_R}\right]}\exp {\left[-\frac{|z|}{h_{z,*}}\right]}, \end{aligned} $$](/articles/aa/full_html/2021/08/aa40851-21/aa40851-21-eq13.gif)
![$$ \begin{aligned} \rho _{\rm d}=\frac{M_{\rm d}}{4\pi h_R^2h_{z,\mathrm{d}}}\exp {\left[-\frac{R}{h_R}\right]}\exp {\left[-\frac{|z|}{h_{z,\mathrm{d}}}\right]}, \end{aligned} $$](/articles/aa/full_html/2021/08/aa40851-21/aa40851-21-eq14.gif)

![$$ \begin{aligned} H_j\,{=}\,&\int _0^\infty \mathrm{d}r \exp {\left[-\frac{r\,\cos i}{h_{z,*}} \right]}\\[.3pc]&\times \ \exp {\left[ -\frac{ \kappa _VM_{\rm d} \exp {\left[-\frac{R}{h_R}\right]}\left(2*j+(-1)^j\exp {\left[-\frac{r\cos i}{h_{z,\mathrm{d}}} \right]}\right)}{4\pi h_R^2\cos i} \right]} . \end{aligned} $$](/articles/aa/full_html/2021/08/aa40851-21/aa40851-21-eq16.gif)

![$$ \begin{aligned} \rho _{*,V}=\left\{ \begin{array}{ll} K_1(h_R)\exp {\left[-\sqrt{R^2+(2.5z)^2}/(2.5\,\mathrm{h})\right]},&R < h_R \\ K_2(h_R)\exp {\left[-\frac{R}{h_R}\right]}\exp {\left[-\frac{|z|}{h_{z,*}}\right]},&R\ge h_R \end{array}\right\} \;, \end{aligned} $$](/articles/aa/full_html/2021/08/aa40851-21/aa40851-21-eq21.gif)








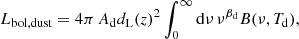


![$$ \begin{aligned} \overline{A_V}=11.6\left[\log _{10}\left(\frac{F_{\rm H_\alpha }}{F_{\rm H_\beta }}\right)-\log _{10} R_{\alpha \beta }\right] , \end{aligned} $$](/articles/aa/full_html/2021/08/aa40851-21/aa40851-21-eq35.gif)

![$$ \begin{aligned} { y}=\log _{10}\left[\overline{\gamma _V}( < 1.5^{\prime \prime })\left(\frac{M_{\rm d}}{M_{\mathrm{d},MW}}\right)^{-1}\right], \end{aligned} $$](/articles/aa/full_html/2021/08/aa40851-21/aa40851-21-eq39.gif)

![$$ \begin{aligned} x_2=\log _{10}\left[\left(\frac{M_{\rm d}}{M_{\mathrm{d},MW}}\right)\left(\frac{1}{h_R(\mathrm{kpc})^2}\right)\right]. \end{aligned} $$](/articles/aa/full_html/2021/08/aa40851-21/aa40851-21-eq41.gif)
![$$ \begin{aligned} \log _{10}\overline{\gamma _V}({ < }1.5^{\prime \prime })\ {=}\ &a^\prime +b^\prime \log _{10}h_R(\mathrm{kpc})\\[.6pc]&+c^\prime \log _{10}\left(\frac{M_{\rm d}(h_R)}{M_{\mathrm{d},MW}}\right),\nonumber \end{aligned} $$](/articles/aa/full_html/2021/08/aa40851-21/aa40851-21-eq43.gif)


![$$ \begin{aligned} c^\prime =\exp \left[-(0.59^{+0.14}_{-0.10})\frac{M_{\rm d}}{M_{\rm d,MW}}\right]. \end{aligned} $$](/articles/aa/full_html/2021/08/aa40851-21/aa40851-21-eq46.gif)
![$$ \begin{aligned} \log _{10}\overline{\gamma _V}(R_{0,\mathrm{max}})&=\infty )\approx 0.22{-}0.19\log _{10}h_R(\mathrm{kpc})\\[.6pc]&+\exp \left[-0.59\frac{M_{\rm d}}{M_{\rm d,MW}}\right]\,\log _{10}\left(\frac{M_{\rm d}}{M_{\rm d,MW}}\right); \ \ \sigma =0.27,\nonumber \end{aligned} $$](/articles/aa/full_html/2021/08/aa40851-21/aa40851-21-eq48.gif)
![$$ \begin{aligned} \log _{10}\left[\overline{\gamma _V}(R_{0,\mathrm{max}}) = \infty )\left(\frac{M_{\rm d}}{M_{\rm d,MW}}\right)^{-1}\right]\approx 0.22 \ \ \ \ \ \end{aligned} $$](/articles/aa/full_html/2021/08/aa40851-21/aa40851-21-eq49.gif)
![$$ \begin{aligned} +\left[2\exp \left[-0.59\frac{M_{\rm d}}{M_{\rm d,MW}}\right] -2.19\right] \log _{10}h_R(\mathrm{kpc}) \end{aligned} $$](/articles/aa/full_html/2021/08/aa40851-21/aa40851-21-eq50.gif)
![$$ \begin{aligned} +\left( \exp \left[-0.59\frac{M_{\rm d}}{M_{\rm d,MW}}\right]-1\right) \log _{10}\left[\left(\frac{M_{\rm d}}{M_{\rm d,MW}}\right)\left(\frac{1}{h_R(\mathrm{kpc})^2}\right)\right]; \ \sigma =0.27 . \end{aligned} $$](/articles/aa/full_html/2021/08/aa40851-21/aa40851-21-eq51.gif)
![$$ \begin{aligned} \gamma _r\ {=}\ &1.06\left[-1.35(c-2.48)^2+1.14\right]\times \\&\left[-0.223(M_r+20.8)^2+1.10\right] ,\nonumber \end{aligned} $$](/articles/aa/full_html/2021/08/aa40851-21/aa40851-21-eq54.gif)

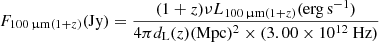


![$$ \begin{aligned} \overline{\gamma _V}=(1.45\pm 0.27)f^{\exp {[-(1.0\pm 0.6)f}]}, \end{aligned} $$](/articles/aa/full_html/2021/08/aa40851-21/aa40851-21-eq69.gif)

![$$ \begin{aligned} \overline{A_V}=(1.45\pm 0.27)f^{\exp {[-(1.0\pm 0.6)f}]} \log _{10}\left(\frac{r_{\rm major}}{r_{\rm minor}}\right). \end{aligned} $$](/articles/aa/full_html/2021/08/aa40851-21/aa40851-21-eq71.gif)


![$$ \begin{aligned} \overline{\gamma _V}=(1.45\pm 0.27)f_M^{\exp {[-(1.0\pm 0.6)f_M]}}, \end{aligned} $$](/articles/aa/full_html/2021/08/aa40851-21/aa40851-21-eq79.gif)
![$$ \begin{aligned} f_M&=1.35\times h_R(\mathrm{kpc})^{-1.75}\times \left(\frac{M_{\rm d}}{M_{\rm d,MW}}\right)^{1.87}\\[.6pc]&=7.6\times 10^{-6} \alpha _{hR}^{-1.75}\times \left(\frac{F_{100\,\upmu \mathrm{m}(1+z)}}{700\ \mathrm{Jy}}\right)^{1.87} \times f_{\rm cosmol.}(z) , \end{aligned} $$](/articles/aa/full_html/2021/08/aa40851-21/aa40851-21-eq80.gif)

