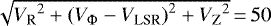| Issue |
A&A
Volume 651, July 2021
|
|
|---|---|---|
| Article Number | A20 | |
| Number of page(s) | 23 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/202140808 | |
| Published online | 02 July 2021 | |
The Gaia RVS benchmark stars
I. Chemical inventory of the first sample of evolved stars and its Rb NLTE investigation★,★★
1
GEPI, Observatoire de Paris, Université PSL, CNRS,
5 Place Jules Janssen,
92190
Meudon,
France
e-mail: Elisabetta.Caffau@obspm.fr
2
Crimean Astrophysical Observatory,
Nauchny
298409,
Republic of Crimea
3
GEPI, Observatoire de Paris, Université PSL, CNRS,
77 Av. Denfert-Rochereau,
75014
Paris,
France
4
UPJV, Université de Picardie Jules Verne,
33 rue St Leu,
80080
Amiens,
France
5
Leibniz-Institut für Astrophysik Potsdam (AIP),
An der Sternwarte 16,
14482
Potsdam,
Germany
6
Dipartimento di Fisica e Astronomia, Università degli Studi di Bologna,
Via Gobetti 93/2,
40129
Bologna,
Italy
7
Centro de Astronomía, Universidad de Antofagasta,
Avda. U.de Antofagasta
02800,
Antofagasta,
Chile
8
European Southern Observatory,
Casilla
19001,
Santiago,
Chile
9
Astronomical Observatory, Odessa, National University,
Shevchenko Park,
65014
Odessa,
Ukraine
10
Université de Nice Sophia-Antipolis, CNRS, Observatoire de la Côte d’Azur, Laboratoire Lagrange,
BP 4229,
06304
Nice,
France
11
Zentrum für Astronomie der Universität Heidelberg,
Landessternwarte, Königstuhl 12,
69117
Heidelberg,
Germany
12
Observatoire astronomique de Strasbourg, Université de Strasbourg, CNRS,
11 rue de l’Université,
67000
Strasbourg,
France
Received:
14
March
2021
Accepted:
23
April
2021
Context. The Radial Velocity Spectrometer (RVS) on board the Gaia satellite is not provided with a wavelength calibration lamp. It uses its observations of stars with known radial velocity to derive the dispersion relation. To derive an accurate radial velocity calibration, a precise knowledge of the line spread function (LSF) of the RVS is necessary. Good-quality ground-based observations in the wavelength range of the RVS are highly desired to determine the LSF.
Aims. Several radial velocity standard stars are available to the Gaia community. The highest possible number of calibrators will surely allow us to improve the accuracy of the radial velocity. Because the LSF may vary across the focal plane of the RVS, a large number of high-quality spectra for the LSF calibration may allow us to better sample the properties of the focal plane.
Methods. We selected a sample of stars to be observed with UVES at the Very Large Telescope, in a setting including the wavelength range of RVS, that are bright enough to allow obtaining high-quality spectra in a short time. We also selected stars that lack chemical investigation in order to increase the sample of bright, close by stars with a complete chemical inventory.
Results. We here present the chemical analysis of the first sample of 80 evolved stars. The quality of the spectra is very good, therefore we were able to derive abundances for 20 elements. The metallicity range spanned by the sample is about 1 dex, from slightly metal-poor to solar metallicity. We derived the Rb abundance for all stars and investigated departures from local thermodynamical equilibrium (NLTE) in the formation of its lines.
Conclusions. The sample of spectra is of good quality, which is useful for a Gaia radial velocity calibration. The Rb NLTE effects in this stellar parameters range are small but sometimes non-negligible, especially for spectra of this good quality.
Key words: stars: abundances / Galaxy: abundances / Galaxy: evolution / Galaxy: formation
Tables B.3 and C.1 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/651/A20
© E. Caffau et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The Gaia satellite (Gaia Collaboration 2016a) was launched on 19 December 2013. Three data releases have been published since then (Gaia Collaboration 2016b, 2018, 2021). These data provide a major breakthrough in our knowledge of the Galaxy, but they have some limitations, and there is still place for improvement in the data analysis phase.
The spectrograph on board Gaia, the Radial Velocity Spectrometer (RVS), is a near infrared (845–872 nm) integral field spectrograph with a medium resolving power (R ≈ 11 500). Radial velocities, Vr, are derived from the RVS spectra. The end-mission Vr precision that can be reached depends on the spectral type, the magnitude of the star, and the number of visits (see Sartoretti et al. 2018, and particularly Fig. 17 from that paper). A limitation in the Vr determination is the relatively small wavelength range and low resolution of the RVS. A crucial point in the absolute radial velocity determination is the zero-point. The RVS is a self-calibrating instrument. It does not have a reference lamp. To transform the pixels into wavelengths, it uses its own observations of stars with known radial velocity. When the zero-point is stable, it is irrelevant to derive the Vr variation, asin the case of hunting binary or multiple systems and planets, but it is crucial to have precise kinematics for the stars. The problem is that in the RVS observation, the zero-point is observed to be time dependent. Ground-based observations can help in defining or understanding the zero-point and correcting for its variations in time. A limited number of reference stars for radial velocity in each location on focal plane should be enough to take this variation into account.
The line spread function (LSF) (i.e., the point spread function, PSF, in the dispersion direction) is also crucial for analysing Gaia data. The knowledge of the RVS LSF is important for extracting the radial and projected rotational velocity information from the RVS spectra. The RVS LSF is calibrated by finding the best fit of bright (Grvs < 9, Sartoretti et al. 2018) RVS spectra with the corresponding ground-based high-resolution spectra with a high signal-to-noise ratio (S/N) convolved with the LSF. However, for only a few sources (on the order of one thousand) do we have a ground-based spectrum with sufficiently high resolution and S/N that covers the RVS wavelength range. This means that we can calibrate the LSF only about once every three months at best, while we know that the LSF varies on a much shorter timescale. To improve the LSF calibration (and the estimation of radial and projected rotational velocities), we need high-resolution spectra with a high S/N of as many bright stars as possible.
The primary radial velocity standards for RVS are the 2800 stars by Crifo et al. (2010) and Soubiran et al. (2018), plus another 6300 radial velocity reference stars (Technical Note OML-002). So far, the vast majority of the available radial velocity standards have been observed from the ground in spectral ranges different from that of the RVS. If there is any physical mechanism, such as convective shifts (see Allende Prieto et al. 2013), that results in the relative shifts of some of the lines with respect to others, the measured radial velocity in different spectral ranges will be slightly different. Since ESO period P104, we started a program with UVES at the Very Large Telescope (VLT; Dekker et al. 2000) in order to collect a library of observed spectra in the wavelength range of the RVS that can be used to calibrate the LSF and determine the radial velocity, so that Gaia can provide measurements that are as reliable and precise as possible.
The observations we secured and will secure in this project will be used for five purposes: (i) to determine the LSF across the entire RVS focal plane, (ii) to compare the radial velocity measured in the RVS range with that measured in other ranges, (iii) to verify the accuracy of the theoretically modelled convective shifts, (iv) to provide high-quality templates for the measurement of RVS radial velocities as an alternative to synthetic spectra, and (v) to compare Vr measured in the RVS range with the RVS resolution with Vr measured with the same range at a resolution that is four times higher to asses any systematic effect. We refer to the sample of stars we defined for this project as Gaia RVS benchmark stars. We would like to stress that the RVS range is close to the maximum of the H− opacity (~ 800 nm). The lines that form in this wavelength range therefore have a rather superficial formation height.
In order to efficiently fulfill all our goals, we need to analyse the spectra. We need (i) to verify the quality, (ii) to derive the stellar parameters, and (iii) the chemical inventory of all the observed stars. The last two points are crucial to allow computing synthetic spectra that can be used as templates for the determination of radial and rotational velocities. In this manuscript we present the project and provide the chemical investigation on the first sample of stars.
We also took advantage of the near-infrared domain of these high-quality observations to investigate a quite neglected element: rubidium. The only two Rb I lines that are typically investigated for the Rb abundance determination are at 780.0 and 794.7 nm (the resonance lines). This wavelength range is too red for many optical spectrographs and too blue for the infrared spectrographs. Recently, this gap has been filled with the Rb abundance investigation of a large sample of stars by Takeda (2021). The author performed detailed computations of the departures from local thermodynamical equilibrium (NLTE).
Rb is a very interesting element: it is formed both in the r- and s- process (Abia et al. 2020) and is useful for quantifying the neutron density in s-process sites. According to the neutron density, one of the two stable (85 Rb) and long-lifetime (87Rb) isotopes is in preference formed from a Kr isotope (Käppeler et al. 2011). The cross-sections of the n-capture of the two Rb isotopes in the two chains are very different. By deriving the 85Rb ∕87Rb ratio, the neutron density of the s-process site might in principle be inferred. Unfortunately, the isotopic shift is too small for a direct measurement of the isotopic ratio. It is possible, however, to derive the Rb abundance with respect to the abundance of the neighbouring elements: the higher the Rb abundance with respect to the neighbouring elements, the higher the neutron density (see Smith & Lambert 1984). We here present the Rb abundance of our sample of stars and investigate the NLTE effects.
2 Target selection
The project aims at observing stars with UVES at the VLT that would normally be considered bright for an 8 m class telescope (magnitude range 8–9). As explained in Sect. 1, however, we need high resolution and S/N. The stars we selected have a preferably southern declination so that they were also easily observable in the case of northern winds. They cover the entire right ascensions of the ESO semester. Because they are bright, a high S/N can also be achieved with poor seeing.
In this first paper, we present a sample of 80 giant stars from solar metallicity to slightly metal poor that were observed in the ESO programme 0104.D-0325. The stars of this ESO period were selected from the Gaia DR2 catalogue, which provides an accurate radial velocity determination. Based on Simbad (Wenger et al. 2000), we preferentially selected stars that were reported in few papers and for which no chemical investigation is reported in the literature so that we would be able to increase the number of bright stars with known chemical composition.
3 Observations
For this project on the UVES spectrograph, we selected the setting 437+760. The choices on the setting were that (i) the 760 range completely covers the RVS range without any gaps, and (ii) the 437 range is the reddest setting that can be coupled with the 760 setting. For metal-rich stars (the majority of our targets), observations in blue settings provide very crowded spectra, and a higher S/N can be achieved in this selected setting than in bluer settings such as the 390 setting.
We chose the highest UVES resolution (slit 0.′′4 in the blue arm and 0.′′3 in the red arm). For all observations, the DIC2 437+760 setting was used. For the stars brighter than V magnitude 8.5, an observing block comprises ten observations of 77.5 s to avoid detector saturation. For the stars fainter than 8.5, five exposures of 202 s allow avoiding detector saturation. In this program, 90 stars have been observed, 80 of which are evolved stars and are analysed here. The 10 unevolved stars will be analysed with stars of similar stellar parameters that are observed or are scheduled to be observed for the following two ESO periods (P105 and P106). The log of the observations is reported in Table B.1. Of the observations we analysed, 71 were graded A, 6 were B, and 3 were C.
The spectra were reduced with the ESO pipeline version 5.8.2 under gasgano. All the exposures for each star were added after correction for the barycentric velocity. To place the spectra at a laboratory wavelength, we used the Gaia DR2 radial velocity. To show the quality of the combined spectra, the range of the Ca triplet line is plotted for two stars in Fig. 1.
 |
Fig. 1 Two spectra (RVS 002 and RVS 038) in the wavelength range of the Gaia RVS. |
4 Analysis
4.1 Stellar parameters
We dereddened the Gaia photometry using the maps from Ivanova et al. (2021). Using the parallax of the Gaia EDR3 catalogue corrected for the zero-point as suggested by Lindegren et al. (2021), we derived the absolute G magnitude. We then compared the dereddened G absolute magnitude and the dereddened BP–RP Gaia EDR3 colour to the synthetic photometry, and assuming solar metallicity, we derived the effective temperature, Teff, and surface gravity, log g, for all stars.
With the derived stellar parameters, we analysed the spectra with MyGIsFOS (Sbordone et al. 2014) to derive the metallicity of all stars. We used this metallicity as input to again derive the stellar parameters. At this point, we adjusted the stellar mass by interpolation into PARSEC isochrones (Bressan et al. 2012; Marigo et al. 2017). The PARSEC isochrones we used are all of solar-scaled composition. The masses were used to estimate the surface gravity through the Stefan-Boltzmann equation. With these new stellar parameters, we ran MyGIsFOS and again derived the metallicity. The process was iterated until the variation in effective temperature was less than 5 K and the variation in surface gravity was less than 0.01 dex.
For a comparison with the isochrones, we used the photometry provided by Gaia DR2 and the PARSEC (Bressan et al. 2012; Marigo et al. 2017) isochrones coloured in the same Gaia data release. The Teff values we adopted match the values derived from the isochrones well. The differences are slightly above 100 K in only five cases. The same comparison for the surface gravities provides good agreement, always within 0.3 dex. We adopted 100 K and 0.3 dex as the uncertainties for the effective temperature and surface gravity.
For the microturbulence (ξ), we had the choice to use the calibration from Monaco et al. (2005), who derived it for stars in the Sagittarius dwarf spheroidal galaxy. Even though the adopted parameters of the stars we analysed are similar to those investigated by Monaco et al. (2005), the range in effective temperatures spanned by our stars is too wide for us to feel comfortable neglecting it in deriving the microturbulence. The calibration from Mashonkina et al. (2017) was conceived for old, metal-poor stars, and our stars are too metal rich and probably too young for us to confidently use this calibration. The calibration by Dutra-Ferreira et al. (2016) was based on theoretical hydrodynamical models and might be correct, but because it is based on theoretical models, it is not expected to take the different ages and masses of our stars into account. These differences might affect the microturbulence. The calibration from Monaco et al. (2005) would provide the highest ξ values (from 1.15 to 1.92 km s−1), the calibration from Mashonkina et al. (2017) spans the range 1.35–1.65 km s−1, and the calibration from Dutra-Ferreira et al. (2016) is systematically lower than this last range by 0.16 km s−1. We decided to allow MyGIsFOS to derive the microturbulence from clean Fe I lines, while we kept the other stellar parameters fixed (Teff and log g). The values for the microturbulence we derive span from 1.18 to 2.9 km s−1, with an average value at 1.6 km s−1. We assumed an uncertainty of 0.3 km s−1 for the microturbulence.
As a test, we allowed MyGIsFOS to derive the microturbulence and the surface gravity from the iron balance simultaneously (see Sbordone et al. 2014, for details). In this case, ξ spans almost the same range (1.18 ≤ ξ ≤ 2.94), and log g is in the range 1.03–3.18, which is slightly lower than with the surface gravity derived from the parallaxes, where log g is in the range 1.05–3.27, but still well within the uncertainties.
The range in the stellar parameters is 4000 < Teff < 5060 K, 1.0 < log g < 3.3, and − 0.9 ≤ [Fe/H] < 0.2. The adopted stellar parameters are shown in Fig. 2. Two PARSEC isochrones (Bressan et al. 2012; Marigo et al. 2017) coloured following Gaia EDR3 are provided to guide the eye, and they are listed in the appendix in Table B.2. The dashed lines delimit the parameters of the grid of the synthetic spectra used by MyGIsFOS in the abundance analysis determination (see Sect. 4.2). The figure shows that we had to extrapolate from the grid in surface gravity for a few stars: stars RVS 099, RVS 127, RVS 148, and RVS 157, whose log g extend from 3.1 to 3.3. These stars were designated to the unevolved star sample of the same program and will be reanalysed with the dwarf grid.
 |
Fig. 2 Observed stars in the (Teff, log g) diagram compared to PARSEC isochrones to guide the eyes. |
4.2 Abundances
With the adopted stellar parameters, the observed spectra were analysed with MyGIsFOS (Sbordone et al. 2014) to derive the metallicity and the detailed chemical abundances. The grid of synthetic spectra, based on ATLAS 12 models (Kurucz 2005), was computed with Synthe (Kurucz 2005) in its Linux version (Sbordone et al. 2004). The grid we used has Teff in the range 4000–5200 K with a step of 200 K, log g from 0.5 to 3.0 with a step of 0.5 dex, metallicity from –1.0 to +0.5 with a step of 0.25 dex, microturbulence of 1, 2, and 3 km s−1, and an enhancement in α-elements of –0.4, 0.0, and +0.4 dex. The atomic data for the lines are taken from the list used in Gaia ESO Survey internal data release 4 (see Smiljanic et al. 2014 and Heiter et al. 2015, see also Heiter et al. 2021). The solar abundances adopted in the models and synthesis computations are reported in Table 1. For consistency, we applied these values in all the figures, and we also scaled the comparison samples to our adopted solar values.
We would like to point out that the automatic analysis performed by MyGIsFOS has the advantage of being fast when the regions to be investigated by the code and the ranges for the pseudo-normalisation are fixed and when the code is optimised for the set of data (see Sbordone et al. 2014). The drawback is that single spectra can be corrupted (e.g. telluric absorption or a cosmic ray) in the wavelength range that is selected for the pseudo-continuum determination or for the line-profile fitting. In several wavelength ranges of these observations, the telluric contamination is an issue, and telluric lines in a selected range may affect the local continuum determination. MyGIsFOS has been built to reject untrustworthy fits, but a manual analysis would allow saving some corrupted features by changing the range for the fit or the continuum, for example. An automatic fast analysis appeared to be the best choice in view of the large set of data that was to be analysed. This is surely the case of surveys such as are expected with WEAVE (Dalton et al. 2018) or 4MOST (de Jong et al. 2019), but the sample of stars expected for this project will hopefully also contain several hundred spectra. The results from the automatic analysis might not be so precise for the single star, for a single element, but if one star looks unusual or an element is particularly determinant, it can be inspected and reanalysed.
Solar abundances.
 |
Fig. 3 [C/Fe] vs. metallicity. |
4.2.1 Metallicity
The metallicity derived from the Fe I lines ranges from –0.90 to +0.16. Many Fe I lines are available in the spectral range (from 71 to 191, with an average of 127 lines) to derive the Fe abundance and provide an average line-to-line scatter of ⟨σFe ⟩ = 0.16 ± 0.02 dex, with a range from 0.12 to 0.21. For all stars we were able to also derive A(Fe) from a limited number of Fe II lines (from three to seven), which provide an average line-to-line scatter of ⟨σFe ⟩ = 0.12 ± 0.04. We used the Fe abundance derived from the Fe I lines to determine the [X/Fe] ratios.
4.2.2 Carbon
Three atomic lines of C I (833, 872, and 911 nm) were investigated by MyGIsFOS in the observed spectra. We know from the solar investigation that the line at 872 nm is formed close to LTE conditions (Caffau et al. 2010; Amarsi et al. 2019), but this line is weak and sometimes distorted. The other two lines suffer from NLTE effects and might also be affected by telluric absorption (depending on the radial velocity of the star and the heliocentric velocity at the observing time). We were able to derive A(C) from the 872 nm line for all but one star. Figure 3 shows the [C/Fe] ratio versus the metallicity, with carbon abundance derived from the 872 nm C I line. A(C) is low for most of the stars, but several of them have mixed their interior material, and a fraction of C has already been converted into nitrogen in their evolution status.
When the errors in the [C/Fe] determinations are taken into account, it is reasonable to consider all stars with − 0.3 ≤ [C/Fe] ≤ +0.3 as having a normal carbon abundance. Four stars in our sample (RVS 014, RVS 029, RVS 065, and RVS 129) stand out from the sample for their relatively high C abundance, with [C/Fe] > 0.3 dex, and 22 stars show a low [C/Fe] ratio (< −0.3). These 22 stars are RVS 008, RVS 015, RVS 022, RVS 042, RVS 044, RVS 050, RVS 064, RVS 102, RVS 101, RVS 103, RVS 123, RVS 124, RVS 133, RVS 134, RVS 146, RVS 147, RVS 150, RVS 153, RVS 154, RVS 160, RVS 163, and RVS 179.
4.2.3 Oxygen
The two forbidden oxygen lines at 630 and 636 nm are both in the observed range. These lines form in conditions close to LTE and in evolved stars they are stronger than in main-sequence stars. We were able to analyse at least one of these lines for all stars. When both lines are not contaminated by blends, the abundance derived from the two lines is good and shows an average difference of 0.02 dex, as found by Caffau et al. (2013) in the case of evolved stars. Figure 4 shows [O/Fe] versus stellar metallicity [Fe/H]. Thisshows the behaviour of increasing [O/Fe] as [Fe/H] decreases. This behaviour is familiar for this element and all α-elements.
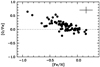 |
Fig. 4 [O/Fe] vs. [Fe/H]. |
4.2.4 Ionisation equilibrium
We recall that the surface gravity was derived using the Gaia EDR3 parallax (see Sect. 4.1) and not from the spectra by imposing the same Fe abundance as when the surface gravity is derived from Fe I and Fe II lines. Figure 5 compares the abundance derived from neutral and singly ionised species for Sc, Ti, and Fe. The trend is good in general. The difference between the abundances derived from neutral and ionised lines are close to zero on average, but the scatter is not negligible. For all stars except for one, the difference in A(Fe) when derived from neutral and ionised Fe lines ranges from –0.24 to +0.25. For the star RVS 160, the disagreement is 0.49 dex.
4.2.5 α elements
As α elements, Mg, Si, S, and Ca were investigated. We show their abundances in Fig. 6 versus stellar metallicity.
To determine the Mg abundance, MyGIsFOS kept from 1 to 13 Mg I features. The line-to-line scatter ranges from 0.02 to 0.14 dex, with an average value of 0.06 dex. A clear increase in [Mg/Fe] for decreasing metallicity is evident in the upper panel of Fig. 6, and the star-to-star scatter is small.
For the Si abundance, MyGIsFOS selected from 16 to 29 features in the wavelength range. In the sample of stars ⟨[Si/Fe]⟩ = 0.15 ± 0.07, and the average line-to-line scatter in the stars is 0.1 dex. The middle panel of Fig. 6 shows [Si/Fe] as a function of [Fe/H].
Using from one to six Ca I features, MyGIsFOS was able to derive the Ca abundance for 77 stars. The line-to-line scatter is small, ⟨σ⟩ = 0.04 ± 0.02.
The sulphur abundance was derived from the S I triplets of Mult. 8 at 675 nm. The lines of Mult. 8 form close to LTE conditions. [S/Fe] behaviour as a function of metallicity is not as clear as for the other α elements (see Fig. 7) and the star-to-star scatter is also quite large, but this is due to the fact that only one or two measurement support the A(S) determination and these features are weak. Some stars show a low S abundance, but this is compatible with the uncertainty with a normal, solar-scaled abundance.
 |
Fig. 5 Comparison of the abundances from neutral and ionised lines. |
 |
Fig. 6 α elements. |
4.2.6 Light elements
MyGIsFOS was able to derive A(Al) for all stars in the sample by using from two to eight Al I features. The line-to-line scatter is always small (from 0.01 to 0.16 dex). All strong Al I lines show effects of departure from LTE. To give an idea of the NLTE effects on the Al lines, we investigated one star, RVS 123. The NLTE corrections for the two lines at 669 nm are about 0.15–0.20 dex, for the two lines at 783 nm, they are in the range 0.13–0.17 dex, and for the two lines at 877 nm, they are about 0.15–0.20 dex. Therefore the LTE analysis of the Al I lines in the near-IR range provides an overestimation of A(Al) for these parameters of about 0.15–0.20 dex.
For all stars in the sample, the Sc abundance was derived from the Sc I and Sc II lines. Only a few lines for neutral and singly ionised Sc lines (from one to five and from one to four, respectively) can be used to determine the abundance. The line-to-line scatter is generally small (0.09 dex on average), but for one and two cases in the two ionisation states with an abundance determination from more than one line (RVS 133 for Sc I, and RVS 042 and RVS 132 for Sc II), the line-to-line scatter is larger than 0.3 dex. Theagreement in the Sc abundance when derived from neutral and singly ionised lines is reasonably good (see Sect. 4.2.4).
For all stars, A(Ti) was derived from Ti I by investigating a large number of lines (MyGIsFOS retained from 41 to 75 lines) and providing a relatively low line-to-line scatter (0.12 dex on average). A(Ti) was also derived by using Ti II lines (from one to four lines), with a slightly smaller line-to-line scatter (0.09 dex on average). The comparison of A(Ti) when derived from neutral or singly ionised lines is similar to the cases of Fe and Sc, and is shown in Fig. 6.
4.2.7 Iron peak elements
A good sample of V I features (from 9 to 38) was used by MyGIsFOS to derive A(V) with a relatively small line-to-line scatter (0.12 dex) on average. For the sample of stars, we derive ⟨[V/Fe]⟩ = 0.02 ± 0.07. Only one star shows a relatively high [V/Fe] ratio of +0.31 (RVS 160).
Several Cr I features (from 18 to 31) were kept by MyGIsFOS in the A(Cr) determination, providing a reasonably good line-to-line scatter (0.11 dex on average). We derive ⟨[Cr/Fe]⟩ = 0.03 ± 0.05 for the sample of stars.
Only a few features (from three to four) of Mn I were retained by MyGIsFOS in the Mn abundance determination. The line-to-line scatter is normally larger than for the other elements (the average value is 0.21 dex) and for the complete sample ⟨[Mn/Fe]⟩ = 0.02 ± 0.05.
A nice sample (from 10 to 27) of Co I features allowed us to derive A(Co) with a good line-to-line scatter (0.14 on average). From the complete sample, we derive ⟨[Co/Fe]⟩ = 0.08 ± 0.06.
From 21 to 46 lines of Ni I we derived the Ni abundance for all stars with a reasonable line-to-line scatter (0.18 on average). For the complete sample, ⟨[Ni/Fe]⟩ = 0.0 ± 0.03.
4.3 Rubidium abundance
Based on the two Rb I lines in the wavelength range, MyGIsFOS was able to derive the Rb abundance for 48 stars using only the line at 794 nm. To be able to use both lines, we also derived the Rb abundance by line-profile fitting of the two Rb I observed lines. A model atmosphere was computed for each star with ATLAS 9 (see Kurucz 2005), with the adopted stellar parameters. In order to find the atomic level populations and the departure coefficients (the b-factors, where b = NNLTE∕NLTE) for Rb I, we employed the code MULTI (Carlsson 1986), modified by Korotin et al. (1999) for the opacity unit of the ATLAS 9 code of stellar atmosphere computations (Castelli & Kurucz 2003) to be applicable in our calculations. The rubidium NLTE atomic model is described in detail in Korotin (2020). The theoretical synthesis was computed with the SynthV software package (Tsymbal 1996), which is designed to model a synthetic stellar spectrum. The synthetic spectrum included all of the lines in a specified wavelength range from the VALD list of lines (Ryabchikova et al. 2015) calculated in LTE and the rubidium lines we are interested in, whose source function and opacities were calculated from the corresponding b-factors. We derived the LTE and NLTE abundances of Rb for all stars.
The NLTE corrections strongly and unambiguously depend on atmospheric parameters and elemental abundance. The values of NLTE corrections can have both positive and negative values. In this relatively small metallicity range, the NLTE effects are weakly dependent on metallicity. In contrast, there is a trend of the NLTE correction with temperature: for the coolest stars, the correction is small and positive and then decreases with increasing temperature. For the hottest stars in the sample, the correction is the maximum in absolute value and is about –0.10 dex. In Fig. 8, the [Rb/Fe] ratio is plotted as a function of [Fe/H], and both the LTE and NLTE A(Rb) are provided for the [Rb/Fe] ratio (empty red and filled black symbols in the figure, respectively). The LTE and the NLTE values are compared to the same solar abundance of A(Rb)⊙ = 2.60 form Lodders et al. (2009) (see Table 1) and to the Fe abundance here derived in LTE.
We compared the results on the Rb abundance derived from the 794 nm line from MyGIsFOS and the fitting procedure of the observed line profile: the abundances we derive are very similar, they have a difference of − 0.00 ± 0.05, and all stars show a difference in the Rb abundance from the two approaches within 0.1 dex.
 |
Fig. 7 [S/Fe]versus metallicity. |
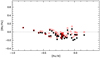 |
Fig. 8 [Rb/Fe] vs. [Fe/H] for the sample stars: NLTE (filled black circles) and LTE values (red empty symbols). For the solar value we used A(Rb) = 2.60 (Lodders et al. 2009) for the NLTE and LTE values to show the effect on NLTE, also because the Fe abundance is in LTE. |
 |
Fig. 9 Heavy elements vs. [Fe/H] for the sample stars. |
4.4 Heavy elements
The heavy elements were derived by matching the observed spectrum around each line of the list with a synthetic spectrum using the LTE spectral line analysis code turbospectrum (Alvarez & Plez 1998; Plez 2012), which treats scattering in detail. We used the ATLAS 9 models computed with the specific stellar parameters for each star as given in Table B.2.
For the heavy elements, we analysed Zn, Sr, Y, Ba, and Eu. We selected the following lines: the 481 nm Zn I line for Zn, the Sr I line at 707.01 nm for Sr, we analysed the 679.5 nm Y I and the 572.8 nm Y II lines for Y, the 664.5 nm Eu II line for Eu, and the two Ba II lines at 585.3 and 614.2 nm for Ba. The trend with respect to [Fe/H] of Sr, Y, Ba, and Eu are shown in Fig. 9. The [Zn/Fe]ratio is negative for all but one star (the most metal-poor star); the average value in the sample is ⟨[Zn∕Fe]⟩ = −0.27 ± 0.13.
4.5 Kinematics and orbital properties of stars in the sample
To study the kinematics and orbital properties of stars in the sample, we calculated the positions and velocities in the galactocentric rest frame by assuming an in-plane distance of the Sun from the Galactic centre, R⊙ = 8.34 kpc (Reid et al 2014), a height of the Sun above the Galactic plane, z⊙ = 27 pc (Chen et al 2001), a velocity for the local standard of rest (LSR), VLSR = 240 km s−1 (Reid et al 2014), and a peculiar velocity of the Sun with respect to the LSR, U⊙ = 11.1 km s−1, V⊙ = 12.24 km s−1, W⊙ = 7.25 km s−1 (Schönrich et al 2010). The transformations from equatorial to galactocentric coordinates were performed by using the Astropy software (Astropy Collaboration 2013, 2018). In Fig. 10 we show the Toomre diagram, that is, the 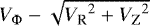 plane, with VR and VZ being the radial and vertical components of the velocity of stars, respectively, and we colour-code stars depending on their [Fe/H] and [Mg/Fe] content.
plane, with VR and VZ being the radial and vertical components of the velocity of stars, respectively, and we colour-code stars depending on their [Fe/H] and [Mg/Fe] content.
In this plane, most of the stars (59 out of 80) in the sample appear to be kinematically associated with the thin disc because the absolute value of their velocity, 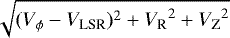 , relative to the LSR, is lower than 50 km s−1. The remaining stars (21 out of 80) all have hotter kinematics: for 19 of them, the absolute value of their velocity lies between 50 and 100 km s−1; the two stars that show the hottest kinematics (RVS065 and RVS138, with
, relative to the LSR, is lower than 50 km s−1. The remaining stars (21 out of 80) all have hotter kinematics: for 19 of them, the absolute value of their velocity lies between 50 and 100 km s−1; the two stars that show the hottest kinematics (RVS065 and RVS138, with 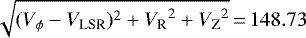 and 140.31 km s−1, respectively) also have the lowest [Fe/H] values and the highest [Mg/Fe] ratios.
and 140.31 km s−1, respectively) also have the lowest [Fe/H] values and the highest [Mg/Fe] ratios.
The cold kinematics of these stars is also reflected in their orbital properties: most of the stellar orbits are indeed confined close to the Galaxy midplane, with zmax (the maximum height from the plane that a star can reach) lower than 500 pc (see Fig. 11).
To integrate the orbits of stars, we used the axisymmetric Galactic potential “PII” (described in Pouliasis et al. 2017), which consists of a thin and a thick stellar disc and a spherical dark matter halo, and which reproduces a number of characteristics of the Milky Way (see Pouliasis et al. 2017, for details). Starting from the current positions and velocities of stars in the galactocentric rest frame, derived as described above, we integrated their orbits backward in time for 5 Gyr by making use of a leap-frog algorithm with a fixed time step Δt = 105 yr. For each star, we thus reconstructed its orbit in the Galactic potential we adopted, and hence estimate the maximum height from the plane, zmax, that it reaches, as well as its (in-plane) apocentre Rmax. To estimate the uncertainties on the orbital parameters, we computed 100 realisations of its orbit for each star by making use of the 100 random realisations of its parallax, proper motions, and line-of-sight velocity, as described above. All these realisations were also integrated in the same Galactic potential and for the same total time interval. The orbits of all stars are reported in Appendix A.
5 Discussion
5.1 Stellar parameters
We compared the derived effective temperatures and surface gravities to the values derived using the calibration by Mucciarelli & Bellazzini (2020): our Teff is systematically lower, overall at the lowest temperatures, by − 55 ± 39 K, with a maximum difference of − 145 K for the star RVS 065. The differences in log g are negligible and simply reflect the difference in the temperature scale.
The ionisation balance we derive in the stars we analysed is acceptable, but far from perfect (see Sect. 4.2.4). It is always a decision to be taken: derive the stellar parameters and abundances from the spectra, or take advantage of other available observations and calibrations (in the case of the microturbulence) for the stars. These stars are bright, and the Gaia EDR3 photometry and the parallaxes are both good. In addition, we have access to precise maps from which to derive the reddening of these relatively close-by stars. We therefore decided to derive the stellar parameters as much as possible without the information available from the spectra.
We recall that we derived the gravity from the parallax corrected for the zero-point. When the abundances derived from neutral and singly ionised species are compared, we also see a certain scatter, if not a systematic trend.
To verify the disagreement of log g derived from the parallax and from the ionisation equilibrium, with fixed effective temperatures (those derived from the photometry), we allowed MyGIsFOS to derive the surface gravity by imposing an ionisation equilibrium of the iron lines of the two ionisations states (see Sbordone et al. 2014, for details). For coherence with the analysis done with fixed log g, we also allowed the microturbulence to be derived by the code. The difference in surface gravities weobtain (from the parallax and from the Fe ionisation equilibrium) is generally tiny (0.01 ± 0.16), from 2.18 ± 0.47, in the range 1.05–3.27, when derived from the parallax to 2.17 ± 0.48, in the range 1.03–3.18, when derived from the Fe ionisation equilibrium. For all except two stars (RVS 155 and RVS 160), the difference is within 0.3 dex. The star RVS 160 showed the strongest ionisation unbalance with the surface gravity derived from the photometry and the parallax. With the ionisation balance, the surface gravity converges to log g = 2.78, providing a good ionisation balance, a surface gravity 0.72 dex higher than from the parallax. To derive a gravity like this from the calibration, a stellar mass of 20 M⊙ would be necessary.
The microturbulence increases by decreasing the surface gravity, as expected, but the stars showing the highest microturbulence are not the most evolved, nor are they the hottest in the sample. Seven stars (RVS 039, RVS 125, RVS 126, RVS 128, RVS 150, and RVS 153) have ξ > 1.95km s−1. This value is higher than any value we derived by using the calibration by Monaco et al. (2005). The question is whether these stars are different from the others, or if the values of microturbulence we derive are unreliable. Based on the isochrones, these stars are young (2–0.2 Gyr), and their masses are high (2 or more solar masses).
The microturbulence derived when log g is a free parameter for MyGIsFOS remains in the same range as when log g is fixed. The difference is small on average (0.0 ± 0.11km s−1), but there are some outliers: seven stars show an absolute difference larger than 0.1 km s−1, and for four stars (RVS 125, RVS 126, RVS 145, and RVS 147), this difference is larger than 0.2 km s−1, All stars except for RVS 126, however, have an absolute difference smaller than 0.4 km s−1. In the case of RVS 126, a microturbulence of 2.45 km s−1 is derived by MyGIsFOS when log g is kept fixed, while a value of 1.72 km s−1 is derived when the surface gravity is a free parameter as well.
 |
Fig. 10 Toomre diagram for stars in the sample, colour-coded by their [Fe/H] content (top panel) and their [Mg/Fe] abundances (bottom panel). The dashed lines separate regions with
|
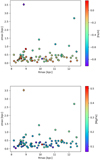 |
Fig. 11 Distribution of stars in the Rmax − zmax plane, colour-coded by their [Fe/H] content (top panel) and their [Mg/Fe] abundances (bottom panel). |
5.2 Abundances
Figure 6 shows that the α-elements present the typical increase in their ratio to iron as metallicity decreases, as is normally expected in this metallicity range (see e.g. Nissen & Schuster 2010). In Fig. 12 our results are compared to the sample of unevolved stars by Bensby et al. (2014). To be fair in the comparison, we scaled their solar abundances to our adopted values. Our sample spans a metallicity subrange of the Bensby et al. (2014) sample, but we see a good agreement for Mg and Si, while our Ca abundances are perhaps slightly lower on average than the comparison sample, but we cannot explain this. Still, fewer lines were investigated than for Mg and Si, and Nissen & Schuster (2010) also reported a quite flat [Ca/Fe] ratio with a tiny difference between the two populations (high-α and low-α stars). As a sanity check, we analysed the UVES-POP (Bagnulo et al. 2003) spectrum of Arcturus (437B, 580L, 580U, and 860L). The analysis for Mg, Si, and Ca is perfectly compatible with the sample of stars we investigated.
Too few of our stars are metal-poor enough for us to be able to show the high- and low-α sequence as presented by Nissen & Schuster (2010). In the metallicity range in which the two populations can be distinguished ([Fe/H] < −0.5), we only have nine stars. These stars probably belong to the Galactic thick disc; they have an average distance of 600 parsec in the range 290–600 parsec. The complete sample is in the distance range 151–1160 parsec from the Sun.
The iron peak elements are derived with reasonably good accuracy, and they trace the Fe abundance well. In Fig. 13 they are compared to the Nissen & Schuster (2010) investigation. The agreement in the overlap metallicity range is good.
In Fig. 14 we compare the Sr and Eu abundances we derive with the analysis by Battistini & Bensby (2016). The two samples behave similarly, although for Sr in the Battistini & Bensby (2016) sample, [Sr/Fe] is predominantly sub-solar, while in our sample it is close to solar except for one star, RVS 125. This star shows high abundance ratios for [Sr/Fe] = 0.89, [Y/Fe] = 0.77, [Ba/Fe] = 0.51, and [Eu/Fe] = 0.74, while this star is normal in Rb, [Rb/Fe] = −0.09. We recall that this star, according to our analysis, is young, and we derived a mass of 3.4 M⊙.
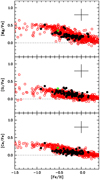 |
Fig. 12 α elements weanalysed (filled black symbols) compared to the sample by Bensby et al. (2014) (open red circles) after scaling it to our solar abundances. The green star represents a consistent chemical analysis of Arcturus. |
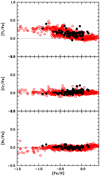 |
Fig. 13 Iron-peak elements we analysed (filled black symbols) compared to the sample by Nissen & Schuster (2010) (open red circles). |
5.3 Rubidium
Figure 15 compares the LTE abundances we derive for Rb to the analysis by Tomkin & Lambert (1999) of the 780 nm Rb I line. The agreement of the two samples is good.
Recently, Takeda (2021) derived the Rb abundance in a large sample of stars by analysing the Rb I 780 nm line. His stellar sample of giant stars is slightly cooler (4490 < Teff < 5625 K) than the sample investigated here and close in surface gravity (1.4 < log g < 3.5) and metallicity (− 0.8 < [Fe/H] < 0.2). Figure 16 compares our NLTE results to his NLTE analysis of his sample of giant stars. We note a general good agreement except at high metallicity, where we find several stars with higher Rb abundance that are not present in the sample of Takeda (2021). The six stars in our sample, at the highest metallicity, standing out for a high [Rb/Fe] ratio, are similar in stellar parameters when compared to the sample by Takeda (2021).
As discussed in Abia et al. (2020) and Figs. 15 and 16 show, the majority of the stars (37 out of 48 for which Rb is detected) show [Rb/Fe] < 0.0. This is also visible in the comparison samples of Tomkin & Lambert (1999) and Takeda (2021). Rubidium shows a sub-solar abundance for stars around solar metallicity. This effect depends on the choice on the solar Rb abundance. The solar reference value of A(Rb) = 2.60 adopted here is higher by about 0.2 dex than the meteoritic value (2.38 ± 0.03, Lodders et al. 2009; 2.36 ± 0.03, Lodders 2019). The solar LTE abundance given by Grevesse et al. (2015) is somewhat lower (A(Rb) = 2.47 ± 0.07) and closer to the meteoritic and solar system values. More recently, Korotin (2020) found that the solar Rb resonance lines deviate substantially from LTE, characterised by an NLTE correction of − 0.12 dex. This leads to a solar NLTE Rb abundance of 2.35 ± 0.05 that is fully consistent with the meteoritic value. This appealing result was challenged by Takeda (2021), who reported smaller solar NLTE corrections of about − 0.05 dex. Nevertheless, taking NLTE effects into account brings the solar Rb abundance close to the meteoritic value. Adopting the meteoritic abundance as the solar reference would result in a super-solar [Rb/Fe] ratio for many stars around solar metallicity.
For the solar case, Grevesse et al. (2015) reported a difference in A(Rb) derived from the two Rb I lines. The line at 794 nm indicates a lower solar Rb abundance than the Rb I 780 nm line; the difference is 0.11 dex (see their Sect. 5.6). Grevesse et al. (2015) suggested that an “unknown blend” in the range of the 780 nm line leads to an overestimation of the Rb abundance inferred from this line. Similarly, Korotin (2020) reported am NLTE Rb abundance of 2.40 and 2.30 from the 780 and the 794 nm line, respectively.NLTE effects cannot explain the abundance discrepancy between the two lines because the NLTE corrections are identical for the two fine-structure components.
Takeda (2021) suggested that a possible cause for the discrepancy in the solar spectrum might be the telluric contamination of the 794 nm line. Over-subtraction of the telluric absorption would lead to an underestimation of the Rb abundance deduced from that spectral line. His reasoning is based on his results for HIP 104214, a K dwarf with relatively strong Rb I lines. Because of the high radial velocity of − 82 km s−1, the 794 nm line is free of telluric contamination. From the NLTE analysis of his high S/N spectrum, the author found that although the abundance difference between the two Rb lines has the same sign as in the Sun, it is too small to be considered significant. A high-resolution spectrum of sunlight reflected off an asteroid with a sufficiently high radial velocity to shift the telluric blend away from the 794 nm line might shed new light on the solar Rb line discrepancy.
We also investigated the possibility that the discrepancy might be related to the fact that the Rb 780 nm line originates on the red shoulder of a strong Si I line. A similar case is the Li doublet at 670.7 nm in metal-poor stars, where the 6Li component falls on the red wing of the stronger 7Li doublet. When the analysis was performed using 1D stellar models, the line asymmetry of 7Li cannot be taken into account and the (possible) presence of the 6Li is overestimated (for details, see Cayrel et al. 2007). Another example is the weak thorium line at 401.9 nm on the red wing of a strong Fe-Ni blend. As shown by Caffau et al. (2008), the abundance derived from this unique Th line in the solar spectrum is lower by 0.1 dex when the analysis is based on a 3D hydrodynamical atmosphere rather than on a 1D hydrostatic model. Convective Doppler shifts cause a slightly stronger absorption in the red wing of the 3D Fe-Ni line profile, reducing the amount of thorium that is required to match the observed spectrum.
To verify whether a similar scenario might lead to a reduction of the Rb abundance derived form the 780 nm line, we analysed the asymmetry of the underlying Si I line profile computed from a 3D solar CO5BOLD (Freytag et al. 2012) model atmosphere. We find that the overall asymmetry of the Si I line is minor, and that somewhat unexpectedly, the blue wing is slightly deeper than the red wing, meaning that the asymmetry is opposite to what would be needed to support the above scenario. We conclude that 3D effects are unlikely to be the cause of the solar Rb line discrepancy. The 3D LTE granulation correction is about − 0.04 and − 0.06 dex for intensityand flux, respectively, and it equally affects both Rb lines.
For the 68 stars for which both lines are retained, we do not see a systematic difference in A(Rb) between thetwo lines in LTE or in NLTE. The abundance difference between the two lines ranges from − 0.05 to + 0.04 in LTE and NLTE, with an average close to zero.
We compared the LTE A(Rb) to the abundances of the s−process elements Sr and Y (see Fig. 17). The average ratios we derive are ⟨[Rb/Sr]⟩ = −0.10 ± 0.13 and ⟨[Rb/Y]⟩ = −0.19 ± 0.16. The stars in our sample do not show high [Rb/Sr] or [Rb/Y], suggesting a low neutron density at the sites of the s−process for these stars (Smith & Lambert 1984). The relatively low values are a consequence of the choice of the high solar A(Rb). Had we adopted the meteoritic value as the solar reference, ⟨[Rb/Y]⟩ would be closer to zero and ⟨[Rb/Sr]⟩ positive. As expected, all stars behave in a similar way, and we do not find abnormally high [Rb/Sr] or [Rb/Y] values for any star in the sample.
The only star that stands out is RVS 125, showing exceptionally low abundance ratios: [Rb/Sr] = –1.0 and [Rb/Y] = –0.89. It is easily detectable as the outstanding low point in Fig. 17. The low values are a consequenceof the exceptionally high Sr and Y abundances of this star, while the Rb abundance is normal. In this star, all the neutron capture elements appear to be enhanced with respect to iron, including Eu. The high mass (M = 3.4 M⊙) we derive for this star and its position with respect to the isochrones suggest that RVS 125 is most likely an AGB star. However, its luminosity is too low to be self-enrichedin s−process elements because this should only happen when the star is in the phase of the thermal pulses (TP-AGB, see e.g. Busso et al. 1999, 2021 and references therein). Furthermore, the overabundance of Eu precludes this interpretation because Eu is a pure r−process element.
A possible concern regarding the spectroscopic analysis might be that (in LTE) the Fe I to Fe II and the Ti I to Ti II ionisation balance of this star is offset by about 0.1 dex, whereas the microturbulence is rather high (2.41 km s−1). To determine to which extent the atmospheric parameters may affect the derived abundances, we repeated the analysis of this star, but now allowing all stellar parameters except for Teff to be automatically adjusted by MyGIsFOS. In this case, the ionisation balance is enforced, the derived surface gravity is higher, and the microturbulence lower. The [Sr/Fe], [Y/Fe], and [Eu/Fe] ratios remain higher than +0.4 dex, however. We conclude that it appears to be unlikely that a different choice of atmospheric parameters may bring these ratios close to zero. It is also difficult to invoke deficiencies in our analysis, such as the neglect of NLTE and 3D effects, because these should equally affect the other stars with similar atmospheric parameters. The abundances of n-capture elements in this star deserve further investigation.
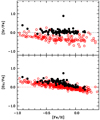 |
Fig. 14 [Sr/Fe] (upper panel) and [Eu/Fe] (lower panel) vs. [Fe/H] for the sample stars (filled black circles). The comparison sample (open red symbols) is from Battistini & Bensby (2016). |
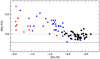 |
Fig. 15 [Rb/Fe] vs. [Fe/H] for our sample stars (LTE values shown as filled black circles) compared to the sample by Tomkin & Lambert (1999) (red squares for giants, and blue squares for dwarfs). The horizontal dotted line is the reference zero value with A(Rb) = 2.60 as the solar abundance, the dashed line would be the zero solar value if the meteoritic Rb abundance, A(Rb) = 2.38, were adopted. |
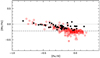 |
Fig. 16 [Rb/Fe] vs. [Fe/H] for our sample stars (filled black circles) compared to the sample of Takeda (2021) (open red squares). The horizontal dotted line is the reference zero value with A(Rb) = 2.60 as the solar abundance, the dashed line would be the zero reference for the meteoritic abundance, A(Rb) = 2.38. Unlike Fig. 15, this plot shows the NLTE Rb abundances. |
 |
Fig. 17 LTE abundance ratios [Rb/Sr] (upper panel) and [Rb/Y] (lower panel) vs. [Fe/H]. |
6 Conclusions
We here presented the chemical investigation of a sample of UVES spectra that will be used to determine the LSF across the focal plane of the RVS on board of Gaia and to improve the radial velocity determination of the Gaia observations. The stars in this sample wereselected from the Gaia DR2 photometry as evolved, possibly slightly metal-poor stars. Selection criteria were also (i) a good precision in the Gaia DR2 radial velocity and (ii) no known chemical investigation, in a way to increase the sample of bright Galactic stars with a detailed chemical inventory. To our knowledge, none of the 80 stars we analysed has a previous chemical investigation. We were able derive a complete chemical analysis for all the stars (α, iron-peak, and heavy elements). No peculiarity in the chemical inventory was found, except for one star, RVS 125, which shows a high Sr, Y, Ba, and Eu abundance, but a normal Rb abundance.
We gave particularly attention to Rb, an element that is often neglected because only few Rb I lines are available in the spectra of cool stars and because of their wavelength position, which is not always covered by optical or infrared spectrographs. We computed NLTE effects for the stars. These effects are generally small and never exceed 0.1 dex. Our LTE and NLTE analyses are comparable to the literature results.
Kinematically, these stars belong in their majority to the thin disc. They lie close to the Galactic plane.
Acknowledgements
We gratefully acknowledge support from the French National Research Agency (ANR) funded projects “Pristine” (ANR-18-CE31-0017) and “MOD4Gai” (ANR-15- CE31-0007). SAK acknowledge financial support from the RFBR and Republic of Crimea, project 20-42-910007. H.G.L. gratefully acknowledges financial support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) Project ID 138713538-SFB 881 (“The Milky Way System”, subproject A04). This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France.
Appendix A Orbits ofstars in the sample
In this appendix, we show the orbits of the 80 stars in the sample. We show the meridional plane, R–Z, and the projection on the X–Y plane. The orbits of the stars are integrated for 5 Gyr backward in time, starting from the current positions and velocities of the stars. The Galactic potential adopted is the model called PII that was presented in Pouliasis et al. (2017), which consists of a thin and a thick disc component, surrounded by a spherical dark matter halo.
 |
Fig. A.1 Projection on the X–Y plane and on the R–Z plane of the orbits of the stars in the sample. The blue line corresponds to the mean orbit of each star, the grey lines to the 100 realisations of this orbit after errors on the observables (parallaxes, proper motions, and line-of-sight velocities) are taken into account, as described in Sect. 4.5. The cyan symbol indicates the position of the Sun, and the red star shows the current position of the star. The ID of each star is reported in the top left corner of each panel. |
Appendix B Stellar information
In this appendix, we report the log of the observations. We also list in Table B.2 the stellar parameters we adopted in this work that are explained in the paper. Table B.3 is available at the CDS and provides detail chemical abundances.
Observation log.
Stellar parameters.
Appendix C Atomic data
Table C.1 with the lines fitted for each star and each element is available at the CDS. We here recall that to derive individual chemical abundances, MyGIsFOS fits a predefined wavelength range. In this range, several lines of the same species can be present. All of them, if they are not too weak, are provided in the table.
References
- Abia, C., Tabernero, H. M., Korotin, S. A., et al. 2020, A&A, 642, A227 [CrossRef] [EDP Sciences] [Google Scholar]
- Allende Prieto, C., Koesterke, L., Ludwig, H.-G., et al. 2013, A&A, 550, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alvarez, R., & Plez, B. 1998, A&A, 330, 1109 [NASA ADS] [Google Scholar]
- Amarsi, A. M., Barklem, P. S., Collet, R., et al. 2019, A&A, 624, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P. et al.), 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Bagnulo, S., Jehin, E., Ledoux, C., et al. 2003, The Messenger, 114, 10 [Google Scholar]
- Battistini, C., & Bensby, T. 2016, A&A, 586, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Feltzing, S., & Oey, M. S. 2014, A&A, 562, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Busso, M., Gallino, R., & Wasserburg, G. J. 1999, ARA&A, 37, 239 [Google Scholar]
- Busso, M., Vescovi, D., Palmerini, S., et al. 2021, ApJ, 908, 55 [Google Scholar]
- Caffau, E., Sbordone, L., Ludwig, H.-G., et al. 2008, A&A, 483, 591 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caffau, E., Ludwig, H.-G., Bonifacio, P., et al. 2010, A&A, 514, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caffau, E., Ludwig, H.-G., Steffen, M., Freytag, B., & Bonifacio, P. 2011, Sol. Phys., 268, 255 [Google Scholar]
- Caffau, E., Ludwig, H.-G., Malherbe, J.-M., et al. 2013, A&A, 554, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carlsson, M. 1986, Uppsala Astronomical Observatory Reports (UK: The Observatory), 33 [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2003, IAU Symp., 210, A20 [Google Scholar]
- Cayrel, R., Steffen, M., Chand, H., et al. 2007, A&A, 473, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, B., Stoughton, C., Smith, J. A., et al. 2001, ApJ, 553, 184 [Google Scholar]
- Crifo, F., Jasniewicz, G., Soubiran, C., et al. 2010, A&A, 524, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dalton, G., Trager, S., Abrams, D. C., et al. 2018, Proc. SPIE, 10 702, 107021B [Google Scholar]
- de Jong, R. S., Agertz, O., Berbel, A. A., et al. 2019, The Messenger, 175, 3 [NASA ADS] [Google Scholar]
- Dekker, H., D’Odorico, S., Kaufer, A., et al. 2000, Proc. SPIE, 4008, 534 [Google Scholar]
- Dutra-Ferreira, L., Pasquini, L., Smiljanic, R., et al. 2016, A&A, 585, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Freytag, B., Steffen, M., Ludwig, H.-G., et al. 2012, J. Comput. Phys., 231, 919 [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016a, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2016b, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grevesse, N., Scott, P., Asplund, M., et al. 2015, A&A, 573, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiter, U., Lind, K., Asplund, M., et al. 2015, Phys. Scr, 90, 054010 [CrossRef] [Google Scholar]
- Heiter, U., Lind, K., Bergemann, M., et al. 2021, A&A, 645, A106 [EDP Sciences] [Google Scholar]
- Ivanova A., Lallement R., Vergely J. L., et al. 2021, A&A, submitted [arXiv:2104.14227] [Google Scholar]
- Käppeler, F., Gallino, R., Bisterzo, S., et al. 2011, Rev. Mod. Physi., 83, 157 [Google Scholar]
- Korotin, S. A. 2020, Astron. Lett., 46, 541 [Google Scholar]
- Korotin, S. A., Andrievsky, S. M., & Kostynchuk, L. Y. 1999, A&A, 342, 756 [Google Scholar]
- Kurucz, R. L. 2005, Mem. Soc. Astron. It. Suppl., 8, 14 [Google Scholar]
- Lindegren, L., Bastian, U., Biermann, M., et al. 2021, A&A 649, A4 [EDP Sciences] [Google Scholar]
- Lodders, K. 2019, ArXiv e-prints [arXiv:1912.00844] [Google Scholar]
- Lodders, K., Palme, H., & Gail, H.-P. 2009, Landolt Börnstein (Berlin: Springer), 712 [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2017, ApJ, 835, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Mashonkina, L., Jablonka, P., Pakhomov, Y., et al. 2017, A&A, 604, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monaco, L., Bellazzini, M., Bonifacio, P., et al. 2005, A&A, 441, 141 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Mucciarelli, A., & Bellazzini, M. 2020, Res. Notes Am. Astron. Soci., 4, 52 [Google Scholar]
- Nissen, P. E., & Schuster, W. J. 2010, A&A, 511, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plez, B. 2012, Astrophysics Source Code Library [record ascl:1205.004] [Google Scholar]
- Pouliasis, E., Di Matteo, P., & Haywood, M. 2017, A&A, 598, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2014, ApJ, 783, 130 [Google Scholar]
- Ryabchikova, T., Piskunov, N., Kurucz, R. L., et al. 2015, Phys. Scr, 90, 054005 [Google Scholar]
- Sartoretti, P., Katz, D., Cropper, M., et al. 2018, A&A, 616, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sbordone, L., Bonifacio, P., Castelli, F., & Kurucz, R. L. 2004, Mem. Soc. Astron. It. Suppl., 5, 93 [Google Scholar]
- Sbordone, L., Caffau, E., Bonifacio, P., & Duffau, S. 2014, A&A, 564, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schönrich, R., Binney, J., & Dehnen, W. 2010, MNRAS, 403, 1829 [NASA ADS] [CrossRef] [Google Scholar]
- Smiljanic, R., Korn, A. J., Bergemann, M., et al. 2014, A&A, 570, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, V. V., & Lambert, D. L. 1984, PASP, 96, 226 [Google Scholar]
- Soubiran, C., Jasniewicz, G., Chemin, L., et al. 2018, A&A, 616, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takeda, Y. 2021, Astron. Nachr., 342, 515 [Google Scholar]
- Tomkin, J., & Lambert, D. L. 1999, ApJ, 523, 234 [Google Scholar]
- Tsymbal, V. 1996, M.A.S.S., Model Atmospheres and Spectrum Synthesis, 108, 198 [Google Scholar]
- Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Two spectra (RVS 002 and RVS 038) in the wavelength range of the Gaia RVS. |
| In the text | |
 |
Fig. 2 Observed stars in the (Teff, log g) diagram compared to PARSEC isochrones to guide the eyes. |
| In the text | |
 |
Fig. 3 [C/Fe] vs. metallicity. |
| In the text | |
 |
Fig. 4 [O/Fe] vs. [Fe/H]. |
| In the text | |
 |
Fig. 5 Comparison of the abundances from neutral and ionised lines. |
| In the text | |
 |
Fig. 6 α elements. |
| In the text | |
 |
Fig. 7 [S/Fe]versus metallicity. |
| In the text | |
 |
Fig. 8 [Rb/Fe] vs. [Fe/H] for the sample stars: NLTE (filled black circles) and LTE values (red empty symbols). For the solar value we used A(Rb) = 2.60 (Lodders et al. 2009) for the NLTE and LTE values to show the effect on NLTE, also because the Fe abundance is in LTE. |
| In the text | |
 |
Fig. 9 Heavy elements vs. [Fe/H] for the sample stars. |
| In the text | |
 |
Fig. 10 Toomre diagram for stars in the sample, colour-coded by their [Fe/H] content (top panel) and their [Mg/Fe] abundances (bottom panel). The dashed lines separate regions with
|
| In the text | |
 |
Fig. 11 Distribution of stars in the Rmax − zmax plane, colour-coded by their [Fe/H] content (top panel) and their [Mg/Fe] abundances (bottom panel). |
| In the text | |
 |
Fig. 12 α elements weanalysed (filled black symbols) compared to the sample by Bensby et al. (2014) (open red circles) after scaling it to our solar abundances. The green star represents a consistent chemical analysis of Arcturus. |
| In the text | |
 |
Fig. 13 Iron-peak elements we analysed (filled black symbols) compared to the sample by Nissen & Schuster (2010) (open red circles). |
| In the text | |
 |
Fig. 14 [Sr/Fe] (upper panel) and [Eu/Fe] (lower panel) vs. [Fe/H] for the sample stars (filled black circles). The comparison sample (open red symbols) is from Battistini & Bensby (2016). |
| In the text | |
 |
Fig. 15 [Rb/Fe] vs. [Fe/H] for our sample stars (LTE values shown as filled black circles) compared to the sample by Tomkin & Lambert (1999) (red squares for giants, and blue squares for dwarfs). The horizontal dotted line is the reference zero value with A(Rb) = 2.60 as the solar abundance, the dashed line would be the zero solar value if the meteoritic Rb abundance, A(Rb) = 2.38, were adopted. |
| In the text | |
 |
Fig. 16 [Rb/Fe] vs. [Fe/H] for our sample stars (filled black circles) compared to the sample of Takeda (2021) (open red squares). The horizontal dotted line is the reference zero value with A(Rb) = 2.60 as the solar abundance, the dashed line would be the zero reference for the meteoritic abundance, A(Rb) = 2.38. Unlike Fig. 15, this plot shows the NLTE Rb abundances. |
| In the text | |
 |
Fig. 17 LTE abundance ratios [Rb/Sr] (upper panel) and [Rb/Y] (lower panel) vs. [Fe/H]. |
| In the text | |
 |
Fig. A.1 Projection on the X–Y plane and on the R–Z plane of the orbits of the stars in the sample. The blue line corresponds to the mean orbit of each star, the grey lines to the 100 realisations of this orbit after errors on the observables (parallaxes, proper motions, and line-of-sight velocities) are taken into account, as described in Sect. 4.5. The cyan symbol indicates the position of the Sun, and the red star shows the current position of the star. The ID of each star is reported in the top left corner of each panel. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.