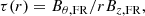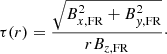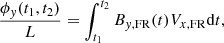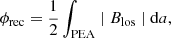| Issue |
A&A
Volume 650, June 2021
|
|
|---|---|---|
| Article Number | A176 | |
| Number of page(s) | 7 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202040070 | |
| Published online | 25 June 2021 | |
Uncovering erosion effects on magnetic flux rope twist
Department of Physics, University of Helsinki, PO Box 64 00014 Helsinki, Finland
e-mail: sanchita.pal@helsinki.fi
Received:
6
December
2020
Accepted:
30
March
2021
Context. Magnetic clouds (MCs) are transient structures containing large-scale magnetic flux ropes from solar eruptions. The twist of magnetic field lines around the rope axis reveals information about flux rope formation processes and geoeffectivity. During propagation MC flux ropes may erode via reconnection with the ambient solar wind. Any erosion reduces the magnetic flux and helicity of the ropes, and changes their cross-sectional twist profiles.
Aims. This study relates twist profiles in MC flux ropes observed at 1 AU to the amount of erosion undergone by the MCs in interplanetary space.
Methods. The twist profiles of two clearly identified MC flux ropes associated with the clear appearance of post eruption arcades in the solar corona are analyzed. To infer the amount of erosion, the magnetic flux content of the ropes in the solar atmosphere is estimated, and compared to estimates at 1 AU.
Results. The first MC shows a monotonically decreasing twist from the axis to the periphery, while the second displays high twist at the axis, rising twist near the edges, and lower twist in between. The first MC displays a larger reduction in magnetic flux between the Sun and 1 AU, suggesting more erosion than that seen in the second MC.
Conclusions. In the second cloud the rising twist at the rope edges may have been due to an envelope of overlying coronal field lines with relatively high twist, formed by reconnection beneath the erupting flux rope in the low corona. This high-twist envelope remained almost intact from the Sun to 1 AU due to the low erosion levels. In contrast, the high-twist envelope of the first cloud may have been entirely peeled away via erosion by the time it reaches 1 AU.
Key words: Sun: coronal mass ejections (CMEs) / magnetic reconnection / Sun: heliosphere / solar-terrestrial relations / Sun: magnetic fields
© ESO 2021
1. Introduction
Coronal mass ejections (CMEs; Webb & Howard 2012) are enormous expulsions of plasma and magnetic flux from the Sun into the heliosphere. The basic structure of the magnetic field of a CME as it erupts is that of a large-scale magnetic flux rope (FR). In interplanetary space, CME-associated FRs that have enhanced magnetic field intensities, smoothly rotating magnetic field vectors, and low proton temperature (Burlaga et al. 1981; Klein & Burlaga 1982; Burlaga & Burlaga 1995) are called magnetic clouds (MCs). Due to their strong magnetic field intensities, high speed, and potential for supporting sustained southward magnetic fields, MCs drive the most intense geomagnetic storms (e.g., Kilpua et al. 2017a). The coherent rotation of magnetic field vectors observed inside MCs as they pass the spacecraft represents the systematic twist of the field lines as they wind around the FR central axis. Twist is an intrinsic property of magnetic flux ropes that is related to the stability of FRs. The distribution of twist has important consequences for energetic particle propagation inside FRs because the twist modifies the length of the FR field lines (e.g., Larson et al. 1997). Along with magnetic field intensity, axis orientation, field line twist (winding of magnetic field lines around the MC axis), and chirality (right- or left-handed sense of twist) are also important FR properties that affect their geoeffectiveness.
Twist distribution also has important implications for the formation of FRs. There is a long-standing debate on whether FRs are formed during the eruption of a CME due to magnetic reconnection (Antiochos et al. 1999; Karpen et al. 2012; Moore et al. 2001) or whether they already exist in the corona prior to the eruption (Kopp & Pneuman 1976; Titov & Démoulin 1999). FRs formed during eruption might have a twist profile where the twist increases gradually from the axis to the periphery of the FR, as illustrated in Moore et al. (2001). In the case of FRs existing prior to the eruption, magnetic flux can also be added during the eruption to the “seed FR” due to reconnection occurring beneath the FR. In this case the reconnected field lines below the FR that are connected to the solar surface form post-eruption arcades (PEAs) and flare ribbons (Priest & Longcope 2017). In contrast, the reconnected field lines above the reconnection site envelop the erupting FR, forming a new outer shell for the FR (e.g., Longcope & Beveridge 2007). The twist profiles in such FRs may show different twists at the core and outer shell. The pre-existing core or seed FR is generally assumed to be highly twisted (Priest & Longcope 2017), while some studies find that the field lines added during the eruption have low twist (van Ballegooijen & Martens 1989). Other studies, however, have suggested that the outer envelope should also have high twist (Longcope & Beveridge 2007). Pal et al. (2017) suggests that the helicity added to the FR through low-coronal reconnection is broadly consistent with the helicity of FRs measured in near-Earth space. While coronal reconnection plays a significant role in shaping the magnetic field of the erupting plasma, the details of the processes are still debated. One possible FR configuration in its minimum energy state is given by the Lundquist model (Lundquist 1950; Lepping et al. 2006), a linear force-free cylindrical and axially symmetric set of solutions for the FR magnetic field. The Lundquist model is one of a number of models that have been proposed to describe the inner magnetic structure of MCs (Kilpua et al. 2017b). In this model the twist of the FR increases toward the FR boundaries as axial field intensity decreases. MCs have also been modeled as nonlinear force-free FRs with uniform twist throughout using the Gold–Hoyle (GH) model (Gold & Hoyle 1960). The Lundquist and GH solutions have been successfully fitted to several magnetic field time series in MCs at different distances from the Sun, and both have also produced good fits for the same MC (Wang et al. 2016; Good et al. 2019; Kilpua et al. 2019). In contrast, studies of twist profiles in MCs have shown the conflict between these and other models, in that the twist distribution obtained depends on the assumed model. For example, Möstl et al. (2009) studied an MC observed on May 20−21, 2007, using the Grad–Shafranov reconstruction technique and found that the twist first increased from the FR core outward, but then declined (i.e., opposite to the twist profile in the Lundquist solution). Hu et al. (2015) found similar results in a statistical study that used the Grad–Shafranov reconstruction and field line length estimates from solar energetic particle observations. Wang et al. (2018) and Zhao et al. (2018), on the other hand, found that twist decreases monotonically from the axis to the periphery of FRs using a velocity-modified GH model (Wang et al. 2016) that considers dynamic evolution of MCs. In contrast, Lanabere et al. (2020) recently applied a superposed epoch analysis to MCs and analyzed their magnetic components in the FR frame, finding that the typical twist distribution of MCs is nearly uniform across the central region and increases moderately (by up to a factor of two) toward the MC periphery.
Regardless of their intrinsic configuration, the magnetic flux and helicity of FRs may be affected by interaction with the ambient solar wind magnetic field as they propagate outward in interplanetary space. This interaction may occur via magnetic reconnection when FR fields are oppositely directed to the local heliospheric magnetic field, which can drape around the FR during its interplanetary propagation (Gosling & McComas 1987; Ruffenach et al. 2015; Pal et al. 2020; McComas et al. 1988). Several studies suggest that reconnection may occur either at the front or back of FRs (Ruffenach et al. 2015; Pal et al. 2020). Reconnection can decrease the flux of the FR by peeling off the FR outer layers. It removes magnetic field lines from the FR outer shell and creates a corresponding number of open field lines (Dasso et al. 2006). It is evident from Dasso et al. (2006) that erosion may remove flux and helicity from FRs and result in asymmetry in the FR azimuthal flux. Pal et al. (2020) further showed that FR erosion is modulated by the solar cycle and may affect the geoeffectiveness of FRs.
In this paper we investigate the effect of FR erosion on twist, an intrinsic FR property. Using in situ magnetic field and plasma data in a frame of reference determined by the FR axis direction, we derive the distribution of twist in the cross-sections of two FRs. In the Sun–Earth domain, we analyze FR magnetic flux in a plane formed by the FR axis and spacecraft trajectory to determine how much magnetic flux is eroded during interplanetary propagation. Finally, we demonstrate how erosion impacts the FR twist profiles. In Sect. 2 the events and methodology selected for this study are described. In Sect. 3 the results of the analysis are presented, with discussion and conclusions in the final sections.
2. Overview of events and methodology
2.1. Event selection and observations
For this study we selected two events with clearly identified MC structures at 1 AU and distinct CMEs accompanied by post eruption arcades (PEAs). The selected events were also required to fulfill two criteria: (1) a small perpendicular distance d between the MC axis and spacecraft trajectory (i.e., small impact parameter p) at 1 AU so that the spacecraft provides a complete sampling from the periphery to the core of the MC, and (2) unambiguously identified front and rear MC boundaries to give accurate least-squares fitting of the MCs. The selected MCs were observed on April 5–6, 2010 (Event 1), and on July 13–14, 2013 (Event 2). Event 1 was the first geoeffective event of solar cycle 24 (Wood et al. 2011) that caused radio bursts, solar energetic particle (SEP) events, and a prolonged geomagnetic storm with minimum Dst of −72 nT. It resulted in a breakdown of the Galaxy 15 satellite. Several studies (Möstl et al. 2010; Liu et al. 2011; Wood et al. 2011) have analyzed the solar source, Sun–Earth propagation, kinematics, and morphology of this event. Event 2 resulted in a moderate geomagnetic storm with minimum Dst of −81 nT. Lugaz et al. (2020) analyzed the coronal and heliospheric observations of this event, and concluded that its long duration (≈39 h) was due to expansion in the corona and innermost heliosphere, and was not the result of rapid heliospheric expansion between Mercury at 0.45 AU and Earth at 1 AU. The front and rear boundaries of the two MCs considered here are very similar to those identified in previous studies, namely Möstl et al. (2010, 2018), Liu et al. (2011), Kilpua et al. (2017c), Palmerio et al. (2018), Lugaz et al. (2020) and available databases such as HELCATS1, the Richardson & Cane (2010) catalogue2 and the Wind ICME catalogue3. We quantify the asymmetry (CB) in the magnetic field profile of the two MCs following a procedure described in Lanabere et al. (2020). To avoid asymmetric events in the FR twist calculation, the study sets the constraint to |CB|≤0.1. In our study the values of CB for Event 1 and Event 2 are negative (i.e., stronger magnetic field at the MC front) and almost equal (CB ≈ −0.04).
The CMEs associated with Event 1 and 2 occurred on April 3, 2010, and July 9, 2013, respectively. The location of the photopsheric magnetic field region involved in eruptions corresponding to Event 1 and 2 were S25E00 and N19E14, respectively (i.e., both located close to the disk center of the Sun). The photospheric eruption region associated with Event 1 was classified as a β-type active region and identified with NOAA number 11059, whereas the region associated with Event 2 was not identified with a NOAA number.
Magnetic field and plasma data at 64 s resolution were obtained from the Advanced Composition Explorer (ACE) spacecraft’s Solar wind Electron, Proton and Alpha Monitor (SWEPAM) and Magnetic Field Experiment (MAG) instruments. The MCs were identified using the standard definition (Burlaga et al. 1981): throughout the MC interval, solar wind magnetic field intensity B is enhanced with respect to that of the ambient solar wind; a smooth rotation exists in the magnetic field components Bx, By, and Bz; the plasma-β is less than one; and plasma temperature Tp is less than the expected ambient solar wind temperature Tex (as subsequently derived by Lopez & Freeman 1986). The MC start (tMCs) and end times (tMCe) are provided in Cols. 2 and 3 of Table 1, respectively; Col. 1 indicates the event number.
Flux rope start and end times, orientation, impact parameter, and radius estimated using FRF methods along with the 1 AU and near-Sun azimuthal magnetic flux of FRs and their percentage of erosion during Sun–Earth propagation.
We observe that the two events analyzed here were associated with distinct halo CMEs detected by the C2 coronagraph of the Large Angle and Spectrometric Coronagraph (LASCO) on board the Solar and Heliospheric Observatory (SOHO; Domingo et al. 1995). The halo CMEs associated with Events 1 and 2 were first detected by the LASCO/C2 coronagraph at 10:33 UT and 15:12 UT on April 3, 2010, and July 9, 2013, respectively. Both CMEs left behind PEAs as coronal signatures. The eruption associated with Event 1 on April 3, 2010, was accompanied by an eruptive filament and a B-class flare, whereas the eruption related to Event 2 on July 9, 2013, only followed an eruptive filament. The associated PEAs were observed using extreme ultraviolet (EUV) observations from the Atmospheric Imaging Assembly (AIA) and Extreme ultraviolet Imaging Telescope (EIT) on board the Solar Dynamics Observatory (SDO) and SOHO, respectively. The solar source location of the progenitor CMEs were obtained online4.
2.2. Analysis methods
In this section the methods used to determine the twist and magnetic flux in the FRs observed in situ at 1 AU and near the Sun are explained. In addition, the method for determining magnetic flux loss during propagation from the Sun to 1 AU is described.
2.2.1. Determination of MC twist profile
The MCs are assumed to be cylindrical FRs and their twists τ as a function of radius r are calculated following Lanabere et al. (2020)
where Bθ, FR and Bz, FR are the azimuthal and axial magnetic field components, respectively. The radial distance from the FR axis is given by 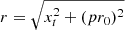 , where the impact parameter p is defined as the perpendicular distance between the FR axis and spacecraft trajectory normalised to the FR radius r0, and xt is the distance traveled by the spacecraft through the MC during time t in a plane perpendicular to its axis. In order to compute τ(r) from the axial and azimuthal field components, the Cartesian components Bx, By, and Bz in geocentric solar ecliptic (GSE) coordinates are converted to the FR frame attached to the MC axis, with axial component Bz, FR and orthogonal components Bx, FR and By, FR. As Bx, FR and By, FR are projections of Bθ, FR, Eq. (1) can be written as
, where the impact parameter p is defined as the perpendicular distance between the FR axis and spacecraft trajectory normalised to the FR radius r0, and xt is the distance traveled by the spacecraft through the MC during time t in a plane perpendicular to its axis. In order to compute τ(r) from the axial and azimuthal field components, the Cartesian components Bx, By, and Bz in geocentric solar ecliptic (GSE) coordinates are converted to the FR frame attached to the MC axis, with axial component Bz, FR and orthogonal components Bx, FR and By, FR. As Bx, FR and By, FR are projections of Bθ, FR, Eq. (1) can be written as
To compute the twist profile, xt is initialized to zero at the FR axis, where By, FR changes its sign. Equation (2) suggests an enhancement in τ near the axis where xt approaches zero and impact parameter p ≈ 0. To determine Bx, FR, By, FR, and Bz, FR, knowledge of the FR axis orientation in terms of latitude θFR and longitude ϕFR is required, where θFR is the angle between the FR axis and ecliptic plane and ϕFR is the angle between the FR axis projected onto the ecliptic plane and the Sun–Earth line. To determine θFR, ϕFR, r0, and p, we apply a least-squares FR fit (FRF) to the in situ measurements using a linear force-free model (Burlaga 1988; Marubashi 1986) that solves ∇ × B = αB in a cylindrical coordinate system (Lepping et al. 1990) during MC intervals and involves FR expansions (Marubashi & Lepping 2007). Here B is the magnetic field vector, and α is a constant that allows self-similar expansion to a cylindrical FR structure. Once θFR and ϕFR are derived, the field components in GSE coordinates are rotated to FR frame (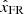 ,
, 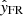 ,
, 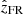 ). In the FR frame
). In the FR frame 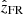 is along the FR axis with Bz, FR > 0 at the axis;
is along the FR axis with Bz, FR > 0 at the axis; 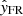 is toward the direction of
is toward the direction of 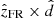 , where
, where 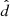 is the direction of the spacecraft’s rectilinear trajectory; and
is the direction of the spacecraft’s rectilinear trajectory; and 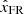 completes the right-handed frame. In Figs. 1a and b the force-free fit to the selected MCs are shown as red curves overplotted on the observed profiles, shown in black. The magnetic field components Bx, By, and Bz are plotted in GSE coordinates. The root mean square error Erms between the observed and modeled FR magnetic field profiles are Erms = 0.32 for Event 1 and 0.24 for Event 2. Figures 1a and b show the solar wind plasma and magnetic field parameters corresponding to Event 1 and Event 2, respectively.
completes the right-handed frame. In Figs. 1a and b the force-free fit to the selected MCs are shown as red curves overplotted on the observed profiles, shown in black. The magnetic field components Bx, By, and Bz are plotted in GSE coordinates. The root mean square error Erms between the observed and modeled FR magnetic field profiles are Erms = 0.32 for Event 1 and 0.24 for Event 2. Figures 1a and b show the solar wind plasma and magnetic field parameters corresponding to Event 1 and Event 2, respectively.
 |
Fig. 1. Observations of MCs associated with (a) Event 1 and (b) Event 2 measured by the ACE spacecraft. From top to bottom, the panels: magnetic field intensity B; the three magnetic field components Bx, By, and Bz in GSE coordinates; plasma velocity Vsw; proton density Np; temperature Tp; and plasma-β. The dashed curves plotted over Tp represent Tex. The vertical black lines indicate the start and end times of the MCs. Time is given (in hours) on the x-axes; the times in UT corresponding to the zero-hour times are indicated below the axes. |
2.2.2. Determination of FR azimuthal flux
When FRs form and erupt from the Sun, they accumulate a certain amount of magnetic flux in the azimuthal plane. We refer here to this initial azimuthal flux close to the Sun as ϕaz, FR. During interplanetary propagation, FRs can interact and reconnect with the ambient interplanetary magnetic field. Reconnection of FR field lines can lead to substantial erosion of FR flux in the azimuthal plane (i.e., the plane formed by the FR axis and spacecraft trajectory in the FR frame), and therefore to the imbalance of the azimuthal flux (Ruffenach et al. 2012, 2015; Pal et al. 2020). In contrast, if no erosion occurs during interplanetary propagation and flux is conserved in the FR azimuthal plane, the MC azimuthal flux measured at 1 AU in situ ideally should be equal to the initial FR flux. Erosion of FRs is expected to also influence the twist profile of the FRs. The amount of reconnected flux and the flux imbalance that results from erosion can be estimated from in situ observations. However, the imbalance estimated from in situ observations does not necessarily give the total reconnected flux due to interplanetary propagation since the reconnected field lines may completely detach from FRs and create a similar number of open field lines. Therefore, to estimate how much the FR has been eroded during its whole Sun-to-Earth transit, fluxes near the Sun (ϕaz, FR) and in situ at 1 AU (ϕaz, MC) must be compared. We employ a technique called the direct method (Dasso et al. 2006, 2007) to estimate the magnetic flux ϕaz, MC (per unit length) that an eroded FR contains upon reaching 1 AU. For this method to be valid it is necessary for the reconnected field lines to still be attached to the FR. In the direct method the accumulated azimuthal magnetic flux per unit length ϕy, MC(t1, t2)/L can be estimated using
where Vx, FR represents the FR speed in the direction of 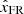 and L is the length of the FR. To compute ϕaz, MC of an eroded FR at 1 AU, t1 and t2 of Eq. (3) are considered as tfront (trear) and tcenter, a time when By, FR changes its sign if the FR’s reconnected field lines are accumulated at its rear (front). The error in flux determination results from ambiguity in the FR boundaries that can impact the model used to determine FR axis orientation (Lepping et al. 2003).
and L is the length of the FR. To compute ϕaz, MC of an eroded FR at 1 AU, t1 and t2 of Eq. (3) are considered as tfront (trear) and tcenter, a time when By, FR changes its sign if the FR’s reconnected field lines are accumulated at its rear (front). The error in flux determination results from ambiguity in the FR boundaries that can impact the model used to determine FR axis orientation (Lepping et al. 2003).
The initial azimuthal flux ϕaz, FR can be alternatively estimated using remote-sensing solar images. Here we compute the low-coronal magnetic reconnection flux ϕrec. Several studies demonstrate that PEAs formed during eruption map to low-coronal reconnection regions associated with eruptive FRs (Longcope & Beveridge 2007; Qiu et al. 2007; Hu et al. 2014). Longcope et al. (2007) show that ϕrec approximately equals ϕaz, FR. We derive ϕrec following the procedure developed by Gopalswamy et al. (2017). Using EUV images, a full-grown PEA at the eruption location on the solar disk is first identified. PEA footpoints are indicated on EUV images, and the footpoints are overlaid on the associated magnetograms. Then magnetic flux is computed using the magnetic field intensity and the area of the region surrounded by the overlaid PEA footpoints. Here ϕrec is measured following
where Blos represents the SDO/HMI line-of-sight (LOS) magnetic field component corresponding to the region surrounded by PEA footpoints and da is the elemental PEA area. In this study the PEA structures are identified using SOHO/EIT 195 Å and SDO/AIA 193 Å images. To determine the 1σ error δϕrec involved in estimating ϕrec, we selected PEAs for multiple times during the interval when full-grown PEAs appear in the solar EUV images.
3. Analysis and results
We computed the azimuthal fluxes for the Event 1 and 2 FRs in the near-Sun region (initial flux) and at 1 AU using Eqs. (3) and (4), respectively. The azimuthal flux ϕaz, MC of the events is calculated using the axis orientations estimated by FRF. By comparing the fluxes of FRs in these two domains any erosion that occurred during interplanetary propagation can be determined. In Col. 9 of Table 1 we present the azimuthal flux of FRs estimated at 1 AU. Twist profiles were derived with Eq. (2), and the effect of erosion on the field line twists were analyzed.
In Figs. 2a and b, we show the accumulated azimuthal flux per unit length ϕy/L (black curve) and azimuthal magnetic field component By, FR (blue curve) corresponding to Event 1 and Event 2, respectively, where the field and velocity components in the FR frame are estimated using FR orientation derived from the FRF method. The x-axis of the plots represents the distance xt. The xt is initialized to zero at the MC front boundary. The imbalance in ϕy/L indicates that both MCs underwent erosion while crossing the spacecraft. The vertical black dashed lines overplotted on Figs. 2a and b indicate the peak of ϕy/L, corresponding to the time tcenter when the spacecraft crossed almost through the center of the MCs in the FR frame. The vertical dash-dotted black lines overplotted on Figs. 2a and b indicate the radial distances xasym when the asymmetry in ϕy/L curves begin. We note that if p is too small, xasym is almost equal to the radius of the eroded MCs in which reconnected field lines are excluded. With the solid vertical lines the boundary of FRs are indicated.
 |
Fig. 2. Accumulated azimuthal flux ϕy/L (black curve) and azimuthal magnetic field component (blue curve) plotted with respect to the distance xt associated with (a) Event 1 and (b) Event 2. The vertical black dashed lines and black dash-dotted lines correspond to tcenter and xasym, respectively. The vertical solid lines represent the MC boundaries. |
The twist τ of Events 1 and 2 as a function of the radial distance r, initialized to zero at the FR center, are presented in Figs. 3a and b, respectively. To avoid significant fluctuations introduced by small-scale irregularities in FR magnetic field and local distortions in the FR twist profile, we apply a 10 min forward-moving average to the time series of the FR magnetic field components. As in Wang et al. (2016, 2018) and Zhao et al. (2018), both events have twist profiles that show an increase toward the FR axis. We observe that the twist in the cross-section of Event 1 monotonically decreases with increasing r and acquires a value of τ ≈ 12 AU−1 at its periphery. The twist profile of Event 2 decreases from the FR center and fluctuates with mean τ ≈ 5 AU−1 until half of its radius r ≈ 0.11 AU. Then the twist increases toward the cloud’s outer boundary and reaches a value of τ ≈ 9 AU−1 at its periphery. The high twist at the edges of Event 2 is consistent with the Lundquist FR model, but a few studies (e.g., Wang et al. 2016, 2018) have recently argued that the high twist observed at the center of FRs is not consistent with the Lundquist flux rope, which has a low-twist core.
 |
Fig. 3. Twist (τ) profile with respect to the radial distance r of MCs associated with (a) Event 1 and (b) Event 2. The plots start from MC centers. |
The initial azimuthal flux of FRs ϕaz, FR is estimated by measuring ϕrec. In the upper and lower panels of Fig. 4, the EUV and LOS magnetograms of the source region of Event 1 and 2 are shown, respectively. The full-grown PEAs associated with Event 1 (detected at 16:24 UT on April 3, 2010) and 2 (detected at 19:13 UT on July 9, 2013), are observed in the SOHO/EIT 195 Å and SDO/AIA 195 Å images, respectively. The PEA footpoints are indicated with red dashed lines on both EUV images and magnetograms. To estimate the error involved in measuring ϕrec, the PEAs are observed for an interval during which they appear on solar EUV images almost with their full-grown structures. The interval for Event 1 and 2 are chosen as 15:36−18:12 UT on April 3, 2010, and 18:00−20:30 UT on July 9, 2013, respectively. The corresponding ϕrec for Event 1 and 2 are thus derived, and then averaged. The average initial azimuthal flux 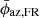 of the FRs are estimated from the average ϕrec and the standard deviation of the ϕrec values are calculated to obtain the 1σ error, δϕaz, FR. In Col. 10 of Table 1,
of the FRs are estimated from the average ϕrec and the standard deviation of the ϕrec values are calculated to obtain the 1σ error, δϕaz, FR. In Col. 10 of Table 1, 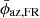 and its 1σ error δϕaz, FR associated with Event 1 and 2 are provided. The percentage of erosion Er of FRs during Sun–Earth travel is derived using
and its 1σ error δϕaz, FR associated with Event 1 and 2 are provided. The percentage of erosion Er of FRs during Sun–Earth travel is derived using 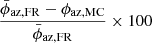 . The Er corresponding to Event 1 and 2 are listed in Col. 11 of Table 1.
. The Er corresponding to Event 1 and 2 are listed in Col. 11 of Table 1.
 |
Fig. 4. Post-eruption arcades (PEAs) observed at EUV wavelengths at the solar sources of FRs corresponding to Event 1 (upper panel) and 2 (lower panel). Arcade footpoints are indicated as red dashed lines on the EUV images and the corresponding LOS magnetograms. The PEA shown in the upper panel is associated with a filament and a flare eruption, whereas the PEA in the lower panel is associated with a filament eruption only. No flare event was observed during the eruption of the Event 2 CME. |
4. Discussion
This work investigates the influence of FR erosion on FR twist profiles. For this analysis we chose two FRs with clear boundaries, a small perpendicular distance between the spacecraft trajectories and FR axes, and clearly identified PEAs at their solar sources. We note that the fit for Event 1 does not capture the magnetic field magnitude profile very well (Fig. 1a). However, when fitting models it is often difficult to reproduce the magnitude, although acceptable values can be found for most of the free parameters (Lepping et al. 2018). Furthermore, only the axis orientation from the fit is used, and the subsequent flux calculations were performed with the direct method (Eq. (3)), which uses the measured field and not the fitted profile. The fit is used to place the data in a coordinate system relative to the axis orientation. The fit captures the axis orientation reasonably well (the polarities of the individual components are accurately reproduced), and the Erms = 0.32. The fit for Event 2 is very good in terms of the components, and it also reproduces the magnitude profile quite well, with an overall Erms = 0.24.
Using superposed epoch analysis (SEA), which emphasizes common features in MC profiles, Lanabere et al. (2020) determined a typical twist distribution inside MCs. The distribution is uniform in the central part of the FRs, and gradually increases by up to a factor of two toward the FR boundaries. The enhancement of twist in the outer shell of FRs may result from helical field lines formed from low-coronal magnetic reconnection beneath erupting FRs at the solar sources that wrap around the FR core (Qiu et al. 2007). However, as discussed in the Introduction, we note that some studies suggest a lower twist in the envelope and higher twist in the core. In our study the twist profile of Event 2 increases moderately toward the periphery from a uniform value in the central part. In contrast, the twist of Event 1 does not show any enhancement at the periphery. The twist profiles we derive here mostly cover the inner part of FR core (i.e., the part close to the FR axis). At this inner core we observe in both events a substantial increase in twist toward the center of the FRs, similar to that found by imposing a velocity-modified, uniform-twist GH model to MCs (Wang et al. 2018; Zhao et al. 2018).
To account for the dissimilarity in the twist profiles of the two events, we determine their azimuthal magnetic flux both near the Sun and in situ (i.e., ∼1 AU), and in particular consider the effect of erosion due to magnetic reconnection between the FR fields and the ambient field (see the Introduction). The reconnection rate is expected to be high close to the Sun and in the inner heliosphere (Lavraud & Borovsky 2008). Lavraud et al. (2014) showed that 47−67% erosion is expected to occur within ≈0.39 AU. However, the available in situ observations of FRs do not allow us to locate the reconnection site in the interplanetary medium. One of the signatures of the ongoing erosion of FRs is the imbalance in azimuthal flux captured at the time of in situ observation. An asymmetry in azimuthal flux due to reconnection close to the Sun may not be identified by in situ observations because, at the time of observation at 1 AU, the reconnected field lines may completely detach from the FRs and create a similar number of open field lines. Therefore, we compare near-Sun and near-Earth azimuthal flux of FRs to determine whether FRs are significantly peeled off during their Sun–Earth propagation. We find that the percentage of erosion Er for Event 1 is greater than that of Event 2. Furthermore, Möstl et al. (2010) concluded that the long-duration, nonrotating magnetic field observed at the back part of Event 1 FR is reminiscent of the events studied by Dasso et al. (2007) where the long back region with nonrotating magnetic fields behind MCs resulted from the reconnection between MC and the interplanetary magnetic field (Dasso et al. 2007).
The dissimilarity in twist profiles observed here may result from the difference in their erosion. We suggest that a significant erosion may have completely removed the twisted outer layer of the FR associated with Event 1. Therefore, for this event, only the outer core along with the inner core remained by the time it reached the orbit of the Earth. As erosion is less in Event 2 than Event 1, the FR’s twisted outer shell is only partly removed and results in a twist profile that rises toward the FR periphery. Wang et al. (2018) found a twist profile monotonically decreasing from core to periphery, which supports the scenario that a twisted seed FR exists prior to the eruption. We note that the study found the degree of imbalance of the MC as 25% and suggested that the erosion affected the MC twist. As the MC was a slow and weak event, its source CME could not be distinguished from other preceding and following CMEs. Its solar source location was thus ambiguous, and therefore, the Wang et al. (2018) study cannot confirm whether a twisted MC outer shell existed before its erosion in interplanetary space.
Unlike Zhao et al. (2018) and Wang et al. (2016), the twist of MCs is computed in this study directly from in situ magnetic field components rotated to the FR frame. Here we consider MC azimuthal flux per unit length because a statistical study by Qiu et al. (2007) found that the ratio of MC azimuthal flux to the coronal reconnection flux equals to unity while considering L = 1 AU. Longcope et al. (2007) showed that the total magnetic helicity transported into the FR from coronal sheared arcades due to low-coronal reconnection closely matches the magnetic helicity of MCs when the length of the MC is considered as 1 AU. In the left and right panels of Fig. 5 we represent two MC cross-sections with their twist distributions using colored contours. The associated FRs have twist profiles similar to those of Event 1 and 2, and undergo the same level of erosion as Event 1 and 2 do while propagating through the interplanetary medium. The highly twisted outer layer is absent in the FR cross-section of left panel, whereas it remains in the other one. The spacecraft propagation paths are represented by black dashed lines.
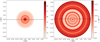 |
Fig. 5. Radial distribution of twist in the cross-section of two MCs replicating Event 1 (left panel) and 2 (right panel) at 1 AU. The color bars represent the twist values and the dashed lines show the spacecraft propagation directions. The light purple dots at the center of the cross-sections indicate the portions for which twist values are not available. |
We note that the twist profiles are partly dependent on the quality of the fits, which provide the FR axis orientation, impact parameter and width. While the fits for the two events analyzed here are broadly satisfactory (e.g., in terms of Erms), more events will need to be analyzed in order to draw firmer and more general conclusions. In particular, it would be worthwhile to analyze more events with twist profiles similar to Event 1 (which are less commonly observed) in order to build a more statistical picture.
5. Conclusion
The twist of the magnetic field lines inside FRs has important implications for the geoeffectiveness of FRs. Moreover, the radial distribution of twist provides significant information on the FR formation processes. When FRs propagate through the interplanetary medium, their outer shell might be partially or entirely eroded due to interaction with the ambient solar wind magnetic field. The erosion of FRs can significantly alter their magnetic properties, including magnetic flux, twist, and helicity. In this study, we select two distinct FRs having typical plasma and magnetic characteristics with well-defined boundaries and investigate the effect of FR erosion on their magnetic flux and twist. The post eruption arcades formed at the FR solar sources during eruption confirm the presence of envelopes of overlying coronal field lines around the erupting, CME-associated FRs. The envelope includes the FR outer shell, where the field line twist depends on the twist of the overlying coronal field. In our study, the field line twist for Event 2 is nearly uniform across the FR mid-region (i.e., outer core) and increases in the FR’s envelope (i.e., outer shell). In contrast, the field line twist of Event 1 shows a decreasing profile near the FR boundary. Both of the twist profiles monotonically increase toward the FR axis. The presence of highly twisted field lines around the FR central axis is consistent with twisted seed FRs pre-existing the eruptions. After comparing the FR azimuthal magnetic flux in the Sun–Earth domain, it is inferred that the percentage of erosion is higher for Event 1 (Er = 54%) than Event 2 (Er = 22%), and that the erosion probably removes the highly twisted outer shell of Event 1. Our result demonstrates that FR eruption involving coronal magnetic reconnection at the solar sources forms an envelope around the FR. The field line twists are greater in the FR envelope (outer shell) than that of the FR outer core, where the twist is almost uniform. During interplanetary propagation, magnetic reconnection that causes erosion of FRs can remove the twisted outer shell altogether, and leave the FR with its core having decreasing field line twist values toward the periphery.
Acknowledgments
S.P., E.K., and D.P. acknowledge the European Research Council (ERC) under the European Union’s Horizon 2020 Research and Innovation Program Project SolMAG 724391. The results presented here have been achieved under the framework of the Finnish Centre of Excellence in Research of Sustainable Space (FORESAIL; Academy of Finland grant numbers 312390), which we gratefully acknowledge. E.K. and S.G. acknowledge Academy of Finland Project 310445 (SMASH). S.P. thanks Dr. Katsuhide Marubashi for providing us with the linear force-free cylindrical model. We thank referee for helpful comments and acknowledge the use of data from SDO, SOHO, and ACE.
References
- Antiochos, S., DeVore, C., & Klimchuk, J. 1999, ApJ, 510, 485 [Google Scholar]
- Burlaga, L. F. 1988, J. Geophys. Res. Space Phys., 93, 7217 [Google Scholar]
- Burlaga, L. F., & Burlaga, L. 1995, Interplanetary Magnetohydrodynamics (Oxford: Oxford University Press) [Google Scholar]
- Burlaga, L., Sittler, E., Mariani, F., & Schwenn, R. 1981, J. Geophys. Res. Space Phys., 86, 6673 [NASA ADS] [CrossRef] [Google Scholar]
- Dasso, S., Mandrini, C. H., Démoulin, P., & Luoni, M. L. 2006, A&A, 455, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dasso, S., Nakwacki, M. S., Démoulin, P., & Mandrini, C. H. 2007, Sol. Phys., 244, 115 [Google Scholar]
- Domingo, V., Fleck, B., & Poland, A. I. 1995, Sol. Phys., 162, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Gold, T., & Hoyle, F. 1960, MNRAS, 120, 89 [NASA ADS] [Google Scholar]
- Good, S. W., Kilpua, E. K. J., LaMoury, A. T., et al. 2019, J. Geophys. Res.: Space Phys., 124, 4960 [CrossRef] [Google Scholar]
- Gopalswamy, N., Yashiro, S., Akiyama, S., & Xie, H. 2017, Sol. Phys., 292, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Gosling, J. T., & McComas, D. J. 1987, Geophys. Res. Lett., 14, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, Q., Qiu, J., Dasgupta, B., Khare, A., & Webb, G. M. 2014, ApJ, 793, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, Q., Qiu, J., & Krucker, S. 2015, J. Geophys. Res.: Space Phys., 120, 5266 [CrossRef] [Google Scholar]
- Karpen, J. T., Antiochos, S. K., & DeVore, C. R. 2012, ApJ, 760, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Kilpua, E., Balogh, A., von Steiger, R., & Liu, Y. 2017a, Space Sci. Rev., 212, 1271 [NASA ADS] [CrossRef] [Google Scholar]
- Kilpua, E., Koskinen, H. E. J., & Pulkkinen, T. I. 2017b, Liv. Rev. Sol. Phys., 14, 5 [Google Scholar]
- Kilpua, E., Koskinen, H. E., & Pulkkinen, T. I. 2017c, Liv. Rev. Sol. Phys., 14, 1 [Google Scholar]
- Kilpua, E. K. J., Good, S. W., Palmerio, E., et al. 2019, Front. Astron. Space Sci., 6, 50 [CrossRef] [Google Scholar]
- Klein, L. W., & Burlaga, L. F. 1982, J. Geophys. Res. Space Phys., 87, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Kopp, R., & Pneuman, G. 1976, Sol. Phys., 50, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Lanabere, V., Dasso, S., Démoulin, P., et al. 2020, A&A, 635, A85 [CrossRef] [EDP Sciences] [Google Scholar]
- Larson, D., Lin, R., McTiernan, J., et al. 1997, Geophys. Res. Lett., 24, 1911 [NASA ADS] [CrossRef] [Google Scholar]
- Lavraud, B., & Borovsky, J. E. 2008, J. Geophys. Res. Space Phys., 113, A00B08 [Google Scholar]
- Lavraud, B., Ruffenach, A., Rouillard, A. P., et al. 2014, J. Geophys. Res. Space Phys., 119, 26 [Google Scholar]
- Lepping, R. P., Jones, J. A., & Burlaga, L. F. 1990, J. Geophys. Res. Space Phys., 95, 11957 [Google Scholar]
- Lepping, R. P., Berdichevsky, D. B., & Ferguson, T. J. 2003, J. Geophys. Res. Space Phys., 108, 1356 [Google Scholar]
- Lepping, R. P., Berdichevsky, D. B., Wu, C. C., et al. 2006, Ann. Geophys., 24, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Lepping, R., Wu, C.-C., Berdichevsky, D., & Kay, C. 2018, Sol. Phys., 293, 1 [Google Scholar]
- Liu, Y., Luhmann, J. G., Bale, S. D., & Lin, R. P. 2011, ApJ, 734, 84 [Google Scholar]
- Longcope, D., & Beveridge, C. 2007, ApJ, 669, 621 [Google Scholar]
- Longcope, D., Beveridge, C., Qiu, J., et al. 2007, Sol. Phys., 244, 45 [Google Scholar]
- Lopez, R. E., & Freeman, J. W. 1986, J. Geophys. Res.: Space Phys., 91, 1701 [Google Scholar]
- Lugaz, N., Winslow, R., & Farrugia, C. 2020, J. Geophys. Res.: Space Phys., 125, e2019JA027213 [Google Scholar]
- Lundquist, S. 1950, Ark. Fys., 2, 361 [Google Scholar]
- Marubashi, K. 1986, Adv. Space Res., 6, 335 [Google Scholar]
- Marubashi, K., & Lepping, R. P. 2007, Ann. Geophys., 25, 2453 [Google Scholar]
- McComas, D. J., Gosling, J. T., Winterhalter, D., & Smith, E. J. 1988, J. Geophys. Res.: Space Phys., 93, 2519 [Google Scholar]
- Moore, R. L., Sterling, A. C., Hudson, H. S., & Lemen, J. R. 2001, ApJ, 552, 833 [Google Scholar]
- Möstl, C., Farrugia, C. J., Miklenic, C., et al. 2009, J. Geophys. Res., 114, A04102 [Google Scholar]
- Möstl, C., Temmer, M., Rollett, T., et al. 2010, Geophys. Res. Lett., 37 [Google Scholar]
- Möstl, C., Amerstorfer, T., Palmerio, E., et al. 2018, Space Weather, 16, 216 [Google Scholar]
- Pal, S., Gopalswamy, N., Nandy, D., et al. 2017, ApJ, 851, 123 [Google Scholar]
- Pal, S., Dash, S., & Nandy, D. 2020, Geophys. Res. Lett., 47, e2019GL086372 [Google Scholar]
- Palmerio, E., Kilpua, E. K., Möstl, C., et al. 2018, Space Weather, 16, 442 [Google Scholar]
- Priest, E. R., & Longcope, D. 2017, Sol. Phys., 292, 1 [Google Scholar]
- Qiu, J., Hu, Q., Howard, T. A., & Yurchyshyn, V. B. 2007, ApJ, 659, 758 [Google Scholar]
- Richardson, I. G., & Cane, H. V. 2010, Sol. Phys., 264, 189 [Google Scholar]
- Ruffenach, A., Lavraud, B., Owens, M. J., et al. 2012, J. Geophys. Res. Space Phys., 117, A09101 [Google Scholar]
- Ruffenach, A., Lavraud, B., Farrugia, C. J., et al. 2015, J. Geophys. Res. Space Phys., 120, 43 [Google Scholar]
- Titov, V., & Démoulin, P. 1999, A&A, 351, 707 [Google Scholar]
- van Ballegooijen, A. A., & Martens, P. 1989, ApJ, 343, 971 [Google Scholar]
- Wang, Y., Zhuang, B., Hu, Q., et al. 2016, J. Geophys. Res.: Space Phys., 121, 9316 [Google Scholar]
- Wang, Y., Shen, C., Liu, R., et al. 2018, J. Geophys. Res.: Space Phys., 123, 3238 [Google Scholar]
- Webb, D. F., & Howard, T. A. 2012, Liv. Rev. Sol. Phys., 9, 3 [Google Scholar]
- Wood, B., Wu, C.-C., Howard, R., Socker, D., & Rouillard, A. 2011, ApJ, 729, 70 [Google Scholar]
- Zhao, A., Wang, Y., Feng, H., et al. 2018, ApJ, 869, L13 [Google Scholar]
All Tables
Flux rope start and end times, orientation, impact parameter, and radius estimated using FRF methods along with the 1 AU and near-Sun azimuthal magnetic flux of FRs and their percentage of erosion during Sun–Earth propagation.
All Figures
 |
Fig. 1. Observations of MCs associated with (a) Event 1 and (b) Event 2 measured by the ACE spacecraft. From top to bottom, the panels: magnetic field intensity B; the three magnetic field components Bx, By, and Bz in GSE coordinates; plasma velocity Vsw; proton density Np; temperature Tp; and plasma-β. The dashed curves plotted over Tp represent Tex. The vertical black lines indicate the start and end times of the MCs. Time is given (in hours) on the x-axes; the times in UT corresponding to the zero-hour times are indicated below the axes. |
| In the text | |
 |
Fig. 2. Accumulated azimuthal flux ϕy/L (black curve) and azimuthal magnetic field component (blue curve) plotted with respect to the distance xt associated with (a) Event 1 and (b) Event 2. The vertical black dashed lines and black dash-dotted lines correspond to tcenter and xasym, respectively. The vertical solid lines represent the MC boundaries. |
| In the text | |
 |
Fig. 3. Twist (τ) profile with respect to the radial distance r of MCs associated with (a) Event 1 and (b) Event 2. The plots start from MC centers. |
| In the text | |
 |
Fig. 4. Post-eruption arcades (PEAs) observed at EUV wavelengths at the solar sources of FRs corresponding to Event 1 (upper panel) and 2 (lower panel). Arcade footpoints are indicated as red dashed lines on the EUV images and the corresponding LOS magnetograms. The PEA shown in the upper panel is associated with a filament and a flare eruption, whereas the PEA in the lower panel is associated with a filament eruption only. No flare event was observed during the eruption of the Event 2 CME. |
| In the text | |
 |
Fig. 5. Radial distribution of twist in the cross-section of two MCs replicating Event 1 (left panel) and 2 (right panel) at 1 AU. The color bars represent the twist values and the dashed lines show the spacecraft propagation directions. The light purple dots at the center of the cross-sections indicate the portions for which twist values are not available. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.