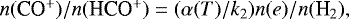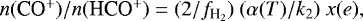| Issue |
A&A
Volume 648, April 2021
|
|
|---|---|---|
| Article Number | A38 | |
| Number of page(s) | 8 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202039915 | |
| Published online | 09 April 2021 | |
CO+ as a probe of the origin of CO in diffuse interstellar clouds★
1
LERMA, Observatoire de Paris, PSL Research University, CNRS, Ecole Normale Supérieure, Sorbonne Université,
75005
Paris,
France
e-mail: maryvonne.gerin@lra.ens.fr
2
National Radio Astronomy Observatory,
520 Edgemont Road,
Charlottesville,
VA
22903,
USA
Received:
15
November
2020
Accepted:
28
January
2021
Context. The chemistry of the diffuse interstellar medium is driven by the combined influences of cosmic rays, ultraviolet (UV) radiation, and turbulence. Previously detected at the outer edges of photodissociation regions and formed from the reaction of C+ and OH, CO+ is the main chemical precursor of HCO+ and CO in a thermal, cosmic-ray, and UV-driven chemistry.
Aims. Our aim was to test whether the thermal cosmic-ray and UV-driven chemistry is producing CO in diffuse interstellar molecular gas through the intermediate formation of CO+.
Methods. We searched for CO+ absorption with the Atacama Large Millimeter Array toward two quasars with known Galactic foreground absorption from diffuse interstellar gas, J1717-3342 and J1744-3116, targeting the two strongest hyperfine components of the J = 2−1 transition near 236 GHz.
Results. We could not detect CO+ but obtained sensitive upper limits toward both targets. The derived upper limits on the CO+ column densities represent about 4% of the HCO+ column densities. The corresponding upper limit on the CO+ abundance relative to H2 is <1.2 × 10−10.
Conclusions. The non-detection of CO+ confirms that HCO+ is mainly produced in the reaction between oxygen and carbon hydrides, CH2+ or CH3+, induced by suprathermal processes, while CO+ and HOC+ result from reactions of C+ with OH and H2O. The densities required to form CO molecules at low extinction are consistent with this scheme.
Key words: ISM: clouds / ISM: molecules / radio lines: ISM
Spectra are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/648/A38.
© M. Gerin and H. Liszt 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The diffuse interstellar medium (ISM) hosts a rich chemistry where many species reach molecular abundances similar to those in denser and darker regions despite the lower densities (a few tens to a few hundred particles per cm−3) and the relatively unattenuated far-ultraviolet (FUV) illumination by the interstellar radiation field (Snow & McCall 2006; Gerin et al. 2016, 2019; Liszt et al. 2014a,b, 2018). Diffuse and translucent interstellar clouds (Snow & McCall 2006) have long been used as testbeds of interstellar chemistry (Glassgold & Langer 1975, 1976; Black & Dalgarno 1977; Van Dishoeck & Black 1986, 1988). These efforts were successful in explaining the measured column densities for H2 and small trace molecules such as CH, OH, and CN using chemical reactions at temperatures 30–80 K corresponding to kinetic temperatures measured in H2 (Savage et al. 1977), but in some cases assuming regions of density ≳1000 cm−3 along the line of sight. However, the observed column densities of CO and the common presence of high column densities of CH+ presented challenges to such models of thermal, cosmic-ray, and UV-driven ion-chemistry in diffuse molecular gas.
The observed CO column densities are empirically explained by the serendipitous detection of unexpectedly high column densities of HCO+ seen in absorption at 89.2 GHz (Lucas & Liszt 1996). A nearly constant abundance of HCO+ relative to H2, X(HCO+) = N(HCO+)/N(H2) = 3 × 10−9 ± 0.2 dex is found in comparison with OH and CH (Gerin et al. 2019), using their fixed abundances relative to H2 established through direct absorption observations at optical and UV wavelengths (Sheffer et al. 2008; Weselak et al. 2009, 2010). With such significant column densities, the observed HCO+ ions will recombine with ambient thermal electrons at densities n(H) ≳100 cm−3 to produce the observed CO column densities (Liszt & Lucas 2000; Visser et al. 2009).
The gas phase chemistry developed during the 1970s–1980s era was qualitatively correct in predicting a fixed abundance ratio N(HCO+)/N(OH) via a dominant chemical chain that proceeds from C+ + OH → CO+ + H (Glassgold & Langer 1975, 1976; Dagdigian 2019) to CO+ + H2 → HCO+ + H and HCO+ + e− → CO + H. However, the observed N(HCO+)/N(OH) ≈ 1/30 is roughly thirty times higher than the predicted value through this simple chemical scheme. Some HCO+ can also be produced in this chemistry by the reaction of C+ and H2O, of which the abundance is 28% of that of OH (Gerin et al. 2016; Wiesemeyer et al. 2016). Both reactions, CO+ + H2 and C+ + H2O, produce equal amounts of HCO+ and the slightly less tightly bonded isomer HOC+ that is observed with N(HOC+)/N(HCO+) = 0.015 ± 0.003 (Gerin et al. 2019). This disparity in the abundances of HCO+ and HOC+ is much too large to be explained by the isomerization reaction H2 + HOC+ → H2 + HCO+ as discussed below.
To reproduce the observed HCO+ abundance at the low mean densities of diffuse clouds, the most successful models include transient production mechanisms that involve dynamical processes in magnetized gas such as low-velocity shocks or turbulent vortices, in which ions and neutral species are partially decoupled (Godard et al. 2014; Lesaffre et al. 2020). The resulting slow velocity drift can therefore be used as an additional energy source to drive endothermic chemical reactions that could not operate otherwise (Sheffer et al. 2008; Visser et al. 2009), especially the reaction C+ + H2 → CH+ + H, which is endothermic by 0.36 eV or about 4300 K. These models therefore include a specific chemical pathway to CO, which starts from CH+ and is followed by a series of rapid hydrogen abstraction reactions producing CH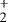 and CH
and CH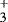 . These two ions react with atomic oxygen to produce the required HCO+, and not HOC+. In this scheme, HCO+ is once again the precursor of CO, but the predicted CO and HCO+ abundances fit the observations well, and therelative rarity of HOC+ arises very naturally.
. These two ions react with atomic oxygen to produce the required HCO+, and not HOC+. In this scheme, HCO+ is once again the precursor of CO, but the predicted CO and HCO+ abundances fit the observations well, and therelative rarity of HOC+ arises very naturally.
Therefore, the relative abundances of the three molecular ions CO+, HCO+, and HOC+ provide key information concerning the mechanisms at the origin of CO in diffuse gas. Despite the pivotal role played by CO+ in some versions of the chemistry, its abundance relative to H2 is much less well constrained than those of HCO+ and HOC+. CO+ was first identified in the interstellar medium toward the bright photodissociation region (PDR) M17SW and the young, high-excitation planetary nebula NGC 7027 (Latter et al. 1993). CO+ is now routinely observed in dense PDRs such as the Orion Bar (Goicoechea et al. 2017) or MonR2 (Treviño-Morales et al. 2016). In such regions, CO+ is located at the very edge close to the HI/H2 transition, and its abundance relative to HCO+ ranges from one to several tens of percent (Fuente et al. 2003). In dense PDRs, the intense FUV radiation can pump H2 into vibrationally excited levels that can reach a significant population (Agúndez et al. 2010). The internal energy of this vibrationally excited H2 can trigger the endothermicreaction of C+ + H2 forming CH+, as shown by the widespread distribution of CH+ emission in such regions (Goicoechea et al. 2019). Paradoxically, the presence of CO+ in dense PDRs is a sign that nonthermal chemical processes are working, while nonthermal processes are invoked in models of diffuse molecular gas to remove the need to produce CO+ on the path to CO.
There are no reported detections of CO+ in the diffuse and translucent interstellar medium: in this paper, we present observations with the Atacama Large Millimeter Array (ALMA) that constrain the abundance of CO+ there for the first time. The observation strategy is presented in Sect. 2, and the results are discussed in Sect. 3 together with the implications for the CO chemistry that are emphasized in Sects. 4 and 5. The conclusions are summarized in Sect. 6.
2 Spectroscopy and observations
2.1 Spectroscopy
Absorption spectroscopy represents the best method to probe the molecular content of diffuse clouds, because the molecular excitation is weak at the low densities (a few tens to a few hundred cm−3) and pressure (p/k ≈ 3 × 103−104 K-cm−3) of these regions (Jenkins & Tripp 2011; Gerin et al. 2015; Goldsmith et al. 2018), and the level populations are concentrated in the lowest rotational levels. As a 2Σ molecular ion, the energy levels of CO+ are described by three quantum numbers; N, the rigid body angular momentum quantum number; S = 1∕2, the electron spin angular momentum quantum number; and J = N + S = N ± 1∕2, the total angular momentum quantum number (Sastry et al. 1981).
The CO+ ground state rotational transitions at 117.7 GHz and 118.1 GHz are close to a strong atmospheric line from molecular oxygen at 118.75 GHz, rendering their observation from the ground very difficult. Hence, observations of CO+ have generally targeted excited transitions where the sky transmission is much better. We chose to search for the N = 2 → 1 transitions because the frequencies of this first excited transition near 236 GHz are easily accessible from ground-based radio observatories, and the level population remains significant even in diffuse interstellar gas. This N = 2 → 1 transition is split into three hyperfine components, with the strongest component at 236.06 GHz. Table 1 lists the three targeted transitions, their frequencies, Einstein A-coefficient, and the conversion factor between the integrated line opacity and the molecule column density N(CO+)∕∫ τ dv assuming that the energy-level population is determined by the cosmic microwave background at 2.73 K.
Apart from CO+, the setting of the ALMA correlator included spectral windows targeting the 13CO(2−1), C18O(2−1) and H2CO(30,3−20,2) transitions that were accessible with the same receiver tuning while including a dedicated continuum spectral window for phase calibration. Properties of the CO lines are given in Table 1, where the column density/optical depth conversion is calculated for an excitation temperature of 5 K that is typical for this more easily excited species in diffuse molecular gas (Goldsmith et al. 2018).
Spectroscopic parameters of observed lines.
2.2 Target directions
The targeted sources are J1717-3342 and J1744-3116, two bright quasars situated at small galactic latitude behind the Galactic bulge that were known to have high intervening column densities of Galactic neutral gas detected in molecular absorption (Gerin & Liszt 2017; Liszt & Gerin 2018; Riquelme et al. 2018). Their positions, continuum flux densities Sν, channel-channel baseline rmsline/continuum noise and line profile integrals, and velocity intervals used here as integration intervals for the targeted CO+ transitions are given in Table 2. Comparable quantities for the 13CO(2-1) and C18O(2-1) lines are given in Table 3.
2.3 ALMA observations
The observations were performed with ALMA Band-6 receivers tuned near 236 GHz during ALMA Cycle 7 under the project code 2019.1.00120.S. The CO+ lines were observed with a channel spacing of 244 kHz, corresponding to a velocity resolution of 0.31 km s−1. The channel spectral resolution is twice the channel spacing. As in our earlier observations toward these sources, the bandpass calibrator was fixed to J1924-2914. Absorption spectra were extracted from the standard pipeline-processed data products at the peak of the continuum map in each spectral window. The ALMA spectra of 13CO, CO+, and HCO+ are displayed in Fig. 1. The H2CO (30,3 − 20,2) line was detected in both directions and will be discussed in a future paper.
Summary of CO+ observations.
 |
Fig. 1 Absorption spectra observed toward J1717-3342 (left) and J1744-3116 (right). The spectra were normalized by the continuum flux density. The CO+ spectra were shifted vertically and multiplied by 10. HCO+ is shown in black, CO+ in red, and 13CO(2–1) in blue for comparison. The HCO+ data are taken from Liszt & Gerin (2018) and Gerin & Liszt (2017). |
CO isotopologue J = 2–1 observations and column densities.
 |
Fig. 2 Comparison of the HCO+ (1–0) (black) and 13CO (2–1) (green) absorption with the 12CO (blue) and scaled HI (gray) emission. J1717-3342 is shown at the top and J1744-3116 at the bottom. C18O(2–1) is also shown in orange for J1744-3116. |
2.4 Other data discussed here
Also shown in Figs. 1 and 2 are 89.2 GHz ALMA HCO+ J=1–0 absorption line profiles with 0.205 km s−1 channel spacing and 0.41 km s−1 spectral resolution from our earlier works (Gerin & Liszt 2017; Liszt & Gerin 2018). Profile integrals are quoted in Table 4, assuming excitation in equilibrium with the CMB and using N(HCO+) = 1.12 × 1012 cm−2 ∫ τ dv as before. Also shown in Fig. 2 are the nearest λ2.6mm CO J = 1–0 emission profiles with an 8.′ 8 beamsize from the work of Bitran et al. (1997) and a λ21cm H I emission profile from Kalberla et al. (2005) taken with a FWHM beam of 0.6°. The CO emission profile for J1744-3116 at l, b = 357.875°,-1° is very nearly along the same sightline; for J1717-3342, the CO profile at 352.75°,2.5° is centered 6.′6 away.
HCO+ and CO+ column densities.
3 Results and discussion
3.1 The sight lines toward J1717-3342 and J1744-3116
Absorption spectra of HCO+, 13CO, and CO+ toward both sources are shown in Fig. 1, and Fig. 2 presents a comparison of the absorption spectra of CO and HCO+ with emission spectra of HI and 12CO(1–0) described in Sect. 2.4. Column densities of HCO+, 13CO, C 18O, and H2 (N(H2) = N(HCO+)/3 × 10−9) are given in Tables 4 and 3. To compute N(13CO) and N(C18O), we assumed an excitation temperature of 5 K (Table 1), which is consistent with the observed brightness of the 12CO emission that is seen toward or near these sources, 1−2.5 K.
The diffuse nature of the gas along these lines of sight has previously been discussed by Gerin & Liszt (2017), Liszt & Gerin (2018), and Riquelme et al. (2018). High gas column densities accumulate over long paths through the Galactic disk at low galactic latitude, even without encountering dense clouds. This is indicated in our new data by the large ratio of 13CO and C 18O integrated optical depths or column densities, N(13CO)/N(C18O) = 29 ± 5 toward J1744-3116 (Table 3). If the oxygen and carbon ratios have the usual interstellar values, 16O/18O ~ 520 and 12C/13C ~ 65 (Wilson & Rood 1994; Milam et al. 2005; Keene et al. 1998; Giannetti et al. 2014), a fully molecular gas would have N(13CO)/N(C18O) = 8 toward J1744-3116. The much larger value we observe arises through a combination of selective photodissociation of C 18O, and, more likely, fractionation of 13CO through endothermic carbon isotope exchange when the majority of the free gas phase carbon is in C+ (Liszt 2017). Our value for N(13CO) toward J1744-3116 in Table 3 agrees with that given by Riquelme et al. (2018) based on J=1–0 absorption, N(13CO) = 6.3 × 1015 cm−2.
In our earlier work we also derived carbon isotope ratios H12CO+ /H13CO+ = 58 ± 9 and 64 ± 4 in the low-velocity gas toward J1717-3342 and J1744-3116, respectively. These values are typical of Galactic disk gas near the Sun and quite different from what is observed inside the Galactic bulge. Therefore, although the sight lines employed here cross the Galactic bulge, the low-velocity gas that is analyzed in CO and CO+ resides relatively nearby in the disk and is discussed under the assumption that local conditions are applicable.
Overall, the CO(1–0) emission is spread over the same velocity range as the HCO+ absorption. Toward J1744-3116, there is a fair correspondence of the main CO emission peaks with the HCO+ absorption features, but the HCO+ absorption profiles are more complex. The positive velocity component toward J1744-3116 is detected in 13CO(2–1) and C18O(2–1) absorption and is associated with a self-absorption feature in the H I spectrum that was discussed in Liszt & Gerin (2018). The presence of the three CO isotopologues indicates that this velocity component probably has the largest extinction and mean density and could be associated with translucent rather than diffuse gas. There is no self-absorption in the HI profile coincident with the negative velocity component, but the main 13CO(2–1) absorption is associated with a faint C18O(2–1) feature.
The CO(1–0) emission differs more from the HCO+ absorption toward J1717-3342, where the direction of the emission spectrum is 6.6′ away. Of the eight main HCO+ absorption features, only one is detected in 13CO(2–1), and none in C18O(2-1), showing that the gas is more diffuse along this line of sight. The CO emission is weaker than toward J1744-3116, barely reaching 1 K. As discussed byLiszt et al. (2010), the CO(1–0) emission is highly variable in diffuse gas as it traces the regions where CO reaches column densities above N(CO) = 1015 cm−2 that are high enough to produce detectable emission. This transition occurs over a small range of H2 column densities and depends on the local physical conditions, but CO emission at the level of 1 K- km s−1 integrated intensity is not observed in regions where the molecular fraction of H-nuclei in H2 is much below 0.6.
The comparison of the emission and absorption profiles therefore demonstrates that the two observed lines of sight encounter matter with variable physical conditions, ranging from diffuse to translucent gas. The upper limits for the CO+ integrated opacities shown in Table 2 provide constraints on the CO+ column densities and abundances for the whole range of physical conditions. For the diffuse molecular gas sampled in absorption the molecule excitation is dominated by the cosmic microwave background because of the low gas densities. Therefore, the CO+ column densities have been derived assuming an excitation temperature of 2.73 K. They are reported in Table 4 together with the HCO+ column densities in the same velocity intervals. The achieved upper limit on CO+ column densities leads to a very low value of about 0.04 for the N(CO+)/N(HCO+) ratio. The corresponding upper limit on the CO+ abundance relative to H2 is X(CO+) < 1.2 × 10−10, using the standard value for the HCO+ abundance relative to H2 in the diffuse molecular gas, 3 × 10−9 (Lucas & Liszt 1996; Gerin et al. 2019). These values are of a factor a few times higher than those established for HOC+, N(HOC+)/N(HCO+) = 0.015, and X(HOC+) = 0.45× 10−11 (Gerin et al. 2019).
3.2 CO+ as a source of HCO+
Despite the excellent sensitivity with achieved fractional rms flux density levels ΔSν∕Sν of 0.22% and 0.83% for J1717-3342 and J1744-3116, respectively, CO+ was not detected toward these sources. The derived 3σ upper limits N(CO+)/N(HCO+) ≲0.04 and N(CO+)/N(H2) < 1.2−1.3 × 10−10 are similar for both sources in Table 2, because J1717-3342, with a smaller intervening column density, is much brighter in the continuum. The achieved upper limit on the relative abundance is somewhat above the values seen in dense PDRs where emission lines from CO+ are detected and X(CO+) reaches a few times 10−11. They are below the relative abundances seen in the exceptional case of the young planetary nebula NGC 7027, where N(CO+)/N(H2) = 5 × 10−9 (Fuente et al. 2003).
It is straightforward to show that the relative abundance of CO+ is too small to provide a major source of the observed HCO+ in diffuse molecular gas, even independent of the HCO+ abundance. In chemical terms, the reaction CO+ + H2 → HCO+ + H forming HCO+ can be compared with the rate at which HCO+ recombines with electrons with rates as given in Table 5.
Equating formation and recombination of HCO+, neglecting photodissociation that is four orders of magnitude slower according to the Kinetic Database for Astrochemistry (KIDA; Wakelam et al. 2015):
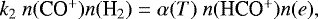
where fH2 is the fraction of H-nuclei in H2, x(e) is the electron fraction, n(H2) is the density of H2 molecules, and n(H) is the total density of H-nuclei. Taking x(e) = 2 × 10−4 corresponding to the observed free gas-phase carbon abundance n(C+)∕n(H) = 1.6 × 10−4 (Sofia et al. 2004) with a small added contribution from cosmic ray ionization of atomic hydrogen in largely molecular gas, the required amount of CO+ needed to restore the HCO+ lost to recombination is
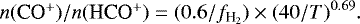
This is some 25 times higher than our upper limit if fH2 = 0.6 and T = 40 K. Wenote above that CO emission, even at the low levels shown in Fig. 2, does not arise in regions of very small molecular fraction and at temperatures high enough to trigger the formation of CH+: these are only characteristic of regions of strong turbulent energy dissipation.
Alternatively, equating the HCO+ formation and recombination rates once again but setting n(HCO+)∕n(H2) = 3 × 10−9 and x(e) = 2 × 10−4 = 2 × 10−4(2n(H2)∕fH2), for the required relative abundance of CO+ one derives
![\[ X(\mbox{{CO$^+$}}) = (1.8\times10^{-9}/\fH2) \times (40/T)^{0.69}. \]](/articles/aa/full_html/2021/04/aa39915-20/aa39915-20-eq9.png)
This is comparable to the CO+ relative abundance seen in NGC 7027 (~5 × 10−9, Fuente et al. 2003) and is at least 15 times above the upper limit achieved here, 1.2 × 10−10, if T = 40 K (Table 2). In this simplified analysis, reducing X(CO+) below our upper limit would require temperatures of about 2000 K, which correspond to the order of magnitude achieved in the turbulence-driven chemistry, which can only be present in small and intermittent regions of space and time, where other thermal and nonthermal processes are operating. CO+ is responsible for producing at most a few percent of the HCO+ that recombines with ambient thermal electrons to form CO in diffuse molecular gas.
Rates and rate coefficients.
4 The thermal chemistry of CO+, HOC+, and HCO+
Our upper limits show that CO+ cannot be responsible for forming the observed CO in diffuse molecular gas, because CO+ does not exist in a sufficient quantity to replenish HCO+ as it recombines with ambient electrons. However, beyond that, our limits combined with the observed relative abundance N(HOC+)/N(HCO+) = 1.4 ± 0.2 × 10−4 (Gerin et al. 2019)can be used to gain further insights into the thermal chemistry that is working in diffuse molecular gas. Most of the reactions that form HCO+ also form HOC+, yet their observed abundances differ by a factor of 70. To explore this, we extended the thermal CO+ and HOC+ chemistry discussed by Gerin et al. (2019) to include some hypotheticals corresponding to uncertainties in reaction rates in the KIDA reaction rate database (Wakelam et al. 2015) and molecular abundances (Gerin et al. 2016). As discussed in Gerin et al. (2019), some of the rates of the reactions controlling the formation of CO+ and HCO+ were not well known, especially the reaction C+ + OH → CO+ + H∕CO + H+ and the isomerization reaction destroying HOC+ and forming HCO+, HOC+ + H2 → HCO+ + H2. The rate of this reaction is reported as 4 × 10−10 cm3 s−1 at 25 and 300 K (Smith et al. 2002), which is about 1/5 the Langevin capture value, and, in this temperature range, it is probably independentof the temperature.
As originally suggested by Glassgold & Langer (1975, 1976), CO+ can be formed by the reaction of C+ with OH, and also by the reaction of O with CH+. CO+ is destroyed by recombination with electrons and in chemical reactions with atomic and molecular hydrogen, and photo-dissociated with a free space rate 1 × 10−10 s−1 that is always at least 300 times slower than the other destruction rates in the calculations discussed here. The OH relative abundance to H2, X(OH) = 1.0 ± 0.14 × 10−7 varies only narrowly and is well-determined in local diffuse clouds (Weselak et al. 2009, 2010) such as those probed in this work. The excellent correspondence of the OH and H2O absorption line profiles and of the H2O and HCO+ profiles along long sight lines across the Galactic plane (Wiesemeyer et al. 2016; Gerin et al. 2019) further indicates that this value of the OH abundance holds for the Galactic disk as well. The rate of the reaction of OH and C+ was recently calculated by Dagdigian (2019), providing accurate information on the rate coefficient and branching ratio over a temperature range 10–1000 K. We approximated the rate constant for C+ + OH forming CO+ as k = 2.2 × 10−9(300/T)0.107 cm3 s−1 (see Table 5). By contrast, the abundance of CH+ is locally variable, and CH+ may not co-exist with the other species if it is predominantly formed in the nonthermal chemistry (Godard et al. 2014; Valdivia et al. 2017). We take X(CH+) as a free parameter with X(CH+) = 10−9 by default in the following discussion.
HOC+ can be formed in the reaction of H2 with CO+ and in the reaction of C+ with H2O, of which we take the fixed relative abundance X(H2O) = 2.4 × 10−8 from Gerin et al. (2016). We ignored HOC+ formation by the reaction of O with CH3+ because the formation of CH3+ is an aspect of the nonthermal chemistry. HOC+ recombines with electrons and is susceptible to photodissociation, but most importantly is isomerized to HCO+ in reaction with H2. The rate constant for the isomerization reaction of H2 and HOC+ has alternatives in the KIDA database as discussed previously. Here, we considered the two extreme values for the rate constant, 10−11 cm3 s−1 given for 10–280 K and 4.7 × 10−10 cm3 s−1 given at 305 K.
The CO+ and HOC+ chemistry is simple when other molecular abundances are held fixed, but it involves the thermal and ionization balance for the temperature-sensitive recombination rates and the atomic/molecular hydrogen balance for various reactions with CO+ and HOC+. To address this, we performed calculations similarly to those described earlier to account for the observations of HF and CF+ (Liszt et al. 2015). In brief, we calculated the self-consistent global atomic/molecular, ionization and thermal equilibrium in gas spheres of constant total hydrogen number and column density, subject to the usual interstellar radiation fields. The hydrogen column density was varied, and molecular abundances were integrated along the central line of sight to form the results that are displayed here. Plotting the results against N(H2) removes some model sensitivities; for instance, to the impact parameter about the cloud center used for the line of sight integration.
The results are shown in Fig. 3. To the left is a baseline model using default values (Table 5). The model produces CO+ relative abundances about 2.5 times smaller than our observed upper limits, and about twice as much HOC+ as observed. Declines in the abundances of CO+ and HOC+ for very high N(H2) arise from the recombination of the free gas-phase carbon from C+ to neutral carbon and CO. In the middle panel, the solid lines show results when H2 -catalyzed HOC+ → HCO+ isomerization has the rate constant 10−11 cm3 s−1, a factor of 2.5 above the default value. The green curve for HOC+ shows that the predicted abundance of HOC+ grows even further above what is observed when the HOC+ → HCO+ interconversion is slow. The orange curves show what happens when the rate constant for HOC+ formation via H2 + CO+ → HOC+ + H is set to 0. The predicted amount of CO+ grows well above our upper limits, and the abundance of HOC+ falls far below the observed mean. We conclude that HOC+ is forming mostly via C+ + OH followed by CO+ + H2, but much or most of the HOC+ produced by these chemical reactions is lost to isomerization into HCO+.
In the right panel of Fig. 3, the solid curves show model results when the reaction of C+ and H2O does not form HOC+: all of the observed HOC+ can indeed be made by the reaction of C+ and OH, and agreement with the observed HOC+/HCO+ ratio is somewhat better when the contribution from H2O is neglected. However, H2O is observed to be present with X(H2O) = 2.4 × 10−8 (Gerin et al. 2016) and would be expected to form some amount of HOC+. The default model may predict an overabundance of CO+ or perhaps some aspect of the reaction of C+ and H2O is not fully understood: a slower rate or a branching ratio that favors HCO+ would lead to a lower contribution of this reaction to the HOC+ formation.
Moreover, CH+ may not co-exist with the other species if it is predominantly formed in the nonthermal chemistry (Godard et al. 2014; Valdivia et al. 2017) and X(CH+) is negligible (10−9) in the default model. The final deviation from the default model is represented by the dash-dot lines in the right-hand panel showing results when X(CH+) = X(OH) = 10−7 is large. The reaction of O + CH+ becomes an important source of CO+ in the thermal chemistry when X(CH+) ≳5 × 10−8 and our upper limits on CO+ by themselves imply X(CH+)/X(OH) ≲3. At such high CH+ abundances the discrepancy in HOC+ grows even larger.
 |
Fig. 3 Models of thermal chemistry for the relative abundances N(CO+)/N(HCO+) and N(HOC+)/N(HCO+) with default rates to the left, and deviations in the middle and right panels. In all panels, results for HOC+ are shown in green and for CO+ in orange. In all cases, N(HCO+) is taken to be the observed value N(HCO+) = 3 × 10−9 N(H2). Left panel: baseline models with the observed upper limit for N(CO+)/N(HCO+) from this work and the mean N(HOC+)/N(HCO+) ratio from Gerin et al. (2019) are illustrated schematically as horizontal dashed lines. Middle panel: the solid lines represent the case that the rate constant of H2 + HOC+ → HOC+ +H2 interconversion is taken as 10−11cm3 s−1. The dashed-dotted lines represent model results when the rate constant for the reaction H2 + CO+ → HOC+ + H is set to 0. Right panel: the solid lines show models in which the reaction of C+ and H2O does not form HOC+ and the dashed-dotted lines show model results when CH+ is as abundant as OH, X(CH+) = 10−7. |
5 Conditions for the growth of CO
Balancing the formation of CO through the dissociative recombination of HCO+ and the destruction of CO by photodissociation can constrain the physical conditions where CO might form in diffuse molecular gas. With a free-space photodissociation rate kd = 2.43 × 10−10 s−1 for the Draine radiation field (defined as G0 = 1) and an attenuation scaling as e−γAV, this balance locally implies
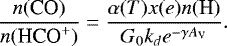
For a uniform slab, integrating the attenuation term from 0 up to half the slab extinction,
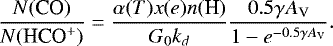
n(H)∕G0 can therefore be expressed as
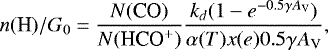
where we approximate AV = 3.1E(B–V) and take E(B–V) from Green et al. (2019), replacing local quantities with line-of-sight averages. The error bar in E(B–V) is a nominal value 0.02 mag. We take γ = 3.88 and use the reaction rates and rate coefficients given in Table 5. Figure 4 presents the variation of n(H)∕G0 as a function of the reddening E(B–V) for the existing sample of quasars sight lines with HCO+ and CO column densities determined in absorption (Liszt & Lucas 1998; Liszt et al. 2019). We used conditions as described in Sect. 2, a uniform temperature of 40 K, and a uniform electron fraction x(e) = 2 × 10−4.
The mean value for the sample is ⟨n(H)∕G0⟩~ 300 cm−3. For a standard interstellar radiation field of G0 = 1, the calculated densities n(H) ~ 100−300 cm−3 are modest for E(B–V) ≳0.5 mag, even in the absence of any consideration of CO shielding by itself or by H2. The higher densities n(H) ~ 1000−2000 cm−3 calculated at E(B–V) ≲ 0.2 mag are higher by a factor of ~5 than those inferred from the brightness of HCO+ emission in these directions (Liszt 2020). Thermal pressures p∕k ~ 40 K × 1000 cm−3 are an order of magnitude higher than typical values in the diffuse molecular gas (Jenkins & Tripp 2011) and would more likely represent the conditions under which a turbulence-driven chemistry forms HCO+. A lower value of the radiation field toward these sight lines would bring the derived densities closer to the mean values. The data shown in this plot include the sight lines with CO and HCO+ detections, which may bias the derived n(H)∕G0 to somewhat high values as a higher density implies a faster CO production rate.
The inverse variation of n(H)∕G0 with E(B–V) in Fig. 4, mirroring the functional dependence on Av, reflects the fact that the observed values of N(CO)/N(HCO+) are not correlated with E(B–V) and show a moderate scatter of at most a factor of 1. A majority of the selected sight lines have N(CO)/N(HCO+) between 1000 and 2000. We also plotted n(H)∕G0 against the molecular fraction fH2 = 2N(H2)/N(H) taking N(H2) = N(HCO+)/3 × 10−9 and N(H) = a×E(B–V). Requiring fH2 ≤ 1 in all cases implies a≳8 × 1021 H-nuclei cm−2 mag−1, but there is no trend for n(H)∕G0 to vary with fH2 calculated in this way.
 |
Fig. 4 Number density n(H)∕G vs. reddening E(B–V) (Green et al. 2019) derived by equating CO formation and photo-destruction for sight lines with HCO+ and CO column densities measured in absorption (Liszt & Lucas 1998; Liszt et al. 2019), as discussed in Sect. 5. |
6 Summary and conclusions
We sought to test the origin of CO in diffuse molecular gas within the generally accepted framework that CO is predominantly formed through the dissociative electron recombination of HCO+. HCO+ is widely observed in diffuse molecular gas, with a relative abundance N(HCO+)/N(H2) = 3 × 10−9.
In a quiescent, thermal, cosmic-ray, and UV-driven chemistry, HCO+ is predominantly formed in the reactions C+ + OH → CO+ + H and CO+ + H2 → HCO+ + H. Using Cycle 7 ALMA Band-6 observations at 236 GHz (Table 1), we searched for CO+ absorption toward two bright compact extragalactic millimeter-wave continuum sources seen at low latitude in the inner Galaxy and known to be occulted by high column densities of HCO+-bearing diffuse molecular gas (see Sect. 2 and Table 2). We failed to detect CO+ at levels sufficient to demonstrate in Sect. 3 that the reaction CO+ + H2 → HCO+ + H cannot replenish more than a few percent of the observed HCO+ that recombines. The non-detection of CO+ confirms that HCO+ is mainly produced in the reaction between oxygen and carbon hydrides CH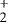 or CH
or CH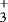 induced by suprathermal processes, while CO+ and HOC+ result from reactions between C+ and OH andH2O in the thermal chemistry that occurs in quiescent diffuse molecular gas. The observed CO+ and HOC+ abundances relative to H2 set an upper limit on the rate coefficient of these reactions.
induced by suprathermal processes, while CO+ and HOC+ result from reactions between C+ and OH andH2O in the thermal chemistry that occurs in quiescent diffuse molecular gas. The observed CO+ and HOC+ abundances relative to H2 set an upper limit on the rate coefficient of these reactions.
In Sect. 4, we have explored the coupled thermal chemistries of CO+ and HOC+ given our observational upper limits on CO+ and existing observations of HOC+ showing N(HOC+)/N(HCO+) = 0.015 ± 0.003. A baseline cosmic-ray and UV-driven thermal chemical model overproduced HOC+ by a factor of two, but by as much as a factor of six if the isomerization reaction HOC+ + H2 → HCO+ + H2 does proceed rapidly. The option of a low rate for this reaction in the KIDA database should probably be ignored. The predicted HOC+ abundance is in better agreement with the observations if the reaction of C+ and H2O preferentially forms HCO+, rather than HOC+. We placed a weak limit on the relative abundance of CH+ in quiescent gas, N(CH+)/N(OH) ≲ 3 or X(CH+)/X(H2) ≲3 × 10−7, such that the reaction O + CH+ does not become a significant source of CO+, substantially overproducing it.
In Sect. 5, we have derived characteristic number densities n(H) at which CO would form in diffuse molecular gas with observed abundances. For E(B–V) ≳ 0.5 mag, the densities are modest, n(H) ~ 100−300 cm−3, but for CO-bright regions of low extinction E(B–V) ~ 0.1−0.2 mag they are an order of magnitude higher n(H) ~ 1−2 × 103 cm−3, and such heavily over-pressured gas is more properly considered in the context of a turbulent dissipation chemistry. The presence of CO in sight lines of low reddening could also indicate a lower radiation field intensity.
Acknowledgements
The authors thanks the referee Helmut Wiesemeyer for his thoughtful comments and suggestions. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2019.1.00120.S.. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), NSC and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. This work was supported by the Programme National “Physique et Chimie du Milieu Interstellaire” (PCMI) of CNRS/INSU with INC/INP co-funded by CEA and CNES.
References
- Agúndez, M., Goicoechea, J. R., Cernicharo, J., Faure, A., & Roueff, E. 2010, ApJ, 713, 662 [NASA ADS] [CrossRef] [Google Scholar]
- Bitran, M., Alvarez, H., Bronfman, L., May, J., & Thaddeus, P. 1997, ApJS, 125, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Black, J. H., & Dalgarno, A. 1977, ApJS, 34, 405 [Google Scholar]
- Dagdigian, P. J. 2019, J. Chem. Phys., 151, 054306 [Google Scholar]
- Endres, C. P., Schlemmer, S., Schilke, P., Stutzki, J., & Müller, H. S. P. 2016, J. Mol. Spectr., 327, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Fuente, A., Rodrıguez-Franco, A., Garcıa-Burillo, S., Martın-Pintado, J., & Black, J. H. 2003, A&A, 406, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerin, M., & Liszt, H. 2017, A&A, 600, A48 [Google Scholar]
- Gerin, M., Ruaud, M., Goicoechea, J. R., et al. 2015, A&A, 573, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerin, M., Neufeld, D. A., & Goicoechea, J. R. 2016, ARA&A, 54, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Gerin, M., Liszt, H., Neufeld, D., et al. 2019, A&A, 622, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giannetti, A., Wyrowski, F., Brand, J., et al. 2014, A&A, 570, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Glassgold, A. E., & Langer, W. D. 1975, ApJ, 197, 347 [Google Scholar]
- Glassgold, A. E., & Langer, W. D. 1976, ApJ, 206, 85 [Google Scholar]
- Godard, B., Falgarone, E., & Pineau des Forêts, G. 2014, A&A, 570, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goicoechea, J. R., Cuadrado, S., Pety, J., et al. 2017, A&A, 601, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goicoechea, J. R., Santa-Maria, M. G., Bron, E., et al. 2019, A&A, 622, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldsmith, P. F., Pineda, J. L., Neufeld, D. A., et al. 2018, ApJ, 856, 96 [Google Scholar]
- Green, G. M., Schlafly, E., Zucker, C., Speagle, J. S., & Finkbeiner, D. 2019, ApJ, 887, 93 [Google Scholar]
- Hamberg, M., Kashperkat, I., Thomas, R. D., et al. 2014, J. Phys. Chem. A., 118, 6034 [Google Scholar]
- Heays, A. N., Bosman, A. D., & van Dishoeck, E. F. 2017, A&A, 602, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jenkins, E. B., & Tripp, T. M. 2011, ApJ, 734, 65 [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keene, J., Schilke, P., Kooi, J., et al. 1998, ApJ, 494, L107 [Google Scholar]
- Latter, W. B., Walker, C. K., & Maloney, P. R. 1993, ApJ, 419, L97 [Google Scholar]
- Lesaffre, P., Todorov, P., Levrier, F., et al. 2020, MNRAS, 495, 816 [Google Scholar]
- Liszt, H. S. 2017, ApJ, 835, 138 [Google Scholar]
- Liszt, H. S. 2020, ApJ, 897, 104 [Google Scholar]
- Liszt, H., & Gerin, M. 2018, A&A, 610, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liszt, H. S., & Lucas, R. 1998, A&A, 339, 561 [NASA ADS] [Google Scholar]
- Liszt, H. S., & Lucas, R. 2000, A&A, 355, 333 [NASA ADS] [Google Scholar]
- Liszt, H. S., Pety, J., & Lucas, R. 2010, A&A, 518, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liszt, H., Lucas, R., Pety, J., & Gerin, M. 2014a, IAU Symp., 297, 163 [Google Scholar]
- Liszt, H. S., Pety, J., Gerin, M., & Lucas, R. 2014b, A&A, 564, A64 [Google Scholar]
- Liszt, H. S., Guzmán, V. V., Pety, J., et al. 2015, A&A, 579, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liszt, H., Gerin, M., Beasley, A., & Pety, J. 2018, ApJ, 856, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Liszt, H., Gerin, M., & Grenier, I. 2019, A&A, 627, A95 [Google Scholar]
- Lucas, R., & Liszt, H. 1996, A&A, 307, 237 [NASA ADS] [Google Scholar]
- Martinez, Jr. O., Betts, N. B., Villano, S. M., et al. 2008, ApJ, 686, 1486 [Google Scholar]
- Milam, S. N., Savage, C., Brewster, M. A., Ziurys, L. M., & Wyckoff, S. 2005, ApJ, 634, 1126 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [Google Scholar]
- Riquelme, D., Bronfman, L., Mauersberger, R., et al. 2018, A&A, 610, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sastry, K. V. L. N., Helminger, P., Herbst, E., & De Lucia, F. C. 1981, ApJ, 250, L91 [Google Scholar]
- Savage, B. D., Drake, J. F., Budich, W., & Bohlin, R. C. 1977, ApJ, 216, 291 [Google Scholar]
- Sheffer, Y., Rogers, M., Federman, S. R., et al. 2008, ApJ, 687, 1075 [Google Scholar]
- Smith, M. A., Schlemmer, S., von Richthofen, J., & Gerlich, D. 2002, ApJ, 578, L87 [Google Scholar]
- Snow, T. P., & McCall, B. J. 2006, ARA&A, 44, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Sofia, U. J., Lauroesch, J. T., Meyer, D. M., & Cartledge, S. I. B. 2004, ApJ, 605, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Treviño-Morales, S. P., Fuente, A., Sánchez-Monge, Á., et al. 2016, A&A, 593, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valdivia, V., Godard, B., Hennebelle, P., et al. 2017, A&A, 600, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Dishoeck, E. F., & Black, J. H. 1986, ApJS, 62, 109 [Google Scholar]
- van Dishoeck, E. F., & Black, J. H. 1988, ApJ, 334, 771 [Google Scholar]
- Visser, R., van Dishoeck, E. F., & Black, J. H. 2009, A&A, 503, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakelam, V., Loison, J. C., Herbst, E., et al. 2015, ApJS, 217, 20 [Google Scholar]
- Weselak, T., Galazutdinov, G., Beletsky, Y., & Krełowski, J. 2009, A&A, 499, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weselak, T., Galazutdinov, G. A., Beletsky, Y., & Krełowski, J. 2010, MNRAS, 402, 1991 [Google Scholar]
- Wiesemeyer, H., Güsten, R., Heyminck, S., et al. 2016, A&A, 585, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, T. L.,& Rood, R. 1994, ARA&A, 32, 191 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Absorption spectra observed toward J1717-3342 (left) and J1744-3116 (right). The spectra were normalized by the continuum flux density. The CO+ spectra were shifted vertically and multiplied by 10. HCO+ is shown in black, CO+ in red, and 13CO(2–1) in blue for comparison. The HCO+ data are taken from Liszt & Gerin (2018) and Gerin & Liszt (2017). |
| In the text | |
 |
Fig. 2 Comparison of the HCO+ (1–0) (black) and 13CO (2–1) (green) absorption with the 12CO (blue) and scaled HI (gray) emission. J1717-3342 is shown at the top and J1744-3116 at the bottom. C18O(2–1) is also shown in orange for J1744-3116. |
| In the text | |
 |
Fig. 3 Models of thermal chemistry for the relative abundances N(CO+)/N(HCO+) and N(HOC+)/N(HCO+) with default rates to the left, and deviations in the middle and right panels. In all panels, results for HOC+ are shown in green and for CO+ in orange. In all cases, N(HCO+) is taken to be the observed value N(HCO+) = 3 × 10−9 N(H2). Left panel: baseline models with the observed upper limit for N(CO+)/N(HCO+) from this work and the mean N(HOC+)/N(HCO+) ratio from Gerin et al. (2019) are illustrated schematically as horizontal dashed lines. Middle panel: the solid lines represent the case that the rate constant of H2 + HOC+ → HOC+ +H2 interconversion is taken as 10−11cm3 s−1. The dashed-dotted lines represent model results when the rate constant for the reaction H2 + CO+ → HOC+ + H is set to 0. Right panel: the solid lines show models in which the reaction of C+ and H2O does not form HOC+ and the dashed-dotted lines show model results when CH+ is as abundant as OH, X(CH+) = 10−7. |
| In the text | |
 |
Fig. 4 Number density n(H)∕G vs. reddening E(B–V) (Green et al. 2019) derived by equating CO formation and photo-destruction for sight lines with HCO+ and CO column densities measured in absorption (Liszt & Lucas 1998; Liszt et al. 2019), as discussed in Sect. 5. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.