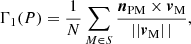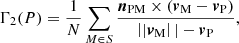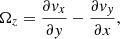| Issue |
A&A
Volume 647, March 2021
|
|
|---|---|---|
| Article Number | A178 | |
| Number of page(s) | 13 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202040172 | |
| Published online | 31 March 2021 | |
Photospheric downflows observed with SDO/HMI, HINODE, and an MHD simulation
1
Institut de Recherche en Astrophysique et Planétologie, Université de Toulouse, CNRS, UPS, CNES, 14 Avenue Edouard Belin, 31400 Toulouse, France
e-mail: thierry.roudier@irap.omp.eu
2
Charles University, Astronomical Institute, V Holešovičkách 2, 18000 Prague 8, Czech Republic
3
Astronomical Institute of the Czech Academy of Sciences, Fričova 298, 25165 Ondejov, Czech Republic
4
Observatoire de Paris, LESIA, 5 Place Janssen, 92195 Meudon, France
5
PSL Research University, CNRS, Sorbonne Universités, Sorbonne Paris Cité, Paris, France
6
Lockheed Martin Solar and Astrophysics Laboratory, Palo Alto, 3251 Hanover Street CA 94303, USA
Received:
18
December
2020
Accepted:
5
February
2021
Downflows on the solar surface are suspected to play a major role in the dynamics of the convection zone, at least in its outer part. We investigate the existence of the long-lasting downflows whose effects influence the interior of the Sun but also the outer layers. We study the sets of Dopplergrams and magnetograms observed with Solar Dynamics Observatory and Hinode spacecrafts and an magnetohydrodynamic (MHD) simulation. All of the aligned sequences, which were corrected from the satellite motions and tracked with the differential rotation, were used to detect the long-lasting downflows in the quiet-Sun at the disc centre. To learn about the structure of the flows below the solar surface, the time-distance local helioseismology was used. The inspection of the 3D data cube (x, y, t) of the 24 h Doppler sequence allowed us to detect 13 persistent downflows. Their lifetimes lie in the range between 3.5 and 20 h with a sizes between 2″ and 3″ and speeds between −0.25 and −0.72 km s−1. These persistent downflows are always filled with the magnetic field with an amplitude of up to 600 Gauss. The helioseismic inversion allows us to describe the persistent downflows and compare them to the other (non-persistent) downflows in the field of view. The persistent downflows seem to penetrate much deeper and, in the case of a well-formed vortex, the vorticity keeps its integrity to the depth of about 5 Mm. In the MHD simulation, only sub-arcsecond downflows are detected with no evidence of a vortex comparable in size to observations at the surface of the Sun. The long temporal sequences from the space-borne allows us to show the existence of long-persistent downflows together with the magnetic field. They penetrate inside the Sun but are also connected with the anchoring of coronal loops in the photosphere, indicating a link between downflows and the coronal activity. A links suggests that EUV cyclones over the quiet Sun could be an effective way to heat the corona.
Key words: Sun: granulation / Sun: photosphere / Sun: atmosphere
© T. Roudier et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Except magnetic structures, the whole solar surface is almost completely renewed every 10−15 min because of the convective motions carrying the energy in the solar envelope. At the solar surface convective cells of hot rising buoyant plasma in which energy is released by radiation exchange are observed. Around these cells, the cold plasma falls down. The cooler plasma flow is more dense than its surroundings, and with triggers the formation of turbulent plumes (Stein & Nordlund 1989; Rieutord & Zahn 1995) and drives the dynamics of the flow. Downdrafts are sinks where the cold plasma goes back into the Sun. These plumes undergo secondary instabilities along their descending trajectories producing a turbulent mixture of vorticity filaments (Rast 1999; Belkacem et al. 2006; Stein et al. 2009; Rincon & Rieutord 2018). The vertical downflows are located in the intergranular regions and occasionally become supersonic (Stein & Nordlund 1998). Their works generally indicate the existence of strong long-lasting downdrafts penetrating into the convection zone. The models of Rast (2003) predict that supergranular downflows are concentrated near the vertices of supergranular cells and merge at deeper layers. This results in large, long-lived downflow regions and, in consequence, the formation of a supergranular flow system. The kinetic energy in the convection zone is tightly connected to the evolution of the innumerable minuscule diving plumes that formed at intergranular lanes (Hanasoge & Sreenivasan 2014).
Various studies revealed the existence of vortex flows (Bonet et al. 2008; Attie et al. 2009) having a wide range of spatial extents from 1 to 20 Mm with lifetimes between 5 min and 2 h. The scale of the vortex flows seem to be comparable to scales of supergranules and mesogranules. Some of the long-lasting vortex flows were located at supergranular junction vertices (Attie et al. 2009, 2016; Requerey et al. 2018). The related downflows also represent transient processes for magnetic field intensification associated with the formation of bright points in the continuum (Berger et al. 2004; Bello González et al. 2009; Narayan 2011).
Recently, the Lagrangian coherent structures (LCS; see, e.g., Chian et al. 2019, 2020) detection method was applied to locate repulsion and attraction regions as well as the shear and swirling of particle motions on the solar surface. With such a contribution, they highlight that supergranular cells are interconnected by ridges of repelling LCSs that facilitate the formation of vortices and magnetic concentration in the valley of the repelling LCS. The attractive LCS reveals the location of sinks of photospheric flows at supergranular junctions associated with persistent vortices and intense magnetic flux.
The downflows are important ingredients of the convective motions. Until now, they had only been studied only in small fields of view and with a short cadence. The only exception known to us is the study by Duvall & Birch (2010), who studied the vertical component of supergranulation. The downflows at mesogranular downdraft boundaries act as ‘collapsars’. Small granules vanish and excite the upward-propagating waves (Rast 1995, 1999; Skartlien & Rast 2000; Skartlien et al. 2000).
The role of surface layers in the global convective simulations was recently discussed by many studies. For instance Nelson et al. (2018) show that the introduction of the near-surface small-scale downflows into the global 3D simulation changes the convective driving motions throughout the convection zone. In particular, the coalescence of downflow plumes into giant cells at larger depths linked to the self-organisation of the near-surface plumes provides a new approach towards the convection conundrum.
Today, the main difficulty seems to be the overestimation of the convective velocity in the convection zone by forward models when forward and inverse models are compared. On the other hand, Hotta et al. (2019) show that the surface region has an unexpectedly weak influence on the deep convection zone and does not resolve the problem of the high convective velocity in the deep solar interior of the state-of-the-art forward models. Nevertheless, Hotta et al. (2019) indicate the possibility of an unknown influence of the unresolved small-scale turbulence.
In this paper, we investigate the properties of near-surface downflows through the observations of the Solar Dynamics Observatory (SDO; Pesnell et al. 2012) and Hinode (Kosugi et al. 2007) satellites and finally a 3D MHD simulation. In Sect. 2, we describe the data selection and reduction. The analysis of the persistent downflows is presented in Sect. 3. Section 4 is devoted to the potential link between vortex and the persistent downflows. The non-detection of a vortex comparable in size to observations at the surface of the Sun in the simulation is described in Sect. 5. The discussion and conclusion are given in Sect. 6.
2. Observations and simulation
To study the properties of the medium-scale surface downflows, we used two 24 h SDO Doppler observations, covering 29 November 2018, and also 2−3 November 2010. Hereafter, we refer to the latter series as the ‘Requerey’s vortex’, where a strong vortical downflow was already studied by Requerey et al. (2018). The regions of interest were around the disc centre in the quiet-Sun regions, with a small inclination of the solar rotation axis with respect to the observer (the heliographic latitudes of the disc centre were B0 = 1.1° in the first case and B0 = 4.25° in the second case). The original pixel size of images were 0.5040″ and 0.5042″, respectively, and a time step of 45 s. Mainly, we used the observations from the Helioseismic and Magnetic Imager (HMI; Schou et al. 2012). The 24 h sequences were aligned, corrected from the satellite motions and the limbshift, and finally tracked with the differential rotation. From the full-disc Dopplergrams we extracted a region around the disc centre having 701 × 701 pixels on a side (353″ × 353″). The tracked Doppler datacube was filtered in the k − ω domain with a threshold phase velocity of 6 km s−1. Line-of-sight HMI magnetograms capturing the longitudinal magnetic induction B∥ were used for both sequences and processed similarly to the Dopplergrams, except for the application of the velocity filter. For the 2018 series, we also used ultraviolet filtergrams from the Atmospheric Imaging Assembly (AIA; Lemen et al. 2012) at a wavelength of 193 Å. The AIA sequence recorded at the original pixel size of 0.6″ was mapped to the HMI frame and tracked to coaling with HMI sequences.
We also used datasets from the Solar Optical Telescope (SOT; Tsuneta et al. 2008) on-board the Hinode mission spacecraft. The observations were recorded continuously on 4 September 2009, from 7:34:34 to 10:16:34 UT. For our study, we used observations of Fe I at λ = 5250 Å from the Hinode/SOT-NFI (Narrow band Filter Imager), where the spectral line was scanned at five wavelength positions along the line profile. The Doppler shift at the disc centre gives us the vertical (radial) flow component vz, the Stokes V and hence the vertical component of the magnetic induction Bz. The pixel size of images is 0.16″ and the time step is 60 s. After the flat field and dark corrections, the images were coaligned and filtered for p-modes in the k − ω space with a threshold phase velocity of 6 km s−1. We note that arcsecond-kilometre conversion, for each dataset considered, takes the distance between the corresponding instrument and the Sun into account.
In order to learn about the structure of the flows also below the solar surface, we utilised time-distance local helioseismology (Duvall et al. 1993). This method comprises tools that measure and analyse the travel times of the waves propagating throughout solar interior.
Travel times of the waves may be measured via cross-correlations of the signals at spatially different points on the solar surface. Doppler shifts of the photospheric absorption lines contain clear indications about solar oscillations. We therefore utilised HMI Dopplergrams and measured travel times using a set of filters, averaging geometries and distances. Since we are dealing with the quiet-Sun region, we measured the travel times using linearised Gizon & Birch (2004) method.
These travel times were then inverted for flows using multi-channel subtractive optimally localised averaging method (MC-SOLA; see Jackiewicz et al. 2012) when involving the cross-talk minimisation (Švanda et al. 2011; Korda & Švanda 2019). When discussing the flows, thanks to the cross-talk minimisation our methodology allows one to not only infer the horizontal velocities (vx in the zonal direction and vy in the meridional direction), but also the vertical component vz. The inferred velocity vector v is a function of the horizontal position r and height z. Horizontal velocities are strong perturbers that may be successfully retrieved to the depth, whereas the vertical velocity is a weak perturber and only inversions in the first 1 Mm of depth are possible with the signal-to-noise ratio larger than one when averaging the data over 24 h or so.
Therefore, except for the surface, the vertical velocity was reconstructed from the horizontal components by integrating the equation of continuity:
where ∇h ⋅ vh indicates the horizontal part of the velocity divergence. The integration does not yield the surface vz(z = 0), where we directly use the inverted values by helioseismology. The surface inversions for plasma flows were validated against the granule-tracking inferences by Švanda et al. (2013).
For the deeper layers, we performed a set of inversions targeted such that the vertical sampling was 2 Mm, starting at the depth of 1 Mm and ending at 25 Mm. We basically followed the vertical sampling given by Greer et al. (2016). With the depth, the extents of the averaging kernels defining the effective resolution increased monotonically, reaching 10 Mm at 1 Mm depth, 34 Mm at 13 Mm depth and finally 58 Mm at 25 Mm depth. The vertical extent defining the vertical resolution increased as well, having 1 Mm at the depth of 1 Mm, 2.9 Mm at the depth of 13 Mm and finally 8.7 Mm at the depth of 25 Mm.
3. Analysis of persistent downflows with HMI, Hinode, and simulation data
The first detection of persistent (long-lived) downflows surviving for at least 4 h is described in Duvall & Birch (2010) (their Figs. 1a and c). The results were obtained by the analysis of the Dopplergrams and magnetograms from SOHO/MDI (Scherrer et al. 1995) with a resolution of 1.2″. Duvall & Birch (2010) selected a 4 h temporal window to average Dopplergrams at the disc centre to follow the evolution of supergranular cells. They tested a possible contamination of the Doppler signal by magnetic fields but concluded that there was a rather small contribution from the magnetic field. Their simultaneous 4 h average of Dopplergrams and magnetograms showed a correlation between the persistent downflows and the magnetic induction. We note that the persistent downflows were called apparent downflows in their paper.
For our study, we selected a 24 h sequence of disc centre quiet-Sun Dopplergrams and magnetograms observed on 29 November 2018 with the SDO/HMI. The spatial resolution of these observations was 1.0″. To mimic the downflow detection like Duvall & Birch (2010), we used the 5 h average Dopplergrams. Figure 1 (left) convincingly shows persistent downflows as localised black areas. The large amplitude of the negative vertical velocity indicates that the downflow survived 24 h averaging. These downflows with sizes around 2−3″ and velocity amplitudes between −0.25 and −0.72 km s−1 spatially correlate with the magnetic field in location (see the middle panel of Fig. 1) and also with the regions of larger activity in the corona (images from AIA 193 Å). Figure 2 shows a zoom-out of the larger downflows from Fig. 1. Figure 3 displays the persistent downflows (red) and |B∥| (blue) at the exact locations relative to the coronal loop. In this example the persistent downflows appear to correlate with the coronal-loop anchor in the photosphere, indicating a link between the persistent downflows and the coronal activity.
 |
Fig. 1. Region of interest on the 29 November 2018 datacube. The region was localised at the disc centre; the field of view has dimensions of 353″ × 353″. Left: 5 h mean of the HMI Dopplergrams, where black areas are considered as persistent downflows. Middle: 5 h mean of the line-of-sight magnetic induction |B∥|. Right: 5 h mean of AIA 193 Å filtergrams. |
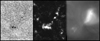 |
Fig. 2. Details of Fig. 1 around one of the persistent downflows, with a field of view of 59.5″ × 73.5″. Left: mean Doppler velocity. Middle: mean |B∥|. Right: mean AIA 193 Å filtergram. |
 |
Fig. 3. Coalignment of panels from Fig. 2. Background: mean AIA 193 Å filtergram. Blue contours: mean |B∥| level = 120 Gauss. Red contours: mean Doppler velocity level = −0.2 km s−1. Red and blue contours largely overlap. |
The inspection of the 3D (x, y, t) Dopplergram datacube from 29 November 2018 allowed us to detect 13 persistent downflows with a minimum duration of 3 h (see below). This gives a rate of occurrence of 2 × 10−4 cases per Mm2 and 24 h. This rate is lower than those found by Requerey et al. (2017) during sequences of 32.0 and 22.7 min of 6.7 × 10−2 per Mm2. These two rates of occurrence are not directly comparable because the first one deals with very long-lasting downflows (a few hours) although the second rate is related to shorter-lasting downflows (30 min).
To detect the supergranule boundaries, horizontal velocities were computed with the local correlation tracking technique (LCT; November 1986) applied to the sequence of Dopplergrams. From the derived horizontal velocities, we computed the 24 h average divergence field and the supergranule boundaries using the watershed method (Roudier et al. 2020). These boundaries plotted over the divergence field are shown as a white network in Fig. 4 (top left). In Fig. 4 (top right) the 24 h mean Doppler map is overlapped by locations of the 13 studied persistent downflows (circles) and supergranular boundaries. Downflows are visible as dark structures in each circle. The persistent downflows are identified in the convergent flows and more particularly at positions, where several supergranules meet. This is in agreement with the conclusion that vortex flows are usually located at supergranular junction vertices found by Attie et al. (2009, 2016). Using the 24 h horizontal-velocity fields, we computed the corks diffusion during that period of time. Figure 4 (bottom left) confirms that the locations of the persistent downflows (circles) at the supergranule boundaries are situated where the corks are accumulate.
 |
Fig. 4. Top left: 24 h divergence field measured with the LCT applied to Dopplergrams. The supergranule boundaries detected by the watershed method are shown as white network. The circles represent the location of the 13 studied a persistent downflows. These persistent downflows are located in convergent flows and more particularly where several supergranules meet. Top right: 24 h mean Doppler map overlapped with the 13 studied persistent downflows (circles) and supergranule boundaries. Downflows are visible as dark structures in each circle. Far from the disc centre, in the lower right part of the figure, some large darker regions are visible. These are caused by the horizontal velocities which become a dominant contribution due to the projection effects. Bottom left: corks position (grey points) after 24 h diffusion by horizontal flows. Their locations are, in accordance with supergranule boundaries, found by the watershed method (superimposed white network). Bottom right: 24 h mean magnetic field and the location of the 13 studied persistent downflows (circles). |
Temporal cuts of the Doppler velocities centred on the 13 persistent downflows are shown in Fig. 5 (top). The downflows are visible as dark structures in the cuts and they last for a long time from 3.5 h to 20 h in our examples. However, the downflows move across the surface during their lifetimes which makes it difficult to catch them on single positional cuts. Nevertheless, the Doppler temporal cuts clearly exhibit their long duration. Some of them are not fully continuous but are visible at the same position. The sizes of these downflows are around 2−3″.
 |
Fig. 5. Doppler (top) and magnetic (bottom) temporal cuts centred on the 13 selected persistent downflows. The time (vertical axis) stands for 24 h, the spatial axis (y cut, horizontal) is 15″ for each column and the numbers indicate the labels of the selected downflows corresponding to the bottom right of Fig. 4. The persistent downflows move across the surface but are visible in the cuts at least from 3.5 h to 20 h. |
Figure 5 (bottom) shows magnetic field temporal cuts centred on the 13 persistent downflows. The correlation between the persistent downflows and the magnetic field is well observed and conforms to the one found by Duvall & Birch (2010). The magnetic field is always observed at the location of the persistent downflows. From our set, only one persistent downflow (number 6) seems to be without a strong magnetic counterpart (see bottom right panel of Fig. 4).
To quantify the velocity-magnetic field correlation, we plotted the mean Doppler velocity versus |B∥| from the 24 h sequence in Fig. 6. In the regions where |B∥| > 60 G, a linear relationship between the magnetic field and the observed Doppler velocity is most clear as described by Duvall & Birch (2010). The strongest magnetic concentrations are found in the strongest downflows. As we observe with high-resolution HMI data (0.5″ per pixel), the positive correlation probably indicates a suppression of the granular flows due to the magnetic field. Our observations thus confirm the hypothesis by Duvall & Birch (2010).
 |
Fig. 6. Scatter plot of the dependence of Doppler velocity and |B∥| obtained for the SDO data on 29 November 2018. |
3.1. Depth structure of the persistent downflows
The persistent downflows identified in the HMI frame were also localised in the helioseismic datacubes. Unlike full-resolution Dopplergrams or velocity fields obtained by LCT, the helioseismic inferences have a much coarser spatial resolution, 10 Mm effective resolution at the surface at best. Therefore these spatially confined persistent downflows cannot be directly identified in the helioseismic frames. We verified that no clear signal of these confined downflows is present in the travel-time maps. This is due to the fact that the typical wavelength of the p-modes and the surface gravity f-modes is a few megametres, which is much larger than the horizontal extent of the identified persistent downflows.
Hence, the downflows were localised by their coordinates. In Fig. 7 we see their locations on the vertical-flow maps derived at the surface (a helioseismic inversion) and at the depth of 25 Mm (estimate obtained from integrating Eq. (1)). At the surface frame the locations of the persistent downflows do not seem to be special except that they are mostly located at the edges of supergranules. On the other hand, at a depth of 25 Mm most of them seem to be present at locations of the negative vertical velocity or very close to it.
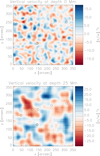 |
Fig. 7. Locations of the 13 selected downflows (open circles) on vertical velocity map at the surface (top) and at the depth of 25 Mm (bottom). The flows were averaged over 24 h on the day of 29 November 2018. |
Vertical cuts through vertical velocity generally show a complicated structure (see an example in Fig. 8). In most cases, it is not possible to track the downflows or upflows through the datacube in a depth strictly vertically. In some cases the vertical velocities create compact regions that are shifted laterally in between the consecutive depths. Merging of the downflows and separation of the upflows are visible in the cuts.
 |
Fig. 8. Example vertical cut through the 3D vertical velocity at y = 210″. |
In this study, we did not focus on a general analysis of downflows, we rather studied the 13 representatives that prevailed for a long time and were associated with the magnetic elements. The vertical cuts through these downflows are seen in Fig. 9. As one can see, in most cases the downflow seems to be present deep, in eight out of 13 cases all the way to the bottom of the domain of interest.
 |
Fig. 9. Vertical cuts through the vertical velocity around the 13 selected downflows from 29 November 2018. Around each downflow, a vicinity of 20″ was segmented and the cut was plotted in both zonal and meridional directions. |
These 13 selected persistent downflows are not the only downflows present in the field of view. By doing an automatic search we identified 183 downflows in the region of interest as the local minima of the vertical velocity which, at the same time, exhibited the negative value. From those downflows we selected the 13 strongest to represent a comparative set to the 13 persistent downflows. For each of the three sets, we computed the average vertical flow profile in the centre of the downflow. These plots are given in Fig. 10. We note that our results are only weakly influenced by the downflow changing the position in the coordinate frame, as these positional changes are rather small (about 5″). These positional changes are significantly smaller than the effective resolution of the helioseismic flow maps (about 13″ at the surface, the number increases with depth).
 |
Fig. 10. Average depth profiles of the vertical flows in downflows. The dashed line represents the average over all 183 downflows located in the field of view. The dot-dashed line is an average over the 13 strongest (at the surface) downflows in the region. The solid line then shows the plot for the 13 persistent downflows. |
There is an obvious difference between the common and the persistent downflows. The persistent downflows, on average, may have a smaller amplitude both at the surface and in the near-surface layers, but on average the flows remain negative all the way to the bottom of our inversion domain. Compared to that the average over all common downflows tends to be zero at the depth of about 8 Mm and remains negligible further down. The comparative set of the strongest downflows has a much larger magnitude peaking at the depth of about 3 Mm on average, but it reaches zeros at the depth of about 13 Mm on average and deeper down it even turns positive.
3.2. Persistent downflows in 2 h 30 min Hinode observations
As a complementary series, we analysed the 2 h 30 min series of Dopplergrams (based on Fe I at λ = 5250 Å line) and the longitudinal magnetic field. SOT/NFI on-board Hinode has a spatial resolution of 0.35″. Two examples of persistent downflows found in the datacube sequences are displayed in Fig. 11. There, in the top row, we see an average of the Doppler and |B∥| over 2 h 30 min. In the bottom row, the cuts in the (x, t) and (y, t) planes through Dopplergram and |B∥| datacubes are plotted at the centres of the two persistent downflows. Here, the persistent downflows are clearly associated with the presence of the magnetic field. The relationship between the magnetic field and the downflows (Fig. 12) is identical to that obtained with the SDO data. It is important to note that the amplitude of the magnetic field is lower in the Hinode data, which is due to the smaller field of view and a quieter region.
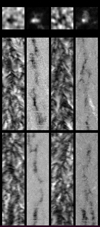 |
Fig. 11. Two persisting downflows during 2 h 30 min of Hinode observations. Top: averaged Dopplergrams and |B∥| around two different persistent downflows in a field of view of 4.4″ × 4.4″. Middle: cuts around the persistent downflows in the (y, t) plane of the Dopplergram and |B∥| datacubes. The dimensions of the arrays are (4.4″ × 2 h 30 min). Bottom: same in the (x, t) plane. |
 |
Fig. 12. Correlation between |B∥| and the Doppler velocity of the mean data 2 h 30 min of the mean Hinode data. |
4. Link between persistent downflows and potential vortex
Requerey et al. (2018) analysed a long-lived and large vortex (having a size of about 5 Mm) using high spatial (0.2″) observations from the Hinode satellite. In the literature, the terms ‘vortex’ and ‘swirl’ are both employed to identify rotating structures in the flows. A large review of the vortex (or swirls) detection is given in Murabito et al. (2020). Photospheric vortex flows are usually correlated with a network of magnetic elements at supergranular vertices (Requerey et al. 2018).
4.1. Vortex detection
Here, medium spatial resolution observations are used over a larger field of view to detect a potential vortex (or swirls). From the horizontal velocity field, we applied the vortex detection to identify ‘swirls’ as described in Giagkiozis et al. (2017), de Souze e Almeida Silva et al. (2018), Liu et al. (2019), with the two dimensionless parameters Γ1(P) and Γ2(P) at the target point P:
where vM and vP are the velocity vectors at the points M and P, S is the two dimensional region with the size N pixels surrounding the target point P, M is the point within the region S, nPM is the normal vector pointing from P to M, and × stands for the vector product (Liu et al. 2019).
Here for convenience, we use only the term vortex and the parameter Γ1 to detect the core of a vortex. More sophisticated vortex detection have been recently developed (LCS approach; see de Souze e Almeida Silva et al. 2018 or Chian et al. 2019) but our small sample allows us to control the vortex detection by eye. For an ideal vortex, Γ1(P) is maximum (value is equal to 1) at the centre of the vortex and decreases towards zero outside of it. Hence, it allows us to determine both the vortex location and the radius. Figure 13 shows the 13 persistent downflows relative to the measured Γ1 parameter computed with the 24 h mean velocity field. In that figure only a few of the 13 downflows correspond to the detected vortex (here via Γ1 > 0.5). However, a detailed inspection reveals a vorticity, at least, in six of them (46%) (downflows 1, 2, 4, 5, 8, and 13) during a portion of their lifetimes, including 9.9 h–17.3 h, 0.9 h–7.1 h, 10.9 h–18.1 h, 10.7 h–19.7 h, and 10.9 h–16.3 h, respectively. Examples of downflows number 5 and 8 are given in the figure.
 |
Fig. 13. Γ1 computed from 24 h mean velocity overlapped by horizontal velocity field. Blue and red represent counter clockwise and clockwise velocities respectively. The locations of the 13 studied persistent downflows are indicated by circles. |
Figure 14 shows the mean Doppler and |Γ1| > 0.4 parameter for the two periods of time relative to the beginning of the sequence: 11.4 h–15.2 h and 15.4 h–19.7 h of downflow number 5. The temporal evolution of the flows indicates, very close to the downdraft, a direction change in the vortex rotation. Therefore, the vortex direction seems to be very sensitive to the evolution of local large-amplitude flows and can be reversed as in our example. Another vortex is presented in Fig. 15, where we observe a clear link between |Γ1| > 0.23 and persistent downflow number 8. One important point is that we never detect a vortex before the appearance of the magnetic field in the downflow, when it is possible to observe that in a few cases. We do not know if this is due to the 1″ of spatial resolution and 45 s temporal step.
 |
Fig. 14. Top: mean Doppler downflow number 5 from time 11.4 h to time 15.2 h (left) and from time 15.2 h to 19.7 h (right) relative to the beginning of the sequence, overlapped with the mean horizontal velocities. Bottom: vorticity characterised by the |Γ1| > 0.4 parameter (downflow number 5) from time 11.4 h to 15.2 h (left) and from time 15.2 h to 19.7 h (right), overlapped with the mean horizontal velocities. White and black represent counter-clockwise Γ1 and clockwise velocities, respectively. |
 |
Fig. 15. Left: mean Doppler downflow number 8 between time 5 h and 10.7 h overlapped with the mean horizontal velocities. Right: vorticity characterised by the |Γ1| > 0.5 parameter (downflow 8). White and black represent counter-clockwise Γ1 and clockwise velocities, respectively. |
4.2. Requerey’s vortex and long-lived downflows
To validate our vortex detection via the parameters Γ1 and Γ2, we used the SDO observation used in the analysis of Requerey et al. (2018), de Souze e Almeida Silva et al. (2018), Chian et al. (2019). Luckily, SDO observations started just before Requerey’s observations were made with the Hinode satellite. We remind the readers that Requerey et al. (2018), de Souze e Almeida Silva et al. (2018), Chian et al. (2019) observed and analysed a nice long-lasting vortex. The advantage of the SDO observations is the access to various kinds of context observations, on the same day, to a larger field of view. Despite the spatial resolution of SDO being lower than that of Hinode, we detected the vortex described in Requerey et al. (2018) without any problem. The locations of Γ1, vortex detection overlapped by a horizontal velocity field are plotted in Fig. 16. The Requerey’s vortex is well detected by the gamma-method and is clearly visible in the plotted horizontal velocities (at the coordinates (62″ × 49″). Figure 17 shows the mean Doppler overlapped by horizontal velocity field and the location of the Γ1 corresponding to downflows around the supergranule.
 |
Fig. 16. Γ1 ‘vortex’ (in circles) overlapped by horizontal velocity field. |
 |
Fig. 17. Mean Dopplergram overlapped by horizontal velocity field and the location of the Γ1 ‘vortex’ (in circles). |
In our observations, five larger-amplitude regions in the Γ1 parameter are seen in total (see Figs. 16 and 17) and only one of them corresponds to the vortex studied by Requerey. The others have vorticity but also a non-negligible shear component which contributes to the final amplitude of Γ1 and hence does not allow for one to call them a vortex. However, Chian et al. (2019, 2020) with higher spatial resolution, reported on the same field of view, more persistent objective vortices with shorter lifetimes corresponding to the gap regions of ‘Lagrangian chaotic saddles’.
In the larger field of view, the horizontal velocity module (Fig. 18) shows, in the central part, the roundish supergranule corresponding to the supergranule shown in Fig. 16, where Requerey’s vortex is observed. This supergranule is a particularly symmetrical, well-formed supergranule with large amplitude horizontal outflows. The large horizontal velocity amplitude of that supergranule and the combination of the velocities from the large supergranules on its right location on the eastern edge, produce the large Requerey’s vortex. The temporal and spatial coincidence is probably the reason for producing this large and long-lasting vortex. The other large amplitude downflows around this supergranule do not show identical properties (see Fig. 19).
 |
Fig. 18. Requerey’s vortex in a large field of view of the module of the mean horizontal velocities (24 h mean). |
 |
Fig. 19. Persisting downflows during 24 h. (y, t) cuts through the Dopplergram (left) and B∥ (right). Requerey’s vortex corresponds to the long-lasting downflow and B∥ is located around y ≈ 120″. |
Helioseismic inversion allows us to study the general properties of the large Requerey’s vortex in depth. In the map of the inverted component, nothing extraordinary is seen at the location of this vortex, likely because the spatial resolution of the flow maps is again coarser than the extent of the vortex. The plot of the vertical profile of the vertical velocity, on the other hand, clearly shows that the downflow extends deep into depth of 20 Mm and more (see Fig. 20). The plotted profile is similar to the profile of the strongest downflows recorded in the studied field of view on 29 November 2018 (compare to the dash-dotted line in Fig. 10).
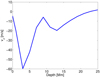 |
Fig. 20. Depth profile of the 24 h averaged vertical velocity in the middle of Requerey’s vortex. |
In the maps of the vertical vorticity computed from the horizontal flow components as
Requerey’s vortex is clearly visible. The depth profile of Ωz shows that the vorticity keeps its integrity to the depth of about 5 Mm (see Fig. 21), where it seems to start to oscillate around zero and vanishes at the depth of about 11 Mm. We do not think that the peak at the depth of 9 Mm that is visible in both vertical velocity and vertical vorticity profiles is particularly real. The formal uncertainty of the vertical velocity at this depth is about 10 m s−1 and that of the vertical velocity vorticity about 10−5 s−1, which corresponds to the magnitude of these ‘peaks’. The comparison of Requerey’s vortex and the downflows in the field of view on 29 November 2018 indicates that the long-living vortex is linked to strong downflows.
 |
Fig. 21. Depth profile of the vertical component of the flow field vorticity in the middle of Requerey’s vortex. |
5. Simulation link between magnetic field and persistent downflows
We used two different datasets based on the 3D MHD numerical simulation. These runs apply to the purely quiet Sun (Stein & Nordlund 1998).
The first dataset provides the velocity vector v(x, y, t) and the magnetic field vector B(x, y, t) over the solar surface (z = 0) for 27 h (spatial resolution: 96 km pixel−1; temporal resolution: 60 s; field of view (FOV): 96 Mm × 96 Mm). The corresponding resolution is 0.13″ on the Sun, as the computational pixel size is 48 km, which is much better than observations. We used the vx, vy, vz as well as Bz quantities. The z axis is positive above the surface. The second dataset, which is much shorter, gives only the vertical velocity vz(x, y, z, t) during 4 h from the surface (z = 0) to z = −20 Mm, with the same horizontal FOV and time step as the first dataset.
In order to eliminate 5 min oscillations, the vertical velocity field vz was filtered in the k − ω diagram low frequencies such that ω < ck were kept and other frequencies were eliminated (c = 6 km s−1). Then, we averaged velocities and magnetic fields over time intervals 12 and 24 h for the first sequence close to the supergranulation lifetime and 4 h for the second sequence in order to keep only long-lasting features.
Figure 22 displays 12 h averages (first dataset) of the vertical magnetic field Bz and the divergence of the horizontal velocities vh = (vx, vy). The long-duration downflows (red points) are spatially much more concentrated and also much more numerous than in observations. They occur almost everywhere, even in non-magnetic areas. Such points are systematically characterised by ∇h ⋅ vh < 0 (converging flows) with the mean value of −1.8 × 10−3 s−1. The second dataset shows that these points are also characterised by dvz/dz > 0 at z = 0, which means that the amplitude of vz decreases with height in these points at the surface. The mean value is 1.9 × 10−3 s−1, so that we are close to ∇ ⋅ v = 0 at the surface. Therefore, the fluid exhibits an uncompressible behaviour in this layer.
 |
Fig. 22. Bz, ∇h ⋅ vh, ∇vz at the surface (FOV 96 × 96 Mm2). Long-lasting downward velocities are displayed as red points using the threshold of −0.25 km s−1. Left: Bz (grey levels), averaged over 12 h. Middle: ∇h ⋅ vh averaged over 12 h. Bright and dark correspond to diverging and converging flows, respectively. Right: dvz/dz averaged over 4 h. Bright and dark correspond to upward and downward vertical gradient, respectively. |
Figure 23 shows two typical cross sections of the vertical flows based on the second dataset, averaged over 4 h. Some downflows extend from the surface down to z = −13 Mm. However, most downflows are not deeper than z = −4 Mm. We also point out that the continuous downflow regions do not extend purely vertically to a certain depth, but they depict a lateral displacement between the depths. This behaviour is very similar to what we found in the helioseismic inversions (cf. Fig. 8).
 |
Fig. 23. Cross sections of the vertical velocity vz (in x × z and y × z planes) at pixel (x = 171 Mm, y = 452 Mm) indicated by the vertical lines, where a typical downflow occurs. The surface is at z = 0 Mm. Bright and dark correspond to upflows and downflows, respectively. |
We conclude that the numerical simulation predicts the existence of spatially concentrated lasting downflows in the quiet Sun with a typical size of about 0.25″. However, the spatial resolution of observations used in this paper does not allow us to confirm simulation results. In the simulations, we did not find evidence of a vortex comparable in size to the observed vortex on the surface of the Sun.
6. Results and conclusion
The properties of solar plasma below the surface is mostly inferred from the observations of solar surface oscillations. The formation of vigorous downflowing plumes and the collective interaction of these (Rast 2003; Cossette & Rast 2016) also provides the opportunity, combined with local helioseismology, to probe the first megameters of the solar interior. Lot of observations of vortices (vortex) associated with downflows are described in the literature (Attie et al. 2009, 2016; Duvall & Birch 2010; Bonet et al. 2010; Vargas Domínguez et al. 2011, 2015; Requerey et al. 2017, 2018), generally studied on short sequences. Three of them are observed on long temporal sequences from 4 h to 24 h (Attie et al. 2009, 2016; Duvall & Birch 2010; Requerey et al. 2018). Taking advantage of the long temporal and homogeneous SDO/HMI observations (24 h here) of the Dopplergrams and magnetograms, we investigate the properties of the downflows, particularly the long-lasting one called persistent downflows here, and their links to a concentrated magnetic field and finally the link with the corona observations (AIA 193 Å).
In the 3D data cube (x, y, t) of the 24 h Doppler sequence (29 November 2018), at the disc centre, we detect 13 persistent downflows giving a rate of occurrence of 2 × 10−4 cases per Mm2 and 24 h. This rate is lower than those found by Requerey et al. (2017) during sequences of 32.0 and 22.7 min of 6.7 × 10−2 per Mm2 which was found with higher spatial resolution but on shorter time sequences. The lifetimes of our 13 persistent downflows were found between 3.5 h to and 20 h with a sizes between 2 and 3″ and speeds between −0.25 and −0.72 km s−1. They are well located at the junction of several supergranules as observed by Attie et al. (2009, 2016), Chian et al. (2019, 2020). In our examples, only 46% of the persistent downflows were connected with an observed vortex, but not all the time and not for all the studied downflows. At higher spatial resolution (Chian et al. 2019, 2020), more persistent objective vortices were found with shorter lifetimes corresponding to the gap regions of ‘Lagrangian chaotic saddles’.
All the studied persistent downflows are always associated with a magnetic field (up to 600 Gauss). No significant downflows were observed before the appearance of the magnetic field as described in Vargas Domínguez et al. (2015). The advantage of their higher spatial resolution (0.15″) probably allows them to detect downflows before the magnetic field appearance and follow the enhancement of this magnetic field by the strong downflows. The detection of the vortex described by Requerey et al. (2018) with our SDO/HMI data gives confidence in our method of vortex detection. This very beautiful vortex, with our large field of view, seems to be the result of the composition of the larger-scale horizontal flows where the combination of the flow phases, temporal and spatial, creates it.
We observe that this downflow is always associated with the presence of the magnetic field. The helioseismic inversion allows us to describe the persistent downflow properties in depth below the solar surface and, for instance, to compare the properties of the persistent downflows to the other (non-persistent) in the field of view. Persistent downflows seem to penetrate deeper, whereas the common downflows seem to reach zero vertical velocity already at the depth of around 7 Mm. The persistent downflows remain slightly negative on average all the way to the bottom of our region of interest, which is 25 Mm.
In the high spatial resolution MHD simulation (0.13″), long-duration downflows (4 h and 12 h) are spatially much smaller and numerous than in observations where the resolution lies around 2 to 3″. We did not find evidence of a vortex comparable in size to observations. The spatial resolution of observations does not allow us to see small scale downflows, so that observations with more precise satellites (as the PHI on-board Solar Orbiter) or ground-based large telescopes are required.
From the space-borne SDO instruments, downflow evolution is studied at different wavelengths. We observe a persistent downflow to be correlated with the coronal-loop anchor in the photosphere, indicating a link between downflows and the coronal activity. This observation is to be compared with the observed EUV cyclones over the quiet Sun, anchored in the rotating magnetic field network magnetic fields, suggesting an effective way to heat the corona Zhang & Liu (2011). The link between the flow evolution at the junctions of supergranular cells, giving mini-coronal-mass ejection and X-ray network flares, is described in Innes et al. (2009), Attie et al. (2016). Hence, the persistent downflows must be investigated with a greater number of time sequences. In the same way, more studies have to be performed on the link between persistent downflows and the coronal phenomena to confirm the link between them and describe the temporal dynamic behaviour of such structures.
The new non-linear methods (Lagrangian Coherent Structure and Lagrangian Chaotic Saddles) developed recently by Chian et al. (2019, 2020), applied to the full Sun SDO/HMI observations, is probably the best way for future research in this domain to access to large-events statistics.
Acknowledgments
This work was granted access to the HPC resources of CALMIP under the allocation 2011-[P1115]. Thanks to SDO/HMI, IRIS, and Hinode/SOT teams. MŠ and DK were supported by the Czech Science Foundation under the grant project 18-06319S.
References
- Attie, R., Innes, D. E., & Potts, H. E. 2009, A&A, 493, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Attie, R., Innes, D. E., Solanki, S. K., & Glassmeier, K. H. 2016, A&A, 596, A15 [CrossRef] [EDP Sciences] [Google Scholar]
- Belkacem, K., Samadi, R., Goupil, M. J., & Kupka, F. 2006, A&A, 460, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bello González, N., Yelles Chaouche, L., Okunev, O., & Kneer, F. 2009, A&A, 494, 1091 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berger, T. E., Rouppe van der Voort, L. H. M., Löfdahl, M. G., et al. 2004, A&A, 428, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonet, J. A., Márquez, I., Sánchez Almeida, J., Cabello, I., & Domingo, V. 2008, ApJ, 687, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Bonet, J. A., Márquez, I., Sánchez Almeida, J., et al. 2010, ApJ, 723, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Chian, A. C.-L., Silva, S. S. A., Rempel, E. L., et al. 2019, MNRAS, 488, 3076 [Google Scholar]
- Chian, A. C.-L., Silva, S. S. A., Rempel, E. L., et al. 2020, Phys. Rev. E, 102, 060201 [Google Scholar]
- Cossette, J.-F., & Rast, M. P. 2016, ApJ, 829, L17 [NASA ADS] [CrossRef] [Google Scholar]
- de Souze e Almeida Silva, S., Rempel, E. L., Pinheiro Gomes, T. F., Requerey, I. S., & Chian, A. C. L. 2018, ApJ, 863, L2 [Google Scholar]
- Duvall, T. L., Jr., & Birch, A. C. 2010, ApJ, 725, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Duvall, T. L., Jr., Jefferies, S. M., Harvey, J. W., & Pomerantz, M. A. 1993, Nature, 362, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Giagkiozis, I., Fedun, V., Scullion, E., & Verth, G. 2017, ArXiv e-prints [arXiv:1706.05428] [Google Scholar]
- Gizon, L., & Birch, A. C. 2004, ApJ, 614, 472 [Google Scholar]
- Greer, B. J., Hindman, B. W., & Toomre, J. 2016, ApJ, 824, 128 [Google Scholar]
- Hanasoge, S. M., & Sreenivasan, K. R. 2014, Sol. Phys., 289, 3403 [Google Scholar]
- Hotta, H., Iijima, H., & Kusano, K. 2019, Sci. Adv., 5, 2307 [Google Scholar]
- Innes, D. E., Genetelli, A., Attie, R., & Potts, H. E. 2009, A&A, 495, 319 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jackiewicz, J., Birch, A. C., Gizon, L., et al. 2012, Sol. Phys., 276, 19 [Google Scholar]
- Korda, D., & Švanda, M. 2019, A&A, 622, A163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3 [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [Google Scholar]
- Liu, J., Nelson, C. J., & Erdélyi, R. 2019, ApJ, 872, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Murabito, M., Shetye, J., Stangalini, M., et al. 2020, A&A, 639, A59 [EDP Sciences] [Google Scholar]
- Narayan, G. 2011, A&A, 529, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelson, N. J., Featherstone, N. A., Miesch, M. S., & Toomre, J. 2018, ApJ, 859, 117 [NASA ADS] [CrossRef] [Google Scholar]
- November, L. 1986, J. Appl. Opt., 25, 392 [Google Scholar]
- Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [Google Scholar]
- Rast, M. 1995, ApJ, 443, 863 [NASA ADS] [CrossRef] [Google Scholar]
- Rast, M. P. 1999, ApJ, 524, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Rast, M. P. 2003, ApJ, 597, 1200 [NASA ADS] [CrossRef] [Google Scholar]
- Requerey, I. S., Del Toro Iniesta, J. C., Bellot Rubio, L. R., et al. 2017, ApJS, 229, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Requerey, I. S., Cobo, B. R., Gošić, M., & Bellot Rubio, L. R. 2018, A&A, 610, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieutord, M., & Zahn, J. P. 1995, A&A, 296, 127 [Google Scholar]
- Rincon, F., & Rieutord, M. 2018, Liv. Rev. Sol. Phys., 15, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Roudier, T., Malherbe, J. M., Gelly, B., et al. 2020, A&A, 641, A50 [EDP Sciences] [Google Scholar]
- Scherrer, P. H., Bogart, R. S., Bush, R. I., et al. 1995, Sol. Phys., 162, 129 [Google Scholar]
- Schou, J., Scherrer, P. H., Bush, R. I., et al. 2012, Sol. Phys., 275, 229 [Google Scholar]
- Skartlien, R., & Rast, M. P. 2000, ApJ, 535, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Skartlien, R., Stein, R. F., & Nordlund, Å. 2000, ApJ, 541, 468 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, R. F., & Nordlund, Å. 1989, ApJ, 342, L95 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stein, R. F., & Nordlund, Å. 1998, ApJ, 499, 914 [Google Scholar]
- Stein, R. F., Nordlund, {\AA}., Georgoviani, D., Benson, D., & Schaffenberger, W. 2009, in Solar-Stellar Dynamos as Revealed by Helio- and Asteroseismology: GONG 2008/SOHO 21, eds. M. Dikpati, T. Arentoft, I. González Hernández, C. Lindsey, & F. Hill, ASP Conf. Ser., 416, 421 [Google Scholar]
- Švanda, M., Gizon, L., Hanasoge, S. M., & Ustyugov, S. D. 2011, A&A, 530, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Švanda, M., Roudier, T., Rieutord, M., Burston, R., & Gizon, L. 2013, ApJ, 771, 32 [Google Scholar]
- Tsuneta, S., Ichimoto, K., Katsukawa, Y., et al. 2008, Sol. Phys., 249, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Vargas Domínguez, S., Palacios, J., Balmaceda, L., Cabello, I., & Domingo, V. 2011, MNRAS, 416, 148 [NASA ADS] [Google Scholar]
- Vargas Domínguez, S., Palacios, J., Balmaceda, L., Cabello, I., & Domingo, V. 2015, Sol. Phys., 290, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, J., & Liu, Y. 2011, ApJ, 741, L7 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Region of interest on the 29 November 2018 datacube. The region was localised at the disc centre; the field of view has dimensions of 353″ × 353″. Left: 5 h mean of the HMI Dopplergrams, where black areas are considered as persistent downflows. Middle: 5 h mean of the line-of-sight magnetic induction |B∥|. Right: 5 h mean of AIA 193 Å filtergrams. |
| In the text | |
 |
Fig. 2. Details of Fig. 1 around one of the persistent downflows, with a field of view of 59.5″ × 73.5″. Left: mean Doppler velocity. Middle: mean |B∥|. Right: mean AIA 193 Å filtergram. |
| In the text | |
 |
Fig. 3. Coalignment of panels from Fig. 2. Background: mean AIA 193 Å filtergram. Blue contours: mean |B∥| level = 120 Gauss. Red contours: mean Doppler velocity level = −0.2 km s−1. Red and blue contours largely overlap. |
| In the text | |
 |
Fig. 4. Top left: 24 h divergence field measured with the LCT applied to Dopplergrams. The supergranule boundaries detected by the watershed method are shown as white network. The circles represent the location of the 13 studied a persistent downflows. These persistent downflows are located in convergent flows and more particularly where several supergranules meet. Top right: 24 h mean Doppler map overlapped with the 13 studied persistent downflows (circles) and supergranule boundaries. Downflows are visible as dark structures in each circle. Far from the disc centre, in the lower right part of the figure, some large darker regions are visible. These are caused by the horizontal velocities which become a dominant contribution due to the projection effects. Bottom left: corks position (grey points) after 24 h diffusion by horizontal flows. Their locations are, in accordance with supergranule boundaries, found by the watershed method (superimposed white network). Bottom right: 24 h mean magnetic field and the location of the 13 studied persistent downflows (circles). |
| In the text | |
 |
Fig. 5. Doppler (top) and magnetic (bottom) temporal cuts centred on the 13 selected persistent downflows. The time (vertical axis) stands for 24 h, the spatial axis (y cut, horizontal) is 15″ for each column and the numbers indicate the labels of the selected downflows corresponding to the bottom right of Fig. 4. The persistent downflows move across the surface but are visible in the cuts at least from 3.5 h to 20 h. |
| In the text | |
 |
Fig. 6. Scatter plot of the dependence of Doppler velocity and |B∥| obtained for the SDO data on 29 November 2018. |
| In the text | |
 |
Fig. 7. Locations of the 13 selected downflows (open circles) on vertical velocity map at the surface (top) and at the depth of 25 Mm (bottom). The flows were averaged over 24 h on the day of 29 November 2018. |
| In the text | |
 |
Fig. 8. Example vertical cut through the 3D vertical velocity at y = 210″. |
| In the text | |
 |
Fig. 9. Vertical cuts through the vertical velocity around the 13 selected downflows from 29 November 2018. Around each downflow, a vicinity of 20″ was segmented and the cut was plotted in both zonal and meridional directions. |
| In the text | |
 |
Fig. 10. Average depth profiles of the vertical flows in downflows. The dashed line represents the average over all 183 downflows located in the field of view. The dot-dashed line is an average over the 13 strongest (at the surface) downflows in the region. The solid line then shows the plot for the 13 persistent downflows. |
| In the text | |
 |
Fig. 11. Two persisting downflows during 2 h 30 min of Hinode observations. Top: averaged Dopplergrams and |B∥| around two different persistent downflows in a field of view of 4.4″ × 4.4″. Middle: cuts around the persistent downflows in the (y, t) plane of the Dopplergram and |B∥| datacubes. The dimensions of the arrays are (4.4″ × 2 h 30 min). Bottom: same in the (x, t) plane. |
| In the text | |
 |
Fig. 12. Correlation between |B∥| and the Doppler velocity of the mean data 2 h 30 min of the mean Hinode data. |
| In the text | |
 |
Fig. 13. Γ1 computed from 24 h mean velocity overlapped by horizontal velocity field. Blue and red represent counter clockwise and clockwise velocities respectively. The locations of the 13 studied persistent downflows are indicated by circles. |
| In the text | |
 |
Fig. 14. Top: mean Doppler downflow number 5 from time 11.4 h to time 15.2 h (left) and from time 15.2 h to 19.7 h (right) relative to the beginning of the sequence, overlapped with the mean horizontal velocities. Bottom: vorticity characterised by the |Γ1| > 0.4 parameter (downflow number 5) from time 11.4 h to 15.2 h (left) and from time 15.2 h to 19.7 h (right), overlapped with the mean horizontal velocities. White and black represent counter-clockwise Γ1 and clockwise velocities, respectively. |
| In the text | |
 |
Fig. 15. Left: mean Doppler downflow number 8 between time 5 h and 10.7 h overlapped with the mean horizontal velocities. Right: vorticity characterised by the |Γ1| > 0.5 parameter (downflow 8). White and black represent counter-clockwise Γ1 and clockwise velocities, respectively. |
| In the text | |
 |
Fig. 16. Γ1 ‘vortex’ (in circles) overlapped by horizontal velocity field. |
| In the text | |
 |
Fig. 17. Mean Dopplergram overlapped by horizontal velocity field and the location of the Γ1 ‘vortex’ (in circles). |
| In the text | |
 |
Fig. 18. Requerey’s vortex in a large field of view of the module of the mean horizontal velocities (24 h mean). |
| In the text | |
 |
Fig. 19. Persisting downflows during 24 h. (y, t) cuts through the Dopplergram (left) and B∥ (right). Requerey’s vortex corresponds to the long-lasting downflow and B∥ is located around y ≈ 120″. |
| In the text | |
 |
Fig. 20. Depth profile of the 24 h averaged vertical velocity in the middle of Requerey’s vortex. |
| In the text | |
 |
Fig. 21. Depth profile of the vertical component of the flow field vorticity in the middle of Requerey’s vortex. |
| In the text | |
 |
Fig. 22. Bz, ∇h ⋅ vh, ∇vz at the surface (FOV 96 × 96 Mm2). Long-lasting downward velocities are displayed as red points using the threshold of −0.25 km s−1. Left: Bz (grey levels), averaged over 12 h. Middle: ∇h ⋅ vh averaged over 12 h. Bright and dark correspond to diverging and converging flows, respectively. Right: dvz/dz averaged over 4 h. Bright and dark correspond to upward and downward vertical gradient, respectively. |
| In the text | |
 |
Fig. 23. Cross sections of the vertical velocity vz (in x × z and y × z planes) at pixel (x = 171 Mm, y = 452 Mm) indicated by the vertical lines, where a typical downflow occurs. The surface is at z = 0 Mm. Bright and dark correspond to upflows and downflows, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} { v}_z (\boldsymbol{r}_0, z_0) = \frac{-1}{\rho (z_0)} \int \limits _0^{z_0} \mathrm{d}z\,\boldsymbol{\nabla }_{\rm h} \cdot [\rho (z)\,\boldsymbol{v}_{\rm h} (\boldsymbol{r}_0, z)], \end{aligned} $$](/articles/aa/full_html/2021/03/aa40172-20/aa40172-20-eq1.gif)