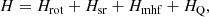| Issue |
A&A
Volume 646, February 2021
|
|
|---|---|---|
| Article Number | L1 | |
| Number of page(s) | 11 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202040210 | |
| Published online | 29 January 2021 | |
Letter to the Editor
Space and laboratory observation of the deuterated cyanomethyl radical HDCCN⋆,⋆⋆
1
Grupo de Astrofísica Molecular, Instituto de Física Fundamental (IFF-CSIC), C/ Serrano 121, 28006 Madrid, Spain
e-mail: carlos.cabezas@csic.es; jose.cernicharo@csic.es
2
Department of Applied Chemistry, Science Building II, National Chiao Tung University, 1001 Ta-Hsueh Rd., Hsinchu 30010, Taiwan
3
LERMA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités, 92190 Meudon, France
4
Observatorio Astronómico Nacional (IGN), C/ Alfonso XII, 3, 28014 Madrid, Spain
5
Centro de Desarrollos Tecnológicos, Observatorio de Yebes (IGN), 19141 Yebes, Guadalajara, Spain
Received:
22
December
2020
Accepted:
10
January
2021
Our observations of TMC-1 with the Yebes 40 m radio telescope in the 31.0–50.3 GHz range allowed us to detect a group of unidentified lines, showing a complex line pattern indicative of an open-shell species. The observed frequencies of these lines and the similarity of the spectral pattern with that of the 20, 2–10, 1 rotational transition of H2CCN indicate that the lines arise from the deuterated cyanomethyl radical, HDCCN. Using Fourier transform microwave spectroscopy experiments combined with electric discharges, we succeeded in producing the radical HDCCN in the laboratory and observed its 10, 1–00, 0 and 20, 2–10, 1 rotational transitions. From our observations and assuming a rotational temperature of 5 K, we derive an abundance ratio H2CCN/HDCCN = 20 ± 4. The high abundance of the deuterated form of H2CCN is well accounted for by a standard gas-phase model, in which deuteration is driven by deuteron transfer from the H2D+ molecular ion.
Key words: astrochemistry / ISM: molecules / ISM: individual objects: TMC-1 / line: identification / molecular data
Data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/646/L1
Based on observations carried out with the Yebes 40 m telescope (projects 19A003, 20A014, and 20D15) and the Institut de Radioastronomie Millimétrique (IRAM) 30 m telescope. The 40 m radiotelescope at Yebes Observatory is operated by the Spanish Geographic Institute (IGN, Ministerio de Transportes, Movilidad y Agenda Urbana).
© ESO 2021
1. Introduction
Recent developments of radio astronomical equipments allow for very sensitive line surveys of molecular sources, where weak lines arising from low-abundance species can be detected. These surveys are the best tool to map out the molecular makeup of astronomical sources by identifying new chemical species. Discovering spectral features of new molecules initially requires a detailed analysis of the spectral contribution of the already identified species, including their isotopologs and vibrationally excited states. In this manner, once all the lines coming from known species are assigned, unidentified lines emerge and open the opportunity to discover new molecules and to deepen in our understanding of the chemical complexity of molecular clouds.
Deuterated molecules show remarkably high D/H abundance ratios (Ceccarelli et al. 2007) even though the deuterium abundance in space is 1.5 × 10−5 relative to hydrogen (Linsky 2003). Hence, deuterated species of abundant interstellar molecules can also contribute to the spectral richness of line surveys. This fact makes the astronomical identification of these deuterated species of utmost importance, not only to gain knowledge about unidentified lines in the lines surveys but also to understand how the deuterium fractionation works and ultimately to constrain molecular formation pathways.
Cyanomethyl radical, H2CCN, has been detected in the cold dark cloud TMC-1 (Saito et al. 1988; Irvine et al. 1988), where its abundance is relatively high. Hence, the deuterated isotopologs of H2CCN are good candidates to be observed in this source. As has been shown previously, a new high sensitivity line survey on TMC-1 has allowed the identification of several transient species such as the anions C3N− and C5N− (Cernicharo et al. 2020a) and the protonated molecules HC5NH+(Marcelino et al. 2020), HC3O+ (Cernicharo et al. 2020b), CH3CO+ (Cernicharo et al. 2021a), and HC3S+ (Cernicharo et al. 2021b).
In this Letter, we report the identification of spectral lines of the deuterated species HDCCN in TMC-1 based on ab initio calculations and accurate line frequencies from laboratory experiments. Column densities for H2CCN and HDCCN species are derived from our observations and the most updated chemical models are used to diagnose the deuterium fractionation ratios for the most abundant molecules in TMC-1.
2. Observations
The observations of TMC-1 (αJ2000 = 4h41m41.9s and 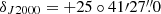 ) on the Q band presented in this work were performed in several sessions between November 2019 and October 2020. They were carried out using a set of new receivers, which were built within the Nanocosmos project1 and installed at the Yebes 40 m radio telescope (hereafter, Yebes 40 m).
) on the Q band presented in this work were performed in several sessions between November 2019 and October 2020. They were carried out using a set of new receivers, which were built within the Nanocosmos project1 and installed at the Yebes 40 m radio telescope (hereafter, Yebes 40 m).
The Q band receiver consists of two HEMT cold amplifiers covering the 31.0–50.3 GHz band with horizontal and vertical polarizations. The temperatures of the receiver vary from 22 K at 32 GHz to 42 K at 50 GHz. The spectrometers formed by 2 × 8 × 2.5 GHz FFTs provide a spectral resolution of 38.1 kHz and cover the whole Q band in both polarizations.
We observed different frequency coverages of 31.08–49.52 GHz and 31.98–50.42 GHz. This permitted us to check for spurious ghosts produced in the down-conversion chain, in which the signal coming from the receiver was down-converted to 1–19.5 GHz and then split into eight bands with a coverage of 2.5 GHz, each of which were analyzed by the FFTs. Frequency switching with a frequency throw of 10 MHz or 8 MHz was chosen as the observing procedure. The nominal spectral resolution of 38.1 kHz was left unchanged for the final spectra. The sensitivity, σ, was derived by removing a polynomial baseline in velocity windows of 24 km s−1 wide, centered on each observed line, and varied along the Q band between ∼0.4 mK (31 GHz), ∼1.0 mK (43 GHz), and ∼2.5 mK (50 GHz).
The intensity scale, antenna temperature (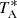 ) used in this work was calibrated using two absorbers at different temperatures and the atmospheric transmission model ATM (Cernicharo 1985; Pardo et al. 2001). Calibration uncertainties were adopted to be 10% based on the observed repeatability of the line intensities between different observing runs. All data were analyzed using the GILDAS package2.
) used in this work was calibrated using two absorbers at different temperatures and the atmospheric transmission model ATM (Cernicharo 1985; Pardo et al. 2001). Calibration uncertainties were adopted to be 10% based on the observed repeatability of the line intensities between different observing runs. All data were analyzed using the GILDAS package2.
3. Results
3.1. TMC-1 observations
Among the unidentified lines of the line survey carried out by our group toward TMC-1 using the Yebes 40 m radio telescope, we found a group of lines with a spectral pattern reminiscent of that produced by a radical with a complex hyperfine structure (see Fig. 1a). The pattern is very similar to the 20, 2–10, 1 rotational transition of H2CCN (see Fig. 1b), which lies at a slightly higher frequency. These facts suggest that the group of unidentified lines could arise from the deuterated species of cyanomethyl radical. In order to check this hypothesis we performed ab initio calculations (see Appendix A) for HDCCN using the spectroscopic available information on H2CCN (Saito & Yamamoto 1997; Ozeki et al. 2004) to scale the spectroscopic parameters calculated. The frequency of the 20, 2–10, 1 transition of HDCCN was predicted in the same frequency region where the group of unidentified lines appear. The hyperfine structure of this transition of HDCCN is slightly different from that of H2CCN resulting from the replacement of a hydrogen nucleus by a deuteron. Motivated by the good agreement between calculated and observed frequency and spectral pattern, we performed additional ab initio calculations and laboratory experiments to assign the complicated hyperfine structure of the rotational spectrum of HDCCN (see Sect. 3.2 and Appendix A). These experiments fully confirm that the carrier of the lines shown in Fig. 1a is HDCCN.
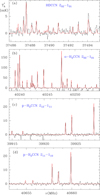 |
Fig. 1. (a) Observed group of lines assigned to the hyperfine structure of the 20, 2–10, 1 transition of HDCCN (black histogram). (b) The observed hyperfine structure of the same transition of o-H2CCN. (c) Selected hyperfine components of the 212–111 transition of p-H2CCN. (d) Selected hyperfine components of the 211–110 transition of p-H2CCN. In all panels, the abscissa represents the rest frequency (in MHz) assuming a local standard of rest velocity for the source of 5.83 km s−1 (Cernicharo et al. 2020c). The ordinate is the antenna temperature in mK. The red curve in each panel represents the best model fit to the emission of this species in TMC-1 for a rotational temperature of 10 K. A similar fit is obtained for other rotational temperatures (see Sect. 4.1 and Table 2). Negative features are due to the folding of the frequency-switching data. |
3.2. Laboratory measurements
The HDCCN radical was produced in a supersonic jet by a pulsed electric discharge of a gas mixture of CH3CN (0.2%) and D2 ( 5%) diluted in Ar. The gas mixture was expanded into a Fabry-Perot cavity of a Fourier transform microwave (FTMW) spectrometer (Endo et al. 1994; Cabezas et al. 2016) with a backing pressure at 2 atm. Synchronized to the gas expansion, a pulse voltage of 1.0 kV with a duration of 450 μs was applied between stainless steel electrodes attached to the exit of the pulsed discharge nozzle (PDN). For measurements of the paramagnetic lines, the Earth’s magnetic field was canceled using three sets of Helmholtz coils placed perpendicularly to one another. Since the PDN is arranged parallel to the cavity of the spectrometer, it is possible to resolve small hyperfine splittings by suppressing the Doppler broadening of spectral lines.
The NKa,Kc = 10, 1–00, 0 pure rotational transition was observed by FTMW spectroscopy while the NKa,Kc = 20, 2–10, 1 transition was measured utilizing a MW-MW double-resonance (DR) technique (Sumiyoshi et al. 2005). In DR measurements, the signal of a known rotational transition is monitored with ordinary FTMW spectroscopy and when the pump radiation is resonant to a transition, connecting the upper or lower level of the monitored microwave transition, a DR spectrum is observed as a change of the intensity of the monitored microwave signal. First, a spectral scan of 100 MHz was done around the predicted frequency region for the NKa,Kc = 10, 1–00, 0 pure rotational transition to observe all the expected hyperfine components. The recorded spectrum for NKa,Kc = 10, 1–00, 0 transition is shown in Fig. 2, where a total of 66 hyperfine components were observed. Other 63 hyperfine components for the NKa,Kc = 20, 2–10, 1 rotational transition could be measured using the DR technique. Hence, a total of 129 hyperfine components (see Appendix B and Table B.1) were analyzed using a Hamiltonian with the following form:
 |
Fig. 2. Section of 10 MHz of the FTMW spectrum of HDCCN showing 36 hyperfine components of the NKa,Kc= 10, 1–00, 0 pure rotational transition. The spectrum was achieved by 100 shots of accumulation and a step scan of 0.5 MHz with a repetition rate of 10 Hz. The coaxial arrangement of the adiabatic expansion and resonator axis produces an instrumental Doppler doubling. The resonances frequencies are calculated as the average of the two Doppler components. |
where Hrot contains rotational and centrifugal distortion parameters, Hsr is the spin-rotational term, Hmhf represents the magnetic hyperfine coupling interaction term due to the nitrogen, hydrogen, and deuterium nuclei, and finally HQ represents the nuclear electric quadrupole interaction due to nitrogen and deuterium nuclei. The coupling scheme used is J = N + S, F1 = J + I(N), F2 = F1 + I(H) and F = F2 + I(D), and thus each energy level is denoted by seven quantum numbers; N, J, Ka, Kc, F1, F2, and F. The results obtained from the least-squares analysis are shown in Table 1. We floated the (B + C)/2 parameter, ΔN centrifugal constant, εbb spin-rotation coupling constant, aF and Taa magnetic hyperfine constants for nitrogen, hydrogen, and deuterium nuclei, and the χaa nuclear electric quadrupole constant for nitrogen nucleus. The A and (B − C)/2 rotational parameters, εaa and εcc spin-rotation coupling constants, and the χaa and χbb nuclear electric quadrupole constants for deuterium nucleus were kept fixed to the theoretical values calculated in this work. The rest of parameters were fixed to the values obtained by Saito & Yamamoto (1997) and Ozeki et al. (2004) for H2CCN radical. The standard deviation of the fit is 4.1 kHz.
Spectroscopic parameters for HDCCN (all in MHz).
4. Discussion
4.1. H2CCN and HDCCN column densities
The N = 2 − 1 line of H2CCN presents a very complex hyperfine structure in addition to the presence of two spin symmetry species, ortho and para. Figure 1b shows the 202–101 ortho line; the ortho species corresponds to even values of the quantum number Ka. Figures 1c and d show a selected range of hyperfine components of the NKa,Kc = 21, 2–11, 1 and 21, 1–11, 0 para lines (Ka odd). Observed line intensities for the ortho species agree very well with those reported by Kaifu et al. (2004). No lines of the para species are reported in that work, which probably results from the limited sensitivity in their spectra. However, some of their unidentified features agree in frequency with the strongest components of this species (see also Ozeki et al. 2004). The detection of all hyperfine components above 1.5 mK of the two para transitions within our line survey confirms the presence of the para species in TMC-1.
Frequency predictions for the ortho and para species of H2CCN are from the CDMS catalog (Müller et al. 2005), which were implemented in the MADEX code (Cernicharo 2012) to compute column densities for these species. Both species have to be considered separately as there are no radiative or collisional transitions between them. The lowest energy level of the para species (11, 1) is 14.1 K above the ortho ground level (000).
In our line survey we only observed one rotational transition of the ortho H2CCN (20, 2–10, 1) and two transitions for the para species (21, 2–11, 1 and 21, 1–11, 0), which involve levels with similar energies. Taking into account that collisional rates are not available for this molecule, column density determinations rely on the assumption of a rotational temperature, Tr, for the two species. Similar assumptions have been adopted in previous studies of this molecule (Irvine et al. 1988; Vastel et al. 2015). In TMC-1, the rotational temperature found for different molecules varies between 5 K and 10 K (see, e.g., Gratier et al. 2016; Cernicharo et al. 2021b, 2020c; Marcelino et al. 2020, and references therein). In particular, for H2CCN, Gratier et al. (2016) find a rotational temperature between 3 K and 5 K. We consider that the lowest value for Tr implies a large opacity for the N = 2 − 1 line of the ortho species (see Fig. 1). The ortho species of the molecule behaves, for low rotational temperatures, as a linear rotor because only levels with Ka = 0 are populated in cold clouds. The first Ka = 2 level (220) is at 55.6 K above the ground level (00, 0). The situation is similar for the para species because only levels with Ka = 1 are populated. The first Ka = 3 level (33, 0) is 110.3 K above the ground level (11, 1). Hence, the rotational partition function, Qr, for both symmetry species has a nearly linear dependence on the rotational temperature (Tr ≤ 30 K).
We computed the ortho and para column densities that best fit the observed transitions shown in Figs. 1b–d and for rotational temperatures between 5 K and 10 K. In these figures the red curve represents the synthetic model spectrum computed at Tr = 10 K. The derived total column density of H2CCN shows a very smooth variation between 5 K and 10 K. This is due to the near linear behavior of the partition function with Tr and the low energy of the involved levels. Therefore the synthetic model spectrum is practically the same for these rotational temperatures. Adopting a value for Tr = 5 K (see Appendix C), we derive N(H2CCN) = (1.48 ± 0.15) × 1013 cm−2 and an ortho/para ratio of 7.7, which is much larger than the statistical ratio of 3. It seems, hence, that the para species, which is higher in energy than the ortho, has suffered interconversion processes through the interaction with XH+ species such as 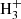 , HCO+, or H3O+. Our derived column density is in good agreement with that derived by Ozeki et al. (2004) and Gratier et al. (2016).
, HCO+, or H3O+. Our derived column density is in good agreement with that derived by Ozeki et al. (2004) and Gratier et al. (2016).
The rotational partition function shows a dependence on 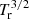 for HDCCN, and hence the column density shows a larger dependence on the assumed Tr. Table 2 gives the derived column densities of o-H2CCN, p-H2CCN, and HDCCN for rotational temperatures between 5 K and 10 K. We derive N(HDCCN) = (7.4 ± 0.7) × 1011 cm−2 and N(H2CCN)/N(HDCCN) = 20 ± 4 for Tr = 5 K. For Tr = 10 K, these values are (10.5 ± 1.1) × 1011 cm−2 and 14 ± 3, respectively. The derived XH/XD abundance ratios for H2CCN and other species are given in Table 3 (see Appendix C and Table C.1).
for HDCCN, and hence the column density shows a larger dependence on the assumed Tr. Table 2 gives the derived column densities of o-H2CCN, p-H2CCN, and HDCCN for rotational temperatures between 5 K and 10 K. We derive N(HDCCN) = (7.4 ± 0.7) × 1011 cm−2 and N(H2CCN)/N(HDCCN) = 20 ± 4 for Tr = 5 K. For Tr = 10 K, these values are (10.5 ± 1.1) × 1011 cm−2 and 14 ± 3, respectively. The derived XH/XD abundance ratios for H2CCN and other species are given in Table 3 (see Appendix C and Table C.1).
H2CCN and HDCCN column densities in TMC-1.
Deuteration enhancement in TMC-1 for selected molecules compared to our gas-phase chemical model.
The H2CCN ortho/para ratio was also derived in L1544 by Vastel et al. (2015). However, the derived values for the column density of the ortho and para species and their abundance ratio show a strong dependency on the assumed rotational temperature. The ortho/para ratio for Tr = 5 K is 0.1 and the column density for the para species is ten times higher than for the ortho species. However, for Tr = 10 K, the column density of the para species decreases by two orders of magnitude and the ortho/para ratio increases to a value of 1. We re-examined their column densities using the data shown in their Fig. 1. Considering, as we have for TMC-1, that the ortho and para spin symmetry states are two different species, we derive for this cloud N(o-H2CCN) = 4 × 1012 cm−2 and N(p-H2CCN) = 5 × 1011 cm−2. Hence, the ortho/para ratio in L1544 is ∼8, that is, very similar to that found in TMC-1. Similar results are obtained for Tr = 10 K.
4.2. Chemical models
After the surprise raised by the detection of DCN in the Orion cloud by Jefferts et al. (1973), it was very quickly suggested that the observed deuterium enrichment is the result of chemical fractionation and not of an exceptional source of deuterium through nucleosynthetic processes. The first determinant step is provided by the deuterium exchange in the 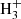 + HD ⇄ H2D+ + H2 reaction. This reaction proceeds essentially in the forward direction in the cold (T ∼ 10 K) interstellar environments, as the endothermicity of the reverse reaction is about 232 K, which results from the difference in zero point energies (ZPE) of the products and reactants. This crucial point was first mentioned by Watson (1976) and extended to the D +
+ HD ⇄ H2D+ + H2 reaction. This reaction proceeds essentially in the forward direction in the cold (T ∼ 10 K) interstellar environments, as the endothermicity of the reverse reaction is about 232 K, which results from the difference in zero point energies (ZPE) of the products and reactants. This crucial point was first mentioned by Watson (1976) and extended to the D +  ⇄ H + H2D+ reaction by Dalgarno & Lepp (1984), which proceeds essentially in the forward direction as the endothermicity of the reverse reaction is then 632 K. The H2D+ molecular ion subsequently transfers the deuteron to various stable molecules, such as CO, N2, H2O, NH3, producing DCO+, N2D+, H2DO+, NH3D+, which disassociatively recombine to produce, for example, HDO and NH2D. This scenario has been further extended to a few other stable molecular ions such as
⇄ H + H2D+ reaction by Dalgarno & Lepp (1984), which proceeds essentially in the forward direction as the endothermicity of the reverse reaction is then 632 K. The H2D+ molecular ion subsequently transfers the deuteron to various stable molecules, such as CO, N2, H2O, NH3, producing DCO+, N2D+, H2DO+, NH3D+, which disassociatively recombine to produce, for example, HDO and NH2D. This scenario has been further extended to a few other stable molecular ions such as  and C2
and C2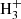 , invoking exchange reactions with HD as in
, invoking exchange reactions with HD as in  + HD ⇄ CH2D+ + H2 and C2
+ HD ⇄ CH2D+ + H2 and C2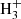 + HD ⇄ C2H2D+ + H2 (Herbst et al. 1987; Gerlich & Schlemmer 2002). The exothermicity achieved in the forward reactions are somewhat larger than that involving H2D+ (Herbst et al. 1987; Roueff et al. 2013; Nyman & Yu 2019), allowing these exchange reactions to occur in somewhat warmer environments such as clumps in the Orion Bar (Roueff et al. 2007; Parise et al. 2009). These exchange reactions can even proceed further toward doubly deuterated molecular ions like D2H+ and
+ HD ⇄ C2H2D+ + H2 (Herbst et al. 1987; Gerlich & Schlemmer 2002). The exothermicity achieved in the forward reactions are somewhat larger than that involving H2D+ (Herbst et al. 1987; Roueff et al. 2013; Nyman & Yu 2019), allowing these exchange reactions to occur in somewhat warmer environments such as clumps in the Orion Bar (Roueff et al. 2007; Parise et al. 2009). These exchange reactions can even proceed further toward doubly deuterated molecular ions like D2H+ and 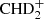 , and up to fully deuterated ions like
, and up to fully deuterated ions like  ,
, 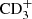 , and C2
, and C2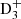 in environments with CO depleted (Walmsley et al. 2004), where the ion-molecule reactions with CO, H2O, and NH3 become negligible in comparison to the reactions with HD (see, e.g., Roberts et al. 2003; Roueff et al. 2005). Additional deuterium enhancements could result from the evaporation of the icy mantles surrounding dust grain as a remnant of cold grain chemistry. Gas-phase chemical processes are reasonably successful to interpret the observations, as reported recently by Bacmann et al. (2020) and Melosso et al. (2020) in their study of the nitrogen hydrides NHD and ND2.
in environments with CO depleted (Walmsley et al. 2004), where the ion-molecule reactions with CO, H2O, and NH3 become negligible in comparison to the reactions with HD (see, e.g., Roberts et al. 2003; Roueff et al. 2005). Additional deuterium enhancements could result from the evaporation of the icy mantles surrounding dust grain as a remnant of cold grain chemistry. Gas-phase chemical processes are reasonably successful to interpret the observations, as reported recently by Bacmann et al. (2020) and Melosso et al. (2020) in their study of the nitrogen hydrides NHD and ND2.
We introduced the deuteration of the carbon chains CnH, CnH2, and nitriles in our gas-phase chemical network, which has been used to study the influence of the C/O ratio on the chemistry of nitriles by Le Gal et al. (2019). That study benefitted from the recent updates reported by Loison et al. (2014, 2017) for nitrogen and carbon-chain chemistry, including the CH3CN isomers. We did not introduce an additional deuterium exchange reaction in the network because the various exchange reactions with HD that we considered (HCNH+, HC3NH+, CH3CNH+) are all hindered by the presence of a barrier of about 56 kcal mol−1 (see Appendix A). Then, deuterium fractionation results directly from the enrichment of H2D+ and, to a lesser extent, from CH2D+ and C2H2D+. In the case of HDCCN, the main route to deuteration is provided by the reaction H2CCN + H2D+ → CH2DCN+ + H2, followed by CH2DCN+ + e− → HDCCN + H. The various dissociative channels of that reaction are reported in Loison et al. (2014) for the hydrogenated ions. We assume, as in our previous studies on nitrogen deuteration (Roueff et al. 2005), that in absence of experimental information the total rate coefficient of dissociative recombination of the deuterated ion is identical to that of the hydrogenated molecular ion. We hypothesize that hydrogen ejection is twice as efficient as deuterium ejection, as found experimentally for HDO+ (Jensen et al. 2000). Our final gas-phase chemical network includes 288 chemical species and more than 7000 chemical reactions3. More details on our gas-phase chemical network will be described in a later publication. We ran steady-state models that are appropriate for the TMC-1 conditions, that is, n(H2) = 104 cm−3, T = 10 K, ζ = 1.3 × 10−17 s−1, and deplete oxygen to get the observed fractional abundance of CO relative to molecular hydrogen of ∼1.2 × 10−5 (Cernicharo & Guélin 1987). The results are shown in Table 3 and compared to the observational ratios. The deuterium ratio of H2CCN is found to be remarkably stable, independent of the assumed N/O ratio and close to the observational value. The other deuterium ratios are within about a factor of two of the observed values, with a couple of exceptions, and are not very sensitive to the N/O ratio. The HCCNC isomer is found by the observations to be more fractionated than theoretically predicted, which may indicate specific chemical rearrangements in the concerned chemical reactions. The main disagreement is obtained for deuterated methyl acetylene, where some additional deuterium enrichment mechanism could be missing. Further studies are desirable.
5. Conclusions
We detected, and fully characterized spectroscopically, the singly deuterated isotopolog of H2CCN from astronomical and laboratory measurements. The observed deuterium ratio for this and other species is well accounted for by a standard gas-phase model, in which deuteration is transferred through the H2D+ molecular ion, followed by dissociative recombination.
The initial network (Le Gal et al. 2019) comprised 190 chemical species and about 3500 chemical reactions.
Acknowledgments
The Spanish authors thank Ministerio de Ciencia e Innovación for funding support through project AYA2016-75066-C2-1-P, PID2019-106235GB-I00 and PID2019-107115GB-C21 / AEI / 10.13039/501100011033. We also thank ERC for funding through grant ERC-2013-Syg-610256-NANOCOSMOS. MA thanks Ministerio de Ciencia e Innovación for grant RyC-2014-16277. Y. Endo thanks Ministry of Science and Technology of Taiwan through grant MOST108-2113-M-009-25. Some of the kinetic data used for the chemical model have been taken from the online database KIDA (Wakelam et al. 2015), http://kida.obs.u-bordeaux1.fr.
References
- Avery, L. W., & Green, S. 1989, ApJ, 337, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Bacmann, A., Faure, A., Hily-Blant, P., et al. 2020, MNRAS, 499, 1795 [CrossRef] [Google Scholar]
- Cabezas, C., Guillemin, J.-C., & Endo, Y. 2016, J. Chem. Phys., 145, 184304 [NASA ADS] [CrossRef] [Google Scholar]
- Ceccarelli, C., Caselli, P., Herbst, E., et al. 2007, Protostars and Planets V eds. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 47 [Google Scholar]
- Cernicharo, J. 1985, Internal IRAM report (Granada: IRAM) [Google Scholar]
- Cernicharo, J. 2012 EAS Publ. Ser. 251 [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., & Guélin, M. 1987, A&A, 176, 289 [Google Scholar]
- Cernicharo, J., Marcelino, N., Pardo, J. R., et al. 2020a, A&A, 641, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Marcelino, N., Agúndez, M., et al. 2020b, A&A, 642, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Marcelino, N., Agúndez, M., et al. 2020c, A&A, 642, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Cabezas, C., Bailleux, S., et al. 2021a, A&A, in press, https://doi.org/10.1051/0004-6361/202040076 [Google Scholar]
- Cernicharo, J., Cabezas, C., Endo, Y., et al. 2021b, A&A, in press, https://doi.org/10.1051/0004-6361/202040013 [Google Scholar]
- Cížek, J. 1969, in Advances in Chemical Physics, ed. P. C. Hariharan (New York: Wiley Interscience), 14, 35 [Google Scholar]
- Dalgarno, A., & Lepp, S. 1984, ApJ, 287, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Dunning, T. H. 1989, J. Chem. Phys., 90, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Endo, Y., Kohguchi, H., & Ohshima, Y. 1994, Faraday Discuss., 97, 341 [CrossRef] [Google Scholar]
- Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2016, Gaussian 16, Revision A.03 [Google Scholar]
- Gerlich, D., & Schlemmer, S. 2002, Planet. Space Sci., 50, 1287 [NASA ADS] [CrossRef] [Google Scholar]
- Gratier, P., Majumdar, L., Ohishi, M., et al. 2016, ApJ, 225, 25 [NASA ADS] [Google Scholar]
- Herbst, E., Adams, N. G., Smith, D., & Defrees, D. J. 1987, ApJ, 312, 351 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Irvine, W. M., Friberg, P., Hjalmarson, A., et al. 1988, ApJ, 334, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Jensen, M., Bilodeau, R. C., Heber, O., et al. 2000, Phys. Rev A, 60, 2970 [CrossRef] [Google Scholar]
- Kaifu, N., Ohishi, M., Kawaguchi, K., et al. 2004, PASJ, 56, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Le Gal, R., Brady, M. T., Öberg, K., et al. 2019, ApJ, 886, 86 [CrossRef] [Google Scholar]
- Linsky, J. L. 2003, Space Sci. Rev., 106, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Loison, J. C., Wakelam, V., & Hickson, K. 2014, MNRAS, 443, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Loison, J. C., Agundez, M., Wakelam, V., et al. 2017, MNRAS, 470, 4075 [NASA ADS] [CrossRef] [Google Scholar]
- Marcelino, N., Agúndez, M., Tercero, B., et al. 2020, A&A, 643, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Melosso, M., Bizzocchi, L., Sipilä, O., et al. 2020, A&A, 641, A153 [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Nyman, G., & Yu, H. G. 2019, AIP Adv., 9, 095016 [CrossRef] [Google Scholar]
- Ozeki, H., Hirao, T., Saito, S., & Yamamoto, S. 2004, ApJ, 617, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Parise, B., Leurini, S., Schilke, P., Roueff, E., Thorwirth, P., & Lis, D. C. 2009, A&A, 508, 737 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pardo, J. R., Cernicharo, J., & Serabyn, E. 2001, IEEE Trans. Antennas Propag., 49, 12 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Raghavachari, K., Trucks, G. W., Pople, J. A., & Head-Gordon, M. 1989, Chem. Phys. Lett., 157, 479 [Google Scholar]
- Roberts, H., Millar, T. J., & Herbst, E. 2003, ApJ, 591, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Roueff, E., & Gerin, M. 2003, Space Sci. Rev., 106, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Roueff, E., Lis, D. C., van der Tak, F. F. S., Gerin, M., & Goldsmith, P. F. 2005, A&A, 438, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roueff, E., Parise, B., & Herbst, E. 2007, A&A, 464, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roueff, E., Gerin, M., Lis, D. C., et al. 2013, J. Phys. Chem. A, 117, 9959 [CrossRef] [Google Scholar]
- Saito, S., & Yamamoto, S. 1997, J. Chem. Phys., 107, 1732 [NASA ADS] [CrossRef] [Google Scholar]
- Saito, S., Yamamoto, Y., Irvine, W. M., et al. 1988, ApJ, 334, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Sumiyoshi, Y., Katsunuma, H., Suma, K., & Endo, Y. 2005, J. Chem. Phys., 123, 054324 [CrossRef] [Google Scholar]
- Thomas, L. F., Sherrard, E. I., & Sheridan, J. 1955, Trans. Farad. Soc., 51, 619 [CrossRef] [Google Scholar]
- Vastel, C., Yamamoto, S., Lefloch, B., & Bachiller, R. 2015, A&A, 582, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakelam, V., Loison, J. C., Herbst, E., et al. 2015, ApJS, 217, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Walmsley, C. M., Flower, D. R., & Pineau des Forêts, G. 2004, A&A, 418, 1035 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watson, W. D. 1976, Rev. Mod. Phys., 48, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, H. J., Knowles, P. J., Knizia, G., et al. 2018, MOLPRO, version 2018.1 [Google Scholar]
- Jefferts, K. B., Penzias, A. A., & Wilson, R. W. 1973, ApJ, 179, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Woon, D. E., & Dunning, T. H. 1995, J. Chem. Phys., 103, 4572 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Quantum chemical calculation
Quantum chemical calculations were carried out to estimate the molecular parameters of HDCCN. Very precise values for the rotational parameters of HDCCN can be obtained using experimetal/theoretical ratios derived for H2CCN species. This is the most common method to predict the expected experimental rotational constants for an isotopic species of a given molecule when the rotational constants for its parent species are known. The geometry optimization calculations were done using a coupled cluster with single, double, and perturbative triple excitation (CCSD(T); Raghavachari et al. 1989) methods with all electrons (valence and core) correlated and Dunning’s correlation-consistent basis sets with polarized core-valence correlation quadruple-ζ (cc-pCVQZ; Woon & Dunning 1995). This calculations were carried out using the Molpro 2018.1 program (Werner et al. 2018). Table A.1 shows the results for these calculations. In addition to the rotational constants, we calculated other parameters necessary to interpret the rotational spectrum of HDCCN. In this manner, the three spin-rotation coupling constants (εaa, εbb and εcc), the magnetic hyperfine constants (aF, Taa and Tbb), and the nuclear electric quadrupole constants for the deuterium nucleus (χaa and χbb) were estimated following the same procedure used for the rotational constants. However, in this case the optimized molecular structure at CCSD(T)/cc-pCVQZ was used. These calculations were carried out via the Becke, three-parameter, Lee-Yang-Parr (B3LYP) hybrid density functional and Dunning’s correlation-consistent basis sets with correlation-consistent polarized valence quadruple-ζ (cc-pVQZ; Dunning 1989). The results for these calculations carried out using the Gaussian16 (Frisch et al. 2016) program package are shown in Table A.1.
Experimental, theoretical, and scaled values for the spectroscopic parameters of H2CCN and HDCCN(all in MHz).
In addition to the structural optimizations, quantum chemical calculations were carried out to examine the potential energy surface for the deuteration reactions of HCNH+, HC3NH+, CH3CNH+ with HD. All the possible stationary points were fully optimized using the coupled cluster singles and doubles correlated method (CCSD; Cížek et al. 1969) along with Dunning’s correlation-consistent polarized valence triple-ζ (cc-pVTZ; Dunning 1989) basis set. The starting point, with the cationic species (HCNH+, HC3NH+ or CH3CNH+) and HD separated from each other, was assumed to be energy zero. The reactions proceed initially by the formation of a pre-reactive complex (HCNH+-HD, HC3NH+-HD, and CH3CNH+-HD), which have energies 2.23, 2.09, and 2.85 kcal mol−1 lower than the separated reactants for HCNH+, HC3NH+ and CH3CNH+, respectively. The barrier heights of the transition states between the pre-reactive complexes and the deuterated species (HCND+, HC3ND+, CH3CND+) are 56.42, 51.87, and 52.76 kcal mol−1, respectively.
Appendix B: Laboratory transition frequencies for HDCCN
The laboratory measurements of HDCCN described in Sect. 3.2 permitted us to measure 132 hyperfine components in the NKa,Kc = 20, 2–10, 1 and 10, 1–00, 0 rotational transitions. The observed frequencies, quantum number assignments, and calculated line intensities are given in Table B.1. We uploaded a file with predictions up to N = 16 to the CDS.
Laboratory observed transition frequencies for HDCCN.
Appendix C: Observed deuteration in other molecular species
In order to compare the derived deuteration enhancement in H2CCN with that of other species, we searched in our data for the lines of the main and singly deuterated isotopologs of CH3CN, CH3CCH, c-C3H2, C4H, and H2C4. The line parameters for the observed rotational transitions of these species are given in Table C.1. For most of these species, only one or two low-J lines were observed in the line survey. We assume a rotational temperature of 10 K for these species. We would like to stress that for most of the species analyzed the variation in column density between Tr = 5−10 K is rather small as was the case for HDCCN (see Sect. 4.1). We observe several rotational transitions for C6H and a rotational diagram was performed. The derived XH/XD abundances are given in Table 3. We now comment on each molecule.
Observed line parameters for selected molecules and their deuterated isotopologs in TMC-1.
In our survey CH3CCH only has a rotational transition for each symmetry species A and E. The data have previously been shown to compare their A/E abundance ratio with that of CH3CO+ (Cernicharo et al. 2021a). The derived line parameters are given in Table C.1. The total column density (A+E) of CH3CCH for Tr = 10 K is (1.3 ± 0.1) × 1014 cm−2. Adopting a Tr = 5 K, we derive practically the same column density. Taking into account the low dipole moment of this species, we could expect that its lowest energy levels are thermalized at the kinetic temperature of the cloud. Two single-deuterated species are observed. We obtain a column density for Tr = 10 of (2.8 ± 0.3) × 1012 cm−2 from the line parameters of CH3CCD given in Table C.1. The H/D abundance ratio for this deuterated isotologue is ∼48. The other single-deuterated substitute, CH2DCCH, is an asymmetric rotor and several lines are observed in our line survey. We derive a column density for Tr = 10 K of (1.4 ± 0.1) × 1013 cm−2 from the derived line parameters (see Table C.1). This value decreases by 15% if a rotational temperature of 5 K is adopted. The H/D abundance ratio for this deuterated isotopolog is ∼10. To compare with the value derived for CH3CCD, we have to take into account a factor of 3 in the abundance ratio coming from the three identical possible substitutions of H by D ina the methyl group. It seems that deuteration in the methyl group is slightly favored (H/D = 30) with respect to deuteration in the acetylenic group of the molecule (H/D = 48). The three 13C isotopologs were detected. Using the integrated lines intensity, we derive an averaged 12C/13C ratio of 75 ± 10. This abundance ratio is in very good agreement with the value derived by Cernicharo et al. (2020c) from the 13C isotopologs of HC5N.
We also show the data previously in the same context as for CH3CCH (Cernicharo et al. 2021a) for CH3CN. The line parameters for all hyperfine components of this molecule are given in Table C.1. We derive N(A-CH3CN) = (2.5 ± 0.2) × 1012 cm−2 and N(E-CH3CN) = (2.2 ± 0.2) × 1012 cm−2 (Tr = 10 K). For CH2DCN, we detect three rotational transitions exhibiting hyperfine splitting. To the best of our knowledge, this hyperfine structure has only been observed in the early years of microwave spectroscopy (Thomas et al. 1955). The reported frequencies, often blends of several hyperfine components, are shifted by 50–100 kHz with respect to the observed frequencies in TMC-1. From these new rest frequencies we derive χaa = −4.194 ± 0.012 MHz. We find that χbb was not necessary to reproduce the observed transitions within our frequency accuracy (10 kHz). The column density derived for this deuterated species is (4.5 ± 0.6) × 1011 cm−2 and the N(CH3CN)/N(CH2DCN) abundance ratio is ∼11, that is, very similar to the value found for the N(CH3CCH)/N(CH2DCCH) abundance ratio.
We observed the 32, 1–31, 2ortho line at 44104.777 MHz for c-C3H2. This line appears in absorption against the cosmic background radiation. This line was not detected in the line survey of TMC-1 performed with the Nobeyama telescope (Kaifu et al. 2004). In addition, we observed in three para lines in our data (see Table C.1). Of these three lines, only the strongest one was reported by Kaifu et al. (2004). One of the para lines (440–331) also appears in our data in absorption against the cosmic background radiation. Hence, it is not possible to adopt a uniform rotational temperature for the lines of both ortho and para species. Nevertheless, collisional rates are available for the system c-C3H2/He (Avery & Green 1989), which allows us to perform excitation models using the large velocity gradient approximation. For the typical volume density of TMC-1 of 4 × 104 cm−3 and TK = 10 K, the three para lines are very well reproduced, including the one in absorption that has a column density for this species of N(p-c-C3H2) = (3.2 ± 0.3) × 1013 cm−2. The absorption produced by the ortho line shows a very strong dependence on the density for a large range of column densities. The line is predicted in absorption for n(H2) ≤ 3 × 104 cm−3 and N(o-c-C3H2) ≥ 5 × 1013 cm−2. The line is predicted to be in emission for larger densities and/or lower column densities. We found that n(H2) = (2–3) × 104 cm−3 and N(o-c-C3H2) = (9 ± 1.0) × 1013 cm−2 reproduce the observed absorption of this species. Hence, the total column density of c-C3H2 is (1.2 ± 0.1) × 1014 cm−2, that is, very similar to that of CH3CCH. The derived ortho/para ratio is 2.8 ± 0.6. The column density and rotational temperature of c-C3HD can be derived from the four observed lines to be (4.5 ± 0.5) × 1012 cm−2 and Tr = 6 ± 1 K, respectively. Therefore, the H/D abundance ratio in this species is 27 ± 5.
Six lines of H2C4 and two of HDC4were found in our survey. The line parameters are given in Table C.1. We explored the column densities and rotational temperatures that reproduce at the best the observed line intensities. We find that for Tr = 10 K N(o-H2C4) = (3.0 ± 0.3) × 1012 cm−2 and N(o-H2C4) = (1.0 ± 0.1) × 1012 cm−2. Similar results are obtained for Tr = 7 K. For Tr = 5 K, the column densities have to be increased by a 25%. The ortho/para abundance ratio is 3 ± 0.3 for this species. We obtain N(HDC4) = (4.8 ± 0.5) × 1010 cm−2 for Tr = 10 K. Consequently, the H/D abundance ratio for H2C4 is 83 ± 15.
For C4H, we modeled the emission for all the lines in our survey, including the weak hyperfine lines that are typically a factor 30–50 weaker than the strongest components. The best fit is obtained for Tr = 7 K and N(C4H) = (1.3 ± 0.1) × 1014 cm−2, although a model with the same column density and Tr = 10 K provides practically the same result. The column density increases by a 20% for Tr = 5 K. Adopting Tr = 7 K for C4D, we derive N(C4D) = (1.1 ± 0.1) × 1011 cm−2. Hence, the H/D abundance ratio for C4H is 118 ± 20.
All Tables
Deuteration enhancement in TMC-1 for selected molecules compared to our gas-phase chemical model.
Experimental, theoretical, and scaled values for the spectroscopic parameters of H2CCN and HDCCN(all in MHz).
Observed line parameters for selected molecules and their deuterated isotopologs in TMC-1.
All Figures
 |
Fig. 1. (a) Observed group of lines assigned to the hyperfine structure of the 20, 2–10, 1 transition of HDCCN (black histogram). (b) The observed hyperfine structure of the same transition of o-H2CCN. (c) Selected hyperfine components of the 212–111 transition of p-H2CCN. (d) Selected hyperfine components of the 211–110 transition of p-H2CCN. In all panels, the abscissa represents the rest frequency (in MHz) assuming a local standard of rest velocity for the source of 5.83 km s−1 (Cernicharo et al. 2020c). The ordinate is the antenna temperature in mK. The red curve in each panel represents the best model fit to the emission of this species in TMC-1 for a rotational temperature of 10 K. A similar fit is obtained for other rotational temperatures (see Sect. 4.1 and Table 2). Negative features are due to the folding of the frequency-switching data. |
| In the text | |
 |
Fig. 2. Section of 10 MHz of the FTMW spectrum of HDCCN showing 36 hyperfine components of the NKa,Kc= 10, 1–00, 0 pure rotational transition. The spectrum was achieved by 100 shots of accumulation and a step scan of 0.5 MHz with a repetition rate of 10 Hz. The coaxial arrangement of the adiabatic expansion and resonator axis produces an instrumental Doppler doubling. The resonances frequencies are calculated as the average of the two Doppler components. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.