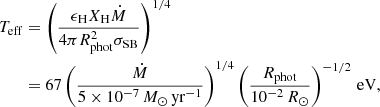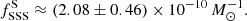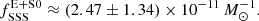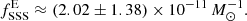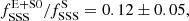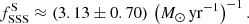| Issue |
A&A
Volume 646, February 2021
|
|
|---|---|---|
| Article Number | A85 | |
| Number of page(s) | 19 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202039522 | |
| Published online | 12 February 2021 | |
Populations of super-soft X-ray sources in galaxies of different morphological types
1
Max Planck Institute for Astrophysics, Karl-Schwarzchild-Str. 1, Garching b. Munchen 85741, Germany
e-mail: ilkham@MPA-Garching.MPG.DE
2
Kazan Federal University, Kremlevskaya Str. 18, 420008 Kazan, Russia
3
Space Research Institute of Russian Academy of Sciences, Profsoyuznaya 84/32, 117997 Moscow, Russia
Received:
24
September
2020
Accepted:
30
November
2020
Aims. We study populations of soft and super-soft X-ray sources (SSSs) in nearby galaxies of various morphological types with particular emphasis on characterizing populations of stable nuclear burning, accreting white dwarfs (WDs).
Methods. Analyzing the content of the Chandra archive, we assembled a sample of nearby galaxies suitable for studying populations of SSSs. Our sample includes four spiral galaxies, two lenticular galaxies, and three ellipticals with stellar mass exceeding 1010 M⊙ and X-ray sensitivity of the order of a few × 1036 erg s−1. We used a combination of hardness ratio and median energy to pre-select X-ray sources with soft spectra, and used the temperature–X-ray luminosity diagram to identify SSSs, likely nuclear-burning, accreting WDs.
Results. For spiral galaxies, there is a distinct and rare population of super-soft sources that are largely detached from the rest of the sources on the kTbb − LX plane. The boundary between these sources and the much more numerous population of harder (but still soft) sources is consistent with the boundary of stable hydrogen burning on the surface of WDs. The combined spectrum of soft sources located outside this boundary shows clear emission lines of Mg and S, the equivalent width of which is similar to that in the combined spectrum of a large number of confirmed supernova remnants in M 83. This supports earlier suggestions that the vast majority of the so-called quasi-soft sources are supernova remnants. In early-type galaxies, populations of super-soft sources are about a factor of eight less abundant, in broad agreement with the population synthesis calculations. Specific frequencies of super-soft sources are (2.08 ± 0.46) × 10−10 M⊙−1 in spiral galaxies and (2.47 ± 1.34) × 10−11 M⊙−1 in lenticular and elliptical galaxies, with the ratio of the latter to the former being 0.12 ± 0.05.
Key words: galaxies: general / X-rays: binaries / white dwarfs / binaries: close
© I. Galiullin and M. Gilfanov 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1. Introduction
CAL 83 and CAL 87, the two prototypical super-soft X-ray sources (SSSs) were discovered by Einstein observatory in the course of a survey of the Large Magellanic Clouds (Long et al. 1981). About a decade later, first light observations of the central region of the LMC with ROSAT observatory led to the discovery of a similar source with a very soft spectrum, RX J0527.8–6954 (Trümper et al. 1991). With the advent of Chandra and XMM-Newton, similar sources were found in other, more distant galaxies. The spectra of these sources are very soft and do not extend beyond ∼1−2 keV, and approximation with the black-body model gives temperatures of the order of ∼10−100 eV and bolometric luminosities in the ∼1036 − 1038 erg s−1 range (Greiner et al. 1991; Kahabka et al. 1994). It is this extreme softness of their spectra that gave rise to their name. The binary nature of some of these sources (CAL 83 and CAL 87 in the first place) was determined soon after their discovery (Pakull et al. 1988; Smale et al. 1988; Cowley et al. 1990) and although they were initially thought to be low-mass X-ray binaries, it was soon realised that the compact object in these binaries is a white dwarf (WD) rather than a neutron star or a black hole (van den Heuvel et al. 1992). The proposition that the main source of energy in SSSs is thermonuclear burning of the accreted hydrogen naturally explained the unusual softness of their X-ray spectra, the combination of the energy output expected in hydrogen fusion and the surface area of a typical WD giving effective temperatures in the correct range, close to the observed values (van den Heuvel et al. 1992).
The details of thermonuclear burning on the surface of WDs are still a matter of debate. Calculations by Nomoto et al. (2007), Wolf et al. (2013; and references therein) find that hydrogen fusion may proceed in a steady manner above some value of the mass accretion rate in the so-called stability strip stretching around Ṁ ∼ few × 10−7 M⊙ yr−1, its exact location depending on the mass of the star. In this regime, classical steady SSSs are observed, while at lower mass-accretion rates hydrogen fusion on the surface of WDs is unstable, giving rise to the explosions of classical and recurrent novae. On the other hand, calculations by Prialnik & Kovetz (1995), Yaron et al. (2005), Starrfield et al. (2013), suggest that nuclear burning is unstable at any mass accretion rate. Although the nova explosion itself is primarily observed in the optical band, nuclear burning of the residual hydrogen on the surface of a WD after the explosion generates soft X-ray emission and the system is observed as a post-nova SSS (Truran & Glasner 1995; Wolf et al. 2013; Soraisam et al. 2016). Thus, the existence of SSSs, steady or not, is envisaged in either scenario.
Although accreting WDs are interesting objects in their own right, they became of broader astrophysical importance as possible progenitors of type Ia supernovae (e.g., Whelan & Iben 1973; Nomoto 1982). However, before exploding as a supernova, a WD needs to increase its mass from the initial value, typically in the ∼0.5−1.0 M⊙ range, to near the Chandrasekhar mass limit of about ∼1.4 M⊙. For an accreting WD, the only way to increase its mass is hydrogen and/or helium fusion on its surface. The mass growth is most efficient when nuclear burning is stable, as in all other regimes it is counteracted by various mass-loss processes. However, growth of the WD mass is also possible in certain domains of the parameter space when the burning is unstable (Starrfield et al. 2013; Hillman et al. 2015). Nevertheless, it was demonstrated that the number of SSSs (Di Stefano 2010) and their total luminosity in the X-ray (Gilfanov & Bogdán 2010; Bogdán & Gilfanov 2011) and UV (Woods & Gilfanov 2013, 2014; Johansson et al. 2014) bands in nearby galaxies is far too insufficient to explain the observed SN Ia rates.
There is still no complete understanding of how the population of nuclear burning, accreting WDs is related to the fundamental properties of their host galaxies, such as their stellar mass, star-formation rate, star-formation history, and metallicity. On the theoretical side, there have been several attempts to address this problem by means of population synthesis calculations (e.g., Yungelson & Livio 1998; Yungelson 2010). Recently, Chen et al. (2014, 2015, 2016) implemented hybrid population synthesis calculations using the MESA code (Paxton et al. 2011, 2013) to compute the mass-transfer phase of binary evolution. Chen et al. produced a model that is in reasonable agreement with a number of existing constraints on the soft X-ray luminosities and average intensity of the ionizing radiation field, as well as with statistics of classical novae in nearby galaxies.
Observational studies of SSS populations are often impeded by the extreme softness of their spectra, making searches for and characterization of these objects difficult. Nevertheless, there have been a number of successful attempts, and this effort intensified with the advent of Chandra and XMM-Newton (e.g., Swartz et al. 2002; Di Stefano & Kong 2003, 2004; Pietsch et al. 2005; Henze et al. 2010, 2011, 2014). It was suggested that the observed number of SSSs differs between various types of galaxies (e.g., Di Stefano 2010). Bogdán & Gilfanov (2011) showed that specific frequencies of SSSs with LX > 1036 erg s−1 in disks of late-type galaxies exceed those found in bulges by factor of approximately two.
In this paper we continue the observational line of investigation of populations of accreting WDs. To this end, we attempted to construct a suitable sample of galaxies from the Chandra archive in order to search for SSSs and implemented efficient source classification algorithms. Our goal is to identify steady nuclear burning WDs and to estimate their specific frequencies in early- and late-type galaxies.
The paper is structured as follows: in Sect. 2 we introduce our sample of nearby galaxies observed by Chandra. Observations and data reduction procedures are described in Sect. 3. In Sect. 4 we introduce the initial source classification procedure based on a combination of median energy and hardness ratio and in Sect. 5 we investigate the properties of soft X-ray sources and separate nuclear burning WDs from the rest of source population with the help of the temperature–luminosity diagram. The nature of soft X-ray sources and SSSs is described in Sect. 6 where we also estimate their specific frequencies and compare our results with those of previous studies, and in Sect. 7 we summarize our findings.
2. Sample of nearby galaxies
We selected galaxies for our analysis from the Chandra observatory archive for cycles 1−20. To this end, we selected observations from the following categories: normal galaxies, active galaxies and quasars, clusters of galaxies, galactic diffuse emission, and surveys. Only archival observations with the Advanced CCD Imaging Spectrometer (ACIS) detector without grating were selected. For each galaxy, we grouped observations made within the same Chandra cycle and selected the group with the largest total exposure time. We then cross-matched aim-point positions of selected Chandra observations with positions of galaxies in the RC3 catalog (de Vaucouleurs et al. 1991) to select potentially interesting observations. For each galaxy, we used a match radius of 0.5 × D25. The parameters of galaxies for further selection were computed as follows. Stellar masses were computed from Ks band luminosities using mass-to-light ratios computed following the prescription of Bell & de Jong (2001). Classifications of galaxies, distances, and Ks-band magnitudes were taken from the HyperLeda1 catalog (Makarov et al. 2014) and the Updated Nearby Galaxy Catalog (Karachentsev et al. 2013). Absorption-corrected (B − V)0 colors were taken from the RC3 catalog.
2.1. Selection criteria
We built our selection procedure based on the following considerations.
(i) Stellar mass of the host galaxy. Population synthesis calculations of Chen et al. (2014, 2015) predict specific frequencies of observable (apparent luminosity LX > 1036 erg s−1) stable nuclear burning, accreting WDs in spiral galaxies after 10 Gyr of evolution at the level of ∼4 × 10−10 (∼2 × 10−9) sources per M⊙, assuming an absorbing column density of 3 × 1021 (3 × 1020) cm−2. For elliptical galaxies, the prediction of these latter authors is ∼10−10 sources per M⊙ for a hydrogen column density of 3 × 1020 cm−2. Based on these predictions we only consider sufficiently massive galaxies with stellar masses M* ≳ 1010 M⊙, in which we can expect to find ≳1 nuclear burning, accreting WDs.
(ii) Distance. We excluded a few large nearby galaxies from our analysis that do not fit, by a large margin, in the Chandra field of view and require the analysis of mosaics of a large number of observations. These are the Magellanic Clouds, M 31 and M 33. We would have also excluded too distant galaxies that suffer from confusion, but they are automatically excluded based on the sensitivity arguments (item (iv) below).
(iii) Inclination angle. Source populations in spiral galaxies which are viewed close to edge-on will be obscured by large intrinsic absorption by gas and dust in the disk, essentially reducing the number of expected super-soft sources to zero. Therefore, in selecting late-type galaxies we applied a criterion i < 70°. For this reason, Sculptor and NGC 4945 for example, were not included from our final sample. No inclination cut was applied to early-type galaxies.
(iv) Sensitivity limit of available archival data. The sensitivity limit of archival data can be estimated as follows:
where D is distance to the galaxy, ECF is the counts-to-ergs conversion factor, S is the limiting number of source counts required to detect and characterize a source, t is the total exposure time of archival data. We assumed a black body model with temperature 60 eV and require S = 20 counts to detect and classify a source. For each galaxy we obtained ECF from the black-body model (kT = 60 eV) modified by the Galactic absorption column density in the direction of the galaxy. For the latter, we used the HI4PI data (HI4PI Collaboration 2016). For cycles 7−20, in computing the ECF, we used the ACIS detector aim-point response files from the Chandra Calibration Database2. For cycles 1−6 we generated aim-point response files ourselves. Circinus (5.3 × 1021 cm−2) and IC 342 (3.6 × 1021 cm−2) galaxies with high Galactic absorption column densities were excluded from our sample. We also excluded M 87 and M 82 due to the presence of bright and complex diffuse emission in these galaxies.
We plot the distribution of galaxies of various morphological types on the distance–sensitivity limit plane in Fig. 1. Based on these data we selected spiral galaxies M 51, M 81, M 83, M 101, lenticular galaxies Cen A and NGC 3115, and elliptical galaxies NGC 3379, 4278, and 4697. For elliptical galaxies, sensitivity limits of the archival Chandra data exceed 1037 erg s−1, but this is compensated by zero intrinsic absorption in these galaxies; see Sect. 5.2.
 |
Fig. 1. X-ray sensitivity–distance diagram of nearby galaxies observed by Chandra up to cycle 20. Each panel corresponds to a certain morphological type of galaxy. Filled (open) symbols correspond to galaxies with stellar mass M* ≥ 1010 M⊙(M* < 1010 M⊙). See Sect. 2 for details. |
We experimented with the selection criteria in order to check whether or not our sample can be improved by adding a few galaxies lying on the boundary of our luminosity and stellar mass selection. Nevertheless, we found that when relaxing the sensitivity threshold, we need to raise the luminosity cut on the kTbb − LX plane (Sect. 5.2) which actually leads to the loss of super-soft sources of lower luminosity and degradation of the statistical accuracy of our analysis. Adding less-massive galaxies below the assumed cut of 1010 M⊙, on the other hand, does not lead to a quick improvement of the sensitivity of our selection to the populations of SSSs as the total mass already included in the analysis exceeds ≈4 × 1011 M⊙. We therefore conclude that the list of galaxies assembled here is reasonably optimal for the current analysis. The basic parameters of these galaxies are summarized in Table 1.
Nearby galaxies used to study populations of soft and SSSs.
3. Observations and data reduction
The observations were processed by following a standard CIAO (Fruscione et al. 2006) threads3 (CIAO version 4.8 and CALDB version 4.7.1). We used tool chandra_repro to reprocess data and create level 2 event files. To improve absolute astrometry we used wcs_match and wcs_update. Astrometry correction was done relative to the observation with the longest exposure time using positions of bright X-ray sources to match frames. Event files were merged by reproject_obs with the aim-point position of the observation with the longest exposure taken as the reference. Combined images and exposure maps were obtained running flux_obs. In Table 2 we present brief information on the observations used in the analysis. Detail information is available in Appendix A.
Properties of galaxies and statistics of their X-ray source populations.
3.1. Source detection
Source detection was performed with the wavdetect tool. We chose to use small  scale series with a power of 0−3 of the wavelet functions to minimize the spurious detections associated with soft diffuse emission in galaxies. Scales of wavelets correspond to variation of the point spread function (PSF) within an aim point of a single ACIS chip. We setup the following parameters of wavdetect to create a background map from the merged image: bkgsigthresh = 0.01, maxiter = 10, iterstop = 10−6. The false-positive source detection probability threshold was chosen at 10−7. Mask filtering was applied to all images of galaxies using exposure maps. Pixels were included in the source-detection region where exposure map values were greater than 20% of the maximum (expthresh = 0.2). False-color X-ray images of all galaxies with their D25 and source-detection regions are presented in Appendix B.
scale series with a power of 0−3 of the wavelet functions to minimize the spurious detections associated with soft diffuse emission in galaxies. Scales of wavelets correspond to variation of the point spread function (PSF) within an aim point of a single ACIS chip. We setup the following parameters of wavdetect to create a background map from the merged image: bkgsigthresh = 0.01, maxiter = 10, iterstop = 10−6. The false-positive source detection probability threshold was chosen at 10−7. Mask filtering was applied to all images of galaxies using exposure maps. Pixels were included in the source-detection region where exposure map values were greater than 20% of the maximum (expthresh = 0.2). False-color X-ray images of all galaxies with their D25 and source-detection regions are presented in Appendix B.
To maximise sensitivity of source detection, we used a combination of the following energy bands: 0.3−1 keV; 1−2 keV; 0.3−2 keV; 0.5−8 keV; 2−8 keV bands. We ran wavdetect in each of these bands and merged their results into a single source list, excluding duplications. To this end we used the STILTS package (Taylor 2006), with the match radius equal to the sum of their PSF radii defined at the 80% encircled fraction. In the final merged list, we chose the coordinates of sources in the band where the significance of detection was maximal. In the very inner regions of some galaxies, wavdetect found multiple overlapping sources. Visual inspection of the images showed that many of these sources are likely false detections caused by the presence of substructures in the bright and complex diffuse emission of the nucleus. In many cases it appears impossible to separate true compact sources from such false detections. We therefore decided to exclude the central circular region of 15″ radius of the M 51, M 83, and Centaurus A galaxies from our analysis. In the case of Centaurus A we also excluded regions around bright X-ray jets similar to Voss & Gilfanov (2006).
To define source and background count extraction regions, we produced PSF maps. In order to account for PSF variations across the combined image, we created a PSF map for each observation with the mkpsfmap tool using encircled energy of 80%, and combined individual maps weighting them with respective exposure maps. Combined source spectra used in the further analysis were extracted using the CIAO tool specextract. For source regions we used circles with a radius equal to that of the 80% PSFs fraction from the exposure-weighted PSF map. The background regions were defined as annuli with inner and outer radii equal to two and four times the radius of the PSFs, respectively. The source count rates were corrected for source count leakage to the background region. When source or background regions of different sources overlapped, we excluded the overlapping parts from the counts summation, correcting the PSF fractions accordingly.
The lists of detected sources were analyzed to identify spurious detection due to fluctuations in local background. For each source, we tested the null hypothesis that observed counts in source and background regions are Poissonian realizations of local background with the same mean (Weisskopf et al. 2007, see Appendix A). We estimated probabilities using source and background counts from merged images in the 0.3−2 keV band. All detections with a statistical confidence of less than 3σ were excluded from the final source list. Additionally, inspection of X-ray images by eye did not reveal any potentially spurious detections. In Table 2 we summarize the numbers of X-ray sources detected in the galaxies of our sample.
3.2. Stellar masses of the final sample of galaxies
Stellar masses of galaxies within D25 and within the source-detection regions listed in Tables 1 and 2 were determined following the prescription of Zhang et al. (2012) as summarized below. We used background-subtracted images from 2MASS Large Galaxy Atlas (Jarrett et al. 2003). Bright sources were visually removed from the images. Net counts of the images S were converted into magnitudes using the zero-point magnitude KMAGZP from the headers of fits files.
We obtained Ks band absolute magnitudes using the distances listed in Table 1. When computing luminosities, solar absolute magnitude in Ks band was assumed to be Ks, ⊙ = 3.27 (Willmer 2018). The final stellar masses of the galaxies were obtained using the Ks band mass-to-light ratio (Bell & de Jong 2001),
where LK is Ks band luminosity and (B − V)0 is the color index corrected for galactic and internal extinction (see Table 1).
4. Source classification
4.1. Method
To classify and separate soft and super-soft sources from sources with more usual spectra we used a combination of hardness ratio HR and median energy Ẽ. The hardness ratio was defined as the ratio of the hard band count rate to the total broad band count rate:
where R is the background subtracted count rate in the respective energy band. The statistical error of the hardness ratio was calculated using standard error propagation.
The median energy Ẽ for each source was calculated from its observed counts spectrum considering the 0.3−8.0 keV energy band. The statistical error was computed using the standard formula for the variance of the sample median (Rider 1960) where the probability density at the median energy was approximately determined from the distribution of observed counts. When computing the median energy, we chose not to subtract background from the source spectrum; the simulations demonstrate that, for the typical source and background spectra we are dealing with, this does not affect our source classification procedure (see Fig. 2 and its discussion below).
 |
Fig. 2. Left: relation of the median energy to the temperature of a black-body model (left-hand curves and y-axis, blue in the color version of this plot) and to the photon index of a power-law model (right curves and y-axis, red). Simulations for the Chandra ACIS-S detector with Cycle 13 (2012) response. An absorption column density of 1021 cm−2 was assumed. Solid lines show models without background, dotted lines show models with 50% contribution of background counts. Parameter ranges are relevant to super-soft sources and X-ray binaries, and the two types of spectra are clearly separated at about Ẽ ≈ 1.0−1.3 keV. Right: verification of the source classification procedure in M 51. Distribution of sources with median energy Ẽ ≤ 2 keV over the photon index of the power-law model. The blue and red dashed histograms show the distributions of sources classified as soft and hard, respectively, and the black solid line indicates the total distribution. |
The motivation behind our choice of the parameters used for source classification is as follows. The median energy characterizes the overall softness of the spectrum. Figure 2 (left panel) shows the median energies of the absorbed black-body and power-law models. As one can see from the plot, in the parameter range relevant to nuclear burning, accreting WDs (kT ≲ 200 eV) and X-ray binaries/AGNs/stars (Γ ≲ 2), the two types of sources occupy different domains along the Ẽ axis with some gap in between4. Therefore one may expect a bi-modal distribution of sources over Ẽ (which may however be smeared by statistical uncertainties).
We use M 51 to illustrate and verify our classification of sources using their median energy (see corresponding panels in Fig. 3). To this end we fit the background-subtracted spectra of all sources with Ẽ ≤ 2 keV5 with an absorbed power-law model. The absorption column density for each source was fixed as described in Sect. 5.1 below. The distributions of soft and hard X-ray sources over photon index are shown in the right panel of Fig. 2. From these distributions it is clear that indeed the sources classified as soft and hard occupy different domains along the photon index axis. The small overlap of the two distributions is caused by statistical uncertainties in measuring the median energy and photon index.
 |
Fig. 3. Hardness ratio vs. median energy diagram for compact X-ray sources in the galaxies of our sample. Only sources with ≥20 net counts are plotted. Dashed lines show the median energy boundary of Ẽ0 = 1.2 keV (see Sect. 4.2). The distributions of sources over median energy are plotted below their corresponding median energy–hardness ratio diagram. |
 |
Fig. 3. continued. |
This comparison shows that a classification scheme based on the median energy is efficient in identifying sources with soft spectra. The hardness ratio on the other hand characterizes the presence of source emission above 2 keV and helps to identify sources with low Ẽ but also featuring hard emission components extending to higher energies. Such hard spectral components are not typical for nuclear burning WDs and may be encountered, for example, in accreting black holes in the soft state and in some supernova remnants.
Finally, we note that the median energy is not efficient in separating the bulk of supernova remnants (SNRs) from WDs. This can be achieved with more detailed spectral fitting, which nevertheless produces meaningful results only for the brightest sources.
Use of the median energy and hardness ratio for characterization of the spectral shape is not entirely new in X-ray astronomy; Hong et al. (2004) for example proposed the use of various quantiles and Prestwich et al. (2003) used a color–color diagram for this purposes. Di Stefano & Kong (2003) used hardness ratio to classify SSSs in external galaxies. Color–color diagrams and hardness ratio techniques were used in numerous other studies not mentioned here. However, to our knowledge, the present study is the first to use the combination of the median energy and hardness ratio for separating super-soft sources from the bulk of the population.
4.2. Distribution of sources in HR–Ẽ plane
The distribution of sources on the hardness ratio–median energy plane is shown in Fig. 3. In producing these plots we applied cuts of 20 net counts to all data sets in order to exclude sources with overly large uncertainties. For each galaxy we also plot distribution of sources over the median energy.
4.2.1. Late-type galaxies
Distributions of the sources over median energy in M 51, M 83, and M 101 are clearly bimodal. Their HR-Ẽ diagrams have distinct and relatively compact populations of soft sources at Ẽ ≲ 1 keV and HR ∼ 0 along with the more extended tail of sources with more usual harder spectra. Based on their distributions over the median energy, we chose the boundary of Ẽ0 = 1.2 keV to select soft sources in these galaxies. Hard sources were excluded from further consideration. We also excluded sources with statistically significant flux (≥3σ) detected above 2 keV. The total numbers of thus-selected soft sources are presented in Table 2.
The median energy distribution of sources in M 81 shows a single peak at Ẽ0 ≈ 1.5 keV with a possible shoulder towards lower values of Ẽ. Lack of bi-modality may be a consequence of the star-formation history of this galaxy as discussed in Sect. 6.4. Due to the absence of obvious bi-modality in the source distribution we applied a selection criterion based on the absence of hard flux. In particular, we excluded sources with statistically significant flux (≥3σ) detected above 2 keV from further analysis. Their numbers are listed in Table 2.
4.2.2. Early-type galaxies
The distribution of sources over median energy for elliptical and lenticular galaxies is also unimodal with the low-energy shoulder present for some galaxies. As for M 81, we only kept sources without statistically significant flux above 2 keV.
5. Observed properties of soft sources
5.1. Equivalent hydrogen column density
Because of the softness of sources under consideration, the value of equivalent hydrogen column density NH is important for accurate spectral analysis. This problem is of relevance for late-type galaxies.
Because of the degeneracy with other parameters NH is difficult to determine from fitting X-ray spectra, especially for fainter sources with a smaller number of counts, which constitute the majority of our sample. Therefore, we chose to fix NH at values determined in the radio band. To this end, we combined CO 2−1 and 21 cm maps from the HI Nearby Galaxy Survey (THINGS, Walter et al. 2008) and the HERA CO-Line Extragalactic Survey (HERACLES, Leroy et al. 2009). For each source we computed absorption column density as
where NH, Gal is the Galactic hydrogen column density in the direction of galaxy (HI4PI Collaboration 2016), and NHI and NH2 are column densities of neutral and molecular gas from THINGS and HERACLES surveys respectively, computed as follows:
where IHI is the velocity-integrated intensities of THINGS maps in units of Jy beam−1 km s−1, and FWHMmaj and FWHMmin are the major and minor axes of the beam in arcsec (Walter et al. 2008, see Eq. (5)). For NH2 we used:
where WCO is the HERACLES velocity-integrated CO J = 2 → 1 map intensity in units of K km s−1, XCO is the CO J = 1 → 0 to H2 conversion factor, and R21 is the ratio of CO J = 2 → 1 to CO J = 1 → 0. We assumed the Galactic value of XCO = 2 × 1020 cm−2 (K km s−1)−1 (Strong & Mattox 1996; Dame et al. 2001) for the majority of galaxies and R21 = 0.8 (see Leroy et al. 2009, Eq. (3) and references therein).
The XCO factor is known to vary between galaxies. In particular, for M 51 it is ∼4 times smaller than the Galactic value (Garcia-Burillo et al. 1993; Guelin et al. 1995). For M 81, no CO maps of sufficient quality are available and we accounted only for absorption by neutral hydrogen. For M 83 we used the CO 1−0 intensity map from NED6 where the galaxy was observed by Crosthwaite et al. (2002) with NRAO 12 m telescope.
Table 3 shows the median values of absorption column density NH of soft sources in late-type galaxies for two cases: f = 0.5 and f = 1. We adopted f = 0.5, which means that sources are subjected to half of the absorption intrinsic to the galaxy. Naively, this corresponds to the assumption that all sources are located close to the midplane of the host galaxy.
Absorption column densities for late-type galaxies.
We analyzed the spectra of bright sources with ≥200 net counts and compared the results of X-ray spectral fits with fixed NH with those where NH was a free parameter of the fit. The results are shown in Fig. 4. As one can see, although there is considerable scatter in NH, values of temperature and especially X-ray luminosity are in reasonable overall agreement. Unfortunately, such an analysis is only possible for a small fraction of the sources. We therefore chose to use fixed absorption column density, computed for each source from Eq. (5).
 |
Fig. 4. Relations between black-body temperature (left) and absorbed X-ray luminosity (center) values computed with NH being a free parameter of X-ray spectral fit (y-axes) and for NH computed from Eq. (5) with f = 0.5 (x-axes). Right-hand panel: relation between bets-fit NH and NH computed from Eq. (5). Only sources with net counts ≥200 are shown. Errors are 1σ. See Sect. 5.1 for more details. |
Elliptical and lenticular galaxies in our sample have much lower intrinsic neutral hydrogen column density, below ∼few × 1019 cm−2 (Serra et al. 2012). We can therefore safely assume NH = NH, Gal for early-type galaxies in our sample, with a caveat regarding Centaurus A. In the dust lanes of this galaxy, absorption column density is at the nearly constant level of ≈5 × 1021 cm−2 and drops rather sharply outside the dust lanes (Struve et al. 2010). Therefore, we accounted for the intrinsic absorption for the sources located in the dust lanes (about one-third of all soft sources in Centaurus A) in the same way as for spiral galaxies, but assuming a constant value of intrinsic absorption of 5 × 1021 cm−2, while we used the Galactic value for the sources outside dust lanes. We find that the particular details of this calculation are unimportant. It should also be noted that Centaurus A also stands out in the early-type galaxy sample because of its ongoing star formation at a level of ∼0.8 M⊙ yr−1 (Espada et al. 2019). It will be further discussed in Sect. 6.2.
5.2. X-ray spectral analysis and kTbb–LX diagram
The spectra of X-ray sources classified as soft were approximated with an absorbed black body model, with the absorption column density fixed at the values computed as described in Sect. 5.1. For spectra with a small number of counts, the absorption correction of X-ray luminosity often bears a large uncertainty and may lead to physically meaningless values. We therefore chose to use the absorbed X-ray luminosities of sources for further analysis and apply absorption to models when comparing them to the data. We used the Tuebingen-Boulder ISM absorption model (Wilms et al. 2000; tbvarabs model in XSPEC). Abundances of late-type galaxies were fixed at values listed in Table 3. For early-type galaxies Wilms et al. (2000) solar elemental abundance was assumed. The spectral fit was performed with XSPEC (Arnaud 1996) in the 0.3−8 keV energy band using C – statistics (Cash 1979). The background spectrum was included in the spectral fitting. Spectra were binned to have at least one count per bin, following the recommendations of the XSPEC manual7. Confidence intervals for the parameters were obtained using the error command in XSPEC.
The distribution of sources on the X-ray luminosity–temperature (hereafter kTbb − LX) plane is shown in Fig. 5. When plotting the kTbb − LX diagram, we applied a cut of 20 net counts in order to exclude faint sources with overly large error bars. X-ray luminosities were computed for the 0.3−2 keV energy band. The thin solid line near the bottom of each panel shows X-ray luminosity corresponding to 20 net counts, as a function of black-body temperature. In plotting these curves we converted counts to rate using the maximal exposure time of the observation. The absorbed X-ray luminosity was computed using a count rate–flux conversion for the black-body spectrum with the given temperature and absorption column density. The luminosity corresponding to 20 counts exceeds the luminosities of faintest sources by a factor of about three, and therefore samples of sources above these curves should not be subject to significant incompleteness effects8.
 |
Fig. 5. kTbb − LX diagram for soft X-ray sources in the galaxies of our sample. A cut of 20 net counts was applied. The luminosities are in the 0.3−2.0 keV band and are not corrected for absorption. All plotted sources have no statistically significant flux above 2 keV (open circles). Sources with median energy Ẽ ≤ 1.2 keV are shown with solid orange circles. Sources with Gaia matches of measured parallax or proper motion are marked by black diamonds. Solid red curves show kTbb − LX relations at the lower boundary of stable nuclear burning. Along these curves, the WD mass increases from 0.51 M⊙ at the lower left end to 1.34 M⊙ at the upper right end. The dotted red line for Centaurus A shows the location of this boundary in the dust lanes of this galaxy. Green lines correspond to the emission spectrum of the general relativistic accretion disk model around a Schwarzschild BH (Ebisawa et al. 1991) for BH masses of 10, 20, 30, and 50 M⊙. The accretion rate changes along the curves from 0.02 ṀEdd to 1 ṀEdd. Horizontally oriented solid black curves show the luminosity corresponding to 20 net counts. The dashed blue line on each plot shows the 20 counts luminosity limit for M 51 corrected for the difference in absorption column density between M 51 and the galaxy under consideration. All model curves show absorbed luminosities. Errors are at 1σ confidence. See Sect. 5.2 for details of calculations. |
On each panel, the blue dashed line shows the luminosity limit for M 51 data corrected for the difference between absorption column densities in M 51 and the galaxy under consideration. The correction factor is close to unity at temperatures exceeding a few hundred eV, but may be considerable at low temperatures for soft spectra. These lines allow us to compare sensitivities of different datasets independently of absorption. In particular, this comparison demonstrates that despite the rather significant scatter in Chandra exposure and distances to galaxies, the selected galaxies have comparable detection sensitivity to sources with soft spectra.
In Fig. 5, solid red curves show the lower bound of the stability strip for the nuclear burning of hydrogen on the WD surface (Wolf et al. 2013). In plotting these curves, we used the Stefan-Boltzmann law to compute the effective temperature and the mass–radius relation for zero-temperature WDs from Panei et al. (2000). The WD mass changes along the curve from 0.51 M⊙ to 1.34 M⊙. We then used the black-body model in XSPEC, applied ISM absorption, and computed the 0.3−2 keV band luminosity corresponding to the given WD mass and effective temperature. For late-type galaxies, absorption column densities were fixed at corresponding median values from Table 3 while for early-type galaxies we used the Galactic value NH, Gal, as explained above. For Centaurus A we also show the location of this boundary for sources located in the dust lanes. Green lines in Fig. 5 show the tracks of the spectral model of the relativistic accretion disk around a Schwarzschild black hole (BH; Ebisawa et al. 1991). Along these lines, the mass accretion rate changes from 0.02 ṀEdd to 1 ṀEdd, and different lines correspond to the different black hole mass as marked by the number near the curves. To compute these tracks, we approximated the accretion disk emission spectrum using an absorbed black-body model. The absorption was applied similar to other models plotted in the figure.
All sources plotted in Fig. 5 have no significant (≥3σ) flux above 2 keV. For three late-type galaxies with bi-modal median energy distributions (M 83, M 51 and M 101) we plot only sources with median energy Ẽ ≲ 1.2 keV. These sources show rather compact distributions in the kTbb − LX plane with temperatures of 20−300 eV and X-ray luminosities in the range of 1036 − 1038 ergs s−1. For other galaxies, we only used the criterion of lack of statistically significant (≥3σ) emission above 2 keV. For these galaxies, distributions of sources extend significantly towards higher temperatures (cross-hair symbols in Fig. 5), which is not surprising as such a selection includes many sources with regular spectra. These sources are dominated by X-ray binaries and background AGNs and their discussion is beyond the scope of this paper. Sources with low median energy Ẽ ≲ 1.2 keV (solid orange symbols) tend to have lower temperatures than the majority of the sources in these galaxies and are discussed in the following section, along with soft sources in M 83, M 51, and M 101.
5.3. Foreground stars
To identify foreground stars we cross-correlated the lists of soft X-ray sources with the Gaia (Gaia Collaboration 2016) catalog, Data Release 2 (Gaia Collaboration 2018). With the search radii of 2″ we typically found two matches per galaxy except for Centaurus A where we found 12 matches. The large number of matches for Centaurus A is caused by its relative proximity to the Galactic plane. Some of the Gaia matches have statistically significant measurements of parallax or proper motion, with S/N > 3. These sources are classified as stars in the Galaxy and are excluded from further analysis; we mark them with open diamonds in Fig. 5.
6. Nature of soft and super-soft X-ray sources
Based on the first Chandra studies of nearby galaxies, Di Stefano & Kong (2003, 2004) proposed that soft sources in external galaxies could be divided into super-soft and quasi-soft. The former are characterized by color temperatures of kT ≲ 100 eV and are believed to be mostly associated with accreting WDs with nuclear burning of hydrogen on their surface, while the latter have temperatures in the range kT ∼ 100−300 eV and are possibly unrelated to WDs.
6.1. Super-soft X-ray sources and accreting WDs
In the commonly used albeit (over)simplified picture, it is assumed that the spectral energy distribution of nuclear burning WDs can be roughly described by a black-body spectrum (cf. Woods & Gilfanov 2013) with a color temperature close to the effective temperature. Observations of well-known SSSs in the Milky Way, Magellanic Clouds (e.g., Greiner 1996; Kahabka & Trumper 1996) seem to broadly support this assumption. The effective temperature of an accreting WD powered by nuclear burning of hydrogen on its surface is given by:
where ϵH = 6 × 1018 erg g−1 is the energy release in hydrogen fusion per unit mass of hydrogen, XH ≈ 0.72 is the hydrogen mass fraction of the accreting material, Ẽ is the mass accretion rate, and Rphot is the photospheric radius of the hydrogen-burning layer. Numerical calculations show that at the bottom of the stability strip, Rphot ∼ RWD and the photospheric radius increases with increasing Ẽ (Wolf et al. 2013).
The red solid line in Fig. 5 shows the temperature–luminosity relation computed at the lower bound of the stability strip and assuming Rphot = RWD. For the definition of the lower boundary of stable nuclear burning (dependent on WD mass) we used the results of Wolf et al. (2013), and for the WD radius we used zero temperature radius (also dependent on WD mass) from Panei et al. (2000). The region on the kTbb − LX diagram above and to the left of this line is permitted for accreting WDs stably burning hydrogen on their surface, while in the part of the diagram to the bottom-right, stable nuclear burning of hydrogen is not possible and this region should be populated with other types of soft X-ray sources. Indeed, Fig. 5 shows that in late-type galaxies (M 83, M 51, M 101 and M 81), there is a distinct group of rare soft and luminous sources located above these line. These sources have temperatures of approximately several tens of eV and seem to clearly stand out in the populations of soft sources in these galaxies. When interpreting the results shown in Fig. 5, one should bear in mind that it shows absorbed luminosities in the 0.3−2.0 keV band and that absorption and bolometric corrections increase roughly exponentially with decreasing color temperature, and therefore the softest sources are truly luminous.
For this reason, we classify sources to the left of the red line in Fig. 5 as classical SSSs. We also include those sources that are located outside the stable nuclear burning boundary but whose error bars cross this boundary. In addition, we added to this list two sources in M 101 that are located outside but close to the stable nuclear burning boundary (the two sources in the upper right panel of Fig. 5 with kT ≳ 100 eV and LX ≳ 1037 erg s−1). The catalog of SSSs is presented in Table C.1, and their numbers in galaxies from our sample are listed in Table 2.
6.2. Specific frequency of super-soft X-ray sources across morphological types
From Fig. 5, it is evident that SSSs are considerably more abundant in late-type galaxies than in early-type galaxies. However, for a statistically sound conclusion one needs to take into consideration the completeness limits of the various data sets. To this end we used the sensitivity limit for M 51 corrected for the difference in the absorption column density as described in Sect. 5.2 to select SSSs. In each galaxy, we selected sources to the left of the thick red line and above the dashed blue line in Fig. 5. This selection is within the 20 counts flux limit (solid black line in Fig. 5) in all galaxies, except for M 83 where at the low temperature end the 20 counts limit for this galaxy is higher by a factor of about two. This may result in slight underestimation of the specific frequency of super-soft sources in late-type galaxies. In Centaurus A, we used different criteria for sources located in and outside the dust lanes (cf. dotted line in Fig. 5), although this does not change the final result.
In order to estimate specific frequencies of SSSs, we group the data separately for early- and late-type galaxies. There are 29 super-soft sources in late-type galaxies (M 83, M 51, M 81, M 101), which, for the total stellar mass of 13.9 × 1010 M⊙ yield the specific frequency of
In computing statistical errors we used Gehrels approximation (Gehrels 1986). Counting lenticular and elliptical galaxies together (Centaurus A, NGC 3115, NGC 3379, NGC 4278, NGC 4697), we find seven SSSs for the total stellar mass of 28.3 × 1010 M⊙, yielding a specific frequency of
Centaurus A galaxy, although classified as S0, shows some star-formation activity within its dust lanes, at the level of ∼0.8 M⊙ yr−1 (Espada et al. 2019). However, its SSS specific frequency is closer to early-type galaxies than to late-type galaxies. In order to check how its inclusion in our sample affects our results, we compute the SSS specific frequency for elliptical galaxies only:
This number is ∼20% smaller but compatible with the value obtained including Centaurus A. The lower limit for the SSS specific frequency in early-type galaxies at the 3σ confidence level is 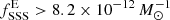 . The ratio of specific frequencies of SSS in late-type to early-type galaxies is
. The ratio of specific frequencies of SSS in late-type to early-type galaxies is
which means that late-type galaxies contain about eight times more SSSs than early-type galaxies. Using a Bayesian approach, we estimate that their specific frequencies are different at the confidence level corresponding to about ≈5.8σ.
We searched for variations of the SSS specific frequency between galaxies of the same morphological type. To this end, we compared observed numbers of SSSs in each galaxy with their expected values computed from the corresponding SSS specific frequency and stellar mass of the galaxy. For early-type galaxies, we find no statistically significant deviations of observed numbers of SSSs from their expected values. This is not surprising, given the small numbers of SSSs in early-type galaxies. However, for the late-type galaxies, we observe statistically significant deviations in M 83 and M 81 where the observed numbers of super-soft sources differ from the expected values at the statistically significant levels exceeding ∼3σ. This can be understood considering that populations of accreting nuclear burning WDs are determined by the long-term star-formation history of their host galaxy rather than by its mass, as discussed in the following section.
For late-type galaxies, we also compute the SSS specific frequency per unit of star formation rate. Using SFR values collected from the literature (Table 1 and references there) we obtain:
Overall, the numbers of SSSs in late-type galaxies appear to somewhat better correlate with their star-formation rate than with stellar mass.
6.3. Comparison with previous work and discussion
The fact that SSSs tend to be predominantly associated with young stellar populations has been noted previously (e.g., Di Stefano & Kong 2004). Studying populations of soft sources in nearby galaxies, Di Stefano (2010) mentioned the difference in the numbers of soft sources in early- and late-type galaxies, but they did not quantify these trends. Using a sample of 12 nearby late-type galaxies, Bogdán & Gilfanov (2011) concluded that specific frequencies (per unit K-band luminosity) of luminous (LX > 1036 erg s−1) super-soft sources in disks of spiral galaxies exceed those of bulges by factor of approximately two. Taking into account the fact that the typical M*/LK ratio for bulges is approximately twice that found for disks, this translates to a factor four difference in specific frequency per unit mass, which is qualitatively the same trend as that seen in our comparison of late-type and early-type galaxies, although the particular numbers are different. The above difference is due to the fact that Bogdán & Gilfanov (2011) used a selection procedure to identify SSSs based on the hardness ratio with the threshold, corresponding to kT = 200 eV.
Population synthesis calculations of nuclear burning, accreting WDs predict a difference in specific frequencies of SSSs in spiral and elliptical galaxies (Chen et al. 2015). Using their model a025qc17, we estimate specific frequencies of SSSs with X-ray luminosities exceeding 1036 erg s−1. For spiral galaxies, these latter authors obtained specific frequencies ranging from 4 × 10−10 to 2 × 10−9 sources per M⊙, corresponding to absorption column densities of 3 × 1021 cm−2 and 3 × 1020 cm−2. For elliptical galaxies, they obtained ≈6 × 10−11 sources per M⊙ (for column density 3 × 1020 cm−2), which is approximately seven times that found for late-type galaxies. The contrast between late- and early-type galaxies is highly consistent with our observations, especially taking into account the dependence of these numbers on the age of the host galaxy (Chen et al. 2015). However, the actual numbers of specific frequencies are larger in simulations than in our data by at least a factor of between about two and three. Among other possibilities, this could be understood as a result of the approximate account for absorption, as the numbers of observable SSSs are highly sensitive to the column density.
Another interesting result of this work is that within the morphological types, the number of SSSs does not seem to obey simple scaling relations with parameters of the host galaxy. In particular, there are large and statistically significant excursions in the specific frequency of SSSs in spiral galaxies normalised to their stellar mass. This could be expected in view of the results of the WD population modeling, which predict that the population of super-soft sources peaks at about 1 Gyr after the star formation event (Chen et al. 2015). For this reason, numbers of super-soft sources in galaxies should not be expected to scale with stellar mass or current star-formation rate. In a more general context, the low specific frequency of SSSs, especially in early-type galaxies, supports the earlier conclusion that they are not the major class of type Ia supernova progenitors (Di Stefano 2010; Gilfanov & Bogdán 2010; Johansson et al. 2014; Woods & Gilfanov 2014).
6.4. Other soft X-ray sources
Along with rare SSSs, in all galaxies from our sample there are much more abundant populations of soft sources with somewhat harder – but still relatively soft – spectra located to the right of the stable nuclear burning boundary in Fig. 5. These sources were previously classified as quasi-soft X-ray sources (Di Stefano & Kong 2004; Orio 2006). Among other hypotheses, it was proposed that they are associated with SNRs or with accreting BHs in the soft spectral state (e.g., Di Stefano & Kong 2004; Patel et al. 2013; Long et al. 2014; Kuntz et al. 2016), although the contribution of the latter should be minimal (Sect. 5.2).
The X-ray-emitting SNRs will be largely unresolved by Chandra and appear as point sources. Indeed, the SNR emission shifts outside the X-ray band when the shock slows down to about ∼200 km s−1 and the post-shock temperature drops below ∼106 K (Vink 2017). This happens about ∼2 × 104 years after the explosion when the remnant size typically reaches ∼10−20 pc (Blondin et al. 1998). At the distances of spiral galaxies of 3.6−7.6 Mpc, the linear dimensions of 10−20 pc correspond to the angular sizes of ∼0.4−0.9″, which can barely be resolved with Chandra ACIS for the brightest sources. Furthermore, the majority of SNRs will be classified as soft sources according to their hardness ratio and median energy.
We used M 83 as a test case to clarify the nature of soft sources located to the right of the stable nuclear burning boundary. This galaxy has one of the best studied X-ray SNR populations. Long et al. (2014) identified 87 X-ray detected SNR candidates based on their X-ray spectral properties and associations with optical emission nebulae and/or radio sources. From this sample, the SNR nature of 67 sources was confirmed with optical spectroscopy using the [SII]/Hα line ratio (Winkler et al. 2017). The list of 87 X-ray-detected SNRs from Long et al. (2014) was cross-correlated with our catalog of X-ray sources detected in M 83. With 1″ matching radius, we found 66 matches, of which 6 sources have statistically significant emission beyond 2 keV and the remaining 60 sources were classified as soft sources in our analysis. We replot the kTbb − LX diagram for M 83 in Fig. 6 marking confirmed SNRs by cyan symbols. As one can see, all confirmed SNRs are located outside the stable hydrogen nuclear burning boundary on the kTbb − LX diagram (i.e., to the right of the thick red line in Fig. 6) and their distribution on the kTbb − LX plane is morphologically quite similar to the distribution of the majority of the quasi-soft sources. We therefore conclude that the majority of the quasi-soft sources must be SNRs.
 |
Fig. 6. kTbb − LX for soft X-ray sources in M 83. Supernova remnants confirmed by optical and radio data are shown by cyan circles. See Fig. 5 for a detailed description of the kTbb − LX diagram. |
For many of the brightest quasi-soft sources in spiral galaxies, the likelihood values obtained from spectral fitting suggest that the spectrum is more complicated than predicted by a featureless black-body model. A more detailed investigation of several such sources revealed that these deviations are mostly associated with the presence of emission lines in their spectra. In the majority of cases, the spectrum of thermal emission of optically thin plasma or a nonequilibrium ionization model significantly improved the quality of the fit, suggesting that these sources may be SNRs. However, such a detailed analysis is only possible for a handful of brightest sources.
In order to compare spectral properties of soft and super-soft sources, we combined their spectra in late- and early-type galaxies. Combined spectra are shown in Fig. 7 separately for sources located inside and outside the stable hydrogen nuclear burning boundary on the kTbb − LX diagram (see Sect. 5.2). For comparison, we also show the combined spectrum of confirmed SNRs in M 83. As seen in Fig. 7, the combined spectrum of soft sources in spiral galaxies shows strong Mg and S lines and closely matches the combined spectrum of SNRs in M 83. Similar values of the equivalent width of Mg and S lines support our conclusion that the vast majority of soft sources in these galaxies must be SNRs. In early-type galaxies on the other hand, the combined spectrum of soft sources is harder and does not show strong emission lines. As discussed in Sect. 5.2, because of the chosen method of selection, soft sources in early-type galaxies should include large numbers of X-ray binaries and background AGNs. On the other hand, SSSs in all galaxies have much softer spectra, as expected. Their spectra are broadly similar in late- and early-type galaxies, although the quality of the latter prevents a more quantitative conclusion.
 |
Fig. 7. Combined spectra of soft and SSSs in late- and early-type galaxies. Black and green symbols show the integrated spectrum of all soft sources located outside the stable nuclear burning region for WDs (i.e., located to the right of the thick red line in Fig. 5) in late- and early-type galaxies. Yellow symbols show integrated spectrum of sources matching confirmed SNRs in M 83. Blue and red symbols show the integrated spectra of SSSs, i.e., sources located to the left of and above the stable nuclear burning boundary in late- and early-type galaxies, respectively. The spectra are normalized to the same flux at 0.35 keV. See Sect. 6.1 for more details. |
We finally note that the numbers and specific frequencies of soft sources in galaxies from our sample seem to follow the same trend as that found for super-soft sources, decreasing from late- to early-type galaxies. However, a detailed investigation of the dependence of the specific frequency of SNRs on morphological type would require a more accurate selection of sources and is outside the scope of the present paper.
7. Summary
Based on public Chandra archival data, we studied populations of soft and super-soft X-ray sources with the aim being to investigate populations of stable nuclear burning, accreting WDs. To this end, we searched the Chandra data archive and constructed an optimal sample of galaxies for studying populations of stable nuclear burning, accreting WDs. We aimed to construct the best possible sample of such galaxies. We selected four late-type and five early-type galaxies with stellar masses ≳1010 M⊙ and Chandra X-ray sensitivity limits comparable to or better than ∼1036 ergs s−1. Our selection presents the nearly full sample of galaxies available in the Chandra archive up to cycle 20 and suitable for such a study (among galaxies fitting within the field of view of Chandra observation).
We proposed a new approach to identify the population of soft and SSSs based on combination of hardness ratio and median energy. The distributions of sources over median energy in late-type galaxies show clear bi-modality with distinct populations of soft and super-soft sources. These sources show a rather compact distribution in the X-ray luminosity–temperature plane with temperatures of 20−300 eV and X-ray luminosities in the 1036 − 1038 ergs s−1 range. The picture is more complex for lenticular and elliptical galaxies, where populations of soft sources smoothly connect to the populations of X-ray binaries and background AGNs in their median energy distributions. For these galaxies, we mainly used the lack of emission above 2 keV to select soft sources for detailed analysis.
We used the X-ray luminosity–temperature diagram to further classify selected sources into super-soft and soft. To this end we used the theoretical boundary of stable hydrogen nuclear burning on the surface of accreting WDs to separate SSSs from the rest of the population of soft sources. In late-type galaxies, we found 29 super-soft sources which yields a specific frequency of 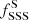 ≈ (2.08 ± 0.46) × 10−10
≈ (2.08 ± 0.46) × 10−10 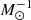 . In lenticular and elliptical galaxies, there are seven super-soft sources, giving a specific frequency of
. In lenticular and elliptical galaxies, there are seven super-soft sources, giving a specific frequency of 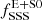 ≈ (2.47 ± 1.34) × 10−11
≈ (2.47 ± 1.34) × 10−11 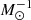 . Specific frequencies in late- and early-type galaxies differ with a statistical confidence of ≈5.8σ. The ratio of specific frequencies of SSSs in late- and early-type galaxies is
. Specific frequencies in late- and early-type galaxies differ with a statistical confidence of ≈5.8σ. The ratio of specific frequencies of SSSs in late- and early-type galaxies is 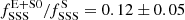 . Our results are broadly consistent with population synthesis modeling of the populations of stable nuclear burning, accreting WDs.
. Our results are broadly consistent with population synthesis modeling of the populations of stable nuclear burning, accreting WDs.
We note that the particular location of the boundary between super-soft sources and X-ray binaries in Fig. 2 depends on the hydrogen column density NH and details of the instrument response. The curves plotted in Fig. 2 (left panel) have been computed for the 2012 (Cycle 13) Chandra ACIS-S response. For other Chandra calibration epochs their shape and location along the x-axis will be (slightly) different.
Some of the hard sources are located at Ẽ ≳ 2 keV, too large for a power-law spectrum with a slope of Γ ≲ 2 (Fig. 2, left panel). These are either sources with genuinely large Ẽ, e.g., absorbed AGNs, or faint sources where the contribution of the instrumental background becomes important and shifts the median energy to unphysically large values.
NASA/IPAC Extragalactic Database: https://ned.ipac.caltech.edu
See, e.g., incompleteness function of Chandra data for Centaurus A in Voss & Gilfanov (2006). From their Fig. A.1, incompleteness effects become relatively small at luminosities of about two to three times the detection limit of the data.
Acknowledgments
This research has made use of data obtained from the Chandra Data Archive and software provided by the Chandra X-ray Center (CXC) in the application packages CIAO. This publication makes use of data products from the HyperLeda and RC3 database. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation; the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. The authors acknowledge partial support of this work by the Russian Government Program of Competitive Growth of Kazan Federal University (IG) and by the RSF grant 19-12-00369 (MG). The authors thank the anonymous referee for useful and inspiring suggestions which helped to improve the manuscript.
References
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Bell, E. F., & de Jong, R. S. 2001, ApJ, 550, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Blondin, J. M., Wright, E. B., Borkowski, K. J., & Reynolds, S. P. 1998, ApJ, 500, 342 [NASA ADS] [CrossRef] [Google Scholar]
- Bogdán, Á., & Gilfanov, M. 2011, MNRAS, 412, 401 [Google Scholar]
- Bresolin, F., Ryan-Weber, E., Kennicutt, R. C., & Goddard, Q. 2009, ApJ, 695, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, H.-L., Woods, T. E., Yungelson, L. R., Gilfanov, M., & Han, Z. 2014, MNRAS, 445, 1912 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, H.-L., Woods, T. E., Yungelson, L. R., Gilfanov, M., & Han, Z. 2015, MNRAS, 453, 3024 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, H.-L., Woods, T. E., Yungelson, L. R., Gilfanov, M., & Han, Z. 2016, MNRAS, 458, 2916 [Google Scholar]
- Ciardullo, R., Feldmeier, J. J., Jacoby, G. H., et al. 2002, ApJ, 577, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Colombo, D., Meidt, S. E., Schinnerer, E., et al. 2014, ApJ, 784, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Cowley, A. P., Schmidtke, P. C., Crampton, D., & Hutchings, J. B. 1990, ApJ, 350, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Crosthwaite, L. P., Turner, J. L., Buchholz, L., Ho, P. T. P., & Martin, R. N. 2002, AJ, 123, 1892 [NASA ADS] [CrossRef] [Google Scholar]
- Dame, T. M., Hartmann, D., & Thaddeus, P. 2001, ApJ, 547, 792 [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin, H. G., Jr., et al. 1991, Third Reference Catalogue of Bright Galaxies (New York: Springer) [Google Scholar]
- Di Stefano, R. 2010, ApJ, 712, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Di Stefano, R., & Kong, A. K. H. 2003, ApJ, 592, 884 [NASA ADS] [CrossRef] [Google Scholar]
- Di Stefano, R., & Kong, A. K. H. 2004, ApJ, 609, 710 [NASA ADS] [CrossRef] [Google Scholar]
- Ebisawa, K., Mitsuda, K., & Hanawa, T. 1991, ApJ, 367, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Espada, D., Verley, S., Miura, R. E., et al. 2019, ApJ, 887, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrarese, L., Mould, J. R., Stetson, P. B., et al. 2007, ApJ, 654, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, W. L., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553, 47 [Google Scholar]
- Fruscione, A., McDowell, J. C., Allen, G. E., et al. 2006, in SPIE Conf. Ser., eds. D. R. Silva, & R. E. Doxsey, 6270, 62701V [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garcia-Burillo, S., Guelin, M., & Cernicharo, J. 1993, A&A, 274, 123 [Google Scholar]
- Gehrels, N. 1986, ApJ, 303, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Gilfanov, M., & Bogdán, Á. 2010, Nature, 463, 924 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Greiner, J. 1996, Catalog of Luminous Supersoft X-ray Sources, 472, 299 [Google Scholar]
- Greiner, J., Hasinger, G., & Kahabka, P. 1991, A&A, 246, L17 [NASA ADS] [Google Scholar]
- Guelin, M., Zylka, R., Mezger, P. G., Haslam, C. G. T., & Kreysa, E. 1995, A&A, 298, L29 [NASA ADS] [Google Scholar]
- Henze, M., Pietsch, W., Haberl, F., et al. 2010, A&A, 523, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henze, M., Pietsch, W., Haberl, F., et al. 2011, A&A, 533, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henze, M., Pietsch, W., Haberl, F., et al. 2014, A&A, 563, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- HI4PI Collaboration (Ben Bekhti, N., et al.) 2016, A&A, 594, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hillman, Y., Prialnik, D., Kovetz, A., & Shara, M. M. 2015, MNRAS, 446, 1924 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, L. C., Li, Z.-Y., Barth, A. J., Seigar, M. S., & Peng, C. Y. 2011, ApJS, 197, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Hong, J., Schlegel, E. M., & Grindlay, J. E. 2004, ApJ, 614, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, N., Wang, E., Lin, Z., et al. 2018, ApJ, 854, 68 [Google Scholar]
- Jarrett, T. H., Chester, T., Cutri, R., Schneider, S. E., & Huchra, J. P. 2003, AJ, 125, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Jarrett, T. H., Masci, F., Tsai, C. W., et al. 2013, AJ, 145, 6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johansson, J., Woods, T. E., Gilfanov, M., et al. 2014, MNRAS, 442, 1079 [NASA ADS] [CrossRef] [Google Scholar]
- Kahabka, P., & Trumper, J. 1996, in Compact Stars in Binaries, eds. J. van Paradijs, E. P. J. van den Heuvel, & E. Kuulkers, 165, 425 [Google Scholar]
- Kahabka, P., Pietsch, W., & Hasinger, G. 1994, A&A, 288, 538 [Google Scholar]
- Karachentsev, I. D., Makarov, D. I., & Kaisina, E. I. 2013, AJ, 145, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Kuntz, K. D., Long, K. S., & Kilgard, R. E. 2016, ApJ, 827, 46 [Google Scholar]
- Leroy, A. K., Walter, F., Bigiel, F., et al. 2009, AJ, 137, 4670 [NASA ADS] [CrossRef] [Google Scholar]
- Long, K. S., Helfand, D. J., & Grabelsky, D. A. 1981, ApJ, 248, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Long, K. S., Kuntz, K. D., Blair, W. P., et al. 2014, ApJS, 212, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Makarov, D., Prugniel, P., Terekhova, N., Courtois, H., & Vauglin, I. 2014, A&A, 570, A13 [CrossRef] [EDP Sciences] [Google Scholar]
- Moustakas, J., Kennicutt, R. C., Jr., Tremonti, C. A., et al. 2010, ApJS, 190, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K. 1982, ApJ, 253, 798 [Google Scholar]
- Nomoto, K., Saio, H., Kato, M., & Hachisu, I. 2007, ApJ, 663, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- Orio, M. 2006, ApJ, 643, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Pakull, M. W., Beuermann, K., van der Klis, M., & van Paradijs, J. 1988, A&A, 203, L27 [NASA ADS] [Google Scholar]
- Panei, J. A., Althaus, L. G., & Benvenuto, O. G. 2000, A&A, 353, 970 [Google Scholar]
- Patel, B., Di Stefano, R., Nelson, T., et al. 2013, ApJ, 771, 6 [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Peletier, R. F., Davies, R. L., Illingworth, G. D., Davis, L. E., & Cawson, M. 1990, AJ, 100, 1091 [NASA ADS] [CrossRef] [Google Scholar]
- Pietsch, W., Fliri, J., Freyberg, M. J., et al. 2005, A&A, 442, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prestwich, A. H., Irwin, J. A., Kilgard, R. E., et al. 2003, ApJ, 595, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Prialnik, D., & Kovetz, A. 1995, ApJ, 445, 789 [NASA ADS] [CrossRef] [Google Scholar]
- Rider, P. R. 1960, J. Am. Stat. Assoc., 55, 148 [Google Scholar]
- Saha, A., Thim, F., Tammann, G. A., Reindl, B., & Sandage, A. 2006, ApJS, 165, 108 [Google Scholar]
- Serra, P., Oosterloo, T., Morganti, R., et al. 2012, MNRAS, 422, 1835 [Google Scholar]
- Smale, A. P., Corbet, R. H. D., Charles, P. A., et al. 1988, MNRAS, 233, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Soraisam, M. D., Gilfanov, M., Wolf, W. M., & Bildsten, L. 2016, MNRAS, 455, 668 [NASA ADS] [CrossRef] [Google Scholar]
- Stanghellini, L., Magrini, L., Casasola, V., & Villaver, E. 2014, A&A, 567, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Starrfield, S., Timmes, F. X., Hix, W. R., et al. 2013, in Binary Paths to Type Ia Supernovae Explosions, eds. R. Di Stefano, M. Orio, & M. Moe, 281, 166 [Google Scholar]
- Strong, A. W., & Mattox, J. R. 1996, A&A, 308, L21 [NASA ADS] [Google Scholar]
- Struve, C., Oosterloo, T. A., Morganti, R., & Saripalli, L. 2010, A&A, 515, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Swartz, D. A., Ghosh, K. K., Suleimanov, V., Tennant, A. F., & Wu, K. 2002, ApJ, 574, 382 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, M. B. 2006, in Astronomical Data Analysis Software and Systems XV, eds. C. Gabriel, C. Arviset, D. Ponz, & S. Enrique, ASP Conf. Ser., 351, 666 [Google Scholar]
- Tonry, J. L., Dressler, A., Blakeslee, J. P., et al. 2001, ApJ, 546, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Trümper, J., Hasinger, G., Aschenbach, B., et al. 1991, Nature, 349, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Truran, J. W., & Glasner, S. A. 1995, in On the Nature of the Soft X-ray Emission from Nova GQ Muscae 1983, eds. A. Bianchini, M. della Valle, & M. Orio, 205, 453 [Google Scholar]
- van den Heuvel, E. P. J., Bhattacharya, D., Nomoto, K., & Rappaport, S. A. 1992, A&A, 262, 97 [Google Scholar]
- Vink, J. 2017, in X-ray Emission Properties of Supernova Remnants, eds. A. W. Alsabti, & P. Murdin, 2063 [Google Scholar]
- Voss, R., & Gilfanov, M. 2006, A&A, 447, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walter, F., Brinks, E., de Blok, W. J. G., et al. 2008, AJ, 136, 2563 [Google Scholar]
- Weisskopf, M. C., Wu, K., Trimble, V., et al. 2007, ApJ, 657, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Whelan, J., & Iben, I., Jr. 1973, ApJ, 186, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Willmer, C. N. A. 2018, ApJS, 236, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [Google Scholar]
- Winkler, P. F., Blair, W. P., & Long, K. S. 2017, ApJ, 839, 83 [Google Scholar]
- Wolf, W. M., Bildsten, L., Brooks, J., & Paxton, B. 2013, ApJ, 777, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Woods, T. E., & Gilfanov, M. 2013, MNRAS, 432, 1640 [NASA ADS] [CrossRef] [Google Scholar]
- Woods, T. E., & Gilfanov, M. 2014, MNRAS, 439, 2351 [NASA ADS] [CrossRef] [Google Scholar]
- Yaron, O., Prialnik, D., Shara, M. M., & Kovetz, A. 2005, ApJ, 623, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Yungelson, L. R. 2010, Astron. Lett., 36, 780 [NASA ADS] [CrossRef] [Google Scholar]
- Yungelson, L., & Livio, M. 1998, ApJ, 497, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Z., Gilfanov, M., & Bogdán, Á. 2012, A&A, 546, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: List of observations
Table A.1 provides a list of the Chandra observations used in this paper. Columns are: (1) Galaxy name; (2) Observation identification number; (3) Date of observations; (4) Exposure time; (5) Type of ACIS camera used during observations.
Chandra observations used for the analysis.
Appendix B: Galaxy images
Figure B.1 shows X-ray images of galaxies in our sample and outlines of analysed regions.
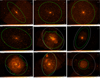 |
Fig. B.1. 0.3−2 keV band false-color images (smoothed) of galaxies in our sample. Dashed white regions correspond to D25. Green lines show regions used for source detection having exposure map values greater than 20% of maximal value (for more detail see Sect. 3.1). Stellar masses listed in Table 2 are computed for these regions. The inside areas of small green regions near the center of Centaurus A, M 83 and M 51 were excluded from analysis. |
Appendix C: Catalog of super-soft X-ray sources
The catalog is comprised of super-soft X-ray sources with more than 20 counts (solid black line in Fig. 5.) The sources are classified as super-soft if they are located to the left of the stable nuclear burning boundary (nearly vertical solid red line in Fig. 5) or their error bars cross this boundary. We also included two sources in M 101, located outside but close to the stable nuclear burning boundary (the two sources in Fig. 5 upper right panel with kT ≳ 100 eV and LX ≳ 1037 erg s−1). The catalog of super-soft X-ray sources in given in Table C.1.
Super-soft X-ray sources.
All Tables
All Figures
 |
Fig. 1. X-ray sensitivity–distance diagram of nearby galaxies observed by Chandra up to cycle 20. Each panel corresponds to a certain morphological type of galaxy. Filled (open) symbols correspond to galaxies with stellar mass M* ≥ 1010 M⊙(M* < 1010 M⊙). See Sect. 2 for details. |
| In the text | |
 |
Fig. 2. Left: relation of the median energy to the temperature of a black-body model (left-hand curves and y-axis, blue in the color version of this plot) and to the photon index of a power-law model (right curves and y-axis, red). Simulations for the Chandra ACIS-S detector with Cycle 13 (2012) response. An absorption column density of 1021 cm−2 was assumed. Solid lines show models without background, dotted lines show models with 50% contribution of background counts. Parameter ranges are relevant to super-soft sources and X-ray binaries, and the two types of spectra are clearly separated at about Ẽ ≈ 1.0−1.3 keV. Right: verification of the source classification procedure in M 51. Distribution of sources with median energy Ẽ ≤ 2 keV over the photon index of the power-law model. The blue and red dashed histograms show the distributions of sources classified as soft and hard, respectively, and the black solid line indicates the total distribution. |
| In the text | |
 |
Fig. 3. Hardness ratio vs. median energy diagram for compact X-ray sources in the galaxies of our sample. Only sources with ≥20 net counts are plotted. Dashed lines show the median energy boundary of Ẽ0 = 1.2 keV (see Sect. 4.2). The distributions of sources over median energy are plotted below their corresponding median energy–hardness ratio diagram. |
| In the text | |
 |
Fig. 3. continued. |
| In the text | |
 |
Fig. 4. Relations between black-body temperature (left) and absorbed X-ray luminosity (center) values computed with NH being a free parameter of X-ray spectral fit (y-axes) and for NH computed from Eq. (5) with f = 0.5 (x-axes). Right-hand panel: relation between bets-fit NH and NH computed from Eq. (5). Only sources with net counts ≥200 are shown. Errors are 1σ. See Sect. 5.1 for more details. |
| In the text | |
 |
Fig. 5. kTbb − LX diagram for soft X-ray sources in the galaxies of our sample. A cut of 20 net counts was applied. The luminosities are in the 0.3−2.0 keV band and are not corrected for absorption. All plotted sources have no statistically significant flux above 2 keV (open circles). Sources with median energy Ẽ ≤ 1.2 keV are shown with solid orange circles. Sources with Gaia matches of measured parallax or proper motion are marked by black diamonds. Solid red curves show kTbb − LX relations at the lower boundary of stable nuclear burning. Along these curves, the WD mass increases from 0.51 M⊙ at the lower left end to 1.34 M⊙ at the upper right end. The dotted red line for Centaurus A shows the location of this boundary in the dust lanes of this galaxy. Green lines correspond to the emission spectrum of the general relativistic accretion disk model around a Schwarzschild BH (Ebisawa et al. 1991) for BH masses of 10, 20, 30, and 50 M⊙. The accretion rate changes along the curves from 0.02 ṀEdd to 1 ṀEdd. Horizontally oriented solid black curves show the luminosity corresponding to 20 net counts. The dashed blue line on each plot shows the 20 counts luminosity limit for M 51 corrected for the difference in absorption column density between M 51 and the galaxy under consideration. All model curves show absorbed luminosities. Errors are at 1σ confidence. See Sect. 5.2 for details of calculations. |
| In the text | |
 |
Fig. 6. kTbb − LX for soft X-ray sources in M 83. Supernova remnants confirmed by optical and radio data are shown by cyan circles. See Fig. 5 for a detailed description of the kTbb − LX diagram. |
| In the text | |
 |
Fig. 7. Combined spectra of soft and SSSs in late- and early-type galaxies. Black and green symbols show the integrated spectrum of all soft sources located outside the stable nuclear burning region for WDs (i.e., located to the right of the thick red line in Fig. 5) in late- and early-type galaxies. Yellow symbols show integrated spectrum of sources matching confirmed SNRs in M 83. Blue and red symbols show the integrated spectra of SSSs, i.e., sources located to the left of and above the stable nuclear burning boundary in late- and early-type galaxies, respectively. The spectra are normalized to the same flux at 0.35 keV. See Sect. 6.1 for more details. |
| In the text | |
 |
Fig. B.1. 0.3−2 keV band false-color images (smoothed) of galaxies in our sample. Dashed white regions correspond to D25. Green lines show regions used for source detection having exposure map values greater than 20% of maximal value (for more detail see Sect. 3.1). Stellar masses listed in Table 2 are computed for these regions. The inside areas of small green regions near the center of Centaurus A, M 83 and M 51 were excluded from analysis. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



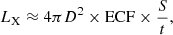
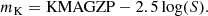
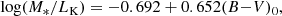
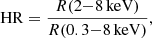
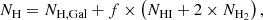
![$$ \begin{aligned} N_{\rm HI} [\mathrm{cm^{-2}}] = \frac{1.11\times 10^{24}\times I_{\rm HI}}{FWHM_{\rm maj}[{}^{\prime \prime }] \times FWHM_{\rm min}[{}^{\prime \prime }]} , \end{aligned} $$](/articles/aa/full_html/2021/02/aa39522-20/aa39522-20-eq12.gif)
![$$ \begin{aligned} N_{\rm H_2}[\mathrm{cm^{-2}}] =\frac{R_{21}}{0.8} \times X_{\rm CO}\times W_{\rm CO}, \end{aligned} $$](/articles/aa/full_html/2021/02/aa39522-20/aa39522-20-eq13.gif)