EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 645 (January 2021) A&A, 645 (2021) A74 Full HTML
Free Access
Issue
A&A
Volume 645, January 2021
Article Number A74
Number of page(s) 11
Section Catalogs and data
DOI https://doi.org/10.1051/0004-6361/202039431
Published online 14 January 2021

© ESO 2021

1. Introduction

The XMM-Newton mission (Jansen et al. 2001) launched in 1999 is the second cornerstone mission of the European Space Agency (ESA). It carries three telescopes with the largest effective area in an X-ray telescope so far (combined 5000 cm2 at 1 keV). These telescopes focus the light on the European Photon Imaging Camera (EPIC) CCD cameras. Owing to its large field of view (∼30 arcmin diameter), it can detect a large number of serendipitous sources in each observation. The Survey Science Centre (SSC), a consortium of ten European Institutes, was formed and is responsible for producing the catalogues of the serendipitous sources detected. The third version of this catalogue (3XMM) has been published and is described in detail in Rosen et al. (2016). The 3XMM covers about 1000 square degrees and contains about half a million unique sources. This is the largest catalogue of X-ray sources ever produced. The median flux of the sources is ∼2.4 × 10−14 erg cm−2 s−1 in the total 0.2–12 keV band.

The large sky area of the 3XMM provides an opportunity to identify rare objects, such as high-luminosity active galactic nuclei (AGNs), that are harder to find in deeper surveys with much smaller sky areas. Moreover, the sensitivity and energy range of the 3XMM allows the detection of X-ray absorbed AGNs, which are elusive in shallower and/or softer surveys. In addition, the SSC provides spectral products for a large number of 3XMM sources, allowing a systematic study of the spectral properties of this latest catalogue.

The goal of this work is the construction of a clean, reliable sample of X-ray absorbed AGNs, after a robust, systematic analysis of their X-ray spectra included in the 3XMM. Given the size of the available dataset (more than 170 000 spectra in the sixth version of the catalogue, 3XMM-DR6), the use of automated spectral modelling techniques is mandatory. The XMM-Newton spectral-FIT CATalogue (XMMFITCAT; Corral et al. 2015) was a previous effort in this direction. This catalogue offers spectral fits for a large fraction of 3XMM sources for which spectral data are available and has been used to identify X-ray absorbed sources (Corral et al. 2014). However, due to the lack of redshift information for the majority of 3XMM sources, it was not possible to provide physical, reliable estimations for the X-ray absorption (i.e. hydrogen column density) or other spectral parameters and derived quantities (e.g. temperature of plasmas or luminosities).

Obtaining spectroscopic redshifts for the bulk of the 3XMM catalogue would be extremely costly in observational terms. Therefore, using photometric redshifts is the only feasible technique to obtain distance information for such a large number of sources. The XMM-Newton Photo-Z CATalogue (XMMPZCAT) offers photometric redshifts for a large fraction of 3XMM sources: In the framework of the ESA Prodex project we derived photometric redshifts for 100 178 X-ray sources, about 50% of the total number of 3XMM sources (205 380) in the XMM-Newton fields selected to build XMMPZCAT (4208 out of 9159). The photometric redshifts were derived using a machine-learning algorithm, Trees for Photo-Z (TPZ; Carrasco Kind & Brunner 2013). The optical photometry used for the derivation of photometric redshifts included the SDSS survey and the PANSTARS survey, with ancillary data in near- (NIR: 2MASS, UKIDSS, VISTA) and mid-infrared (MIR; All-WISE survey) bands. See Ruiz et al. (2018) for a complete description of this catalogue.

In this work we combine the results of XMMPZCAT with the automated spectral fitting approach of XMMFITCAT in order to estimate X-ray models and the corresponding spectral properties for 30 816 3XMM detections. These results are collected in the XMM-Newton spectral-fit z catalogue (XMMFITCAT-Z).

As a demonstration of the scientific potential of XMMFITCAT-Z, we searched for sources showing spectral features of X-ray absorbed AGNs. We found 1421 spectra with signs of X-ray absorption (∼5% of the total catalogue), corresponding to 1037 unique sources. After further examination of their X-ray properties, we selected 977 detections for our final sample, corresponding to 765 unique sources, showing highly reliable absorption features and redshift estimations.

The structure of the paper is as follows: in Sect. 2 we describe the XMMFITCAT-Z, including the data and techniques used to build the catalogue. Section 3 explains our methodology for identifying X-ray absorption and presents the final atlas of X-ray absorbed AGNs. In Sect. 4 we discuss our results, while Sect. 5 summarises the main conclusions of this work.

2. XMMFITCAT-Z: A catalogue of automatic X-ray spectral fitting

In this work we present the XMM-Newton spectral-fit z catalogue1 (XMMFITCAT-Z): using the pipeline spectral products from the 3XMM catalogue (see Sect. 2.1.1) and the redshifts we derived in XMMPZCAT (see Sect. 2.1.2), we built a catalogue of X-ray spectral fits, similar to XMMFITCAT (Corral et al. 2015) but now including the distance information in an automated spectral fitting process. This allows the estimation of important physical parameters from the X-ray spectra, such as rest-frame column densities, temperature of emitting plasma, intrinsic fluxes, and luminosities.

XMMFITCAT-Z contains spectral-fitting results for 30 816 source detections, corresponding to 22 677 unique sources. The version of the catalogue used to construct the current catalogue is 3XMM-DR6. Not all detections with extracted spectra are included in this database. To ensure the reliability of the spectral-fitting results, a constraint has been imposed on the number of counts collected in the X-ray spectra (Sect. 2.1.1), and as a result some detections are rejected in the automated spectral-fit pipeline. Moreover, only detections with redshifts in XMMPZCAT have been included (Sect. 2.1.2). We offer two main products to the final user: A single FITS table containing the most useful data from XMMFITCAT-Z, and a relational database with all information.

The main results of the XMMFITCAT-Z database are summarised in a table in FITS format. It contains one row for each detection included in the database, and 157 columns containing information about the source detection and the spectral-fitting results. The first 14 columns contain information about the source and observation, including redshift information, and the remaining 143 columns contain, for each model applied, model spectral-fit flags, parameter values and errors, fluxes, luminosities, and five columns to describe the goodness of the fit. See Appendix A for a full description of all the columns included in the table.

We also offer the full XMMFITCAT-Z database as a file in SQLite format, which can be downloaded by the final user. The SQLite version contains significantly more information than the FITS table and allows advanced queries to be performed using SQL language. It is composed of 11 tables, which store all the information about the detections, the spectra used in the automatic fitting, and the results: fit statistics, best-fit parameters, fluxes, and luminosities. A complete description of all tables and parameters is available at the XMMFITCAT-Z website2.

2.1. Data

2.1.1. XMM-Newton data

3XMM-DR6 is the third-generation catalogue of serendipitous X-ray sources from the ESA’s XMM-Newton observatory, and was created by the XMM-Newton SSC on behalf of ESA. The 3XMM-DR6 catalogue contains X-ray photometric information for 678 680 X-ray detections.

Each XMM-Newton observation considered for the construction of the 3XMM goes through the SSC source-detection pipeline independently, obtaining a list of detections for each observation. As some of these observations correspond to overlapping sky areas, a fraction of these detections can be associated to the same physical object (i.e. unique source). The 3XMM catalogue groups detections, which are assumed to be the same physical source, as a single entry. When taking this into account, the 678 680 detections included in the 3XMM-DR6 are reduced to 468 440 unique sources.

As part of the catalogue production, spectra and time series are also extracted in the case of detections with more than 100 counts collected in the EPIC camera. This corresponds to 149 998 detections, and 102 157 unique sources. The spectral data from the 3XMM-DR6 catalogue were screened before applying our automated spectral-fitting pipeline so that spectral fits are only performed if the data fulfil the following criteria:

– Only spectra corresponding to a single instrument and observation with more than 50 net counts (i.e. background subtracted) in the 0.5–10 keV band are used in the spectral fits. This means that some detections with more than 100 EPIC counts in the total band, but less than 50 counts in each different EPIC instrument (EPIC-pn, EPIC-MOS1, or EPIC-MOS2), are excluded from the automated fits, and these are therefore not included in the spectral-fit database.

– Complex models (see Sect. 2.3), are only applied if the number of EPIC counts is larger than 500 net counts in the total 0.5–10 keV band.

As a result of the application of these criteria, the spectral-fit database contains results corresponding to the simple models for 30 816 source detections, corresponding to 22 677 unique sources (see Table 1). Spectral-fitting results for complex models are available for 4797 detections. The distribution of spectral counts per observation used during the automated fits is plotted in Fig. 1. Observations with more than 10 000 counts, which amounts to 2% of the 30 816 detections, are excluded from this plot for clarity.

thumbnail Fig. 1.

Distribution of net counts (background-subtracted spectral counts) per observation used in the automated spectral fits. Observations with more than 10 000 counts are not included in this plot.

Table 1.

Number of sources.

2.1.2. Photometric redshifts

The XMM-Newton Photo-Z Catalogue3 (XMMPZCAT, Ruiz et al. 2018) contains photometric redshifts for 100 178 X-ray sources in the 3XMM, which is about 50% of the X-ray sources within the selected XMM-Newton observations used to build the catalogue. XMMPZCAT contains sources outside the Galactic plane (|b| > 20 deg) with highly reliable optical counterparts in the SDSS-DR13 or Pan-STARRS-DR1 catalogues and was produced through a machine-learning algorithm, MLZ-TPZ (Carrasco Kind & Brunner 2013)4. using optical (SDSS and Pan-STARRS) and (if available) NIR (2MASS, UKIDSS, VISTA) and/or MIR (All-WISE) photometry to derive photometric redshifts. The version of the catalogue used to construct the current XMMPZCAT is 3XMM-DR6. Optical and IR data were obtained from multiwavelength cross-matched catalogues using tools and results from the ARCHES project (Motch et al. 2017; Pineau et al. 2017).

XMMPZCAT also includes spectroscopic redshifts for 12 693 sources obtained either from the SDSS or other spectroscopic surveys, such as XXL (Menzel et al. 2016), XMS (Barcons et al. 2007) or XBS (Della Ceca et al. 2004); these were used to train the machine-learning algorithm. See Mountrichas et al. (2017a); Ruiz et al. (2018) for a detailed description of these surveys. If available, we used these spectroscopic redshifts for the X-ray spectral fits.

2.2. Bayesian X-ray analysis

We used the fitting and modelling software Sherpa 4.9.1 (Freeman et al. 2001) to perform the automated spectral fits. We followed the Bayesian technique proposed in Buchner et al. (2014) using the Bayesian X-ray Analysis (BXA) software, which connects the nested sampling algorithm MultiNest (Feroz et al. 2009) with Sherpa.

We use BXA to incorporate the whole probability distribution for each photometric redshift as a prior in the model fitting. Moreover, a nested sampling algorithm like MultiNest allows for a full exploration of the parameter space, and helps to avoid only finding solutions for local minima, a common problem that arises when using standard minimisation techniques like for example the Levenberg-Marquardt algorithm.

In the BXA framework, the use of Cash statistics (Cash 1979) is mandatory. We used the wstat implementation in Sherpa, which allows background datasets to be used as background models. wstat is used for modelling Poisson data with Poisson background when no physically motivated background model is available. It assumes a background model with as many parameters as bins in the background spectrum. Under certain assumptions, there is an analytical solution for calculating the values of these parameters (see e.g. Appendix B of the Xspec user guide)5. For using the wstat statistics, the grouped spectra from the 3XMM-DR6 catalogue were ungrouped and then grouped to one count per bin.

All available instruments and exposures for a single observation of a source were fitted together using spectral data within the 0.5–10 keV band. All model parameters for different instruments are tied together except for a relative normalisation, which accounts for the differences in flux calibration between instruments.

2.3. Models and priors

Most sources included in XMMPZCAT are extragalactic and hence the population is dominated by AGNs. Given this fact, we reduced the number of spectral models with respect to XMMFITCAT. These are phenomenological models selected to reproduce the spectral emission of AGNs. We also included a simple thermal model to deal with the X-ray emission of stars (about 10% of XMMPZCAT sources) and other hot plasmas (e.g. intra-cluster medium emission).

There are four different models, two simple and two more complex models, as follows:

Simple models.

− Absorbed power-law model (“wapo”, XSPEC: zwabs* pow): Variable parameters are the hydrogen column density of the absorber, the power-law photon index, and the power-law normalisation.

− Absorbed thermal model (“wamekal”, XSPEC: zwabs* mekal): Variable parameters are the hydrogen column density of the absorber, the plasma temperature of the thermal component, and the normalisation of the thermal component.

Complex models.

− Absorbed thermal plus power-law model (“wamekalpo”, XSPEC: zwabs*(mekal + zwabs*pow)): Variable parameters are the hydrogen column density of both absorbers, the plasma temperature, the photon index, and the normalisation of the power-law and thermal components.

− Absorbed double power-law model (“wapopo”, XSPEC: zwabs*(pow + zwabs*pow)): Variable parameters are the hydrogen column density of both absorbers, the photon indices of both power-law components, and the corresponding normalisations.

All models include an additional absorption component, wabs, to take into account the Galactic absorption, with the hydrogen column density fixed to the value in the direction of the source from the Leiden/Argentine/Bonn (LAB) survey of Galactic HI (Kalberla et al. 2005).

In the BXA framework we employed for the spectral fitting, a probability prior should be assigned to each free parameter in the model. The priors we selected are as follows:

– Hydrogen column density: Jeffreys prior (i.e. a uniform prior in the logarithmic space) with limits 1020 − 1025 cm−2.

– Power-law photon index: Gaussian prior with a mean of 1.9 and a standard deviation of 0.15. This prior corresponds to the photon index distribution for the AGN population as described in Nandra & Pounds (1994).

– Thermal plasma temperature: Uniform prior with limits 0.08–20 keV.

– Redshift: For sources with known spectroscopic redshift, this is included as a fixed parameter in the models. When only a photometric redshift is available, the redshift is treated as a free parameter using the photo-z probability density distribution calculated in XMMPZCAT as the prior.

– Normalisation: Jeffreys prior with limits 10−30 − 1.

– Relative normalisation constants: Jeffreys prior with limits 0.01–100.

2.4. Goodness of fit

Cash maximum likelihood statistics lacks a direct estimate of goodness of fit (GoF). We followed the method proposed in Buchner et al. (2014) and used quantile–quantile (Q–Q) plots to obtain an estimate of the GoF of our spectral fits.

A Q–Q plot compares the cumulative counts of the data (source + background) with the predicted counts (source + background) of the model (see Fig. 2). These plots gives a quick visual idea of how well the model can reproduce the data. For a quantitative estimate of the GoF we calculated the Kolmogorov-Smirnov (KS) statistic between the two cumulative distributions, and the corresponding p-value. A low KS (or a high p-value) means that the data are well reproduced by the model.

thumbnail Fig. 2.

Q–Q plots for a 3XMM spectrum (EPIC-pn) fitted with an absorbed power law (blue, solid line) and an absorbed thermal model (orange, dashed line).

However, we note that in this case the p-values for the KS statistic cannot be calculated the usual way. The cumulative distribution of the model depends on the parameters that were estimated from the data distribution, and therefore the condition of independence between the two compared distributions does not hold, and p-values estimated using the KS probability distribution are grossly incorrect. Nevertheless, we can get an estimate of the p-value through a permutation test. For each source, we did 1000 resamplings, randomly splitting the original data+model sample into two subsamples of equal size, and estimated the corresponding KS statistic. The correct p-value was estimated as the quotient between the number of resamplings that have higher statistics than those of the original sample, and the total number of resamplings.

Any model showing a KS p-value < 0.01 is considered as an acceptable fit. If we find at least one acceptable fit for a given data set, the A_FIT parameter is set to True. The XBA MultiNest algorithm also estimates the evidence for each model (logZ). The model with the highest evidence (lowest logZ) is selected as the preferred model (P_MODEL parameter). A preferred model is always included, even in cases where it is not an acceptable fit and shows a KS p-value above 0.01. We also list the remaining models (A_MODELS parameter) with ‘relative evidence’ taking a value of lower than 30 with respect to the preferred model, that is, ‘very strong evidence’ according to the scale of Jeffreys (1961) (see also Robert et al. 2009; Buchner et al. 2014). Assuming that all models are a priori equally probable, there is no statistical reason to rule out any of the models in the set formed by P_MODEL and A_MODELS. Without additional information favouring a particular model, if the fit is acceptable, the simplest model should be selected as the best-fit model.

We find that 28 887 detections have an acceptable fit, which is 94% of the XMMFITCAT-Z detections. Specifically, 22 427 detections (73%) have a single absorbed power law (‘wapo’) as the preferred model, and 27 659 detections (90%) have this model either as preferred or in the accepted models.

2.5. Parameter and error estimation

The MultiNest algorithm implemented in BXA gives the marginalised posterior probability distribution for all free parameters in the fitted model. We used these distributions to estimate the best-fit parameters and the corresponding errors. The best-fit values correspond to the mode (the most probable value) of the posterior distribution, estimated using a half-sample algorithm (Robertson & Cryer 1974). Errors were estimated using the posterior distributions to calculate a 90% credible interval around the mode.

Figure 3 shows an example of the marginal and conditional (for two parameters) posterior distributions for a source fitted using an absorbed power law. This example shows how the structure of the original photo-z probability distribution is preserved.

thumbnail Fig. 3.

Posterior distributions for a 3XMM detection (DETID 106909002010001) fitted with an absorbed power law. Left column: marginal distributions for hydrogen column density, photon index, redshift, and power-law normalisation. Right column: two-parameter conditional distributions. Blue circles with error bars show the best-fit value of the parameters and the corresponding 90% credible intervals.

2.6. X-ray fluxes and luminosities

The posterior probability distribution of the free parameters was propagated to estimate the flux and errors for each model. This method preserves the structure of the uncertainty (degeneracies, multimodal structure, etc.). Reported fluxes and luminosities in the catalogue correspond to the mode of the posterior distribution, with errors estimated as 90% credible intervals. These are EPIC fluxes, meaning that, in the case of multiple instrument spectra for a single observation, the reported flux is the average of the different fluxes for each instrument and exposure.

For sources with spectroscopic redshifts, luminosities were estimated using the intrinsic fluxes and the luminosity distance corresponding to that redshift. For sources with photometric redshifts, z is a free parameter and hence is propagated with the posterior distribution to estimate the corresponding luminosity distance in each case. We assumed a ΛCDM cosmology with H0 = 67.7, Ωm = 0.307 (Planck Collaboration XIII 2016).

We estimated fluxes and luminosities in the soft (0.5–2 keV) and hard (2–10 keV) bands. For observed fluxes, these bands correspond to the observer frame; for intrinsic fluxes and luminosities they correspond to the rest frame of the source.

EPIC soft fluxes obtained from the spectral fits (using results for P_MODEL, see Appendix A) are plotted against those from the 3XMM-DR6 catalogue (EP_2_FLUX + EP_3_FLUX) in the left panel of Fig. 4, and the hard X-ray luminosity is plotted against redshift in the right panel. Fluxes from the automated fits and from the 3XMM-DR6 are consistent within errors for ∼70% of the detections. The conversion from count rates to fluxes in the 3XMM assumes a simple power-law model with photon index of 1.7. Therefore, we can expect that XMMFITCAT-Z sources with different spectral shapes will show larger discrepancies in flux. That is indeed the case: significant differences between flux values are more frequent among sources displaying a soft spectrum, that is, sources that are best fitted by a power-law with a steep photon index or by a thermal model. More than 80% of the non-matching fluxes correspond to any of these cases.

thumbnail Fig. 4.

Left: soft fluxes (in cgs units) computed from the automated fits (P_MODEL) against fluxes in the 3XMM-DR6 catalogue. Right: hard luminosity versus redshift (in cgs units) computed from the automated fits (P_MODEL). Darker colours show a higher density of points.

3. Search for X-ray absorbed sources

The basic mechanism that explains the panchromatic emission of an AGN is the accretion of gas onto the central supermassive black hole of the host galaxy. The high temperatures in the inner-most regions of the accretion disc ionise the surrounding gas, creating a ‘hot corona’ of energetic electrons. Optical and UV photons interact with the electrons in the corona through inverse Compton scattering, causing the characteristic X-ray emission of AGNs (Haardt & Maraschi 1991; Haardt et al. 1994).

This primary emission can then be reprocessed through other physical processes: absorption due to ionised, warm, or cold material (Turner & Miller 2009); reflection by the material in the accretion disc or by farther neutral gas (Fabian et al. 2006; Turner & Miller 2009); scattering by an absorbing medium (Netzer et al. 1998); or fluorescent emission of ionised iron (Mushotzky et al. 1995; Fabian et al. 2000).

The combination of these processes can produce a relatively complex X-ray spectrum in the observing spectral range of XMM-Newton (∼0.2 − 12 keV). However, this complexity is reasonably well captured by the phenomenological models we present in Sect. 2.3: the X-ray primary emission can be modelled by a power law with a photon index of ∼1.9; Compton-thin neutral absorbers (1022 <  NH <  1024 cm−2) are modelled by the different absorption components included in our models; Partial absorption can be mimicked through double power-law models; Compton-thick absorption (NH >  1024 cm−2), where all primary emission is suppressed below 10 keV, can also be roughly approximated by a double power law (see below); and reflection effects are roughly modelled through power laws or thermal emission components (‘wapopo’ or ‘wamekalpo’ model). Using these simple models, we find acceptable fits for 28 887 out of 30 816 (94%) X-ray spectra included in XMMFITCAT-Z.

Our first goal was to identify AGNs in XMMFITCAT-Z that show spectral features of X-ray absorption. Although low-luminosity AGNs do exist (see e.g. Ho 1999; Panessa et al. 2007), any persistent astronomical source with an intrinsic (i.e. absorption-corrected) 2–10 keV luminosity above 1042 erg s−1 can be associated to an AGN, and no other known mechanism can produce such luminosity.

Compton-thin absorbed sources can be identified by a significant absorption component with NH ≳ 1022 cm−2. Compton-thick sources are harder to identify within the XMM-Newton spectral range because, as stated above, all primary emission is suppressed below a rest frame of 10 keV. Only the X-ray emission scattered by the absorbing medium is observable in this range. This emission shows a flatter spectral shape with a prominent iron Kα emission line (equivalent width above 500 eV). We must note that the models used in XMMFITCAT-Z did not include iron emission lines, and therefore any Compton-thick sources detectable thanks to this spectral feature alone could be missed in our final sample of X-ray absorbed AGNs.

In summary, our selection criteria to identify X-ray absorbed AGNs were as follows.

  • We first selected sources with a single absorbed power law (‘wapo’) as an accepted model (P_MODEL or in A_MODELS, and A_FIT true). Those sources showing NH >  1022 cm−2 or Γ <  1.4 with 90% confidence6 are classified as absorbed.

  • Among those sources without ‘wapo’ as an accepted model, we select those with a double power law with two absorbers (‘wapopo’) as an accepted model. Compton-thin sources can be identified as those showing NH >  1022 cm−2 in the inner absorber (logNH2). This model also allows a crude approximation of the spectrum of Compton-thick objects: those showing a high obscuration in the inner absorber (NH >  1023 cm−2) and Γ <  1.4 in the outer power law (PhoIndex2).

  • Finally, among those sources classified as absorbed, we selected only those showing an intrinsic 2–10 keV luminosity consistent with being greater than 1042 erg s−1 (i.e. upper error bars are above 1042).

Applying these selection criteria we found 1421 spectra with signs of X-ray absorption (∼5% of the total catalogue), corresponding to 1037 unique sources (out of 22 677 unique sources in the total catalogue); 1385 out of 1421 show NH >  1022 cm−2 and 38 show a flat spectrum with Γ <  1.4. Two of them show both high NH and a flat emission spectrum.

Figure 5 show two examples of 3XMM detections included in XMMFITCAT-Z and classified as absorbed AGNs following these criteria. The plots show their EPIC-pn spectra, including the best-fit model, and the corresponding best-fit parameters and their probability distributions.

thumbnail Fig. 5.

XMM-Newton spectra (EPIC-pn) of two X-ray absorbed AGNs identified through our selection criteria. For improved visualisation, spectral data (blue circles) have been grouped to obtain a signal-to-noise ratio per bin of at least five. Solid red lines show the background plus model and dashed red lines show the model only. Red areas indicate the 2σ model uncertainty. Panels in the lower part of the plots show the ratio between the observed and the model-predicted count rate. Histograms in the right column show the posterior probability distribution of the model parameters; the corresponding best-fit values (mode), and their 90% credible intervals are shown as symbols with error bars. Solid grey histograms and blue circles correspond to the outer model components. Open histograms and orange triangles correspond to the inner model components. Top: detection best fitted with a single absorbed power law (‘wapo’ model). Bottom: detection best fitted using a double power law with two absorbers (‘wapopo’ model).

To build our final selection of X-ray absorbed AGNs we further examined the X-ray properties of XMMFITCAT-Z AGNs (see Sect. 4). We find that our X-ray modelling for a significant fraction of sources overestimates their X-ray luminosity. This was caused by either incorrect estimation of their photometric redshifts or modelling artifacts introduced when using a double power-law model (wapopo). As we explain in Sect. 4, after applying an additional filtering for selecting objects with more reliable redshifts and X-ray modelling, our atlas of X-ray absorbed AGNs contains 977 detections, corresponding to 765 unique sources. We provide this sample as a FITS table7.

4. Discussion

In Fig. 6 we present the ratio of absorbed to unabsorbed AGNs as a function of redshift (top panel) and X-ray luminosity (lower panel). Redshift and luminosity bins were estimated using the Bayesian Block Algorithm (Scargle et al. 2013). This algorithm uses a fitness function calculated on the actual data for estimating an optimal binning. It allows the user to vary the bin size for better reproduction of the underlying distribution. Blue circles show the results after applying the absorption criteria we present in Sect. 5 based solely on the X-ray spectral fits.

thumbnail Fig. 6.

Ratio between X-ray absorbed and unabsorbed AGNs identified in XMMFITCAT-Z for different redshift (top) and luminosity (bottom) ranges. Blue circles correspond to ratios estimated using all X-ray absorbed AGNs; the ratios shown as orange stars are estimated using only absorbed AGNs with a reliable best-fit model (see Sect. 4).

It appears that there is an excess of absorbed sources at low redshift. This is easily explained as the absorbed sources have a lower flux and are therefore detected at shorter distances. The fraction of absorbed AGNs remains roughly constant with luminosity, except for the highest luminosity bin where the number of absorbed sources increases significantly. Although we emphasise that our sample is not statistically complete and is indeed biased towards the brightest sources, regarding both the X-ray and the optical selection we should not expect a strong correlation for the fraction of absorbed AGNs with X-ray luminosity (see e.g. Sazonov et al. 2015).

The blue solid line in Fig. 7 shows the 2–10 keV luminosity distribution for all XMMFITCAT-Z sources classified as AGNs, again based solely in their X-ray properties. There is a long, significantly high-luminosity tail for these sources, reaching X-ray luminosities above 1047 erg s−1. Such high luminosities are clearly non-physical.

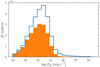thumbnail Fig. 7.

X-ray luminosity distribution for XMMFITCAT-Z sources classified as AGNs. The solid blue line shows the whole sample without any additional filtering. The solid orange histogram includes only AGNs with a reliable best-fit model (see Sect. 4).

These results strongly suggest that our X-ray spectral modelling is overestimating the intrinsic 2–10 keV luminosity for some objects. We therefore tried to identify those sources with unreliable modelling. There are two main effects that can overestimate the X-ray luminosity: On one hand, the photometric redshifts calculated for some sources could be incorrect. When building XMMFITCAT-Z, we did not apply any filtering regarding the quality of the photometric redshifts. In Ruiz et al. (2018) we presented several quality diagnostics for photo-z based on the shape of its probability density function. For example, using the peak strength (PS) parameter included in XMMPZCAT, we can select sources for which the photo-z probability distribution is narrowly concentrated around a single redshift, avoiding highly multimodal distributions. We considered objects with PS < 0.7 as having an unreliable X-ray spectral modelling.

On the other hand, the complex models we used for sources with high counts (the absorbed double power-law model, ‘wapopo’, or the absorbed thermal plus power-law model, ‘wamekalpo’; see Sect. 2.3) can introduce artifacts in the X-ray modelling leading to non-physical parameters: some of these sources are not well fitted by a single power law or thermal emission because they have a small but significant excess emission at the high-energy end of the spectrum. This excess, which is associated with the AGN Compton reflection hump (Magdziarz & Zdziarski 1995; Reynolds 1999), can easily be modelled by introducing a highly absorbed power law with NH ≳ 1023cm−2. When such an artifact appears in the selected best-fit model, it can clearly lead to overestimation of the intrinsic 2–10 keV luminosity. Our selection criteria for X-ray absorbed sources will identify these kinds of sources as highly absorbed, misinterpreting them as a heavily buried AGN components when in fact they do not show any real spectral feature for X-ray absorption. We therefore classified as unreliable those X-ray sources that are well modelled using any of our complex models and are classified as absorbed, but show a 2–10 keV luminosity above 1045.3 erg s−1. This luminosity limit corresponds to the last luminosity bin in Fig. 6.

Finally, we also excluded sources with a loosely constrained NH (i.e. the 90% credible interval for log NH is greater than 2 dex). Once we had applied these quality criteria for selecting sources with a reliable X-ray modelling, we rejected 8871 detections: 444 absorbed AGNs and 8427 unabsorbed AGNs. Orange stars in Fig. 6 and the orange solid histogram in Fig. 7 include only AGNs with reliable X-ray modelling. The figures clearly show that the effects due to overestimated luminosities disappear after applying this filtering.

Figure 8 shows the relationships between hydrogen column density and photon index (left) and between redshift and 2–10 keV luminosity (right) for detections classified as AGNs in XMMFITCAT-Z (objects with unreliable X-ray modelling are not included); the corresponding normalised distribution is also shown for each parameter. These plots show the data for unabsorbed (17 158 detections) and X-ray absorbed AGNs (977 detections).

thumbnail Fig. 8.

Photon index vs. hydrogen column density (left) and redshift vs. 2–10 keV absorption-corrected luminosity (right) for detections classified as AGNs with reliable X-ray modelling (see Sect. 4). Red triangles are X-ray absorbed AGNs, and unabsorbed AGNs are shown as grey circles. Errors are not included in the plots in order to improve visualisation; instead, we include error bars in the corners showing the median error of the corresponding parameters. The histograms in the upper and right sides of the plots show the normalised distribution of the parameters for X-ray absorbed (red) and unabsorbed AGNs (grey).

The use of MIR colours is a common tool for AGN identification (Stern et al. 2005; Donley et al. 2007, 2012; Mateos et al. 2012; Assef et al. 2013), in particular using data in the W1 (3.4 μm) and W2 (4.6 μm) bands from the WISE all-sky surveys (Wright et al. 2010; Mainzer et al. 2011; Cutri et al. 2013), because galaxies are expected to display bluer colours than AGNs in the MIR. In Fig. 9 we present the W1–W2 distribution (lower panel) for XMMFITCAT-Z AGN with counterparts in the All-WISE catalogue (Cutri et al. 2013).

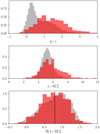thumbnail Fig. 9.

(g–i; top), (r–W2; middle), and (W1–W2; bottom) normalised colour distributions. Solid red histograms show unique sources classified as X-ray absorbed AGNs in XMMFITCAT-Z; solid grey histograms show X-ray unabsorbed AGNs. Only AGNs with reliable modelling are included (see discussion in Sect. 4). The vertical dotted line in the bottom panel shows the Stern et al. (2012) MIR criterion for AGN selection (W1 − W2 >  0.8).

The W1–W2 colour was proposed by Stern et al. (2005) as an efficient diagnostic for the selection of AGNs. The idea is that the heated torus dust results in increased emission in the W2 band. No difference is seen between absorbed and unabsorbed objects in terms of MIR colours, as expected if the MIR emission is from the torus and is therefore inclination independent. We find that a considerable fraction of our sources are classified as AGNs following the W1–W2 criterion. However, an almost equally large number of X-ray sources would not be classified as AGNs following the W1–W2 criterion.

These objects are associated with AGNs where the galaxy starts to dominate over the AGN colours (see also Barmby et al. 2006). Assef et al. (2013) propose a more elaborate criterion where the W1–W2 cut-off is a function of the W2 magnitude. This selection curve (90% completeness) is shown in Fig. 10. It is evident that a significant number of X-ray-selected AGNs would evade identification if we used MIR colour criteria alone. In the same figure, we plot the sources that were not classified as AGNs in our spectral fits (i.e. objects with a good X-ray spectral fit with at least one of our models, but with 2–10 keV luminosity below 1042 erg s−1). The vast majority of these lie outside the AGN locus. This suggests that the X-ray spectral criteria alone are quite efficient in selecting AGNs. As stated above, AGN selections based on WISE colours are efficient for identifying sources where the MIR torus emission dominates over the host galaxy contribution, that is, for luminous, unobscured AGNs (see e.g. Eckart et al. 2010; Hickox et al. 2017; Pouliasis et al. 2020). Our results show how X-ray spectral criteria can select AGNs with lower luminosities. Figure 10 also shows some contamination of sources within the AGN wedge but for which there is no evidence in X-rays of hosting an AGN (light green crosses). Georgakakis et al. (2020) suggested that these sources could be star forming galaxies at redshift ≲0.5 that scatter into the AGN MIR wedge because of the photometric uncertainties on the WISE magnitudes.

thumbnail Fig. 10.

W2 versus W1–W2 for XMMFITCAT-Z unique sources with WISE counterparts. Red triangles show X-ray absorbed AGNs, and grey circles show X-ray unabsorbed AGNs. Light-green crosses are objects not classified as AGNs but with an acceptable fit in XMMFITCAT-Z. Only sources with reliable modelling are included (see discussion in Sect. 4). The black dashed line shows the Assef et al. (2013) criterion for AGN selection.

We now discuss the obscuration properties of our sample. In the top panel of Fig. 9 we present the (g–i) colours of the absorbed versus the unabsorbed sources. X-ray absorbed sources are optically redder compared to unabsorbed sources, as expected. However, there is a non-negligible number of X-ray unabsorbed sources with very red colours. Some of these could be absorbed objects that were missed by our selection criteria, but they could also be truly peculiar sources. The catalogue is therefore quite useful for identifying these kinds of objects for further study.

In the middle panel of Fig. 9 we present the r–W2 colour distribution. Yan et al. (2013) suggested that this colour (r–W2 > 6) offers a powerful diagnostic for the selection of obscured AGNs, and can be used in combination with pure MIR diagnostics to identify AGNs (W1–W2 > 0.8 and W2 < 15.8) This is because in the presence of reddening, the ‘r’ band is easily diminished while the W2 emission remains relatively unscathed. As expected, the X-ray-obscured sources have a redder tail compared to the unobscured sources. However, it is worth noting that a considerable fraction of X-ray unabsorbed sources have r–W2 > 6. Hickox et al. (2017) show that the r–W2 criterion is only really effective above z >  1. The fact that the bulk of our absorbed AGNs have redshift values of below 1 (see Fig. 8, right panel) could explain our result.

Our analysis of XMMFITCAT-Z sources is consistent with the results of many previous studies (Eckart et al. 2010; Stern et al. 2012; Assef et al. 2013; Yan et al. 2013; Mateos et al. 2012, 2013; Mountrichas et al. 2017b, 2020; Pouliasis et al. 2020) showing that MIR diagnostics are powerful for the identification of luminous AGNs but that they fail for AGNs with lower luminosity and/or mild absorption, where the stellar contribution to the optical/MIR emission is non-negligible. By focusing on the X-ray properties, we can identify these objects.

5. Summary

We present a catalogue of automated X-ray spectral fits using the 3XMM-DR6 spectral products. Photometric redshifts were previously estimated (Ruiz et al. 2018) using machine-learning techniques (TPZ; Carrasco Kind & Brunner 2013). We present 22 677 X-ray sources with an X-ray spectrum of reasonable quality, meaning that each XMM-Newton detector has over 50 counts, and for which a photometric or spectroscopic redshift is available. X-ray spectral fits were performed using a Bayesian X-ray analysis (Buchner et al. 2014), including the PDF of photometric redshift as a prior.

As a brief demonstration of the potential of this X-ray spectral catalogue, we present the properties of the 765 sources showing strong evidence of being X-ray absorbed AGNs. We show that a considerable fraction of our sample would not be classified as AGNs based on their MIR colours, W1–W2 versus W2. About one-third of the X-ray absorbed AGNs present red r − W2  >   6 colours. It therefore appears that the r–W2 criterion, often used in the literature for the selection of obscured AGNs, produces very different samples compared to the X-ray criteria based on the hydrogen column density.

6

The lower limit of the 90% credible interval for the parameter is above our selection limit.

Acknowledgments

This work is part of the Enhanced XMM-Newton Spectral-fit Database project, funded by the European Space Agency (ESA) under the PRODEX program. AR acknowledges support of this work by the PROTEAS II project (MIS 5002515), which is implemented under the “Reinforcement of the Research and Innovation Infrastructure” action, funded by the “Competitiveness, Entrepreneurship and Innovation” operational programme (NSRF 2014-2020) and co-financed by Greece and the European Union (European Regional Development Fund). AC acknowledges financial support from the Spanish Ministry MCIU under project RTI2018-096686-B-C21 (MCIU/AEI/FEDER/UE), cofunded by FEDER funds and from the Agencia Estatal de Investigación, Unidad de Excelencia María de Maeztu, ref. MDM-2017-0765. This research has made use of data obtained from the 3XMM XMM-Newton serendipitous source catalogue compiled by the 10 institutes of the XMM-Newton Survey Science Centre selected by ESA. This work is based on observations made with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and NASA. Funding for the Sloan Digital Sky Survey IV has been provided by the Alfred P. Sloan Foundation, the US Department of Energy Office of Science, and the Participating Institutions. SDSS-IV acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS web site is www.sdss.org. SDSS-IV is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, the Chilean Participation Group, the French Participation Group, Harvard-Smithsonian Center for Astrophysics, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU)/University of Tokyo, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatário Nacional/MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University. This publication makes use of data products from the Wide-field Infrared Survey Explorer, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, funded by the National Aeronautics and Space Administration. This research made use of Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration 2012).

References

  1. Assef, R. J., Stern, D., Kochanek, C. S., et al. 2013, ApJ, 772, 26 [Google Scholar]
  2. Astropy Collaboration (Price-Whelan, A. M., et al.) AJ, 156, 123 [Google Scholar]
  3. Barcons, X., Carrera, F. J., Ceballos, M. T., et al. 2007, A&A, 476, 1191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Barmby, P., Alonso-Herrero, A., Donley, J. L., et al. 2006, ApJ, 642, 126 [NASA ADS] [CrossRef] [Google Scholar]
  5. Buchner, J., Georgakakis, A., Nandra, K., et al. 2014, A&A, 564, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Carrasco Kind, M., & Brunner, R. J. 2013, MNRAS, 432, 1483 [NASA ADS] [CrossRef] [Google Scholar]
  7. Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
  8. Corral, A., Georgantopoulos, I., Watson, M. G., et al. 2014, A&A, 569, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Corral, A., Georgantopoulos, I., Watson, M. G., et al. 2015, A&A, 576, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Cutri, R. M., Wright, E. L., Conrow, T., et al. 2013, VizieR Online Data Catalog, 2328 [Google Scholar]
  11. Della Ceca, R., Maccacaro, T., Caccianiga, A., et al. 2004, A&A, 428, 383 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Donley, J. L., Rieke, G. H., Pérez-González, P. G., Rigby, J. R., & Alonso-Herrero, A. 2007, ApJ, 660, 167 [NASA ADS] [CrossRef] [Google Scholar]
  13. Donley, J. L., Koekemoer, A. M., Brusa, M., et al. 2012, ApJ, 748, 142 [Google Scholar]
  14. Eckart, M. E., McGreer, I. D., Stern, D., Harrison, F. A., & Helfand, D. J. 2010, ApJ, 708, 584 [NASA ADS] [CrossRef] [Google Scholar]
  15. Fabian, A. C. 2006, in ESA SP-604: The X-ray Universe 2005, ed. A. Wilson, 463 [Google Scholar]
  16. Fabian, A. C., Iwasawa, K., Reynolds, C. S., & Young, A. J. 2000, PASP, 112, 1145 [NASA ADS] [CrossRef] [Google Scholar]
  17. Feroz, F., Hobson, M. P., & Bridges, M. 2009, MNRAS, 398, 1601 [NASA ADS] [CrossRef] [Google Scholar]
  18. Freeman, P., Doe, S., & Siemiginowska, A. 2001, in Proc. SPIE, eds. J. L. Starck, & F. D. Murtagh, 4477, 76 [NASA ADS] [CrossRef] [Google Scholar]
  19. Georgakakis, A., Ruiz, A., & LaMassa, S. M. 2020, MNRAS, 499, 710 [CrossRef] [Google Scholar]
  20. Haardt, F., & Maraschi, L. 1991, ApJ, 380, L51 [NASA ADS] [CrossRef] [Google Scholar]
  21. Haardt, F., Maraschi, L., & Ghisellini, G. 1994, ApJ, 432, L95 [NASA ADS] [CrossRef] [Google Scholar]
  22. Hickox, R. C., Myers, A. D., Greene, J. E., et al. 2017, ApJ, 849, 53 [NASA ADS] [CrossRef] [Google Scholar]
  23. Ho, L. C. 1999, ApJ, 516, 672 [NASA ADS] [CrossRef] [Google Scholar]
  24. Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Jeffreys, H. 1961, The Theory of Probability, Texts in the Physical Sciences (Oxford Univ. Press) [Google Scholar]
  26. Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Magdziarz, P., & Zdziarski, A. A. 1995, MNRAS, 273, 837 [NASA ADS] [CrossRef] [Google Scholar]
  28. Mainzer, A., Bauer, J., Grav, T., et al. 2011, ApJ, 731, 53 [NASA ADS] [CrossRef] [Google Scholar]
  29. Mateos, S., Alonso-Herrero, A., Carrera, F. J., et al. 2012, MNRAS, 426, 3271 [NASA ADS] [CrossRef] [Google Scholar]
  30. Mateos, S., Alonso-Herrero, A., Carrera, F. J., et al. 2013, MNRAS, 434, 941 [NASA ADS] [CrossRef] [Google Scholar]
  31. Menzel, M.-L., Merloni, A., Georgakakis, A., et al. 2016, MNRAS, 457, 110 [NASA ADS] [CrossRef] [Google Scholar]
  32. Motch, C., Carrera, F., Genova, F., et al. 2017, in Astronomical Data Analysis Software and Systems XXV, eds. N. P. F. Lorente, K. Shortridge, R. Wayth, et al., ASP Conf. Ser., 512, 165 [Google Scholar]
  33. Mountrichas, G., Corral, A., Masoura, V. A., et al. 2017a, A&A, 608, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Mountrichas, G., Georgantopoulos, I., Secrest, N. J., et al. 2017b, MNRAS, 468, 3042 [NASA ADS] [CrossRef] [Google Scholar]
  35. Mountrichas, G., Georgantopoulos, I., Ruiz, A., & Kampylis, G. 2020, MNRAS, 491, 1727 [CrossRef] [Google Scholar]
  36. Mushotzky, R. F., Fabian, A. C., Iwasawa, K., et al. 1995, MNRAS, 272, L9 [NASA ADS] [CrossRef] [Google Scholar]
  37. Nandra, K., & Pounds, K. A. 1994, MNRAS, 268, 405 [Google Scholar]
  38. Netzer, H., Turner, T. J., & George, I. M. 1998, ApJ, 504, 680 [NASA ADS] [CrossRef] [Google Scholar]
  39. Panessa, F., Barcons, X., Bassani, L., et al. 2007, in The Multicolored Landscape of Compact Objects and Their Explosive Origins, eds. T. di Salvo, G. L. Israel, L. Piersant, et al., Am. Inst. Phys. Conf. Ser., 924, 830 [Google Scholar]
  40. Pineau, F.-X., Derriere, S., Motch, C., et al. 2017, A&A, 597, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Pouliasis, E., Mountrichas, G., Georgantopoulos, I., et al. 2020, MNRAS, 495, 1853 [CrossRef] [Google Scholar]
  43. Reynolds, C. S. 1999, in High Energy Processes in Accreting Black Holes, eds. J. Poutanen, & R. Svensson, ASP Conf. Ser., 161, 178 [Google Scholar]
  44. Robert, C. P., Chopin, N., & Rousseau, J. 2009, Stat. Sci., 24, 141 [CrossRef] [Google Scholar]
  45. Robertson, T., & Cryer, J. 1974, J. Am. Stat. Assoc., 69, 1012 [CrossRef] [Google Scholar]
  46. Rosen, S. R., Webb, N. A., Watson, M. G., et al. 2016, A&A, 590, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Ruiz, A., Corral, A., Mountrichas, G., & Georgantopoulos, I. 2018, A&A, 618, A52 [CrossRef] [EDP Sciences] [Google Scholar]
  48. Sazonov, S., Churazov, E., & Krivonos, R. 2015, MNRAS, 454, 1202 [NASA ADS] [CrossRef] [Google Scholar]
  49. Scargle, J. D., Norris, J. P., Jackson, B., & Chiang, J. 2013, ApJ, 764, 167 [NASA ADS] [CrossRef] [Google Scholar]
  50. Stern, D., Eisenhardt, P., Gorjian, V., et al. 2005, ApJ, 631, 163 [NASA ADS] [CrossRef] [Google Scholar]
  51. Stern, D., Assef, R. J., Benford, D. J., et al. 2012, ApJ, 753, 30 [NASA ADS] [CrossRef] [Google Scholar]
  52. Turner, T. J., & Miller, L. 2009, A&A Rev., 17, 47 [NASA ADS] [CrossRef] [Google Scholar]
  53. Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [Google Scholar]
  54. Yan, L., Donoso, E., Tsai, C.-W., et al. 2013, AJ, 145, 55 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Description of the XMMFITCAT-Z

The XMMFITCAT-Z table contains one row for each detection, and 157 columns containing information about the source detection and the spectral-fitting results. Unavailable values are represented by an empty “NULL” value. The first 14 columns contain information about the source and observation, including redshift information, whereas the remaining 143 columns contain, for each model applied, spectral-fit flags, parameter values and errors, fluxes, luminosities, and five columns to describe the goodness of the fit.

Source and observation

– IAUNAME: The IAU name assigned to a unique source in the 3XMM-DR6 catalogue.

– SC_RA, SC_DEC: Right ascension and declination in degrees (J2000) of the unique source, as in the 3XMM-DR6 catalogue. RA and DEC correspond to the SC_RA and SC_DEC columns in the 3XMM-DR6 catalogue. These are corrected source coordinates and, in the case of multiple detections of the same source, they correspond to the weighted mean of the coordinates for the individual detections.

– SRCID: A unique number assigned to a group of catalogue entries that are assumed to be the same source in 3XMM-DR6.

– DETID: A consecutive number that identifies each entry (detection) in the 3XMM-DR6 catalogue.

– OBS_ID: The XMM-Newton observation identification, as in 3XMM-DR6.

– SRC_NUM: The (decimal) source number in the individual source list for this observation (OBS_ID), as in 3XMM-DR6. In the pipeline products this number is used in hexadecimal form.

– PHOT_Z, PHOT_ZERR: Photometric redshift of the source (from XMMPZCAT) and the corresponding 1σ error.

– SPEC_Z: Spectroscopic redshift of the source, if available.

– T_COUNTS/H_COUNTS/S_COUNTS: Spectral-background-subtracted counts in the full/hard/soft bands computed by adding all available instruments and exposures for the corresponding observation.

– NHGAL: Galactic column density in the direction of the source from the Leiden/Argentine/Bonn (LAB) Survey of Galactic HI.

Model-related columns

Columns referring to any particular model start with the name of the model (wapo, wamekal, wamekalpo, wapopo).

(a) Spectral-fit summary columns

– A_FIT: The value is set to True if an acceptable fit, i.e. KS p-value > 0.01, has been found for at least one of the models applied, and to False otherwise.

– P_MODEL: The data-preferred model, that is the model with the highest evidence (lowest logZ). A spectral model is always listed regardless of the fit being an acceptable or an unacceptable fit.

– A_MODELS: List of acceptable models. This column contains the remaining models with relative evidence (with respect to P_MODEL) lower than 30 (‘very strong evidence’ accordingly to the scale of Jeffreys 1961). Assuming all models a priori equally probable, there is no statistical reason to rule out any of the models in the set formed by P_MODEL and A_MODELS. Therefore, if the fit is acceptable, the simplest model should be selected as the best-fit model.

(b) Parameters and errors

Columns referring to parameters and errors start with the model name and the parameter name (logNH[1, 2], PhoIndex[1, 2], kT, and z). Values for the normalisations of the models and the relative normalisation factors between instruments are not included in the table (but they are available in the SQL database).

– < MODEL> _< PARAMETER> : parameter value.

– < MODEL> _< PARAMETER> _min,

< MODEL> _< PARAMETER> _max: upper and lower limits of the 90% credible interval for the parameter.

(c) Fluxes and luminosities

– < MODEL> _flux_< BAND> : the mean observed flux (in erg cm−2 s−1) of all instruments and exposures for the corresponding observation, in < BAND> (soft/hard). Observed fluxes were corrected of Galactic absorption.

– < MODEL> _fluxmin_< BAND>,

< MODEL> _fluxmax_< BAND> : lower and upper limits of the 90% credible interval.

– < MODEL> _intflux_< BAND> : the mean intrinsic flux (rest-frame, corrected of intrinsic absorption, in erg cm−2 s−1) of all instruments and exposures for the corresponding observation, in < BAND> (soft/hard).

– < MODEL> _intfluxmin_< BAND>,

< MODEL> _intfluxmax_< BAND> : lower and upper limits of the 90% credible interval.

– < MODEL> _lumin_< BAND> : the mean luminosity (rest-frame, corrected of intrinsic absorption, in erg s−1) of all instruments and exposures for the corresponding observation, in < BAND> (soft/hard).

– < MODEL> _luminmin_< BAND>,

< MODEL> _luminmax_< BAND> : lower and upper limits of the 90% credible interval.

(d) Fitting statistics

– < MODEL> _wstat: W-stat (Cash statistics) value.

– < MODEL> _dof: Degrees of freedom.

– < MODEL> _ks: Kolmogorov-Smirnov (KS) statistic.

– < MODEL> _ks_pvalue: KS p-value.

– < MODEL> _logZ: Natural logarithm of the evidence, estimated by the MultiNest algorithm.

All Tables

Table 1.

Number of sources.

In the text

All Figures

thumbnail Fig. 1.

Distribution of net counts (background-subtracted spectral counts) per observation used in the automated spectral fits. Observations with more than 10 000 counts are not included in this plot.
In the text
thumbnail Fig. 2.

Q–Q plots for a 3XMM spectrum (EPIC-pn) fitted with an absorbed power law (blue, solid line) and an absorbed thermal model (orange, dashed line).
In the text
thumbnail Fig. 3.

Posterior distributions for a 3XMM detection (DETID 106909002010001) fitted with an absorbed power law. Left column: marginal distributions for hydrogen column density, photon index, redshift, and power-law normalisation. Right column: two-parameter conditional distributions. Blue circles with error bars show the best-fit value of the parameters and the corresponding 90% credible intervals.
In the text
thumbnail Fig. 4.

Left: soft fluxes (in cgs units) computed from the automated fits (P_MODEL) against fluxes in the 3XMM-DR6 catalogue. Right: hard luminosity versus redshift (in cgs units) computed from the automated fits (P_MODEL). Darker colours show a higher density of points.
In the text
thumbnail Fig. 5.

XMM-Newton spectra (EPIC-pn) of two X-ray absorbed AGNs identified through our selection criteria. For improved visualisation, spectral data (blue circles) have been grouped to obtain a signal-to-noise ratio per bin of at least five. Solid red lines show the background plus model and dashed red lines show the model only. Red areas indicate the 2σ model uncertainty. Panels in the lower part of the plots show the ratio between the observed and the model-predicted count rate. Histograms in the right column show the posterior probability distribution of the model parameters; the corresponding best-fit values (mode), and their 90% credible intervals are shown as symbols with error bars. Solid grey histograms and blue circles correspond to the outer model components. Open histograms and orange triangles correspond to the inner model components. Top: detection best fitted with a single absorbed power law (‘wapo’ model). Bottom: detection best fitted using a double power law with two absorbers (‘wapopo’ model).
In the text
thumbnail Fig. 6.

Ratio between X-ray absorbed and unabsorbed AGNs identified in XMMFITCAT-Z for different redshift (top) and luminosity (bottom) ranges. Blue circles correspond to ratios estimated using all X-ray absorbed AGNs; the ratios shown as orange stars are estimated using only absorbed AGNs with a reliable best-fit model (see Sect. 4).
In the text
thumbnail Fig. 7.

X-ray luminosity distribution for XMMFITCAT-Z sources classified as AGNs. The solid blue line shows the whole sample without any additional filtering. The solid orange histogram includes only AGNs with a reliable best-fit model (see Sect. 4).
In the text
thumbnail Fig. 8.

Photon index vs. hydrogen column density (left) and redshift vs. 2–10 keV absorption-corrected luminosity (right) for detections classified as AGNs with reliable X-ray modelling (see Sect. 4). Red triangles are X-ray absorbed AGNs, and unabsorbed AGNs are shown as grey circles. Errors are not included in the plots in order to improve visualisation; instead, we include error bars in the corners showing the median error of the corresponding parameters. The histograms in the upper and right sides of the plots show the normalised distribution of the parameters for X-ray absorbed (red) and unabsorbed AGNs (grey).
In the text
thumbnail Fig. 9.

(g–i; top), (r–W2; middle), and (W1–W2; bottom) normalised colour distributions. Solid red histograms show unique sources classified as X-ray absorbed AGNs in XMMFITCAT-Z; solid grey histograms show X-ray unabsorbed AGNs. Only AGNs with reliable modelling are included (see discussion in Sect. 4). The vertical dotted line in the bottom panel shows the Stern et al. (2012) MIR criterion for AGN selection (W1 − W2 >  0.8).
In the text
thumbnail Fig. 10.

W2 versus W1–W2 for XMMFITCAT-Z unique sources with WISE counterparts. Red triangles show X-ray absorbed AGNs, and grey circles show X-ray unabsorbed AGNs. Light-green crosses are objects not classified as AGNs but with an acceptable fit in XMMFITCAT-Z. Only sources with reliable modelling are included (see discussion in Sect. 4). The black dashed line shows the Assef et al. (2013) criterion for AGN selection.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.