| Issue |
A&A
Volume 645, January 2021
|
|
|---|---|---|
| Article Number | A31 | |
| Number of page(s) | 7 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202039304 | |
| Published online | 23 December 2020 | |
Origin of the zebra structure in the Jovian decameter radio emission
1
Institute of Applied Physics of Russian Academy of Sciences,
Nizhny Novgorod,
Russia
e-mail: sh130@appl.sci-nnov.ru
2
National Research University Higher School of Economics,
Nizhny Novgorod,
Russia
3
Institute of Radio Astronomy,
Kharkiv,
Ukraine
e-mail: gallitv@rian.kharkov.ua
Received:
31
August
2020
Accepted:
11
November
2020
Context. We discuss the origin of quasi-harmonic emission bands that have been observed in the dynamic spectra of the Jovian decameter emission.
Aims. We aim to show that the interpretation of the observed structure can be based on the effect of double plasma resonance (DPR) at ion cyclotron harmonics.
Methods. According to the proposed model, in the extended source in the upper ionosphere of Jupiter, where the DPR condition is satisfied for one of the ion cyclotron frequency harmonics, the ion cyclotron waves are effectively excited at the frequency of the lower hybrid resonance. The observed electromagnetic radiation with a quasi-harmonic structure arises due to scattering of ion cyclotron waves by supra-thermal electrons.
Results. Based on the VIP4 magnetic field model, we determine the longitudes at which the source of the considered radiation can be located. The obtained estimates of the plasma density and its height distribution in the source, as well as the energies of emitting ions and scattering electrons provide information about the plasma parameters in the upper ionosphere of Jupiter. Furthermore, these estimates are in good agreement with the observational data.
Key words: planets and satellites: individual: Jupiter / radiation mechanisms: non-thermal / methods: analytical
© ESO 2020
1 Introduction
Intensive observations of Jupiter’s sporadic decameter radiation (DAM) began from the moment of its discovery in 1955 (Burke & Franklin 1955). The radiation consists of noise storms formed by powerful sporadic bursts that have been registered by both ground-based telescopes and space missions in the range from a few MHz to almost 40 MHz. Sporadic radiation from Jupiter is an extraordinary astrophysical phenomenon because it is the result of an unique combination of Jupiter and its satellite Io, which is manifested by the unusual complexity of the frequency-time structure in the dynamic spectra (see, e.g., Zarka 1998; Litvinenko et al. 2009, 2016, and literature cited therein). In particular, the quasi-equidistant stripes of increased and decreased brightness, drifting synchronously in time, are observed in the dynamic spectra of Io-dependent decameter radio emission (Litvinenko et al. 2016; Panchenko et al. 2018). This structure is very similar to Jupiter’s broadband kilometer radio emission (bKOM) spectrum measured during the flight of the Cassini spacecraft (Kurth et al. 2001) as well as to the quasi-harmonic emission stripes in the microwave radiation of the pulsar in the Crab Nebula (Hankins & Eilek 2007) and to the “zebra structure” (ZS) in the solar radio emission (see, e.g., Chernov 2006, and the literature cited there).
In Fig. 1, we present an example of a dynamic spectrum with a ZS obtained with the Ukrainian T-shape radio telescope UTR-2. In the spectrum, the time of 07 : 15 : 41.5 corresponds to the switching of receiving equipment due to the shift of the observed object from the receiving antenna line of sight.
It is generally accepted (see, e.g., Zarka 1998, and literature cited therein) that the decameter radio emission from Jupiter is generated due to the electron cyclotron maser (ECM) at frequencies near the local cyclotron frequency of electrons. However, it should be noted that within the frame of the ECM model of the Jovian radiation origin, it is not possible to explain the quasi-harmonic structure of the zebra type in the dynamic spectra. Zaitsev et al. (1986) proposed a plasma generation mechanism as an explanation of the origin of the narrow-band decameter emission spectral structure with frequency splitting (the dynamic spectrum consists of two quasi-harmonic bands drifting synchronously in time Flagg et al. 1976). In Zaitsev et al. (1986), the appearance of two frequency-separated emission bands is associated with the presence of several maxima of the plasma instability growth rate. However, this mechanism cannot provide the generation of a big number of quasi-harmonic bands, which are observed in the radiation with ZS. The point is that the growth rate decreases significantly with increasing frequency of the growth rate maximum and there is no way to generate a sufficiently large number of emission stripes of approximately equal intensity. In addition, as seen from Fig. 1, the emission stripes of ZS are superimposed with the system of rapidly drifting S-bursts, occupying a much wider frequency interval and having a much lower intensity. The origin of S-bursts is usually associated with fluxes of electrons, moving along the magnetic field lines and being emitting via the ECM mechanism (see, e.g., Ryabov et al. 2014). The existence of quite different spectral structures in the dynamic spectrum indicates that the mechanisms of generation for every radiation spectrum may be different.
The theoretical research discussing the origins of ZS mainly refer to the solar radio emission. In most of these works, the appearance of ZS is associated with the generation mechanism features. In the solar radio emission case, preference is given to plasma generation mechanisms, whereby plasma (electrostatic) waves are first excited and then these waves are transformedinto electromagnetic radiation (see, e.g., Chernov 1976; Zheleznyakov et al. 2016). In a number of works, the appearance of ZS is explained by the interference of waves during their propagation in plasma with a regular non-uniform density (Barta & Karlicky 2006; Ledenev et al. 2006). Treumann et al. (2011) associate the appearance of quasi-harmonic emission bands with the modulation of continuum by the harmonics of the ion cyclotron frequency. A review of the proposed models of the origin of ZS in the solar radio emission, along with the arguments for and against, can be found in Chernov (2006, 2010), Zlotnik (2009) and Zheleznyakov et al. (2016).
The most developed theory of the origin of ZS in solar radio emission is based on the effect of double plasma resonance (DPR) at the electron cyclotron frequency harmonics (Zheleznyakov & Zlotnik 1975a,b,c; Kuijpers 1975). In plasma physics, DPR at electron cyclotron harmonics results from the coincidence of the frequency of the upper hybrid resonance, fUH, with one of the electron cyclotron harmonics, sfBe,
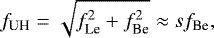 (1)
(1)
where 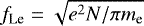 and fBe = eB∕2πmec are the Langmuir and cyclotron frequencies of electron, accordingly, s is the cyclotron harmonic number, N and B are the plasma density and the magnetic field in the generation region, accordingly, e and me are the charge and mass of electron, c is the speed of light. The DPR effect the electron cyclotron harmonics consists in efficient excitation due to the cyclotron instability (the instability growth rate increases by about one to two orders of magnitude) of plasma waves at the upper hybrid resonance frequency.
and fBe = eB∕2πmec are the Langmuir and cyclotron frequencies of electron, accordingly, s is the cyclotron harmonic number, N and B are the plasma density and the magnetic field in the generation region, accordingly, e and me are the charge and mass of electron, c is the speed of light. The DPR effect the electron cyclotron harmonics consists in efficient excitation due to the cyclotron instability (the instability growth rate increases by about one to two orders of magnitude) of plasma waves at the upper hybrid resonance frequency.
The observed electromagnetic radiation with ZS can arise due to the several processes: nonlinear coupling of two exited high-frequency plasma waves with each other, scattering of excited waves by plasma particles, or coupling of exited high-frequency waves with low-frequency waves (Zheleznyakov et al. 2016). The multiband dynamic spectrum can occur to the fact that in a plasma with an inhomogeneous magnetic field and plasma density, DPR effect is realized in spatially separated regions where condition (1) is satisfied (see Fig. 2).
The model based on the DPR effect at electron cyclotron harmonics makes it possible to consistently explain the origin of almost all the main features of the dynamic spectra of solar radiation with ZS. However, using this model to explain ZS in the decameter radiation of Jupiter is not possible. As follows from Eq. (1), for the realization of DPR effect at the electron cyclotron harmonics, it is necessary for the electron Langmuir frequency to significantly exceed the electron cyclotron frequency, fLe ≫ fBe. In most parts of Jupiter’s magnetosphere, including the region where decameter radio emission with ZS is generated, this condition is not satisfied. In these regions, the reverse inequality is true, fLe ≪ fBe. Actually, according toPanchenko et al. (2018), the decameter radio emission from Jupiter with ZS is observed in the range from 12.6 to 29.7 MHz. Taking into account that the decameter radio emission is generated at frequencies close to the local electron cyclotron frequency, from the condition fLe ≫ fBe, Panchenko et al. (2018) obtained the following magnitude of the magnetospheric plasma density in the generation region N > 106−107 cm−3. The obtained values of plasma density significantly exceed the observed value even at the maximum of the ionospheric layer, which is approximately equal to 2 × 105 cm−3 (Hinson et al. 1997, 1998).
Zlotnik et al. (2016) proposed a model based on DPR at ion cyclotron harmonics to explain the generation of the kilometer radio emission of Jupiter with ZS. Double plasma resonance at ion cyclotron harmonics is the coincidence of the lower hybrid resonance frequency with one of the harmonics of the ion cyclotron frequency. According to Zlotnik et al. (2016), radiation sources, each of which generates radiation corresponding to one of the so-called zebra stripes, are located along the magnetic field lines at heights where the lower hybrid resonance frequency coincides with one of the local ion cyclotron harmonics. Excited ion cyclotron waves are converted due to the scattering by supra-thermal magnetized electrons into extraordinary electromagnetic waves with frequencies close to the local electron cyclotron frequency 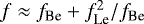 (Shaposhnikov et al. 2018). As a result, a zebra-like structure is formed in the dynamic spectrum of the Jovian radiation. This model of ZS origin in Jupiter’s kilometer radio emission makes it possible to explain the main features of the observed dynamic spectrum.
(Shaposhnikov et al. 2018). As a result, a zebra-like structure is formed in the dynamic spectrum of the Jovian radiation. This model of ZS origin in Jupiter’s kilometer radio emission makes it possible to explain the main features of the observed dynamic spectrum.
It should be noted that the ion cyclotron waves are considered in Treumann et al. (2011) in the possible mechanism of ZS formation in the solar radio emission. According to Treumann et al. (2011), non-equilibrium weakly relativistic ions generate waves at the harmonics of the ion cyclotron frequency, which modulate the electron flux. These electrons then become the source of the observed electromagnetic emission. As a result, this electromagnetic radiation is modulated by frequencies corresponding to the ion cyclotron harmonics. However, for the formation of ZS in the decameter radio emission of Jupiter, the above-mentioned mechanism, as well as the mechanism based on the excitation of ion or electron Bernstein modes in the radiation source (Zheleznyakov & Zlotnik 1975a) are not suitable. The problem is that in these models the frequency spacing between the stripes in the ZS corresponds to the ion cyclotron frequency value in the first case or to the electron cyclotron frequency in the case of the Bernstein electron waves excitation. As we know, the typical value of the ion cyclotron frequency in the regions where decameter radio emission is generated is several tens of kHz, and the electron cyclotron frequency is several tens of MHz, while the observed emission band spacing is 0.3− 1.5 MHz (Panchenko et al. 2018). In the dynamic spectrum, which is shown in Fig. 1, the spacing between the zebra stripes is Δf ≈ 0.45 MHz.
In this paper, we present an interpretation of the observed ZS in the Jovian decameter radio emission that is based on the effect of DPR at ion cyclotron harmonics. This approach allows us to obtain new important theoretical information about the plasma parameters in the upper ionosphere of Jupiter and to compare it with the known observational data. Section 2 provides the necessary information about the DPR theory at the ion cyclotron harmonics. In Sect. 3, on the basis of the DPR effect, which takes place in a magnetic tube passing either through the satellite Io or through its trace in orbit, we present an explanation of the origin of the quasi-harmonic emission bands in the spectrum of the Jovian decameter radio emission observed with the Ukrainian T-shape radio telescope UTR-2 on September 17, 2016. In Sect. 4, we discuss a number of consequences arising from the proposed in Sect. 3 interpretation of ZS origin, followed by a comparative analysis with the known experimental data.
 |
Fig. 1 Example of a dynamic spectrum with a ZS. The spectrum gap at time 07 : 15 : 41.5 is caused byswitching the receiving antenna. |
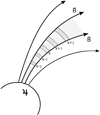 |
Fig. 2 Schematic presentation of a decameter radio emission source, in which radiation is generated due to the DPR effect. The active magnetic tube, in which radiation with a ZS is generated, is marked in gray. The shaded areas indicate the DPR regions where ion cyclotron waves are excited due to the DPR effect. |
2 DPR effect at the ion cyclotron harmonics
The theory of the DPR effect at the ion cyclotron harmonics is presented in Shaposhnikov et al. (2018). Here, we limit our discussion to the information that allows us to understand the proposed interpretation of the origin of the ZS in the decameter emission of Jupiter. As noted above, the double plasma resonance at ion cyclotron harmonics is a coincidence of the lower hybrid frequency, fLH, with one of the harmonics of the ion cyclotron frequency sfBi,
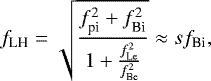 (2)
(2)
where 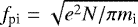 and fBi = eB∕2πmi are the plasma and cyclotron ion frequencies, accordingly, mi is the mass of ion, s is the ion cyclotron harmonic number. In the case when
and fBi = eB∕2πmi are the plasma and cyclotron ion frequencies, accordingly, mi is the mass of ion, s is the ion cyclotron harmonic number. In the case when 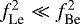 and
and 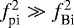 , the condition of double plasma resonance at ion cyclotron harmonics takes a simpler form (Zlotnik et al. 2016; Shaposhnikov et al. 2018):
, the condition of double plasma resonance at ion cyclotron harmonics takes a simpler form (Zlotnik et al. 2016; Shaposhnikov et al. 2018):
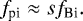 (3)
(3)
Relation (3) differs from the DPR condition at the electron cyclotron harmonics only by the replacing subscript “e” with subscript “i”. Condition (3) shows that DPR is only possible for harmonics with s ≥ 2.
The DPR effect at ion cyclotron harmonics consists in the efficient excitation of the ion cyclotron waves propagating practically across the magnetic field due to the cyclotron instability (the instability growth rate increases about one to two orders of magnitude). The growth rate increasing occurs in a narrow frequency range of Δf ≪ f, located above the value of the cyclotron harmonic frequency sfBi ≈ fpi (Shaposhnikov et al. 2018). It should be noted that a small difference between the frequency of the excited wave and the frequency of the ion cyclotron harmonic is insignificant for our study, thus for simplicity, we assume f = sfBi = fpi.
The inequalities 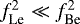 and
and 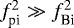 can be rewritten as follows (Zlotnik et al. 2016)
can be rewritten as follows (Zlotnik et al. 2016)
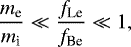 (4)
(4)
where the left side of the inequality corresponds to the condition of a weak magnetic field for ions, 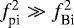 . Condition (4) is satisfied everywhere in the lower magnetosphere, including the ionospheric layer maximum. It means that the necessary conditions for the implementation of DPR at ion cyclotron harmonics exist in those regions of Jupiter’s magnetosphere where sources of Io-dependent decameter radiation are located.
. Condition (4) is satisfied everywhere in the lower magnetosphere, including the ionospheric layer maximum. It means that the necessary conditions for the implementation of DPR at ion cyclotron harmonics exist in those regions of Jupiter’s magnetosphere where sources of Io-dependent decameter radiation are located.
In addition, for the implementation of the DPR effect and the amplification of ion cyclotron waves, the fluxes of fast ions (vi ≫ vTi, vi is the bulk velocity of fast ions, vTi is the thermal velocity of the ionic component of an equilibrium plasma) with a non-equilibrium velocity distribution function are required. This condition is due to the requirement of the absent the ion cyclotron waves absorption by particles of equilibrium plasma. Thenecessary fluxes of fast ions (protons) are observed, in particular, on L-shells associated with Jupiter’s satellite Io (see, e.g., Bhardwaj & Marykutty 2002, and the literature cited there).
Since ion cyclotron waves are low-frequency plasma waves, they cannot go beyond Jupiter’s magnetosphere and be recorded by ground-based equipment. To register the emission, it is necessary to transform ion cyclotron waves into electromagnetic waves that are capable of leaving the magnetosphere of Jupiter. Such waves can be ordinary waves and fast extraordinary waves. The frequency of the latter exceeds the so-called cutoff frequency fc of the extraordinary wave 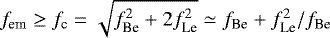 .
.
As noted in Sect. 1, the conversion of the excited ion cyclotron waves into electromagnetic waves is possible as a result of several processes. One of them is the process of coupling of a low-frequency ion cyclotron wave with a high-frequency plasma wave (Zlotnik et al. 2016). However, as shown in Shaposhnikov et al. (2018), under DPR conditions, this process can provide conversion only into an ordinary electromagnetic wave. At the same time, it is generally accepted that the polarization of Io-depended decameter radio emission corresponds to an extraordinary electromagnetic wave (see, e.g., Dulk et al. 1994; Zarka 1998).
Conversion of the excited ion cyclotron waves into the fast extraordinary electromagnetic waves is possible as a result of scattering of ion cyclotron waves by non-equilibrium supra-thermal particles. Scattering by particles with an equilibrium distribution function occurs with a decrease in the frequency of the scattered wave, while the conversion into a fast extraordinary wave requires a significant increase in frequency during the scattering process. As shown in Shaposhnikov et al. (2018), the conversion as a result of scattering by ion beams is possible only if particles have the unrealistically high energy, vi ≥ (mi∕me)vTi.
In the case of scattering by fluxes of supra-thermal non-equilibrium electrons, two scenarios are possible for the conversion of ion cyclotron waves into the fast extraordinary waves. The first scenario, proposed in Shaposhnikov et al. (2018) as an the explanation of the observed ZS in Jupiter’s kilometer radio emission, is realized at small values of the orthogonal (relative to the magnetic field) component of the velocity of scattering electrons 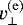 , that is, at electron velocities satisfying the condition:
, that is, at electron velocities satisfying the condition:
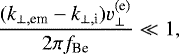 (5)
(5)
where k⊥,em and k⊥,i are the orthogonal component of the wave vector of the electromagnetic wave (em) and the ion cyclotron wave (i). In this case, the law of conservation of energy during scattering takes the form (Melrose & Sy 1972; Tsytovich 1977):
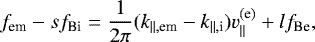 (6)
(6)
where the subscript (∥) denotes the longitudinal component of the wave vectors of the electromagnetic and ion cyclotron waves and the longitudinal component of the velocity of scatteringelectrons, and l is the number of the electron cyclotron harmonic. The appearance of the electron cyclotron harmonics in the law of conservation of energy (6) is due to the fact that the scattering electrons move along a spiral trajectory. Shaposhnikov et al. (2018) show that the conversion of the ion cyclotron wave at the frequency sfBi into the extraordinary electromagnetic wave occurs as a result of scattering at the first electron cyclotron harmonic (l = 1) by electrons with velocities 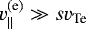 .
.
The second conversion scenario on fluxes of supra-thermal electrons is realized at large values of the orthogonal component of the velocity of scattering electrons, when their orthogonal velocities 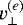 satisfies the condition:
satisfies the condition:
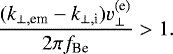 (7)
(7)
In this case, the law of conservation of energy in the presence of scattering takes the form:
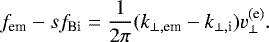 (8)
(8)
The law of conservation of energy (Eq. (8)) takes into account the fact that the wave vectors of excited ion cyclotron waves are concentrated in a small range of angles in the area of the direction orthogonal to the magnetic field, that is, k∥,i ≪ k⊥,i (see Shaposhnikov et al. 2018, for details). Additionally taking into account that the growth rate of the ion cyclotron waves instability under DPR conditions is at maximum for wave vectors k⊥,i ≈ 0.6πfBi∕vTi (Shaposhnikov et al. 2018), it follows from Eq. (8) that for the conversion of ion cyclotron waves into fast extraordinary waves, the electrons should have velocities of 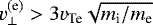 .
.
It should be noted that during the scattering by particles, the conversion to an ordinary wave is possible. What is also possible is the conversion to a fast extraordinary wave with frequency value that is significantly differ from the cutoff frequency, fc (the expressions for law of conservation of energy (Eqs. (6) and (8)) allow for such conversion). Nevertheless, in the radiation emerging from the source region, the electromagnetic waves corresponding to the extraordinary mode with frequencies belonging to a narrow frequency range, Δf ≪ fem, near the cutoff frequency fc. That is to say that with frequencies at which the refractive index of the extraordinary wave is small, ne ≪ 1, these waves are dominated (Shaposhnikov et al. 2018). This is due to two reasons. The first reason is associated with an increase of the spectral flux, Ff, of waves with the low refractive index. This flux is inversely proportional to the cube of the wave refractive index (Zaitsev et al. 1986):
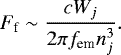 (9)
(9)
With comparable values of the wave energy density in the source, Wj (j = e – for an extraordinary wave and j = o – for an ordinary wave), the radiation flux leaving the source is by a factor of 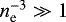 greater for the above-mentioned waves than at the same frequencies for an ordinary wave (for it no ≃ 1), or for an extraordinary wave, outside a narrow interval near fc. The second reason is associated with a larger (as compared to that of other waves) spatial amplification of waves with a low refractive index, which is due to their small group velocity (Zaitsev et al. 1986). Due to the small value of group velocity, the waves are significantly amplified during their propagation in the source region, Wj ~ exp(κieL∕cne). Here, κie is the coefficient of conversion of ion cyclotron waves into fast extraordinary waves, L is the source size.
greater for the above-mentioned waves than at the same frequencies for an ordinary wave (for it no ≃ 1), or for an extraordinary wave, outside a narrow interval near fc. The second reason is associated with a larger (as compared to that of other waves) spatial amplification of waves with a low refractive index, which is due to their small group velocity (Zaitsev et al. 1986). Due to the small value of group velocity, the waves are significantly amplified during their propagation in the source region, Wj ~ exp(κieL∕cne). Here, κie is the coefficient of conversion of ion cyclotron waves into fast extraordinary waves, L is the source size.
In Shaposhnikov et al. (2018), one more consequence of the smallness of the refractive index is mentioned. Due to refraction, when the radiation leaves the source region where ne ≪ 1 to outside the source where ne ~ 1, the radiation acquires a directional character, even in the case where the conversion is the same in all directions. Radiation is concentrated in a narrow angle 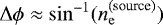 along the source inhomogeneity gradient.
along the source inhomogeneity gradient.
Thus, regardless of the magnitude of the thermal spread of the scattering electrons, the radiation leaving the source region is concentrated in a narrow frequency range Δf ≪ fem, near the local gyrofrequency, fem ≈ fBe, and its polarization corresponds to the extraordinary waves, that is, during scattering there is no appreciable frequency broadening of the radiation bands in the ZS. In addition, due to refraction, the outgoing radiation is concentrated in a narrow range of angles along the source inhomogeneity gradient (Shaposhnikov et al. 2018).
3 Formation of the quasi-harmonic stripes in the emission region
As we notedabove, the peculiarity of the formation mechanism of the ZS, based on the DPR effect, is that its different emission stripes of the are generated in the various regions of the extended source with the inhomogeneous magnetic field and plasma. Figure 2 shows a schematic presentation of a decameter radio emission source, in which radiation is generated due to the DPR effect.
We construct the source model as follows (as seen in Fig. 3). Since the discussed spectrum (Fig. 1) is of the Io-dependent radiation, so the emission source is on the L-shells of the magnetic field, where the satellite Io is located. For the sake of certainty, let us take L ≈ 6. The VIP4 model was used as a magnetic field model (Connerney et al. 1998). The frequency interval in which the radiation with a ZS is observed equals ≈24−27 MHz and its value is the same as the value of local electron cyclotron frequency range in the generation region. So, according to the VIP4 model, it occupies a small region along the field lines Δls ≪ RJ. This region is located in the lower magnetosphere or upper ionosphere of Jupiter, that is, near the so-called planet “surface”’. Therefore, when constructing the model and calculating the cyclotron frequencies, the magnetic latitude of the source is assumed to be approximately equal to the magnetic latitude of the Io footprint φ = 65°. The exact value of the source longitude is unknown, and, for the sake of certainty, we assumed that the source of the observed radiation with a ZS is located at the instantaneous Io’s magnetic tube. The longitude of the instantaneous Io’s magnetic tube is estimated as follows. At the time marked with a dotted line in the dynamic spectrum in Fig. 1, the longitude of the central meridian (λCML) is approximately λCML ≈ 168°, and the phase of Io (γIo) is γIo ≈ 231°. The longitude of the satellite Io in system III (magnetic longitude) is found by the formula λIo = λCML + 180° − γIo. For the values of λCML = 168° and γIo = 231° we get λIo = 117°.
Figure 3 shows a scheme of the DAM generation, which contains the ZS, based on the assumption that the source is located along the magnetic field lines that intersect satellite Io λIo = 117°, and the harmonic numbers of the ion cyclotron frequency s vary from 2 to 8. In Fig. 3, the dash-dotted and dashed lines show the dependence of the electron cyclotron frequency, fBe, and harmonics of the ion cyclotron frequency, sfBi, accordingly, on the distance from the center of the planet r = R∕RJ (RJ is the radius of Jupiter) along the active magnetic tube. The horizontal lines in the upper part of the figure mark the frequencies (fzp) at which the emission stripes of the ZS are observed. Since the expected frequencies of the ZS in the proposed model should be slightly differ from the local electron cyclotron frequency, the intersection points of the horizontal lines, fzp, with the dash-dotted line, fBe, indicate the positions of the double plasma resonance regions in the active magnetic flux tube. The intersections of dotted vertical straight lines with dashed lines, sfBi, determine the frequencies of ion cyclotron harmonics and the local plasma ion frequency, fpi, in the regions of double plasma resonance.
The distribution of plasma density along an active magnetic tube located at a longitude of λs = λIo = 117° is shown in Fig. 4, where the dots mark the plasma density values obtained as a result of our model implementation. The lower boundary of the source is located at an altitude of h ≈ 2000 km, where the plasma concentration is ≈3 × 105 cm−3. The solid line shows the approximating curve ∝exp(rRJ∕H) with height scale of H ≈ 740 km.
As noted above, the exact location of the active magnetic flux tube is unknown. The active magnetic flux tube can be a magnetic tube passing through the satellite Io. In turn, observations carried out onboard the Galileo spacecraft show the existence of energetic electrons and ions fluxes, as well as fluxes of cold plasma in the tail of Io (Williams et al. 1996; Frank & Paterson 1999; Mauk et al. 2001). In addition, there is an extended (up to 100° in longitude) Io footprint in the ultraviolet and infrared frequency ranges that is caused by plasma flow from Io’s tail (see Bhardwaj & Marykutty 2002, and literature cited therein). These observations indicate that the source can be located not only on the magnetic field lines directly crossing Io (instantaneous Io’s magnetic tube), but also on the on magnetic field lines which cross Io’s tail, that is, at longitudes of λs < λIo. However, it is necessary to take into consideration that the magnitude of the magnetic field and, as a result, the local electron cyclotron frequency and cutoff frequency, fc, change along Io’s trail on the planet’s “surface”. Since the maximum emission frequency (fmax ≈ 27 MHz) must exceedthe cutoff frequency on the planet’s “surface”, this requirement imposes a limitation of the choice of the possible active tubes. This means that the distance to the lower boundary of the source (Rl) must exceed the radius of Jupiter, Rl > RJ (see Fig. 2). Due to the obtained plasma density distribution in the source (Fig. 4), it is possible to define the location of lower possible boundary of the double plasma resonance region in the active tube. It can be seen from Fig. 4 that the plasma density decreases with the altitude increasing. Thus, the altitude of the region in which a double plasma resonance is possible is expected to be higher than the altitude of the ionospheric maximum location, which is of ~ 1000−2000 km (Hinson et al. 1997, 1998). According to the VIP4 magnetic field model this requirement is satisfied for longitudes, λs ≥ 109°. So, at the time moment marked with a dashed vertical line in Fig. 1, the tubes with longitudes of 109° ≤ λs ≤ 117° can be the necessary active magnetic tubes. Figure 4 shows the plasma change in a source located in a magnetic tube with a longitude λs = 109°. In this case, the lower boundary of the double plasma resonance region is located at an altitude of h ≈ 900 km, where the plasma concentration is ≈3 × 105 cm−3. The solid line shows the approximating curve ∝exp(rRJ∕H) with height scale of H ≈ 730 km.
 |
Fig. 3 Scheme of generation of the radiation with ZS at the instant marked by a dashed line in Fig. 1. Electron cyclotron frequency fBe and harmonics of ion cyclotron frequency sfBi with harmonic s varying from2 to 8 as function of the distance r = R∕RJ from the planet center along the active magnetic tube (λIo = 117°) are shown. Horizontal solid lines denote the frequency of observed zebra stripes fzp. The regions where fBe = fzp are marked by circles on the fzp lines. The DPR regions are marked by filled circles on the sfBi curves. Starson the r axis show the distances at which the DPR regions at the harmonics s varying 2 to6 are located. |
 |
Fig. 4 Plasma density as function of distance r = R∕RJ from the planet center along the active magnetic tube when the harmonic numbers of the ion cyclotron frequency s vary from 2 to 8 (hard lines) and from 5 to 11 (dashed lines) for two possible positions of the active magnetic power tube λs = λIo = 117° and λs = 109°. Plasma concentration values that follow from the model are marked by circles, the lines represent exponential fitting lines. |
4 Discussion
In this work, we propose the generation scheme for the Jovian decameter emission with a fine frequency structure in the form of quasi-harmonic radiation stripes, based on the DPR effect at the ion cyclotron harmonics. From the proposed scheme (see Figs. 3 and 4), it follows that radiation sources with a ZS are located in the upper ionosphere, and their lower boundary, depending on the longitude, λs, is set at altitude of 900−2000 km above the planet’s “surface”. The plasma density at these altitudes is ≈3 × 105 cm−3 and decreases with increasing height with the characteristic scale of approximately 730−740 km. The obtained values are in a good agreement with the ionospheric plasma measurement data obtained by the Voyager 2 and Galileo spacecraft (Hinson et al. 1997, 1998). The localization of radiation sources with a ZS in the upper ionosphere facilitates the suggestion that the transverse velocity component of the supra-thermal electrons arriving from the region of Io’s orbit is predominant. This is caused by the increasing of electron pitch angles due to their propagation to the region with strong magnetic field. Thus, we can assume that in the region of radiation with the ZS, the second scenario assuming the conversion of ion cyclotron waves into the electromagnetic radiation is realized. Taking the temperature of the equilibrium plasma in the ionosphere equal to 103 K, we obtain the following estimate of the electron transverse energy, E⊥≥ 20 keV, due to which the conversion of the ion cyclotron waves into the fast extraordinary waves occurs. We note here that the measurements made in Io’s tail reveal the intense energetic electron beams (> 20 keV) flowing along Io’s flux tube (Williams et al. 1996). In the proposed generation scheme, the number of ion cyclotron harmonics s at which DPR occursis a free parameter. As follows from Eq. (3), in the considered magnetic field (which is determined by observed radiation frequency), the harmonic numbers depend only on the plasma distribution in the generation region. Figure 4 shows the plasma distribution for two variants of changing the number s of ion cyclotron harmonics, from 2 to 8 and from 5 to 11. It can be seen from Fig. 4 that with the increase of the harmonic number, the value of the plasma density, required for the implementation of DPR, increases. For s = 5−11, the plasma density at the lower boundary of the source (where DPR occurs at harmonics s = 10, 11) exceeds the plasma density at the maximum of the ionospheric layer obtained from measurements. This result imposes a restriction on the harmonic numbers at which the DPR can be realized in the source of the radiation discussed in the work, and the harmonic number, s, can vary only from 2 to about 9.
Our model is developed on the assumption that plasma in the generation region contains only one ion species, which are the ions of hydrogen H+. At the same time, the ionosphere of Jupiter contains other species of ions. Observations in the IR and UV from Io’s footprint indicate that the region of generation can contain ions of tritium H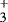 and deuterium H
and deuterium H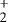 (see, for example, Connerney et al. 1993; Tao et al. 2011; Gerard et al. 2014). According to the ionosphere model calculated by Tao et al. (2011), these ions are the main minor species above the ionospheric maximum, that is, where the source of DPR radiation is located. In this region of the ionosphere, the ion tritium density is approximately one order of magnitude lower, and the ion deuterium density is more than two orders of magnitude smaller, than the density of hydrogen ions. It can be shown that the presence of minor species in the DPR radiation source has a negligible effect on the spectrum of radiation generated by the DPR effect. Indeed, the source model is based on the DPR effect, the implementation of which is condition (2). In the region where decameter radio emission is generated, this condition is reduced to the equality of the plasma frequency of ions to the frequency of one of the ion cyclotron harmonics (Eq. (3)). In principle, the consideration of minor ions can first lead to a change in the frequency of the lower hybrid resonance and, second, to the appearance of new cyclotron harmonics corresponding to the minor ions, on which double plasma resonance can occur. In the first case, accounting for minor species gives a correction of order mi Nm∕mmNi (where Nm and mm are the equilibrium density and the mass of the ion minor species, respectively) to the frequency of the lower hybrid resonance. For the largest minor species, H
(see, for example, Connerney et al. 1993; Tao et al. 2011; Gerard et al. 2014). According to the ionosphere model calculated by Tao et al. (2011), these ions are the main minor species above the ionospheric maximum, that is, where the source of DPR radiation is located. In this region of the ionosphere, the ion tritium density is approximately one order of magnitude lower, and the ion deuterium density is more than two orders of magnitude smaller, than the density of hydrogen ions. It can be shown that the presence of minor species in the DPR radiation source has a negligible effect on the spectrum of radiation generated by the DPR effect. Indeed, the source model is based on the DPR effect, the implementation of which is condition (2). In the region where decameter radio emission is generated, this condition is reduced to the equality of the plasma frequency of ions to the frequency of one of the ion cyclotron harmonics (Eq. (3)). In principle, the consideration of minor ions can first lead to a change in the frequency of the lower hybrid resonance and, second, to the appearance of new cyclotron harmonics corresponding to the minor ions, on which double plasma resonance can occur. In the first case, accounting for minor species gives a correction of order mi Nm∕mmNi (where Nm and mm are the equilibrium density and the mass of the ion minor species, respectively) to the frequency of the lower hybrid resonance. For the largest minor species, H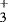 , the correction value does not exceed 0.1. In the second case, in an inhomogeneous plasma, implementation of DPR for minor ions occurs in regions of the source that can not be the DPR regions for H+ ions. This fact can lead to the stripes smearing. However, it should be taken into account that the instability growth rate of electrostatic cyclotron ion waves due to the DPR effect is proportional to N1,α∕mα (where mα is the mass of the ion of species α, at the cyclotron harmonic of which DPR occurs, N1,α is the density of non-equilibrium component of ions α), and under any other equal conditions will be significantly less for minor ions. For instance, the instability growth rate at the ion cyclotron harmonics of the H+ ion will be more than an order of magnitude larger than the corresponding instability growth rate at the cyclotron harmonics of the tritium ion H
, the correction value does not exceed 0.1. In the second case, in an inhomogeneous plasma, implementation of DPR for minor ions occurs in regions of the source that can not be the DPR regions for H+ ions. This fact can lead to the stripes smearing. However, it should be taken into account that the instability growth rate of electrostatic cyclotron ion waves due to the DPR effect is proportional to N1,α∕mα (where mα is the mass of the ion of species α, at the cyclotron harmonic of which DPR occurs, N1,α is the density of non-equilibrium component of ions α), and under any other equal conditions will be significantly less for minor ions. For instance, the instability growth rate at the ion cyclotron harmonics of the H+ ion will be more than an order of magnitude larger than the corresponding instability growth rate at the cyclotron harmonics of the tritium ion H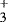 . As a result, the radiation at frequencies corresponding to the cyclotron harmonics of minor ions will be significantly lower and can be neglected.
. As a result, the radiation at frequencies corresponding to the cyclotron harmonics of minor ions will be significantly lower and can be neglected.
It should be noted, in particular, that the quasi-harmonic stripes presented in the dynamic spectrum (Fig. 1) have an interesting feature. Narrowband continuous radiation transforms into a quasi-periodic sequence of negatively drifting bursts (see the time interval ≈ 07 : 15 : 44.5−07 : 15 : 45.4 in Fig. 1). The transformation of continuous narrow-band radiation (Δf ≪ f) for the decameter radio emission from Jupiter is discussed in Shaposhnikov et al. (2011). In this work, a model based on effect of the amplitude-frequency modulation and the broadening of the frequency spectrum during the emission propagation in a medium with frequency dispersion and parameters that vary over time, is proposed. Shaposhnikov et al. (2011) show that the structure of the initially continuous radiation generated in Jupiter’s ionosphere at frequencies close to the cutoff frequency of a fast extraordinary wave and propagated through a region with a nonstationary magnetic field can significantly change. Depending on the conditions in and near the radiation source, various types of finestructure will be observed in the dynamic spectrum, including quasiperiodic sequences of negatively drifting bursts. The frequency dispersion of the medium is due to the frequency dependence on the refractive index, while the negative frequency drift of the burst is due to the frequency dependence on the group velocity of the extraordinary electromagnetic wave at frequencies near the cutoff frequency. A necessary condition for the appearance of quasiperiodic sequences of S-bursts in the model proposed in Shaposhnikov et al. (2011) is the presence of unsteady perturbations of the planet’s magnetic field in Jupiter’s ionosphere. One of the reasons for the necessary disturbance may be, for example, oscillations of the magnetic field in the ionospheric Alfvén resonator (in this regard see Ergun et al. 2006; Shaposhnikov et al. 2011). The conditions in the radiation source with a ZS correspond to the above-mentioned requirements necessary for the frequency spectrum transformation model proposed in Shaposhnikov et al. (2011). In this case, the observed frequency drift is due to the frequency dependence on the group wave velocity, and its magnitude is connected with the plasma parameters in the source by the relation (Zaitsev et al. 1986):
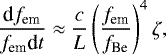 (10)
(10)
where L is the length of the radiation propagation trajectory part where the dependence of the group wave velocity on frequency is essential (i.e., the length of the radiation propagation path in the ionosphere), And the factor ζ is equal to 0.1−1, depending on the tendency of the extraordinary wave refractive index, ne, to approach to the vicinity of zero if fem → fc. From our model of the ZS formation assume that Ne ≈ 2 × 105 cm−3 and fBe ≈ fem = 26 MHz, the frequency drift is d fem∕dt ≈−6 MHz s−1, as found from the analysis of the dynamic spectrum (Fig. 1), and ζ = 0.5, we obtain the following estimation of the value L ≈ 4 × 107 cm.
Thus, in this work, on the basis of the DPR effect at the ion cyclotron harmonics, an explanation is given for the origin of quasi-harmonic emission bands observed in the dynamic spectrum of Jupiter decameter radio emission, is given. According to the proposed scheme, Jovian radiation is generated in the upper ionosphere of the planet, where the DPR condition fpi ≈ sfBi is satisfied. Once this condition is satisfied, the growth rate of the instability of the ion cyclotron waves increases by approximately one or two orders of magnitude. Electromagnetic radiation with a frequency spectrum in the form of quasi-harmonic stripes appears as a result of the ion cyclotron waves scattering by supra-thermal electrons. The obtained estimates of the magnitude and distribution of the equilibrium plasma concentration in the source, the energy of supra-thermal ions and electrons required for efficient generation of ion cyclotron waves and their conversion into electromagnetic radiation are in good agreement with modern concepts of the structure of the upper ionosphere of Jupiter.
In the present work, the problem of the quasi-harmonic emission stripes origin is considered in detail. The numerical solution of the problem of ion cyclotron waves conversion into electromagnetic radiation remains beyond the scope of this work. The numerical solutions to this problem make it possible to determine the parameters of supra-thermal ions and electrons with a nonequilibrium distribution function, which are necessary for the generation of the observed radiation level. In addition, it should be pointed out that quasi-harmonic emission stripes are not the only feature of the fine structure presented in the dynamic spectrum under discussion (Fig. 1). The “bursts in absorption” (in the time interval ≈ 07 : 15 : 40−07 : 15 : 43) and “S-bursts rain” are also seen in the dynamic spectrum of Fig. 1. The study of the formation mechanism of these fine structure elements is not the purpose of this work, but it is important for the creation of a complex source model of the Jovian DAM emission. For subsequent studies, it is interesting to note the fact that both of these structures demonstrate a negative frequency drift, the magnitude of which is close to the magnitude of the frequency drift of bursts appearing as a result of the continuous emission bands transformation into a sequence of quasi-periodic bursts. The solution to all these problems is necessary toconfirm the proposed mechanism for the formation of emission bands and diagnostics of plasma parameters in the upper ionosphere of Jupiter.
Acknowledgements
The work is supported by the Russian Science Foundation under grant No. 20-12-00268. Part of this work was supported by the Russian Foundation for Basic Research (projects 19-02-00704a and 20-02-00108a, Sect. 2), the State Assignment No. 0035-2019-0002. The work of the Ukrainian team was supported by the National Academy of Sciences of Ukraine (project “Plasmospheres” 012U102592, observation of DAM).
References
- Barta, M., & Karlicky, M. 2006, A&A, 450, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bhardwaj, A., & Marykutty, M. 2002, Earth-Like planets and moons: Proceedings of the 36th ESLAB Symposium, June 3–8, 2002, ESTEC, Noordwijk, The Netherlands, eds. B. Foing, & B. Battrick (European Space Agency), 115 [Google Scholar]
- Burke, B. F., & Franklin, K. L. 1955, J. Geophys. Res., 60, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Chernov, G. P. 1976, Sov. Astron., 20, 582 [Google Scholar]
- Chernov, G. P. 2006, Space Sci. Rev., 127, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Chernov, G. P. 2010, Res. Astron. Astrophys., 10, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Connerney, J. E. P., R. Baron, R., Saton, T., & Owen, T. 1993, Science, 262, 1035 [NASA ADS] [CrossRef] [Google Scholar]
- Connerney, J. E. P., Acuna, M. H., Ness, N. F., & Satoh, T. 1998, J. Geophys. Res., 103, 11929 [NASA ADS] [CrossRef] [Google Scholar]
- Dulk, G. A., Leblanc, Y., & Lecacheux, A. 1994, A&A, 286, 683 [NASA ADS] [Google Scholar]
- Ergun, R. E., Su, Y. J., Andersson, L., et al. 2006, J. Geophys. Res., 111, A06212 [Google Scholar]
- Flagg, R. S., Krausche, D. S., & Lebo, G. R. 1976, Icarus, 29, 477 [CrossRef] [Google Scholar]
- Frank, L., & Paterson, W. 1999, J. Geophys. Res., 104, 28657 [CrossRef] [Google Scholar]
- Gerard, J., Bonfond, B., Grodent, D., et al. 2014, J. Geophys. Res., 119, 9072 [NASA ADS] [CrossRef] [Google Scholar]
- Hankins, T. H., & Eilek, J. A. 2007, ApJ, 670, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Hinson, D. P., Flasar, F. M., Kliore, A., et al. 1997, Geophys. Res. Lett., 24, 2107 [NASA ADS] [CrossRef] [Google Scholar]
- Hinson, D. P., Kliore, A., Flasar, F. M., et al. 1998, J. Geophys. Res., 103, 29343 [NASA ADS] [CrossRef] [Google Scholar]
- Kuijpers. 1975, A&A, 40, 405 [Google Scholar]
- Kurth, W. S., Hospodarsky, G. B., Gurnett, D. A., et al. 2001, in Planetary Radio Emission V: Proceedings of the 5th International Workshop, April 2–4, 2001, Graz, Austria, eds. H. O. Rucker, M. L. Kaiser, & Y. Leblanc (Graz: Austrian Academy of Sciences Press), 15 [Google Scholar]
- Ledenev, V. G., Yan, Y., & Fu, Q. 2006, Sol. Phys., 233, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Litvinenko, G. V., Rucker, H. O., Vinogradov, V. V., Leiner, M., & Shaposhnikov, V. E. 2009, A&A, 493, 651 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Litvinenko, G. V., Shaposhnikov, V. E., Konovalenko, A. A., et al. 2016, Icarus, 272, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Mauk, B., Williams, D., & Eviatar, A. 2001, J. Geophys. Res., 106, 26195 [CrossRef] [Google Scholar]
- Melrose, D. B., & Sy, W. N. 1972, Aust. J. Phys., 25, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Panchenko, M., Rošker, S., Rucker, H. O., et al. 2018, A&A, 610, A69 [CrossRef] [EDP Sciences] [Google Scholar]
- Ryabov, V. B., Zarka, P., Hess, S., et al. 2014, A&A, 568, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shaposhnikov, V. E., Korobkov, S. V., Rucker, H. O., et al. 2011, J. Geophys. Res., 116, A03205 [Google Scholar]
- Shaposhnikov, V. E., Zaitsev, V. V., & Litvinenko, G. V. 2018, J. Geophys. Res., 123, 9395 [CrossRef] [Google Scholar]
- Tao, C., Badman, S. V., & Fujimoto, M. 2011, Icarus, 213, 581 [CrossRef] [Google Scholar]
- Treumann, R. A., Nakamura, R., & Baumjohann, W. 2011, Ann. Geophys., 29, 1673 [NASA ADS] [CrossRef] [Google Scholar]
- Tsytovich, V. 1977, Theory of Turbulent Plasma (New York: Springer), 535 [Google Scholar]
- Williams, D. J., Mauk, B. H., McEntire, R. E., et al. 1996, Science, 274, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Zaitsev, V. V., Zlotnik, E. Y., & Shaposhnikov, V. E. 1986, A&A, 169, 345 [NASA ADS] [Google Scholar]
- Zarka, P. 1998, J. Geophys. Res., 103, 20159 [NASA ADS] [CrossRef] [Google Scholar]
- Zheleznyakov, V. V., & Zlotnik, E. Y. 1975a, Sol. Phys., 43, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Zheleznyakov, V. V., & Zlotnik, E. Y. 1975b, Sol. Phys., 44, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Zheleznyakov, V. V., & Zlotnik, E. Y. 1975c, Sol. Phys., 44, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Zheleznyakov, V. V., Zlotnik, E. Y., Zaitsev, V. V., & Shaposhnikov, V. V. 2016, Phys. Usp., 59, 997 [NASA ADS] [CrossRef] [Google Scholar]
- Zlotnik, E. Y. 2009, Central Eur. Astrophys. Bull., 33, 281 [Google Scholar]
- Zlotnik, E. Y., Shaposhnikov, V. E., & Zaitsev, V. V. 2016, J. Geophys. Res., 121, 5307 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Example of a dynamic spectrum with a ZS. The spectrum gap at time 07 : 15 : 41.5 is caused byswitching the receiving antenna. |
| In the text | |
 |
Fig. 2 Schematic presentation of a decameter radio emission source, in which radiation is generated due to the DPR effect. The active magnetic tube, in which radiation with a ZS is generated, is marked in gray. The shaded areas indicate the DPR regions where ion cyclotron waves are excited due to the DPR effect. |
| In the text | |
 |
Fig. 3 Scheme of generation of the radiation with ZS at the instant marked by a dashed line in Fig. 1. Electron cyclotron frequency fBe and harmonics of ion cyclotron frequency sfBi with harmonic s varying from2 to 8 as function of the distance r = R∕RJ from the planet center along the active magnetic tube (λIo = 117°) are shown. Horizontal solid lines denote the frequency of observed zebra stripes fzp. The regions where fBe = fzp are marked by circles on the fzp lines. The DPR regions are marked by filled circles on the sfBi curves. Starson the r axis show the distances at which the DPR regions at the harmonics s varying 2 to6 are located. |
| In the text | |
 |
Fig. 4 Plasma density as function of distance r = R∕RJ from the planet center along the active magnetic tube when the harmonic numbers of the ion cyclotron frequency s vary from 2 to 8 (hard lines) and from 5 to 11 (dashed lines) for two possible positions of the active magnetic power tube λs = λIo = 117° and λs = 109°. Plasma concentration values that follow from the model are marked by circles, the lines represent exponential fitting lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


