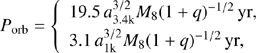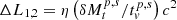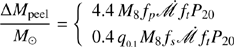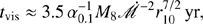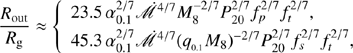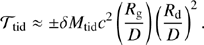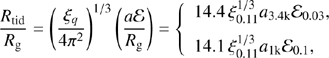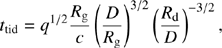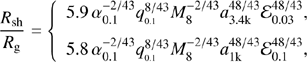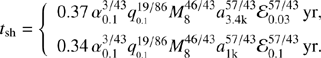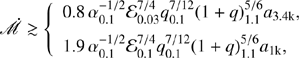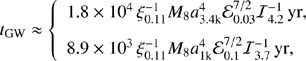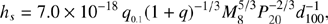EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 643 (November 2020) A&A, 643 (2020) L9 Full HTML
Free Access
Issue
A&A
Volume 643, November 2020
Article Number L9
Number of page(s) 6
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202039368
Published online 03 November 2020

© ESO 2020

1. Introduction

Seyfert galaxies are commonly classified into type 1 and 2 active galactic nuclei (AGNs) corresponding to ones with and without broad emission lines, respectively. The two kinds of AGNs have been successfully unified by obscurations of a dusty torus differently orientated to observers (Antonucci 1993; Netzer 2015). Despite its success, five outliers were detected between the 1970-1980s: NGC 3516 (Andrillat 1968), NGC7603 (Tohline & Osterbrock 1976), Fairall 9 (Kollatschny & Fricke 1985), NGC 4151 and 3C 390.3 (Penston & Perez 1984), and Mrk 1080 (Cohen et al. 1986). They undergo transitions from type 1 to type 2 on a timescale of less than one year according to Hβ line, or vice versa, they also show Mg II (Guo et al. 2019) and C IV (Ross et al. 2019) lines. They are known today as changing-look (CL) AGNs (CL-AGNs), which are a fast-increasing population discovered in time domaine surveys (e.g., MacLeod et al. 2016; Yang et al. 2018; MacLeod et al. 2019; Graham et al. 2020; Wang et al. 2019; Frederick et al. 2019). Their continuum changes from a factor of a few to several tens when a type transition occurs. Typical Eddington ratios are λEdd ≈ 0.1 for CL-AGNs in the type 1 state (MacLeod et al. 2019). Moreover, CL cannot be explained by obscuration variations according to polarization observations (Hutsemékers et al. 2019; Marin et al. 2019). This greatly enhances it as a puzzle.

Several hypotheses have been suggested to explain CL. Inspired by changes in the accretion states of X-ray binaries, Noda & Done (2018) showed that evaporation of the inner part of the disk drives a change in accretion states into a drop, which causes the CL of Mrk 1018. This appears to be supported by the analogy of CL-AGNs to X-ray binaries (Ruan et al. 2019; Ai et al. 2020; Liu et al. 2019). Cooling fronts driven by a sudden change in the magnetic torque at the innermost stable circular orbit (Ross et al. 2018), or magnetic fields supporting a geometrically thick disk (Dexter & Begelman 2019), or the radiation pressure instability (Sniegowska et al. 2020) lead to a changing state. With the standard model of a single SMBH system for AGNs (Rees 1984), we can hardly reconcile the shorter timescales of CL properties with the various instabilities of accretion disks because accretion-disk timescales are far longer (Stern et al. 2018; Ross et al. 2018; Lawrence 2018), even if they could last a few months, as in the CL-AGN 1ES 1927+654 (Trakhtenbrot et al. 2019). These facts strongly imply an external torque required for the fast type transition. Considering highly asymmetric profiles of CL-AGNs, we could think that the most natural sources driving the transitions are the secondary black hole at the galactic center.

In this Letter, we show one possibility: CB-SMBHs with highly eccentric orbits can trigger type transitions. In this context, the tidal torque of black holes acting on the mini-disks can efficiently exchange angular momentum (AM) with the binary orbit, giving rise to fast and violent variations in ionizing sources. Consequently, the appearance of the AGNs changes.

2. Accretion onto binary black holes

2.1. Close binaries of SMBHs

Numerous studies have been performed for CB-SMBHs based on Artymowicz & Lubow (1996) and Armitage & Natarajan (2002). The basic conclusions are that (1) the circumbinary disk (CBD) surrounding the CB-SMBHs has a central cavity with a radius of RCBD ≈ 2a(1 + e), which is formed by tidal torque of the binary with a half-major axis (a) and eccentricity (e); (2) each black hole efficiently peels streams of gas off the inner edge of the CBD that rapidly traverse the cavity (MacFadyen & Milosavljević 2008; Roedig & Sesana 2014; Farris et al. 2015a,b; Shi & Krolik 2015; Bowen et al. 2018); and (3) the peeled streams form two mini-disks around each member of the binary (Roedig & Sesana 2014; Farris et al. 2014, 2015a,b; D’Orazio et al. 2016; Tang et al. 2018; d’Ascoli et al. 2018; Moody et al. 2019; Bowen et al. 2018, 2019; Muñoz et al. 2020).

We consider one CB-SMBH system, whose separation with phases is described by D = a(1 − e2)/(1+e cos θ)​, and θ is the orbital phase angles. Periastron and apastron are given by Dmin, max = a(1 ∓ e), respectively, where tidal interaction is strongest and weakest. The CB-SMBH periods are

P orb = { 19.5 a 3.4 k 3 / 2 M 8 ( 1 + q ) − 1 / 2 yr , 3.1 a 1 k 3 / 2 M 8 ( 1 + q ) − 1 / 2 yr , $$ \begin{aligned} P_{\rm orb}=\left\{ \begin{array}{l} 19.5\,a_{\rm 3.4k}^{3/2}M_{8}(1+q)^{-1/2}\,\mathrm{yr},\\ 3.1\,a_{\rm 1k}^{3/2}M_{8}(1+q)^{-1/2}\,\mathrm{yr}, \end{array}\right. \end{aligned} $$(1)

where a1k, 3.4k = a/(1, 3.4)×103Rg was chosen for two types of eccentricities to create a turn-off (for a few years of viscosity time for the innermost part of the disks, see Eqs. (7) and (4), and also for high-e orbits), 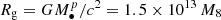R g = G M ∙ p / c 2 = 1.5 × 10 13 M 8 $ {R_{\text{g}}}=GM_{\bullet}^{p}/c^{2}=1.5\times 10^{13}\,M_8\, $cm is the gravity radius, 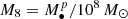M 8 = M ∙ p / 10 8 M ⊙ $ M_{8}=M_{\bullet}^{p}/10^{8}\,{M_\odot} $ is the primary black hole mass, 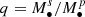q = M ∙ s / M ∙ p $ q=M_{\bullet}^{s}/M_{\bullet}^{p} $ is the mass ratio, G is the gravitational constant, and c is the speed of light. Hβ-BLR (broad-line region) radius follows 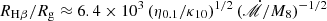R H β / R g ≈ 6.4 × 10 3 ( η 0.1 / κ 10 ) 1 / 2 ( M ˙ / M 8 ) − 1 / 2 $ R_{\mathrm{H\beta}}/{R_{\text{g}}}\approx 6.4\times 10^{3}\left(\eta_{0.1}/\kappa_{10}\right)^{1/2}({\dot{\mathscr{M}}}/M_{8})^{-1/2} $ (Bentz et al. 2013; Du & Wang 2019), indicating that the BLR is located in the CBD, where η0.1 = η/0.1 is the radiation efficiency and κ10 = κbol/10 is the bolometric factor, 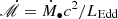M ˙ = M ˙ ∙ c 2 / L Edd $ {\dot{\mathscr{M}}}=\dot{M}_{\bullet}c^{2}/L_{\mathrm{Edd}} $ is the dimensionless accretion rate (Ṁ∙), and LEdd is the Eddington luminosity. CB-SMBHs are assumed to have two solitary BLRs (e.g., Shen & Loeb 2010; Popović 2012; Wang et al. 2018).

2.2. Building-up of mini-disks

As characteristic configurations, we show the simplest four coplanar cases of mini-disks and orbital AM of CB-SMBHs in Fig. 1. The complexity arises from the random accretion of peeled gas and supply onto the SMBHs. There are solid reasons for fully chaotic and random accretion onto CB-SMBHs making both prograde and retrograde accretions possible in the context of merged galaxies (Nixon et al. 2011, 2013; Dunhill et al. 2014, see also for details in Roedig et al. 2012; Roedig & Sesana 2014 and hereafter). Observationally, there is increasing evidence for random accretion. SINFONI observations, for example, showed two tongues from the south and north in ∼10 pc regions in NGC 1068 (Müller Sánchez et al. 2009), dual AGNs with an antiparallel AM in Arp 220 (Wheeler et al. 2020), and other evidence (Tremblay et al. 2016; Temi et al. 2018). The inner edge of the CBD significantly differs from the accretion disk around a single black hole: (1) part of the lumps (from the m = 1 mode) receive AM from the binary and are flung at the inner edge; but (2) via the turbulence of the CBD disk, AM is transferred outward, which drives the lumps inward. Moreover, the peeled gas has a very low AM on average, but the AM direction of individual clumps might be random to some degree.

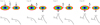thumbnail Fig. 1.

Simplest AM configurations (AMC) of CB-SMBHs and corresponding light curves when the companions pass through periastron. ℓp, ℓorb, and ℓs denote the AM of the primary, the orbital, and the secondary black holes, respectively. O is the mass center of the binary. Tidal interaction between mini-disks and SMBHs leads to two types of quenching modes: (1) fast gains of AM for prograde mini-disks (Case A) from the binary orbit, and (2) precursor-flaring and quenching for a retrograde mini-disk (the secondary in Case B). The precursor flaring is caused by the rapid loss of AM of the tidal part so that accretion in the remainder of the mini-disk is accelerated. Here Δ L 1 , 2 = η ( δ M t p , s / t v p , s ) c 2 $ \Delta L_{1,2}=\eta \left(\delta M_{t}^{p,s}/t_{\mathit{v}}^{p,s}\right)c^{2} $ represents the increased luminosity due to the enhanced accretion for the primary and the secondary BHs, respectively (see text for details).

Following Roedig et al. (2014), we assumed that the pealing accretion rates of the primary and secondary black holes are Ṁp = fpṀ∙ and Ṁs = fsṀ∙, respectively, but fp + fs ≲ 1, where Ṁ∙ is the accretion rate of the CBD, fp and fs are fractions depending on the orbits of the CB-SMBHs. For simplicity, we assumed them to be free parameters. We roughly divided the orbit into two parts: (1) the apastron phase (ftPorb; ft ≈ 1), and (2) the periastron phase of tperi ≈ (1 − e)3/2Porb ≲ 0.03Porb for e ≳ 0.9. The mini-disk is accumulating to have a mass of ΔMp = ftPorbfpṀ∙ during the apastron phase (tide is weak), but the disk strongly interacts with individual black holes during the periastron phase (the peeling is negligible). It has been shown that the peeling rates are significantly modulated by eccentric orbits (Bogdanović et al. 2008), but only the total peeled mass is important for exploring whether CB-SMBHs can make a type transition due to tidal interaction.

The peeled gas forms mini-disks around each black hole. During one apastron phase, the peeled gas is

Δ M peel M ⊙ = { 4.4 M 8 f p M ˙ f t P 20 0.4 q 0.1 M 8 f s M ˙ f t P 20 $$ \begin{aligned} \frac{\Delta M_{\rm peel}}{M_\odot }=\left\{ \begin{array}{l} 4.4\,M_{8}f_{p}\dot{\fancyscript {M}}f_{t}P_{20}\\ 0.4\,q_{_{0.1}}M_{8}f_{s}\dot{\fancyscript {M}}f_{t}P_{20} \end{array}\right. \end{aligned} $$(2)

for the primary and the secondary, respectively, where q0.1 = q/0.1 and P20 = Porb/20 yr. At the inner edge, the cooling timescale of the peeled gas is 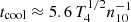t cool ≈ 5.6 T 4 1 / 2 n 10 − 1 $ t_{\mathrm{cool}}\approx 5.6\,T_{4}^{1/2}n_{10}^{-1}\, $h, where T4 = T/104 K, and n10 = n/1010 cm−3 is the density. We find that tcool is much shorter than the free fall of 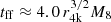t ff ≈ 4.0 r 4 k 3 / 2 M 8 $ t_{\mathrm{ff}}\approx 4.0\,r_{\mathrm{4k}}^{3/2}M_{8}\, $yr ≲Porb, where r4k = R/4 × 103Rg. Neglecting the complicated processes, we assumed the mini-disks to be described by the inner region of the standard model (Shakura & Sunyaev 1973). The surface density, mid-plane temperature, and radial velocity of the disks are (see Kato et al. 2008)

{ Σ = 3.5 × 10 2 α 0.1 − 1 M ˙ − 1 r 3 / 2 g cm − 2 , T c = 1.1 × 10 6 ( α 0.1 M 8 ) − 1 / 4 r − 3 / 8 K , υ r = 4.3 × 10 8 α 0.1 M ˙ 2 r − 5 / 2 cm s − 1 , $$ \begin{aligned} \left\{ \begin{array}{l} \Sigma =3.5\times 10^{2}\,\alpha _{0.1}^{-1}\dot{\fancyscript {M}}^{-1}r^{3/2}\,\mathrm{g\,cm^{-2}},\\ T_{c}=1.1\times 10^{6}\,\left(\alpha _{0.1}M_{8}\right)^{-1/4}r^{-3/8}\,\mathrm{K},\\ \upsilon _{r} =4.3\times 10^{8}\,\alpha _{0.1}\dot{\fancyscript {M}}^{2}r^{-5/2}\,\mathrm{cm\,s^{-1}}, \end{array}\right. \end{aligned} $$(3)

provided 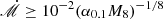M ˙ ≥ 10 − 2 ( α 0.1 M 8 ) − 1 / 8 $ {\dot{\mathscr{M}}}\ge 10^{-2}(\alpha_{0.1}M_8)^{-1/8} $, and this works within the outer radius of 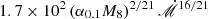1.7 × 10 2 ( α 0.1 M 8 ) 2 / 21 M ˙ 16 / 21 $ 1.7\times 10^{2}\left(\alpha_{0.1}M_{8}\right)^{2/21}{\dot{\mathscr{M}}}^{16/21} $, where α0.1 = α/0.1 is the viscosity. The viscosity timescale (or radial motion one) is

t vis ≈ 3.5 α 0.1 − 1 M 8 M ˙ − 2 r 10 7 / 2 yr , $$ \begin{aligned} t_{\rm vis}\approx 3.5\,\alpha _{0.1}^{-1}M_{8}\dot{\fancyscript {M}}^{-2}r_{10}^{7/2}\,\mathrm{yr}, \end{aligned} $$(4)

where r10 = R/10Rg, which is sensitive to 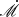M ˙ $ {\dot{\mathscr{M}}} $ and the radius. Given r = r* = 10, we have tvis = 3.5 M8 yr, denoted 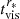t vis r * $ t_{\rm vis}^{r_*} $ for α = 0.1 and 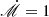M ˙ = 1 $ {\dot{\mathscr{M}}}=1 $, which agrees with the characterized transition of CL-AGNs. In order to create a CL, the suggested external torque has to remove the AM of the R ≳ 10Rg disk.

By integrating the surface density of Eq. (3), we obtained a mini-disk mass of 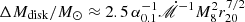Δ M disk / M ⊙ ≈ 2.5 α 0.1 − 1 M ˙ − 1 M 8 2 r 20 7 / 2 $ \Delta M_{\mathrm{disk}}/{M_\odot}\approx2.5\,\alpha_{0.1}^{-1}{\dot{\mathscr{M}}}^{-1}M_{8}^{2}r_{20}^{7/2} $, where r20 = R/20Rg, yielding outer boundary radii of the primary and the secondary mini-disks from ΔMdisk = ΔMpeel,

R out R g ≈ { 23.5 α 0.1 2 / 7 M ˙ 4 / 7 M 8 − 2 / 7 P 20 2 / 7 f p 2 / 7 f t 2 / 7 , 45.3 α 0.1 2 / 7 M ˙ 4 / 7 ( q 0.1 M 8 ) − 2 / 7 P 20 2 / 7 f s 2 / 7 f t 2 / 7 , $$ \begin{aligned} \frac{R_{\rm out}}{R_{\rm g}}\approx \left\{ \begin{array}{ll} 23.5\,\alpha _{0.1}^{2/7}\dot{\fancyscript {M}}^{4/7}M_{8}^{-2/7}P_{20}^{2/7}f_{p}^{2/7}f_{t}^{2/7},\\ 45.3\,\alpha _{0.1}^{2/7}\dot{\fancyscript {M}}^{4/7}(q_{_{0.1}}M_{8})^{-2/7}P_{20}^{2/7}f_{s}^{2/7}f_{t}^{2/7}, \end{array}\right. \end{aligned} $$(5)

respectively. Circularization of the peeled gas relies on its AM, but our model takes a conservative estimate of low AM (because Rout ≪ RCBD). The disks retain vertical equilibrium with a very short timescale of 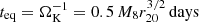t eq = Ω K − 1 = 0.5 M 8 r 20 3 / 2 days $ t_{\mathrm{eq}} =\Omega_{\mathrm{K}}^{-1}=0.5\,M_{8}r_{20}^{3/2}\,\mathrm{days} $, which is equal to the free-fall timescale (tff) after the accretion disk AM is removed. With the sound speed of 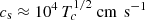c s ≈ 10 4 T c 1 / 2 cm s − 1 $ c_{\mathrm{s}}\approx 10^{4}\,T_{c}^{1/2}{\text{ cm}\,\text{ s}^{-1}} $, we have a radial dynamical timescale of 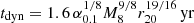t dyn = 1.6 α 0.1 1 / 8 M 8 9 / 8 r 20 19 / 16 yr $ t_{\mathrm{dyn}} = 1.6\,\alpha_{0.1}^{1/8}M_{8}^{9/8}r_{20}^{19/16}\,\mathrm{yr} $ for keeping a whole disk under tidal perturbations. Moreover, the viscosity time scales of the mini-disks are 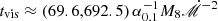t vis ≈ ( 69.6 , 692.5 ) α 0.1 − 1 M 8 M ˙ − 2 $ t_{\mathrm{vis}}\approx (69.6,692.5)\,\alpha_{0.1}^{-1}M_{8}{\dot{\mathscr{M}}}^{-2}\, $yr at Rout given by Eq. (5), which are much longer than Porb. The peeled-gas rates are modulated by orbital motion (e.g., Bogdanović et al. 2008; Miranda et al. 2017) with about Porb, but the modulated rates are smeared by the viscosity so that temporal radiation (light curves) from the mini-disks does not follow the orbital modulations. Thus only the total peeled mass is important for the current issues.

2.3. Tidal torque from a black hole

The effects of tidal torques acting on mini-disks depend on the AMC. For a prograde mini-disk (ℓi​ ∥ ​ℓorb, i = 1, 2), the tidal torque will physically divide the mini-disk into two parts at radius Rtid (in Eq. (7)). In such a case, the inner part of the mini-disks (≤Rtid) is tidal free, whereas its tidal part is accelerated through delivering orbital AM to the part, and it becomes a “decretion disk”, leading to dramatical decrease in accretion rates with 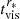t vis r * $ t_{\rm vis}^{r_*} $ and quenching accretion. For a retrograde mini-disk, the tidal part in contrast efficiently looses AM and is rapidly squeezed into the tidal radius (∼tff), dramatically accelerating the ongoing accretion rates and creating a flare until the inner part diminishes. The tidal interaction between the black holes and the mini-disks causes diverse phenomena of CL-AGNs.

The tidal force acting on the secondary disk by the primary black hole is 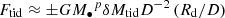F tid ≈±G M • p δ M tid D −2 ( R d /D ) $ F_{\rm tid}\approx \pm G{M_{\bullet}}^{p} \delta M_{\rm tid}{D^{-2}}\left(R_{\rm d}/{D}\right) $, where δMtid is the mass of the tidal part at radius Rd. This net tidal force depends on the AMCs in Fig. 1. Here the plus-minus sign represents gain and loss of AM from tidal interaction for prograde and retrograde mini-disks, respectively. The tidal torque is

T tid ≈ ± δ M tid c 2 ( R g D ) ( R d D ) 2 . $$ \begin{aligned} \mathcal{T}_{\rm tid}\approx \pm \delta M_{\rm tid}c^{2}\left(\frac{R_{\rm g}}{D}\right)\left(\frac{R_{\rm d}}{D}\right)^{2}. \end{aligned} $$(6)

The AM of the tidal part is approximated by δℒd ≈ δMtidℓd, where 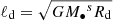ℓ d = G M ∙ s R d $ \ell_{\mathrm{d}}=\sqrt{G{M_{\bullet}}^{s} R_{\mathrm{d}}} $ is the specific AM, yielding the tidal radius from the balance given by δℒd = 𝒯tidtperi

R tid R g = ( ξ q 4 π 2 ) 1 / 3 ( a E R g ) = { 14.4 ξ 0.11 1 / 3 a 3.4 k E 0.03 , 14.1 ξ 0.11 1 / 3 a 1 k E 0.1 , $$ \begin{aligned} \frac{R_{\rm tid}}{R_{\rm g}}=\left(\frac{\xi _{q}}{4\pi ^{2}}\right)^{1/3} \left(\frac{a\mathcal{E}}{R_{\rm g}}\right) =\left\{ \begin{array}{l} 14.4\,\xi _{0.11}^{1/3}a_{\rm 3.4k}\mathcal{E} _{0.03},\\ 14.1\,\xi _{0.11}^{1/3}a_{\rm 1k}\mathcal{E} _{0.1}, \end{array}\right. \end{aligned} $$(7)

where ξq = q(1 + q), ξ0.11 = ξq/0.11 for q = 0.1, ℰ = (1 − e) and ℰ0.03, 0.1 = ℰ/(0.03, 0.1) for e = (0.97, 0.9), respectively.

Density waves excited by the torque in the tidal part are strong enough to form shocks and to transport AM (Spruit 1987). Recent simulations showed that this is a powerful way of transporting AM outward (Ju et al. 2016), even stronger than the known. With the help of δℒd, we have the timescale within which the AM is exchanged, ttid = δℒd/|𝒯tid|,

t tid = q 1 / 2 R g c ( D R g ) 3 / 2 ( R d D ) − 3 / 2 , $$ \begin{aligned} t_{\rm tid}=q^{1/2}\frac{R_{\rm g}}{c}\left(\frac{D}{R_{\rm g}}\right)^{3/2}\left(\frac{R_{\rm d}}{D}\right)^{-3/2}, \end{aligned} $$(8)

with the wave density pattern velocity Vsp. The mini-disks respond to the tidal perturbations with tdyn. The spiral shocks excited by the tidal torque are nonlocal with Mach numbers of ℳ = Vsp/cs = tdyn/ttid beyond a radius at ℳ = 1,

R sh R g = { 5.9 α 0.1 − 2 / 43 q 0.1 8 / 43 M 8 − 2 / 43 a 3.4 k 48 / 43 E 0.03 48 / 43 , 5.8 α 0.1 − 2 / 43 q 0.1 8 / 43 M 8 − 2 / 43 a 1 k 48 / 43 E 0.1 48 / 43 , $$ \begin{aligned} \frac{R_{\rm sh}}{R_{\rm g}}=\left\{ \begin{array}{l} 5.9\,\alpha _{0.1}^{-2/43}q_{_{0.1}}^{8/43}M_{8}^{-2/43}a_{\rm 3.4k}^{48/43}\mathcal{E} _{0.03}^{48/43},\\ 5.8\,\alpha _{0.1}^{-2/43}q_{_{0.1}}^{8/43}M_{8}^{-2/43}a_{\rm 1k}^{48/43}\mathcal{E} _{0.1}^{48/43}, \end{array}\right. \end{aligned} $$(9)

and the propagation timescale (tsh = tdyn = ttid) is

t sh = { 0.37 α 0.1 3 / 43 q 0.1 19 / 86 M 8 46 / 43 a 3.4 k 57 / 43 E 0.03 57 / 43 yr , 0.34 α 0.1 3 / 43 q 0.1 19 / 86 M 8 46 / 43 a 1 k 57 / 43 E 0.1 57 / 43 yr . $$ \begin{aligned} t_{\rm sh}=\left\{ \begin{array}{l} 0.37\,\alpha _{0.1}^{3/43}q_{_{0.1}}^{19/86}M_{8}^{46/43}a_{\rm 3.4k}^{57/43}\mathcal{E} _{0.03}^{57/43}\,\mathrm{yr},\\ 0.34\,\alpha _{0.1}^{3/43}q_{_{0.1}}^{19/86}M_{8}^{46/43}a_{\rm 1k}^{57/43}\mathcal{E} _{0.1}^{57/43}\,\mathrm{yr}. \end{array}\right. \end{aligned} $$(10)

Here we take D = Dmin for the shortest timescale. We find that tsh <  tvis, indicating that spiral shocks can efficiently exchange the AM of the mini-disk with the binary. Moreover, the condition of tvis ≲ Porb is necessary for a turn-off of accretion onto SMBHs. Combining Eqs. (1), (4), (7), we have

M ˙ ≳ { 0.8 α 0.1 − 1 / 2 E 0.03 7 / 4 q 0.1 7 / 12 ( 1 + q ) 1.1 5 / 6 a 3.4 k , 1.9 α 0.1 − 1 / 2 E 0.1 7 / 4 q 0.1 7 / 12 ( 1 + q ) 1.1 5 / 6 a 1 k , $$ \begin{aligned} \dot{\fancyscript {M}}\gtrsim \left\{ \begin{array}{l} 0.8\,\alpha _{0.1}^{-1/2}\mathcal{E} _{0.03}^{7/4}q_{0.1}^{7/12}(1+q)_{1.1}^{5/6}a_{\rm 3.4k},\\ 1.9\,\alpha _{0.1}^{-1/2}\mathcal{E} _{0.1}^{7/4}q_{0.1}^{7/12}(1+q)_{1.1}^{5/6}a_{\rm 1k}, \end{array}\right. \end{aligned} $$(11)

implying 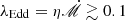λ Edd = η M ˙ ≳ 0.1 $ \lambda_{\mathrm{Edd}}=\eta{\dot{\mathscr{M}}}\gtrsim0.1 $, otherwise the turn-off cannot be achieved within one orbital period. Considering the large uncertainties of M• and the bolometric luminosity, Eq. (11) is roughly consistent with the λEdd ≳ 0.1 CL-AGNs (see Fig. 6 in MacLeod et al. 2019), showing the validity of this turn-off mechanism.

For the prograde case, on the other hand, the decretion disk could be changed into elliptical shapes so that some of it will be accreted onto SMBHs, leading to an inefficient turn-off. We keep this effect in mind for numerical simulations in the future.

2.4. Gravitational waves

Owing to gravitation waves (GWs), the binary orbit shrinks on a timescale given by (see Eq. (5.6) in Peters 1964),

t GW ≈ { 1.8 × 10 4 ξ 0.11 − 1 M 8 a 3.4 k 4 E 0.03 7 / 2 I 4.2 − 1 yr , 8.9 × 10 3 ξ 0.11 − 1 M 8 a 1 k 4 E 0.1 7 / 2 I 3.7 − 1 yr , $$ \begin{aligned} t_{\rm GW}\approx \left\{ \begin{array}{l} 1.8\times 10^{4}\,\xi _{0.11}^{-1}M_{8}a_{\rm 3.4k}^{4}\mathcal{E} _{0.03}^{7/2}\mathcal{I} _{4.2}^{-1}\,\mathrm{yr},\\ 8.9\times 10^{3}\,\xi _{0.11}^{-1}M_{8}a_{\rm 1k}^{4}\mathcal{E} _{0.1}^{7/2}\mathcal{I} _{3.7}^{-1}\,\mathrm{yr}, \end{array}\right. \end{aligned} $$(12)

corresponding to Norb ≈ (908, 2881) orbits, where ℐe = 1 + 73e2/24 + 37e4/96, and ℐ4.2, 3.7 = ℐe/(4.2, 3.7)  for e previously given. The intrinsic strain amplitude is

h s = 7.0 × 10 − 18 q 0.1 ( 1 + q ) − 1 / 3 M 8 5 / 3 P 20 − 2 / 3 d 100 − 1 , $$ \begin{aligned} h_{s} =7.0\times 10^{-18}\,q_{_{0.1}}(1+q)^{-1/3}M_{8}^{5/3}P_{20}^{-2/3}d_{100}^{-1}, \end{aligned} $$(13)

from hs = (128/5)1/2(GMc)5/3(πfGW)2/3/c4dL, 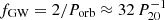f GW = 2 / P orb ≈ 32 P 20 − 1 $ f_{\mathrm{GW}}=2/P_{\mathrm{orb}}\approx 32\,P_{20}^{-1}\, $nHz is the frequency of GWs, 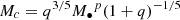M c = q 3/5 M • p (1+q) −1/5 $ M_{c}=q^{3/5}{{M_{\bullet}}^{p}}(1+q)^{-1/5} $ is the chirping mass, and d100 = dL/100 Mpc is the distance (e.g., Graham et al. 2015). For pure GW-driven evolution, te ≈ (32.7, 9.3)tGW, and the initial e0 = (0.97, 0.9) will reduce to (0.95, 0.84) by dropping half of a, where te = (dlne/dt)−1 is the evolutionary timescale of eccentricity. However, a monotonic e-gain (for e ≳ 0.6) with accretion of the secondary black hole in a retrograde binary can keep high-e orbits prior to the merger (Amaro-Seoane et al. 2016). With the complicated e-evolution, the high-e orbits can be kept in some orbits that result in CL.

We focus on the extreme cases here in which CL transition is triggered by one tidal interaction during one orbit. If the initial e of CB-SMBH orbits is not as high as e ≈ 0.9, the binaries may undergo tidal interaction for several orbits and lead to CL transition, or they undergo increases in e in the case of retrograde accretion, which finally leads to a transition. In this context, the mini-disks can accumulate more during several orbital periods; CL-AGNs have different variations from what we discussed here. A future paper will study the intermediate-e cases.

3. Turn-on and turn-off

As shown in Fig. 1, we focused on four simplest configurations: (1) Case-A (↑, ↑, ↑); (2) Case-B (↑, ↓, ↑); (3) Case-C (↑, ↓, ↓), and (4) Case-D (↓, ↓, ↑). We neglected spins of black holes, avoiding more configurations. We note that the appearance of Cases B and C could be less common than that of Cases A and D. For a convenient discussions, we use 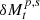δ M t p , s $ \delta M_{t}^{p,s} $ as the masses of the tidal parts of the primary and secondary mini-disks, and 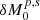δ M 0 p , s $ \delta M_{0}^{p,s} $ as the mass of the remaining parts. We stress that the discussions are only valid for the characterized properties of the process.

3.1. Case A

In Case A, both mini-disks are prograde. Tidal torque transfers orbital AM to both disks simultaneously so that the tidal parts (with mass of 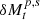δ M t p , s $ \delta M_{t}^{p,s} $) become decretion disks that rotate outward (e.g., Rafikov 2016), and accretion onto the binary is interrupted after the mass ( 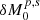δ M 0 p , s $ \delta M_{0}^{p,s} $) of the nontidal part is depleted. We call this the rest accretion, which radiates at luminosities of 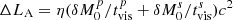Δ L A = η ( δ M 0 p / t vis p + δ M 0 s / t vis s ) c 2 $ \Delta L_{\mathrm{A}}=\eta (\delta M_{0}^{p}/t_{\mathrm{vis}}^{p}+\delta M_{0}^{s}/t_{\mathrm{vis}}^{s})c^{2} $, where 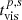t vis p , s $ t_{\mathrm{vis}}^{p,s} $ are viscosity timescales of the primary and secondary mini-disks. According to the standard disk model, photons (ϵ) are emitted from 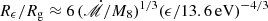R ϵ / R g ≈ 6 ( M ˙ / M 8 ) 1 / 3 ( ϵ / 13.6 eV ) − 4 / 3 $ R_{\epsilon}/{R_{\text{g}}}\approx 6\,(\dot{\mathscr{M}}/M_{8})^{1/3}(\epsilon/13.6\,\mathrm{eV})^{-4/3} $ as the innermost regions of the mini-disks. The expansion of the tidal part can simply be estimated by ΔRd/Rd ≈ 2Δ(δℒd)/δℒd = 2 because the balance of δℒd = 𝒯tidtperi. As a consequence, gas supply to the Rϵ-region is interrupted by the torque, leading to violent variations in both UV and Hβ line. Turn-off occurs then with a transition from type 1 to type 2 after periastron.

Turn-on transition starts from accumulation via peeling gas from the CBD after the periastron phase. First, the tidal part begins to fall back, but on a timescale that is longer than tvis by a factor of (ΔRd/Rd)7/2 ≈ 11.3 (> Porb). Second, peeled gas continues to accumulate because the outward-rotating gas is still bounded by its black hole in the same disk plane (because teq ≪ tdyn). This results in continuous growth of the mini-disks from peeled gas over every orbiting cycle until the mini-disk radii exceed the Roche radius given by RH ≈ 0.27q∓0.3a for the primary and secondary mini-disks (Bowen et al. 2017). With limitation of GW-driven timescales of orbit decays, on the other hand, the CB-SMBHs will undergo cycles of ncyc ≈ tGW/Porb ∼ 103 around the apastron phase for Porb ∼ 20 yr and tGW ∼ 2 × 104 yr. Mini-disks then grow to an outer radius of Rout/Rg ≈ (88, 170) (by multiplying the factor ft with ncyc in Eq. (5)) but Rout/Rg ≤ RH for the primary and secondary. This disk is able to produce optical continuum like normal AGNs. The innermost regions undergo violent variations that cause fast and large variabilities only in the UV, but they are relatively less variable in the optical, agreeing with that of CL-AGNs (Ross et al. 2018; Lawrence 2018).

The growth of prograde mini-disks results from the circularization of the peeled gas through AM composition. Kinetic energy isdissipated in this process to radiate some energy (but the spectral energy distributions depend on the composition). Consequently, this causes complicated variations in the continuum on various timescales. More work needs to be done for details through numerical simulations in the future.

3.2. Cases B and C

In Case B, the primary mini-disk is prograde to the orbit, but the secondary is retrograde. The primary disk receives AM from the orbit, and the UV emission declines as in Case A, but the secondary shows a flare in UV before quenching. This is caused by a fast increase in the accretion rates within Rtid through a rapid squeezing of the 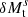δ M t s $ \delta M_{\mathrm{t}}^{s} $ caused by loss of its AM. The enhanced accretion rates can be roughly estimated by 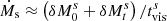M ˙ s ≈ ( δ M 0 s + δ M t s ) / t vis s $ \dot{M}_{\mathrm{s}}\approx \left(\delta M_{0}^{s}+\delta M_{t}^{s}\right)/{t_{\mathrm{vis}}^{s}} $. The enhanced accretion leads to an increased luminosity 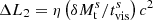Δ L 2 = η ( δ M t s / t vis s ) c 2 $ \Delta L_{2}=\eta \left(\delta M_{\mathrm{t}}^{s}/t_{\mathrm{vis}}^{s}\right)c^{2} $. After fast accretion within Rtid, the mini-disk is quenched, and consequently, turn-off occurs on a timescale of ∼1 yr (Eq. (4)). Interestingly, a flare like this was found as a precursor of CB-SMBHs in numerical simulations by Chang et al. (2010). In this case, the primary contributes optical emissions, but both components contribute to violent variations in UV emissions. In particular, the gas squeezed by the tidal torque undergoes supersonic infall and may lead to γ-ray emission on short timescales (Kolykhalov & Syunyaev 1979; Meszaros & Ostriker 1983). This might be detectable by Fermi.

Case C is similar to Case B, but the primary mini-disk in Case C is retrograde to the orbit. It first undergoes a flare and then decays. The secondary mini-disk is quenched as in Case A, which is driven to rotate outward, but it causes optical emissions similar to Case B. We note that the flaring and quenching timescales of the two mini-disks might be different depending on black hole masses, accretion rates, and the binary orbit.

3.3. Case D

In Case D, both mini-disks are retrograde. Both tidal parts of the disks are squeezed rapidly into ≲Rtid regions, which accelerates the accretion rates of the disks. Then a turn-off transition occurs. In this case, the total accretion rates of the flare luminosity of the binary are about Ṁtot = Ṁp + Ṁs, where 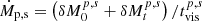M ˙ p , s = ( δ M 0 p , s + δ M t p , s ) / t vis p , s $ \dot{M}_{\mathrm{p,s}}=\left(\delta M_{0}^{p,s}+\delta M_{t}^{p,s}\right)/t_{\mathrm{vis}}^{p,s} $. The enhanced accretion depends on the black hole mass, and thus the two flares of the mini-disks have different timescales. These characterized light curves depend on the ratios of 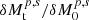δ M t p , s / δ M 0 p , s $ \delta M_{\mathrm{t}}^{p,s}/\delta M_0^{p,s} $ and their relative viscosity timescales. For cases of extremely eccentric orbits, the mini-disks may be completely tidal destroyed if Rtid ∼ 6Rg for extreme cases with very high-e orbits. In this case, the flares are stronger because all mini-disks are squeezed into the black hole.

Real situations of mini-disks or orbits in CB-SMBHs may be more complicated than that in Fig. 1. They might be warped and noncoplanar, such as in OJ 287 (Sillanpaa et al. 1988). Moreover, the relative appearance of the four cases remains open, but Cases A and D might be more common than others. Finally, we would pointed out that the current scenario provides a cycle of CL transition with orbit period in the nonperiodical light curves of the continuum. Turn-on and turn-off timescales are determined by the orbit, but they might have a quasi-periodicity when the CBD is self-gravitating to form clumps.

4. Conclusions and discussions

The rapidity of the change in CL-AGNs is a puzzle. Based on heuristic information from observations, we demonstrated the extreme case in which CB-SMBHs with low mass ratios and high eccentricities might cause a fast transition of states within one orbit. Both black holes peel gas off the inner edge of the circumbinary disk to form mini-disks around them. In a system like this, the tidal torque on the mini-disks caused by companion black holes is strong enough to exchange AM between the disks and the binary orbit for rapid changes in the innermost regions of the disk. The mini-disks are either being squeezed into the innermost regions or are expanded outward (to form a decretion disk), depending on the AMC of the binary system. The different configurations cause the diverse properties of CL-AGNs, including flaring precursors of type transitions. CB-SMBHs drive the changing look of AGNs to appear in transition cycles, likely with orbital periods (or quasi-periodical transition due to complications at the inner edge of the CBD). This scenario can be tested by the turn-on and turn-off behaviors in historical data of spectral variations over several decades. CL-AGNs might contribute a significant fraction of the low-frequency gravitational wave background.

Several aspects should be investigated to explain the nature of CL-AGNs. First, details of their host morphology should be searched for signatures of disrupted or ripples as may be caused by merged remnants. This is inspired by results reported by Charlton et al. (2019), who clearly found such features in Gemini images of four CL-quasars. Second, CL-AGNs could be characterized by profile asymmetries in their broad emission lines. We visually confirmed the broadline profiles of CL-AGNs and found that all of them have either highly – asymmetric or double-peaked profiles, but the reverse is not supported by current observations. AGNs are monitored with the Hβ Asymmetry (MAHA), which is a long-term campaign searching for CB-SMBHs (Du et al. 2018). We hope to see signals of CB-SMBHs from their 2D transfer functions (Wang et al. 2018; Kovačević et al. 2020a; Songsheng et al. 2020, see a recent review of Wang & Li 2020) as well as signals revealed by GRAVITY/VLTI (Songsheng et al. 2019; Kovačević et al. 2020b). CL-AGNs could be the best candidates of CB-SMBHs. Third, the spectral energy distributions of CL-AGNs are poorly understood at epochs of type transitions. CB-SMBHs drive far more violent variations in the UV than in the optical, which apparently supports our scenario, but the complicated processes of the tidal interaction may lead to γ-rays from the inflows with low AM. Monitoring campaigns of CL-AGN multi-λ continuum will greatly help understand the physics of these processes.

We will study the temporal details of the tidal interaction and accretion rates of the mini-disks in a binary orbit in future work. This allows us to compare with observed light curves of CL-AGNs or to predict some precursors of CL transition, and reveal the physics of the peeling between the binary and the CBD from observations. In this context, time-dependent accretion (and decretion) disks should be employed, including the spectral energy distributions. Finally, CL-AGNs might significantly contribute to the GW background, and this will be studied in the future.

Acknowledgments

We are grateful to an anonymous referee, and T. Bogdanović for helpful discussions as well as Z. Yu, Y.-R. Li and Y.-Y. Songsheng from the IHEP AGN group. JMW thanks the support by National Key R&D Program of China through grant -2016YFA0400701, by NSFC through grants NSFC-11991050, -11991054, -11833008, -11690024, and by grant No. QYZDJ-SSW-SLH007 and No.XDB23010400. EB acknowledges the Serbian support through contract number 451-03-68/2020-14/200002, and CA16104.

References

  1. Ai, Y., Dou, L., Yang, C., et al. 2020, ApJ, 890, L29 [CrossRef] [Google Scholar]
  2. Amaro-Seoane, P., Maureira-Fredes, C., Dotti, M., et al. 2016, A&A, 591, A114 [CrossRef] [EDP Sciences] [Google Scholar]
  3. Andrillat, Y. 1968, AJ, 73, 862 [CrossRef] [Google Scholar]
  4. Antonucci, R. 1993, ARA&A, 31, 473 [Google Scholar]
  5. Armitage, P. J., & Natarajan, P. 2002, ApJ, 567, L9 [NASA ADS] [CrossRef] [Google Scholar]
  6. Artymowicz, P., & Lubow, S. H. 1996, ApJ, 467, L77 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bentz, M. C., Denney, K. D., Grier, C. J., et al. 2013, ApJ, 767, 149 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bogdanović, T. S., Britton, D., Sigurdsson, S., et al. 2008, ApJS, 174, 455 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bowen, D. B., Campanelli, M., Krolik, J. H., et al. 2017, ApJ, 838, 42 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bowen, D. B., Mewes, V., Campanelli, M., et al. 2018, ApJ, 853, L17 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bowen, D. B., Mewes, V., Noble, S. C., et al. 2019, ApJ, 879, 76 [NASA ADS] [CrossRef] [Google Scholar]
  12. Chang, P., Strubbe, L. E., Menou, K., & Quataert, E. 2010, MNRAS, 407, 2007 [NASA ADS] [CrossRef] [Google Scholar]
  13. Charlton, P. J. L., Ruan, J. J., Haggard, D., et al. 2019, ApJ, 876, 75 [CrossRef] [Google Scholar]
  14. Cohen, R. D., Rudy, R. J., Puetter, R. C., et al. 1986, ApJ, 311, 135 [NASA ADS] [CrossRef] [Google Scholar]
  15. d’Ascoli, S., Noble, S. C., Bowen, D. B., et al. 2018, ApJ, 865, 140 [NASA ADS] [CrossRef] [Google Scholar]
  16. Dexter, J., & Begelman, M. C. 2019, MNRAS, 483, L17 [NASA ADS] [CrossRef] [Google Scholar]
  17. D’Orazio, D. J., Haiman, Z., Duffell, P., et al. 2016, MNRAS, 459, 2379 [NASA ADS] [CrossRef] [Google Scholar]
  18. Du, P., & Wang, J.-M. 2019, ApJ, 886, 42 [NASA ADS] [CrossRef] [Google Scholar]
  19. Du, P., Brotherton, M. S., Wang, K., et al. 2018, ApJ, 869, 142 [CrossRef] [Google Scholar]
  20. Dunhill, A. C., Alexander, R. D., Nixon, C. J., et al. 2014, MNRAS, 445, 2285 [NASA ADS] [CrossRef] [Google Scholar]
  21. Farris, B. D., Duffell, P., MacFadyen, A. I., et al. 2014, ApJ, 783, 134 [NASA ADS] [CrossRef] [Google Scholar]
  22. Farris, B. D., Duffell, P., MacFadyen, A. I., et al. 2015a, MNRAS, 447, L80 [NASA ADS] [CrossRef] [Google Scholar]
  23. Farris, B. D., Duffell, P., MacFadyen, A. I., et al. 2015b, MNRAS, 446, L36 [NASA ADS] [CrossRef] [Google Scholar]
  24. Frederick, S., Gezari, S., Graham, M. J., et al. 2019, ApJ, 883, 31 [NASA ADS] [CrossRef] [Google Scholar]
  25. Graham, M. J., Djorgovski, S. G., Stern, D., et al. 2015, MNRAS, 453, 1562 [NASA ADS] [CrossRef] [Google Scholar]
  26. Graham, M. J., Ross, N. P., Stern, D., et al. 2020, MNRAS, 491, 4925 [NASA ADS] [Google Scholar]
  27. Guo, H., Sun, M., Liu, X., et al. 2019, ApJ, 883, L44 [CrossRef] [Google Scholar]
  28. Hutsemékers, D., Agís González, B., Marin, F., et al. 2019, A&A, 625, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Ju, W., Stone, J. M., & Zhu, Z. 2016, ApJ, 823, 81 [NASA ADS] [CrossRef] [Google Scholar]
  30. Kato, S., Fukue, J., & Mineshige, S. 2008, Black-Hole Accretion Disks – Towards a New Paradigm (Kyoto: Kyoto University Press) [Google Scholar]
  31. Kollatschny, W., & Fricke, K. J. 1985, A&A, 146, L11 [NASA ADS] [Google Scholar]
  32. Kolykhalov, P. I., & Syunyaev, R. A. 1979, Sov. Ast., 23, 189 [Google Scholar]
  33. Kovačević, A. B., Wang, J.-M., & Popović, L. Č. 2020a, A&A, 635, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Kovačević, A. B., Songsheng, Y. Y., Wang, J. M., & Popović, L. 2020b, A&A, accepted [arXiv: 2010.01317] [Google Scholar]
  35. Lawrence, A. 2018, Nat. Astron., 2, 102 [NASA ADS] [CrossRef] [Google Scholar]
  36. Liu, H., Wu, Q., Lyu, B., & Yan, Z. 2019, ArXiv e-prints [arXiv: 1912.03972] [Google Scholar]
  37. MacFadyen, A. I., & Milosavljević, M. 2008, ApJ, 672, 83 [Google Scholar]
  38. MacLeod, C. L., Ross, N. P., Lawrence, A., et al. 2016, MNRAS, 457, 389 [NASA ADS] [CrossRef] [Google Scholar]
  39. MacLeod, C. L., Green, P. J., Anderson, S. F., et al. 2019, ApJ, 874, 8 [NASA ADS] [CrossRef] [Google Scholar]
  40. Marin, F., Hutsemékers, D., & Agís González, B. 2019, SF2A-2019: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, eds. P. Di Matteo, O. Creevey, A. Crida, et al., 509 [Google Scholar]
  41. Meszaros, P., & Ostriker, J. P. 1983, ApJ, 273, L59 [NASA ADS] [CrossRef] [Google Scholar]
  42. Miranda, R., Muñoz, D. J., & Lai, D. 2017, MNRAS, 466, 1170 [NASA ADS] [CrossRef] [Google Scholar]
  43. Moody, M. S. L., Shi, J.-M., & Stone, J. M. 2019, ApJ, 875, 66 [NASA ADS] [CrossRef] [Google Scholar]
  44. Muñoz, D. J., Lai, D., Kratter, K., & Miranda, R. 2020, ApJ, 889, 114 [CrossRef] [Google Scholar]
  45. Müller Sánchez, F., Davies, R. I., Genzel, R., et al. 2009, ApJ, 691, 749 [NASA ADS] [CrossRef] [Google Scholar]
  46. Netzer, H. 2015, ARA&A, 53, 365 [NASA ADS] [CrossRef] [Google Scholar]
  47. Nixon, C. J., Cossins, P. J., King, A. R., et al. 2011, MNRAS, 412, 1591 [NASA ADS] [CrossRef] [Google Scholar]
  48. Nixon, C., King, A., & Price, D. 2013, MNRAS, 434, 1946 [CrossRef] [Google Scholar]
  49. Noda, H., & Done, C. 2018, MNRAS, 480, 3898 [NASA ADS] [CrossRef] [Google Scholar]
  50. Penston, M. V., & Perez, E. 1984, MNRAS, 211, 33P [NASA ADS] [CrossRef] [Google Scholar]
  51. Peters, P. C. 1964, Phys. Rev., 136, 1224 [Google Scholar]
  52. Popović, L. Č. 2012, NewAR, 56, 74 [NASA ADS] [CrossRef] [Google Scholar]
  53. Rafikov, R. R. 2016, ApJ, 830, 7 [NASA ADS] [CrossRef] [Google Scholar]
  54. Rees, M. J. 1984, ARA&A, 22, 471 [NASA ADS] [CrossRef] [Google Scholar]
  55. Roedig, C., & Sesana, A. 2014, MNRAS, 439, 3476 [NASA ADS] [CrossRef] [Google Scholar]
  56. Roedig, C., Sesana, A., Dotti, M., et al. 2012, A&A, 545, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Roedig, C., Krolik, J. H., & Miller, M. C. 2014, ApJ, 785, 115 [NASA ADS] [CrossRef] [Google Scholar]
  58. Ross, N. P., Ford, K. E. S., Graham, M., et al. 2018, MNRAS, 480, 4468 [CrossRef] [Google Scholar]
  59. Ross, N. P., Graham, M. J., & Calderone, G. 2020, MNRAS, 498, 2339 [CrossRef] [Google Scholar]
  60. Ruan, J. J., Anderson, S. F., Eracleous, M., et al. 2019, ApJ, 883, 76 [CrossRef] [Google Scholar]
  61. Ryan, G., & MacFadyen, A. 2017, ApJ, 835, 199 [NASA ADS] [CrossRef] [Google Scholar]
  62. Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 500, 33 [NASA ADS] [Google Scholar]
  63. Shen, Y., & Loeb, A. 2010, ApJ, 725, 249 [NASA ADS] [CrossRef] [Google Scholar]
  64. Shi, J.-M., & Krolik, J. H. 2015, ApJ, 807, 131 [NASA ADS] [CrossRef] [Google Scholar]
  65. Sillanpaa, A., Haarala, S., Valtonen, M. J., et al. 1988, ApJ, 325, 628 [NASA ADS] [CrossRef] [Google Scholar]
  66. Sniegowska, M., Czerny, B., Bon, E., & Bon, N. 2020, A&A, 641, A167 [CrossRef] [EDP Sciences] [Google Scholar]
  67. Songsheng, Y.-Y., Wang, J.-M., Li, Y.-R., & Du, P. 2019, ApJ, 881, 140 [CrossRef] [Google Scholar]
  68. Songsheng, Y.-Y., Xiao, M., Wang, J.-M., & Ho, L. C. 2020, ApJS, 247, 3 [NASA ADS] [CrossRef] [Google Scholar]
  69. Spruit, H. C. 1987, A&A, 184, 173 [NASA ADS] [Google Scholar]
  70. Stern, D., McKernan, B., & Graham, M. J. 2018, ApJ, 864, 27 [NASA ADS] [CrossRef] [Google Scholar]
  71. Tang, Y., Haiman, Z., & MacFadyen, A. 2018, MNRAS, 476, 2249 [CrossRef] [Google Scholar]
  72. Temi, P., Amblard, A., Gitti, M., et al. 2018, ApJ, 858, 17 [NASA ADS] [CrossRef] [Google Scholar]
  73. Tohline, J. E., & Osterbrock, D. E. 1976, ApJ, 210, L117 [NASA ADS] [CrossRef] [Google Scholar]
  74. Trakhtenbrot, B., Arcavi, I., MacLeod, C. L., et al. 2019, ApJ, 883, 94 [CrossRef] [Google Scholar]
  75. Tremblay, G. R., Oonk, J. B. R., Combes, F., et al. 2016, Nature, 534, 218 [NASA ADS] [CrossRef] [Google Scholar]
  76. Wang, J.-M., & Li, Y.-R. 2020, RA&A, 20, 160 [Google Scholar]
  77. Wang, J.-M., Songsheng, Y.-Y., Li, Y.-R., & Yu, Z. 2018, ApJ, 862, 171 [NASA ADS] [CrossRef] [Google Scholar]
  78. Wang, J., Xu, D. W., Wang, Y., et al. 2019, ApJ, 887, 15 [CrossRef] [Google Scholar]
  79. Wheeler, J., Glenn, J., Rangwala, N., & Fyhrie, A. 2020, ApJ, 896, 43 [CrossRef] [Google Scholar]
  80. Yang, Q., Wu, X.-B., Fan, X., et al. 2018, ApJ, 862, 109 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

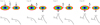thumbnail Fig. 1.

Simplest AM configurations (AMC) of CB-SMBHs and corresponding light curves when the companions pass through periastron. ℓp, ℓorb, and ℓs denote the AM of the primary, the orbital, and the secondary black holes, respectively. O is the mass center of the binary. Tidal interaction between mini-disks and SMBHs leads to two types of quenching modes: (1) fast gains of AM for prograde mini-disks (Case A) from the binary orbit, and (2) precursor-flaring and quenching for a retrograde mini-disk (the secondary in Case B). The precursor flaring is caused by the rapid loss of AM of the tidal part so that accretion in the remainder of the mini-disk is accelerated. Here Δ L 1 , 2 = η ( δ M t p , s / t v p , s ) c 2 $ \Delta L_{1,2}=\eta \left(\delta M_{t}^{p,s}/t_{\mathit{v}}^{p,s}\right)c^{2} $ represents the increased luminosity due to the enhanced accretion for the primary and the secondary BHs, respectively (see text for details).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.