| Issue |
A&A
Volume 643, November 2020
|
|
|---|---|---|
| Article Number | A121 | |
| Number of page(s) | 13 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202039085 | |
| Published online | 10 November 2020 | |
Sustained oscillations in interstellar chemistry models
1
LERMA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Université,
92190
Meudon, France
e-mail: Evelyne.Roueff@obspm.fr; jacques.lebourlot@obspm.fr
2
Université de Paris,
Paris, France
Received:
1
August
2020
Accepted:
29
September
2020
Context. Nonlinear behavior in interstellar chemical models has been recognized for 25 years now. Different mechanisms account for the possibility of multiple fixed-points at steady-state, characterized by the ionization degree of the gas.
Aims. Chemical oscillations are also a natural behavior of nonlinear chemical models. We study under which conditions spontaneous sustained chemical oscillations are possible, and what kind of bifurcations lead to, or quench, the occurrence of such oscillations.
Methods. The well-known ordinary differential equations (ODE) integrator VODE was used to explore initial conditions and parameter space in a gas phase chemical model of a dark interstellar cloud.
Results. We recall that the time evolution of the various chemical abundances under fixed temperature conditions depends on the density over cosmic ionization rate nH∕ζ ratio. We also report the occurrence of naturally sustained oscillations for a limited but well-defined range of control parameters. The period of oscillations is within the range of characteristic timescales of interstellar processes and could lead to spectacular resonances in time-dependent models. Reservoir species (C, CO, NH3, ...) oscillation amplitudes are generally less than a factor two. However, these amplitudes reach a factor ten to thousand for low abundance species, e.g. HCN, ND3, that may play a key role for diagnostic purposes. The mechanism responsible for oscillations is tightly linked to the chemistry of nitrogen, and requires long chains of reactions such as found in multi-deuteration processes.
Key words: astrochemistry / instabilities / methods: numerical / ISM: abundances / evolution / molecular processes
© E. Roueff and J. Le Bourlot 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The evolution of interstellar chemical abundances through formation/destruction chemical processes is described by a set of nonlinear differential equations that fall under the frame of dynamical systems. Then, it is not surprising to find some of the standard features characteristic of these systems. In particular multiple fixed-points for a given set of control parameters have been demonstrated by Pineau des Forets et al. (1992) and first analyzed by Le Bourlot et al. (1993, 1995a,b). The two stable solutions correspond to very different chemical signatures and have been labelled as LIP, corresponding to a Low Ionization Phase and HIP for an High Ionization Phase. LIP features are described by abundant saturated molecules and molecular ions whereas HIP signatures rather point to abundant radicals, carbon chains and atomic ions. Although these results led to some debate (e.g. Shalabiea & Greenberg 1995), they were later confirmed by various groups (Lee et al. 1998; Charnley & Markwick 2003; Boger & Sternberg 2006; Dufour & Charnley 2019). Some puzzling observations were even suggested to be representative of the HIP phase by, e.g., Gerin et al. (1997) or Ceccarelli et al. (2011).
However, apart from a passing mention in Le Bourlot et al. (1995a), no steady chemical oscillations have been reported to date. This is rather surprising, as such a behavior is a normal feature of nonlinear sets of chemical equations (see Gray & Scott 1994) and results probably from the limited range of integration time and parameter values considered in the current time-dependent chemical studies applied to interstellar clouds (Wakelam et al. 2015). Various time dependent behaviors including oscillations are explicitly quoted in Maffucci et al. (2018). This paper will be discussed below, as we believe their study to be not fully complete. Furthermore, our analysis explains naturally a large fraction of their findings.
In this paper, we describe in some details naturally occurring oscillations in a model of dark cloud chemistry. The underlying formalism is presented in Sect. 2, a fiducial oscillatory solution is introduced in Sect. 3. We discuss the effect of various control parameters in Sect. 4 and present our analysis and a discussion in Sect. 5.
2 Time dependent chemical equations
We restrict ourself to an idealized dark cloud. That is, photo processes come only from secondary photons following the creationof high energy electrons by cosmic-ray. These electrons excite the different electronic states of H2 that eventually decay by emitting ultraviolet photons in the 750–1750 Å window (Gredel et al. 1989).
We also make two very strong restrictions by assuming a constant temperature and discarding gas-grain chemical interactions. We are fullyaware that, as a consequence, the resulting models cannot be readily applied to “real” astrophysical objects, nor be compared to observations. But this is a necessary preliminary step to try and understand the chemical mechanisms at work. Extended models that overcome one or both of these approximations will be introduced later (note however a brief discussion in the last section).
On the other hand, our chemical model includes an extended and detailed chemical network including 254 species, coupled by 4872 reactions taken from our previous studies (Roueff et al. 2015; Cernicharo et al. 2018). In particular, it includes a detailed deuteration scheme with multiple deuterated species from NH3 to ND3 (Roueff et al. 2005), H2CO to D2CO, H2 CS to D2 CS (Marcelino et al. 2005), CH4 to CD4. We introduce the value of the ortho-to-para ratio of molecular hydrogen, (O/P), which drives the deuteration efficiency through the  reaction (Pagani et al. 1992) as an external fixed parameter, following Roueff et al. (2015). This parameter is also critical for the initial step of the nitrogen hydrogenation reaction N+ + H2 →NH+ + H which is slightly endothermicwhen H2 is in its para form as first emphasized by Le Bourlot (1991). We follow the prescription of Dislaire et al. (2012) based on the experimental studies of Marquette et al. (1988) to account for this reaction. We also include the experimental reaction rate coefficients to account for N+ + HD and N+ + D2 reactions.
reaction (Pagani et al. 1992) as an external fixed parameter, following Roueff et al. (2015). This parameter is also critical for the initial step of the nitrogen hydrogenation reaction N+ + H2 →NH+ + H which is slightly endothermicwhen H2 is in its para form as first emphasized by Le Bourlot (1991). We follow the prescription of Dislaire et al. (2012) based on the experimental studies of Marquette et al. (1988) to account for this reaction. We also include the experimental reaction rate coefficients to account for N+ + HD and N+ + D2 reactions.
Parameters used for various models are displayed in Table 1. The range shown is typical of the values explored, although we did not compute all possible models1.
Control parameters.
2.1 Nondimensional equations
One major advantage of using a constant temperature is that it leads to constant chemical reaction rates once the other external parameters are chosen. In a low-density gas, only two body collisions are possible. So the time evolution of any species Xi abundance  writes:
writes:
 (1)
(1)
Two bodies rates  are in cm3 s−1 and one body rates
are in cm3 s−1 and one body rates  are in s−1. These condensed equations account both for formation/destruction processes with appropriate signs. Given our hypothesis, all
are in s−1. These condensed equations account both for formation/destruction processes with appropriate signs. Given our hypothesis, all  are proportional to the molecular hydrogen cosmic-ray ionization rate ζ. This suggests to use 1∕ζ as a characteristic timescale, and to introduce a nondimensional time variable τ = ζ t. Writing now ni = nH xi, with xi the relative abundance of species Xi, we can introduce nondimensional rates for all chemical reactions by writing:
are proportional to the molecular hydrogen cosmic-ray ionization rate ζ. This suggests to use 1∕ζ as a characteristic timescale, and to introduce a nondimensional time variable τ = ζ t. Writing now ni = nH xi, with xi the relative abundance of species Xi, we can introduce nondimensional rates for all chemical reactions by writing:  .
.
Subsequently, Eq. (1) reduces to:
 (2)
(2)
This analysis shows that we can lower the number of control parameters by defining an “ionization efficiency parameter”  or
or  (unitless), which leads to values of Iep from 1 to 10 for typical interstellar conditions. This property has been previously recognized for steady-state results (Lepp & Dalgarno 1996; Boger & Sternberg 2006) or for the maxima corresponding to so-called early-time results (Lee et al. 1998). However, to our knowledge, this occurrence was never taken full advantage of for interstellar applications. Let us also point out that this property is maintained for gas–grain interactions as long as a single grain temperature is considered and a standard rate equations formalism is used to describe surface chemistry (Hasegawa et al. 1992).
(unitless), which leads to values of Iep from 1 to 10 for typical interstellar conditions. This property has been previously recognized for steady-state results (Lepp & Dalgarno 1996; Boger & Sternberg 2006) or for the maxima corresponding to so-called early-time results (Lee et al. 1998). However, to our knowledge, this occurrence was never taken full advantage of for interstellar applications. Let us also point out that this property is maintained for gas–grain interactions as long as a single grain temperature is considered and a standard rate equations formalism is used to describe surface chemistry (Hasegawa et al. 1992).
2.2 Dynamical system properties
Equation (2) is in the standard form of a dynamical system:
 (3)
(3)
where X is the vector of (unknown) variables, α a set of (fixed) control parameters, and F a vector of functions. Below, we summarize the main properties of dynamical systems as described in the literature; for example Gray & Scott (1994). Fixed points of this system are found by setting  . The (possibly multiple) solutions may or may not be stable. The stability can be assessed by computing the eigenvalues of the Jacobian matrix J at the fixed point. If
. The (possibly multiple) solutions may or may not be stable. The stability can be assessed by computing the eigenvalues of the Jacobian matrix J at the fixed point. If  is a fixed point, then:
is a fixed point, then:
 (4)
(4)
Close to  , the system (2) can be linearized. Its evolution is then given by
, the system (2) can be linearized. Its evolution is then given by
 (5)
(5)
where λi are the eigenvalues of  . We see that, if all real parts
. We see that, if all real parts  , then the fixed point is stable, and evolution may lead to it, provided that all control parameters remain constant during the evolution. If a single λi has a positive real part, then the fixed point is unstable, and the system leaves its vicinity. As soon as
, then the fixed point is stable, and evolution may lead to it, provided that all control parameters remain constant during the evolution. If a single λi has a positive real part, then the fixed point is unstable, and the system leaves its vicinity. As soon as  is no longer infinitely small, the linearized approximation does not apply and higher order terms control the evolution.
is no longer infinitely small, the linearized approximation does not apply and higher order terms control the evolution.
This is independent of whether λi eigenvalues have an imaginary part or not. If they do, then they occur in pairs of complex conjugates. Writing λi = μi + i ωi, all  include a contribution of the form
include a contribution of the form  , which is an oscillatory contribution.
, which is an oscillatory contribution.
-
If the fixed point is stable, then the system behaves as a damped oscillator, with a damping characteristic time of
 , where μj
is the smallest eigenvalue (in absolute value). If the associated λi
has an imaginary part, then there is an oscillatory damping;
, where μj
is the smallest eigenvalue (in absolute value). If the associated λi
has an imaginary part, then there is an oscillatory damping; -
If the fixed point is unstable, the system leaves its vicinity with a timescale associated to the most positive eigenvalue. Here again, an oscillatory component may or may not be present.
The subsequent evolution depends on the topology of the phase space. Evolution may lead to another (stable) fixed point (steady-state), or to sustained oscillations if a stable limit cycle exists. In the following, we show how a stable fixed point undergoes a Hopf bifurcation, giving birth to a stable limit cycle at a specific value of a control parameter. This occurs when the real part of an eigenvalue of the Jacobian matrix crosses a value of zero. We note that this also explains the phenomenon of “critical slow-down” observed in the vicinity of a bifurcation point. As the evolution depends on  , the damping or growing time diverges as μi → 0. An example is given below in Sect. 4.2.
, the damping or growing time diverges as μi → 0. An example is given below in Sect. 4.2.
2.3 The role of initial conditions
If several attractors exist (e.g., one or more stable fixed points, and a stable limit cycle) then the evolution depends critically on the chosen initial conditions. Different initial conditions may lead to one or the other attractor as previously shown in Le Bourlot et al. (1993). The initial part of the evolution has thus no particular meaning, depending solely on an arbitrary choice of initial conditions. Relaxation to the attractor depends mainly on its stability character and its distance – in parameter space – from a possible bifurcation point. We would like to stress here that the so-called early-time behavior is entirely dependent on an arbitrary choice of initial conditions; it should be considered with great care as it provides almost no information on the intrinsic behavior of the system.
When application to interstellar medium conditions is examined, one should remember that interstellar clouds do not form out of nothing at a given time, but rather result from fluctuations within a turbulent medium that is permanently stirred by various dynamical process (e.g., supernovae or the differential rotation of the galaxy). Part of the gas disappears in new stars and fresh material is constantly added to the medium by the evolution of stars (stellar winds, loss of envelopes, supernova) or cooling flows from intergalactic material.
Thus, when a dense cloud separates from its environment, its composition is typical of the diffuse medium and quite different from the arbitrary simple values often found in the literature (e.g., H2, C+, O, N,...). Model results obtained with such initial conditions may therefore be significantly misleading.
3 The oscillatory fiducial model
We report and discuss now our finding of oscillatory solutions obtained through a mixture of serendipity and systematic exploration of the model parameters displayed in Table 1.
3.1 Typical oscillations
Table 2 shows the values of the physical parameters leading to an oscillatory behavior of the reduced abundances, and defines our fiducial model.
Examples of oscillations are shown in Fig. 1.
All quantities are nondimensional (x relative to nH and time in units of τ). Panel a shows how the reservoir of carbon oscillates from C to CO and back. Oscillations are simple and in perfect phase opposition. We note that the C/CO ratio is of the order of 1, which corresponds to unusual but observationally found situations with a significant neutral carbon abundance such as TMC1 (Schilke et al. 1995). The oscillatory behavior has indeed been found for a C/O elemental ratio of 1 corresponding to carbon-rich environments. We also point out that the electronic fraction displayed in panel b of Fig. 1 oscillates around 4 × 10−7, with an amplitude of ~2 × 10−7, corresponding to a relatively high value for dense interstellar cloud conditions. The chemical properties of the corresponding solutions are similar to those of the HIP phase (Le Bourlot et al. 1993). Panel c shows how minor species react to this balance. NH3 oscillation amplitudes are mild, but the full isotopic substituted ND3 shows spectacular amplitude variations, which is the case for all fully deuterated substituted species. The maximum variation is over three orders of magnitude for 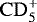 . Panel d shows, for SH, that more complex oscillations are achievable that probably emerge from intricate coupling terms in the chemical evolution.
. Panel d shows, for SH, that more complex oscillations are achievable that probably emerge from intricate coupling terms in the chemical evolution.
We can also display the dependence between different evolving variables in phase space. After dissipation of the transitory regime, the phase trajectory converges towards a limit cycle as displayed for NH3, CH4, and CO in Fig. 2.
Reference model parameters  .
.
3.2 Initial conditions effects
Most if not all time-dependent studies use initial conditions where carbon is totally ionized as C+, sulfur as S+, whereas oxygen and nitrogen are atomic. Hydrogen is most often taken as fully molecular but atomic initial conditions are also used sometimes. These assumptions are obviously far from reality as a dense cloud results from the previous evolution of diffuse clouds which are found to be chemically diverse from absorption observations in front of randomly available continuum radio sources; see for example Liszt et al. (2019). The partitioning of elemental carbon amongst the different potential reservoirs, C+, C, and CO is much more likely to represent plausible initial conditions. If some amount of CO is present as an initial condition, this impacts the sharing of oxygen as well in order to maintain the full elemental abundances. Figure 3 demonstrates this effect on the time evolution of the fractional abundance of a typical complex molecule, D2 CO2. All initial abundances are identical except for C+, O, and CO. Initial C is kept to a vanishingly low value here, but qualitatively identical results are obtained if we use C in place of C+. For these, the total amount of carbon and oxygen is distributed with a fraction α on C+ and O and a fraction 1 − α on CO (recall that C∕O = 1 here). We see that D2CO oscillations are exactly the same after about two periods, exhibiting only a phase shift. The transitory regime occurring before the oscillations take place shows amplified response to initial conditions that are far from the asymptotic behavior. But that initial variation can either be towards a stronger peak (the so-called early-time regime) or a very low abundance, with all intermediate values possible. We see that the resulting abundances are entirely a consequence of the choice of initial conditions. It is therefore very important to select physically plausible conditions, which excludes the usual choice of a single species found in theoretical papers. A reasonable solution is for example to run a first case until a permanent regime is reached, and then to change the control parameters (e.g., the density) and start from the solution of the previous run.
 |
Fig. 1 Typical oscillations obtained in the fiducial model. τ = 10−3 corresponds to ~0.634 Myr for ζ = 5× 10−17 s−1. |
 |
Fig. 2 Projection of a limit cycle on a 3D slice of phase space for the fiducial model. Any triple combination of species could be used in place of NH3, CH4, and CO. |
3.3 Timescales
The period of the oscillations can be deduced from the position of successive maxima. We find a period of τ0 = 1.1562 × 10−3 with Iep = 4, which translates to0.73274 Myr for ζ = 5 × 10−17 s−1.
To convert from a nondimensional period τ0 to “real” time, one needs only to divide by the value of ζ in s −1. If Iep is given, then:
 (6)
(6)
For a given value of Iep, the oscillation period decreases as 1∕nH. Figure 4 shows the relation between nH and tosc for the range of Iep found in Sect. 4.1.
Using initial conditions leading to a high first maximum of the time evolution (e.g., α =1 in Fig. 3), we can also study how these maxima converge towards a steady-state behavior by plotting the differences between successive maxima Δx and the asymptotic value. Figure 5 shows a typical example3. A clear exponential decrease emerges from which we deduce a characteristic damping time for the transitory regime, τr ≃ 6.5 × 10−4, slightly above a half period.
The oscillations are also clearly visible when performing a Fourier transform of the abundances. The equations were integrated over 1400 periods, which allows us to reach a resolution of δν = 0.7736 (unit-less). The corresponding spectra are shown in Fig. 6, where the Fourier transform power P of  and
and  evolutions are displayed for comparison.
evolutions are displayed for comparison.
Although very close, the peak intensities are slightly different at low frequency. First, the main peak at ν0 = 864.93 confirms the value of the period of τ0 = 1.1562 × 10−3 reported above. All the harmonics at n × ν0 are very strong. Additional weaker peaks arise at two other frequencies, ν1 = 298.63 and ν2 = 566.27. However, subsequent peaks at ν2 + n × ν0 get increasingly stronger when those at ν1 + n × ν0 disappear. This is particularly perceptible for SH. We also point out that ν1 is close to ν0∕3 and ν2 is close to 2ν0∕3 but the difference between these fractions is markedly greater than the frequency resolution, and is therefore significant. These additional peaks are therefore not sub-harmonics of the main frequency.
 |
Fig. 3 Time dependence of D2CO for different initial conditions defined by α (see text) reported on the top with different colors for the fiducial model. α = 1 corresponds to all elemental carbon put on C+ initially. |
 |
Fig. 4 Oscillation period as a function of density nH for various Iep values. |
 |
Fig. 5 Relaxation timescale and period evaluation from successive maxima for the fiducial model. |
4 Dependence of the oscillatory behavior on the control parameters
Such a chemical evolution could affect the dynamics of the environment if its occurrence complies with likely observable conditions, as discussed in Sect. 5. Here, we study within which range of control parameters oscillations are obtained.
 |
Fig. 6 Fourier transform power spectrum P of oscillating fractional abundances in the fiducial model as a function of the dimensionless frequency parameter ν. Upper panel:C, lower panel: SH. |
4.1 Effect of the ionization efficiency parameter Iep
The standard method to find the extent of an oscillatory zone in parameter space is the following:
- 1.
Fix a value of the parameter Iep and find the exact value of T at the bifurcation. This should be achieved by computing the eigenvalues of the Jacobian matrix and solving for
 , where λm is the highest eigenvalue real part.
, where λm is the highest eigenvalue real part. - 2.
Then use a continuation scheme to follow the bifurcation point in parameter space. To this end, we require that a variation δIep of Iep leads to a variation δT of T to still be at a bifurcation point.
 (8)
(8)
If  , we can solvethe 1D ordinary differential equation (ODE):
, we can solvethe 1D ordinary differential equation (ODE):
 (10)
(10)
Unfortunately, this scheme breaks down in the present case. The Jacobian matrix happens to be very ill-conditioned, and the computation of the eigenvalues becomes unstable close to the bifurcation. This has been confirmed using two different numerical routine libraries: the latest LAPACK version of DGEEVX, and the oldest but quadruple precision version of EISPACK routine “rg”. Both routines agree very well on all eigenvalues, except in the vicinity of a bifurcation point where the smallest eigenvalues in norm are unreliable4.
We therefore resorted to a less accurate but robust method to explore parameter space: brute force. Figure 7 shows the domain of oscillations in the Iep –T parameter space obtained from systematic sampling, together with the oscillation period represented by the color coding. The domain of oscillation spans a narrow range of temperatures between about 7 and 15 K with ionization efficiency parameters between 1.3 and 10.4. For a typical cosmic-ray ionization parameter ζ = 5 × 10−17 s−1, the range of density is 5 × 103–5 × 104 cm−3. We stress that all these values are compatible with physical conditions found in interstellar clouds. The oscillatory period varies by less than a factor of two, between 450 and 900 kyr for this value of cosmic-ray ionization rate. Such values are also similar to the expected evolution time of interstellar clouds. Small ionization efficiency parameters lead to larger values of the oscillation period. We can therefore consider that these findings are much more than a numerical curiosity and could significantly impact our knowledge of the interstellar medium.
 |
Fig. 7 Oscillation domain in the Iep − T plane. The oscillation period is color-coded. |
4.2 Effect of the temperature
Keeping other parameters from Table 2 fixed, we now explore the range of temperatures over which oscillations are found. Figure 8 is a bifurcation diagram displaying the steady-state solutions when T is varied from 8.5 K to 13 K, keeping Iep = 4. A single fixed point is obtained for Tc1 < 8.752 K and Tc2 > 12.347 K, which is exhibited in green. Stable oscillations are present in between and the corresponding maxima and minima values of the fractional abundances are also reported in green. The fixed point itself does not disappear, but becomes unstable, and this is displayed in red in Fig. 8. This behavior is standard, and representative of a Hopf bifurcation, as detailed for example in Gray & Scott (1994).
This effect of temperature is illustrated using HCN, but the behavior is generic and identical for all species. Below Tc1 = 8.752 K, there is a stable fixed point. Starting from various (but not necessarily any) initial conditions, the system converges towards it. However, convergence is slower and slower corresponding to an increasing relaxation time of the initial conditions, as seen in Fig. 9, which displays the relaxation time deduced from the decline of successive maxima as a function of temperature.
This is the critical slow-down phenomenon, characteristic of bifurcations. Close to Tc1, the fixed point becomes unstable, and oscillations appear through a Hopf bifurcation. Their amplitudes are initially vanishingly small, but they grow fast as T is increased. The time evolution for two values of the temperature that bracket the bifurcation point is shown in Fig. 10. In the close vicinity of Tc1 and for T <Tc1, a nice damped oscillatory structure is shown for the ND3 fractional abundance, which converges slowly towards the stable fixed point (in green on Fig. 10). The red curve displays the sustained oscillations taking place immediately after Tc1. One can see that many oscillations are necessary before reaching the permanent regime.
The amplitude of the oscillations remains significant until the vicinity of Tc2 = 12.347 K where a second Hopf bifurcation occurs. Beyond this second bifurcation point, the fixed point is stable again. A fixed point is still present between the two bifurcation points but the corresponding solution is unstable. These points are displayed in red in Fig. 8 and were computed using a Newton-Raphson scheme by directly solving the d ∕d t = 0 coupled chemical equations.
The critical slow-down in the vicinity of a bifurcation point is important, because it leads to timescales that are totally unrelated toany other characteristic times of the system, either chemical or dynamical. Hence, the system may seem to behave strangely given the chosen parameters. This is simply the direct consequence of a close-by bifurcation point in parameter space. It is also remarkable that the range of temperatures where the oscillatory behavior takes place is within the values derived from interstellar cloud observations.
The value Tc2 is driven by our hypothesis on (O/P), the H2 ortho-to-para ratio. Here, we assume that it is the thermal equilibrium value, where T is the gas temperature. Increasing T increases (O/P), which has a dramatic effect on the N+ + H2 →NH+ + H reaction rate coefficient (see discussion on the chemistry in Sect. 5.1 and Appendix A and on the (O/P) valuein Sect. 5.3).
 |
Fig. 8 Bifurcation diagram for HCN. Within the unstable fixed-point region, the two outer curves show the range of oscillations (minimum and maximum values). |
 |
Fig. 9 Relaxation time of initial conditions. We highlight the large uncertainties far from the bifurcation points. Conversely, close to Tc1 and Tc2 the large relaxation time allows for a very accurate determination. |
 |
Fig. 10 ND3 evolution before and after the first bifurcation point. |
 |
Fig. 11 Bifurcation diagram for δN. Note a small error in the value of the fixed point computed with the Newton-Raphson scheme below the lowest Hopf bifurcation. |
4.3 Effect of the elemental abundances
Elemental abundances in the gas phase constitute another set of control parameters. We focus our study on the most abundant elements after hydrogen and helium, namely C, N, and O, and introduce a relation between δC and δO. Instead of varying the latter independently, we explore the influence of the δC ∕δO ratio at constant total δC + δO (total metallicity) or the influence of metallicity for a constant δC∕δO = 1.
Figure 11 shows a bifurcation diagram for δN. All other parameters are kept at the values of our fiducial model (cf. Table 2). As the density nH is kept constant, we chose the ionization degree of the gas as a representative variable, as it does not require a rescaling by elemental abundances. Two Hopf bifurcations are present, with oscillations maintained up to a very high (and somewhat unrealistic) abundance value for nitrogen (over 7 × 10−4).
Keeping δN at its fiducial value (6 × 10−5), Fig. 12 shows that oscillations encompass typical values of δC ∕δO and not only the selected value of 1 we used up to here. Figure 13 shows in a similar way that the total metallicity can be varied up to values found in many environments, although somewhat lower than in the solar vicinity.
We conclude that the occurrence of oscillations does not require very specific values of the elemental abundances, although our studies are more representative of low-metallicity or depleted environments.
The chance occurrence of a spectacular critical slow-down found during the exploration of this parameter space is presented in Appendix B.
 |
Fig. 12 Bifurcation diagram for δC∕δO. |
 |
Fig. 13 Bifurcation diagram for the total metallicity with varying δC + δO. Other abundances are kept as in Table 2. |
5 Discussion
5.1 Chemistry
Elucidating the chemical mechanisms responsible for oscillations is much more challenging than for steady-state results. There is indeed no set of equations to solve that would provide the answer. One has to follow the time variations of leading species to point to the relevant interactions. Here, we do not know which are the leading species. We can however derive some chemical properties that comply with the oscillatory behavior:
- 1.
The full evolution remains within HIP chemistry. This corresponds to a significant electronic fraction (~ a few 10−7) which further implies the presenceof C at a level close tothat of CO.
- 2.
Full deuteration appears compelling (within our set of chemical reactions). This implies thatlong chains of reactions exist leading from some very simple species (say, e.g., N+) to fully deuterated species (say, e.g., ND3,
 ). It may be possible that other long chains of reactions also lead to oscillations, for example the formation of cyanopolyines, but we did not explore this point further.
). It may be possible that other long chains of reactions also lead to oscillations, for example the formation of cyanopolyines, but we did not explore this point further. - 3.
Nitrogen chemistry plays a central role. The slightly endothermic N+ + H2 →NH+ + H reaction, which is subject to large uncertainties (Dislaire et al. 2012; Marquette et al. 1988), has a huge impact on the collective behavior.
A first clue as to the underlying mechanism is seen from the successive maxima of chemically linked species. Figure 14 shows the sequence of different deuterated compounds of NH3 as a function of time. The abundances are rescaled to the (dimensionless) interval [0 : 1] through 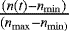 to enable comparison. We first observe the peak of NH3 itself. Then, offset by nearly half a period, we find the peak of NH2D, which is closely followed by that of ND2H, and finally by that of ND3. Meanwhile, NH3 has time to decrease to its minimum, which quenches the deuteration process. The deuterated species are then destroyed more efficiently than they are formed, and they fall to very low levels. The process then starts again.
to enable comparison. We first observe the peak of NH3 itself. Then, offset by nearly half a period, we find the peak of NH2D, which is closely followed by that of ND2H, and finally by that of ND3. Meanwhile, NH3 has time to decrease to its minimum, which quenches the deuteration process. The deuterated species are then destroyed more efficiently than they are formed, and they fall to very low levels. The process then starts again.
Figure 15 shows the ratio of the maximum to minimum abundances of all species as a function of their peak abundance time with respect to that of NH3. The peak of NH3 is well separated from all other species (by at least one-tenth of a period), which is a strong indication that it plays a particular role. This latter peak is followed by a small number of “lead” molecules, half of which are hydrogenated nitrogen with no or one deuterium. Then, at about 0.6 τ0, most species peak, with an amplitude that may exceed a factor of 104. This is where all multiply deuterated molecules are found, with the single exception of  . This peak extends over a limited time interval, which expresses the trigger of successive interconnected maxima. We interpret these features as a signature of the importance of nitrogen deuteration in the mechanism responsible for oscillations.
. This peak extends over a limited time interval, which expresses the trigger of successive interconnected maxima. We interpret these features as a signature of the importance of nitrogen deuteration in the mechanism responsible for oscillations.
 |
Fig. 14 Scaled oscillations of NH3 and its deuterated isotopologs. The amplitude of the oscillations is fixed to [0 : 1] for each species as described in the text. |
 |
Fig. 15 Ratio of maximum to minimum abundances as a function of phase shift with respect to NH3. “multi-D” are molecules with two or more D. The two vertical lines delineate the time range where multideuterated species peak. |
NH3/CN connection
Formation of NH3 and its deuterated substitutes proceeds progressively in time as shown in Fig. 14. The initial step is provided by the reaction of N+ with H2, HD, and D2 as shown in Fig. 16.
In the HIP environment considered here, atomic carbon C (Bourgalais et al. 2015; Hickson et al. 2015)and ionized carbon C+ are the main destruction agents (see Fig. 17) which finally lead to the formation of a CN bond within a large variety of species (HCN, HNC, HCNH+,...), as displayed in Fig. 18.
Focusing on these H, C, and N compounds as displayed on the left of Fig. 18, we see that the CN radical emerges. Reactions ofCN with C and O then lead back to atomic N whereas the reaction with N produces N2 as found experimentally by Daranlot et al. (2012). N+ is subsequently restored via reactions of N2 with He+ and cosmic-ray ionization ofatomic N, and the full cycle starts again.
During the whole process, minor reactions may create leaks towards other branches of the full chemical set (e.g., through NO for a coupling to oxygen chemistry), and so it is very sensitive, which explains why we find oscillations only within a restricted part of parameter space. We further study nitrogen chemistry in Appendix A.
5.2 Thermal balance
Our current model does not include a sophisticated treatment of thermal balance, as found for example in the Meudon PDR code (Le Petit et al. 2006). However, simple analytic formulae of the main heating and cooling processes are included, following Flower & Pineau des Forêts (2015), that allow the derivation of the temperature within a given equation of state, namely n = Cte here, with n the density of the gas, that is, 
Solving for thermal balance removes one control parameter from the system, as temperature is now computed by solving its evolution equation and is not set arbitrarily. However, the cooling and heating terms do not scale in the same way with ζ and nH, and so the ionization efficiency Iep cannot be used as a single parameter. The number of control parameters is therefore unchanged.
We did not conduct a full exploration of that parameter space, but we checked that thermal oscillations can be found and are fully compatible with the mechanism described here. For Iep = 4, Fig. 19 shows a Hopf bifurcation close to nH = 9.5 × 103 cm−3. We kept a constant value for Iep, to help comparisons with Fig. 7. One can see that the range of temperatures spanned within the oscillations is compatible with the values found at constant temperature.
This example shows that oscillations can be expected within a detailed model using a more sophisticated thermal balance. However, it is not yet possible to determine the precise domain of parameters involved.
5.3 (O/P)
Even in steady-state, (O∕P) is not equal to its ETL value. Destruction of H2 by cosmic rays and reactions with H+ and  are compensated by formation on grains with a different (O/P). However, this latter process is very poorly understood. (O ∕P) is usually supposed to be three at the formation process on grains, but this is true only if a significant fraction of the formation enthalpy is used to that end. Some mechanisms may also lead to a significant transfer of energy to the grain, or favor a different statistical equilibrium. For example, a strong interaction with the surface could lead to independent spins for the two protons, resulting in a (O ∕P) value of one at formation.
are compensated by formation on grains with a different (O/P). However, this latter process is very poorly understood. (O ∕P) is usually supposed to be three at the formation process on grains, but this is true only if a significant fraction of the formation enthalpy is used to that end. Some mechanisms may also lead to a significant transfer of energy to the grain, or favor a different statistical equilibrium. For example, a strong interaction with the surface could lead to independent spins for the two protons, resulting in a (O ∕P) value of one at formation.
However, our choice is certainly a lower limit, and higher values are expected, as found by Flower et al. (2006). The thermal value of (O ∕P) for the fiducial model at T = 11 K is 1.67× 10−6. We explored the influence of using a higher value of (O∕P) and found that oscillations persist up to (O∕P) = 1.65 × 10−4 in this case. We therefore find that oscillations are entirely compatible with typical values of (O/P).
We checked that the impact of the fraction of ortho-H2 on the occurrence of oscillations is entirely due to N+ + H2 →NH+ + H. The other (O∕P)-sensitive reaction, namely  , has no impact on whether or not oscillations occur.
, has no impact on whether or not oscillations occur.
 |
Fig. 16 NH3 and deuterated isotopolog formation. |
 |
Fig. 17 NH3 and deuterated isotopolog destruction. The dissociative recombination reactions of HCNH+ and deuterated substitutes are not displayed. |
5.4 Grain chemistry
The present study is restricted to pure gas-phase chemistry. However, recombination of atomic ions on the grain surfaces reduces the ionization fraction as emphasized by Shalabiea & Greenberg (1995) in their discussion of the effects of grains on bistability properties. We recall that Le Bourlot et al. (1995b) showed that the bistability domain is shifted, but not suppressed, when only neutralization on grains is introduced.
Following the treatment reported in Le Bourlot et al. (1995b) and summarized in Cuppen et al. (2017), we obtain
![\begin{equation*} \frac{\textrm{d}\left[\mathrm{X}^{+}\right]}{\textrm{d}t}=-\pi\,a^{2}\,(1+f_{\textrm{C}})\,v_{\mathrm{X^{+}}}\,x_{\textrm{gr}}\,n_{\mathrm{H}}\,\left[\mathrm{X}^{+}\right], \end{equation*}](/articles/aa/full_html/2020/11/aa39085-20/aa39085-20-eq40.png) (11)
(11)
where a is the grain radius,  is the velocity of X+, fC is the Coulomb factor
is the velocity of X+, fC is the Coulomb factor  , and xgr is the dust-to-gas density ratio. For a typical grain radius a of 0.1 μ, a dust-to-gas mass ratio G = 10−2, a volumic mass density ρ of 3 g cm−3, and a temperatureT = 10 K, (1 + fC) = 12,
, and xgr is the dust-to-gas density ratio. For a typical grain radius a of 0.1 μ, a dust-to-gas mass ratio G = 10−2, a volumic mass density ρ of 3 g cm−3, and a temperatureT = 10 K, (1 + fC) = 12,  and the equation reduces to:
and the equation reduces to:
![\begin{equation*} \frac{\textrm{d}\left[\mathrm{X}^{+}\right]}{\textrm{d}t}=-3.2\times 10^{-16}\,\frac{1}{\sqrt{M_{\mathrm{X^{+}}}}}\,n_{\mathrm{H}}\,\left[\mathrm{X}^{+}\right], \end{equation*}](/articles/aa/full_html/2020/11/aa39085-20/aa39085-20-eq44.png) (12)
(12)
where  is the atomic massof X+ in amu. We find that such a value is compatible with the oscillatory behavior.
is the atomic massof X+ in amu. We find that such a value is compatible with the oscillatory behavior.
In addition, the neutralization rates are reduced significantly in low-metallicity regions where the dust-to-gas mass ratio is small, and in dense cores where coagulation leads to a large mean grain radius5.
 |
Fig. 18 CN links destruction and nitrogen recycling. |
 |
Fig. 19 Bifurcation diagram for temperatures at Iep = 4. |
5.5 Discussion of the oscillatory behavior reported in Maffucci et al. (2018)
In a paper devoted to cyanopolyynes and other oxygenated complex organic molecules in TMC1, Maffucci et al. (2018) mention oscillatory solutions for their time-dependent model. Unfortunately, the authors do not extend their calculations further than two millions years. Thus, one cannot be sure that these oscillations are maintained over a large period of time. There are nevertheless striking similarities between our findings:
-
The oscillatory behavior takes place for specific physical conditions, corresponding to a large C∕O ratio, low densities, and a large cosmic ionization rate, which probably would correspond to a chemical HIP phase, with large abundance of carbon chains;
-
The largest amplitude of the oscillations is obtained for the large cyanopolyynes whereas we find a similar feature for the highly substituted deuterated species. These species correspond to the extremities of successive complex chemical reactions.
These authors did not try to further explore such a behavior, and the origin of these oscillations could be more thoroughly investigated. However, we note that this model includes grain surface chemistry, which shows that this is not restricted to a pure gas-phase chemical network. We also anticipate that the oscillatory behavior concerns all chemical species, as this is a basic mathematical property of the chemical equations, as mentioned above. The observed fluctuations of long chains in TMC1 could come from oscillations triggered with different initial conditions from place to place. Therefore, variations in abundances would result from a common origin and common environment.
We also note that these latter authors use initial conditions with all abundances set to zero except for a single atom or atomic ion for each element (except for hydrogen). This is not likely to happen in a real cloud that condensates from diffuse conditions. Hence, their “early-time” results are entirely a consequence of this unfortunate choice and tell us nothing about the age of the cloud (see Sect. 3.2 above). In particular, we can expect that starting from conditions where most carbon is locked in CO would quench the formation of long cyanopolyyne chains entirely if oscillations do not restore some C to the gas phase.
6 Summary and conclusions
The present study reveals for the first time a well-known feature of nonlinear effects of chemical kinetics in the context of interstellar chemistry, namely the occurrence of oscillatory solutions of the chemical abundances over a restricted but representative physical parameter space. The oscillations are still present in an isochoric model where the thermal balance is solved concomitantly with the chemistry. We obtained different bifurcation diagrams by varying several control parameters, such as nH∕ζ, temperature, and elemental depletions. The spectacular outcome, in our point of view, lies in the range of physical parameters where the oscillatory behavior is obtained, which corresponds to the values derived from interstellar observations in terms of density, temperature, cosmic ionization rate, and elemental abundances. In addition, the timescales obtained for the oscillation periods are between some hundred thousand years and some million years, which are also within the same order of magnitude as other important timescale values relevant to the interstellar medium, such as the free-fall time or the crossing time (Klessen & Glover 2016).
The oscillatory behavior occurs within the so-called HIP phase, corresponding to electronic fractions which are typically of the order of several 10−7, significantly larger than those corresponding to the standard LIP chemical cloud conditions. These conditions are favored by a relatively high C∕O elemental ratio which in turn leads to a significant number of carbon chains, as found in several interstellar conditions.
The triggering mechanism of the oscillations is not precisely identified but the detailed analysis of the differential behavior of the various species points to the role of long chains of reactions. In our study, these are provided by the sequential deuteration processes which end up with fully deuterated species, such as CD4 and ND3, and the corresponding molecular ions  and
and  . The amplitude of the oscillations increases dramatically with the number of substituted deuterium nuclei. We also find that nitrogen chemistry plays a critical role through the link between carbon and oxygen. Finally, we want to emphasize the crucial importance of realistic initial conditions for deriving sensible conclusions on early-time behaviors of the chemical abundances.
. The amplitude of the oscillations increases dramatically with the number of substituted deuterium nuclei. We also find that nitrogen chemistry plays a critical role through the link between carbon and oxygen. Finally, we want to emphasize the crucial importance of realistic initial conditions for deriving sensible conclusions on early-time behaviors of the chemical abundances.
We can expect that the (magneto-)hydrodynamical behavior of a fluid subject to chemical oscillations could be quite distinct from that ofa more inert fluid. Various timescales might couple and lead to unexpected consequences. In particular, we propose that some characteristic length scales could emerge, which would be a natural explanation for variations in the star formation rate and in the mass distribution of young stars in a giant molecular complex, depending on whether or not chemical oscillations, and the induced oscillation of the cooling function, are triggered during the collapse.
Acknowledgements
This work was supported by the Programme National “Physique et Chimie du Milieu Interstellaire” (PCMI) of CNRS/INSU with INC/INP co-funded by CEA and CNES.
Appendix A Nitrogen chemistry
The formation routes of NH3,..., ND3 from the initial N+ + H2, N+ + HD and N+ + D2 are displayed in Fig. 16. These reactions have been the subject of a number of experimental (Marquette et al. 1988; Zymak et al. 2013 and references therein) and theoretical (Grozdanov et al. 2016) studies. The major issues involved are due to the mixing of the reactive, rotational, and fine structure channels of N+, H2, HD, NH+, ND+, meaning that the reaction proceeds very differently depending on whether H2 is in its J = 0, para, or J = 1, ortho level, as first noticed by Le Bourlot (1991). Nevertheless, the actual value of the reaction rate coefficient is still uncertain. The present study was performed by including the experimental values of Marquette et al. (1988) and following the analytic prescription of Dislaire et al. (2012), who derived two different analytic expression for the reactions with para and ortho-H2. (O/P) is computed from the gas temperature in our study as we did not try to separate the full ortho-to-para species as performed in some other studies (Hily-Blant et al. 2018; Sipilä et al. 2015). The fine tuning of this parameter would allow also to monitor the deuteration via the  reaction, which also critically depends on (O/P) as the endothermicity of the reaction (192 K) is of the same order of magnitude as the energy between the J = 1 and J = 0 levels of H2 (170.5 K).
reaction, which also critically depends on (O/P) as the endothermicity of the reaction (192 K) is of the same order of magnitude as the energy between the J = 1 and J = 0 levels of H2 (170.5 K).
As the oscillations take place for low values of the ortho-to-para ratio of H2, an alternative more efficient formation route of NH+ in our conditions is in fact obtained though the charge exchange reaction of H+ with NH 6. The corresponding chemical network is displayed in Fig. A.1.
 |
Fig. A.1 Different formation channels of NH+ and ND+. |
NH itself is formed through the dissociative recombination of  . We notice at this point also the crucial importance of the branching ratio of this reaction, which has been the object of several contradicting experiments. The present value is taken as 0.10, following the latest experimental value of Shapko et al. (2020).
. We notice at this point also the crucial importance of the branching ratio of this reaction, which has been the object of several contradicting experiments. The present value is taken as 0.10, following the latest experimental value of Shapko et al. (2020).
On the other hand, Marquette et al. (1988) found a relatively rapid rate coefficient for the N+ + HD reaction (3.17 × 10−10 cm3 s−1), which was used in the present study. The formation of deuterated ammonia then follows the reactions starting from N+ + HD as shown in Figs. 16 and A.1.
We also briefly mention NH2 and its deuterated isotopologs which are obtained from the dissociative recombination of different protonated molecular ions, as displayed in Fig. A.2, and lead back to N2 via reactions with atomic nitrogen. This reaction is specifically introduced in Wakelam et al. (2013).
 |
Fig. A.2 Cycle between NH2 and its deuterated isotopologs and molecular nitrogen. |
Appendix B Spectacular critical slow-down
While investigating these bifurcations, we found a nice illustration of the possible pitfalls offered by systems with multiple possible asymptotic behaviors (i.e., stable and/or unstable fixed points and limit cycles). Figure B.1 shows the time evolution of the ionization degree for δN = 7.36 × 10−4 (which happens, by chance, to be close to the upper bifurcation point). For more than 1000 periods, the system seems to have stabilized at a constant value, which would be the signature of a stable fixed point. Subsequently, some small fluctuations set in, and the evolution switches quite abruptly towards large oscillations. This behavior is hard to interpret if one only looks at the time evolution of one or another variable; but it becomes much clearer in phase space. Figure B.2 shows one of the many possible projections of the phase-space trajectory. The initial conditions are on the far left of the figure. The trajectory relaxes very quickly towards the unstable fixed point (seen in light blue), close to one of the (many) incoming heteroclinic orbits. However, once in the immediate vicinity of the fixed point, the influence of the outgoing heteroclinic orbits associated with positive eigenvalues of the Jacobian matrix begins to be felt. The trajectory spirals around the fixed point, with an exponentially increasing size. It goes almost unnoticed for quite a while, but eventually the trajectory leaves the vicinity of this fixed point and converges towards the stable limit cycle, giving rise to oscillations. Starting from different initial conditions, the trajectory can converge directly towards this limit cycle within a single period.
 |
Fig. B.1 Critical slow-down for initial conditions approaching an unstable fixed point. |
 |
Fig. B.2 Phase space trajectory of the simulation of Fig. B.1. The projection of the final limit cycle on each of the three 2D plans is shown for clarity. |
References
- Boger, G. I., & Sternberg, A. 2006, ApJ, 645, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Bourgalais, J., Capron, M., Abhinavam Kailasanathan, R. K., et al. 2015, ApJ, 812, 106 [CrossRef] [Google Scholar]
- Ceccarelli, C., Hily-Blant, P., Montmerle, T., et al. 2011, ApJ, 740, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., Lefloch, B., Agúndez, M., et al. 2018, ApJ, 853, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Charnley, S. B., & Markwick, A. J. 2003, A&A, 399, 583 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cuppen, H. M., Walsh, C., Lamberts, T., et al. 2017, Space Sci. Rev., 212, 1 [Google Scholar]
- Daranlot, J., Hincelin, U., Bergeat, A., et al. 2012, Proc. Natl. Acad. Sci. USA, 109, 10233 [NASA ADS] [CrossRef] [Google Scholar]
- Dislaire, V., Hily-Blant, P., Faure, A., et al. 2012, A&A, 537, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dufour, G., & Charnley, S. B. 2019, ApJ, 887, 67 [CrossRef] [Google Scholar]
- Flower, D. R., & Pineau des Forêts, G. 2015, A&A, 578, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flower, D. R., Pineau des Forêts, G., & Walmsley, C. M. 2006, A&A, 449, 621 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerin, M., Falgarone, E., Joulain, K., et al. 1997, A&A, 318, 579 [NASA ADS] [Google Scholar]
- Gray, P., & Scott, S. 1994, Chemical Oscillations and Instabilities: Non-linear Chemical Kinetics, International series of monographs on chemistry (Clarendon Press) [Google Scholar]
- Gredel, R., Lepp, S., Dalgarno, A., & Herbst, E. 1989, ApJ, 347, 289 [Google Scholar]
- Grozdanov, T. P., McCarroll, R., & Roueff, E. 2016, A&A, 589, A105 [CrossRef] [EDP Sciences] [Google Scholar]
- Hasegawa, T. I., Herbst, E., & Leung, C. M. 1992, ApJS, 82, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Hickson, K. M., Loison, J.-C., Bourgalais, J., et al. 2015, ApJ, 812, 107 [CrossRef] [Google Scholar]
- Hily-Blant, P., Faure, A., Rist, C., Pineau des Forêts, G., & Flower, D. R. 2018, MNRAS, 477, 4454 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S., & Glover, S. C. O. 2016, Saas-Fee Adv. Course, 43, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Le Bourlot, J. 1991, A&A, 242, 235 [NASA ADS] [Google Scholar]
- Le Bourlot, J., Pineau des Forets, G., Roueff, E., & Schilke, P. 1993, ApJ, 416, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Le Bourlot, J., Pineau des Forets, G., & Roueff, E. 1995a, A&A, 297, 251 [Google Scholar]
- Le Bourlot, J., Pineau des Forets, G., Roueff, E., & Flower, D. R. 1995b, A&A, 302, 870 [Google Scholar]
- Lee, H. H., Roueff, E., Pineau des Forets, G., et al. 1998, A&A, 334, 1047 [Google Scholar]
- Le Petit, F., Nehmé, C., Le Bourlot, J., & Roueff, E. 2006, ApJS, 164, 506 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lepp, S., & Dalgarno, A. 1996, A&A, 306, L21 [NASA ADS] [Google Scholar]
- Liszt, H., Gerin, M., & Grenier, I. 2019, A&A, 627, A95 [Google Scholar]
- Maffucci, D. M., Wenger, T. V., Le Gal, R., & Herbst, E. 2018, ApJ, 868, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Marcelino, N., Cernicharo, J., Roueff, E., Gerin, M., & Mauersberger, R. 2005, ApJ, 620, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Marquette, J. B., Rebrion, C., & Rowe, B. R. 1988, J. Chem. Phys., 89, 2041 [NASA ADS] [CrossRef] [Google Scholar]
- Pagani, L., Salez, M., & Wannier, P. G. 1992, A&A, 258, 479 [NASA ADS] [Google Scholar]
- Pineau des Forets, G., Roueff, E., & Flower, D. R. 1992, MNRAS, 258, 45P [NASA ADS] [CrossRef] [Google Scholar]
- Roueff, E., Lis, D. C., van der Tak, F. F. S., Gerin, M., & Goldsmith, P. F. 2005, A&A, 438, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roueff, E., Loison, J. C., & Hickson, K. M. 2015, A&A, 576, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schilke, P., Keene, J., Le Bourlot, J., Pineau des Forets, G., & Roueff, E. 1995, A&A, 294, L17 [NASA ADS] [Google Scholar]
- Shalabiea, O. M., & Greenberg, J. M. 1995, A&A, 296, 779 [NASA ADS] [Google Scholar]
- Shapko, D., Dohnal, P., Kassayová, M., et al. 2020, J. Chem. Phys., 152, 024301 [CrossRef] [Google Scholar]
- Sipilä, O., Harju, J., Caselli, P., & Schlemmer, S. 2015, A&A, 581, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakelam, V., Smith, I. W. M., Loison, J. C., et al. 2013, ArXiv e-prints, [arXiv:1310.4350] [Google Scholar]
- Wakelam, V., Loison, J. C., Herbst, E., et al. 2015, ApJS, 217, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Zymak, I., Hejduk, M., Mulin, D., et al. 2013, ApJ, 768, 86 [NASA ADS] [CrossRef] [Google Scholar]
The code is made available at http://ism.obspm.fr
All Tables
All Figures
 |
Fig. 1 Typical oscillations obtained in the fiducial model. τ = 10−3 corresponds to ~0.634 Myr for ζ = 5× 10−17 s−1. |
| In the text | |
 |
Fig. 2 Projection of a limit cycle on a 3D slice of phase space for the fiducial model. Any triple combination of species could be used in place of NH3, CH4, and CO. |
| In the text | |
 |
Fig. 3 Time dependence of D2CO for different initial conditions defined by α (see text) reported on the top with different colors for the fiducial model. α = 1 corresponds to all elemental carbon put on C+ initially. |
| In the text | |
 |
Fig. 4 Oscillation period as a function of density nH for various Iep values. |
| In the text | |
 |
Fig. 5 Relaxation timescale and period evaluation from successive maxima for the fiducial model. |
| In the text | |
 |
Fig. 6 Fourier transform power spectrum P of oscillating fractional abundances in the fiducial model as a function of the dimensionless frequency parameter ν. Upper panel:C, lower panel: SH. |
| In the text | |
 |
Fig. 7 Oscillation domain in the Iep − T plane. The oscillation period is color-coded. |
| In the text | |
 |
Fig. 8 Bifurcation diagram for HCN. Within the unstable fixed-point region, the two outer curves show the range of oscillations (minimum and maximum values). |
| In the text | |
 |
Fig. 9 Relaxation time of initial conditions. We highlight the large uncertainties far from the bifurcation points. Conversely, close to Tc1 and Tc2 the large relaxation time allows for a very accurate determination. |
| In the text | |
 |
Fig. 10 ND3 evolution before and after the first bifurcation point. |
| In the text | |
 |
Fig. 11 Bifurcation diagram for δN. Note a small error in the value of the fixed point computed with the Newton-Raphson scheme below the lowest Hopf bifurcation. |
| In the text | |
 |
Fig. 12 Bifurcation diagram for δC∕δO. |
| In the text | |
 |
Fig. 13 Bifurcation diagram for the total metallicity with varying δC + δO. Other abundances are kept as in Table 2. |
| In the text | |
 |
Fig. 14 Scaled oscillations of NH3 and its deuterated isotopologs. The amplitude of the oscillations is fixed to [0 : 1] for each species as described in the text. |
| In the text | |
 |
Fig. 15 Ratio of maximum to minimum abundances as a function of phase shift with respect to NH3. “multi-D” are molecules with two or more D. The two vertical lines delineate the time range where multideuterated species peak. |
| In the text | |
 |
Fig. 16 NH3 and deuterated isotopolog formation. |
| In the text | |
 |
Fig. 17 NH3 and deuterated isotopolog destruction. The dissociative recombination reactions of HCNH+ and deuterated substitutes are not displayed. |
| In the text | |
 |
Fig. 18 CN links destruction and nitrogen recycling. |
| In the text | |
 |
Fig. 19 Bifurcation diagram for temperatures at Iep = 4. |
| In the text | |
 |
Fig. A.1 Different formation channels of NH+ and ND+. |
| In the text | |
 |
Fig. A.2 Cycle between NH2 and its deuterated isotopologs and molecular nitrogen. |
| In the text | |
 |
Fig. B.1 Critical slow-down for initial conditions approaching an unstable fixed point. |
| In the text | |
 |
Fig. B.2 Phase space trajectory of the simulation of Fig. B.1. The projection of the final limit cycle on each of the three 2D plans is shown for clarity. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




