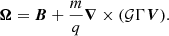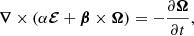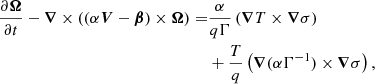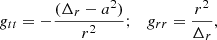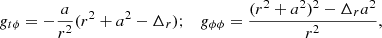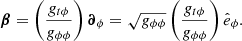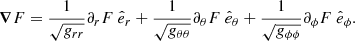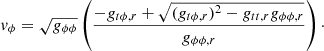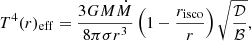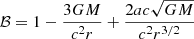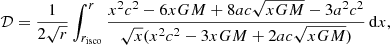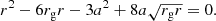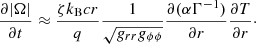| Issue |
A&A
Volume 642, October 2020
|
|
|---|---|---|
| Article Number | L6 | |
| Number of page(s) | 5 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202039127 | |
| Published online | 02 October 2020 | |
Letter to the Editor
Vortex generation in the early Universe
The spacetime curvature drive in primordial black hole accretion disks
1
Department of Physics, New York Institute of Technology, Old Westbury, NY 11458, USA
e-mail: usa.chinmoy@gmail.com
2
Los Alamos National Laboratory, Los Alamos, NM 87545, USA
e-mail: djstark@lanl.gov
Received:
7
August
2020
Accepted:
10
September
2020
Context. Accretion disks formed near primordial black holes can be sources of seed magnetic fields in the early Universe. In particular, the Biermann battery mechanism has been shown to generate primordial magnetic fields in an unmagnetized and turbulence-free accretion disk, but this depends on a delicate misalignment of density and pressure gradients in plasmas.
Aims. We aim to reformulate the question of magnetogenesis in the context of plasma generalized vorticity and to search for a more robust mechanism of vorticity generation in the early Universe.
Methods. We utilize the electro-vortical formalism in curved spacetime, which treats the plasma flow and electromagnetic field on an equal footing, and apply it to a thin accretion disk model near a rotating black hole.
Results. We present a spacetime curvature-driven mechanism that persists even in the absence of the Biermann battery. We explore the vorticity and enstrophy generation rate dependencies on black hole masses and spin rates.
Conclusions. Analysis indicates that the accretion disks around lower-mass, faster rotating black holes contribute the greatest amount to the enstrophy and vorticity generation rates from the spacetime curvature drive. The shorter turning radii at which the sign of the vorticity changes – corresponding with this region of phase space – may favor these length scales in vortical structure formation and subsequent evolution.
Key words: black hole physics / accretion, accretion disks / plasmas / magnetic fields / early Universe
© ESO 2020
1. Introduction
Fluid vorticity, defined as the curl of the fluid velocity field v, is essential to understanding early Universe structure formation, turbulence, and dynamos in accretion disks (Blackman 2001; Klahr & Bodenheimer 2003; Porter et al. 2015; Jelic-Cizmek et al. 2018). For a charged fluid, the definition of vorticity is generally extended by adding the magnetic field to the fluid vorticity, which can be called the generalized vorticity (Steinhauer & Ishida 1998; Mahajan & Yoshida 1998). Similar to the fluid theory, the generalized vorticity of an ideal plasma that is initially zero remains zero in the absence of external drives (forces). One can also characterize this result through the invariance of a topological property, namely the generalized helicity (Moffatt 1969). Based on the observation of our present Universe, which shows signatures of both a primordial magnetic field and solenoidal structure of fluid in galaxy clusters, the question of how the generalized vortex is formed in the early Universe remains open (Zucca et al. 2017; Vacca et al. 2018; Akahori et al. 2018; Subramanian 2019; Christopherson et al. 2011; Cutting et al. 2020; Brandenburg et al. 1996; Wittor et al. 2017; Zhu et al. 2010).
The origin of the primordial magnetic field has been explored via different mechanisms, such as the density perturbation, the Biermann battery, etc. (Martin & Davis 1995; Ichiki et al. 2006; Naoz & Narayan 2013). In the present work, we investigate the seed vortex generation in the context of primordial black holes (PBHs), which were formed in the early Universe due to density fluctuations (Zel’dovich & Novikov 1966; Carr & Hawking 1974; Novikov et al. 1979) and which then grew by accreting gas or dark matter. Recently, using the magnetohydrodynamics (MHD) approximation, it has been shown that the magnetic field can be generated via the Biermann battery mechanism in a plasma due to the misalignment of pressure p and density n gradients, that is, ∇n−1 × ∇p ≠ 0 in an initially unmagnetized PBH accretion disk (Safarzadeh 2018). Once created, this seed magnetic field is amplified by nonlinear processes – such as the magneto-rotational instability, the α-Ω dynamo, etc. – and exponentially grows with time (Reinhardt & Rosenblum 1974). However, for a barotropic fluid obeying an equation of state p = p(n), the Biermann battery vanishes, which usually happens in most long-lived plasma systems (Mahajan & Yoshida 2011).
Here, we adopt the relativistic multifluid electro-vortical approach to investigate the primordial vortex generation near the PBH accretion disk. In this formalism, the relativistic plasma dynamics are expressed in terms of a hybrid field tensor, which is constructed by adding the electromagnetic and thermally modified flow field tensors together (Mahajan 2003). This has been utilized to investigate initial seed vortex generation, vortex evolution in quark-gluon plasmas produced in heavy ion collisions, and Beltrami equilibria in black hole accretion disks (Asenjo et al. 2013; Bhattacharjee et al. 2015a,b, 2018; Gao et al. 2014; Dash et al. 2018). It is found that in the absence of the Biermann battery, a novel relativistic drive due to spacetime curvature can generate seed vorticity. We extend the analysis here to investigate the generation of seed vorticity in PBHs. To simplify the analysis, we ignore the exact cause of accretion and assume the disk to be unmagnetized and without any turbulence. In addition to calculating the magnitude of the vorticity generation rate, we analyze the effect of the temperature profile and spacetime geometry on both the vortical field profile and the enstrophy (a measure of vorticity strength) generation rate in the PBH accretion disk. The paper is organized as follows: first, we discuss the basics of the electro-vortical formalism, and then we present the vortical dynamics of plasmas in a PBH accretion disk. Finally, we present our results and conclusions.
2. Relativistic plasma dynamics
2.1. Covariant Electro-vortical formulation
We present the vortical formalism of a relativistically hot electron fluid – with an arbitrary charge-neutralizing background – which can be obtained by taking the covariant divergence of the energy-momentum tensor. Unless stated explicitly, we chose G = c = 1 in this section. In the stationary axisymmetric spacetime (Kerr metric) described by (Harko & Lobo 2014; Choquet-Bruhat 2015),
a relativistic perfect fluid obeys the following equation of motion:
where Uμ is the four velocity of a plasma element, Fμν = ∇μAν − ∇νAμ is the Faraday tensor, and 𝒢 = (ρ + p)/mn is the thermodynamic factor (related to enthalpy density), with p and ρ being the pressure and mass density of the fluid, respectively. Additionally, m and n are the mass and number density of the plasma constituents. We assumed a local Maxwellian closure and pressure p = nkBT, where kB is the Boltzmann constant.
Equation (2) can be simplified by defining a new temperature-transformed flow field tensor (Bekenstein 1987; Mahajan 2003), Sμν := ∇μ(𝒢Uν) − ∇ν(𝒢Uμ); with this definition, Eq. (2) can be rewritten as (Bhattacharjee et al. 2015c)
where ℳμν = Fμν + (m/q)Sμν is the magnetofluid tensor and the entropy density σ for the fluid satisfies T∇νσ = (mn∇ν𝒢−∇νp)/n.
2.2. 3+1 splitting
The spatial part of the covariant plasma in Eq. (3) was obtained by breaking the spacetime into a family of fiducial space-like 3D differentially rotating hypersurfaces such that each hypersurface Σt is defined by a constant Boyer-Lindquist time coordinate t. Thus, the line element in Eq. (1) can be written as
where α is the lapse function, βi is the shift vector, and hij is the spatial metric (the induced metric) for the hypersurface Σt; collectively, α, βi, and hij form the Arnowitt-Deser-Misner (ADM) variables. In this 3+1 splitting, the 3D Eulerian velocity is written as V = 1/α (v + β), where vi is the ith component of the coordinate fluid velocity vi = dxi/dt and 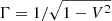 is the associated Lorentz factor.
is the associated Lorentz factor.
Under these ADM variables, the 3D equation of motion of the magnetofluid becomes (Bhattacharjee et al. 2018)
with ℰ and Ω as the generalized electric and magnetic fields expressed as:
Here, ℒβ(𝒢ΓV)) = [β, 𝒢ΓV], K = hμνKμν is the mean curvature and 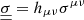 corresponds to the trace-free part of the extrinsic curvature tensor for the hypersurface Σt. To compute Kμν and σμν, one uses the following definitions:
corresponds to the trace-free part of the extrinsic curvature tensor for the hypersurface Σt. To compute Kμν and σμν, one uses the following definitions: 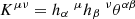 and σμν = Kμν − 1/3 hμνK, where θμν = ∇(μnν) with nμ = (1/α, −βi/α) being the unit normal vector to the hypersurface and nμnμ = −1.
and σμν = Kμν − 1/3 hμνK, where θμν = ∇(μnν) with nμ = (1/α, −βi/α) being the unit normal vector to the hypersurface and nμnμ = −1.
Finally, using the generalized Faraday’s law
we can cast Eq. (5) as the vorticity evolution equation
where we assume ∇ ⋅ β = 0 and 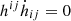 (Bhattacharjee et al. 2018).
(Bhattacharjee et al. 2018).
The first term on the right-hand side of Eq. (9) is the standard Biermann battery drive and the second is a new spacetime geometry-driven vorticity source. This equation, unlike the standard vorticity equation, has a unique structure because the plasma flow field is now endowed with an attribute associated with the inherent rotation (identified with the shift vector β) of background spacetime, which embedded in the Lorentz factor through the flow velocity V.
3. Vorticity generation in an accretion disk near a Kerr black hole
For a Kerr black hole, the metric elements in Boyer-Lindquist coordinates are
where Δr = (r2 + a2)−2rgr. It should be noted here that hij = gij and the parameters of the black hole are its mass M and normalized angular momentum a = J/Mc.
The shift vector is then given by
We note that the 3-gradient in the above equations is defined, for an arbitrary scalar function F, as
To simplify our analysis, we assumed vϕ ≫ vr, vθ in the equatorial plane θ = π/2. We further assumed that the plasma itself does not contribute to the background spacetime geometry, which indicates that, at a given radius, the azimuthal plasma velocity vϕ in the accretion disk can be approximated by the corresponding component of a test mass’s geodesic velocity. For vϕ, we therefore used the expression for the plasma velocity in the accretion disk
The lapse function is given by 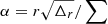 , where
, where 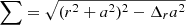 . Due to electromagnetic and thermal interactions, however, the plasma in the disk does not exactly follow a geodesic trajectory, and we will account for that in calculating the relativistic curvature drive below.
. Due to electromagnetic and thermal interactions, however, the plasma in the disk does not exactly follow a geodesic trajectory, and we will account for that in calculating the relativistic curvature drive below.
Since our formalism is based on a perfect fluid, we can also assume the plasma to be barotropic with its pressure depending on density only, which in terms of entropy and temperature can be written as σ(T) = f(T). Therefore, the Biermann battery term ∇T × ∇σ = 0 and the remaining source term is a purely spacetime curvature drive (kB/q)∇(αΓ−1)×∇T. Here, we assumed an equation of state T∇σ = ϵkB∇T, where ϵ is a constant of order unity. At this point, it is instructive to take the classical limit of Eq. (9), where we set V ≪ c, α ≈ 1, β = 0 and Γ ≈ 1. Therefore, under the barotropic assumption in classical ideal dynamics, both the Biermann battery and spacetime curvature drive vanish (i.e., the right-hand side of Eq. (9) is zero), which implies that vorticity cannot emerge from a zero initial value and that helicity is an invariant of the dynamics. On the other hand, in the relativistic limit, the right-hand side of Eq. (9) is non-zero even in a barotropic ideal fluid, which shows that vorticity can be generated due to the spacetime curvature drive.
The effective temperature profile of the disk from the balance of cooling and heating is given by (Novikov & Thorne 1973):
where σ is the Stefan-Boltzmann constant and 𝒟 and ℬ are relativistic factors. They are given by
and the inner-most circular orbit risco is obtained by solving the following equation in a co-rotating disk (Hobson et al. 2006):
This temperature profile is applicable to an axisymmetric disk, and it can be used to characterize deviations from geodesic circular motion in the disk. Here we adopted a spiral structure, also observed in protostellar disks (Lee et al. 2020), to approximate the plasma non-geodesic motion, and this implicitly creates an azimuthal dependence of the temperature profile in the disk.
A spiral orbit is defined by a radial coordinate 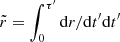 and azimuthal angle
and azimuthal angle 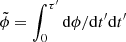 that are related through
that are related through ![$ \tilde{r}(\tau^\prime)=\tilde{r}_0\exp{[-\zeta \tilde{\phi}(\tau^\prime)}] $](/articles/aa/full_html/2020/10/aa39127-20/aa39127-20-eq27.gif) . Here ζ is the spiraling parameter, which measures the tightness of the orbit and can also be considered as a parameter characterizing the deviation from a stable circular orbit, and τ′ is the time parameter on which the plasma element evolves. The value of the spiraling parameter, in general, depends on different processes, such as viscosity, instabilities, and gravitational radiation from in-falling plasmas. Denoting the temperature
. Here ζ is the spiraling parameter, which measures the tightness of the orbit and can also be considered as a parameter characterizing the deviation from a stable circular orbit, and τ′ is the time parameter on which the plasma element evolves. The value of the spiraling parameter, in general, depends on different processes, such as viscosity, instabilities, and gravitational radiation from in-falling plasmas. Denoting the temperature 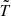 of the accreting plasma in the disk, we can approximate the azimuthal temperature gradient through
of the accreting plasma in the disk, we can approximate the azimuthal temperature gradient through 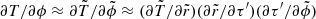 . Then, approximating
. Then, approximating 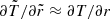 , we can write the poloidal (
, we can write the poloidal (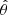 ) component of Eq. (9) as
) component of Eq. (9) as
The linear growth rate of vorticity obtained here from Eq. (9) remains valid as long as the dynamo term remains negligible relative to the terms on the other side of the equation during a dynamical time defined as 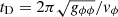 . One can compute the total vorticity generated over time τ′ ∼ tD at a given radius by multiplying Eq. (19) by τ′. This vorticity is crucial to seeding the amplification of ordered magnetic and flow field structure, which may occur via the standard processes mentioned in the introduction.
. One can compute the total vorticity generated over time τ′ ∼ tD at a given radius by multiplying Eq. (19) by τ′. This vorticity is crucial to seeding the amplification of ordered magnetic and flow field structure, which may occur via the standard processes mentioned in the introduction.
4. Results and discussion
Next we examine the parametric dependencies of the vorticity generation rate and their implications for vorticity and large-scale structural development in the early Universe. In Fig. 1, we plot the magnitude of the vorticity generation rate in the accretion disk near a 10 Ms black hole for several different values of the spin parameter a, all using a spiraling parameter ζ = 0.01, which corresponds with a small deviation from a closed circular orbit and an accretion rate 10−10 Ms year−1. For simplicity and ease of comparison with future figures, we kept the values of the spiraling parameter and accretion rate to be the same.
 |
Fig. 1. Vorticity generation rate as a function of radius for several different values of a, M = 10 Ms, ζ = 0.01, and an accretion rate of 1010 Ms year−1. |
The sharp drop in the vorticity generation rates seen in Fig. 1 occurs at the radius where the vorticity switches signs due to the temperature profile reaching its maximum. Such a peak in temperature is predicted in the thin disk model, which may not exist in the real disk model (Novikov & Thorne 1973; Shafee et al. 2008; Kulkarni et al. 2011). For higher values of a, we observe that the vorticity generation rate is higher for fixed r/rg values (apart from the sign change region) because the spacetime effect is stronger. As r → ∞, the vorticity generation rate for different spin parameters converges. For reference, the dashed line in the figure shows the semi-relativistic vorticity generation rate for a = 0.99, which is obtained by dropping the terms 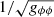 and
and 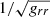 in Eq. (19). This indicates that the vorticity generation rates can be significantly overestimated if the appropriate spacetime metric elements are not incorporated into the calculation.
in Eq. (19). This indicates that the vorticity generation rates can be significantly overestimated if the appropriate spacetime metric elements are not incorporated into the calculation.
The vorticity generation rate in the accretion disk similarly has a strong dependence on the mass of the black hole. Figure 2 shows the magnitude of the vorticity generation rate for different black hole masses for a fixed a = 0.8 (and thus fixed risco) and masses ranging from 20 Ms to 100 Ms. The vorticity rate sharply decreases with increasing black hole mass, and, at a fixed r/rg, the vorticity rate scales as M−9/4. We correspondingly observe an almost two order of magnitude reduction at larger radii transitioning from 20 Ms to 100 Ms.
 |
Fig. 2. Vorticity generation rate as a function of radius for several different values of black hole masses with fixed a = 0.8, ζ = 0.01, and an accretion rate of 10−10 Ms year−1. An “x” mark is overlayed at the risco location for each curve. |
Next we examine the role of a in greater detail, as this determines the risco as well as the turning radius at which the sign of the vorticity generation rate changes. Changing the radius scale to units of risco and then comparing the vorticity generation rate at fixed radius r = 2 risco and mass M = 5 Ms for different a values (see blue curve of Fig. 3), we observe an increase in rate by multiple orders of magnitude as a increases from 0 toward 1. This is a more striking change than that observed in Fig. 1, now that the radius is normalized in an a-dependent manner. From a qualitative physics perspective, the vorticity generation rate is higher for low-mass, high-spin black holes likely because of the more extreme tidal forces present in the plasma around these black holes (Hobson et al. 2006).
 |
Fig. 3. Vorticity generation rate at fixed 2 risco (blue curve) and turning radius in rg (red curve) as a function of a for M = 5 Ms, ζ = 0.01, and an accretion rate of 10−10 M⊙ year−1. |
The red curve of Fig. 3 depicts the turning radius (now back in rg units) using the same 5 Ms black hole and spanning the same range in a values. This length scale could potentially be important for structure formation because the change in vorticity sign is expected to change the flow and magnetic field behavior. The curve suggests that this length scale contracts with increased spin rates, and thus small-scale structures may arise from the faster rotating black hole accretion disks and contribute to astrophysical formations on these scales at later points in the Universe’s evolution.
The final point of analysis considers the enstrophy of the plasma (defined as ∫Ω2dA with area element  ) in the accretion disk as a measure of energy associated with generalized vorticity. With this metric, we can consider which region of parameter space contributes the greatest enstrophy to the early Universe from the considered spacetime drive. Enstrophy, largely used as a measure of turbulence and dissipation in astrophysical systems, can have lasting implications for the subsequent evolution of PBHs as well as during the structure formation in the Universe (Vazza et al. 2017; Yoshida & Mahajan 2002). We chose to calculate the enstrophy generation rate dΩ2/dt = 2ΩdΩ/dt integrated over the area of the accretion disk (out to 40 rg, at which point the vorticity generation rate has dropped several orders of magnitude and there is not a substantial contribution). For Ω in the expression, we chose a reference timescale of tf = 2πrisco/vϕ for the point M = 200 Ms, a = 0 and assumed linear growth, as discussed at the end of Sect. 3. This provides a point of comparison between accretion disks, and we explore a, M space. Figure 4 is a color plot showing ∫dΩ2/dtdA across a select region of phase space along with contour lines to illustrate the trend more clearly.
) in the accretion disk as a measure of energy associated with generalized vorticity. With this metric, we can consider which region of parameter space contributes the greatest enstrophy to the early Universe from the considered spacetime drive. Enstrophy, largely used as a measure of turbulence and dissipation in astrophysical systems, can have lasting implications for the subsequent evolution of PBHs as well as during the structure formation in the Universe (Vazza et al. 2017; Yoshida & Mahajan 2002). We chose to calculate the enstrophy generation rate dΩ2/dt = 2ΩdΩ/dt integrated over the area of the accretion disk (out to 40 rg, at which point the vorticity generation rate has dropped several orders of magnitude and there is not a substantial contribution). For Ω in the expression, we chose a reference timescale of tf = 2πrisco/vϕ for the point M = 200 Ms, a = 0 and assumed linear growth, as discussed at the end of Sect. 3. This provides a point of comparison between accretion disks, and we explore a, M space. Figure 4 is a color plot showing ∫dΩ2/dtdA across a select region of phase space along with contour lines to illustrate the trend more clearly.
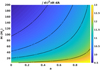 |
Fig. 4. Color plot of ∫dΩ2/dtdA in a, M space assuming linear growth over a fiducial timescale of τ = 2πrisco/vϕ for M = 200 Ms, a = 0 for Ω. Select contour lines are overlayed. |
The greatest integrated enstrophy generation rates are at the high spin rates of a ∼ 1 and the lowest black hole masses considered. Conversely, the lowest rates exist with the slowest spin rates and the most massive black holes considered here. This manner of comparison indicates more clearly what the other figures suggested: low-mass, fast-rotating black holes contribute the greatest amount to the spacetime-driven enstrophy generation in the early Universe. The relative abundance of the different black hole systems will also factor into the contributions to enstrophy from each region of phase space, but the 1:1 analysis is nevertheless very suggestive. Furthermore, given the smaller turning radius seen in the faster rotating and smaller black hole systems, the smaller length scales of vortical structure could therefore play more prominent roles in the ensuing magnetic field and plasma flow development in the Universe.
5. Conclusions
To summarize the study, we employed an electro-vortical formalism, combining the magnetic field and a thermally modified flow vorticity, to explore the spacetime curvature vorticity drive in accretion disks surrounding PBHs. This mechanism is inherent to the spacetime of the system and thus is not subject to the delicate gradient balance required for the Biermann battery. A fully general relativistic model is shown to be required in order to avoid overpredicting the vorticity generation rates.
Both increasing rotation rates and reducing black hole masses result in greater vorticity and enstrophy generation rates, the latter integrated throughout the accretion disk area to capture the full system’s role. All of the considered vorticity generation rate radial profiles reveal the presence of a turning radius at which the sign of the vorticity changes. This turning radius is relatively small in the considered low-mass, high-spin regime of phase space and thus may factor prominently into the length scales found in the early Universe (and ongoing) vortical structure. Following the amplification of a seed vortex, processes such as magnetic reconnection, magnetic buoyancy, outflows, and flares can act as means of transporting vortical field lines beyond the confines of the accretion disk, thus potentially inducing wide-spread vortex structure (magnetic and fluid vorticity) formation in the early Universe.
This work identifies and explores a potentially significant source of vorticity and vortical structure in the early Universe, but further analysis is required to understand the nonlinear evolution of vorticity and to incorporate more sophisticated models of accretion, turbulence, and thermal profiles relevant to this era. This can then result in a greater understanding of the interplay of the vorticity generation mechanisms in the early Universe and how large of a role PBHs played in structure formation.
Acknowledgments
The authors thank Justin C. Feng for helpful discussions and the anonymous referee for helping to clarify the explanations. CB acknowledges the New Faculty Scholarship and Research Program at New York Institute of Technology for funding this work.
References
- Akahori, T., Nakanishi, H., Sofue, Y., et al. 2018, PASJ, 70, R2 [Google Scholar]
- Asenjo, F. A., Mahajan, S. M., & Qadir, A. 2013, Phys. Plasmas, 20, 022901 [CrossRef] [Google Scholar]
- Bekenstein, J. D. 1987, ApJ, 319, 207 [CrossRef] [Google Scholar]
- Bhattacharjee, C., Das, R., & Mahajan, S. M. 2015a, Phys. Rev. D, 91, 123005 [CrossRef] [Google Scholar]
- Bhattacharjee, C., Das, R., Stark, D. J., & Mahajan, S. 2015b, Phys. Rev. E, 92, 063104 [CrossRef] [Google Scholar]
- Bhattacharjee, C., Das, R., & Mahajan, S. 2015c, Phys. Rev. D, 91, 064055 [CrossRef] [Google Scholar]
- Bhattacharjee, C., Feng, J. C., & Stark, D. J. 2018, MNRAS, 481, 206 [CrossRef] [Google Scholar]
- Blackman, E. G. 2001, MNRAS, 323, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Enqvist, K., & Olesen, P. 1996, Phys. Rev. D, 54, 1291 [NASA ADS] [CrossRef] [Google Scholar]
- Carr, B. J., & Hawking, S. W. 1974, MNRAS, 168, 399 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Choquet-Bruhat, Y. 2015, Introduction to General Relativity, Black Holes, and Cosmology (Oxford: Oxford University Press) [Google Scholar]
- Christopherson, A. J., Malik, K. A., & Matravers, D. R. 2011, Phys. Rev. D, 83, 123512 [CrossRef] [Google Scholar]
- Cutting, D., Hindmarsh, M., & Weir, D. J. 2020, Phys. Rev. Lett., 125, 021302 [CrossRef] [Google Scholar]
- Dash, A., Roy, V., & Mohanty, B. 2018, J. Phys. G: Nucl. Part. Phys., 46, 015103 [CrossRef] [Google Scholar]
- Gao, J.-H., Qi, B., & Wang, S.-Y. 2014, Phys. Rev. D, 90, 083001 [CrossRef] [Google Scholar]
- Harko, T., & Lobo, F. S. N. 2014, Galaxies, 2, 410 [CrossRef] [Google Scholar]
- Hobson, M. P., Efstathiou, G. P., & Lasenby, A. N. 2006, General Relativity: An Introduction for Physicists (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Ichiki, K., Takahashi, K., Ohno, H., Hanayama, H., & Sugiyama, N. 2006, Science, 311, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Jelic-Cizmek, G., Lepori, F., Adamek, J., & Durrer, R. 2018, JCAP, 2018, 006 [CrossRef] [Google Scholar]
- Klahr, H. H., & Bodenheimer, P. 2003, ApJ, 582, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Kulkarni, A. K., Penna, R. F., Shcherbakov, R. V., et al. 2011, MNRAS, 414, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, C.-F., Li, Z.-Y., & Turner, N. J. 2020, Nat. Astron., 4, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Mahajan, S. M. 2003, Phys. Rev. Lett., 90, 035001 [CrossRef] [Google Scholar]
- Mahajan, S., & Yoshida, Z. 1998, Phys. Rev. Lett., 81, 4863 [CrossRef] [Google Scholar]
- Mahajan, S., & Yoshida, Z. 2011, Phys. Plasmas, 18, 055701 [CrossRef] [Google Scholar]
- Martin, A. P., & Davis, A.-C. 1995, Phys. Lett. B, 360, 71 [CrossRef] [Google Scholar]
- Moffatt, H. K. 1969, J. Fluid Mech., 35, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Naoz, S., & Narayan, R. 2013, Phys. Rev. Lett., 111, A77 [Google Scholar]
- Novikov, I., & Thorne, K. S. 1973, Astrophysics of Black Holes [Google Scholar]
- Novikov, I., Polnarev, A., Starobinskii, A., & Zeldovich, I. B. 1979, A&A, 80, 104 [Google Scholar]
- Porter, D. H., Jones, T., & Ryu, D. 2015, ApJ, 810, 93 [CrossRef] [Google Scholar]
- Reinhardt, M., & Rosenblum, A. 1974, A&A, 34, 23 [Google Scholar]
- Safarzadeh, M. 2018, MNRAS, 479, 315 [CrossRef] [Google Scholar]
- Shafee, R., McKinney, J. C., Narayan, R., et al. 2008, ApJ, 687, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Steinhauer, L., & Ishida, A. 1998, Phys. Plasmas, 5, 2609 [CrossRef] [Google Scholar]
- Subramanian, K. 2019, Galaxies, 7, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Vacca, V., Murgia, M., Govoni, F., et al. 2018, MNRAS, 479, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Vazza, F., Jones, T. W., Brüggen, M., et al. 2017, MNRAS, 464, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Wittor, D., Jones, T., Vazza, F., & Brüggen, M. 2017, MNRAS, 471, 3212 [CrossRef] [Google Scholar]
- Yoshida, Z., & Mahajan, S. 2002, Phys. Rev. Lett., 88, 095001 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Zel’dovich, Y. B., & Novikov, I. 1966, AZh, 43, 758 [Google Scholar]
- Zhu, W., Feng, L.-L., & Fang, L.-Z. 2010, ApJ, 712, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Zucca, A., Li, Y., & Pogosian, L. 2017, Phys. Rev. D, 95, 063506 [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Vorticity generation rate as a function of radius for several different values of a, M = 10 Ms, ζ = 0.01, and an accretion rate of 1010 Ms year−1. |
| In the text | |
 |
Fig. 2. Vorticity generation rate as a function of radius for several different values of black hole masses with fixed a = 0.8, ζ = 0.01, and an accretion rate of 10−10 Ms year−1. An “x” mark is overlayed at the risco location for each curve. |
| In the text | |
 |
Fig. 3. Vorticity generation rate at fixed 2 risco (blue curve) and turning radius in rg (red curve) as a function of a for M = 5 Ms, ζ = 0.01, and an accretion rate of 10−10 M⊙ year−1. |
| In the text | |
 |
Fig. 4. Color plot of ∫dΩ2/dtdA in a, M space assuming linear growth over a fiducial timescale of τ = 2πrisco/vϕ for M = 200 Ms, a = 0 for Ω. Select contour lines are overlayed. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



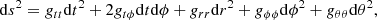
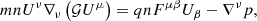
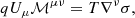
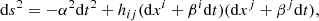
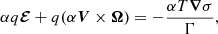
![$$ \begin{aligned}&\boldsymbol{\mathcal{E} }=\boldsymbol{E}-\frac{m}{\alpha q}{\boldsymbol{\nabla }}(\alpha \mathcal{G} \Gamma )-\frac{m}{q}\left[2\underline{\underline{{\sigma }}} \cdot (\mathcal{G} \Gamma {\boldsymbol{V}})+\frac{2}{3} K \mathcal{G} \Gamma {\boldsymbol{V}}\right]\nonumber \\&\qquad -\frac{m}{q\alpha }\left(\partial _t(\mathcal{G} \Gamma {\boldsymbol{V}}) -\mathcal{L} _{\boldsymbol{\beta }}(\mathcal{G} \Gamma {\boldsymbol{V}})\right);\end{aligned} $$](/articles/aa/full_html/2020/10/aa39127-20/aa39127-20-eq7.gif)