| Issue |
A&A
Volume 693, January 2025
|
|
|---|---|---|
| Article Number | A134 | |
| Number of page(s) | 5 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202452803 | |
| Published online | 10 January 2025 | |
Magnetic seed generation by plasma heat flux in accretion disks
1
Departmento de Física, Facultad de Ciencias, Universidad de Chile, Las Palmeras 3425, 7800003 Ñuñoa, Santiago, Chile
2
Facultad de Ingeniería y Ciencias, Universidad Adolfo Ibáñez, 7941169 Peñalolén, Santiago, Chile
⋆ Corresponding authors; nicolas.villarroel@ug.uchile.cl; felipe.asenjo@uai.cl; pablo.moya@uchile.cl
Received:
29
October
2024
Accepted:
19
November
2024
Context. Magnetic batteries are potential sources that may drive the generation of a seed magnetic field, even if this field is initially zero. These batteries can be the result of nonaligned thermodynamic gradients in plasmas, as well as of special and general-relativistic effects. So far, magnetic batteries have only been studied in ideal magnetized fluids.
Aims. We studied the nonideal fluid effects introduced by the energy flux in the vortical dynamics of a magnetized plasma in curved space-time. We propose a novel mechanism for generating a heat-flux-driven magnetic seed within a simple accretion disk model around a Schwarzschild black hole.
Methods. We used the 3 + 1 formalism for the splitting of the space-time metric into space-like and time-like components. We studied the vortical dynamics of a magnetized fluid with a heat flux in the Schwarzschild geometry in which thermodynamic and hydrodynamic quantities are only dependent on the radial coordinate. Assuming that the magnetic field is initially zero, we estimated the linear time evolution of the magnetic field due to the inclusion of nonideal fluid effects.
Results. When the thermodynamic and hydrodynamic quantities vary only radially, the effect of the coupling between the heat flux, the space-time curvature, and the fluid velocity acts as the primary driver for an initial linearly time-growing magnetic field. The plasma heat flux completely dominates the magnetic field generation at a specific distance from the black hole, where the fluid vorticity vanishes. This distance depends on the thermodynamical properties of the Keplerian plasma accretion disk. These properties control the strength of the nonideal effects in the generation of seed magnetic fields.
Conclusions. We find that heat flux is the main driver of a seed magnetic field in black hole accretion disks if the geometry, plasma dynamics, and thermodynamics share the same axial symmetry. This suggests that nonideal fluid effects may play a major role in the magnetization of astrophysical plasmas.
Key words: accretion, accretion disks / magnetic fields / plasmas
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Large-scale magnetic fields appear to be ubiquitous in the known physical universe. Dynamo mechanisms can significantly amplify a small magnetic field, but cannot do so if the field is initially absent. This has led to growing interest in exploring new methods for creating small magnetic fields that can act as seeds for these large-scale structures. In recent years, magnetic seed generation through mechanisms such as the Weibel instability (Zhang et al. 2020) and the Biermann battery (Pilgram et al. 2022) has been successfully observed in laboratory plasmas.
In this article, we explore the generation of a seed magnetic field through a heat-flux-induced battery mechanism in the plasma surrounding a spherically symmetric, static black hole. We will consider a nongravitating plasma fluid with heat flux, which evolves in a background curved space-time defined by the Schwarzschild metric. Our treatment of this system follows the framework of the unified magnetofluid theory (Mahajan 2003), which describes the coupling between plasma hydrodynamics, thermodynamics, and electrodynamics in curved spacetime. We also adopted the 3 + 1 formalism for the foliation of space-time (Arnowitt et al. 2008), which allows the separation of four-dimensional vectorial and tensorial quantities into space-like and time-like components in the reference frame of a Eulerian (or fiducial) observer (Gourgoulhon 2012).
In this case, its stress-energy tensor, Tμν, is
where Thμν accounts for the energy transfer within the fluid due to the heat flux vector, qμ (Misner et al. 2017). Here, c is the speed of light, h = ρ + p is related to the fluid’s enthalpy density, ρ is the mass-energy density, p is the thermodynamic pressure, and gμν is the metric of the particular geometry. The plasma fluid four-velocity is Uμ = Γ(c, v), with v being the plasma three-velocity, and Γ is the general-relativistic Lorentz factor. For simplicity, the heat flux term is the only nonideal component of the magnetofluid’s stress-energy tensor that we considered. Besides, the plasma fluid obeys the continuity equation ∇μ(nUμ) = 0, where n is the plasma density, and ∇μ is a covariant derivative. The whole system is coupled to the curved space-time Maxwell equations ∇νFμν = (4π/c)Jμ and ∇ν(⋆Fμν) = 0, where Fμν is the electromagnetic tensor, ⋆Fμν = (1/2)ϵμνρσFρσ is its Hodge dual, and Jμ = qnUμ is the fluid’s four-current, with q being the charge of the plasma species.
The equation of motion governing the plasma dynamics is
By introducing the quantity f = h/mn, we defined the fully antisymmetric tensor Sμν = [∇μ(fUν)−∇ν(fUμ)]/c. By incorporating Sμν in Eq. (2), we obtained (Mahajan 2003; Asenjo et al. 2013)
where Mμν = Fμν + (m/q)Sμν is the fully antisymmetric magnetofluid tensor (Mahajan 2003), and σ is the fluid entropy per baryon obtained from the first law of thermodynamics dρ = (h/n)dn + nTdσ. The inclusion of the analogous electromagnetic tensor, Sμν, resulting from the antisymmetric gradient of the enthalpy flux, fUμ, is not arbitrary. This quantity accounts for the coupling between the magnetic vector potential, Aμ, and the fluid’s momentum through the generalized momentum, Πμ = (f/c2)mUμ + (q/c)Aμ, which results in an equation shared by the time evolution of the magnetic field and fluid vorticity in the classical derivation of the Biermann battery (Biermann 1950; Kulsrud 2005).
It is worth mentioning that the mathematical framework of the unified magnetofluid formalism is not unique when it comes to the study of coupling between hydrodynamics, electrodynamics, and general relativity. Khanna (1998b) derived the magnetohydrodynamic equations of a two-component plasma in an axisymmetric motion around a Kerr black hole by employing the 3 + 1 formalism. Following this work, Khanna (1998a) showed that gravitational contributions to the partial pressure of electrons are able to sustain currents that work as a gravitomagnetic Biermann battery in Kerr space-time. A different approach was taken by Contopoulos & Kazanas (1998), who proposed Poynting-Robertson radiation drag as a source for an azimuthal current that induces poloidal magnetic fields in an electron-ion plasma. This mechanism was dubbed the Cosmic Battery and has been discussed extensively in the context of Kerr black hole accretion disks, including its general-relativistic effects (Koutsantoniou & Contopoulos 2014; Sadowski et al. 2017; Contopoulos et al. 2018).
2. Equation for general-relativistic vorticity
Eq. (3) is the starting point for obtaining the seed magnetic field from the contribution of the plasma heat flux. For this, we analyzed this equation in the background Schwarzschild space-time. We used a 3 + 1 decomposition of this metric in terms of the lapse function α, the future-oriented unit four-vector as nμ = (1/α, 0, 0, 0), and the space-like projector, γμν = gμν + nμν, such that nμγμν = 0. The set {α, nμ, γμν} is often referred to as the ADM variables of the foliation. The components of the metric can be inferred from the Schwarzschild line element, ds2 = −α(r)2dt2 + α(r)−2dr2 + r2dΩ2, where Ω is the spherical solid angle. Since the Schwarzschild space-time possesses no extrinsic curvature, the gradient of the unit-time-oriented dual 1-form is given by ∇νnμ = −nνaμ, where aμ = nν∇νnμ = ∂μα/α. The above formalism allows the decomposition of physical quantities as 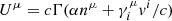 and Mμν = nμξν − nνξμ − ϵμνρσΩρnσ (Asenjo et al. 2013). The components
and Mμν = nμξν − nνξμ − ϵμνρσΩρnσ (Asenjo et al. 2013). The components
represent generalized electric-like and magnetic-like fields, respectively, in the unified magnetofluid formalism, the latter being referred to as the plasma’s generalized vorticity. In vectorial notation, these space-like four-vectors are given by
where E and B are the electric and magnetic fields, respectively (Asenjo et al. 2013).
Using the above 3 + 1 decomposition, we could calculate the space-like projection of Eq. (3) by contraction with 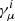 . Thus, we obtained
. Thus, we obtained
Here, the gradients, ∇i, were used interchangeably with the space-like projection of the four-gradient, 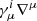 , since for a nonrotating geometry ni = 0, and therefore
, since for a nonrotating geometry ni = 0, and therefore 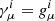 .
.
The last term on the right-hand side contains new, nonideal effects on describing the generalized vorticity dynamics. Explicit calculation of it, using the definitions in (1a) and (1b), yields 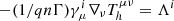 , with
, with
We used the properties of Mμν to find the dynamical behavior of the general-relativistic vorticity. The governing equations could be obtained from the constraint 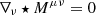 , where ⋆Mμν = Ωμnν − Ωνnμ − ϵμνρσξρnσ is the Hodge dual of the magnetofluid tensor. Projecting this equation onto nμ results in the generalized magnetic Gauss’s law, (∇μ − aμ)Ωμ = 0. On the other hand, its space-like projection becomes
, where ⋆Mμν = Ωμnν − Ωνnμ − ϵμνρσξρnσ is the Hodge dual of the magnetofluid tensor. Projecting this equation onto nμ results in the generalized magnetic Gauss’s law, (∇μ − aμ)Ωμ = 0. On the other hand, its space-like projection becomes
which is completely equivalent to the analogous equation found in Asenjo et al. (2013). Here, we have related the zero-gradient (∇ϵ = 0) covariant Riemann volume form, ϵ, to the Levi-Civita symbol, ε, as 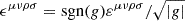 . We thereby obtained the vorticity equation by replacing Eq. (8) in Eq. (10), to obtain
. We thereby obtained the vorticity equation by replacing Eq. (8) in Eq. (10), to obtain
In vector notation, Eq. (11) is equivalent to ∂Ω/∂t − ∇ × (v × Ω) = ∇ × (T∇σ/(qΓ)+Λ), where the three-vectors and three-gradients are obtained by taking the space-like projection of the corresponding four-vectors and covariant derivatives, respectively. The previous expression contains three feasible magnetic seed drives. The first is the relativistic baroclinic drive (Biermann battery) corrected by space-time curvature, ΞB = ∇T × ∇σ/(qΓ), which can produce a seed magnetic field under particular configurations of the plasma’s thermodynamic properties in Schwarzschild space-time (Asenjo et al. 2013). The second is the relativistic drive, ΞR = −T ∇Γ × ∇σ/(qΓ2) (Mahajan & Yoshida 2010; Asenjo et al. 2013), which can generate magnetic fields through the interaction of relativity and plasma thermodynamics. The last one, the heat flux drive,
is the main result of this work. This nonlinear drive, being the curl of vector (9), has a completely different nature compared to the others. Below, we show that in the most simple scenario for a plasma in an accretion disk around a Schwarzschild black hole, the only possibility of generating a seed magnetic field is the action of the heat flux drive.
3. Vorticity seed generation by heat flux in accretion disks
For a plasma in a thin accretion disk (in equatorial plane θ = π/2) around a Schwarzschild black hole, the lapse function, α(r) = (1 − rS/r)1/2, depends only on the radial coordinate, r. Here, we have defined the Schwarzschild radius, rS = 2GM/c2, with M being the black hole’s mass, and G the universal gravitational constant. Also, ![$ \gamma_{ij}={\alpha^{-2}}\delta^{r}_{i}\delta^{r}_{j}+r^2[\delta^{\theta}_{i}\delta^{\theta}_{j}+\sin^2\theta\delta^{\phi}_{i}\delta^{\phi}_{j}] $](/articles/aa/full_html/2025/01/aa52803-24/aa52803-24-eq21.gif) .
.
The simplest scenario consists of every single plasma variable depending only on the radial Schwarzschild coordinate. In this case, it is straightforward to realize that the baroclinic drive ΞB = 0, and the relativistic drive ΞR = 0 (as all gradients are parallel). Only the heat flux drive (12) does not vanish under this simple assumption (as shown below). Of course, one can invoke more sophisticated dynamical plasma scenarios where ΞB or ΞR do not vanish in accretion disks. For example, in Asenjo et al. (2013), a nonradial plasma temperature profile was assumed, and in Bhattacharjee et al. (2015), the orbit of the particles in the accretion plasma disk was not stable, but inwardly spiraled into the event horizon. In those cases, the heat flux drive will also contribute.
Although the plasma orbits in accretion disks are not in general stable (Vietri 2008), this process is expected to occur very slowly. Therefore, for this work, we considered the plasma to be in stable Keplerian orbits in the black hole equatorial plane. We also return to the simplest assumption, that all plasma quantities depend on radial direction only; thus, the baroclinic and relativistic drives vanish identically. We thereby considered only Keplerian orbits with an angular velocity 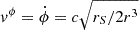 . Since v2 ≈ (rvϕ)2, we obtain the Lorentz factor Γ(r) = (1 − rph/r)−1/2, which allows any orbit beyond r ≥ rph, where rph = 3rS/2 is the radius of the photosphere, describing the innermost unstable circular orbit for massless particles.
. Since v2 ≈ (rvϕ)2, we obtain the Lorentz factor Γ(r) = (1 − rph/r)−1/2, which allows any orbit beyond r ≥ rph, where rph = 3rS/2 is the radius of the photosphere, describing the innermost unstable circular orbit for massless particles.
To evaluate the heat flux drive, we first assumed that the heat flux 1-form, qμ, has components given by the general-relativistic Tolman’s law (Misner et al. 2017):
where the temperature-dependent collision-driven thermal conductivity coefficient is given by the Spitzer-Härm relation, κ(T) = κ0(T/T0)5/2 (Spitzer & Härm 1953), where κ0 and T0 are dimensional constants yet to be determined. We note that the thermal conduction coefficient, κ0, has been normalized to the referential temperature, T0, and therefore has cgs units of [gram ⋅ centimeter ⋅ Kelvin−1 ⋅ second−3], which are those of the thermal conduction coefficient in Fourier’s law of heat conduction. A conductive heat flux of this kind has often been utilized in the literature regarding general-relativistic plasmas and fluids (Misner et al. 2017; Tanaka & Menou 2006; Chandra et al. 2015; Schobert et al. 2019).
The temperature is considered to be a product of the accretion disk’s blackbody radiation; T = (ℱ(r)/σSB)1/4, where σSB is the Stefan-Boltzmann constant and ℱ(r) is the time-averaged radiation flux (Thorne 1974), which is given by 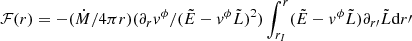 (Page & Thorne 1974). Here, Ṁ is the black hole’s accretion rate, which is assumed to be constant,
(Page & Thorne 1974). Here, Ṁ is the black hole’s accretion rate, which is assumed to be constant, 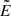 and
and 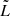 are the disk’s specific energy-at-infinity and specific angular momentum, respectively, and rI = 3rS is the radius of the innermost stable circular orbit (ISCO). The analytical integral expression for temperature can be approximated by
are the disk’s specific energy-at-infinity and specific angular momentum, respectively, and rI = 3rS is the radius of the innermost stable circular orbit (ISCO). The analytical integral expression for temperature can be approximated by
where β and λ characterize the power-law behavior of the temperature. Here, the constant T0[K] encloses the constants of the blackbody radiation temperature derived by Thorne (1974). This behavior is based on analytical expressions for the surface temperature of matter in an accretion disk around a black hole with β = 3/4 and λ = 1/4 (Shakura & Sunyaev 1973; Page & Thorne 1974; Bhattacharyya et al. 2000).
The plasma density in the accretion disk can be obtained from the continuity equation 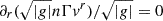 . To compute the value of the density, we approximate the orbits as spirals given by r(ϕ) = r0e−ζϕ, where ζ is a function of r but can be considered as a constant for very tightly bound orbits (Bhattacharjee et al. 2015). We then take the limit ζ → 0, which vanishes vr. The resulting plasma density satisfies
. To compute the value of the density, we approximate the orbits as spirals given by r(ϕ) = r0e−ζϕ, where ζ is a function of r but can be considered as a constant for very tightly bound orbits (Bhattacharjee et al. 2015). We then take the limit ζ → 0, which vanishes vr. The resulting plasma density satisfies
where n0 is a dimensional constant with units of [cm−3]. By replacing (13a), (13b), (14), and (15) in Eq. (9), we obtain that the only nonvanishing term is in the azimuthal direction
where
We note that (16) is unavoidably singular at the black hole singularity and at r = rph, due to the appearance of the Lorentz factor in both (17) and the ratio vϕ(r)/n(r). However, the function d(r) that arises as a consequence of the factor (1 − rI/r)λ in (14) implies that the vorticity obtained from (11) will be singular at the ISCO for any λ < 6/7, for which the domain of the final solution will be limited to that of stable orbits only.
In general, the curl of vector (16) does not vanish, and then the heat flux drive (12) does indeed produce an initial temporal variation of the generalized vorticity in the polar direction.
Since we are interested in studying the generation of magnetic fields, it is useful to explicitly separate the generalized vorticity into the magnetic field, which will initially be null, and the fluid vorticity, which will be nonzero in our model. Because of the initial lack of electromagnetic fields in (2), we considered an initial equilibrium state in which the time derivatives of the fluid velocity, particle density, temperature, and pressure were zero. The second term in the left-hand side of (11) is zero for our initial conditions, and we are left with the following equation for the time evolution of the magnetic field
Here, the magnetic field is multiplied by r to obtain a result in magnetic field units, since the choice of a spherical coordinate basis implies that the angular components of vectors are divided by r.
Because of the inclusion of a heat flux, the system will be unstable, as energy will be injected into it. The time derivative of the enthalpy-related quantity, f, can be obtained from the energy equation Uμ∇νTμν = 0, which yields ∂tf = [ − (1/Γ)∇νqν + (Γv2/rc2)qr]/mn(r).
Following Asenjo et al. (2013), if the magnetic field is zero at the initial instant, t = t0, its time evolution can be approximated to first order as ∂tBi(t)|t = t0t = ς ≈ Bi(ς)/ς, where ς = r/|v|α ≈ 1/vϕα is the timescale for a linear generation of a magnetic seed. Considering initially stable orbits and, therefore, a total axial symmetry of the system, then the baroclinical Biermann battery and the general-relativistic drive both vanish (Asenjo et al. 2013). Under these conditions, a careful treatment of (11) yields the magnetic seed that is generated in a time interval ς:
Equation (21) is solved numerically for β = 3/4, λ = 1/4, which indicates a blackbody radiation-dominated temperature, as well as n0 = 1010cm−3, T0 = 106K (Bhattacharyya et al. 2000; Narzilloev & Ahmedov 2022) and κ0 = 109 g ⋅ s−3 ⋅ K−1, following Meyer-Hofmeister & Meyer (2006). The charge and mass are taken to be those of the electron. We focused on solutions for r < 20rs, as this is the region where gravity is strong and the effects of the generalized vorticity batteries are most important. Fig. 1 displays the strength in Gauss of the magnetic field generated in the time interval, ζ, in the equatorial plane, as a function of r/rS. For this choice of the parameters β and λ, the poloidal magnetic field generated in a time interval, ζ, diverges at rI and becomes 0 at r0B/rS = 9.6. Similarly, the time derivative of the enthalpy-weighted fluid vorticity, ∂ω/∂t, where ω = ∇ × (fΓv), vanishes at r0ω/rS = 9.8. The heat flux battery, Ξq, becomes zero at r0q/rS = 11.9.
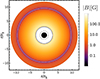 |
Fig. 1. Magnitude of the magnetic field produced in the equatorial plane in a time interval, ς. The shaded area represents the inside of the horizon, the dashed line indicates the photosphere, the solid black line is the ISCO, and the solid white line is the radius at which the generated magnetic field passes through zero and inverts its sign. |
The vanishing radii for B, ∂ω/∂t, and Ξq are strongly dependent on β and λ, which in this work were chosen according to values commonly associated with black hole accretion disks. In general, an increment in λ will increase the values of r0B, r0ω, and r0q, while an increase in β has the opposite effect.
Fig. 2a displays the amplitude of the magnetic field, |B|, generated in a time interval, ζ, as well as the absolute values of the linear-time evolution of the heat flux battery, ζ|Ξq|, and fluid vorticity, ζ(m/q)|∂ω/∂t|, in magnetic field units (first and second terms in Eq. (21), respectively), all as functions of r/rs. Fig. 2b depicts the ratio, |Ξq|/(m/q)|∂ω/∂t|, between the heat flux battery and the time evolution of the fluid vorticity. Both figures are displayed to show that, since r0ω ≠ r0q, there is a domain for which the magnetic field generated in an initial time interval, ζ, will be driven by the heat flux battery. This domain is characterized by having |Ξq|/(m/q)|∂ω/∂t|> 1, and for this case study, the latter inequality is satisfied for 3 < r/rS < 3.2 and 9.6 < r/rS < 9.9. As with the vanishing radii, the location of this domain is highly dependent on the particular choice of the parameters β and λ in (14).
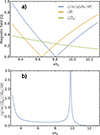 |
Fig. 2. Radial domain of heat-flux-induced seed magnetic field. (a) Magnitude of the linear-time evolution of the magnetic field, |B|, heat flux battery, ζ|Ξq|, and fluid vorticity, ζ(m/q)|∂ω/∂t|, as functions of r/rS. (b) Ratio of the strengths of the heat flux battery and the time evolution of the fluid vorticity as a function of r/rS. |
Fig. 3 displays the behavior of the heat flux battery, Ξq, as a function of r/rS. As previously discussed, this quantity diverges at rI. The value r0q at which Ξq vanishes is where this battery switches its sign. For r > r0q, Ξq reaches a local maximum and vanishes as r/rS → ∞. The asymptotic behavior of this quantity is a consequence of the choice of the temperature profile in (14).
 |
Fig. 3. Generalized vorticity generated by the heat flux battery in a time interval, ζ, as a function of r/rS. |
4. Discussion
In this article, we show that the inclusion of nonideal thermodynamic effects in the description of a charged fluid orbiting a nonmagnetized black hole contributes to the generation of a magnetic field in the system. In particular, if the system is axisymmetric and well described by Keplerian dynamics, only the novel heat flux battery, Ξq, induces the time evolution of initially nonexistent generalized vorticity, since both the Biermann (ΞB) and the relativistic (ΞR) batteries vanish because of this symmetry (see Khanna 1998a and Asenjo et al. 2013 for further discussion on the role of the symmetric properties of the plasma and geometry on the generation of magnetic fields). To our knowledge, this is the first time that nonideal thermodynamic effects are considered in deriving a general-relativistic generalized vorticity equation for magnetic fields in plasmas. However, heat flux has been widely considered in general-relativistic hydrodynamics and black hole accretion disk theory, both from the point of view of physics and of astrophysics Page & Thorne (1974), Misner et al. (2017), Meyer-Hofmeister & Meyer (2006).
By proposing a simple model of a thin plasma disk with no accretion and a conduction-dominated heat flux, we demonstrate that the heat flux battery, Ξq, is the only initial source for the time evolution of the magnetofluid’s generalized vorticity. In particular, if the system’s magnetic field is initially zero, inclusion of the heat flux is directly responsible for generating a magnetic seed at small temporal scales. We show that the heat flux battery is the primary source of the magnetic field in the region 9.6 < r/rS < 9.9, which is where our assumptions regarding the model are most valid. Our model can be extended by considering more sophisticated velocity profiles that include disk accretion and by addressing the full nonlinear time evolution of the magnetofluid vorticity equation. The role of accretion on the time evolution of the magnetic field has been discussed extensively in the context of the Cosmic Battery (Contopoulos et al. 2015).
It is important to note that the use of the Spitzer-Härm thermal conductivity model is only valid in an electron-proton plasma. We are thus working over that supposition ab initio. The heat flux discussed in this article is driven mainly by electrons and results from the gradients of the red-shifted radiation temperature, 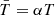 , of the disk in (13b). The coupling between the plasma velocity and the energy flux contributes to a nonzero Λϕ in (9), which gives rise to an azimuthal generalized electric field in (8). The generalized electric field, in turn, can be related to an azimuthal generalized current through an analogous Ohm’s law in the unified magnetofluid formalism, which draws parallelisms to the Cosmic Battery proposed by Contopoulos & Kazanas (1998). In the Cosmic Battery, the radiation temperature is also the source of an azimuthal current through the aberration of the radiation force acting on the electrons due to the azimuthal motion of the plasma (see Koutsantoniou & Contopoulos (2014) for a detailed discussion).
, of the disk in (13b). The coupling between the plasma velocity and the energy flux contributes to a nonzero Λϕ in (9), which gives rise to an azimuthal generalized electric field in (8). The generalized electric field, in turn, can be related to an azimuthal generalized current through an analogous Ohm’s law in the unified magnetofluid formalism, which draws parallelisms to the Cosmic Battery proposed by Contopoulos & Kazanas (1998). In the Cosmic Battery, the radiation temperature is also the source of an azimuthal current through the aberration of the radiation force acting on the electrons due to the azimuthal motion of the plasma (see Koutsantoniou & Contopoulos (2014) for a detailed discussion).
The final results shown in this article depend strongly on the particular choices of the velocity and temperature profiles and the heat flux considered in our model. The underlying physical consequences of these results, however, are far-reaching. Eqs. (9) and (11) show that the only restriction for this new generalized vorticity battery to exist is that ∇jΛk ≠ 0, which can be achieved by a wide variety of functions describing the velocity profile and heat flux within the accretion disk. Thus, our results are not limited to the particular magnetofluid configuration treated as an example in this article. On the contrary, this general result should be applied to any study that explores the generation of magnetic fields via a Biermann battery-like mechanism in both classical and relativistic regimes where energy fluxes are present, whether these fluxes are due to convection, radiation, conduction, or even a particle flux through the lens of the mass-energy equivalence (Landau et al. 1959). This implies that our results can be further extended by including other possible sources of magnetic field generation, as well as black hole rotation, accretion, and explicit time dependence of thermodynamic and hydrodynamic quantities.
Acknowledgments
We thank Prof. Kinwah Wu (UCL-MSSL) for helpful discussions. N.V.S. is supported by ANID, Chile, through National Doctoral Scholarship N° 21220616. F.A.A thanks to FONDECYT grant No. 1230094 that partially supported this work. P.S.M is supported by FONDECYT Grant No. 1240281, and by the Research Vice-Rectory of the University of Chile (VID) through Grant ENL08/23.
References
- Arnowitt, R., Deser, S., & Misner, C. W. 2008, General Relativ. Gravit., 40, 1997 [CrossRef] [Google Scholar]
- Asenjo, F. A., Mahajan, S. M., & Qadir, A. 2013, Phys. Plasmas, 20, 022901 [NASA ADS] [CrossRef] [Google Scholar]
- Bhattacharjee, C., Das, R., & Mahajan, S. 2015, Phys. Rev. D, 91, 123005 [NASA ADS] [CrossRef] [Google Scholar]
- Bhattacharyya, S., Thampan, A. V., Misra, R., & Datta, B. 2000, ApJ, 542, 473 [NASA ADS] [CrossRef] [Google Scholar]
- Biermann, L. 1950, Zeitschrift für Naturforschung A, 5, 65 [CrossRef] [Google Scholar]
- Chandra, M., Gammie, C. F., Foucart, F., & Quataert, E. 2015, ApJ, 810, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Contopoulos, I., & Kazanas, D. 1998, ApJ, 508, 859 [Google Scholar]
- Contopoulos, I., Nathanail, A., & Katsanikas, M. 2015, ApJ, 805, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Contopoulos, I., Nathanail, A., Sadowski, A., Kazanas, D., & Narayan, R. 2018, MNRAS, 473, 721 [CrossRef] [Google Scholar]
- Gourgoulhon, E. 2012, Lecture Notes in Physics, 3+1 Formalism in General Relativity, 1st edn. (Berlin: Springer), 846 [CrossRef] [Google Scholar]
- Khanna, R. 1998a, MNRAS, 295, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Khanna, R. 1998b, MNRAS, 294, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Koutsantoniou, L. E., & Contopoulos, I. 2014, ApJ, 794, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Kulsrud, R. M. 2005, Plasma Physics for Astrophysics (Princeton University Press) [Google Scholar]
- Landau, L. D., Lifshitz, E. M., Sykes, J. B., & Reid, W. H. 1959, Fluid Mechanics (Oxford, England: Pergamon Press) [Google Scholar]
- Mahajan, S. M. 2003, Phys. Rev. Lett., 90, 035001 [NASA ADS] [CrossRef] [Google Scholar]
- Mahajan, S. M., & Yoshida, Z. 2010, Phys. Rev. Lett., 105, 095005 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer-Hofmeister, E., & Meyer, F. 2006, A&A, 449, 443 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Misner, C. W., Thorne, K. S., & Wheeler, J. A. 2017, Gravitation (Princeton University Press) [Google Scholar]
- Narzilloev, B., & Ahmedov, B. 2022, Symmetry, 14, 1765 [NASA ADS] [CrossRef] [Google Scholar]
- Page, D. N., & Thorne, K. S. 1974, ApJ, 191, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Pilgram, J. J., Adams, M. B. P., Constantin, C. G., et al. 2022, High Power Laser Sci. Eng., 10, e13 [NASA ADS] [CrossRef] [Google Scholar]
- Sadowski, A., Wielgus, M., Narayan, R., et al. 2017, MNRAS, 466, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Schobert, B. N., Peeters, A. G., & Rath, F. 2019, ApJ, 881, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Spitzer, L., & Härm, R. 1953, Phys. Rev., 89, 977 [Google Scholar]
- Tanaka, T., & Menou, K. 2006, ApJ, 649, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Thorne, K. S. 1974, ApJ, 191, 507 [Google Scholar]
- Vietri, M. 2008, Foundations of high-energy astrophysics (University of Chicago Press) [CrossRef] [Google Scholar]
- Zhang, C., Hua, J., Wu, Y., et al. 2020, Phys. Rev. Lett., 125, 255001 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Magnitude of the magnetic field produced in the equatorial plane in a time interval, ς. The shaded area represents the inside of the horizon, the dashed line indicates the photosphere, the solid black line is the ISCO, and the solid white line is the radius at which the generated magnetic field passes through zero and inverts its sign. |
| In the text | |
 |
Fig. 2. Radial domain of heat-flux-induced seed magnetic field. (a) Magnitude of the linear-time evolution of the magnetic field, |B|, heat flux battery, ζ|Ξq|, and fluid vorticity, ζ(m/q)|∂ω/∂t|, as functions of r/rS. (b) Ratio of the strengths of the heat flux battery and the time evolution of the fluid vorticity as a function of r/rS. |
| In the text | |
 |
Fig. 3. Generalized vorticity generated by the heat flux battery in a time interval, ζ, as a function of r/rS. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



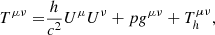
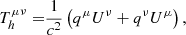
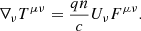
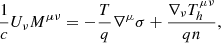
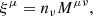
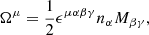
![$$ \begin{aligned} \boldsymbol{\xi }&=\boldsymbol{E}-(m/\alpha q)[\boldsymbol{\nabla }(f\alpha ^2\Gamma )+\partial _t (f\Gamma \boldsymbol{v})],\end{aligned} $$](/articles/aa/full_html/2025/01/aa52803-24/aa52803-24-eq8.gif)
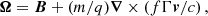
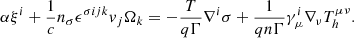
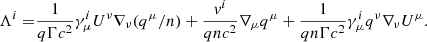
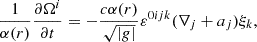
![$$ \begin{aligned}&\frac{\partial \Omega ^i}{\partial t}-\varepsilon ^{0ijk}\varepsilon _{0k\ell m}\nabla _jv^{\ell }\Omega ^{m}=\frac{c\alpha (r)}{\sqrt{|g|}}\varepsilon ^{0ijk}\nabla _j\Big [\frac{T\nabla _{k}\sigma }{q\Gamma }+\Lambda _{k}\Big ]. \end{aligned} $$](/articles/aa/full_html/2025/01/aa52803-24/aa52803-24-eq19.gif)
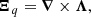
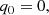
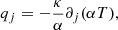
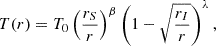
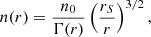
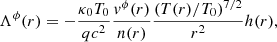
![$$ \begin{aligned} h(r)&=-\left(2-\frac{\Gamma ^2(r)}{2}-\frac{7}{2}\left[\beta -\frac{\lambda }{2}d(r)\right]\right)k(r)\nonumber \\&+\frac{\lambda }{4}d(r)\left(d(r)+1\right)+\left(\frac{1}{2}+\beta -\frac{\lambda }{4}\big [3+d(r)\big ]\right) \frac{r_S}{r} ,\end{aligned} $$](/articles/aa/full_html/2025/01/aa52803-24/aa52803-24-eq32.gif)
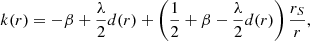
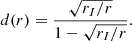
![$$ \begin{aligned} r\partial _t B^{\theta }&=-c\alpha (r)[\partial _r\Lambda ^{\phi }+\frac{1}{r}\Lambda ^{\phi }]\nonumber \\&\quad +r\Big (\frac{m\alpha (r)}{qc}\Big )[\partial _r(\Gamma v^{\phi }\partial _t f)+\frac{1}{r}(\Gamma v^{\phi }\partial _t f)]. \end{aligned} $$](/articles/aa/full_html/2025/01/aa52803-24/aa52803-24-eq35.gif)
![$$ \begin{aligned} r B^{\theta }(t_0)\approx&-\frac{c}{v^{\phi }}[\partial _r\Lambda ^{\phi }+\frac{1}{r}\Lambda ^{\phi }]\nonumber \\&+r\Big (\frac{m}{qcv^{\phi }}\Big )[\partial _r(\Gamma v^{\phi }\partial _t f)+\frac{1}{r}(\Gamma v^{\phi }\partial _t f)]. \end{aligned} $$](/articles/aa/full_html/2025/01/aa52803-24/aa52803-24-eq36.gif)