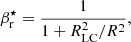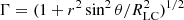© B. Cerutti et al. 2020

1. Introduction

Large-scale current sheets are generic features of planetary and stellar magnetospheres. Their formation can be externally driven, as in the Earth magnetotail shaped by the Solar wind, or internally driven by the intrinsic magnetic activity of the star or by the rapid rotation of the magnetosphere, like in Jupiter. Perhaps the most extreme example of rotationally driven current sheets in an astrophysical environment is found in the vicinity of pulsars. The short rotation period of the star (P ∼ 1−10³ ms) combined with strong surface magnetic fields (B ∼ 10⁹ − 10¹² G) lead to significant field line winding and opening beyond the light cylinder, a virtual cylindrical surface of radius R_LC = cP/2π ∼ 50−50 000 km, beyond which the co-rotation velocity becomes superluminal. A large-scale current sheet forms outside the light cylinder where both magnetic polarities of the star meet (Michel 1971; Coroniti 1990). The magnetic and current structures are supported by a plasma of relativistic electron-positron pairs that are self-generated near the stellar surface via pair production. This plasma flows along open field lines in the form of a radially expanding, relativistic magnetized wind, simply referred to as the pulsar wind in the following (Rees & Gunn 1974; Kennel & Coroniti 1984).

If the magnetic axis is aligned with the rotation axis, the magnetosphere is axisymmetric and the current sheet is a flat disk lying in the equatorial plane. If the magnetic axis is inclined, the current sheet has the shape of an oscillatory structure of wavelength 2πR_LC confined within an equatorial wedge of a half-opening angle set by the magnetic inclination angle (Bogovalov 1999). A cut through this surface at a constant latitude gives rise to a succession of narrow stripes of currents separated by smooth wind regions (Fig. 1). For this reason, this structure is usually referred to as the “striped wind” (Coroniti 1990; Kirk et al. 2009). Away from this region, the wind is smooth and is well described by a rotating monopole-like configuration (Michel 1973).

Fig. 1. 3D rendering of plasma density isosurfaces for χ = 60° from the star surface (yellow dot at the center) up to 50 RLC. A spherical wedge has been removed to show the internal structure of the striped wind.

One fundamental question regards the fate of the stripes as the wind propagates outward, and so far this issue has led to contradictory conclusions (Coroniti 1990; Lyubarsky & Kirk 2001; Lyubarsky 2003; Kirk & Skjæraasen 2003; Cerutti & Philippov 2017). It is generally accepted that relativistic reconnection occurs within the current layer (e.g., Kagan et al. 2015), leading to a transfer of magnetic energy into particle kinetic energy. The main uncertainty lies in the rate of dissipation and its feedback on the global dynamics of the wind. In a collisionless plasma, the current layer thickness is determined by the plasma kinetic scales (i.e., on the order of plasma skin-depth and particle Larmor radius scales). In pulsars, this scale is microscopic such that the aspect ratio of the current sheet is very large, meaning that the layer will most likely reconnect into the plasmoid-dominated regime, a regime where reconnection is fast (Uzdensky et al. 2010). Recent particle-in-cell (PIC) simulations of plane-parallel reconnection have confirmed the efficiency of relativistic reconnection mediated by the plasmoid instability at dissipating the field and accelerating particles (e.g., Zenitani & Hoshino 2001; Cerutti et al. 2012; Sironi & Spitkovsky 2014; Werner et al. 2018). In a parallel effort, global PIC simulations of pulsar magnetospheres have shown the major role that reconnection has at dissipating a sizeable fraction of the Poynting flux into high-energy particles and pulsed gamma-ray emission (Cerutti et al. 2016; Philippov & Spitkovsky 2018; Kalapotharakos et al. 2018). These simulations were focused on the inner magnetospheric regions and restricted to a few light-cylinder radii only so that the large-scale evolution of dissipation was not probed.

In this study, we aim at reconciling global models of pulsar wind dynamics, reconnection, and particle acceleration in the stripes within the same numerical framework, using large three-dimensional (3D) PIC simulations. The latter are supplemented by a series of two-dimensional (2D) simulations restricted to the equatorial plane to explore the parameter space and the effect of numerical resolution. This work is the logical continuation of our previous effort in this direction (Cerutti & Philippov 2017). We begin by introducing the numerical setup in Sect. 2. Simulation results are presented in Sect. 3 and discussed in Sect. 4 with an emphasis on dissipation and particle acceleration. Radiative signatures will not be discussed in this paper and will be left to a future study.

2. Methodology and setup

We used the relativistic electromagnetic PIC code ZELTRON (Cerutti et al. 2013; Cerutti & Werner 2019) in its full 3D spherical coordinate (r, θ, ϕ) version that was first introduced in Cerutti et al. (2016). The numerical grid is logarithmically spaced along the r-axis. This choice is well suited for this problem, in which the plasma density and the field strength present a sharp gradient in the vicinity of the star; it also allows us to probe large physical distances, the key objective in this work. The grid along the θ-direction follows a cosθ-spacing. This is a natural choice for a 3D spherical grid as it keeps the volume of the cell constant at a given radius, that is to say, the grid is refined at the equator but is coarser at the poles. This choice is also motivated by the fact that the pulsar wind power is concentrated within the equatorial regions (for a monopole it scales as ∝sin²θ). The grid is uniformly spaced along the ϕ-direction.

The full numerical grid is composed of (2016×1024×512) cells along the r-, θ-, and ϕ-directions, respectively. The box extends from the stellar surface r_min = r_⋆ up to r_max = 100 R_LC, where we fixed R_LC/r_⋆ = 3, θ = [0.03π,0.97π] and ϕ = [0,2π]. A damping layer absorbs all outgoing electromagnetic waves and particles to mimic an open boundary (Cerutti et al. 2015). We applied reflective boundary conditions along the θ-boundaries for the particles and axial symmetry to the fields (Holland 1983). As for the ϕ-direction, we applied standard periodic boundary conditions to the fields and the particles. The rotation axis of the star is aligned with the axis of the spherical domain (i.e., θ = 0). The magnetic axis is inclined at an angle χ with respect to the rotation axis and rotates at the angular velocity of the star Ω. Following Cerutti & Philippov (2017), we chose a split-monopole magnetic configuration (Michel 1973; Bogovalov 1999), which is a good proxy for the asymptotic structure of the pulsar wind, the main region of interest in this work. At t = 0, the magnetic field configuration is purely radial,

$$\begin{array}{c}\hfill B_{\mathrm{r}}=\pm B_{\star }{\left(\frac{r_{\star }}{r}\right)}^2,\end{array}$$(1)

where B_⋆ is the magnetic field strength at the surface of the star (+B_⋆ in the northern hemisphere and −B_⋆ in the southern hemisphere). At any instant t, the plane that separates both magnetic polarities at the stellar surface is given by the following condition:

$$\begin{array}{c}\hfill sin\theta sin\chi cos(\mathrm{\Omega }t-\varphi )+cos\chi cos\theta =0.\end{array}$$(2)

The solid rotation of field lines is enforced by applying the co-rotation electric field at the stellar surface at every time step. Assuming a perfectly conducting neutron star yields

$$\begin{array}{c}\hfill \mathit{E}=-\frac{(\mathbf{\Omega }\times \mathit{r})\times \mathit{B}}{c}·\end{array}$$(3)

Fresh plasma exclusively composed of electron-positron pairs is uniformly injected at the stellar surface. The plasma is in co-rotation with the star and has a net radial velocity determined by the E × B drift velocity of the monopole solution. Normalized by the speed of light, the initial particle velocity components are (Cerutti & Beloborodov 2017)

$$\begin{array}{cc}& {\beta }_{\mathrm{r}}^{\star }=\frac{1}{1+R_{\mathrm{LC}}^2/R^2},\hfill \end{array}$$(4)

$$\begin{array}{cc}& {\beta }_{\theta }^{\star }=0,\hfill \end{array}$$(5)

$$\begin{array}{cc}& {\beta }_{\varphi }^{\star }=\frac{R/R_{\mathrm{LC}}}{1+R^2/R_{\mathrm{LC}}^2},\hfill \end{array}$$(6)

where R = rsinθ is the cylindrical radius. The injected plasma is neutral and has a multiplicity ${\kappa }_{\star }=n^{\star }/n_{\mathrm{GJ}}^{\star }=10$, where $n_{\mathrm{GJ}}^{\star }=\mathrm{\Omega }{B}_{\star }/2\pi ec$ is the fiducial plasma density (Goldreich & Julian 1969) and e the elementary electric charge. This prescription is a simple numerical recipe to efficiently fill the magnetosphere with plasma and therefore reach a quasi force-free configuration, which is most appropriate for modeling active pulsars (Cerutti et al. 2015). In this work, we are not aiming at modeling pair production, which is most likely happening in the inner magnetosphere, but focus our numerical resources on the wind region instead, assuming that plenty of pairs are produced along all field lines. On average, one new pair is injected per cell at the neutron star surface every eight time steps. At the end of the simulation, when most of the numerical box has been filled with plasma, there are about ∼10¹⁰ particles, which represents about ten particles per cell on average.

In addition to the Lorentz force, particles feel the radiation-reaction force due to both curvature and synchrotron radiation (see Cerutti et al. 2016 for its implementation). The simulation time step is fixed at half the Courant-Friedrichs-Lewy time step, Δt = 0.5Δt_CFL. One pulsar period is 3.6 × 10⁴Δt. All simulations were evolved for about ten rotation periods (i.e., for about 3.6 × 10⁵Δt). The fiducial plasma magnetization at the star surface is set at

$$\begin{array}{c}\hfill {\sigma }_{\star }=\frac{B_{\star }^2}{4\pi n^{\star }{m}_{\mathrm{e}}{c}^2}=250,\end{array}$$(7)

where m_e is the electron rest mass. The shortest plasma time scale, ${\omega }_{\mathrm{pe}}^{-1}$, as well as the shortest radiative cooling time scale, ${\omega }_{\mathrm{c}}^{-1}$, are well resolved in all simulations, with ω_peΔt ≈ 20 and ω_cΔt ≈ 14. The smallest plasma scale, the local skin depth d_e = c/ω_pe, is also very well resolved everywhere in the simulation box with d_e/Δr ≳ 10−30, where Δr is the radial size of a cell. At the light cylinder, the local plasma skin depth is d_e/R_LC ≈ 3 × 10⁻².

We performed 3D simulations with three different magnetic obliquity angles: χ = 30°, 60°, and 85°; all other parameters remained identical. We ran another 3D run for χ = 60° and r_max = 50 R_LC with a constant spacing along the radial direction to evaluate the role of the grid on magnetic dissipation. We also performed a series of 2D runs limited to the equatorial plane, as in Cerutti & Philippov (2017), to explore the parameter space and to investigate the role of numerical resolution on the dissipation of the striped wind. To this end, we performed a first series of six simulations with κ_⋆ = 10 and σ_⋆ = 250 using a logarithmic or a constant radial grid spacing with different numerical resolutions both in r and ϕ. In a second set, we aimed at assessing the role of the wind magnetization σ_⋆ = 125, 250, 750 while keeping κ_⋆ = 10. In the last set, we explored the role of the plasma multiplicity while keeping the stellar magnetic field the same, with κ_⋆ = 0.2, 0.6, 2, 6, 20, 60. Table 1 shows the full listing of all runs used in this work.

3. Simulation results

3.1. Plasma structures

Shortly after the onset of the simulations, the plasma blown from the star establishes a force-free split-monopole-like configuration as it propagates out. It is characterized by a toroidal-dominated magnetic structure whose polarity reverses across the current sheet. The shape of this sheet is consistent with the prediction of Bogovalov (1999): It is a 3D spherical Archimedean spiral of wavelength 2πR_LC defined within the spherical wedge π/2 − χ ≤ θ ≤ π/2 + χ (Figs. 1 and 2). This region, which includes both the sheet and the plasma in between, is the striped wind (Michel 1971; Coroniti 1990; Kirk et al. 2009). Away from the stripes, the wind closely resembles a single rotating magnetic monopole (Michel 1973).

Fig. 2. 2D slices of the plasma density $r^2(n/n_{\mathrm{GJ}}^{\star })$ for χ = 60°. Top: rθ-plane containing the magnetic axis at the phase ϕ = Ωt. Bottom: rϕ-plane at the equator (θ = 90°). The radius is expressed in units of RLC. Right panels: zoomed-in views of the regions delimited by the white boxes drawn on the left panels. The striped wind region is contained within π/2 − χ ≤ θ ≤ π/2 + χ (white dashed lines).

The current sheet fragments soon after its formation near the light cylinder. It is unstable to the relativistic tearing mode (Zelenyi & Krasnoselskikh 1979; Pétri & Kirk 2007), which mediates fast magnetic reconnection. It results in the formation of a dynamical chain of plasma overdensities trapped in magnetic loops, or plasmoids, separated by secondary current sheets where the field reconnects. These features are clearly visible in the zoomed-in view of the plasma density in both the toroidal and poloidal planes in Fig. 2. In full 3D, these structures form a network of interconnected flux ropes reminiscent of plane-parallel reconnection simulations (Kagan et al. 2013; Cerutti et al. 2014; Werner & Uzdensky 2017). Secondary flux ropes are produced within secondary current sheets, which then merge with others to form bigger structures. The dynamical nature of reconnection is most pronounced within ≲10 R_LC and is quenched by the expansion of the wind at larger radii. Although severely fragmented, the striped wind structure retains its global coherent structure. Hence, the 2D picture drawn in Cerutti & Philippov (2017) qualitatively holds in full 3D.

We observe that the sheet is also mildly kink unstable (Zenitani & Hoshino 2005; Cerutti et al. 2014). It appears as wiggles, which are most visible in the zoomed-in view of the poloidal plane in Fig. 2, but these distortions do not lead to the complete disruption of the sheet. The kink is more effective at low magnetic obliquities (Philippov et al. 2015; Cerutti et al. 2016) and can lead to a significant latitudinal spreading of the striped wind region, well outside of its natural boundaries. At χ = 30°, the kink instability may be responsible for a widening of the stripes of about 10°, whereas there are no noticeable deviations for χ = 60° and above (Fig. 2, top panel). The plasma density is distributed in a highly inhomogeneous and anisotropic manner. The unstriped wind is composed of a low-density uniform plasma, of multiplicity κ = n/n_GJ of order unity, except close to the axis where numerical plasma fluctuations are artificially enhanced by the spherical grid. In the striped zone, there is a strong plasma density contrast between, in order of increasing density, the wind (κ ∼ 2−3), secondary current layers (κ ∼ 4−5), and the far denser flux ropes (κ ∼ 10−10³). The wind zone between two stripes is itself inhomogeneous, in contrast with the unstriped region. There is a clear plasma depletion on the leading edge of the spiral, which was already reported in previous studies (Philippov et al. 2015; Cerutti & Philippov 2017; Philippov & Spitkovsky 2018). In this sense, reconnection proceeds in a highly asymmetric way.

3.2. Poynting flux and dissipation

We now turn our attention to the central question of magnetic dissipation. In a dissipationless steady-state split-monopole magnetosphere, the outgoing Poynting flux integrated over a spherical radius is conserved in virtue of the Poynting flux theorem. The predicted value is

$$\begin{array}{c}\hfill L_0=\frac{c}{4\pi }{\displaystyle \int \int (\mathit{E}\times \mathit{B})}{r}^{2}sin\theta \mathrm{d}\theta \mathrm{d}\varphi =\frac{2c{B}_{\star }^2{r}_{\star }^4}{3R_{\mathrm{LC}}^2}·\end{array}$$(8)

Figure 3 shows the radial and latitudinal dependence of the Poynting flux, L, for all 3D simulations. The first element to notice is that the numerical values are closer to L ≈ L₀/5 at the star surface. This discrepancy is explained by the fact that the analytical split-monopole solution used in Eq. (8) assumes that all field lines cross the light cylinder and therefore participate in the pulsar spindown. In all runs, a large fraction of initially open field lines reconnects in the equatorial region to form a series of closed field lines nearly co-rotating with the star up to the light cylinder, and thus they do not contribute to the outflowing Poynting flux. Only polar field lines remain open so that the magnetospheric structure simulated here qualitatively resembles a force-free dipole inside the light cylinder. Nonetheless, the Poynting flux does not present a strong dependence with magnetic obliquity as expected from the split-monopole solution (Bogovalov 1999). More formally, we can express the spindown power as a function of the flux of open magnetic field lines per hemisphere, Ψ_open. For an aligned monopole,

$$\begin{array}{c}\hfill {\mathrm{\Psi }}_{\mathrm{open}}=2\pi r^2{B}_{\mathrm{r}}(1-cos{\theta }_{\mathrm{open}}),\end{array}$$(9)

Fig. 3. Left panels: radial evolution of the Poynting flux normalized to the expected monopole solution $L_0=2c{B}_{\star }^2{r}_{\star }^4/3R_{\text{LC}}^2$ (top) and dissipated fraction relative to the light-cylinder value ΔL = L(r) − LLC normalized by LLC (bottom). Right panels: latitude dependence of the normalized Poynting flux per unit of solid angle dL/dΩ (top) and dissipated fraction (bottom) averaged over the radial range 40 ≤ r/RLC ≤ 50. Vertical dotted lines show the predicted maximal latitudinal extension of the striped wind. The dot-dashed line is a sin2θ profile for comparison with the monopole prediction (top-right panel). The full dissipation model of the striped wind proposed by Lyubarsky (2003), Komissarov (2013) is shown by the dashed black line in the lower-right panel. In all panels, these quantities are shown for all 3D runs performed in this study, including the constant radial grid spacing solution for χ = 60°, represented by the dashed red line.

so that Eq. (8) should be changed into the more general expression (e.g., Tchekhovskoy et al. 2016)

$$\begin{array}{c}\hfill L=\frac{{\mathrm{\Omega }}^2{\mathrm{\Psi }}_{\mathrm{open}}^2}{6{\pi }^{2}c}=L_0{(1-cos{\theta }_{\mathrm{open}})}^2.\end{array}$$(10)

Thus, physically, L/L₀ ≈ 0.2 is a measure of the fraction of the solid angle squared filled by open field lines in the inclined split-monopole simulations.

The presence of reconnection in the current sheet leads to significant dissipation, which translates into a decay of the radial Poynting flux. Here, dissipation is by no means spurious numerical dissipation, but it has a real physical origin: The reservoir of Poynting flux provided by the star is gradually consumed by reconnection, which converts magnetic free energy into particle kinetic energy and radiation such that the total energy in the system is conserved to a good accuracy, as shown in Fig. 4. Irregularities in the total power curve reflect the intermittent nature of reconnection. The radial profile of the Poynting flux first drops by about 20% within a few light-cylinder radii after launching, a number consistent with past studies that have focused on the magnetosphere and inner wind zone (Parfrey et al. 2012; Philippov & Spitkovsky 2014; Cerutti et al. 2015; Belyaev 2015). Dissipation continues further at a much slower but steady rate beyond r ≳ 10 R_LC until it reaches about 40−50% of the total initial flux at r = 50 R_LC (Fig. 3). This rate seems to be independent of the magnetic obliquity. It does not seem to be sensitive to the choice of the grid spacing either: After a brief overshoot at low radii, likely due to the low numerical resolution in comparison with the log-spacing run, the constant r-spacing simulation asymptotically converges toward the same amount and rate of dissipation (see the solid and the dashed red lines in Fig. 3). To strengthen this point further, 2D simulations restricted to the equatorial plane with different numerical resolutions, box sizes, and grid spacing present the same evolution of Poynting flux and the same amount of dissipation (top panel in Fig. 5).

Fig. 4. Radial evolution of the kinetic energy flux carried by the particles, Lpart = ∬n(γ − 1)mec2vrr2sinθdθdϕ (dashed blue line), along with the Poynting flux, L (solid red line) and the total power, Ltot = L + Lpart (thick solid black line) for χ = 60°. Luminosities are normalized by the monopole spindown power L0.

Fig. 5. Top: convergence study of dissipation with grid spacing and numerical resolution using 2D simulations (see Table 1 for grid parameters). The 3D run with χ = 85° is reported here for comparison with 2D runs (black solid line). Middle: dependence of dissipation with the plasma magnetization for κ⋆ = 20. Bottom: dependence of dissipation with the plasma multiplicity for σ⋆ = 250. The dashed lines are best-fit models to the analytical solution proposed in Sect. 4, Eq. (20). In all panels, the Poynting flux is normalized to its light-cylinder value, L/LLC.

Figure 3 also shows the latitudinal dependence of the Poynting flux and of its dissipation. As expected, the Poynting flux is preferentially distributed within the equatorial regions, and the θ-profiles closely resemble the split-monopole solution (i.e., dL/dΩ ∝ sin²θ). We note that the profiles are slightly sharper than predicted, although not as much as reported in Tchekhovskoy et al. (2013) where dL/dΩ ∝ sin⁴θ for an initially dipolar magnetic field configuration. The transition between the striped and the unstriped wind regions is smooth, except at χ = 30° where small dips are visible. An interesting feature is that the same fraction of power is dissipated at all latitudes within the striped wind region. This fraction reaches about 40−50% depending on the obliquity and vanishes within the dissipationless unstriped wind region (see lower-right panel in Fig. 3)¹. Incidentally, the kink-induced widening of the sheet at χ = 30° described in Sect. 3.1 results in a broader angular dissipation rate profile, well outside the boundaries 60° ≤θ ≤ 120°.

In Fig. 5 (middle and bottom panels), we report on the dependence of dissipation with the plasma magnetization, σ_⋆, and multiplicity, κ_⋆, based on our large set of 2D simulations. While there is no noticeable dependence on magnetization (at least as long as σ_⋆ ≫ 1), dissipation monotonically increases with increasing plasma multiplicity. Low-multiplicity solutions (κ_⋆ <  1) present 10−20% dissipation rates at r/R_LC = 50. In contrast, high-multiplicity solutions (κ ≫ 1) show up to 70−80% dissipation without any sign of saturation with the radius, indicating that the striped wind structure most likely disappears far before the pulsar wind terminates in isolated systems (Sect. 4). Putting everything together, simulations reported in this work suggest that reconnection proceeds efficiently and homogeneously within the striped wind regardless of magnetic inclination, numerical resolution, grid spacing, or plasma magnetization, but that there is a clear distinction between charge-starved (slow dissipation) and high-multiplicity (fast dissipation) winds.

3.3. Wind kinematics and particle spectra

In this section, we exploit the particle data to reconstruct the bulk motion of the wind and the particle spectrum in the context of magnetic dissipation and particle acceleration. Figure 6 focuses on the radial and latitudinal dependence of the wind bulk Lorentz factor Γ. Here, all quantities are averaged over azimuth so that the wind can be referred to as a single homogeneous entity. Within r/R_LC ≲ 4, the wind accelerates quasi-linearly with the cylindrical radius as expected from the monopole prediction, that is to say $\mathrm{\Gamma }={(1+r^2{\sin }^2\theta /R_{\text{LC}}^2)}^{1/2}$ if the plasma follows the E × B drift velocity (see Eqs. (4)–(6)). Then, the wind quickly reaches the fast magnetosonic point defined by ${\mathrm{\Gamma }}_{\mathrm{fms}}={\mu }_{\mathrm{M}}^{1/3}\approx 4$, where

$$\begin{array}{c}\hfill {\mu }_{\mathrm{M}}\equiv \frac{B^2}{4\pi n{m}_{\mathrm{e}}{c}^2}=\mathrm{\Gamma }\sigma \end{array}$$(11)

Fig. 6. Top: ϕ-averaged plasma bulk Lorentz factor in the striped wind region within 80° ≤θ ≤ 100° as a function of radius Γ(r). The dotted black line is the monopole prediction, $\mathrm{\Gamma }={(1+r^2{\sin }^2\theta /R_{\text{LC}}^2)}^{1/2}$. The dashed green line is the Michel magnetization parameter, μM (see Eq. (11)), to the power 1/3. The fast magnetosonic point is located at the yellow star, where ${\mathrm{\Gamma }}_{\mathrm{fms}}={\mu }_{\mathrm{M}}^{1/3}$. Bottom: θ-dependence of Γ(θ). Vertical dashed lines delimit the extension of the striped wind region. The black dotted line is a sinθ profile, as expected from the monopole solution.

is Michel’s magnetization parameter (Kirk et al. 2009). With σ ≈ 15 at the fast point, the wind remains highly magnetized. Past this point, the wind acceleration slows significantly and saturates at Γ_∞ ≈ 11 for r/R_LC ≳ 30 within the equatorial regions. This result is not sensitive to the magnetic obliquity angle and confirms theoretical expectations (Tomimatsu 1994; Beskin et al. 1998) as well as our previous findings in 2D, although here we obtain significantly larger asymptotic values in full 3D (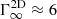${\mathrm{\Gamma }}_{\infty }^{2\mathrm{D}}\approx 6$ reported in Cerutti & Philippov 2017). The latitudinal dependence of the bulk Lorentz factor is consistent with the monopole solution in the unstriped region with Γ(θ) ∝ sinθ. At large radii in the striped region, the profile is much flatter and departs significantly from the ideal solution (bottom panel in Fig. 6). These deviations are most likely due to dissipation and particle acceleration within the current sheets, whose effects are not negligible at large radii.

The wind acceleration is an ideal process governed solely by the E × B drift velocity. It should not be confused with non-thermal particle acceleration that is due to reconnection or other nonideal dissipative processes, which come in addition to this ideal process. Figure 7 shows the radial and latitudinal evolution of the individual particle Lorentz factor spectrum, (γ/N)dN/dγ. The r-dependence highlights the formation of a broad non-thermal particle spectrum as magnetic energy is consumed and transferred to the particles via reconnection. The saturated-looking state of the particle spectrum at large radii hides a strong latitude dependence, as shown in the middle panel of Fig. 7. The spectrum is narrow and peaks at low energies near the rotation axis (⟨γ⟩∼3). The mean energy shifts to higher energy without any significant spectral broadening in the unstriped zone. This evolution follows the ideal bulk acceleration of the wind, which is not accompanied by non-thermal acceleration. In contrast, the particle spectrum dramatically widens inside the striped region, where non-thermal particle acceleration pushes particles up to γ ≫ Γ_∞. This evolution is not very sensitive to the magnetic obliquity.

Fig. 7. Top panel: normalized particle energy spectrum, (γ/N)dN/dγ, within the spherical shells of radius r and r + RLC as a function of radius (color-coded) for χ = 60°. Middle panel: latitudinal dependence (color-coded) of the particle energy spectrum averaged between 40 ≤ r/RLC ≤ 50 for χ = 60°. Bottom panel: total particle spectra beyond r = 40 RLC and 80° ≤θ ≤ 100° for χ = 30°, 60°, and 85°.

The asymptotic spectrum in the striped wind can be decomposed into two parts: a thermal bath peaking at γ ≈ Γ_∞ and a hard power-law spectrum dN/dγ ∝ γ⁻¹ cutting at ${\mu }_{\mathrm{M}}^{\mathrm{LC}}=B_{\mathrm{LC}}^2/4\pi n_{\mathrm{LC}}{m}_{\mathrm{e}}{c}^2={\mathrm{\Gamma }}_{\mathrm{LC}}{\sigma }_{\mathrm{LC}}\approx 50$, where Γ_LC ≈ 1.4. To uncover the origin of these two components, it is useful to look at the ϕ-resolved particle spectrum (see Fig. 8). This analysis clearly shows that the low-energy particles are associated with the wind region located far upstream from the current layers, where the ideal monopole wind acceleration mechanism applies. A closer look reveals that the wind itself is composed of two distinct parts with slightly different energies: a low-energy component at the leading edge of the spiral sheet corresponding to the low-density region with ⟨γ⟩≈8 and a high-energy component at the trailing edge of the spiral with ⟨γ⟩≈15. There is a sharp spatial segregation about halfway between two current sheets (around ϕ = 0° and ϕ = 180° in Fig. 8), which marks the zone of influence of each reconnecting layer on the plasma in the wind. As for the hard power-law component, it is unambiguously associated with non-thermal particle acceleration within the reconnection layers. The spectral index of ≈ − 1 is consistent with high-σ reconnection simulation studies (Zenitani & Hoshino 2001; Sironi & Spitkovsky 2014; Guo et al. 2015; Werner et al. 2016). Therefore, to a first order, the asymptotic particle spectrum within the striped wind can be approximatively described as

$$\begin{array}{c}\hfill \frac{\mathrm{d}N}{\mathrm{d}\gamma }\propto {\gamma }^{-1},{\mu }_{\mathrm{M}}^{1/3}\lesssim \gamma \lesssim {\mu }_{\mathrm{M}}^{\mathrm{LC}}.\end{array}$$(12)

Fig. 8. Top: ϕ-profile of the normalized current density flowing along the θ-direction in the equatorial plane (θ = 90°) for r = 48 RLC and χ = 60°. The locations of the current sheets and wind regions are labeled “Layer 1,” “Layer 2,” and “wind,” respectively. Middle: corresponding ϕ-resolved particle energy spectrum. Bottom: decomposition of the total particle spectrum in the striped region (dashed black line) into a wind component (solid red line) and a layers component (solid blue line). The vertical dotted lines show γ = Γ∞ ≈ 11 and γ = σLC ≈ 50.

The asymptotic spectrum does not seem to collapse into a narrower distribution at large radii, in contrast to our previous 2D runs. This suggests that 3D effects may be important in producing a power-law spectrum.

4. Interpretation and discussion

4.1. A toy model for dissipation

We propose a simple analytical model for the evolution of magnetic dissipation inspired by our simulations in an attempt to extrapolate our results to realistic pulsar winds. In a steady state, the radial variations of the Poynting flux is governed solely by Joule dissipation between two spherical shells that we will choose here to be of radius r = R_LC and an arbitrary radius r >  R_LC, such that

$$\begin{array}{c}\hfill L(r)-L_0=-{\displaystyle {\int }_{R_{\mathrm{LC}}}^r{\int }_0^{\pi }{\int }_0^{2\pi }\mathit{J}·\mathit{E}{r}^{2}sin\theta \mathrm{d}r\mathrm{d}\theta \mathrm{d}\varphi .}\end{array}$$(13)

To a very good accuracy, we have

$$\begin{array}{c}\hfill \mathit{J}·\mathit{E}\approx J_{\theta }{E}_{\theta }\approx J_{\theta }{B}_{\varphi }.\end{array}$$(14)

To make further progress, we need to take a closer look at the distribution of currents and fields in the vicinity of current sheets where Joule dissipation is localized. Figure 9 shows the radial profile of B_ϕ, J_θ and the product of the two for κ_⋆ = 0.2, 2, and 20 at a pulsar phase ϕ chosen such that it crosses only current sheets and avoids magnetic islands. The spatial distribution of J ⋅ E within islands is dipolar such that there is no net contribution integrated over their volume, in contrast to secondary current sheets. The magnitude of the current carried by the particles depends on the plasma multiplicity and is localized in the form of thin sheets, as expected. At low multiplicities (κ_⋆ <  1), the conduction current is small, too small in fact to explain the magnetic reversal, and it is not localized at the magnetic nulls. In this regime, the current is mostly carried by the displacement current (∂E/∂t, only possible for an oblique rotator), which is a logical consequence of charge starvation in the wind. With increasing multiplicities, the magnetic profile changes from a nearly sinusoidal shape at low-κ_⋆ to an asymmetric square shape at high-κ_⋆, with sharp gradients where the field reverses and where a strong conduction current is localized. Thus, the electric field in Joule’s terms may be understood as the reconnection electric field, E_rec, which represents a fraction of the upstream magnetic field, $B_{\varphi }^{\mathrm{up}}$, such that

$$\begin{array}{c}\hfill E_{\mathrm{rec}}={\beta }_{\mathrm{rec}}{B}_{\varphi }^{\mathrm{up}},\end{array}$$(15)

Fig. 9. Radial profile of Jθ (dashed black line), Bϕ (red line), and JθBϕ (blue line) for κ⋆ = 0.2 (top), 2 (middle), and 20 (bottom). Jθ is normalized to the Goldreich-Julian current density, JGJ = (B⋆/P)(r⋆/r)2, and Bϕ is normalized by the monopole solution, $B_{\varphi }^{\mathrm{Michel}}=B_{\star }(R/R_{\mathrm{LC}}){(r_{\star }/r)}^2$.

where β_rec is the dimensionless reconnection rate (Lyubarskii 1996; Uzdensky & Spitkovsky 2014).

Another important observation we can make from Fig. 9 is that the magnetic field strength that contributes to dissipation is always on the trailing edge of the spiral because of the asymmetric nature of reconnection in the striped wind, the most pronounced effect being visible at high multiplicities. This conclusion is also compatible with the asymmetry in the phase-resolved particle spectrum reported in Sect. 3.3. We find that the upstream magnetic field strength at the trailing edge of the sheet, $B_{\varphi }^{\mathrm{up}}$, is on the order of the ideal split monopole field at all radii, even though the striped-averaged field strength decreases with radius due to dissipation, that is:

$$\begin{array}{c}\hfill B_{\varphi }^{\mathrm{up}}\approx B_{\varphi }^{\mathrm{Michel}}=\mp \frac{R}{R_{\mathrm{LC}}}{B}_{\star }{\left(\frac{r_{\star }}{r}\right)}^2,\end{array}$$(16)

such that the sheet is always fed with a fresh, non-reconnected magnetic field. The electric current is given by Ampère’s law. Assuming perfect symmetry on both sides of the current layer for the sake of simplicity, we have (e.g., Cerutti & Philippov 2017)

$$\begin{array}{c}\hfill \frac{4\pi }{c}{J}_{\theta }\delta =2B_{\varphi }^{\mathrm{up}},\end{array}$$(17)

where δ is the layer thickness. Putting everything together, the Joule’s term within a single current sheet can be approximately estimated as

$$\begin{array}{c}\hfill \mathit{J}·\mathit{E}\approx \frac{c{\beta }_{\mathrm{rec}}{(B_{\varphi }^{\mathrm{up}})}^2}{2\pi \delta }=\frac{3{\beta }_{\mathrm{rec}}{L}_0}{4\pi \delta }\frac{{sin}^2\theta }{r^2}·\end{array}$$(18)

The integral over ϕ at a constant radius and latitude vanishes everywhere, except at two phases where the layers are located. The angular width of each layer can be estimated as Δϕ ∼ δ/r, such that Eq. (13) becomes

$$\begin{array}{c}\hfill L(r)-L_0\approx -\frac{3{\beta }_{\mathrm{rec}}{L}_0}{2\pi }{\displaystyle {\int }_{R_{\mathrm{LC}}}^r{\int }_0^{\pi }\frac{\mathrm{d}r}{r}{sin}^3\theta \mathrm{d}\theta ,}\end{array}$$(19)

that is to say, dissipation is independent of the width of the current layer. The integrals over θ and r lead to the final result,

$$\begin{array}{c}\hfill \frac{L(r)}{L_0}=1-{\beta }_{\mathrm{rec}}ln\left(\frac{r}{R_{\mathrm{LC}}}\right),\end{array}$$(20)

where we absorbed the constant 2/π of order unity into the reconnection rate, (i.e., β_rec ← 2β_rec/π). Applying this model to simulation data provides a good description of the Poynting flux decay and a direct measure of the rate of dissipation. Figure 10 shows the evolution of the dissipation rate with the plasma multiplicity. It is determined from the best-fit model to the dissipation curves in Fig. 5 (bottom panel), assuming the evolution given in Eq. (20). As expected, dissipation is low at low multiplicities because the current is mostly carried away by the displacement current. The contribution from the conduction current increases with the plasma supply until it reaches an approximate saturation at high multiplicities where β_rec ∼ 0.1−0.2. One should keep in mind that the rate measured from the simulations includes additional physical effects neglected in the above toy model, which are of order unity, such as asymmetries, deviations from the split monopole solutions, or the filling factor of plasmoids, which do not contribute to dissipation. These effects may account for the slow increase in the dissipation rate at high multiplicities.

Fig. 10. Evolution of the dissipation rate βrec (blue line, dots, and axis) and the extrapolated full dissipation radius of the stripes $R_{\mathrm{diss}}/R_{\mathrm{LC}}=exp({\beta }_{\mathrm{rec}}^{-1})$ (red line, dots, and axis) with the typical plasma multiplicity measured at secondary current sheets, κX. The estimated radius of the Crab pulsar wind termination shock is shown by the horizontal dotted line (RTS/RLC ∼ 109) for comparison.

Another effect not captured by this simple model is dissipation due to the formation of vacuum gaps in the low-multiplicity solutions, as reported in Cerutti et al. (2015) for an aligned rotator. In the 2D equatorial plane simulations used here, Ω ⋅ B = 0, and therefore no gap can form in this special configuration. We would expect an additional source of dissipation at low, but finite multiplicities in a full 3D setup, which we did not explore in this work. In this sense, the model gives a lower limit of dissipation in this regime. This being said, the real solution must smoothly connect to the fully dissipationless vacuum solution (Deutsch 1955), meaning that dissipation should necessarily cease as we asymptotically approach the vacuum regime, as reported here.

4.2. Implications

If the model presented above is a fair description of real astrophysical pulsar winds, it has important astrophysical implications. The first observation to make is that dissipation depends only on the reconnection rate. Studies of local plane-parallel reconnection consistently find a high reconnection rate, β_rec ∼ 0.1−0.2 (see, e.g., Kagan et al. 2015, and references therein), similar to what is reported here. This rate does not seem to depend on anything as long as the layer is thin, meaning that it is on the order of the plasma kinetic scales, δ ∼ d_e. In particular, it should not depend on the plasma multiplicity as long as κ ≫ 1, as reported in Fig. 10, and thus the radius at which the striped wind has fully dissipated should be similar for all pulsars producing pairs (e.g., gamma-ray pulsars). In this sense, our results suggest that there is a universal dissipation radius for all pulsar winds loaded with pairs. Using Eq. (20) and assuming a naive extrapolation of the model to any radius, we predict a complete decay of the Poynting flux at a radius

$$\begin{array}{c}\hfill R_{\mathrm{diss}}=R_{\mathrm{LC}}exp\left({\beta }_{\mathrm{rec}}^{-1}\right)\sim {10}^2-{10}^4{R}_{\mathrm{LC}}\end{array}$$(21)

for β_rec = 0.1−0.2. Although this radius is quite sensitive to the exact value of the reconnection rate, simulations show that β_rec is high, meaning that the striped wind will most certainly decay entirely far before reaching its termination (Coroniti 1990; Cerutti & Philippov 2017) unless it is truncated at short distances by an accretion disk or a companion star wind.

At this stage, it is important to emphasize that the expansion of the current layer plays no role in dissipating the field, as long as the layer thickness remains small compared with the stripe half-wavelength, δ/πR_LC ≪ 1 (Lyubarsky & Kirk 2001; Kirk & Skjæraasen 2003; Zrake & Arons 2017), which is the case in all of the simulations reported here. In contrast to Eq. (21), this condition explicitly depends on the plasma multiplicity: A denser sheet is also a thinner one, thus the condition for which two consecutive sheets would overlap is pushed further away as the multiplicity increases (Cerutti & Philippov 2017). Therefore, R_diss should be seen as an upper limit for the radius of full dissipation. It is also worth noting that we do not find any evidence for a significant bulk acceleration of the wind due to magnetic dissipation as anticipated by Lyubarsky & Kirk (2001) and Kirk & Skjæraasen (2003). Here, reconnection proceeds at a similar rate even past the fast point where the bulk Lorentz factor remains constant (Fig. 6). As discussed further below, dissipation does not perform work on the wind as a bulk but rather benefits hot pairs trapped within plasmoids.

The wind kinematics and the shape of the particle spectrum reported here also have important astrophysical consequences. The commonly accepted picture is that the wind is composed of cold, nearly monoenergetic pairs traveling at ultra-relativistic velocities such that Γ ∼ 10⁴ − 10⁶ (Rees & Gunn 1974; Wilson & Rees 1978; Kennel & Coroniti 1984). While most of the predicted wind properties are recovered here, we find that the bulk Lorentz factor may not be as relativistic as previously thought. A good proxy is given by the wind Lorentz factor at the fast magnetosonic point, ${\mathrm{\Gamma }}_{\infty }\sim {\mu }_{\mathrm{M}}^{1/3}$. The magnetization at the light cylinder is poorly constrained mostly because of the uncertainty of the plasma multiplicity, but it could be on the order of

$$\begin{array}{c}\hfill {\mu }_{\mathrm{M}}^{\mathrm{LC}}=\frac{B_{\mathrm{LC}}^2}{4\pi \kappa n_{\mathrm{GJ}}{m}_{\mathrm{e}}{c}^2}=\frac{eP{B}_{\mathrm{LC}}}{4\pi m_{\mathrm{e}}c\kappa }=1.4\times {10}^6{P}_{100}{B}_5{\kappa }_4^{-1},\end{array}$$(22)

where P₁₀₀ = P/100 ms is the pulsar period, B₅ = B_LC/10⁵ G and κ₄ = κ/10⁴, for a typical young gamma-ray pulsar. Hence, we expect ${\mathrm{\Gamma }}_{\infty }\sim {\mu }_{\mathrm{M}}^{1/3}\sim 100$ at most, that is to say, more similar to what is usually inferred in gamma-ray burst jets². This gives a good estimate of the bulk particle Lorentz factor throughout the pulsar wind. It is also a fair estimate of the individual particle Lorentz factor located within ideal regions, that is to say the unstriped polar regions and the inter-stripe medium where the particle spectrum remains narrow and cold. Within the current layers, relativistic reconnection leads to the formation of a broad power law of index p ∼ −1, with a low-energy cutoff at γ ≈ Γ_∞ ∼ 10² and a high-energy cutoff at $\gamma \approx {\mu }_{\mathrm{M}}^{\mathrm{LC}}\sim {10}^6$.

The fundamental difference with the standard picture is that the pairs accelerated in the sheet are not cold with γ = Γ, but instead the particles remain hot and trapped within the flux ropes in the wind frame. Thus, we expect the pulsar wind to inject ultra-relativistic pairs with a hard spectrum into the nebula and not just at a single energy scale. Interestingly, applying this model to the Crab Nebula with the typical magnetization scale quoted above, μ_M ∼ 10⁶, could provide a natural explanation for the mysterious radio-electron component responsible for the hard, low-energy emission from the nebula. In the spectral modeling by Meyer et al. (2010), this population is well fitted by a single power law of index −1.6 cutting off at γ_min ∼ 20 and γ_max ≈ 2 × 10⁵, which fits well within our results. Although our spectrum is slightly too hard, a larger and therefore more realistic separation of scales between the layer thickness and the light-cylinder scale could lead to a significant spectral steepening (Petropoulou & Sironi 2018). Pairs injected into the shock could be further accelerated into the nebula by some other mechanisms to form the softer X-ray to gamma-ray electron component, which would naturally result in a smooth transition between both components.

5. Summary

We performed large 3D PIC simulations of pulsar winds with a focus on magnetic dissipation and particle acceleration within the striped region. The global structure of the striped wind is consistent with the split-monopole prediction (Michel 1973; Bogovalov 1999). The current sheet is prone to the plasmoid instability shortly after its launching at the light cylinder. This instability leads to an efficient fragmentation of the sheet into a network of interconnected flux ropes separated by secondary thin current layers where the field reconnects, a structure reminiscent of 3D plane-parallel reconnection studies. This chain is highly dynamical and flux ropes form and merge to form bigger structures, which may result in bright, short bursts of radio emission (Philippov et al. 2019; Lyubarsky 2019) aligned with the incoherent gamma-ray-pulsed emission from the sheet (Cerutti et al. 2016). The sheet is also kink unstable, which leads to a significant widening of the striped wind region at low magnetic obliquity. Reconnection in this environment proceeds in a highly asymmetric way, in a qualitatively similar manner as the dayside of the Earth’s magnetopause. More efforts are needed to better understand asymmetric reconnection in the relativistic regime using local studies.

Relativistic reconnection gradually consumes the oscillatory component of the toroidal magnetic field. This feature is robust against numerical resolution, grid spacing, and plasma magnetization. The Poynting flux monotonically decreases with the distance to the light cylinder, reaching up to about 40% dissipation at the outer parts of the box (i.e., r = 50 R_LC). The dissipation rate weakly depends on latitude within the striped region and on the magnetic obliquity angle. Based on a large set of 2D simulations restricted to the equatorial plane, we can establish that the fate of the striped wind is not sealed by the sheet width as previously thought, but it is instead controlled by the dimensionless reconnection rate β_rec ≈ 0.2, which lies well within reported values in plane-parallel reconnection studies where β_rec ∼ 0.1−0.2. This rate is known to weakly depend on the system size and plasma magnetization in the ultra-relativistic regime (σ ≫ 1, Werner et al. 2018), meaning here that dissipation should not depend on other parameters such as the plasma multiplicity as long as there is a large supply of pairs (κ ≫ 1). Therefore, we propose that there is a universal dissipation radius valid in all pair-producing pulsars of order $R_{\mathrm{diss}}/R_{\mathrm{LC}}=exp\left({\beta }_{\mathrm{rec}}^{-1}\right)\sim {10}^2-{10}^4$, meaning that the stripes should disappear long before reaching the wind termination shock radius in isolated systems such as the Crab pulsar where R_TS/R_LC ∼ 10⁹.

The wind bulk Lorentz is not as relativistic as previously imagined. After crossing the fast magnetosonic point, the wind speed quickly saturates to ${\mathrm{\Gamma }}_{\infty }\approx {\mu }_{\mathrm{M}}^{1/3}$ and thus does probably not exceed Γ_∞ ≲ 100, which is closer to the gamma-ray burst jet Lorentz factor than the standard Crab pulsar wind model where Γ ∼ 10³ − 10⁶ (Rees & Gunn 1974; Wilson & Rees 1978; Kennel & Coroniti 1984). On top of the wind acceleration driven by ideal processes, non-thermal particle acceleration proceeds in the striped region, driven by reconnection. The particle spectrum is consistent with high-σ reconnection simulations, meaning a hard power-law distribution of index p ∼ −1 between ${\gamma }_{\min }\sim {\mu }_{\mathrm{M}}^{1/3}$ and γ_max ∼ μ_M. Scaled up to realistic Crab-like parameter yields, the pulsar wind would be composed of ultra-relativistic pairs distributed as dN/dγ ∝ γ⁻¹ between 10² ≲ γ ≲ 10⁵. Injected at the shock front, the wind particles could then naturally explain the mysterious hard radio component in the Crab Nebula (Meyer et al. 2010).

Acknowledgments

We thank the referee, Ioannis Contopoulos, for his careful review of the manuscript. BC warmly thanks Benjamin Crinquand for insightful discussions about this study. This work has been supported by the Programme National des Hautes Énergies of CNRS/INSU and CNES. We acknowledge PRACE and GENCI (allocation A0070407669) for awarding us access to Joliot-Curie at GENCI@CEA, France.

References

All Tables

All Figures

	Fig. 1. 3D rendering of plasma density isosurfaces for χ = 60° from the star surface (yellow dot at the center) up to 50 RLC. A spherical wedge has been removed to show the internal structure of the striped wind.
In the text

Fig. 2. 2D slices of the plasma density $r^2(n/n_{\mathrm{GJ}}^{\star })$ for χ = 60°. Top: rθ-plane containing the magnetic axis at the phase ϕ = Ωt. Bottom: rϕ-plane at the equator (θ = 90°). The radius is expressed in units of RLC. Right panels: zoomed-in views of the regions delimited by the white boxes drawn on the left panels. The striped wind region is contained within π/2 − χ ≤ θ ≤ π/2 + χ (white dashed lines).

In the text

Fig. 3. Left panels: radial evolution of the Poynting flux normalized to the expected monopole solution $L_0=2c{B}_{\star }^2{r}_{\star }^4/3R_{\text{LC}}^2$ (top) and dissipated fraction relative to the light-cylinder value ΔL = L(r) − LLC normalized by LLC (bottom). Right panels: latitude dependence of the normalized Poynting flux per unit of solid angle dL/dΩ (top) and dissipated fraction (bottom) averaged over the radial range 40 ≤ r/RLC ≤ 50. Vertical dotted lines show the predicted maximal latitudinal extension of the striped wind. The dot-dashed line is a sin2θ profile for comparison with the monopole prediction (top-right panel). The full dissipation model of the striped wind proposed by Lyubarsky (2003), Komissarov (2013) is shown by the dashed black line in the lower-right panel. In all panels, these quantities are shown for all 3D runs performed in this study, including the constant radial grid spacing solution for χ = 60°, represented by the dashed red line.

In the text

	Fig. 4. Radial evolution of the kinetic energy flux carried by the particles, Lpart = ∬n(γ − 1)mec2vrr2sinθdθdϕ (dashed blue line), along with the Poynting flux, L (solid red line) and the total power, Ltot = L + Lpart (thick solid black line) for χ = 60°. Luminosities are normalized by the monopole spindown power L0.
In the text

Fig. 5. Top: convergence study of dissipation with grid spacing and numerical resolution using 2D simulations (see Table 1 for grid parameters). The 3D run with χ = 85° is reported here for comparison with 2D runs (black solid line). Middle: dependence of dissipation with the plasma magnetization for κ⋆ = 20. Bottom: dependence of dissipation with the plasma multiplicity for σ⋆ = 250. The dashed lines are best-fit models to the analytical solution proposed in Sect. 4, Eq. (20). In all panels, the Poynting flux is normalized to its light-cylinder value, L/LLC.

In the text

Fig. 6. Top: ϕ-averaged plasma bulk Lorentz factor in the striped wind region within 80° ≤θ ≤ 100° as a function of radius Γ(r). The dotted black line is the monopole prediction, $\mathrm{\Gamma }={(1+r^2{\sin }^2\theta /R_{\text{LC}}^2)}^{1/2}$. The dashed green line is the Michel magnetization parameter, μM (see Eq. (11)), to the power 1/3. The fast magnetosonic point is located at the yellow star, where ${\mathrm{\Gamma }}_{\mathrm{fms}}={\mu }_{\mathrm{M}}^{1/3}$. Bottom: θ-dependence of Γ(θ). Vertical dashed lines delimit the extension of the striped wind region. The black dotted line is a sinθ profile, as expected from the monopole solution.

In the text

	Fig. 7. Top panel: normalized particle energy spectrum, (γ/N)dN/dγ, within the spherical shells of radius r and r + RLC as a function of radius (color-coded) for χ = 60°. Middle panel: latitudinal dependence (color-coded) of the particle energy spectrum averaged between 40 ≤ r/RLC ≤ 50 for χ = 60°. Bottom panel: total particle spectra beyond r = 40 RLC and 80° ≤θ ≤ 100° for χ = 30°, 60°, and 85°.
In the text

Fig. 8. Top: ϕ-profile of the normalized current density flowing along the θ-direction in the equatorial plane (θ = 90°) for r = 48 RLC and χ = 60°. The locations of the current sheets and wind regions are labeled “Layer 1,” “Layer 2,” and “wind,” respectively. Middle: corresponding ϕ-resolved particle energy spectrum. Bottom: decomposition of the total particle spectrum in the striped region (dashed black line) into a wind component (solid red line) and a layers component (solid blue line). The vertical dotted lines show γ = Γ∞ ≈ 11 and γ = σLC ≈ 50.

In the text

	Fig. 9. Radial profile of Jθ (dashed black line), Bϕ (red line), and JθBϕ (blue line) for κ⋆ = 0.2 (top), 2 (middle), and 20 (bottom). Jθ is normalized to the Goldreich-Julian current density, JGJ = (B⋆/P)(r⋆/r)2, and Bϕ is normalized by the monopole solution, $B_{\varphi }^{\mathrm{Michel}}=B_{\star }(R/R_{\mathrm{LC}}){(r_{\star }/r)}^2$.
In the text

Fig. 10. Evolution of the dissipation rate βrec (blue line, dots, and axis) and the extrapolated full dissipation radius of the stripes $R_{\mathrm{diss}}/R_{\mathrm{LC}}=exp({\beta }_{\mathrm{rec}}^{-1})$ (red line, dots, and axis) with the typical plasma multiplicity measured at secondary current sheets, κX. The estimated radius of the Crab pulsar wind termination shock is shown by the horizontal dotted line (RTS/RLC ∼ 109) for comparison.

In the text