| Issue |
A&A
Volume 641, September 2020
|
|
|---|---|---|
| Article Number | A103 | |
| Number of page(s) | 20 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202038289 | |
| Published online | 15 September 2020 | |
Gas and dust from metal-rich AGB stars
1
INAF, Observatory of Rome, Via Frascati 33, 00077 Monte Porzio Catone (RM), Italy
e-mail: paolo.ventura@inaf.it
2
Konkoly Observatory, Research Centre for Astronomy and Earth Sciences, Konkoly Thege Miklós út 15-17, 1121 Budapest, Hungary
3
ELTE Eötvös Loránd University, Institute of Physics, Budapest 1117, Pázmány Péter sétány 1/A, Hungary
4
School of Physics and Astronomy, Monash University, VIC 3800, Australia
5
INAF, Astrophysics and Space Science Observatory, Via Piero Gobetti 93/3, 40129 Bologna, Italy
6
Dipartimento di Fisica e Astronomia “Galileo Galilei”, Univ. di Padova, Vicolo dell’Osservatorio 3, Padova 35122, Italy
Received:
29
April
2020
Accepted:
29
June
2020
Context. Stars evolving through the asymptotic giant branch (AGB) phase provide significant feedback to their host system, which is both gas enriched in nuclear-burning products, and dust formed in their winds, which they eject into the interstellar medium. Therefore, AGB stars are an essential ingredient for the chemical evolution of the Milky Way and other galaxies.
Aims. We study AGB models with super-solar metallicities to complete our vast database, so far extending from metal-poor to solar-chemical compositions. We provide chemical yields for masses in the range 1−8 M⊙ and metallicities Z = 0.03 and Z = 0.04. We also study dust production in this metallicity domain.
Methods. We calculated the evolutionary sequences from the pre-main sequence through the whole AGB phase. We followed the variation of the surface chemical composition to calculate the chemical yields of the various species and model dust formation in the winds to determine the dust production rate and the total dust mass produced by each star during the AGB phase.
Results. The physical and chemical evolution of the star is sensitive to the initial mass: M > 3 M⊙ stars experience hot bottom burning, whereas the surface chemistry of the lower mass counterparts is altered only by third dredge-up. The carbon-star phase is reached by 2.5−3.5 M⊙ stars of metallicity Z = 0.03, whereas all the Z = 0.04 stars (except the 2.5 M⊙) remain O-rich for the whole AGB phase. Most of the dust produced by metal-rich AGBs is in the form of silicate particles. The total mass of dust produced increases with the mass of the star, reaching ∼0.012 M⊙ for 8 M⊙ stars.
Key words: stars: AGB and post-AGB / stars: evolution / stars: abundances / stars: winds, outflows
© ESO 2020
1. Introduction
In recent years, we have witnessed a growing interest in stars evolving through the asymptotic giant branch (AGB) phase because they have been recognised to play an important role in several astrophysical contexts, from the interpretation of the chemical patterns traced by Milky Way stars (e.g. Romano et al. 2010), to the formation of multiple populations in globular clusters (Ventura et al. 2001; D’Ercole et al. 2008) and the contribution to the overall dust budget in the local Universe and at high redshift (Valiante et al. 2009). Several groups have modelled this stellar evolutionary phase, which is characterised by the occurrence of a series of thermal pulses (TP), providing an accurate description of the main evolutionary and structural properties of AGB stars of different mass and metallicity and the chemical yields from these objects. These are essential ingredients to understanding the feedback from these stars to the host system (Cristallo et al. 2011, 2015; Karakas 2010; Karakas & Lattanzio 2014; Karakas et al. 2018).
Recent models also couple the modelling of the AGB evolution with the description of the dust formation process that takes place in the wind expanding from the central star (e.g. Ventura et al. 2012, 2014a; Nanni et al. 2013, 2014). Our research has so far been mostly focused on metal-poor (Ventura et al. 2012; Di Criscienzo et al. 2013) and sub-solar metallicity (Ventura et al. 2014b) AGB models. The former were used to explore the dust contribution from AGB stars at high redshift and in Local Group galaxies harbouring only metal-poor populations (Dell’Agli et al. 2019). The Z = 4−8 × 10−3 models were the starting point to characterise the evolved populations of the Magellanic Clouds (Dell’Agli et al. 2014a; Dell’Agli et al. 2015a; Dell’Agli et al. 2015b). The advent of Gaia pushed the interest towards solar metallicities, which were studied by Di Criscienzo et al. (2016) and Ventura et al. (2018). In this paper, we take a further step forward, studying the behaviour of super-solar metallicity AGB stars, Z = 0.03 and Z = 0.04.
The exploration of the super-solar metallicity regime is particularly important given the recent results from Galactic surveys (Casagrande et al. 2011; Bensby et al. 2014), that showed that stars with ages in the range of 5−10 Gyr currently found in the solar neighbourhood span the metallicity range from 0.2 to 2.5 solar, which can be interpreted as the effects of migration mechanisms taking place within the Galaxy (Minchev et al. 2013; Kubryk et al. 2015; Spitoni et al. 2015). Furthermore, recent studies showing evidence of a significant fraction of metal-rich stars in the Galactic centre (Schultheis et al. 2019) suggest that this region is characterised by a very high average metallicity, to the order of 1.5 solar. Thorsbro et al. (2020) analysed a sample of giants in the Galactic centre and found a metallicity distribution extended to [Fe/H] = +0.5. Lastly, we recall recent results selected from LAMOST, combined with Gaia DR2 data, which outline the presence of super-metal-rich stars, both with thin-disc and thick-disc kinematics, which again invokes radial migration. Out of the Milky Way, super metal-rich stars were suggested as possible major components in the nuclear regions of massive elliptical galaxies (Bertola et al. 1995).
While understanding that the gas pollution from metal-rich stars is crucial to the study of the Milky Way and other galaxies, most current grids of stellar yields in literature only cover up to solar metallicity. When the yields are implemented in galactic chemical evolution models, some interpolation is needed between adjacent metallicity grids. Unless the yields vary monotonically with metallicity, this is clearly an unsafe procedure. When the metallicity exceeds solar, the yields are either kept the same as their solar values or extrapolated somehow, with the first choice being the most common one. While this does not affect the results of chemical evolution studies focusing on dwarf galaxies or the external regions of the Milky Way, it might severely affect the predictions regarding the inner Galaxy evolution, as well as the interpretation of data for massive ellipticals at both low and high redshifts. In fact, when large fractions of super-solar metallicity stars are formed, the adoption of solar-metallicity yields may result in spurious results. As far as AGB stars are concerned, this is especially true for elements such as He, 13C, 14N, and 17O that are produced in significant amounts by intermediate-mass stars.
Models of nucleosynthesis and dust formation for AGB stars of super-solar metallicity are also needed to address the origin of meteoritic stardust grains, the vast majority of which originated from AGB stars (see, e.g. the review by Zinner 2014). Based on their isotopic anomalies, it has been proposed that a significant fraction of silicon carbide (SiC) grains extracted from meteorites originated from AGB stars of super-solar metallicity (Lugaro et al. 2014, 2018), and that the efficiency of the formation of SiC dust around AGB stars as function of the metallicity may be responsible for the higher than expected number of grains from super-solar metallicity AGB stars (Lewis et al. 2013). Furthermore, SiC grains from such AGB stars of super-solar metallicity are the best candidates to be the mineral carriers responsible for the anomalies in the elements heavier than iron predominant in different Solar System bodies, and they provide us information on the evolution of dust in the protosolar disc (Ek et al. 2019). Also, to address the problems related to meteoritic stardust, the models of metallicities above solar, including both nucleosynthesis and dust formation, represent one of the most promising current tools.
The paper is organised as follows: in Sect. 2, we discuss the main uncertainties affecting the modelling of the AGB phase; Sect. 3 presents the numerical and physical ingredients used to model the evolution of the stars and of the dust formation process; the evolution of stars before and during the AGB phase are described in Sects. 4 and 5, respectively; and Sect. 6 regards the chemical yields of the stars. In Sect. 7, our results are compared to models of similar metallicities available in the literature; in Sect. 8, we report the properties of the dust formed in the wind of AGB stars in terms of grain size distribution, the dust production rate, and the mass of dust formed; and conclusions are made in Sect. 9.
2. The uncertainties affecting AGB modelling
Before describing the physical and numerical ingredients used in the present investigation, we believe it is important to stress that the results regarding the AGB modelling are rendered uncertain by the scarce knowledge of two physical mechanisms. These mechanisms are relevant to the description of the evolution of these stars, which are still poorly known from first principles: convection and mass loss (Karakas & Lattanzio 2014).
The importance of convection on the AGB evolution is twofold, as the description of convective regions concerns both the efficiency of the convective modality of transport of energy and the location of the border of the instability regions, within which chemical mixing takes place.
The efficiency of convection reflects into the temperature gradient and is particularly relevant when determining the temperature at the base of the external mantle, which, in turn, is connected with the possible ignition of hot bottom burning (HBB), which consists of the activation of proton captures in the innermost regions of the convective envelope, once the temperatures exceed ∼30 MK (Renzini & Voli 1981; Blöcker & Schöenberner 1991; Sackmann & Boothroyd 1991). Ventura & D’Antona (2005a) showed that the strength of HBB is extremely sensitive to convection modelling, and, within the classic mixing length theory schematization, to the choice of the free parameter α, giving the mixing length in terms of the local value of the pressure scale height. The AGB phase is the only case, within the stellar astrophysical context, where the choice of the convective model affects not only the external temperature and the colours, but also the physical evolution of the star, namely the luminosity reached and the duration of this peculiar evolutionary phase (Ventura & D’Antona 2005a).
An important point related to convection is the location of the borders of the instability regions. Within the context of AGB modelling, it is of paramount importance to determine the extent of the third dredge-up (hereinafter TDU). The TDU is the inwards penetration of the convective envelope, taking place after each thermal pulse of the He burning shell, down to layers previously affected by nucleosynthesis via the triple-alpha reactions, thus enriched in carbon (Iben 1974). When the plain Schwartzschild criterion is adopted, with no assumptions regarding possible extra-mixing from the bottom of the convective envelope, the extent of TDU is too small to reproduce the observational evidence, particularly the luminosity function of carbon stars in the Magellanic Clouds (however, see Straniero et al. 1997 regarding the possibility that models without extra mixing are able to produce a deep TDU). An early algorithm aimed at calculating the extent of the extra-mixed zone was proposed by Lattanzio (1986) and is still used by the team using the MONASH code (Karakas 2014; Karakas & Lattanzio 2014; Karakas et al. 2018). Several research groups adopt a velocity profile decaying from the base of the envelope towards the stellar interior, with the e-folding distance of the decay being treated as a free parameter (Herwig 2000, 2005; Cristallo et al. 2009; Weiss & Ferguson 2009). We reiterate here that all these treatments require some ad hoc assumptions, because the details of the mixing mechanism, and more generally of the convective phenomenon, close to the borders, is substantially unknown from first principles: the extent of TDU can be empirically determined by fitting the observational scenario, but cannot be found on the basis of solid physical arguments.
The description of mass loss has an extreme importance in the modelling of the AGB phase, comparable to the role played by convection. The rate at which the mass of the envelope of AGB stars is expelled into the interstellar medium affects the duration of the AGB phase and has relevant effects on the largest luminosity reached, the degree of nucleosynthesis associated with HBB, and the amount of carbon that is gradually accumulated in the surface regions via TDU (Ventura & D’Antona 2005b).
Mass loss is commonly described by analytical relations, that allow the computation of Ṁ as a function of the main stellar parameters, in particular the radius and the surface gravity.
Several evolutionary codes adopt the classic period–mass loss rate relation by Vassiliadis & Wood (1993), which was calibrated on the basis of Galactic Mira variables and pulsation OH/IR stars in the Galaxy and the Large Magellanic Cloud. The Vassiliadis & Wood (1993) recipe is used both for O-rich and carbon stars (Cristallo et al. 2009; Karakas & Lattanzio 2014).
Some groups (Weiss & Ferguson 2009) model mass loss during the O-rich AGB phases via the empirical period–mass loss relation by van Loon et al. (2005), which is based on the observations of dust-enshrouded M-stars in the Magellanic Clouds. One of the most widely used prescriptions for mass loss by M-rich AGBs is the treatment by Blöcker (1995), based on hydrodynamical models of pulsating M-type stars (Karakas et al. 2018; Pignatari 2016).
Regarding the C-rich phase, alternatively to Vassiliadis & Wood (1993), several research teams based their computations on the theoretical radiation-hydrodynamical models published by the Berlin group (Wachter et al. 2002, 2008), which considered dust production in C-rich winds and the effects of radiation pressure on the carbonaceous dust particles formed in the circumstellar envelope (Weiss & Ferguson 2009; Ventura et al. 2018).
The main shortcoming of the use of the above prescriptions is their application to a wide range of mass and metallicities, despite the fact that these relationships have been derived on the basis of limited samples of stars, mostly homogeneous in the chemical composition. Furthermore, some of these prescriptions contain free parameters (e.g. the Reimers parameter entering the Blöcker (1995) recipe) that require further calibration.
The situation is even more complex for C-stars if we consider that the formulae of Wachter et al. (2002, 2008) do not include any dependence on the actual carbon excess with respect to oxygen, which intuitively should affect the amount of dust formed in the wind of the stars. Wachter et al. (2002) showed that the dependence of the mass loss rate on this quantity is weak enough to be ignored in comparison with all other uncertainties, but this statement was seriously disputed by Mattsson et al. (2008), who stressed the decisive role of the carbon excess in the dust formation process and in the determination of the mass loss rate.
3. Physical and numerical input
3.1. Stellar evolution modelling
The models presented in this paper were calculated with the ATON stellar evolution code (Ventura et al. 1998). An exhaustive description of the numerical details of the code and the most recent updates can be found in Ventura et al. (2013). The models span the mass interval 1M⊙ ≤ M ≤ 8 M⊙. The metallicities used are Z = 0.03 and Z = 0.04, and the scaled-solar mixture adopted is taken from Grevesse & Sauval (1998). The initial helium is Y = 0.30. The models not undergoing the helium flash were evolved from the pre-main sequence until the almost total consumption of the envelope. Low-mass models (M ≤ 2 M⊙) experiencing the helium flash were evolved from the horizontal branch, starting from the total mass, core mass, and surface chemical composition calculated up to the tip of the red giant branch.
The temperature gradient within convective regions is calculated via the full spectrum of turbulence (FST) model (Canuto & Mazzitelli 1991). The overshoot of convective eddies within radiatively stable regions is modelled by assuming that the velocity of convective elements decay exponentially beyond the neutrality point, fixed via the Schwartzschild criterion. The e-folding distances of the velocity decays that occur during the core (hydrogen and helium) burning phases and during the AGB phase are taken as 0.02HP and 0.002HP, respectively. The former was calibrated on the basis of the observed width of the main sequences of open clusters (Ventura et al. 1998), while the latter was found by reproducing the luminosity function of carbon stars in the Magellanic Clouds (Ventura et al. 2014b).
The mass-loss rate for oxygen-rich models is determined via the Blöcker (1995) treatment with the parameter entering the Blöcker (1995) formula set to η = 0.02, following the calibration given in Ventura et al. (2000). For carbon stars, we implemented the description of mass loss from the Berlin group (Wachter et al. 2002, 2008).
The radiative opacities are calculated according to the OPAL release, in the version documented by Iglesias & Rogers (1996). The molecular opacities in the low-temperature regime (T < 104 K) are calculated with the AESOPUS tool (Marigo & Aringer 2009). The opacities are constructed self-consistently and by following the changes in the chemical composition of the envelope, particularly of the individual abundances of carbon, nitrogen, and oxygen.
3.2. Dust production
The formation and growth of dust particles in the wind of AGB stars is described according to the schematization proposed by the Heidelberg group (Ferrarotti & Gail 2006), previously used by our team (Ventura et al. 2012, 2014a, 2015; Ventura et al. 2016), and in a series of papers by the Padua group (Nanni et al. 2013, 2014, 2016; Nanni et al. 2018, 2019, 2020). All the relevant equations can be found in Ventura et al. (2012). Here, we only provide a brief description of the methodology.
Dust particles are assumed to form and grow in the wind, which expands isotropically from the central star. The wind dynamics are described by the momentum equation, where the acceleration is determined by the balance between gravity and radiation pressure acting on the newly formed dust grains. The coupling between grain growth and wind dynamics is given by the extinction coefficients, describing absorption and scattering of the radiation by dust particles. The evolution of the dust grains over time is determined by the balance between the growth and the vaporisation rate. The former is given by the gas molecules hitting the already formed grains, and the latter is related to the vapour pressure of gaseous molecules over the solid compounds. Regarding the dust species formed, in oxygen-rich environments, the most stable compounds are considered: silicates, alumina dust (Al2O3), and solid iron. In the winds of carbon stars, the species considered are silicon carbide (SiC), solid carbon, and solid iron. This description allows the determination of the surface fraction of gaseous silicon, aluminium, iron, and carbon condensed into dust particles (see eq. 20–23 and 34–35 in Ferrarotti & Gail 2006) and the dust production rate for each dust species, which depends on the mass-loss gas rate, the surface mass fractions of the aforementioned chemical elements, and the fraction of the latter species condensed into dust (see Sect. 5.2 in Ferrarotti & Gail 2006).
4. The evolutionary phases before the AGB
The Z = 0.03 and Z = 0.04 evolutionary sequences discussed in the present investigation were calculated from the pre-MS phase until the almost complete ejection of the external mantle. A summary of the main properties of the models presented here, regarding the core hydrogen and helium burning phases and the AGB evolution, are reported in Table 1.
Main structural properties of our stellar models.
Before the beginning of the AGB phase, stars experience two episodes during which the surface convection penetrates inwards, until reaching zones of the star previously contaminated by nuclear activity: the first dredge-up episode takes place during the ascent of the red giant branch, while the second dredge-up episode occurs after the core helium burning phase, before the ignition of the first TP. These mixing events are extremely important, as they determine the surface chemical composition of the star at the beginning of the AGB phase. While the first dredge-up changes the surface chemical composition of all stars, the second dredge-up, in the metallicity domain investigated here, is experienced only by M ≥ 4.5 M⊙ stars. This second dredge-up event is relevant for the subsequent evolution of the stars during the AGB phase, as it causes a significant decrease in the core mass of the star, which affects the main properties of the AGB evolution. Figure 1 shows the changes in the surface mass fractions of helium and of the most relevant CNO isotopes determined by the two dredge-up events.
 |
Fig. 1. Changes in the surface mass fraction of helium (top-left panel), 12C (top right), 14N and 16O after the first (full points) and the second (open points) dredge-up episode of the AGB stars of metallicity Z = 0.03 (red squares) and Z = 0.04 (blue diamonds). The horizontal lines in each panel indicate the initial mass fractions of the same species. |
The first dredge-up favours the rise in the surface helium content, which on average increases by δY ∼ 0.02, although concerning stars of masses close to ∼2 M⊙, δY is limited to ∼0.01. A well known consequence of the first dredge-up is the drop in the surface mass fraction of 12C, which we find to be between −0.002 < δX(12C) < −0.001, and the rise in the nitrogen content. The latter quantity is sensitive to the mass of the star, with the percentage increase ranging from ∼50% for solar mass stars, to a factor ∼3 in M ≥ 3 M⊙ stars. The surface content of 16O decreases by less than 10%, the largest depletion taking place in the interior of M > 4 M⊙ stars. In stars of initial mass above 3 M⊙, the base of the envelope reaches regions where sodium was produced by 22Ne(p,γ)23Na reactions: in this mass domain, the surface sodium increases by 40−50%.
The extent of the changes in the mass fractions of the various species given above must be considered as lower limits, because the present results have been obtained by considering only convective mixing, without considering additional effects such as thermohaline or rotation-induced mixing. Such effects might trigger further changes in the chemical composition of the surface regions (Pinsonneault 1997; Charbonnel & Lagarde 2010; Lagarde et al. 2012).
In the discussion of the effects of the second dredge-up, we focus on stars of masses above 4 M⊙. In lower mass objects, the inwards penetration of the convective envelope following the end of the core helium burning phase is not sufficiently deep to reach regions that were previously sites of nuclear activity. As discussed previously, one of the most important effects of the second dredge-up is the decrease in the core mass, which is highly sensitive to the initial mass of the star: in 4.5 M⊙ stars δMC ∼ −0.03 M⊙, while in 8 M⊙ stars δMC ∼ −0.6 M⊙.
The decrease in core mass is related to the capability of the external mantle to penetrate inwards, past the H-He discontinuity. This process, which is made easier by the temporary extinction of the H-burning shell, favours the transportation of helium-rich material towards the surface layers, which become more and more enriched in helium (Boothroyd & Sackmann 1999). This effect is stronger the higher the mass of the star (Ventura 2010); the helium enrichment spans the range from δY = 0.01 for M = 4.5 M⊙ stars, to δY = 0.07 for M > 6M⊙ stars.
Additional consequences of the occurrence of the second dredge-up are a further reduction of the surface mass fractions of 12C and 16O and the increase in the surface 14N. For all these chemical species, similarly to helium, the extent of the change in the surface content increases with the mass of the star. This is almost null in stars of masses around 4.5 M⊙, and it reaches a maximum extent in M > 6 M⊙ stars. These results are shown in Fig. 1.
5. The AGB phase of metal-rich stars
After the end of the core helium burning phase, the stars of masses M ≤ 8 M⊙ develop a core composed of carbon and oxygen, which evolves under conditions of electron degeneracy. The only exceptions to this general behaviour are the stars of mass M ≥ 7 M⊙, which experience off-centre carbon burning and develop a convective flame that moves inwards, forming a zone enriched in oxygen and neon close to the stellar centre. The subsequent evolution is commonly referred to as “super-AGB” (e.g. Garcia-Berro & Iben 1994; Siess 2007).
The energy supply is provided for ∼95% of the time by a CNO burning shell: periodically a helium-rich region just above the core is ignited in conditions of thermal instability (Schwarzschild & Härm 1965), which explains the use of the terminology “thermal pulse” to refer to these episodes. The inter-shell zone between the He-rich buffer where the TPs develop and the CNO burning shell is composed essentially of helium, carbon, oxygen, and neon, with mass fractions (He, C, O, Ne)∼(55%,38%,4%,3%). This distribution, which is relevant to the s-process nucleosynthesis and the relative surface enrichment, is extremely sensitive to the treatment of convective borders and to the assumption of extra mixing from the base of the pulse driven convective shell.
The core mass is the key factor in the AGB evolution: the higher the core mass, the higher the degree of degeneracy in the internal regions. This translates into larger pressures and temperatures within the CNO burning shell, which most of the time supports these structures energetically. This is the reason for the tight relationship between the core mass and luminosity of AGB stars, which was initially predicted in a classic paper by Paczyński (1970). The core mass–luminosity trend for some of the stars considered here is shown in Fig. 2; the evolutionary sequences in this plane are similar to those published in Karakas & Lattanzio (2014, see their Fig. 18).
 |
Fig. 2. Evolution of high-metallicity AGB models in the core mass–luminosity plane. The black line shows the theoretical relationship derived by Paczyński (1970). |
The top panels of Fig. 3 show the highest luminosity and temperature at the base of the envelope attained during the AGB phase. To understand the role of metallicity we also show the solar metallicity models published in Ventura et al. (2018). These plots highlight the difference between the evolution of the stars with initial masses M > 3 M⊙ and their lower-mass counterparts, which evolve to much lower luminosities and temperatures. The sudden drop of Tbce occurring around 3 M⊙ is clearly visible. This behaviour is related to the ignition of HBB, which requires core masses to the order of ∼0.8 M⊙ (Ventura et al. 2013) and strongly affects the surface chemistry. The results reported in the bottom-right panel of Fig. 3 show the significant effect of HBB on the final C/O surface ratio, defined as the ratio of the sum of the surface number densities of the carbon isotopes, divided by the sum of the number densities of oxygen isotopes; at the base of the convective envelope, 12C nuclei are exposed to p-capture reactions, which decrease the surface carbon content and the C/O ratio.
 |
Fig. 3. Maximum luminosity (top-left panel) and temperature at the base of the envelope (top, right) experienced by our AGB models of metallicity Z = 0.03 (red squares) and Z = 0.04 (blue diamonds) as a function of the initial mass. The bottom panels show the duration of the TP-AGB phase (left) and the final C/O (right). For comparison, we also show solar metallicity models by Ventura et al. (2018) (black points), Z = 0.03 models by Karakas (2014) (green triangles), and Z = 0.04 models by Weiss & Ferguson (2009) (magenta asterisks). |
The ignition of HBB also has profound effects on the physical evolution of AGB stars: it results in a fast rise in luminosity (Blöcker & Schöenberner 1991), with significant deviations (see Fig. 2) from the core mass–luminosity relationship predicted by Paczyński (1970). This is accompanied by the increase in the mass-loss rate, which shortens the duration of the AGB phase. This is shown in the bottom-left panel of Fig. 3, where the timescale of the AGB phase of M > 3 M⊙ stars is on average more than one order of magnitude shorter than for the lower masses. Specifically, in the low-mass domain, the behaviour of the duration of the TP-AGB phase, τAGB, is not monotonically related to the initial mass of the star. In the 1−2.5 M⊙ range, τAGB increases with the initial mass, because the higher the mass, the larger the number of TPs experienced before the entire envelope is lost, which makes the AGB phase longer (see bottom, left panel of Fig. 3). For higher mass stars, the most relevant point to τAGB is that the core mass, and hence the luminosities, are larger, which leads to shorter timescales. In the low-mass domain, the stars evolving faster along the AGB phase, with τAGB ∼ 1 Myr, are the 1 M⊙ and 3.5 M⊙ stars. The stars with the longest AGB life, to the order of 2.5 Myr, are those with initial masses of 2.5 M⊙ (see Col. 5 of Table 1).
The comparison between the present models and those by Ventura et al. (2013, 2014b, 2018) indicates that the threshold mass at which the ignition of HBB occurs is in the range of 3−3.5 M⊙ for all the metallicities Z ≥ 4 × 10−3. The metallicity trends illustrated in Fig. 3 reflect a well-established property of AGB stars: the lower the metallicity, the larger the temperature at the base of the envelope (Tbce), and, as a consequence, the luminosity (Ventura et al. 2013). This is particularly important in the M > 3 M⊙ domain, where the degree of the p-capture nucleosynthesis due to HBB is extremely sensitive to Tbce (Dell’Agli et al. 2018). The metallicity effect on the evolutionary timescales for the stars experiencing HBB is straightforward: the higher the metallicity, the lower the luminosity, and the longer the duration of the AGB phase. In the low-mass domain, the behaviour is the opposite: higher metallicity stars evolve at lower effective temperatures and larger radii, thus they experience higher mass-loss rates, which shortens the AGB phase.
Besides HBB, the surface chemical composition of AGB stars can be modified by the occurence of a third dredge-up (TDU). This is the inwards penetration of the convective envelope that takes place after each thermal pulse (TP) of the He-burning shell and goes down to layers previously affected by nucleosynthesis via the triple-alpha reactions, and thus enriched in carbon (Iben 1974). The alteration determined by TDU is significantly different than HBB: in this case the main effect is the gradual increase in the surface carbon, which can lead to the formation of a carbon star, once the number density of carbon atoms exceeds the number density of oxygen. The efficiency of each TDU event is commonly described by λ, which is defined as the ratio between the decrease in the core mass favoured by TDU, and the increase in the core mass that occurred since the previous TP (during the quiescent CNO burning phase).
In Table 2, we report for each stellar mass and for the two metallicities discussed here, the relevant information describing the occurrence and the effects of TDU. By this we mean the core masses of the star when the first TDU takes place, the core mass and luminosity when the C-star stage is reached, the duration of the C-star phase, and the maximum λ experienced. Given the significant difference in their evolutions, we describe the stars in the low-mass domain (M ≤ 3.5 M⊙) and the higher mass stars that experience HBB separately.
Properties of the stars related to the occurrence of TDU events and the achievement (if any) of the C-star stage.
5.1. The evolution of massive AGB stars
The variation of the main physical properties of metal-rich, massive AGB stars over time are shown in Fig. 4. These stars experience an initial phase during which the luminosity and Tbce increase (see top panels of Fig. 4), owing to the gradual rise in the mass of the core (bottom-left panel of Fig. 4); both quantities decline in the final AGB phases after a significant fraction of the envelope is lost. The mass-loss rate shown in the bottom-right panel of Fig. 4 follows a similar trend considering the link between mass loss and luminosity, which is generally expected and is particularly tight according to the Blöcker (1995) treatment of mass loss adopted in the present investigation. The effective temperature Teff of the Z = 0.03 stars decreases during the AGB lifetime, with Teff ∼ 3500 K during the initial TPs, and Teff ∼ 2300 K during the final AGB phases; this behaviour is substantially independent of the initial mass of the star. Furthermore, Z = 0.04 stars follow a similar decreasing trend, the difference with respect to the Z = 0.03 case being that the effective temperatures are ∼100 K cooler.
 |
Fig. 4. Variation with time (starting from the beginning of the TP-AGB phase) of the luminosity (top-left panel), temperature at the base of the envelope (top-right panel), core mass (bottom left) and mass-loss rate (bottom right) during the AGB phase of stars of metallicity Z = 0.03 (red squares) and Z = 0.04 (blue diamonds) of initial mass 4, 5, 6, 7 M⊙. The points along the different tracks refer to the middle of the inter-pulse phase. |
Both the average and the peak luminosity (the latter in the 20−80 × 103 L⊙ range) are strongly sensitive to the initial stellar mass. The differences in the luminosity among stars of different masses are reflected in the duration of the AGB phase, which varies from ∼5 × 104 yr for 8 M⊙ stars, to ∼3 × 105 yr for 4 M⊙ stars. The luminosities and temperatures reached by the Z = 0.03 stars are generally higher than their Z = 0.04 counterparts, the differences being below ∼15% in all cases.
Figure 5 shows the variation in the surface chemical composition of the stars reported in Fig. 4. The alteration of the surface chemistry is mostly due to HBB, because the efficiency of TDU is low in this mass domain. Generally speaking, this behaviour is associated with the strength of TPs, which is weaker than in the lower mass counterparts. A further effect that is particularly relevant when convection is described by means of the FST is related to the strong HBB experienced, which accelerates the AGB evolution in such a way that the external mantle is lost before deep TDU events take place. As reported in Table 2, the TDU efficiency is λ < 0.2 for the stars experiencing HBB. Similar behaviour was found in the solar metallicity models discussed in Ventura et al. (2018).
 |
Fig. 5. Variations with time of the surface mass fraction of 12C (top-left panel), 14N (top right), lithium (bottom left), and the 12C/13C ratio (bottom right) of the same models shown in Fig. 4 (except for the 6 M⊙ model, omitted here for the sake of readibility). The black dots refer to a 4 M⊙ star of solar metallicity, published in Ventura et al. (2018), while the other symbols are the same as in Fig. 4. |
The ignition of HBB triggers the reduction of the surface carbon: the final surface 12C is depleted by a factor of 15 (20) in Z = 0.03 (Z = 0.04) stars (see top-left panel of Fig. 5); the final 12C/13C reaches the equilibrium value of ∼4 in all cases. This is consistent with the results shown in the bottom-right panel of Fig. 3, where we see that the final C/O is below ∼0.1 in the high-mass domain. The initial mass affects the timing when the modification of the surface chemistry occurs: while in the higher mass stars, carbon depletion starts from the very first thermal pulses. In the 4 M⊙ case, this takes place only after the star has experienced several TPs. This is consistent with the evolution of the Tbce of stars of different masses, which is shown in the right panel of Fig. 4.
In this metallicity domain, the surface oxygen is only scarcely affected by HBB. This is consistent with the results of Ventura et al. (2018), who found that oxygen destruction is negligible in massive AGB stars of solar metallicity. Therefore, the nucleosynthesis experienced at the base of the envelope is essentially pure CN cycling, which results in a direct relationship between the number of 12C nuclei destroyed and the number of 14N synthesized (see top-right panel of Fig. 5). The nitrogen abundance is higher in Z = 0.04 stars compared to Z = 0.03, due to the larger initial abundance of 12C.
While HBB is potentially able to activate all the p-capture channels, until the synthesis of silicon, we find that in the stars discussed here the Mg-Al chain is not activated; this is related to the temperatures attained at the bottom of the convective envelope (see Fig. 4), below 108 K, which is the threshold required to ignite the first reaction of the chain, meaning proton capture by 24Mg nuclei. This is consistent with the analysis of Dell’Agli et al. (2018), which focused on the temperatures at the base of the external mantle required to activate the different nuclear channels and the largest degree of nucleosynthesis activated in massive AGB stars of different metallicities.
The temperatures at the base of the convective envelope (Fig. 4) are above 40 MK, which is the threshold required to activate the series of reactions that leads to the synthesis of lithium (Cameron & Fowler 1971). As shown in the bottom-left panel of Fig. 5, the stars evolve as lithium-rich for a significant fraction of the AGB phase; this is different to the behaviour of their lower metallicity counterparts, where the survival of lithium in the surface regions, particularly in the most massive stars, is limited to very few TPs (Ventura et al. 2000). The long duration of the Li-rich phase is due to the metallicity trend of the temperatures at the bottom of the envelope (discussed above). In metal-rich stars, the Tbce are lower than in solar and sub-solar AGBs, which allows a longer survival of 3He, the essential ingredient to lithium production (Sackmann & Boothroyd 1992). While lithium production by massive AGB stars is larger in the high metallicity domain, the overall lithium expelled by AGB stars is not sufficient to explain the lithium versus metallicity trend exhibited by Milky Way stars (Romano et al. 2001), which suggests that other sources must be responsible for the lithium enrichment of the interstellar medium.
5.2. Low-mass AGB stars
Stars of initial mass M ≤ 3 M⊙ do not experience HBB. The variation in their surface chemical composition during the AGB lifetime is only driven by TDU. In this section, we include stars of initial mass 3.5 M⊙, because they experience such weak HBB that the TDU plays the dominant role in the modification of their surface chemistry.
Figure 6 shows the variation of the luminosity and of the surface C/O ratio as a function of the current mass of the star. We report the evolution of all the stars with initial masses in the range of 1−3.5 M⊙, with the exception of the 1.25 M⊙ model, which was omitted for readability. The variation over time in the core mass and the mass-loss rate of AGB stars beloning to the low-mass domain are shown in Fig. 7. The gradual increase in the luminosity is determined by the growth of the core mass. The maximum luminosity reached correlates with the initial mass of the star. Additionally, the larger the initial mass, the higher the number of TPs experienced before the envelope is lost, and the larger the final core mass. The efficiency of TDU increases as more and more TPs are experienced; consequently, the stars undergoing the deepest TDU events are those of initial masses around 3 M⊙, for which λ ∼ 0.6 during the final part of the AGB phase (see Table 2). This can be seen in the left panel of Fig. 7.
 |
Fig. 6. Variation with the current mass of the star of the luminosity (left panel) and surface C/O (right panel) of Z = 0.03 (red squares) and Z = 0.04 (blue diamond) stars with initial masses in the range of 1−3.5 M⊙. |
 |
Fig. 7. Variation with time (counted since the beginning of the TP phase) of the core mass (left panel) and mass-loss rate (right panel) of Z = 0.03 and Z = 0.04 models of initial mass 1 M⊙, 1.5 M⊙, 2.5 M⊙, 3 M⊙ and 3.5 M⊙. |
Similarly to their higher mass counterparts, the external regions of the star become cooler and cooler during the AGB phase, with the effective temperatures spanning the same Teff range (2500–3500 K) given in Sect. 5.1. The only exceptions to this common behaviour are the 1 M⊙ models, of which the effective temperatures during the final AGB phase are ∼2800 K, and the 3 M⊙ of metallicity Z = 0.03, which, after becoming carbon stars readjust on a largely expanded configuration with Teff ∼ 2000 K.
The variations of the surface chemistry reflect the effect of the recurrent TDU events, which results in the gradual increase in surface carbon and the consequent rise in the C/O ratio. The accumulation of the surface carbon increases with the initial mass of the star because of the higher number of TDU episodes experienced. We find that at Z = 0.03, only models with initial masses in the range of 2.5−3.5 M⊙ become C-stars in the final evolutionary phases. The present computations show that formation of C-stars is not expected for metallicities Z > 0.03, except in the case of the 2.5 M⊙ star of Z = 0.04 (see Table 3).
Chemical yields of AGB stars of metallicities Z = 0.03, Z = 0.04, and (initial) masses in the range of 1−8 M⊙.
6. The stellar yields
Observations of chemical abundances and abundance ratios can be used to constrain the timescales of galaxy formation (Matteucci 2012), as well as to pin down the shape of the stellar initial mass function (IMF) in galaxies where direct measurements are unfeasible (Romano et al. 2017, 2019; Zhang et al. 2018, and references therein). To interpret the observations, galactic chemical evolution models are needed, which require input stellar yields from stellar evolution calculations. As highlighted in the introduction, it is crucial to provide grids of stellar yields that cover the whole range of metallicities spanned by the observations.
Here, we follow the classical definition of the stellar yield, which is that the yield of a given element i is the net amount of newly produced element that is ejected in the interstellar medium by a star during its life:
The integral is calculated over the entire stellar lifetime, 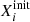 is the mass fraction of species i at the beginning of the evolution, and Ṁ is the mass-loss rate. If the element is destroyed in the stellar interior, then the yield is negative.
is the mass fraction of species i at the beginning of the evolution, and Ṁ is the mass-loss rate. If the element is destroyed in the stellar interior, then the yield is negative.
Figure 8 shows the yields of helium and of the CNO elements of the high-metallicity models discussed in the present work. The helium yield increases with mass, ranging from almost null at the lowest masses, and reaching values to the order of ∼0.6 M⊙ for M ∼ 8 M⊙. The change in the slope of the Y(He) versus the mass relationship is due to the onset of the second dredge-up, which occurs after the exhaustion of the core helium in stars of masses above ∼4 M⊙. This results in a significant increase in the surface helium. The trend with mass is positive, because the higher the mass of the star, the larger the extent of the inwards penetration of the convective envelope taking place during the second dredge-up (Ventura 2010). Since the second dredge-up occurs before the beginning of the TP-AGB phase, its results are more robust than those related to nucleosynthesis and mixing during the TP-AGB phase, whose description is affected by several uncertainties in the physical ingredients adopted (Karakas & Lattanzio 2014). The 12C yields are positive in the low-mass domain, owing to the effect of the TDU, which results in the increase of the surface carbon (see right panel of Fig. 6). The largest yields of 12C, to the order of 0.015 M⊙, are produced by ∼3 M⊙ stars. Massive AGB stars destroy carbon via HBB (see top-left panel of Fig. 5), which is why they produce negative carbon yields. The 16O yields (not shown) are negative for M ≥ 4 M⊙, owing to the effects of HBB. However, even in the most extreme cases such as that of the ∼8 M⊙ stars, the yields are not smaller than ∼ − 0.02 M⊙. This is because the HBB experienced by stars of the metallicities discussed here is not efficient enough to significantly deplete the surface oxygen abundance.
 |
Fig. 8. Yields in solar masses of helium (top-left panel), 12C and 14N (top, right), 13C (bottom, left), and 17O (bottom, right) of our Z = 0.03 (red squares) and Z = 0.04 (blue diamond) AGB models and of solar-metallicity models by Ventura et al. (2018). Green triangles indicate the helium, carbon, and nitrogen yields published in Karakas & Lugaro (2016). |
The nitrogen yields are always positive. In the low-mass domain, this is due to the effects of the first dredge-up, which increases the surface N abundance. No significant further rise in the nitrogen content of the envelope is expected during the TP-AGB phase. The N yields of massive AGB stars reflect the effects of HBB; independently of whether the sole CN or the full CNO cycle is activated, the outcome is the synthesis of significant quantities of nitrogen. The N yields increase with the mass of the star, reaching ∼0.06 M⊙ in the most massive cases.
The yields of the minor isotopes 13C and 17O are found to increase almost monotonically as a function of both stellar mass and metallicity. They increase with the initial mass and metallicity of the star, with the exception of a spike in 13C (17O) production occurring around 3.5(2.5) M⊙ (Fig. 8: left- and right-hand lower panels, respectively). The prominent peak in the 13C yield is related to the combined effects of TDU and HBB in ∼3.5 M⊙ stars, with the former mechanism favouring the increase in the surface 12C, which is later converted into 13C by proton captures. It has recently been pointed out (Romano et al. 2017, 2019; Zhang et al. 2018) that the CNO isotopic ratios may be used to probe the shape of the galaxy-wide IMF in high-redshift, massive dusty starbursts where direct measurements are unfeasible. These objects are thought to host a non-negligible fraction of super-solar metallicity stars (see, e.g. Johansson et al. 2012). Grids of super-solar metallicity yields such as those presented in this study will therefore be extremely useful for spotting IMF variations in extreme environments. The future implementation of our grids of super-solar metallicity stars into chemical evolution models for massive dusty starbursts will allow more robust predictions.
7. Comparison to other studies
Super-solar metallicity models were published by Karakas (2014, hereinafter K14) and Weiss & Ferguson (2009). The K14 models with metallicities Z = 0.03 were calculated by means of the MONASH code. The authors present an exhaustive discussion on the efficiency of the TDU in the high-metallicity domain and how the initial mass and helium affect the AGB evolution. In a subsequent paper, Karakas & Lugaro (2016, hereainfter KL16) presented the gas yields of K14 models, which we compare with the results presented in Sect. 6.
Because the evolution of AGB stars is driven by the mass of the degenerate core, we checked for consistency between the K14 core masses and ours at the beginning of the AGB phase. The core masses reported in Col. 6 of Table 1 are similar to those by K14 for M ≤ 4 M⊙ stars. In the larger mass domain, our core masses are slightly higher than K14, with a ∼0.5 M⊙ shift in the initial mass versus core mass relationship.
The structure differences between our Z = 0.03 models and those published by K14 can be seen in the two panels of Fig. 3, where the peak luminosities and the hottest temperatures reached during the AGB phase are shown. A remarkable difference is that our massive AGB models are brighter and hotter than those of K14, with larger discrepancies for higher initial masses. These differences tend to vanish in the M < 3 M⊙ domain.
Similar differences between our models and MONASH models were found for solar (Ventura et al. 2018) and sub-solar metallicities (Ventura et al. 2015). The main reason for the dissimilarities is the treatment of turbulent convection: we calculated the temperature gradient within regions that are unstable in the face of convection motions via the FST model (see Sect. 3.1), whereas K14 used the mixing length theory (Vitense 1953). As discussed in Sect. 2, the treatment of convection in the envelope deeply affects the physical behaviour of AGB stars, particularly under HBB conditions. Ventura & D’Antona (2005a) showed that FST modelling favours a more efficient nucleosynthesis in the internal regions of the envelope than in the MLT case, which leads to higher luminosities and rates of mass loss.
The differences with K14 are particularly evident in stars of masses corresponding to the minimum threshold required to activate HBB, which is ∼3.5 M⊙ in the present analysis, and ∼4.5 M⊙ in K14. This discrepancy is entirely due to the treatment of convection; we rule out that dissimilarities in the core mass play a role here, because our values (Col. 6 of Table 1) are the same (within 0.02 M⊙) as those of K14 in the same mass range.
The bottom-left panel of Fig. 3 shows the overall duration of the TP-AGB phase. The results presented here and those of K14 are similar in the M > 3 M⊙ domain, despite the large difference in the luminosity, which should make the duration of the AGB phase of our models much shorter than that of K14. Ventura et al. (2018) found that at solar metallicity, the timescale of the AGB phase calculated with the ATON code is between two and three times shorter than the MONASH models of the same mass. The reason for this is in the treatment of mass loss. In fact, ATON uses the description by Blöcker (1995), according to which Ṁ is strongly dependent on the luminosity. The K14 computations are instead based on the Vassiliadis & Wood (1993) treatment, where the mass-loss rate is set to increase with the period of the star. In AGB stars of lower metallicities than presented in this paper, the Blöcker (1995) description leads to higher Ṁ because of the large luminosities typical of the stars experiencing HBB. In this case, the differences between the ATON and MONASH models is enhanced by the larger luminosities attained by ATON models. For the higher metallicities presented in this paper, the situation is different because: (a) HBB is weaker than at lower metallicities, thus the luminosities are smaller (compare the Z = 0.014 and Z = 0.03 lines in the top-left panel of Fig. 3); (b) metal-rich stars evolve to larger radii, which result in generally longer periods. Consequently, at Z = 0.03, the mass-loss rate of Vassiliadis & Wood (1993) is more efficient than that of Blöcker (1995). In massive AGB stars, these effects partly counterbalance those related to the higher luminosities experienced by the ATON models calculated with the FST convection description, making the duration of the whole TP-AGB phase of the present models similar to that of K14. The higher mass-loss rates predicted by the Vassiliadis & Wood (1993) treatment is also the reason why in the Z = 0.03 low-mass domain the duration of the K14 models is shorter than in our models.
The KL16 yields are compared to ours in Fig. 8. The helium yields are similar, with a ∼0.5 M⊙ shift related to the differences in the core masses outlined at the beginning of this section, and to the fact that most of the surface helium enrichment occurs during the second dredge-up, of which the results presented by different research groups are in strong agreement (Ventura 2010). The carbon and nitrogen yields present significant differences related to the different physical behaviour discussed above. The carbon yields presented here are significantly smaller than KL16 for M > 3 M⊙ stars, owing to the much more efficient HBB nucleosynthesis experienced. This is particularly evident in the 3.5−4.5 M⊙ mass range, which exhibits the largest differences in the temperatures at the bottom of the envelope, as shown in the right panel of Fig. 3. The M > 3 M⊙Z = 0.03 models experience a much stronger HBB than KL16, thus producing more nitrogen via 12C proton capture reactions. This is the reason for the differences in the N yields in the right panel of Fig. 8.
The Z = 0.04 models by Weiss & Ferguson (2009) are compared to ours and to K14 in Fig. 3. The comparison is limited to the duration of the AGB phase and to the final C/O, because neither the largest luminosity and temperature at the base of the envelope nor the chemical yields are given in Weiss & Ferguson (2009).
For stars of masses below ∼2.5 M⊙ the final carbon-to-oxygen ratio by Weiss & Ferguson (2009) is practically the same as the results presented here and by K14, indicating that the efficiencies of TDU are similar in the three cases. For higher mass stars, the results by Weiss & Ferguson (2009) are somewhat intermediate between the final C/O found in the present work and those by K14, suggesting that: (a) the HBB experienced is weaker than in our case; and (b) the TDU efficiency is smaller than in K14. While the weaker HBB is explained by the difference in convection modelling, point (b) above is related to the description of convective borders adopted (as discussed in Sect. 2, K14 results are based on the algorithm proposed by Lattanzio (1986), whereas Weiss & Ferguson (2009) imposed an exponential decay of velocities from the border of all the convective regions formed).
The results shown in the bottom-left panel of Fig. 3 indicate that the AGB evolution predicted by Weiss & Ferguson (2009) is faster than in the present study and in K14, for almost all the masses considered. This is due to the treatment of mass loss, because the fitting formula by van Loon et al. (2005) leads to mass-loss rates 2−7 times higher than the predictions based on the Blöcker (1995) and Vassiliadis & Wood (1993) formulae in the super-solar metallicity domain.
8. Dust production
The amount and mineralogy of the dust formed in the circumstellar envelope of AGB stars are determined by the surface chemical composition and by global physical parameters, in particular by (a) the mass-loss rate, which determines the density of the wind, and in turn the number of gaseous molecules available to condensation; (b) the luminosity of the star, which affects the radiation pressure acting on the newly formed dust grains; and (c) the effective temperature, which sets the location of the condensation zone (Ferrarotti & Gail 2006). Among the various species, those most thermodynamically stable are alumina dust and SiC, for oxygen-rich AGBs and carbon stars, respectively. The condensation zone of these compounds is more internal than that of silicates and solid carbon, which are characterised by higher extinction coefficients (Ferrarotti & Gail 2006).
In the schematisation adopted here, the dust grains of the different species form in the condensation zone and grow from nano-sized dimensions until they reach an asymptotic size, which happens when the gas densities drop below the level at which the growth rate becomes much smaller than the velocity with which the wind moves outwards. It is to this asymptotic dimension that we refer in the following discussion and in Fig. 9, where we show the size of the grains of the considered dust species, formed in the wind of stars of different masses.
 |
Fig. 9. Sizes (radius) of the different dust species (listed in the legend) formed in the wind of AGB stars as a function of the current stellar mass. The left and right panels refer to the Z = 0.03 and Z = 0.04 metallicities, respectively. For the sake of readability, we only show the 1.25 M⊙ and 3 M⊙ cases for the low-mass domain (top panels), and the 4 M⊙ and 7 M⊙ models for the HBB domain (bottom panels). |
Before discussing the results obtained in the present investigation, we believe it is important to underline that the modelling of dust formation used here, mostly based on the schematisation proposed by the Heidelberg group, is a simplified description of a much more complex situation. This is where the combination of shocks and pulsation effects carry gas molecules into more external and cooler regions of the circumstellar envelope, and where dust formation may occur in conditions substantially different to those found in the static wind proposed here. The most serious limitation in the present description is that mass loss is assumed a priori, whereas it should be the outcome of a self-consistent treatment of the wind dynamics, which is in agreement with the studies by Mattsson et al. (2008) and the most recent investigations by Bladh et al. (2019a, b). The results in terms of dust production presented here must be taken with some caution, particularly for what concerns the production of carbonaceous species. Indeed, the present findings are based on the mass-loss rate calculated by means of the Wachter et al. (2002, 2008) works, which, as discussed in Sect. 2, neglects any role of the carbon excess: this assumption may lead to an overestimation of the Ṁ’s found here (Bladh et al. 2019b), considering that in the few models that reach the C-star stage, the carbon excess is small. This is due to the high oxygen content of the surface regions of the star. It goes without saying that the growth of dust particles, particularly of the carbon grains, might be overestimated as well.
Table 4 reports the mass of the total and the different species of dust produced by our models of different masses during the AGB lifetime. Given the significant differences in the evolution properties of AGB stars of different masses, we divide the description below into three mass ranges.
Total dust mass and the masses of the individual species produced by our Z = 0.03 and Z = 0.04 models during the AGB phase.
8.1. Production of silicates in low-mass AGB stars (<2 M⊙)
The 1.25 M⊙ models shown in Fig. 6 represent the low-mass AGB stars with initial masses below 2 M⊙ that experience only a few (∼10) TPs before losing the entire envelope. Considering the small number of TDU events, these stars do not reach the C-star phase, and they evolve as O-rich stars for the whole AGB lifetime (right panel of Fig. 6). Based on the previous discussion, the dust formed in their envelope is composed of silicates, alumina dust, and solid iron, with no traces of carbonaceous particles.
The dominant contribution to the dust budget is provided by silicates, particularly by olivine grains, whose size increases steadily during the AGB phase until it reaches dimensions of the order of 0.12 μm towards the final evolutionary stages, where the percentage of silicon locked into dust particles approaches ∼20%. Negligible quantities of alumina dust are formed, owing to the low mass-loss rates experienced below ∼10−6 M⊙ yr−1. We see in Fig. 9 that the size of the solid iron particles formed is anti-correlated with olivine; this is because the iron dust formation layer is more external than that of silicates, thus a significant production of the latter results in a significant wind acceleration, which favours the drop in the gas density and the decrease in the iron grain growth rate. During the first TPs, almost 25% of the gaseous iron is condensed into dust grains sized slightly below 0.1 μm; the size of iron particles drops to ∼0.05 μm during the final AGB stages, where silicates form in significant quantities and the fraction of iron locked into dust is below 10%.
The metallicity has some effects on the dust formed by low-mass AGBs. The Z = 0.04, 1.25 M⊙ star produces more dust than its Z = 0.03 counterpart, owing to the higher quantities of silicon, aluminium, and iron in the surface layers, and to the higher rates of mass loss experienced. However, as shown in Fig. 9, the differences in the size of the particles formed are within 10%.
8.2. Dust production by stars close to the mass threshold to activate HBB (2 M⊙ < M < 3.5 M⊙)
Stars of initial mass close to ∼3 M⊙ experience several TPs and TDU episodes, with a consequent increase in the surface carbon. These stars are represented by the 3 M⊙ models in Fig. 9. A distinction based on metallicity is mandatory here, because, as discussed in Sect. 5.2, the Z = 0.03 stars in this mass domain reach the C-star stage, whereas most of the Z = 0.04 stars evolve as O-rich ones (see right panel of Fig. 6).
We start from the Z = 0.04 case, which is similar to the lower-mass stars discussed in Sect. 8.1. The dust formed in the wind has a dominant contribution from silicates, and the amounts of iron dust and silicates are anti-correlated. The size of the silicate grains formed is ≃0.15 μm, with ∼25% of the silicon locked into dust. The production of silicates is more efficient than in the 1.25 M⊙ case, because the mass-loss rate goes up to ∼10−5 M⊙ yr−1 in the final evolutionary phases. An additional difference, also due the higher mass-loss rate, is that the formation of alumina dust is non-negligible in this case. During the final phases, the fraction of aluminium condensed into alumina dust is ∼15%, and the size of Al2O3 grains is ∼0.05 μm (see the red squares in the top-right panel of Fig. 9, which represent the size of Al2O3 grains). According to the present modelling, the C-star stage is reached only by stars of initial masses ∼2 M⊙ during the final AGB phases: however, the carbon excess with respect to oxygen is very small, thus the formation of carbonaceous dust particles is negligible.
The behaviour of the 3 M⊙ star of metallicity Z = 0.03 is qualitatively different, because it becomes a C-star during the final 10% (in time) of the AGB evolution. We note that although the duration of the phase during which the star is O-rich is much longer than the C-star phase, 80% of the mass is lost after the star becomes a C-star (see right panel of Fig. 6). The dust produced by these stars is therefore dominated by carbonaceous particles and solid iron. The amount of silicates produced is smaller than in the higher metallicity 3 M⊙ star, and the formation of alumina dust is negligible: this is because the production of these species is limited to the first part of the AGB phase, where the mass-loss rate is below a few ∼10−6 M⊙ yr−1.
During the C-star phase, the dust mineralogy is dominated by SiC and solid iron, due to the low surface C excess, with a C/O ratio below ∼1.2 for a significant fraction of the C-rich phase. The SiC grains reach dimensions ∼0.13 μm, whereas the size of solid carbon particles is below ∼0.1 μm. The results reported in the top-left panel of Fig. 9 indicate that the size of SiC grains remains constant during the whole AGB phase: this is a saturation effect due to the fact that all the residual silicon not already locked into SiS molecules, which is ∼55% of the original silicon abundance, is condensed into dust. Conversely, only ∼5% of carbon is locked into solid particles. The consumption of gaseous silicon by formation of SiC dust was explored in AGB stars of sub-solar metallicities by Ventura et al. (2014a).
These conditions prove extremely favourable to the formation of large amounts of solid iron; we see in Fig. 9 that during the phases just before and immediately after the star becomes a C-star, solid iron is the dominant species, with the grain size reaching ∼0.1 μm and almost half of the gaseous iron condensed into dust. The formation of solid iron grains is partly due to the wide availability of iron in the surface regions of high-metallicity stars. Furthermore, compared to lower metallicity stars, the low-C excess affects the efficiency of the growth of solid carbon grains and favours the formation of solid iron grains, which is otherwise inhibited by the fast acceleration of the wind triggered by the large extinction coefficients of solid carbon particles.
During the last evolutionary phases, after more carbon is accumulated in the surface regions via the recurrent TDU events, and the surface C/O exceeds 1.2, the size of carbon grains formed reaches ∼0.18 μm, with 10−15% of carbon condensed into dust. The amount of carbon dust exceeds SiC only during these late phases.
The extinction properties of solid carbon grains favour the acceleration of the wind, which in the 3 M⊙ star shown in the top-left panel of Fig. 9, reaches velocities slightly below 30 Km s−1. These results indicate that the winds of carbon stars in the super-solar metallicity domain are slower than they are in the lower metallicity case, owing to the smaller values of the carbon excess in the surface regions. In the Z = 0.03 stars with initial masses of 2.5 M⊙ and 3.5 M⊙, we find smaller velocities during the C-star phase, which are in the 20–30 Km s−1 range. These results must be taken with some caution, because the analysis by Wachter et al. (2002, 2008), used in the present investigation to derive the mass loss rates, holds for values of the carbon excess above 8.2, whereas in these stars, as reported in Table 2, we find C −0 < 8.1.
Ventura et al. (2012) warned that the model predictions for the production of silicates during part of the O-rich phase of low-mass stars are not robust. This is due to the fact that the wind is not accelerated, which renders the results sensitive to the assumed velocity with which the wind enters the condensation zone. We stress that in all the cases discussed here so far regarding dust production in low-mass AGB stars and the formation of silicates during the O-rich AGB phases of the 3 M⊙ star of metallicity Z = 0.03, the wind is accelerated after the formation of dust, until it reaches velocities to the order of 10 Km s−1. This result is due to the large amounts of silicon and aluminium available in the envelope of super-solar metallicity stars, and renders the present findings more robust than for stars of lower metallicities, as they are independent of the assumptions regarding the initial velocity (Ventura et al. 2012).
8.3. HBB and dust formation (M > 3.5 M⊙)
One of the most significant differences between the evolution of low-mass and massive AGB stars is the overall energy release: comparing the results in the left panel of Fig. 4 and the left panel of Fig. 6, it is clear that while the luminosities of low-mass AGBs are in the 5 × 103 − 2 × 104 L⊙ range, the stars experiencing HBB evolve at higher luminosities: 2 × 104 L⊙ < L < 8 × 104 L⊙. This difference affects the mass-loss rate, when considering the high sensitivity of the mass-loss description by Blöcker (1995) to the luminosity.
In fact, massive AGB stars experience mass-loss rates in the range of 10−5 − 10−4 M⊙ yr−1, which is significantly larger than those experienced by their lower mass counterparts. These high rates of mass loss favour high wind densities, which triggers the production of large quantities of dust (Ventura et al. 2012). The bottom panels of Fig. 9 show that the dimension of olivine, alumina dust, and solid iron grains are generally higher than in the low-mass domain, shown in the top panels of the same figure. The mass trends, mostly due to the behaviour of the luminosity and mass loss rate, are clear in Fig. 9: the size of olivine grains slightly increases from ∼0.14 μm for the 4 M⊙ star, to ∼0.16 μm in the 7 M⊙ case. The fraction of silicon condensed into dust is in the 30−40% range. The mass-loss rates experienced by massive AGB stars are sufficiently large to favour copious production of alumina dust; the Al2O3 grains formed reach dimensions ranging from ∼0.05 μm (4 M⊙) to ∼0.08 μm (7 M⊙). The percentage of aluminium locked into Al2O3 is generally above 50%. In the models of higher mass we see in Fig. 9 that the size of alumina dust particles, ∼0.08 μm, are unchanged during the AGB phase; this is due to the saturation effect, first described in massive AGB stars of solar chemical composition by Dell’Agli et al. (2014b), with almost all the gaseous aluminium available locked into dust grains. The formation of silicates enhances the effects of radiation pressure acting on dust grains. For the stars experiencing HBB, we find that the final wind velocities are slightly in excess of 20 Km s−1. This result is very similar to the velocities found by Ventura et al. (2018) for solar metallicity stars: the latter models produce lower amounts of silicates (see Fig. 11) than their higher metallicity counterparts, but this is compensated by the larger luminosities (see Fig. 3), which increases the effects of radiation pressure on the acceleration of the wind. We note some metallicity effects where the higher metallicity stars form slightly larger dust particles, though the differences are within 5%.
8.4. The dust production rate
To understand the feedback from AGB stars to the cycle of matter of the host system, we discuss the rate at which AGB stars eject dust in the interstellar medium: this is known as the dust production rate (DPR). The determination of the DPR is crucial not only to understanding how dust is produced in single galaxies (Srinivasan et al. 2009, 2016; Schneider et al. 2014; Dell’Agli et al. 2016; Dell’Agli et al. 2018; Dell’Agli et al. 2019), but also, more generally, to assess whether the dust produced by stars is able to reproduce interstellar dust abundances (Zhukovska et al. 2008).
In Fig.10, we show the variation in the DPR of the same models shown in Figs. 4 and 6 during the AGB lifetime. The lines represent the overall DPR at each evolutionary stage obtained by summing up the contributions from all the individual dust species.
 |
Fig. 10. Variation of the dust production rate with the stellar mass for low-mass stars (left panel) and massive AGBs (right panel). Red squares and blue diamonds refer to Z = 0.03 and Z = 0.04, respectively. Full points indicate stages during which the star is O-rich, while open points refer to carbon stars. The track referring to the 2.5 M⊙ stars of metallicity Z = 0.03 is green, to better distinguish it from the 2 M⊙ and 3 M⊙ models. |
The DPR of low-mass stars increases during the AGB phase, which is consistent with the earlier discussion and the results shown in the top panels of Fig. 9. The DPR are generally in the 10−8 − 10−7 M⊙ yr−1 range and the main contribution is provided by silicates. The sole exceptions to this general behaviour are given by 2.5−3.5 M⊙ stars of metallicity Z = 0.03: these stars become carbon stars, and during the C-star phase they form dust with rates up to ∼5 × 10−7 M⊙ yr−1 in the final evolutionary stages.
Massive AGB stars (right panel of Fig.10) behave differently: the DPR trend follows the variation of the luminosity because the dust production is strictly connected to the efficiency of HBB, as it is the overall energy flux. The DPR is higher during the initial AGB phases, where the luminosities and the temperatures at the base of the convective envelope are higher (see Fig. 4), and then it decreases towards the end of the AGB evolution. A DPR mass trend is clearly visible in Fig. 10: the largest DPR grows from a few 10−8 M⊙ yr−1 in the stars of masses 4 M⊙, up to ∼5 × 10−7 M⊙ yr−1 in the 7 M⊙ case.
8.5. The overall dust mass of super-solar metallicity AGB stars
The amounts of dust produced by our models of different masses during the AGB life are summarised in Fig.11, where we also show, for comparison, the dust masses of the solar-metallicity models of Ventura et al. (2018), the results at Z = 0.02 and Z = 0.04 of Ferrarotti & Gail (2006), and the Z = 0.04 models of Nanni et al. (2014).
 |
Fig. 11. Dust mass produced during the whole AGB phase of our models of different masses and metallicities. We also show, for comparison, the solar metallicity models by Ventura et al. (2018) and the results from Ferrarotti & Gail (2006) and Nanni et al. (2014). |
The dust mass increases with the initial mass of the star, spanning the range of 0.0001−0.012 M⊙ for Z = 0.03 and 0.0001−0.014 M⊙ for Z = 0.04. Most of the dust is in the form of silicates, with the exception of the Z = 0.03 stars with initial masses of 2.5−3.5 M⊙, which produce mostly carbonaceous dust; this is consistent with the earlier study by Nanni et al. (2014). On average, the amount of dust produced is higher than in solar metallicity AGB stars. A striking difference between stars of different metallicities is the behaviour of the 2−3 M⊙ solar-metallicity stars, which produce large amounts of carbon dust, to the order of 0.01−0.015 M⊙, which is comparable with those of the most massive AGB stars. This important difference is due to the higher carbon excess reached by solar-metallicity stars with respect to the Z = 0.03 counterparts studied here.
Our Z = 0.04 results are on average a factor of ∼2 lower than those of Ferrarotti & Gail (2006). This difference is due to the adopted description of the mass loss. While we used the treatment of Blöcker (1995), Ferrarotti & Gail (2006) and K14 adopted the mass loss versus period relationship method of Vassiliadis & Wood (1993). As discussed in Sect. 7, in metal-rich AGB models, the mass-loss rates determined by applying the Vassiliadis & Wood (1993) method are generally higher than those of Blöcker (1995), which leads to higher rates of dust production in the wind.
The difference in the total dust produced during the AGB lifetime is particularly relevant in the low-mass domain, where the dust masses of Ferrarotti & Gail (2006) are 2−3 times higher than those calculated here. The difference is smaller for the stars experiencing HBB, as the present models experience stronger HBB conditions and evolve at larger luminosities compared to those of Ferrarotti & Gail (2006).
The dust masses found by Nanni et al. (2014), indicated with orange triangles in Fig. 11, are similar to those of Ferrarotti & Gail (2006) in the low- and intermediate-mass domain. For stars of masses ∼6 M⊙, the amount of dust by Nanni et al. (2014) is substantially higher; this is connected with the formation reaction for silicates used by Nanni et al. (2014) (discussed in Nanni et al. 2013), which makes the formation of silicates take place at temperatures to the order of 1400 K, closer to the stellar surface than in the present model and in that of Ferrarotti & Gail (2006).
9. Conclusions
We studied the evolution through the AGB phase of 1−8 M⊙ super-solar metallicity stars, Z = 0.03 and Z = 0.04. We find that stars with masses above ∼3 M⊙ experience HBB at the base of the convective mantle. These objects evolve at luminosities of 20−80 × 103L⊙ during the AGB phase, with timescales ranging from ∼1 Myr for M ∼ 4 M⊙ stars, to ∼5 × 104 yr for M ∼ 8 M⊙. The surface chemical composition is driven by proton captures in the internal regions of the convective envelope, with the destruction of the surface 12C and the synthesis of large quantities of 14N. Significant amounts of lithium and sodium are produced, whereas the destruction of the surface 16O is modest.
Low-mass stars not exposed to HBB experience several TDU events, which gradually increase the surface carbon. The C-star stage is reached only by 2.5−3.5 M⊙ stars of metallicity Z = 0.03, with the surface C/O reaching a maximum of ∼1.2. C-stars are not expected to be formed at Z = 0.04.
Dust production at super-solar metallicity is dominated by the formation of mostly olivine silicate particles with a ∼10% contribution of alumina dust and solid iron. The only exception is represented by 2.5−3.5 M⊙ stars of metallicity Z = 0.03, whose dust production is dominated by the carbonaceous species, silicon carbide, and solid carbon: formed during the final AGB phases. The total mass of the dust formed depends on the initial mass of the star, and it ranges from ∼0.001 M⊙ for stars of mass 1 M⊙, to ∼0.012 M⊙ for M = 8 M⊙.
Regarding the gas pollution, our new models extend the available grids of stellar yields to super-solar metallicity. Nearly 70% of solar 14N is synthesised in AGB stars according to recent chemical evolution model results (Romano et al. 2019). This number is expected to be even higher in the inner disc of the Galaxy. Since the 14N yield continues to increase with stellar metallicity (see Fig 8), with the highest yields found for the most metal-rich stars, stellar yields from super-solar metallicity models are required in chemical evolution studies to properly assess the 14N enrichment in the most evolved environments. Another example is 12C, whose yields are also dependent on metallicity. Carbon is observed in massive local ellipticals, as well as in their dust-obscured progenitors at high redshifts, and can be used to constrain the timescales of formation of these systems (e.g. Johansson et al. 2012). A meaningful quantification of the timescale for the most massive ellipticals requires the adoption of stellar yields computed for super-solar metallicity stars. Finally, as mentioned in Sect. 4, the adoption of super-solar metallicity yields of 13C and 17O derived from self-consistent, low- and intermediate-mass star models is mandatory for improving the modelling of dusty starburst galaxies at high redshifts, and, consequently, the derivation of their galaxy-wide stellar IMF (see Romano et al. 2017; Zhang et al. 2018).
Future work also involves comparing the nucleosynthetic predictions from the ATON AGB models to the isotopic composition of meteoritic stardust grains. For ATON, such a comparison has the advantage, with respect to those performed using other codes, of also being able to predict the expected types, amounts, and sizes of the dust produced by the potential AGB parent stars of the meteoritic grains. Such a comprehensive and comparative investigation should include both carbonaceous and oxide dust, and both the light elements and those heavier than iron, which are produced in AGB stars by neutron captures. For the latter, an initial application of this innovative approach of combining AGB nucleosynthesis and dust formation predictions is presented in relation to large (∼μm-sized) SiC grains by Lugaro et al. (2020), who conclude that these large grains originated from AGB stars of super-solar metallicity, and that the initial number of dust seeds should decrease with increasing metallicity. However, such work combined neutron-capture nucleosynthesis predictions from the MONASH models and dust formation predictions from the ATON models. As the development of tools allowing predictions for neutron-capture nucleosynthesis using ATON is almost complete (Yague et al., in prep.), a more self-consistent approach will be possible in the near future.
Acknowledgments
P. V. and D. R. benefited from the International Space Science Institute (ISSI, Bern, CH, and ISSI-BJ, Beijing, CN) thanks to the funding of the team ‘‘Chemical abundances in the ISM: the litmus test of stellar IMF variations in galaxies across cosmic time”. M. L. acknowledges the financial support of the Hungarian National Research, Development and Innovation Office (NKFI), grant KH_18 130405 and the Lendület grant (LP17-2014) of the Hungarian Academy of Sciences.
References
- Bensby, T., Feltzing, S., & Oey, M. S. 2014, A&A, 562, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertola, F., Bressan, A., Burstein, D., et al. 1995, ApJ, 438, 680 [CrossRef] [Google Scholar]
- Bladh, S., Eriksson, K., Marigo, P., et al. 2019a, A&A, 623, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bladh, S., Liljegren, S., Höfner, S., et al. 2019b, A&A, 626, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blöcker, T. 1995, A&A, 297, 727 [NASA ADS] [Google Scholar]
- Blöcker, T., & Schöenberner, D. 1991, A&A, 244, L43 [Google Scholar]
- Boothroyd, A. I., & Sackmann, I.-J. 1999, ApJ, 510, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, A. G. W., & Fowler, W. A. 1971, ApJ, 164, 111 [Google Scholar]
- Canuto, V. M. C., & Mazzitelli, I. 1991, ApJ, 370, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Schönrich, R., Asplund, M., et al. 2011, A&A, 530, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charbonnel, C., & Lagarde, N. 2010, A&A, 522, A10 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Chen, Y. Q., Zhao, G., Zhao, J. K., et al. 2019, AJ, 158, 249 [CrossRef] [Google Scholar]
- Cox, J. P. 1980, Theory of Stellar Pulsation (Princeton: Princeton University Press), 165 [CrossRef] [Google Scholar]
- Cox, A. N. & Stewart, J. N., 1969, Academia Nauk, Scientific Information, 15, 1 [Google Scholar]
- Cristallo, S., Straniero, O., Gallino, R., et al. 2009, ApJ, 696, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Piersanti, L., Straniero, O., et al. 2011, ApJS, 197, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Straniero, O., Piersanti, L., et al. 2015, ApJS, 219, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Dell’Agli, F., García-Hernández, D. A., Rossi, C., et al. 2014a, MNRAS, 441, 1115 [NASA ADS] [CrossRef] [Google Scholar]
- Dell’Agli, F., Ventura, P., Garcia Hernandez, D. A., et al. 2014b, MNRAS, 442, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Dell’Agli, F., Ventura, P., Schneider, R., et al. 2015a, MNRAS, 447, 2992 [NASA ADS] [CrossRef] [Google Scholar]
- Dell’Agli, F., García-Hernández, D. A., Ventura, P., et al. 2015b, MNRAS, 454, 4235 [NASA ADS] [CrossRef] [Google Scholar]
- Dell’Agli, F., Di Criscienzo, M., Boyer, M. L., et al. 2016, MNRAS, 460, 4230 [CrossRef] [Google Scholar]
- Dell’Agli, F., García-Hernández, D. A., Ventura, P., et al. 2018, MNRAS, 475, 2282 [Google Scholar]
- Dell’Agli, F., Di Criscienzo, M., García-Hernández, D. A., et al. 2019, MNRAS, 482, 4733 [CrossRef] [Google Scholar]
- D’Ercole, A., Vesperini, E., D’Antona, F., et al. 2008, MNRAS, 391, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Di Criscienzo, M., Dell’Agli, F., Ventura, P., et al. 2013, MNRAS, 433, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Di Criscienzo, M., Ventura, P., García-Hernández, D. A., et al. 2016, MNRAS, 462, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Ek, M., Hunt, A. C., Lugaro, M., et al. 2019, Nat. Astron., 4, 273 [CrossRef] [Google Scholar]
- Ferrarotti, A. S., & Gail, H.-P. 2006, A&A, 447, 553 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garcia-Berro, E., & Iben, I. 1994, ApJ, 434, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, SSrv, 85, 161 [Google Scholar]
- Herwig, F. 2000, A&A, 360, 952 [NASA ADS] [Google Scholar]
- Herwig, F. 2005, ARA&A, 43, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, I., Jr 1974, ARA&A, 12, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Johansson, J., Thomas, D., & Maraston, C. 2012, MNRAS, 421, 1908 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A. I. 2010, MNRAS, 403, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A. I. 2014, MNRAS, 445, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A. I., & Lattanzio, J. C. 2014, PASA, 31, e030 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A. I., & Lugaro, M. 2016, ApJ, 825, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A. I., Lugaro, M., Carlos, M., et al. 2018, MNRAS, 477, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Kubryk, M., Prantzos, N., & Athanassoula, E. 2015, A&A, 580, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagarde, N., Decressin, T., Charbonnel, C., et al. 2012, A&A, 543, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lattanzio, J. C. 1986, ApJ, 311, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, K. M., Lugaro, M., Gibson, B. K., et al. 2013, ApJ, 768, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Lugaro, M., Tagliente, G., Karakas, A. I., et al. 2014, ApJ, 780, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Lugaro, M., Karakas, A. I., Pető, M., et al. 2018, Geochim. Cosmochim. Acta, 221, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Lugaro, M., Cseh, B., Világos, B., et al. 2020, ApJ, 898, 96 [CrossRef] [Google Scholar]
- Marigo, P., & Aringer, B. 2009, A&A, 508, 1538 [Google Scholar]
- Matteucci, F. 2012, Chemical Evolution of Galaxies (Berlin Heidelberg: Springer-Verlag) [CrossRef] [Google Scholar]
- Mattsson, L., Wahlin, R., Höfner, S., & Eriksson, K. 2008, A&A, 484, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Chiappini, C., & Martig, M. 2013, A&A, 558, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nanni, A., Bressan, A., Marigo, P., et al. 2013, MNRAS, 434, 2390 [NASA ADS] [CrossRef] [Google Scholar]
- Nanni, A., Bressan, A., Marigo, P., et al. 2014, MNRAS, 438, 2328 [NASA ADS] [CrossRef] [Google Scholar]
- Nanni, A., Marigo, P., Groenewegen, M. A. T., et al. 2016, MNRAS, 462, 1215 [NASA ADS] [CrossRef] [Google Scholar]
- Nanni, A., Marigo, P., Girardi, L., et al. 2018, MNRAS, 473, 5492 [NASA ADS] [CrossRef] [Google Scholar]
- Nanni, A., Groenewegen, M. A. T., Aringer, B., et al. 2019, MNRAS, 487, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Nanni, A., Marigo, P., Groenewegen, M. A. T., et al. 2020, IAU General Assembly, 405 [Google Scholar]
- Paczyński, B. 1970, Acta Astron., 20, 287 [Google Scholar]
- Pignatari, M., et al. 2016, ApJS, 225, 24 [Google Scholar]
- Pinsonneault, M. 1997, ARA&A, 35, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Renzini, A., & Voli, M. 1981, A&A, 500, 221 [Google Scholar]
- Romano, D., Matteucci, F., Ventura, P., et al. 2001, A&A, 374, 646 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romano, D., Karakas, A. I., Tosi, M., et al. 2010, A&A, 522, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romano, D., Matteucci, F., Zhang, Z.-Y., et al. 2017, MNRAS, 470, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., Matteucci, F., Zhang, Z.-Y., et al. 2019, MNRAS, 490, 2838 [NASA ADS] [CrossRef] [Google Scholar]
- Sackmann, I.-J., & Boothroyd, A. I. 1991, ApJ, 366, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Sackmann, I.-J., & Boothroyd, A. I. 1992, ApJ, 392, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, R., Valiante, R., Ventura, P., et al. 2014, MNRAS, 442, 1440 [NASA ADS] [CrossRef] [Google Scholar]
- Schultheis, M., Rich, R. M., Origlia, L., et al. 2019, A&A, 627, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwarzschild, M., & Härm, R. 1965, ApJ, 142, 855 [NASA ADS] [CrossRef] [Google Scholar]
- Siess, L. 2007, A&A, 476, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitoni, E., Romano, D., Matteucci, F., et al. 2015, ApJ, 802, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Srinivasan, S., Meixner, M., Leitherer, C., et al. 2009, AJ, 137, 4810 [NASA ADS] [CrossRef] [Google Scholar]
- Srinivasan, S., Boyer, M. L., Kemper, F., et al. 2016, MNRAS, 457, 2814 [NASA ADS] [CrossRef] [Google Scholar]
- Straniero, O., Chieffi, A., Limongi, M., et al. 1997, ApJ, 478, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Thorsbro, B., Ryde, N., Rich, R. M., et al. 2020, ApJ, 894, 26 [CrossRef] [Google Scholar]
- Valiante, R., Schneider, R., Bianchi, S., et al. 2009, MNRAS, 397, 1661 [NASA ADS] [CrossRef] [Google Scholar]
- van Loon, J., Cioni, M.-R., Zijlstra, A., & Loup, C. 2005, A&A, 438, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vassiliadis, E., & Wood, P. R. 1993, ApJ, 413, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P. 2010, Light Elements in the Universe, 147 [Google Scholar]
- Ventura, P., & D’Antona, F. 2005a, A&A, 431, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ventura, P., & D’Antona, F. 2005b, A&A, 439, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ventura, P., Zeppieri, A., Mazzitelli, I., & D’Antona, F. 1998, A&A, 334, 953 [Google Scholar]
- Ventura, P., D’Antona, F., & Mazzitelli, I. 2000, A&A, 363, 605 [Google Scholar]
- Ventura, P., D’Antona, F., Mazzitelli, I., et al. 2001, ApJ, 550, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., Di Criscienzo, M., Schneider, R., et al. 2012, MNRAS, 420, 1442 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., Di Criscienzo, M., Carini, R., & D’Antona, F. 2013, MNRAS, 431, 3642 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., Di Criscienzo, M., D’Antona, F., Vesperini, E., Tailo, M., Dell’Agli, F., & D’Ercole, A. 2014a, MNRAS, 437, 3274 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., Dell’Agli, F., Schneider, R., et al. 2014b, MNRAS, 439, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., Karakas, A. I., Dell’Agli, F., et al. 2015, MNRAS, 450, 3181 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., Karakas, A. I., Dell’Agli, F., et al. 2016, MNRAS, 457, 1456 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., Karakas, A., Dell’Agli, F., García-Hernández, D. A., & Guzman-Ramirez, L. 2018, MNRAS, 475, 2282 [NASA ADS] [Google Scholar]
- Vitense, E. 1953, ZAp, 32, 135 [Google Scholar]
- Wachter, A., Schröder, K. P., Winters, J. M., Arndt, T. U., & Sedlmayr, E. 2002, A&A, 384, 452 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wachter, A., Winters, J. M., Schröder, K. P., & Sedlmayr, E. 2008, A&A, 486, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wegg, C., Rojas-Arriagada, A., Schultheis, M., et al. 2019, A&A, 632, A121 [CrossRef] [EDP Sciences] [Google Scholar]
- Weiss, A., & Ferguson, J. W. 2009, A&A, 508, 1343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, Z.-Y., Romano, D., Ivison, R. J., et al. 2018, Nature, 558, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Zhukovska, S., Gail, H.-P., & Trieloff, M. 2008, A&A, 479, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zinner, E. 2014, Meteor. Cosmochem. Processes, 181, [Google Scholar]
All Tables
Properties of the stars related to the occurrence of TDU events and the achievement (if any) of the C-star stage.
Chemical yields of AGB stars of metallicities Z = 0.03, Z = 0.04, and (initial) masses in the range of 1−8 M⊙.
Total dust mass and the masses of the individual species produced by our Z = 0.03 and Z = 0.04 models during the AGB phase.
All Figures
 |
Fig. 1. Changes in the surface mass fraction of helium (top-left panel), 12C (top right), 14N and 16O after the first (full points) and the second (open points) dredge-up episode of the AGB stars of metallicity Z = 0.03 (red squares) and Z = 0.04 (blue diamonds). The horizontal lines in each panel indicate the initial mass fractions of the same species. |
| In the text | |
 |
Fig. 2. Evolution of high-metallicity AGB models in the core mass–luminosity plane. The black line shows the theoretical relationship derived by Paczyński (1970). |
| In the text | |
 |
Fig. 3. Maximum luminosity (top-left panel) and temperature at the base of the envelope (top, right) experienced by our AGB models of metallicity Z = 0.03 (red squares) and Z = 0.04 (blue diamonds) as a function of the initial mass. The bottom panels show the duration of the TP-AGB phase (left) and the final C/O (right). For comparison, we also show solar metallicity models by Ventura et al. (2018) (black points), Z = 0.03 models by Karakas (2014) (green triangles), and Z = 0.04 models by Weiss & Ferguson (2009) (magenta asterisks). |
| In the text | |
 |
Fig. 4. Variation with time (starting from the beginning of the TP-AGB phase) of the luminosity (top-left panel), temperature at the base of the envelope (top-right panel), core mass (bottom left) and mass-loss rate (bottom right) during the AGB phase of stars of metallicity Z = 0.03 (red squares) and Z = 0.04 (blue diamonds) of initial mass 4, 5, 6, 7 M⊙. The points along the different tracks refer to the middle of the inter-pulse phase. |
| In the text | |
 |
Fig. 5. Variations with time of the surface mass fraction of 12C (top-left panel), 14N (top right), lithium (bottom left), and the 12C/13C ratio (bottom right) of the same models shown in Fig. 4 (except for the 6 M⊙ model, omitted here for the sake of readibility). The black dots refer to a 4 M⊙ star of solar metallicity, published in Ventura et al. (2018), while the other symbols are the same as in Fig. 4. |
| In the text | |
 |
Fig. 6. Variation with the current mass of the star of the luminosity (left panel) and surface C/O (right panel) of Z = 0.03 (red squares) and Z = 0.04 (blue diamond) stars with initial masses in the range of 1−3.5 M⊙. |
| In the text | |
 |
Fig. 7. Variation with time (counted since the beginning of the TP phase) of the core mass (left panel) and mass-loss rate (right panel) of Z = 0.03 and Z = 0.04 models of initial mass 1 M⊙, 1.5 M⊙, 2.5 M⊙, 3 M⊙ and 3.5 M⊙. |
| In the text | |
 |
Fig. 8. Yields in solar masses of helium (top-left panel), 12C and 14N (top, right), 13C (bottom, left), and 17O (bottom, right) of our Z = 0.03 (red squares) and Z = 0.04 (blue diamond) AGB models and of solar-metallicity models by Ventura et al. (2018). Green triangles indicate the helium, carbon, and nitrogen yields published in Karakas & Lugaro (2016). |
| In the text | |
 |
Fig. 9. Sizes (radius) of the different dust species (listed in the legend) formed in the wind of AGB stars as a function of the current stellar mass. The left and right panels refer to the Z = 0.03 and Z = 0.04 metallicities, respectively. For the sake of readability, we only show the 1.25 M⊙ and 3 M⊙ cases for the low-mass domain (top panels), and the 4 M⊙ and 7 M⊙ models for the HBB domain (bottom panels). |
| In the text | |
 |
Fig. 10. Variation of the dust production rate with the stellar mass for low-mass stars (left panel) and massive AGBs (right panel). Red squares and blue diamonds refer to Z = 0.03 and Z = 0.04, respectively. Full points indicate stages during which the star is O-rich, while open points refer to carbon stars. The track referring to the 2.5 M⊙ stars of metallicity Z = 0.03 is green, to better distinguish it from the 2 M⊙ and 3 M⊙ models. |
| In the text | |
 |
Fig. 11. Dust mass produced during the whole AGB phase of our models of different masses and metallicities. We also show, for comparison, the solar metallicity models by Ventura et al. (2018) and the results from Ferrarotti & Gail (2006) and Nanni et al. (2014). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned}&Y_i=\int {[X_i-X_i^\mathrm{init}] \dot{M} \,\mathrm{d}t.} \end{aligned} $$](/articles/aa/full_html/2020/09/aa38289-20/aa38289-20-eq6.gif)