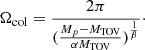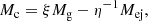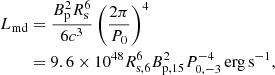| Issue |
A&A
Volume 641, September 2020
|
|
|---|---|---|
| Article Number | A56 | |
| Number of page(s) | 10 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201936671 | |
| Published online | 09 September 2020 | |
Protomagnetar research through an analysis of the X-ray plateau in the multi-messengar era
1
Key Laboratory of Dark Matter and Space Astronomy, Purple Mountain Observatory, Chinese Academy of Sciences, Nanjing, Jiangsu 210008, PR China
e-mail: renxx@pmo.ac.cn, dmwei@pmo.ac.cn
2
School of Astronomy and Space Science, University of Science and Technology of China, Hefei, Anhui 230026, PR China
3
Department of Astronomy, Xiamen University, Xiamen, Fujian 361005, PR China
4
School of Mathematics and Physics, Changzhou University, Changzhou, Jiangsu 213164, PR China
5
Department of Physics, Nanjing University, Nanjing, Jiangsu 210093, PR China
Received:
11
September
2019
Accepted:
22
June
2020
The joint detection of the gravitational wave signal and the electromagnetic emission from a binary neutron star merger can place unprecedented constraint on the equation of state of supranuclear matter. Although a variety of electromagnetic counterparts have been observed for GW170817, including a short gamma-ray burst, kilonova, and the afterglow emission, the nature of the merger remnant is still unclear, however. The X-ray plateau is another important characteristics of short gamma-ray bursts. This plateau is probably due to the energy injection from a rapidly rotating magnetar. We investigate what we can learn from the detection of a gravitational wave along with the X-ray plateau. In principle, we can estimate the mass of the merger remnant if the X-ray plateau is caused by the central magnetar. We selected eight equations of state that all satisfy the constraint given by the gravitational wave observation, and then calculated the mass of the merger remnants of four short gamma-ray bursts with a well-measured X-ray plateau. If, on the other hand, the mass of the merger remnant can be obtained by gravitational wave information, then by comparing the masses derived by these two different methods can further constrain the equation of state. We discuss the possibility that the merger product is a quark star. In addition, we estimate the possible mass range for the recently discovered X-ray transient CDF-S XT2 that probably originated from a binary neutron star merger. Finally, under the assumption that the post-merger remnant of GW170817 was a supramassive neutron star, we estimated the allowed parameter space of the supramassive neutron star and find that in this case, the magnetic dipole radiation energy is so high that it may have some effects on the short gamma-ray burst and kilonova emission. The lack of detection of these effects suggests that the merger product of GW170817 may not be a supermassive neutron star.
Key words: gravitational waves / gamma-ray burst: individual: GRB170817 / stars: neutron / equation of state
© ESO 2020
1. Introduction
On August 17, 2017, the first gravitational wave (GW) event from a binary neutron star (NS) merger was detected by the Advanced Laser Interferometer Gravitational-wave Observatory (aLIGO) and Virgo. This event is called GW170817 (Abbott et al. 2017). In addition, 1.74 seconds later, a weak short gamma-ray burst (sGRB) was detected by Fermi GBM (Goldstein et al. 2017) and INTEGRAL (Savchenko et al. 2017). This historical event confirmed that a binary NS merger can produce an sGRB and a GW, which marks a breakthrough in the field of gravitational-wave multi-messenger astronomy. After 11 hours, a coincidence following optical singal SSS17a was caught in NGC 4993 (Coulter et al. 2017). This electromagnetic (EM) counterpart comes from the radioactive decay of lanthanide-rich dynamical ejecta and is called AT2017gfo (Li & Paczyński 1998; Metzger 2017a). Although a variety of electromagnetic counterparts has been observed, including a short GRB, kilonova, and the afterglow emission, the nature of the merger remnant is still unclear. From analyzing the GW and EM signals, it has been suggested that the merger remnant may be a hypermassive neutron star (HMNS; Margalit & Metzger 2017; Shibata & Kiuchi 2017; Radice et al. 2018a) or a long-lived neutron star (Li et al. 2018; Yu et al. 2018; Piro et al. 2019).
The product of a binary NS merger is thought to have four different types, which mainly depend on the mass, spin, and equation of state (EOS; Piro et al. 2017). First, a binary NS with sufficiently low mass may result in a stable NS. Second, if the total binary NS mass exceeds the maximum allowable mass of an NS, the merger product may directly collapse to become a black hole (BH). Third, for binary NSs whose masses are slightly lower than the maximum allowable mass, the merger product may be an HMNS. Finally, for binary NSs with even lower total mass, the product may be a supermassive neutron star (SMNS) that is initially supported by sufficiently high spin and eventually collapses to a BH.
Electromagnetic signals, such as afterglow and kilonova, can give insight into the nature of sGRBs. For instance, the X-ray plateau has been invoked to cause the formation of a long-lived magnetar (Dai & Lu 1998; Zhang & Mészáros 2001; Fan & Xu 2006; Metzger et al. 2008; Lyons et al. 2010; Rowlinson et al. 2010). In general, the X-ray plateau (a nearly flat light-curve plateau of about some hundreds of seconds followed by a rapid decay) is thought to be produced by the energy injection from a central SMNS. The turning point marks the collapse to a black hole due to spindown caused by dipole radiation or GW radiation. Some studies have shown that X-ray plateau and GW emission can be used to constrain the EOS and some other physical properties (Gao et al. 2016; Piro et al. 2017; Ma et al. 2018). The X-ray plateau is a common phenomenon. It can probably be detected along with GW signals in the coming years. We investigate the possibility that the mass of merger product of sGRBs might be estimated by analyzing the X-ray plateau.
The paper is organized as follows. In Sect. 2 we describe how the GW can be used to place constraints on the NS EOS and then select eight EOSs that satisfy the GW constraint. In Sect. 3 we estimate the protomagnetar masses of four sGRBs with well-measured X-ray plateaus. We consider two cases. In the first case, we only consider the magnetic dipole radiation. In the other case, both GW emission and the dipole radiation are considered. In Sect. 4 we discuss the situation of quark stars (QS) as merger remnants. In Sect. 5 we apply our method to estimate the possible remnant mass of the newly discovered X-ray transient CDF-S XT2. In Sect. 6 we discuss the properties of the remnant of GW170817 by assuming that its merger product is an SMNS. Finally, the summary and future perspective are presented in Sect. 7.
2. Select the NS EOS from the GW constraint
The detection of GW170817 has placed a strong and unprecedented constraint on the tidal deformability, which is induced by the gravitational field of the companion during the inspiral phase. The tidal deformability depends on the properties of the NS. It can be quantified as (Hinderer et al. 2010; Abbott et al. 2017, 2018)
where k2 is the second Love number. It clearly depends on the EOS as well as on the stellar mass M and radius R. Initially, the LIGO/VIRGO set a 90% credible upper bounds of Λ1.4 ≤ 800 for a 1.4 M⊙ neutron star (Abbott et al. 2017). In a recent analysis, which employed EOS-insensitive relations, the new results were tightened to 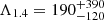 at 90% confidence (Abbott et al. 2019).
at 90% confidence (Abbott et al. 2019).
We used the EOSs from Read et al. (2009). We selected the EOSs with maximum gravitational masses not lower than the detection constraint of 2 M⊙ (Demorest et al. 2010; Antoniadis et al. 2013) that satisfied the constraints of GW170817. The remains are SLy, APR3, APR4, WFF1, WFF2, ENG, MPA1, and ALF2. We plot their macroscopic properties Λ and NS mass relation in Fig. 1, as well as the tidal deformability parameter Λ1 versus Λ2 using the low-spin and high-spin priors in Fig. 2.
 |
Fig. 1. Relation between tidal deformability (Λ) and NS mass for different EOSs. The vertical dotted line marks the canonical NS mass of 1.4 M⊙. From top to bottom, the three horizontal dotted lines are for Λ = 800, 580, and 70. Currently, all EOSs satisfy the constraints from GW observations, and are indistinguishable from each other. |
 |
Fig. 2. Tidal deformability Λ1 and Λ2 calculated using the 90% credible region of the component masses for GW170817 (Abbott et al. 2019). The 90% and 50% credible region contours determined by the GW are also shown by dashed lines from the outside to the inside. Left panel: situation of low-spin priors, and right panel: high-spin priors. |
Although a GW can place good constraints on the NS EOS, some open questions remain. The Bayesian inference of the GW can only constrain the NS properties before the merger, and it is obvious that the EOSs in the above figures are located too close to each other to be further distinguished from each other. As we know, double NSs merger events may carry a variety of multi-messenger information, including a GW, kilonova, sGRBs, and other afterglow radiation. Taking full advantage of these GW and EM signals might therefore reveal more essential physical properties.
3. Constraining the NS EOS from the X-ray plateau
3.1. sGRB samples and parameterization of the EOSs
We focus on the X-ray plateau to study the properties of merger remnants. It is generally recognized that the X-ray plateau, followed by a steep decay, indicates the existence of an SMNS as the GRB central engine. This SMNS collapses to a BH due to spin down. We selected four sGRBs with well-measured X-ray plateaus. These are GRB 080905A, GRB 060801, GRB 100702A, and GRB 101219A. The values of the initial spin period P0 and of the surface dipolar magnetic field Bp were obtained by fitting the Swift light curves (the detailed data are shown in Table 1) (Rowlinson et al. 2013). We assumed a redshift z = 0.72 for GRB 100702A.
Parameters of four sGRBs with an X-ray plateau.
The parameterization of the EOS is a good way to study the property of an NS. For a given EOS, Mmax can be expressed as a function of the spin period P and MTOV (Lasky et al. 2014; Gao et al. 2016; Li et al. 2017),
where MTOV and Mmax are the maximum NS mass for the static and rotational condition, respectively. α and β are function of the stellar mass, radius, and moment of inertia. We used the code RNS1 to calculate equilibrium sequences of the rapidly rotating condition to obtain the fitting results for each EOS. More information about the code can be found in Komatsu et al. (1989), Cook et al. (1994). Details are tabulated in Table 2. In Table 2, α and β are the fitting values of different EOSs in Eq. (2); σ2 is the deviation between the parameterized and the real EOS. Our fitting deviations are consistent with the errors in Li et al. (2017).
Eight EOSs.
3.2. Spindown only caused by magnetic dipole radiation
It is generally recognized that the rapid decay after the X-ray plateau indicates the collapse of an SMNS to a BH due to spindown caused by magnetic dipole radiation and GW emission (Fan et al. 2013a; Zhang & Mészáros 2001). For simplicity, we first only consider the magnetic dipole radiation. The standard magnetic dipole radiation reads (Lasky et al. 2014; Li et al. 2017)
Here I is the moment of inertia during the rapidly spinning phase. Combining Eq. (3) and Eq. (2), we obtain the relation about the moment of inertia I,
where the collapse time tcol, the surface dipole magnetic field Bp, and the initial spin period P0 can be obtained from Table 1 (Rowlinson et al. 2013; Lasky et al. 2014). Here Mp represents the protomagnetar mass. Following Li et al. (2017), we took as the values of the NS radius the values shown in Table 2. Considering the latest estimate of the radius of 1.4 M⊙ (Abbott et al. 2018), we also adopted a comparatively larger radius (13 km) to determine whether the value of the radius would change the result significantly.
The relationship between moment of inertia (I) and mass (M) for the four sGRBs is represented in Fig. 3, in which the dashed black line shows the I − M relation for the Keplerian spin case. We obtain the possible protomagnetar mass from the intersection of these lines. For GRB 080905A, GRB 060801, and GRB 100702A, whose spin periods are longer than the Keplerian period, the protomagneter masses are approximately equal to the nonspinning maximum mass MTOV of the corresponding EOSs. As shown in Fig. 3, the maximum offset does not exceed 0.01 M⊙. In particular, the mass of GRB 080905A is nearly equal to the MTOV because its period is rather long.
 |
Fig. 3. Moment of inertia as a function of the protomagnetar mass for eight EOSs using four sGRB samples. GRB 080905A is shown in yellow, GRB 060801 in green, GRB 100702A in red, and GRB 101219A in blue. We also plot the results with a radius of 13 km for GRB 101219A (magenta). Each group of curves has three lines. The middle solid lines correspond to the best-fit (Pi, Bp) values, and the bottom and upper dashed lines take the error of the fitting results into account. Detailed data are listed in Table 3. The eight EOSs are SLy, APR3, APR4, WFF1, WFF2, ENG, MPA1, and ALF2. In each EOS panel, the dashed black line represents the relation of the moment of inertia and mass in the case of Keplerian rotation. The intersection parts represent the theoretical mass of the nascent NS. |
The initial spin period of GRB 101219A is about 1 ms, which is close to the NS Keplerian limit. This is therefore a promising event for calculating the possible protomagneter mass, which would higher than MTOV. The theoretical mass ranges for GRB 101219A with different EOSs are shown in the left column of Table 3. Considering the latest estimate of the radius for 1.4 M⊙, which is 9 km–13 km (Abbott et al. 2018), we add the discussion of the case R = 13 km. The results are shown in the right column in Table 3. Figure 3 also shows that the mass range changes only slightly, which means that the mass is weakly dependent on the radius.
Theoretical protomagnetar mass range for GRB 101219A.
Our results clearly show that the characteristics of the protomagnetar depend on the spin period. The protomagnetar mass mainly depends on the spin periods, and fast rotation can produce more massive SMNS. This conclusion is well known and consistent with many researches (Gao et al. 2016; Radice et al. 2018b). Fig. 3 shows that if the initial spin period of a newly born SMNS is longer than the Keplerian period, then the mass of this SMNS should be close to the MTOV. In other words, if the spin period of the SMNS is close to the Keplerian period, the mass can be much higher than MTOV. For GW170817, the value of MTOV is estimated to be about 2.17 M⊙ under the assumption of Kepler rotation (Ruiz et al. 2018; Rezzolla et al. 2018; Ma et al. 2018). However, Shibata et al. (2019), Shao et al. (2020) recently revisited the constraint on MTOV using the observational results of GW170817. The authors found that MTOV could be as high as about 2.3 M⊙ when energy and angular momentum conservation are considered. We expect that more binary NS merger events will be detected in the future, which will place more constraints on the value of MTOV.
3.3. Spindown caused by magnetic dipole radiation and GW emission
We considered the more general situation that the loss of the spin energy of an SMNS includes both magnetic dipole radiation and GW emission (Fan et al. 2013a; Zhang & Mészáros 2001). As discussed in Gao et al. (2016), when the GW emission is included, the new spindown formula can be written as
where 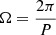 is the angular frequency and
is the angular frequency and 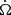 is its time derivative, and ε is the ellipticity of the SMNS. To simplify the equation, we define
is its time derivative, and ε is the ellipticity of the SMNS. To simplify the equation, we define 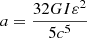 and
and 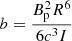 . With the initial condition
. With the initial condition 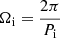 and
and 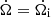 for T = 0, Eq. (5) can be solved, and we obtain a new relationship between the moment of inertia I and the protomagnetar mass Mp as
for T = 0, Eq. (5) can be solved, and we obtain a new relationship between the moment of inertia I and the protomagnetar mass Mp as
and
We also assume that the ellipticity of the SMNS is ε = 0.005 (Gao et al. 2016), which can release strong GW radiation after a merger. The new results including the GW emission are shown in Fig. 4 and Table 4. By comparing this with the results of Table 3, we can see that the protomagnetar mass deviations between this two cases (considering EM radiation alone and considering both EM and GW radiation) are not very significant. When GW emission is included, the nascent NS mass predicted by the model becomes slightly lower. This is easy to understand because GWs can take away some energy.
 |
Fig. 4. Moment of inertia as a function of the protomagnetar mass for 8 EOSs using 4 sGRB samples considering the magnetic dipole radiation and GW emission. The parameter of ellipticity is ε = 0.005, which is the same value in Gao et al. (2016). Like Fig. 3, the 4 sGRBs are represeted by different colors and the black dashed line represents the relation of moment of inertia and mass in the case of Kepler rotation. we also painted the situation of R = 13 km. The theoretical mass estimates are shown in Table 4. |
Theoretical protomagnetar mass range for GRB 101219A considering magnetic dipole radiation and GW emission.
For binary NS mergers, the merger product is of great interests because it sensitively depends on the EOS. Here we provide a way to estimate the protomagnetar mass based on the simultaneous detection of a GW and an sGRB in the X-ray plateau. On the other hand, the protomagnetar mass can also be estimated by numerical simulation, that is, the measured total mass is subtracted from the ejected mass, the disk mass, and other possible lost mass. This can be compared with our results and then used further to constrain the EOS.
4. Central engine of a quark star
At present, GW observations can only detect the waveform in the in-spiral phase. The questions remain about the nature of the merger product of a binary NS merger, and if the EOS before merging and after merging is the same. Moreover, we do not know whether there a phase transition in massive merger products. The possibility that a QS is the central engine of sGRBs and the conversion of an NS into a QS have been studied by many authors (Cheng & Dai 1996; Dai & Lu 1998; Wang et al. 2000; Ouyed & Sannino 2002; Drago et al. 2004; Paczyński & Haensel 2005). Li et al. (2016) discussed the model of a QS as the central engine of sGRBs based on the statistical analysis of the X-ray plateau. We used the same QS EOSs to calculate the mass of the post-merger product. The results are presented in Figs. 5 and 6.
 |
Fig. 5. Moment of inertia as a function of the merger product mass for the EOSs of the three QSs when EM radiation alone is considered. The detailed QSs information is provided by Li et al. (2016). |
 |
Fig. 6. Moment of inertia as a function of the merger product mass for the EOSs of the three QSs when EM and GW emission are considered. For the ellipticity of the QS, we used the same selection of an NS with ε = 0.005. |
When we consider the macroscopic physical properties, there are many differences between QS and NS. QS can support a higher mass than NS for the rotating case. The rotation speed and moment of inertia of a QS can be higher than that of an NSs. In the statistical analysis of Li et al. (2016) it was made clear that one of the most important advantages is that the EOSs of QS predict a much more narrow break time tb distribution than the EOSs of NS. This is more consistent with the observed data. The mass of the merger product when the magnetic dipole radiation alone is considered is shown in Fig. 5 and Table 3 for the EOSs of the three QSs. When GW radiation is included, the new results are shown in Fig. 6 and Table 4. The masses of QSs can clearly be more massive than the masses of NSs. This is probably a simple but reasonable way to distinguish QSs from NSs.
5. Protomagnetar mass estimation for CDF-S XT2
Recently, Xue et al. (2019) detected an X-ray transient (CDF-S XT2) whose light curve is analogous to the X-ray plateau of a GRB afterglow. CDF-S XT2 is thought to be powered by a millisecond magnetar. It is associated with a galaxy at redshift z = 0.738 and lies in the outskirts of the host galaxy with a moderate offset from the galaxy center. The event-rate density of simliar transients is also consistent with the binary NS merger rate density. The light curve can be well fit by a broken power-law model, with the power-law slopes being 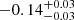 before the break (the break time
before the break (the break time 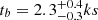 ) and
) and 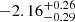 after the break (Xue et al. 2019). All these features of CDF-S XT2 imply that this X-ray transient may have originated from a binary NS merger, and that the merger product is a long-lived magnetar.
after the break (Xue et al. 2019). All these features of CDF-S XT2 imply that this X-ray transient may have originated from a binary NS merger, and that the merger product is a long-lived magnetar.
Based on the magnetar model, Xiao et al. (2019) have obtained some key properties of the protomagnetar, such as its initial spin period P0, the surface magnetic field strength B, and the wind saturation Lorentz factor Γsat. The authors calculated the parameters for five different values of Γsat and found that the most likely case is Γsat ∼ 103 − 104. For Γsat = 103, the parameters of the initial spin period and the magnetic field strength are 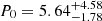 ms and
ms and 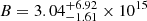 G. For Γsat = 104, these two parameters are
G. For Γsat = 104, these two parameters are 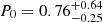 ms and
ms and 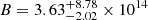 G, respectively.
G, respectively.
We used these two best-fitting results to estimate the protomagnetar mass. The results are shown in Fig. 7. It is obvious that the masses for Γsat = 103 are all close to MTOV, which is similar to the cases of GRB 060801, GRB 070724A, and GRB 080905A, because the initial spin period of Γsat = 103 is rather long. For Γsat = 104, however, the mass of the magnetar is higher than MTOV because the initial spin is close to the Keplerian limit. If the mass of the central magnetar can be determined by some other ways, then we can constrain the EOS subsequently. For example, if the mass of this millisecond magnetar is approximately 2.3 M⊙, we find that a softer EOSs would be favored, such as SLy, APR4, WFF1, WFF2, ENG, and ALF2. If the mass of this magnetar were close to 2.6 M⊙, however, then the allowed EOSs are APR3, APR4, WFF2, ENG, and MPA1.
 |
Fig. 7. Theoretical mass range of the central engine of CDF-S XT2. Left panel: results of Γsat = 103, right panel: results of Γsat = 104. |
6. Central engine of GW170817: an SMNS?
The central remnant of GW170817 is still unknown. There is no strong evidence to determine whether the merger product is an HMNS or SMNS, or even a stable NS. Considering the observed properties of AT 2017gfo, Yu et al. (2018) suggested that the central engine may be a long-lived NS with a surface magnetic field of ∼1011 − 1012 G. Ai et al. (2018) investigated the allowed parameter space of the long-lived NS and obtained similar results. Margalit & Metzger (2017) discussed the properties of GW170817 and claimed that the product of GW170817 is more likely to be an HMNS or a short-lived SMNS with Bp ≫ 1015 G.
We estimated the possible parameter space of an SMNS by assuming that the merger product of GW170817 is an SMNS. First we need to infer the possible mass of the protomagnetar. For GW170817, the total mass of the binary NS is 2.74 M⊙ (Abbott et al. 2017). According to the numerical simulations, the mass of the central remnant could be formulated as (Rezzolla et al. 2018)
where Mc represents the uniformly rotating central remnant. Mg is the initial total gravitational mass of the binary system, and ξ (ξ = 0.95 ± 0.03) is the mass fraction of the core after dynamical mass ejection (Hanauske et al. 2017; Rezzolla et al. 2018). Mej is the mass of ejecta from the core and can be estimated from the blue kilonova ejecta (Metzger 2017a,b; Shibata & Kiuchi 2017). According to Cowperthwaite et al. (2017), a reasonable value is Mej = 0.02 ± 0.01 M⊙. η = 1.171 is the conversion factor between baryonic mass and gravitational mass (Rezzolla et al. 2018). We considered two typical mass values of an SMNS as the merger outcome of GW170817. One is a remnant mass of 2.58 M⊙, which corresponds to ξ = 0.95 and Mej = 0.02 M⊙. The other is a remnant mass of 2.49 M⊙, which corresponds to ξ = 0.92 and Mej = 0.03 M⊙. These two values are also consistent with the numerical simulation results of Shibata & Kiuchi (2017).
For a given EOS, to form an SMNS the remnant mass should satisfy the condition MTOV ≤ Mc ≤ Mmax. This means that only five of the eight EOSs (APR3, APR4, WFF2, ENG and MPA1) satisfy this mass constraint. Furthermore, the maximum value of the initial spin period P0 can be obtained from Eq. (2) (by taking Mmax = 2.58 M⊙ and 2.49 M⊙). We find that the P0 of these EOSs is very close to the Keplerian limit. Then we can calculate the lower limit of the dipolar magnetic field Bp by assuming the collapse time tcol. We considered four cases of collapse time: tcol = 10 s, 100 s, 1000 s, and 10 000 s, wich are commonly shown in GRB X-ray afterglows.
The magnetic dipole radiation luminosity Lmd of an NS can be expressed as
where Rs, 6 = Rs/106 cm, Bp, 15 = Bp/1015 G, and P0, −3 = P0/1 ms are the radius, the polar magnetic field, and the initial spin period of the remnant, respectively (Yu et al. 2018). All of these SMNS properties are presented in Table 5 and 6.
Possible parameter space of the SMNS with 2.49M⊙.
Possible parameter space of the SMNS with 2.58 M⊙.
In all cases, the magnetic field strength lies between 1013 G–1015 G, so that the formed SMNS is a millisecond magnetar, and the magnetic dipole radiation luminosity is in the range 1046 − 1049 erg s−1, which is comparable to the luminosity of the GRB X-ray plateau (Nousek et al. 2006), and is much higher than the luminosity of a kilonova (∼1041 erg s−1). For GRB 1708117A at a distance of 40 Mpc, this early X-ray emission can be easily detected if the source can be well localized shortly after the GW and sGRB are detected. We also note that in all cases, the total magnetic dipole radiation energy is > 1050 erg (the values of Bp and Lmd given in Tables 5 and 6 are only lower limits, the actual values can be far higher), a large fraction of which would be deposited into the post-merger environment, such as GRB jet and merger ejecta. Because this energy is comparable to that of the GRB jet and merger ejecta (Margalit & Metzger 2017; Troja et al. 2019), this energy input may induce some additional signatures in the GRB and/or kilonova emission, such as an bump or flat segment in the GRB afterglow light curve or a higher kilonova luminosity (Fan et al. 2013b; Yu et al. 2013). The lack of detection of such signatures suggests that the merger product of GW170817 may be not an SMNS.
7. Conclusions and discussions
The detection of GW170817 and its EM counterpart have opened the era of multi-messenger astronomy. We have considered the appearance of the X-ray plateau along with a GW. This can be used to study some properties of protomagnetar. If the outcome of a binary NS merger is a magnetar, we can obtain the values of the initial spin period P0 and the magnetic field Bp by fitting the X-ray plateau and then calculating the mass of the magnetar. For four sGRBs with well-measured P0 and Bp, we find that for three of them, that is, GRB 080905A, GRB 060801, and GRB 100702A, the masses of their magnetars are all close to the MTOV because their spin periods are relatively long. For GRB 101219A, whose spin period is close to the Keplerian period, the mass of the central engine can be higher than MTOV. We also discussed the possibility that a QS is the protomagnetar after the merger. The most essential feature is that a QS can reach a higher mass than an NS. On the other hand, the protomagnetar mass can also be estimated by GW detection and numerical simulation, that is, the measured total mass is subtracted from the ejected mass, the disk mass, and other possible lost mass, which can be compared with our results and then be used to further constrain the EOS.
The event-rate density of an NS merger inferred from GW170817 is 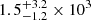 Gpc−3 yr−1 (Abbott et al. 2017). As discussed in Lasky et al. (2014), the coincident GW and EM detection of an sGRB with an X-ray plateau is estimated to be 0.4 events per year. When we consider the ISS-Lobster (a proposed all-sky X-ray telescope), the coincident events can rise to one per year (Lasky et al. 2014). This means that the coincidence of GW and X-ray plateau might be detected in the near future.
Gpc−3 yr−1 (Abbott et al. 2017). As discussed in Lasky et al. (2014), the coincident GW and EM detection of an sGRB with an X-ray plateau is estimated to be 0.4 events per year. When we consider the ISS-Lobster (a proposed all-sky X-ray telescope), the coincident events can rise to one per year (Lasky et al. 2014). This means that the coincidence of GW and X-ray plateau might be detected in the near future.
In addition, we applied our method to the recent observation of CDF-S XT2 to estimate the mass of the central engine. Xue et al. (2019) suggested that this X-ray transient is powered by a millisecond magnetar. We calculated the mass for Γsat = 103 and Γsat = 104. For a millisecond magnetar with a period about 6 ms, the mass is in the range of 2.1 M⊙ ∼ 2.46 M⊙. For a period of approximately 0.8 ms, the possible mass value falls in the interval of 2.1 M⊙ ∼ 3.0 M⊙. If in the future, this type of X-ray transient is also caught by GW observations, we can make further constraints on the NS EOS.
The central remnant of GW170817 is still unknown. We investigated the possibility that an SMNS is the merger product and discussed its properties. It is interesting to show that the SMNS is a millisecond magnetar and its magnetic dipole radiation luminosity is very high. The energy input to the GRB jet and merger ejecta may induce some specific emission features. The lack of detection of such features suggests that the merger product of GW170817 may not be an SMNS. However, we note that the data for GW170817 suggest an MTOV ≤ 2.17 M⊙ if the newly formed remnant has been a short-lived HMNS (Margalit & Metzger 2017; Rezzolla et al. 2018; Ai et al. 2020), while in order to account for X-ray plateaus, MTOV would need to be relatively high, MTOV ∼ 2.3 M⊙ (Fan et al. 2013a; Gao et al. 2016). This difference may be reduced if the remnant formed in GW170817 had quickly or effectively lost its angular momentum through the GW radiation, for which MTOV ≤ 2.3 M⊙ is allowed for the general cases (Shibata et al. 2019; Shao et al. 2020). Fan et al. (2020) showed that the properties of the binary NSs involved in GW170817 are in favor of strong post-merger GW radiation. In addition, as discussed in Ai et al. (2020), the merger remnant of GW170817 may also have been a long-lived massive NS or even a stable NS. This question needs further investigation. The exact value of MTOV and the nature of the merger remnant may be identified when more NS-NS merger events have been detected.
In the advanced LIGO/Virgo O3 run, it is expected that more GW170817-like events are detected. For X-ray observations, Sarin et al. (2018) have developed a GW detection pipeline for a long-lived binary NS merger remnant guided by X-ray counterpart observations. The coincidence of GW and X-ray afterglow can help us to solve more puzzles of the central engine, such as the NS EOS, ellipticity, and spin-down mechanism. All these progresses will help us to reveal the essential properties of binary NS mergers.
Acknowledgments
We thank the anonymous referee for valuable comments. This work was supported by NSFC (No. 11921003, 11933010), by the Chinese Academy of Sciences via the Strategic Priority Research Program (No. XDB23040000), Key Research Program of Frontier Sciences (No. QYZDJ-SSW-SYS024).
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017, Phys. Rev. Lett., 119, 161101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2018, Phys. Rev. Lett., 121, 161101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2019, Phys. Rev. X, 9, 011001 [Google Scholar]
- Ai, S., Gao, H., & Zhang, B. 2020, ApJ, 893, 146 [CrossRef] [Google Scholar]
- Ai, S., Gao, H., Dai, Z.-G., et al. 2018, ApJ, 860, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Antoniadis, J., Freire, P. C. C., Wex, N., et al. 2013, Science, 340, 448 [Google Scholar]
- Cheng, K. S., & Dai, Z. G. 1996, Phys. Rev. Lett., 77, 1210 [NASA ADS] [CrossRef] [Google Scholar]
- Cook, G. B., Shapiro, S. L., & Teukolsky, S. A. 1994, ApJ, 422, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Coulter, D. A., Foley, R. J., Kilpatrick, C. D., et al. 2017, Science, 358, 1556 [NASA ADS] [CrossRef] [Google Scholar]
- Cowperthwaite, P. S., Berger, E., Villar, V. A., et al. 2017, ApJ, 848, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, Z. G., & Lu, T. 1998, Phys. Rev. Lett., 81, 4301 [NASA ADS] [CrossRef] [Google Scholar]
- Demorest, P. B., Pennucci, T., Ransom, S. M., Roberts, M. S. E., & Hessels, J. W. T. 2010, Nature, 467, 1081 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Drago, A., Lavagno, A., & Pagliara, G. 2004, Phys. Rev. D, 69, 057505 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Y.-Z., & Xu, D. 2006, MNRAS, 372, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Y.-Z., Wu, X.-F., & Wei, D.-M. 2013a, Phys. Rev. D, 88, 067304 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Y.-Z., Yu, Y.-W., Xu, D., et al. 2013b, ApJ, 779, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Y.-Z., Jiang, J.-L., Tang, S.-P., Jin, Z.-P., & Wei, D.-M. 2020, ArXiv e-prints [arXiv:2005.10482] [Google Scholar]
- Gao, H., Zhang, B., & Lü, H.-J. 2016, Phys. Rev. D, 93, 044065 [NASA ADS] [CrossRef] [Google Scholar]
- Goldstein, A., Veres, P., Burns, E., et al. 2017, ApJ, 848, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Hanauske, M., Takami, K., Bovard, L., et al. 2017, Phys. Rev. D, 96, 043004 [CrossRef] [Google Scholar]
- Hinderer, T., Lackey, B. D., Lang, R. N., & Read, J. S. 2010, Phys. Rev. D, 81, 123016 [Google Scholar]
- Komatsu, H., Eriguchi, Y., & Hachisu, I. 1989, MNRAS, 237, 355 [NASA ADS] [Google Scholar]
- Lasky, P. D., Haskell, B., Ravi, V., Howell, E. J., & Coward, D. M. 2014, Phys. Rev. D, 89, 047302 [NASA ADS] [CrossRef] [Google Scholar]
- Li, A., Zhang, B., Zhang, N.-B., et al. 2016, Phys. Rev. D, 94, 083010 [NASA ADS] [CrossRef] [Google Scholar]
- Li, A., Zhu, Z.-Y., & Zhou, X. 2017, ApJ, 844, 41 [CrossRef] [Google Scholar]
- Li, L.-X., & Paczyński, B. 1998, ApJ, 507, L59 [Google Scholar]
- Li, S.-Z., Liu, L.-D., Yu, Y.-W., & Zhang, B. 2018, ApJ, 861, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Lyons, N., O’Brien, P. T., Zhang, B., et al. 2010, MNRAS, 402, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, P.-X., Jiang, J.-L., Wang, H., et al. 2018, ApJ, 858, 74 [CrossRef] [Google Scholar]
- Margalit, B., & Metzger, B. D. 2017, ApJ, 850, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Metzger, B. D. 2017a, Liv. Rev. Relativ., 20, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Metzger, B. D. 2017b, ArXiv e-prints [arXiv:1710.05931] [Google Scholar]
- Metzger, B. D., Quataert, E., & Thompson, T. A. 2008, MNRAS, 385, 1455 [NASA ADS] [CrossRef] [Google Scholar]
- Nousek, J. A., Kouveliotou, C., Grupe, D., et al. 2006, ApJ, 642, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Ouyed, R., & Sannino, F. 2002, A&A, 387, 725 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paczyński, B., & Haensel, P. 2005, MNRAS, 362, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Piro, A. L., Giacomazzo, B., & Perna, R. 2017, ApJ, 844, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Piro, L., Troja, E., Zhang, B., et al. 2019, MNRAS, 483, 1912 [NASA ADS] [CrossRef] [Google Scholar]
- Radice, D., Perego, A., Zappa, F., & Bernuzzi, S. 2018a, ApJ, 852, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Radice, D., Perego, A., Bernuzzi, S., & Zhang, B. 2018b, MNRAS, 481, 3670 [CrossRef] [Google Scholar]
- Read, J. S., Lackey, B. D., Owen, B. J., & Friedman, J. L. 2009, Phys. Rev. D, 79, 124032 [NASA ADS] [CrossRef] [Google Scholar]
- Rezzolla, L., Most, E. R., & Weih, L. R. 2018, ApJ, 852, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Rowlinson, A., O’Brien, P. T., Tanvir, N. R., et al. 2010, MNRAS, 409, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Rowlinson, A., O’Brien, P. T., Metzger, B. D., Tanvir, N. R., & Levan, A. J. 2013, MNRAS, 430, 1061 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiz, M., Shapiro, S. L., & Tsokaros, A. 2018, Phys. Rev. D, 97, 021501 [NASA ADS] [CrossRef] [Google Scholar]
- Sarin, N., Lasky, P. D., Sammut, L., & Ashton, G. 2018, Phys. Rev. D, 98, 043011 [CrossRef] [Google Scholar]
- Savchenko, V., Ferrigno, C., Kuulkers, E., et al. 2017, ApJ, 848, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Shao, D.-S., Tang, S.-P., Sheng, X., et al. 2020, Phys. Rev. D, 101, 063029 [CrossRef] [Google Scholar]
- Shibata, M., & Kiuchi, K. 2017, Phys. Rev. D, 95, 123003 [NASA ADS] [CrossRef] [Google Scholar]
- Shibata, M., Zhou, E., Kiuchi, K., & Fujibayashi, S. 2019, Phys. Rev. D, 100, 023015 [CrossRef] [Google Scholar]
- Troja, E., van Eerten, H., Ryan, G., et al. 2019, MNRAS, 489, 1919 [NASA ADS] [Google Scholar]
- Wang, X. Y., Dai, Z. G., Lu, T., Wei, D. M., & Huang, Y. F. 2000, A&A, 357, 543 [NASA ADS] [Google Scholar]
- Xiao, D., Zhang, B.-B., & Dai, Z.-G. 2019, ApJ, 879, L7 [CrossRef] [Google Scholar]
- Xue, Y. Q., Zheng, X. C., Li, Y., et al. 2019, Nature, 568, 198 [CrossRef] [Google Scholar]
- Yu, Y.-W., Zhang, B., & Gao, H. 2013, ApJ, 776, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, Y.-W., Liu, L.-D., & Dai, Z.-G. 2018, ApJ, 861, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B., & Mészáros, P. 2001, ApJ, 552, L35 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Theoretical protomagnetar mass range for GRB 101219A considering magnetic dipole radiation and GW emission.
All Figures
 |
Fig. 1. Relation between tidal deformability (Λ) and NS mass for different EOSs. The vertical dotted line marks the canonical NS mass of 1.4 M⊙. From top to bottom, the three horizontal dotted lines are for Λ = 800, 580, and 70. Currently, all EOSs satisfy the constraints from GW observations, and are indistinguishable from each other. |
| In the text | |
 |
Fig. 2. Tidal deformability Λ1 and Λ2 calculated using the 90% credible region of the component masses for GW170817 (Abbott et al. 2019). The 90% and 50% credible region contours determined by the GW are also shown by dashed lines from the outside to the inside. Left panel: situation of low-spin priors, and right panel: high-spin priors. |
| In the text | |
 |
Fig. 3. Moment of inertia as a function of the protomagnetar mass for eight EOSs using four sGRB samples. GRB 080905A is shown in yellow, GRB 060801 in green, GRB 100702A in red, and GRB 101219A in blue. We also plot the results with a radius of 13 km for GRB 101219A (magenta). Each group of curves has three lines. The middle solid lines correspond to the best-fit (Pi, Bp) values, and the bottom and upper dashed lines take the error of the fitting results into account. Detailed data are listed in Table 3. The eight EOSs are SLy, APR3, APR4, WFF1, WFF2, ENG, MPA1, and ALF2. In each EOS panel, the dashed black line represents the relation of the moment of inertia and mass in the case of Keplerian rotation. The intersection parts represent the theoretical mass of the nascent NS. |
| In the text | |
 |
Fig. 4. Moment of inertia as a function of the protomagnetar mass for 8 EOSs using 4 sGRB samples considering the magnetic dipole radiation and GW emission. The parameter of ellipticity is ε = 0.005, which is the same value in Gao et al. (2016). Like Fig. 3, the 4 sGRBs are represeted by different colors and the black dashed line represents the relation of moment of inertia and mass in the case of Kepler rotation. we also painted the situation of R = 13 km. The theoretical mass estimates are shown in Table 4. |
| In the text | |
 |
Fig. 5. Moment of inertia as a function of the merger product mass for the EOSs of the three QSs when EM radiation alone is considered. The detailed QSs information is provided by Li et al. (2016). |
| In the text | |
 |
Fig. 6. Moment of inertia as a function of the merger product mass for the EOSs of the three QSs when EM and GW emission are considered. For the ellipticity of the QS, we used the same selection of an NS with ε = 0.005. |
| In the text | |
 |
Fig. 7. Theoretical mass range of the central engine of CDF-S XT2. Left panel: results of Γsat = 103, right panel: results of Γsat = 104. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



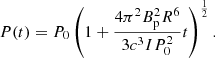
![$$ \begin{aligned} I =\frac{4\pi ^2B_{\rm p}^2R^6t_{\rm col}}{3c^3}\left[\left(\frac{M_{\rm p}-M_{\rm TOV}}{\alpha M_{\rm TOV}}\right)^{\frac{2}{\beta }}-P_0^2\right]^{-1}, \end{aligned} $$](/articles/aa/full_html/2020/09/aa36671-19/aa36671-19-eq13.gif)
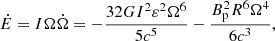
![$$ \begin{aligned} \frac{a}{2b^2}\ln \left[\left(\frac{a\Omega _{\rm i}^2 + b}{a\Omega _{\rm col}^2 + b}\right)\frac{\Omega _{\rm col}^2}{\Omega _{\rm i}^2}\right] + \frac{\Omega _{\rm i}^2 - \Omega _{\rm col}^2}{2b\Omega _{\rm i}^2\Omega _{\rm col}^2} - t_{\rm col} = 0, \end{aligned} $$](/articles/aa/full_html/2020/09/aa36671-19/aa36671-19-eq21.gif)