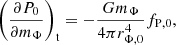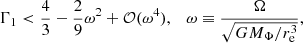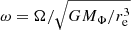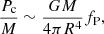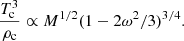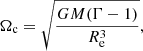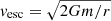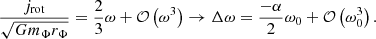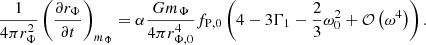EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 640 (August 2020) A&A, 640 (2020) L18 Full HTML
Free Access
Issue
A&A
Volume 640, August 2020
Article Number L18
Number of page(s) 8
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202038902
Published online 17 August 2020

© ESO 2020

1. Introduction

Very massive stars have long been predicted to undergo pair-instability supernovae (PISNe, Fowler & Hoyle 1964; Rakavy & Shaviv 1967) and pulsational-PISNe (PPISNe, Fraley 1968; Woosley 2017) due to pair-creation in their cores, which softens the equation of state and induces instability. Collapse in these conditions leads to runaway oxygen burning and energetic mass ejections. Although there are various candidate electromagnetic transients that could have been powered by this mechanism (cf. Gal-Yam et al. 2009; Terreran et al. 2017; Arcavi et al. 2017; Lunnan et al. 2018), there is no unambiguous event that indicates that these transients do occur in nature.

Indirect evidence for PPISNe and PISNe is provided by gravitational wave observations. PISNe (which leave no remnant) and PPISNe (which result in mass loss before iron-core collapse) have been predicted to result in a gap in black hole (BH) masses between ∼45 M⊙ and 120 M⊙ (Heger & Woosley 2002; Yoshida et al. 2016; Woosley 2017; Marchant et al. 2019), which is expected to be an observable feature in the population of binary BH mergers observed by ground-based detectors (Belczynski et al. 2014, 2016; Marchant et al. 2016; Spera & Mapelli 2017). Results from the first two observing runs of the LIGO and Virgo detectors indicate that there is a dearth of BHs with masses ≳45 M⊙, consistent with the lower edge of the predicted PISNe gap (Fishbach & Holz 2017; Abbott et al. 2019a). In the next years, additional measurements will further constrain this upper mass gap from PISNe, allowing it to be used as a standard candle for cosmology (Farr et al. 2019) and as a tool for constraining uncertain nuclear reaction rates (Farmer et al. 2020).

Currently, significant work is conducted to study what can modify the predicted location of this mass gap, including uncertainties in nuclear reaction rates (Takahashi 2018; Farmer et al. 2019), convection (Renzo et al. 2020), the presence of a massive hydrogen envelope at iron-core collapse (Di Carlo et al. 2019), and accretion after BH formation (van Son et al. 2020). Regarding rotation, work has been done to study how it affects the evolution of a star prior to a PPISN or PISN (Chatzopoulos et al. 2013; Mapelli et al. 2020), but there is still a large uncertainty on how rotation affects the actual hydrodynamics of these events. Early work performed by Glatzel et al. (1985) showed that rapid rotation can shift the boundaries of instability upward in mass, but provided no predictions on the resulting properties of BHs that formed through this process.

The objective of this Letter is to provide a first estimate on how the hydrodynamics of PPISNe or PISNe are affected by rotation, and how this affects the upper mass gap. In Sect. 2 we describe how rotation modifies the criterion for instability. We describe the setup of our numerical simulations of PPISNe and PISNe in Sect. 3, and present our results in Sect. 4. We conclude by discussing the implications of our results in Sect. 5.

2. Rotation and pair instability

We modeled rotation following the shellular approximation, in which all thermodynamical properties of the star are assumed to be constant through rigidly rotating Roche equipotentials. Under this assumption, the equations of stellar structure and evolution retain their one-dimensional form but include rotation using two coefficients, fP and fT, that are computed from integrals over the Roche potential (Endal & Sofia 1976; Heger & Langer 2000). The momentum equation in this approximation is given by

( ∂ P ∂ m Φ ) t = − G m Φ 4 π r Φ 4 f P − 1 4 π r Φ 2 ( ∂ r Φ ∂ t ) m Φ , $$ \begin{aligned} \left(\frac{\partial P}{\partial m_{\Phi }}\right)_{\rm t} = -\frac{Gm_\Phi }{4\pi r_\Phi ^4}f_{\rm P}-\frac{1}{4\pi r_{\Phi }^2}\left(\frac{\partial r_\Phi }{\partial t}\right)_{m_\Phi }, \end{aligned} $$(1)

where rΦ and mΦ represent the volume-equivalent radius and the mass associated with each equipotential surface. In the shellular approximation, the standard radiative temperature gradient ∇r is also scaled by a factor fT/fP.

The effect of rotation on the hydrodynamics of PPISNe and PISNe can be understood in terms of two different effects that are produced by centrifugal support: a modification of the stability criterion, and that rotating stars follow an evolution that resembles that of lower mass stars. The variation in the stability criterion can be described by considering a hydrostatic solution of Eq. (1),

( ∂ P 0 ∂ m Φ ) t = − G m Φ 4 π r Φ , 0 4 f P , 0 , $$ \begin{aligned} \left(\frac{\partial P_0}{\partial m_{\Phi }}\right)_{\rm t} = -\frac{Gm_\Phi }{4\pi r_{\Phi ,0}^4}f_{\rm P,0}, \end{aligned} $$(2)

and performing a Lagrangian perturbation on rΦ, 0,

r Φ = r Φ , 0 + Δ r Φ , Δ r Φ = α r Φ , 0 , $$ \begin{aligned} r_{\Phi }=r_{\Phi ,0}+\Delta r_{\Phi }, \quad \Delta r_{\Phi } = \alpha r_{\Phi ,0}, \end{aligned} $$(3)

with |α|≪1 being a constant. Requiring that the resulting acceleration is in the same direction as the perturbation, we obtain a sufficient instability criterion (see Appendix A),

Γ 1 < 4 3 − 2 9 ω 2 + O ( ω 4 ) , ω ≡ Ω G M Φ / r e 3 , $$ \begin{aligned} \Gamma _1 < \frac{4}{3}-\frac{2}{9}\omega ^2 + \mathcal{O} (\omega ^4),\quad \omega \equiv \frac{\Omega }{\sqrt{GM_\Phi /r_{\rm e}^3}}, \end{aligned} $$(4)

where Γ1 ≡ (d log P/d log ρ)ad is the first adiabatic index of the fluid, Ω is the rotational frequency of a shell, and re is its equatorial radius. This resembles the standard instability criterion Γ1 <  4/3 for a nonrotating self-gravitating body. As a real star does not have a constant Γ1 or ω, Eq. (4) can be true or false in different regions of the star, and whether this drives a global instability can be assessed by integrating the difference between the left- and right-hand sides of the equation through the star (Stothers 1999).

Figure 1 shows the instability region given by Eq. (4) for different values of ω in the ρ − T plane. Three profiles of nonrotating stellar models at the onset of a PPISN or PISN from Marchant et al. (2019) are included; the 50 M⊙ model undergoes a PPISN, and the 61 M⊙ and 72 M⊙ models result in full disruption through a PISN. For ω = 0.4, all three models fall outside of the instability region.

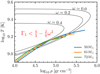thumbnail Fig. 1.

Instability region from pair-creation for different values of the ratio ω = Ω / G M Φ / r e 3 $ \omega=\Omega/\sqrt{GM_\Phi/r_{\mathrm{e}}^3} $, computed for material composed of 90% oxygen and 10% carbon by mass. For reference, the profile of three nonrotating stripped star models at the onset of PPISNe or PISNe from Marchant et al. (2019) are included. The masses given correspond to the mass at the onset of instability.

The second effect that can stabilize a rotating star is that its evolution resembles that of a lower mass star. This can be understood in terms of an order-of-magnitude analysis of Eq. (1), where when we assume that there is a characteristic value for fP throughout the star, we can estimate the central pressure as

P c M ∼ GM 4 π R 4 f P , $$ \begin{aligned} \frac{P_{\rm c}}{M}\sim \frac{GM}{4\pi R^4}f_{\rm P}, \end{aligned} $$(5)

where R and M are the radius and mass of the star. Using Eq. (A.2) for fP, taking ρc ∝ M/R3 and assuming a gas strongly dominated by radiation pressure such that P ∝ T4, we find that

T c 3 ρ c ∝ M 1 / 2 ( 1 − 2 ω 2 / 3 ) 3 / 4 . $$ \begin{aligned} \frac{T_{\rm c}^3}{\rho _{\rm c}}\propto M^{1/2}(1-2\omega ^2/3)^{3/4}. \end{aligned} $$(6)

This implies that more massive stars follow an evolution in the ρc − Tc plane at higher Tc for a given ρc, thus approaching the region where Γ1 <  4/3. Rotation lowers the value of the central temperature at a fixed central density, causing the star to evolve farther away from the instability region.

3. Methods

We performed our numerical simulations using version 13311 of the MESA code for stellar structure and evolution (Paxton et al. 2011, 2013, 2015, 2018, 2019), with the setup described in Marchant et al. (2019). A detailed description of our simulation setup is provided in Appendix B.

As initial conditions we used pure helium stars, which are representative of binary BH progenitors formed through the isolated evolution of close binaries. To maximize the angular momentum content of our models at the onset of PPISNe or PISNe, we considered helium stars at a metallicity of Z⊙/50 with Z⊙ = 0.0142 (Asplund et al. 2009). One important process we take into account is the Spruit-Tayler (ST) dynamo for angular momentum transport (Spruit 1999, 2002). The inclusion of the ST dynamo in stripped stars leads to nearly solid-body rotation and efficient loss of angular momentum from winds. In particular, Qin et al. (2019) showed that binary models without the ST dynamo can reproduce the nearly critical spins of BHs that are observed in high-mass X-ray binaries, while models that include it result in BHs with nearly zero spin. The physical nature of the ST dynamo is currently a topic of active discussion (cf. Denissenkov & Pinsonneault 2007; Zahn et al. 2007; Fuller et al. 2019), therefore we consider models with and without this mechanism.

Initial rotation rates were set in our simulations as solid-body rotation at the beginning of core helium burning. The angular frequency was taken to be 90% of its critical value at the surface Ωcrit, which is given by (Langer 1997)

Ω c = G M ( Γ − 1 ) R e 3 , $$ \begin{aligned} \Omega _{\rm c} = \sqrt{\frac{GM(\Gamma -1)}{R_{\rm e}^3}}, \end{aligned} $$(7)

where Re is the equatorial radius of the star, and the Eddington factor Γ is defined as

Γ ≡ κ L 4 π c G M · $$ \begin{aligned} \Gamma \equiv \frac{\kappa L}{4\pi c G M}\cdot \end{aligned} $$(8)

Our choice of 90% of the critical rotation at birth is meant to explore the variations from rotation for the most extreme cases. In the context of binary BH formation, such rapidly rotating naked helium stars are expected from chemically homogeneous evolution (Mandel & de Mink 2016; Marchant et al. 2016) and from tidal synchronization in very compact post-common-envelope systems consisting of a helium star and a BH (Kushnir et al. 2016; Qin et al. 2018)

For comparison, we also computed nonrotating models. The initial masses in our simulations were chosen to cover the range of masses at which PPISNe occur, while resolving the boundaries between nonpulsating and pulsating models and between pulsating and fully disrupted models. We modeled evolution until either the star was completely disrupted in a PISN or an iron-core was formed and collapsed. Tables summarizing each individual simulation we performed are included in Appendix C.

4. Results

The properties of our models at the onset of pair instability are illustrated in Fig. 2 and also indicate the outcome of the simulations in terms of the occurrence of PPISNe or PISNe. We define the specific angular momentum j as the total angular momentum of the star divided by its mass. As expected, models that do not include the ST dynamo retain more angular momentum. We find that all our models with the ST dynamo evolve toward critical rotation at their surface (Ω/Ωc = 1) during the contraction phase between core helium depletion and core carbon ignition. To prevent models from evolving above critical rotation, we considered enhanced wind mass-loss as described in Paxton et al. (2015), such that the star removes sufficient angular momentum to remain below critical. This results in enhanced mass-loss at this late stage (Aguilera-Dena et al. 2018). As the models with the ST dynamo evolve as solid-body rotators even at these late phases, these simulations represent an upper limit on the angular momentum content at the onset of pair instability if such stars have strong angular momentum coupling.

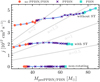thumbnail Fig. 2.

Specific angular momentum j and masses at the onset of PPISNe or PISNe for all of our simulations. For models that do not undergo pair instability, the values correspond to the moment of iron-core collapse. Gray lines correspond to constant values of the spin parameter a = jc/MG.

Our nonrotating models can be used as a baseline to assess the effect of rotation. Without rotation, we find that PPISNe occur for masses between 36.7 M⊙ and 62.6 M⊙. Models below this range evolve hydrostatically until iron-core collapse, and models above this range are disrupted in a PISN. Rotating models with the ST dynamo shift this range upward to 37.7 M⊙ − 64.7 M⊙, while the range is between 43.2 M⊙ and 76.5 M⊙ when the ST dynamo is not included. Thus, between our nonrotating and rotating simulations we find a ∼20% shift in the mass range for the onset of PPISNe.

Figure 3 summarizes the masses and angular momentum of our models at the point of iron-core collapse. The reduction of the spin parameter a = jc/MG at core-collapse compared to that at the onset of PPISNe is of particular interest. For example, in our simulations with the ST dynamo, the most massive model at core collapse has 47.4 M⊙ and a spin of 0.17, while at the onset of the PPISN, it had 56.1 M⊙ and a spin of 0.84. This large reduction in spin is caused not only by mass loss, but is also due to angular momentum transport between a compact core and an extended envelope. As shown by Marchant et al. (2019), heat injected by the thermonuclear pulses leads to a quiescent phase that lasts up to ten thousand years, in which the outer layers of the star can expand beyond 100 R⊙. Our rotating simulations with the ST dynamo transport angular momentum efficiently to these extended layers, which are ejected in later pulses. In contrast, simulations without the ST dynamo do not undergo efficient angular momentum transport during this phase; the model with the highest mass at core collapse has 57.7 M⊙ and a spin of 1.39, and it corresponds to a pre-PPISN star of 63.7 M⊙ with a spin of 1.57.

thumbnail Fig. 3.

Same as Fig. 2, but for the properties at the onset of iron-core collapse. MCC corresponds to the baryonic mass of the star at core collapse.

Many of our simulations at core collapse have spin parameters in excess of unity, such that assuming direct collapse to a BH is not an adequate model. Instead, we assumed that the innermost 3 M⊙ of the star collapse to a BH with a maximum spin parameter of unity and used the model of Batta & Ramirez-Ruiz (2019) to grow the BH from the remainder of the star. In this approximation parts of the star that have sufficient angular momentum to form a disk around the BH increase its mass and spin following Bardeen et al. (1972), while parts with insufficient angular momentum collapse directly to the BH. This results in BHs with spins smaller than unity and gravitational masses lower than the baryonic mass of the collapsing star. In determining the final gravitational mass of the BH we ignored energy losses from neutrino emission. This is justified because even if the star undergoes collapse to a BH through an intermediate proto-neutron star phase, this would only reduce the gravitational mass of the collapsing iron core (which is just ∼10% of the total mass of the star) by ∼10% (cf. Appendix A.2 of Zevin et al. 2020).

The resulting gravitational masses of the BHs, together with their spins, are shown in Fig. 4. The lower edge of the PISNe mass gap for nonrotating models is at 45.5 M⊙, and the maximum masses for rotating models with and without the ST dynamo are 47.4 M⊙ and 52.4 M⊙, respectively. This represents an upward shift in the mass at the edge of the gap of ∼4% and ∼15% for the cases with and without the ST dynamo.

thumbnail Fig. 4.

Final gravitational BH masses and spins predicted from the properties of our simulations at iron core-collapse combined with the model of Batta & Ramirez-Ruiz (2019) for BH formation.

5. Discussion

In order to study how rotation affects the lower edge of the BH mass gap predicted from PISNe, we have performed simulations of PPISNe and PISNe from rapidly rotating helium star progenitors by using a 1D approximation for hydrodynamics. We find that the final outcome of our simulations depends on the strength of angular momentum transport. Compared to nonrotating models, rotating simulations that include strong coupling through the ST dynamo produce a small increase (∼4%) on the mass range at which PPISNe occur, as well as on the final masses of the BHs that are produced. The effect is larger in simulations without the ST dynamo, with an increase of ∼15% in the mass range for PPISNe and their resulting BH masses. This indicatest that the lower edge of the PISNe mass gap increases in mass at higher BH spins (a ≳ 0.8), as shown in Fig. 4.

Assessing this prediction with observations of merging binary BHs presents important complications. In most cases, only the effective spin χeff rather than the individual BH spins can be measured to any accuracy, and there is a significant degeneracy with respect to the mass ratio of the system (Hannam et al. 2013). Additionally, BHs produced in binary BH mergers can also produce a population of high-spin and high-mass BHs in the upper mass gap (Gerosa & Berti 2017). Furthermore, we did not study the case where a star retains a significant hydrogen envelope at the onset of instability, although BHs formed from stars rich in hydrogen are expected to spin down their cores significantly (Fuller & Ma 2019), which leads to low-spin BHs for which rotation should not affect the dynamics of PPISNe.

Despite these uncertainties, one particular object of interest in the first catalog of gravitational wave transients is GW170729 (Abbott et al. 2019b), for which the effective spin was reported to be 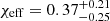χ eff = 0 . 37 − 0.25 + 0.21 $ \chi_{\mathrm{eff}}=0.37^{+0.21}_{-0.25} $ with a mass of the primary BH of 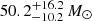50 . 2 − 10.2 + 16.2 M ⊙ $ 50.2^{+16.2}_{-10.2}\,M_\odot $. Although the mass of the primary BH in GW170729 is consistent with the edge of the mass gap as predicted by nonrotating models, most of the 90% credible interval falls within the gap. This has motivated discussions that GW170729 might be a second-generation BH merger (Kimball et al. 2020). Analyzing the posterior distributions provided by the LIGO-Virgo collaboration, we find that the individual spin of this BH is 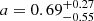a = 0 . 69 − 0.55 + 0.27 $ a=0.69^{+0.27}_{-0.55} $ (see Appendix D), which makes it a candidate for a BH that formed through a rapidly rotating star that underwent PPISN. Even with imperfect measurements, a large number of detections can be used to derive the intrinsic properties of the population (Mandel et al. 2019), which will provide stronger evidence than inferences based on individual objects.

One additional aspect that we did not consider here is the relevance of our simulations in the context of long gamma-ray burst (LGRB) progenitors. The standard model for LGRBs invokes a so-called collapsar, where the collapse of a star with a sufficiently high angular momentum can lead to the formation of a massive disk around a newly formed BH (Woosley 1993; MacFadyen & Woosley 1999). The stellar origin of LGRBs is supported by the observation of associated SNe (cf. Galama et al. 1998), for which the lack of hydrogen and helium in their spectra indicate that stripped stars are the progenitors (cf. Campana et al. 2006).

From our simulations of rotating stripped stars we can study whether the occurrence of pulsational mass loss prior to collapse can affect a potential LGRB or its associated SNe. As shown by Marchant et al. (2019), strong pulses are expected to deposit energy throughout the layers of the star that remain bound, leading to an expansion of the star by orders of magnitude prior to iron-core collapse. This is illustrated in Fig. 5, where we plot the radius at core collapse of our models computed without the ST dynamo versus the mass coordinate measured inward from the surface. Models that do not pulsate have radii ≲1 R⊙, while pulsating models cover a wide range of radii that extend well beyond 10 R⊙. If all these collapsing models resulted in LGRBs, the large variety of free-fall timescales for these extended envelopes might translate into different LGRB durations, reaching into the regime of ultra-long GRBs (e.g., Levan et al. 2014). The free-fall timescales of the progenitors with radii above 10 R⊙ exceeds 104 s and corresponds to those observed for ultra-long GRBs (∼104 s). Many progenitors here have free-fall timescales exceeding 105 s, which are well beyond the duration of known ultra-long GRBs, but the accretion could be suppressed at some moment as a result of the accompanying SN, for instance. A candidate GRB with a duration of about 107 s is known (Quataert & Kasen 2012), and it matches the free-fall timescales of the most extended progenitors (∼103 R⊙) produced by PPISNe. In the accompanying paper (Moriya et al. 2020), we investigate the explosion properties of one extended GRB progenitor presented here and show that it can also explain the peculiar SN component associated with the ultra-long GRB 111209A (Greiner et al. 2015).

thumbnail Fig. 5.

Radii as a function of outer mass coordinate for all our simulations without the ST dynamo at the point of iron-core collapse. The total mass M is defined as the innermost mass coordinate for which the velocity is below the local escape velocity v esc = 2 G m / r $ \mathit{v}_{\mathrm{esc}}=\sqrt{2Gm/r} $.

As already mentioned, the objective of this study is to provide a first analysis of the effect of rotation on the hydrodynamic evolution of stars undergoing PPISNe, but an important caveat needs to be pointed out. The use of one-dimensional simulations is dependent on the shellular approximation, but during rapid hydrodynamical phases, horizontal turbulence, which is the process believed to produce near-shellular rotation in radiative layers of a rotating star (Chaboyer & Zahn 1992), cannot operate fast enough. This implies that our simulations can be used to determine the masses for which PPISNe or PISNe occur, but there is still an important quantitative uncertainty on the final BH masses that are produced by these thermonuclear events. Nevertheless, our results can serve to study the growing sample of gravitational-wave sources with non-negligible spins, while motivating multidimensional calculations of PPISNe and PISNe.

1

These low-temperature tables are for hydrogen-rich material, which does not correspond to the case in our simulations. These low temperatures are reached on the outermost layers of our models that expand to large radii (R >  103 R⊙), but do not affect the conclusion that these stars would expand to such a large size after pulsations.

Acknowledgments

PM acknowledges support from the FWO junior postdoctoral fellowship No. 12ZY520N. TJM is supported by the Grants-in-Aid for Scientific Research of the Japan Society for the Promotion of Science (JP18K13585, JP20H00174). The authors would also like to thank the anonymous referee for their helpful comments.

References

  1. Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2019a, ApJ, 882, L24 [NASA ADS] [CrossRef] [Google Scholar]
  2. Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2019b, Phys. Rev. X, 9, 031040 [Google Scholar]
  3. Aguilera-Dena, D. R., Langer, N., Moriya, T. J., & Schootemeijer, A. 2018, ApJ, 858, 115 [NASA ADS] [CrossRef] [Google Scholar]
  4. Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
  5. Arcavi, I., Howell, D. A., Kasen, D., et al. 2017, Nature, 551, 210 [NASA ADS] [CrossRef] [Google Scholar]
  6. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bardeen, J. M., Press, W. H., & Teukolsky, S. A. 1972, ApJ, 178, 347 [NASA ADS] [CrossRef] [Google Scholar]
  8. Batta, A., & Ramirez-Ruiz, E. 2019, ArXiv e-prints [arXiv:1904.04835] [Google Scholar]
  9. Belczynski, K., Buonanno, A., Cantiello, M., et al. 2014, ApJ, 789, 120 [NASA ADS] [CrossRef] [Google Scholar]
  10. Belczynski, K., Heger, A., Gladysz, W., et al. 2016, A&A, 594, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Biscoveanu, S., Isi, M., Vitale, S., & Varma, V. 2020, ArXiv e-prints [arXiv:2007.09156] [Google Scholar]
  12. Bohé, A., Shao, L., Taracchini, A., et al. 2017, Phys. Rev. D, 95, 044028 [CrossRef] [Google Scholar]
  13. Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
  14. Campana, S., Mangano, V., Blustin, A. J., et al. 2006, Nature, 442, 1008 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  15. Caughlan, G. R., & Fowler, W. A. 1988, At. Data Nucl. Data Tables, 40, 283 [Google Scholar]
  16. Chaboyer, B., & Zahn, J.-P. 1992, A&A, 253, 173 [Google Scholar]
  17. Chatzopoulos, E., Wheeler, J. C., & Couch, S. M. 2013, ApJ, 776, 129 [NASA ADS] [CrossRef] [Google Scholar]
  18. Cox, J. P., & Giuli, R. T. 1968, Principles of Stellar Structure (New York: Gordon and Breach) [Google Scholar]
  19. Denissenkov, P. A., & Pinsonneault, M. 2007, ApJ, 655, 1157 [NASA ADS] [CrossRef] [Google Scholar]
  20. Di Carlo, U. N., Giacobbo, N., Mapelli, M., et al. 2019, MNRAS, 487, 2947 [NASA ADS] [CrossRef] [Google Scholar]
  21. Endal, A. S., & Sofia, S. 1976, ApJ, 210, 184 [NASA ADS] [CrossRef] [Google Scholar]
  22. Endal, A. S., & Sofia, S. 1978, ApJ, 220, 279 [NASA ADS] [CrossRef] [Google Scholar]
  23. Farmer, R., Renzo, M., de Mink, S. E., Marchant, P., & Justham, S. 2019, ApJ, 887, 53 [CrossRef] [Google Scholar]
  24. Farmer, R., Renzo, M., de Mink, S., Fishbach, M., & Justham, S. 2020, ApJ, submitted [arXiv:2006.06678] [Google Scholar]
  25. Farr, W. M., Fishbach, M., Ye, J., & Holz, D. E. 2019, ApJ, 883, L42 [CrossRef] [Google Scholar]
  26. Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
  27. Fishbach, M., & Holz, D. E. 2017, ApJ, 851, L25 [NASA ADS] [CrossRef] [Google Scholar]
  28. Fowler, W. A., & Hoyle, F. 1964, ApJS, 9, 201 [Google Scholar]
  29. Fraley, G. S. 1968, Ap&SS, 2, 96 [NASA ADS] [CrossRef] [Google Scholar]
  30. Fricke, K. 1968, Z. Astrophys., 68, 317 [NASA ADS] [Google Scholar]
  31. Fuller, J., & Ma, L. 2019, ApJ, 881, L1 [NASA ADS] [CrossRef] [Google Scholar]
  32. Fuller, J., Piro, A. L., & Jermyn, A. S. 2019, MNRAS, 485, 3661 [NASA ADS] [Google Scholar]
  33. Galama, T. J., Vreeswijk, P. M., van Paradijs, J., et al. 1998, Nature, 395, 670 [NASA ADS] [CrossRef] [Google Scholar]
  34. Gal-Yam, A., Mazzali, P., Ofek, E. O., et al. 2009, Nature, 462, 624 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  35. Gerosa, D., & Berti, E. 2017, Phys. Rev. D, 95, 124046 [NASA ADS] [CrossRef] [Google Scholar]
  36. Glatzel, W., Fricke, K. J., & El Eid, M. F. 1985, A&A, 149, 413 [NASA ADS] [Google Scholar]
  37. Goldreich, P., & Schubert, G. 1967, ApJ, 150, 571 [Google Scholar]
  38. Greiner, J., Mazzali, P. A., Kann, D. A., et al. 2015, Nature, 523, 189 [NASA ADS] [CrossRef] [Google Scholar]
  39. Hamann, W.-R., Koesterke, L., & Wessolowski, U. 1995, A&A, 299, 151 [NASA ADS] [Google Scholar]
  40. Hannam, M., Brown, D. A., Fairhurst, S., Fryer, C. L., & Harry, I. W. 2013, ApJ, 766, L14 [CrossRef] [Google Scholar]
  41. Hannam, M., Schmidt, P., Bohé, A., et al. 2014, Phys. Rev. Lett., 113, 151101 [CrossRef] [Google Scholar]
  42. Heger, A., & Langer, N. 2000, ApJ, 544, 1016 [NASA ADS] [CrossRef] [Google Scholar]
  43. Heger, A., & Woosley, S. E. 2002, ApJ, 567, 532 [NASA ADS] [CrossRef] [Google Scholar]
  44. Heger, A., Langer, N., & Woosley, S. E. 2000, ApJ, 528, 368 [NASA ADS] [CrossRef] [Google Scholar]
  45. Herwig, F. 2000, A&A, 360, 952 [NASA ADS] [Google Scholar]
  46. Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
  47. Kimball, C., Berry, C., & Kalogera, V. 2020, Res. Notes Am. Astron. Soc., 4, 2 [CrossRef] [Google Scholar]
  48. Kippenhahn, R. 1974, IAU Symp., 66, 20 [Google Scholar]
  49. Kushnir, D., Zaldarriaga, M., Kollmeier, J. A., & Waldman, R. 2016, MNRAS, 462, 844 [NASA ADS] [CrossRef] [Google Scholar]
  50. Langer, N. 1997, ASP Conf. Ser., 120, 83 [Google Scholar]
  51. Langer, N., Fricke, K. J., & Sugimoto, D. 1983, A&A, 126, 207 [NASA ADS] [Google Scholar]
  52. Levan, A. J., Tanvir, N. R., Starling, R. L. C., et al. 2014, ApJ, 781, 13 [NASA ADS] [CrossRef] [Google Scholar]
  53. Lunnan, R., Fransson, C., Vreeswijk, P. M., et al. 2018, Nat. Astron., 2, 887 [NASA ADS] [CrossRef] [Google Scholar]
  54. MacFadyen, A. I., & Woosley, S. E. 1999, ApJ, 524, 262 [NASA ADS] [CrossRef] [Google Scholar]
  55. Mandel, I., & de Mink, S. E. 2016, MNRAS, 458, 2634 [NASA ADS] [CrossRef] [Google Scholar]
  56. Mandel, I., Farr, W. M., & Gair, J. R. 2019, MNRAS, 486, 1086 [NASA ADS] [CrossRef] [Google Scholar]
  57. Mapelli, M., Spera, M., Montanari, E., et al. 2020, ApJ, 888, 76 [CrossRef] [Google Scholar]
  58. Marchant, P., Langer, N., Podsiadlowski, P., Tauris, T. M., & Moriya, T. J. 2016, A&A, 588, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Marchant, P., Renzo, M., Farmer, R., et al. 2019, ApJ, 882, 36 [Google Scholar]
  60. Moriya, T. J., Marchant, P., & Blinnikov, S. I. 2020, A&A, submitted [arXiv:2007.06221] [Google Scholar]
  61. Nieuwenhuijzen, H., & de Jager, C. 1990, A&A, 231, 134 [NASA ADS] [Google Scholar]
  62. Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
  63. Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [NASA ADS] [CrossRef] [Google Scholar]
  64. Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
  65. Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  67. Potekhin, A. Y., & Chabrier, G. 2010, Contrib. Plasma Phys., 50, 82 [NASA ADS] [CrossRef] [Google Scholar]
  68. Qin, Y., Fragos, T., Meynet, G., et al. 2018, A&A, 616, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Qin, Y., Marchant, P., Fragos, T., Meynet, G., & Kalogera, V. 2019, ApJ, 870, L18 [NASA ADS] [CrossRef] [Google Scholar]
  70. Quataert, E., & Kasen, D. 2012, MNRAS, 419, L1 [NASA ADS] [CrossRef] [Google Scholar]
  71. Rakavy, G., & Shaviv, G. 1967, ApJ, 148, 803 [NASA ADS] [CrossRef] [Google Scholar]
  72. Renzo, M., Farmer, R. J., Justham, S., et al. 2020, MNRAS, 493, 4333 [CrossRef] [Google Scholar]
  73. Rogers, F. J., & Nayfonov, A. 2002, ApJ, 576, 1064 [Google Scholar]
  74. Saumon, D., Chabrier, G., & van Horn, H. M. 1995, ApJS, 99, 713 [NASA ADS] [CrossRef] [Google Scholar]
  75. Spera, M., & Mapelli, M. 2017, MNRAS, 470, 4739 [Google Scholar]
  76. Spruit, H. C. 1999, A&A, 349, 189 [NASA ADS] [Google Scholar]
  77. Spruit, H. C. 2002, A&A, 381, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Stothers, R. B. 1999, MNRAS, 305, 365 [NASA ADS] [CrossRef] [Google Scholar]
  79. Takahashi, K. 2018, ApJ, 863, 153 [Google Scholar]
  80. Terreran, G., Pumo, M. L., Chen, T.-W., et al. 2017, Nat. Astron., 1, 713 [NASA ADS] [CrossRef] [Google Scholar]
  81. Timmes, F. X., & Swesty, F. D. 2000, ApJS, 126, 501 [NASA ADS] [CrossRef] [Google Scholar]
  82. Toro, E. F., Spruce, M., & Speares, W. 1994, Shock Waves, 4, 25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. van Son, L. A. C., De Mink, S. E., Broekgaarden, F. S., et al. 2020, ApJ, 897, 100 [CrossRef] [Google Scholar]
  84. Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. Woosley, S. E. 1993, ApJ, 405, 273 [NASA ADS] [CrossRef] [Google Scholar]
  86. Woosley, S. E. 2017, ApJ, 836, 244 [NASA ADS] [CrossRef] [Google Scholar]
  87. Yoshida, T., Umeda, H., Maeda, K., & Ishii, T. 2016, MNRAS, 457, 351 [NASA ADS] [CrossRef] [Google Scholar]
  88. Zahn, J. P. 1974, IAU Symp., 59, 185 [Google Scholar]
  89. Zahn, J. P., Brun, A. S., & Mathis, S. 2007, A&A, 474, 145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  90. Zevin, M., Spera, M., Berry, C. P. L., & Kalogera, V. 2020, ApJ, 899, L1 [CrossRef] [Google Scholar]

Appendix A: Derivation of a sufficient instability criterion

In terms of the small parameter |α|≪1 from Eq. (3), the corresponding Lagrangian perturbations for density and pressure are given by

Δ ρ = − 3 α ρ 0 , Δ P = Δ ρ ρ Γ 1 P 0 = − 3 α Γ 1 P 0 . $$ \begin{aligned} \Delta \rho = -3\alpha \rho _0,\quad \Delta P=\frac{\Delta \rho }{\rho }\Gamma _1 P_0=-3\alpha \Gamma _1 P_0. \end{aligned} $$(A.1)

As a star contracts or expands, its rotation changes, leading to a variation in the fP correction. From Paxton et al. (2019) we have that fP can be approximated as

f P = 1 − 2 3 ω 2 + O ( ω 4 ) . $$ \begin{aligned} f_{\rm P}=1-\frac{2}{3}\omega ^2+\mathcal{O} \left(\omega ^4\right). \end{aligned} $$(A.2)

The perturbation in fP, 0 can then be described in terms of the perturbation on ω,

Δ f P f P , 0 = ( − 4 3 ω 0 + O ( ω 0 3 ) ) Δ ω . $$ \begin{aligned} \frac{\Delta f_{\rm P}}{f_{\rm P,0}}=\left(-\frac{4}{3}\omega _0+\mathcal{O} \left(\omega _0^3\right)\right)\Delta \omega . \end{aligned} $$(A.3)

To compute Δω, we consider that the perturbation preserves the specific angular momentum jrot of each shell. In this case, we have that (Paxton et al. 2019)

j rot G m Φ r Φ = 2 3 ω + O ( ω 3 ) → Δ ω = − α 2 ω 0 + O ( ω 0 3 ) . $$ \begin{aligned} \frac{j_{\rm rot}}{\sqrt{Gm_\Phi r_\Phi }}=\frac{2}{3}\omega + \mathcal{O} \left(\omega ^3\right)\rightarrow \Delta \omega =\frac{-\alpha }{2}\omega _0+\mathcal{O} \left(\omega _0^3\right). \end{aligned} $$(A.4)

Combining Eqs. ((1), (A.1)−(A.4)), the acceleration after the perturbation is

1 4 π r Φ 2 ( ∂ r Φ ∂ t ) m Φ = α G m Φ 4 π r Φ , 0 4 f P , 0 ( 4 − 3 Γ 1 − 2 3 ω 0 2 + O ( ω 4 ) ) . $$ \begin{aligned} \frac{1}{4\pi r_{\Phi }^2}\left(\frac{\partial r_\Phi }{\partial t}\right)_{m_\Phi } = \alpha \frac{Gm_\Phi }{4\pi r_{\Phi ,0}^4}f_{\rm P,0}\left(4-3\Gamma _1-\frac{2}{3}\omega _0^2 + \mathcal{O} \left(\omega ^4\right)\right). \end{aligned} $$(A.5)

We can now derive a sufficient condition for instability by considering whether a contraction of the star, given by α <  0, leads to runaway collapse, which gives the result of Eq. (4).

Appendix B: Details of MESA simulations

In this appendix we briefly summarize the physical assumptions and ingredients we used in our simulations. MESA uses an equation of state that is constructed from a patchwork of results that have different ranges of validity, including OPAL (Rogers & Nayfonov 2002), SCVH (Saumon et al. 1995), PC (Potekhin & Chabrier 2010) and HELM (Timmes & Swesty 2000). Opacities are computed using tables from the OPAL project (Iglesias & Rogers 1996), with metal abundances corresponding to scaled solar values as measured by Asplund et al. (2009). At low temperatures, we rely on the opacity tables of Ferguson et al. (2005)1. Nuclear reaction rates are taken from Angulo et al. (1999) and Caughlan & Fowler (1988) with a preference for the former when available. During PPISNe and PISNe we make use of the nuclear network approx_21_plus_co56.net, which is the same 21-isotope network described in Marchant et al. (2019) with the inclusion of 56Co to better account for the radioactive decay of 56Ni. Mass-loss rates are computed as a combination of the prescriptions of Vink et al. (2001), Hamann et al. (1995), and Nieuwenhuijzen & de Jager (1990), as described in Marchant et al. (2019). We model convection using the mixing-length theory (Böhm-Vitense 1958; Cox & Giuli 1968) and a mixing-length parameter αMLT = 2 with exponential overshooting at convective boundaries (Herwig 2000) defined by parameters f = 0.01 and f0 = 0.005. Semiconvective mixing is modeled as as in Langer et al. (1983) with an efficiency parameter αsc = 1.

Hydrodynamical evolution is computed using the HLLC Riemann solver developed by Toro et al. (1994), with gravity being scaled by the fP parameter as described in Eq. (1). The value of fP is computed following Paxton et al. (2019). In addition to the ST dynamo, we include angular momentum transport in our simulations from Eddington-Sweet circulations (cf. Kippenhahn 1974), the GSF instability (Goldreich & Schubert 1967; Fricke 1968) and both secular (Endal & Sofia 1978) and dynamical (Zahn 1974) shear, following the method of Heger et al. (2000). There can be long periods of quiescence between events of pulsational mass loss and iron-core collapse. When a model restores hydrostatic equilibrium after a pulse, we therefore remove the ejected material from our simulation grid by following the method described in Paxton et al. (2018) and Marchant et al. (2019).

All necessary input files to reproduce our simulations, as well as machine-readable tables with our results, are available for download2.

Appendix C: Tabulated results

The results of our simulations are summarized in Tables C.1–C.3 for our models that are nonrotating, rotating with the ST dynamo, and rotating without the ST dynamo, respectively. The properties listed are

  • Mi: Initial mass of the helium star.

  • MHe dep: Mass of the star at core-helium depletion.

  • MCO,  He dep: Mass of the carbon-oxygen core of the star at core-helium depletion, defined as the innermost mass boundary where the mass fraction of helium is below 1%.

  • Mpre PPISN/PISN: Mass at the onset of the PPISN or PISN.

  • Mejecta: Mass ejected through pulsations. For models undergoing a PISN, this is equal to Mpre PPISN/PISN.

  • MCC: Baryonic mass of the star at iron-core collapse. We note that MCC ≠ Mpre PPISN/PISN + Mejecta as wind mass-loss during quiescent periods between pulsations and iron-core collapse can contribute.

  • # of pulses: Number of mass ejections produced by a PPISN or PISN.

  • Duration: Time from the onset of the PPISN until iron-core collapse

  • max KE: Maximum kinetic energy of ejected material achieved in an individual pulse.

  • ai, aHe dep, apre PPISN/PISN and aCC: Spin parameter a = jc/MG for the layers of the star that are below the escape velocity at different phases.

  • MBH, aBH: Final gravitational mass and spin of the BH.

Table C.1.

Summary of results for nonrotating models.

Table C.2.

Summary of results for rotating models including angular momentum transport via the ST dynamo.

Table C.3.

Summary of results for rotating models without angular momentum transport via the ST dynamo.

Appendix D: Spin posterior of the primary BH of GW170729

Although the first catalog of gravitational-wave transients (Abbott et al. 2019b) does not provide confidence intervals for individual BH spins, the posterior samples they computed are openly available and can be used to obtain this information3. These posteriors are computed using two waveform models, IMRPhenonPv2 (Hannam et al. 2014) and SEOBNRv3 (Bohé et al. 2017), as well as a set that combines an equal number of samples from both waveform models. Figure D.1 shows the posterior distributions compared to the prior used for parameter estimation, which corresponds to a flat distribution in spin between 0 ≤ a ≤ 0.99. From the combined distribution we find a median value with a 90% confidence interval of a = 0 . 69 − 0.55 + 0.27 $ a=0.69^{+0.27}_{-0.55} $. It has also recently been pointed out that for systems whose mass ratios are not far from unity, the individual spins can be better constrained when one simply aims to measure the highest and lowest spin of the BHs in the system, without directly specifying to which BH they correspond (Biscoveanu et al. 2020).

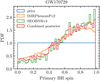thumbnail Fig. D.1.

Posterior distribution for the spin of the more massive BH in GW170729 using different waveform models compared to the flat prior distribution we used. The “Combined posterior” is obtained by using an equal number of random samples from each of the other two.

All Tables

Table C.1.

Summary of results for nonrotating models.

In the text
Table C.2.

Summary of results for rotating models including angular momentum transport via the ST dynamo.

In the text
Table C.3.

Summary of results for rotating models without angular momentum transport via the ST dynamo.

In the text

All Figures

thumbnail Fig. 1.

Instability region from pair-creation for different values of the ratio ω = Ω / G M Φ / r e 3 $ \omega=\Omega/\sqrt{GM_\Phi/r_{\mathrm{e}}^3} $, computed for material composed of 90% oxygen and 10% carbon by mass. For reference, the profile of three nonrotating stripped star models at the onset of PPISNe or PISNe from Marchant et al. (2019) are included. The masses given correspond to the mass at the onset of instability.
In the text
thumbnail Fig. 2.

Specific angular momentum j and masses at the onset of PPISNe or PISNe for all of our simulations. For models that do not undergo pair instability, the values correspond to the moment of iron-core collapse. Gray lines correspond to constant values of the spin parameter a = jc/MG.
In the text
thumbnail Fig. 3.

Same as Fig. 2, but for the properties at the onset of iron-core collapse. MCC corresponds to the baryonic mass of the star at core collapse.
In the text
thumbnail Fig. 4.

Final gravitational BH masses and spins predicted from the properties of our simulations at iron core-collapse combined with the model of Batta & Ramirez-Ruiz (2019) for BH formation.
In the text
thumbnail Fig. 5.

Radii as a function of outer mass coordinate for all our simulations without the ST dynamo at the point of iron-core collapse. The total mass M is defined as the innermost mass coordinate for which the velocity is below the local escape velocity v esc = 2 G m / r $ \mathit{v}_{\mathrm{esc}}=\sqrt{2Gm/r} $.
In the text
thumbnail Fig. D.1.

Posterior distribution for the spin of the more massive BH in GW170729 using different waveform models compared to the flat prior distribution we used. The “Combined posterior” is obtained by using an equal number of random samples from each of the other two.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.