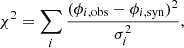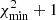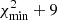| Issue |
A&A
Volume 638, June 2020
|
|
|---|---|---|
| Article Number | L5 | |
| Number of page(s) | 4 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202037762 | |
| Published online | 15 June 2020 | |
Letter to the Editor
Evidence for a rapid decrease of Pluto’s atmospheric pressure revealed by a stellar occultation in 2019
1
Astronomical Observatory, Graduate School of Science, Kyoto University Kitashirakawa-oiwake-cho, Sakyo-ku, Kyoto 606-8502, Japan
e-mail: arimatsu@kwasan.kyoto-u.ac.jp
2
Department of Earth Science, Okayama University, 1-1-1 Kita-ku, Tsushimanaka, Okayama 700-8530, Japan
3
Planetary Plasma and Atmospheric Research Center, Graduate School of Science, Tohoku University, 6-3 Aramaki -aza-aoba, Aoba-ku, Sendai 980-8578, Japan
4
Institute of Astronomy, Graduate School of Science, The University of Tokyo, 2-21-1 Osawa, Mitaka, Tokyo 181-0015, Japan
5
Japan Spaceguard Association, Bisei Spaceguard Center, 1716-3 Okura, Bisei, Ibara, Okayama 714-1411, Japan
Received:
18
February
2020
Accepted:
15
May
2020
We report observations of a stellar occultation by Pluto on 2019 July 17. A single-chord high-speed (time resolution = 2 s) photometry dataset was obtained with a CMOS camera mounted on the Tohoku University 60 cm telescope (Haleakala, Hawaii). The occultation light curve is satisfactorily fitted to an existing atmospheric model of Pluto. We find the lowest pressure value at a reference radius of r = 1215 km among those reported after 2012. These reports indicate a possible rapid (approximately 21−5+4% of the previous value) pressure drop between 2016, which is the latest reported estimate, and 2019. However, this drop is detected at a 2.4σ level only and still requires confirmation from future observations. If real, this trend is opposite from the monotonic increase of Pluto’s atmospheric pressure reported by previous studies. The observed decrease trend is possibly caused by ongoing N2 condensation processes in the Sputnik Planitia glacier associated with an orbitally driven decline of solar insolation, as predicted by previous theoretical models. However, the observed amplitude of the pressure decrease is larger than the model predictions.
Key words: Kuiper belt objects: individual: Pluto / planets and satellites: atmospheres / planets and satellites: physical evolution / occultations
© ESO 2018
1. Introduction
The existence of a substantial atmosphere around Pluto, primarily consisting of N2 with trace amounts of CH4, CO, HCN, and other species, makes it unique among known trans-Neptunian objects (TNOs) since no clear observational evidence for an atmosphere with a surface pressure greater than ∼10 nbar is found on the other bodies (Sicardy et al. 2011; Ortiz et al. 2012; Arimatsu et al. 2019a). After its confirmation in 1988 (Hubbard et al. 1988; Elliot et al. 1989), stellar occultation observations have been a powerful tool to explore Pluto’s atmosphere; clear refraction features in the light curve of an occulted star probes the number density, temperature, and pressure profiles. Pluto’s stellar occultations especially provide unique opportunities to monitor seasonal evolutions of the atmospheric pressure, which was discovered by Sicardy et al. (2003). The pressure evolution is caused by surface sublimation-condensation processes of Pluto’s N2 and other volatiles, which are thought to account for the large diversity of surface structures revealed by the New Horizons spacecraft (hereafter NH; Stern et al. 2015). Revealing pressure evolution through stellar occultations is thus critical not only to obtaining basic physical properties of the atmosphere, but also to understanding the geology of this unique TNO.
Although Pluto has receded from the Sun since 1989, its observed atmospheric pressure shows a monotonic increase (e.g., Sicardy et al. 2003; Young 2013; Olkin et al. 2015; Dias-Oliveira et al. 2015; Sicardy et al. 2016; Meza et al. 2019). The observed increase trend has been modeled (Bertrand & Forget 2016; Forget et al. 2017; Meza et al. 2019) based on surface topographic features and volatile ice distributions observed by NH (Moore et al. 2016). According to the models, the surface N2 ice glacier covering Sputnik Planitia, which is the largest confirmed basin, plays an important role in the seasonal pressure evolution. Model predictions indicate that the pressure was increasing and reached its maximum value in ∼2015. These models predict the decrease of pressure after 2015–2020 since the insolation in Sputnik Planitia decreased. Further continuous observations are required to test the model predictions. Unfortunately, Pluto has been receded away from the Galactic plane and the probability of occultation events has decreased since ∼2015. Observations of stellar occultations thus become rare opportunities to examine the current state of Pluto’s atmosphere.
In this Letter, we report observations of a stellar occultation by Pluto on 2019 July 17, approximately three years after the latest reported stellar occultation event (2016 July 19; Meza et al. 2019). Photometric data of the occultation were obtained with a CMOS camera mounted on the Tohoku University 60 cm Cassegrain/Coude (T60) telescope (Haleakala, Hawaii). Section 2 presents the outline of the stellar occultation observation and the data reduction method to derive the light curve. The results of the observation and the pressure estimate are given in Sect. 3. Discussions based on the obtained results are provided in Sect. 4. Finally, we summarize the results and discussions in Sect. 5.
2. Observation and data reduction
2.1. Observation
The occultation of a star UCAC5 340-173206 (Gaia DR2 catalog source ID: 6772059623498733952, ICRS position at epoch J2000: 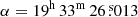 , δ = −22° 07′ 58.42″, Gaia Gmag = 13.0; Gaia Collaboration 2018) on 2019 July 17 was originally predicted by ERC Lucky Star project1. The project predicts stellar occultations by Pluto using Numerical Integration of the Motion of an Asteroid (NIMA) version 8 orbital elements (Desmars et al. 2019). The prediction confirmed that Pluto’s shadow swept over the major islands of Hawaii at a geocentric velocity vrel = 24.18 km s−1. The geocentric distance of Pluto during the occultation corresponds to D = 32.83 au.
, δ = −22° 07′ 58.42″, Gaia Gmag = 13.0; Gaia Collaboration 2018) on 2019 July 17 was originally predicted by ERC Lucky Star project1. The project predicts stellar occultations by Pluto using Numerical Integration of the Motion of an Asteroid (NIMA) version 8 orbital elements (Desmars et al. 2019). The prediction confirmed that Pluto’s shadow swept over the major islands of Hawaii at a geocentric velocity vrel = 24.18 km s−1. The geocentric distance of Pluto during the occultation corresponds to D = 32.83 au.
On 2019 July 17, we observed UCAC5 340-173206 at the Tohoku University Haleakala Observatory (latitude: 20° 42′30″ N, longitude: 156° 15′30″ W, altitude: 3040 m), Hawaii. At Haleakala, photometric data were obtained using a ZWO Co., Ltd. ASI178MM CMOS camera mounted on the Coude focus of the T60 telescope. The field of view (FoV) for the CMOS camera is 120″ × 80″ with an angular pixel scale of 0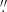 038. The exposure time was 2 s for each frame corresponding to the frame rate of ∼0.5 Hz. No filter was used in the present observation. During the observation, a dataset consisting of 1305 image frames were obtained in a 43.5 min window centered on the predicted central time of the occultation (12:42 on 2019 July 17 UTC) with an imaging capture software Firecapture version 2.4.
038. The exposure time was 2 s for each frame corresponding to the frame rate of ∼0.5 Hz. No filter was used in the present observation. During the observation, a dataset consisting of 1305 image frames were obtained in a 43.5 min window centered on the predicted central time of the occultation (12:42 on 2019 July 17 UTC) with an imaging capture software Firecapture version 2.4.
2.2. Data reduction
Aperture photometry for the occulted star (plus Pluto and Charon) is performed using the image data after bias and flat-field corrections and sky background subtraction. Owing to possible rapid changes in atmospheric conditions, the obtained flux values for individual data points can incur time-dependent flux fluctuations. To correct the possible flux fluctuations and calibrate the flux value of the target star, we carried out differential photometry with three reference stars (Gaia DR2 G-band magnitude range of 11−14) that are detected simultaneously. The calibrated light curve is then normalized to the unocculted flux.
We also obtained a Pluto + Charon flux relative to the total flux (including the occulted star) with resolved images obtained approximately 40 min before the occultation event. To obtain an accurate Pluto + Charon flux, we subtracted a radial brightness profile of UCAC5 340-173206 located close to Pluto and Charon in the original images based on a digital coronagraphic method developed by Assafin et al. (2009). The derived relative flux ratio is ∼0.241. We should note that, however, the imperfect flat-field correction, the residual of the stellar radial brightness profile, the airmass variation (1.5 during calibration versus 1.7 during the occultation), and Pluto’s rotational albedo variation can cause a systematic uncertainty of the flux ratio. We thus use this flux ratio only as a reference value for the light curve fit (see Sect. 3.1).
3. Results
3.1. Light curve fitting
Figure 1 shows the light curve of the target star after calibration and normalization. The observed duration of the occultation is roughly ∼50 s. No significant asymmetric profile or spike-like feature was detected from the light curve. To obtain the pressure of the atmosphere, synthetic light curves as a function of the pressure at a radius of r = 1215 km, which has been referred to be a reference radius by previous studies (Yelle & Elliot 1997; Sicardy et al. 2016; Meza et al. 2019), p1215, the distance of closest approach of Haleakala Observatory to Pluto’s shadow center, ρ the central time of the occultation, and the Pluto + Charon flux relative to the total flux, are generated using a ray-tracing technique described by Sicardy et al. (1999). For Pluto’s atmospheric refraction model, we consider atmospheric profiles provided by Dias-Oliveira et al. (2015) with assumptions that Pluto has a pure N2, spherically symmetric and transparent (haze-free) atmosphere with a time-independent thermal structure derived from the observed light curves. In the present model, the contribution from the near-limb (primary) image and far-limb (secondary) images are considered with a focusing factor provided by Sicardy et al. (1999); this factor is the ratio of the observer’s distance to the shadow center and the closest approach of the corresponding ray in Pluto’s atmosphere assuming a circular limb curvature of Pluto. The validity of these assumptions is discussed by Meza et al. (2019) with the NH results. According to Meza et al. (2019), the fixed temperature profile appears to be close to the results derived from NH and is thus useful for at least estimating the relative pressure changes. The physical parameters used for the fit are presented in Table 1. We adopted these parameters following Dias-Oliveira et al. (2015) and Meza et al. (2019) to avoid systematic uncertainties caused by using different values.
 |
Fig. 1. Light curve of the occultation obtained with T60. The data are normalized to the unocculted flux. An error bar for each data point represents the detector readout noise, target shot noise, and sky background noise. The sky background noise is the dominant noise source since the background level was irregularly high because of the apparent proximity of Moon during the observations (angular distance to the object corresponds to ∼10deg). The solid curve corresponds to the best-fit synthetic light curve. The horizontal dashed line shows the best-fit Pluto + Charon contribution to the total flux, corresponding to 0.261. The residuals are shown in the lower panel. |
Adopted parameters for the light curve fit and results.
The synthetic light curve is fitted to the observed data points (77 data points shown in Fig. 1 are used for the fit) by minimizing χ2;
where ϕi, obs, ϕi, syn, and σi are the observed and synthetic stellar fluxes, and the 1σ error at a data point i, respectively. Figure 2 shows the χ2 map for the fit to the light curve as a function of p1215 and ρ. The χ2 value for the best fit is 61.9 with 73 degrees of freedom (corresponding to 77 data points – 4 free parameters), indicating a satisfactory fit with a reduced χ2 of ∼0.848. The best-fit parameters are shown in Table 1, and the best-fit synthetic data points are overlaid with the observed data points in Fig. 1. According to the best-fit model, observed stellar rays come from above r ∼ 1214 km, which is comparable to the adopted reference radius. The obtained reference radius pressure is 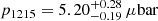 (1σ level error bars; see Fig. 2). Assuming the lower atmosphere temperature profile provided by Dias-Oliveira et al. (2015), this value corresponds to a surface (r = 1187 km) pressure of
(1σ level error bars; see Fig. 2). Assuming the lower atmosphere temperature profile provided by Dias-Oliveira et al. (2015), this value corresponds to a surface (r = 1187 km) pressure of 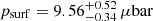 .
.
 |
Fig. 2. Fit to the light curve χ2 map as a function of the distance of closest approach of Haleakala Observatory to Pluto’s shadow center, ρ, and the pressure at a radius of 1215 km, p1215, which has been referred to be a reference radius by previous studies (Yelle & Elliot 1997; Sicardy et al. 2016; Meza et al. 2019). Darker zones correspond to lower χ2 values. The white circular point is the best-fit value corresponding to the minimum χ2 value of |
The best-fit ρ is derived to be 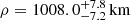 . The central time of the occultation derived from the fit is 12:41:52.02 ± 0.18 on 2019 July 17 UTC. We should note that the value derived from time stamps of the image data have a constant offset of several seconds due to imperfect time synchronizations of the capture software (Arimatsu et al. 2017). The best-fit Pluto + Charon flux ratio is 0.261 ± 0.012, which is slightly higher but comparable to that observed before the occultation event (0.241, see Sect. 2.2).
. The central time of the occultation derived from the fit is 12:41:52.02 ± 0.18 on 2019 July 17 UTC. We should note that the value derived from time stamps of the image data have a constant offset of several seconds due to imperfect time synchronizations of the capture software (Arimatsu et al. 2017). The best-fit Pluto + Charon flux ratio is 0.261 ± 0.012, which is slightly higher but comparable to that observed before the occultation event (0.241, see Sect. 2.2).
3.2. Pressure evolution
Figure 3 shows the reference radius pressure p1215 as a function of time; our result is compared with pressure values obtained by previous studies (Meza et al. 2019) using the same atmosphere model profile. The present pressure value is the lowest among those reported after 2012. We report a diminution of pressure of 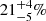 (1σ error bars) between 2016 (when p1215 = 6.61 ± 0.22 μbar, Meza et al. 2019) and our measurement in 2019 (
(1σ error bars) between 2016 (when p1215 = 6.61 ± 0.22 μbar, Meza et al. 2019) and our measurement in 2019 ( , see above). This corresponds to a decrease rate of
, see above). This corresponds to a decrease rate of 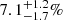 per Earth year. Examination of the χ2 map in Fig. 2, however, shows that this drop is detected at the 2.4σ level and thus remains marginally significant. Previous occultation studies using the same atmospheric model profile have reported a continuous increase of the pressure by a factor of approximately three between 1988 and 2016 (Meza et al. 2019), corresponding to an average increase rate of ∼4% per Earth year. Taken at face value, our result thus indicates that Pluto’s atmospheric pressure is decreasing nearly twice as rapidly as it increased in the previous three decades.
per Earth year. Examination of the χ2 map in Fig. 2, however, shows that this drop is detected at the 2.4σ level and thus remains marginally significant. Previous occultation studies using the same atmospheric model profile have reported a continuous increase of the pressure by a factor of approximately three between 1988 and 2016 (Meza et al. 2019), corresponding to an average increase rate of ∼4% per Earth year. Taken at face value, our result thus indicates that Pluto’s atmospheric pressure is decreasing nearly twice as rapidly as it increased in the previous three decades.
 |
Fig. 3. Atmospheric pressure of Pluto at r = 1215 km, p1215, as a function of time. The red square indicates the pressure value obtained in our present study (see Sect. 3), overlaid with those obtained between 1988 and 2016 using the same atmosphere model profile (black points; Meza et al. 2019; Sicardy, priv. commun.). The solid and dashed lines (horizontally shifted by +0.1 years for better visibility) represent 1σ and 3σ error bars for the data points, respectively. The 3σ error bar of the 1988 June 09 data point is not shown since the corresponding error value was not provided. |
4. Discussion
The pressure evolution of Pluto’s atmosphere has been due to seasonal cycles of surface volatiles, especially of N2 (Hansen & Paige 1996; Young 2013; Hansen et al. 2015). Recent exploration by NH gives a much tighter constraints on seasonal cycle models of Pluto’s surface volatiles (Bertrand & Forget 2016; Forget et al. 2017; Bertrand et al. 2018; Meza et al. 2019), several of which predict an ongoing (or near-future) decrease in Pluto’s atmospheric pressure.
According to a seasonal volatile transport model by Bertrand & Forget (2016), the observed trend is related to the seasonal sublimation-condensation of the glacier in Sputnik Planitia. Since the subsolar point was close to the latitudes of northern areas (30°N–50°N) of Sputnik Planitia in ∼1988−2015, the insolation and the sublimation of N2 ice in its glacier reached maximal. The model predicted that the pressure reached its peak value in ∼2015 and then decreased because the subsolar point moves to higher latitudes, leading to an enhanced N2 condensation rate. A recent model proposed by Meza et al. (2019) also predicts a similar pressure drop trend after ∼2020. However, our decrease rate of pressure is larger than that predicted by the seasonal evolution models. For instance, the Bertrand & Forget (2016) model predicts that the pressure decrease rate around 2019 is ∼0.7−1.0% (assuming a seasonal thermal inertia range of 500−1500 J s−1/2 m−2 K−1) per Earth year, approximately an order of magnitude smaller than our estimated value. Meza et al. (2019) predict almost no change or slight upward trend in the pressure around 2019 for their assumed N2-ice albedo range (0.72−0.73). These models assume that the decrease of the atmosphere is mainly attributed to the condensation of N2 in Sputnik Planitia. The present result would imply that the current N2 condensation rate at Sputnik Planitia is significantly higher than that predicted by existing models. Another possibility is that topographic features other than Sputnik Planitia may play an important role in a rapid N2 ice condensation. The present rapid decrease may imply an additional non-negligible deposit(s), especially in the hemisphere opposite from that better observed by NH, the so-called far side hemisphere (Stern et al. 2019). In any case, further continuous observations are required to obtain more detailed constraints.
5. Conclusions and future prospects
Single-chord high-speed photometric observations of the stellar occultation by Pluto on 2019 July 17 provided its latest atmospheric pressure. Contrary to the recent increasing pressure trend revealed by previous occultation studies, our analysis shows a rapid (approximately 21% of the previous value) pressure drop between 2016 and 2019; this decrease, however, is at a 2.4σ significance level, which is marginally significant. This decreasing trend is possibly caused by ongoing N2 condensation processes associated with the orbitally driven decline of solar insolation in Sputnik Planitia N2 ice. However, the observed amplitude of the pressure decrease is larger than the model predictions.
Our single-date and single-chord data do not bring further constraints on the seasonal evolution. Continuous ground-based stellar occultation observations are thus important to assess and to understand the transitional phase of Pluto’s atmospheric pressure trend. However, as already mentioned in Sect. 1, since Pluto is receding away from the Galactic plane, the probability of occultation events of bright stars is decreasing. High-sensitivity and high-cadence observations with CMOS cameras mounted on ∼ meter class telescopes will become more important to observe occultation events of fainter stars (with magnitudes fainter than ∼15, e.g., Arimatsu et al. 2019a), which occur more frequently than those of brighter stars. Observations with airborne telescopes such as SOFIA (Person 2012) and with portable telescope systems for high-cadence observations (e.g., Arimatsu et al. 2017, 2019b) will also be useful to observe rare and local occultation events.
Acknowledgments
We thank Dr. Bruno Sicardy for careful reading and providing constructive suggestions. This research has been partly supported by Japan Society for the Promotion of Science (JSPS) Grants-in-Aid for Scientific Research (KAKENHI) Grant Numbers 15J10278, 16K17796, and 18K13606.
References
- Arimatsu, K., Tsumura, K., Ichikawa, K., et al. 2017, PASJ, 69, 68 [CrossRef] [Google Scholar]
- Arimatsu, K., Ohsawa, R., Hashimoto, G. L., et al. 2019a, AJ, 158, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Arimatsu, K., Tsumura, K., Usui, F., et al. 2019b, Nat. Astron., 3, 301 [CrossRef] [Google Scholar]
- Assafin, M., Vieira-Martins, R., Braga-Ribas, F., et al. 2009, AJ, 137, 4046 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertrand, T., & Forget, F. 2016, Nature, 540, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Bertrand, T., Forget, F., Umurhan, O. M., et al. 2018, Icarus, 309, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Desmars, J., Meza, E., Sicardy, B., et al. 2019, A&A, 625, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dias-Oliveira, A., Sicardy, B., Lellouch, E., et al. 2015, ApJ, 811, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Elliot, J. L., Dunham, E. W., Bosh, A. S., et al. 1989, Icarus, 77, 14 [Google Scholar]
- Forget, F., Bertrand, T., Vangvichith, M., et al. 2017, Icarus, 287, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration 2018, A&A, 595, A1 [Google Scholar]
- Grundy, W. M., Binzel, R. P., & Buratti, B. J. 2016, Science, 351, aad9189 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, C. J., & Paige, D. A. 1996, Icarus, 120, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, C. J., Paige, D. A., & Young, L. A. 2015, Icarus, 246, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Hubbard, W. B., Hunten, D. M., Dieters, S. W., et al. 1988, Nature, 336, 452 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meza, E., Sicardy, B., Assafin, M., et al. 2019, A&A, 625, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moore, J. M., McKinnon, W. B., Spencer, J. R., et al. 2016, Science, 351, 1284 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Olkin, C. B., Young, L. A., Borncamp, D., et al. 2015, Icarus, 246, 220 [Google Scholar]
- Ortiz, J. L., Sicardy, B., Braga-Ribas, F., et al. 2012, Nature, 491, 566 [NASA ADS] [CrossRef] [Google Scholar]
- Person, M. J. 2019, Icarus, in press, https://doi.org/10.1016/j.icarus.2019.113572 [Google Scholar]
- Sicardy, B., Ferri, F., Roques, F., et al. 1999, Icarus, 142, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Sicardy, B., Widemann, T., Lellouch, E., et al. 2003, Nature, 424, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Sicardy, B., Ortiz, J. L., Assafin, M., et al. 2011, Nature, 478, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Sicardy, B., Talbot, J., Meza, E., et al. 2016, ApJ, 819, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Stern, S. A., Bagenal, F., & Ennico, K. 2015, Science, 350, aad1815 [Google Scholar]
- Stern, S. A., Weaver, H. A., Young, L. A., et al. 2019, in Pluto System After New Horizons, Abstract #7024. LPI Contribution No. 2133 (Houston: Lunar and Planetary Institute) [Google Scholar]
- Washburn, E. W. 1930, International Critical Tables of Numerical Data: Physics, Chemistry and Technology (New York: McGraw-Hill), 7 [Google Scholar]
- Yelle, R. V., & Elliot, J. L. 1997, in Pluto and Charon, Eds. Stern, S. A., & Tholen, D. J. (Tucson: University of Arizona Press), 347 [Google Scholar]
- Young, L. A. 2013, ApJ, 766, L22 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Light curve of the occultation obtained with T60. The data are normalized to the unocculted flux. An error bar for each data point represents the detector readout noise, target shot noise, and sky background noise. The sky background noise is the dominant noise source since the background level was irregularly high because of the apparent proximity of Moon during the observations (angular distance to the object corresponds to ∼10deg). The solid curve corresponds to the best-fit synthetic light curve. The horizontal dashed line shows the best-fit Pluto + Charon contribution to the total flux, corresponding to 0.261. The residuals are shown in the lower panel. |
| In the text | |
 |
Fig. 2. Fit to the light curve χ2 map as a function of the distance of closest approach of Haleakala Observatory to Pluto’s shadow center, ρ, and the pressure at a radius of 1215 km, p1215, which has been referred to be a reference radius by previous studies (Yelle & Elliot 1997; Sicardy et al. 2016; Meza et al. 2019). Darker zones correspond to lower χ2 values. The white circular point is the best-fit value corresponding to the minimum χ2 value of |
| In the text | |
 |
Fig. 3. Atmospheric pressure of Pluto at r = 1215 km, p1215, as a function of time. The red square indicates the pressure value obtained in our present study (see Sect. 3), overlaid with those obtained between 1988 and 2016 using the same atmosphere model profile (black points; Meza et al. 2019; Sicardy, priv. commun.). The solid and dashed lines (horizontally shifted by +0.1 years for better visibility) represent 1σ and 3σ error bars for the data points, respectively. The 3σ error bar of the 1988 June 09 data point is not shown since the corresponding error value was not provided. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.