| Issue |
A&A
Volume 638, June 2020
|
|
|---|---|---|
| Article Number | A23 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201936183 | |
| Published online | 05 June 2020 | |
“TNOs are Cool”: A survey of the trans-Neptunian region
XV. Physical characteristics of 23 resonant trans-Neptunian and scattered disk objects
1
Konkoly Observatory, Research Centre for Astronomy and Earth Sciences, Hungarian Academy of Sciences,
Konkoly Thege 15-17,
1121
Budapest,
Hungary
e-mail: farkas.aniko@csfk.mta.hu
2
Eötvös University, Faculty of Science,
Pázmány P. sétány 1/A,
1171
Budapest,
Hungary
3
ELTE Eötvös Loránd University, Institute of Phyiscs,
Pázmány P. sétány 1/A,
1171
Budapest,
Hungary
4
Max-Planck-Institut für Sonnensystemforschung,
Justus-von-Liebig-Weg 3,
37077
Göttingen,
Germany
5
Max-Planck-Institut für extraterrestrische Physik,
Giessenbachstrasse,
85748
Garching,
Germany
6
Lowell Observatory,
1400 W. Mars Hill Rd.,
Flagstaff,
AZ
86001,
USA
7
Space Telescope Science Institute,
3700 San Martin Dr.,
Baltimore,
MD
21218,
USA
8
Observatoire de Paris, Laboratoire d’Études Spatiales et d’Instrumentation en Astrophysique (LESIA),
5 Place Jules Janssen,
92195
Meudon Cedex,
France
9
Astrophysics Research Centre, School of Mathematics and Physics, Queen’s University Belfast,
Belfast,
UK
Received:
26
June
2019
Accepted:
2
March
2020
The goal of this work is to determine the physical characteristics of resonant, detached and scattered disk objects in the trans-Neptunian region, observed mainly in the framework of the “TNOs are Cool” Herschel open time key programme. Based on thermal emission measurements with the Herschel/PACS and Spitzer/MIPS instruments, we determine size, albedo, and surface thermal properties for 23 objects using radiometric modeling techniques. This is the first analysis in which the physical properties of objects in the outer resonances are determined for a notable sample. In addition to the results for individual objects, we compared these characteristics with the bulk properties of other populations of the trans-Neptunian region. The newly analyzed objects show a large variety of beaming factors, indicating a diversity of thermal properties, and in general they follow the albedo-color clustering identified earlier for Kuiper belt objects and Centaurs, further strengthening the evidence for a compositional discontinuity in the young Solar System.
Key words: Kuiper belt: general
© ESO 2020
1 Introduction
Trans-Neptunian objects in mean motion resonance with Neptune (RTNOs; see, e.g., Gladman et al. 2012, and references therein) show a dynamical behavior that their resonance angle ϕjk = jλ − kλN − (j-k)ϖ (where λ is the longitude of object, λN the longitude of Neptune, and ϖ the longitude of perihelion of the RTNO, for a specific j:k resonance) cannot have all values between 0° and 360°. Typically, the resonance angle is confined to a mean value with some relatively small libration amplitude. An important feature of the resonances is that they may provide protection against perturbations and allow large eccentricity orbits to survive for the age of the Solar System. Even so, the chaotic nature of the resonance border allows temporary trapping of objects near the border of the resonance, and nearly resonant objects can escape into a dynamical regime where perturbations may direct them out of the Kuiper belt toward the inner Solar System. Resonant objects also serve as a diagnostic tool of the planetary migration era. Current population estimates of RTNOs are consistent with a scenario that they were likely put in place in the resonances during the planet migration era at the end of the giant-planet formation process (Gladman et al. 2012). RTNOs show dynamical characteristics (e.g., inclination distribution) different from those of the classical Kuiper belt, but may be connected to the scattered disk population (Gomes et al. 2008), objects on high eccentricity orbits with perihelia beyond Neptune, and semi-major axes beyond the 2:1 resonance. Recent studies (Yu et al. 2018) indicate that a significant fraction of all scattered objects are transiently stuck in mean motion resonances, suggesting that these objects originated from the same single population.
The Outer Solar System Origins Survey (OSSOS, Bannister et al. 2018) recently provided a significant increase in the number of RTNOs, adding 313 new objects of which 132 are plutinos. This survey also detected two objects in the distant 9:1 resonance (Volk et al. 2018) that may have originated in the scattered population, and that became trapped in this resonance within the last ~1 Gyr, but could also be remnants of a larger, primordial population.
In addition to dynamical properties, Sheppard (2012) obtained broad-band color of 58 resonant objects, with significantly different color distributions in the different resonances. For example, those in the 5:3 and 7:4 resonances are dominated by ultra-red material, similar to that in the cold classical belt. Objects in the inner 4:3 and distant 5:2 resonances show mostly moderate red colors, similar to the scattered and detached populations, while the 2:1 and 3:2 resonances show a wide range of colors. Apart from the dynamical properties, color, albedo, and size are very crucial physical characteristics of these objects; however, they can be determined only when thermal emission data or occultation measurements are available.
In the framework of the “TNOs are Cool”: a survey of the trans-Neptunian region, a Herschel open time key programme (Müller et al. 2009), several papers have been published on the physical characteristics of Centaurs and trans-Neptunian objects in population-specific papers, and in other papers concentrating on specifically selected objects (Pál et al. 2012; Fornasier et al. 2013) or on the general properties of these small bodies (Lellouch et al. 2013). These papers used thermal emission data obtained with the PACS photometer camera of the Herschel Space Observatory in the far-infrared, at 70, 100, and 160 μm. The population-specific papers included the Centaurs (Duffard et al. 2014), classical Kuiper belt objects (Vilenius et al. 2012, 2014), plutinos (Mommert et al. 2012), some scattered disk and detached objects (Santos-Sanz et al. 2012), and also the members of the Haumea collisional family (Vilenius et al. 2018).
Using these data, in particular the size and albedo derived using radiometric models that were supplemented by color information, Lacerda et al. (2014) found evidence for a compositional discontinuity in the early Solar System, identifying two distinct types of planetary bodies: objects with dark (geometric albedo of pV ≈ 0.05) and neutrally colored surfaces, or with bright (pV ≈ 0.15) and red surfaces. Objects in relic populations (cold classicals, detached objects, and outer resonances, i.e., the 2:1 mean-motion resonance and beyond) show exclusively bright-red surfaces, while objects in dynamically less stable populations (Centaurs, plutinos, scattered disk object, and hot classicals) contain a mixture of bright-red and dark-neutral surfaces.
The largest set of RTNOs with reliable size and albedo information available are the plutinos. Mommert et al. (2012) derived these physical characteristics for 18 objects as part of the “TNOs Are Cool” program. They found sizes ranging from 150 to 730 km and geometric albedos varying between 0.04 and 0.28, with an average albedo of 0.08 ± 0.03, similar to the mean albedo of Centaurs, Jupiter family comets, and other TNOs except cold classicals and detached objects. Based on these results, the cumulative power law of the size distribution in this dynamical group is q = 2 between sizes of 120 and 400 km, and q = 3 for larger objects.
In a similar study (Santos-Sanz et al. 2012) investigated 15 scattered disk and detached objects and found notably different albedos between the scattered disk and detached subpopulations (mean geometric albedos of 6.9 and 17%, respectively).
Data from both studies were incorporated in the paper by Lacerda et al. (2014), with additional objects from the incomplete Herschel sample of RTNOs in non-3:2 resonances and additional scattered disk objects from Lellouch et al. (2013). A recent summary of thermal infrared observations of Centaurs and trans-Neptunian objects can be found in Müller et al. (2020).
In this paper we present the results of an investigation similar to those in the “TNOs are Cool” sample papers, focusing on Herschel/PACS observations of as-yet unpublished resonant and scattered disk objects. We derive size and albedo from Herschel/PACS measurements and derive radiometric models of 15 resonant, 7 scattered disk, and 1 detached object, in some cases supplemented by data from the MIPS camera of the Spitzer Space Telescope, not presented in earlier papers. We also reconsidered the data of a scattered disk and a detached object with inconsistent flux densities or problematic radiometric fits in previous papers, derived new flux densities using the final version of our data reduction pipeline, and obtained updated radiometric size and albedo estimates. Our results are then compared with color-albedo data of the trans-Neptunian dynamical populations derived in previous papers.
2 Observations, data reduction, and radiometric modeling
2.1 Herschel/PACS data
All Herschel/PACS measurements presented in this paper as new data were taken in scan-map mode with the PACS photometer arrays, following the observation strategy of the “TNOs are Cool” open time key programme (Müller et al. 2009; Vilenius et al. 2012; Kiss et al. 2014). Reduction of PACS photometer data is performed using the latest version of the “TNOs are Cool” pipeline. Both the key program observation strategies and the main characteristics and features of the pipeline are summarized in Kiss et al. (2014).
All Herschel/PACS measurements presented here as new reduction followed the same observation strategy: the target is observed at two epochs, typically separated by a day, and the data of the two epochs are combined to allow for optimal background elimination. At each epoch we observed the target with two 70/160 μm and two 100/160 μm filter astronomical observation requests (AORs), corresponding to 70° and 110° scan direction orientations. Altogether we obtained eight AORs per target, and correspondingly eight individual observation idendifiers (OBSIDs; see Table 1). Then the data of these OBSIDs are combined to obtain the final products. We note that 2003 UY117 was measured with Herschel/PACS using the 70/160 μm filter combination only, while all other targets were observed with both filter combinations.
We used the following main settings to obtain Level-2 flux-calibrated PACS scan maps from the raw PACS measurements:
scan legs are extended based on the slew speed 15 and 25′′ s−1, around the commanded 20′′ s−1 scan speed;
high pass filtering with filter width of 8, 9, and 16 is used at 70, 100, and 160 μm, respectively (high pass filter width sets the number of frames [2n+1] used for median subtraction from the detector timeline; see Popesso et al. 2012 and Balog et al. 2014 for a detailed description of the method);
pixel masking is used above 2σ, and at the source position with 2 × FWHM radius;
second-level deglitching is applied with nσ = 30, the sigma-clipping parameter of this deglitching method working on the map level (see the PACS Data Reduction Guide 2015 for more details);
correction for the apparent motion of the target is not applied to allow an optimal evaluation of the sky background using multiple measurements;
the drizzle method is used to project the time-line data and to produce the single maps using the photProject() task in HIPE, with a pixel fraction parameter of 1.0.
As a standard setting for all “TNOs are Cool” data products we use pixel sizes of 1.′′1, 1.′′4, and 2.′′1 in the PACS 70, 100, and 160 μm bands, different from the “physical” pixel sizes of 3.2′′ and 6.4′′ for the blue and red detectors, respectively. This allows an optimal sampling of the respective point spread functions (see Kiss et al. 2014). Our flux calibration is based on a set of standard stars with the same basic data reduction settingsas in the case of our Solar System targets. Determination of the photometric uncertainty in scan maps is performed using the implanted source method, as described in Kiss et al. (2014). The flux densities of Solar System targets are derived from the double-differential products (see Kiss et al. 2014, for details). These double-differential images, as well as co-added and simple differential images, are available in the Herschel Science Archive1 as User Provided Data Products (UPDPs), along with a detailed description of the processing steps and the data products (UPDP Release Note Version 1.0, May 5, Kiss et al. 2017). The summary of the observations, as well as the derived in-band flux densities, are measured with the specific instrument–filter combinations presented in Table 1.
We reanalyzed the PACS observations of two targets from Santos-Sanz et al. (2012), 1999 KR16 and 2005 QU182. In both cases in the earlier evaluation the 100 μm flux densities were inconsistently low compared with the 70 and 160 μm flux densities. While there are some differences between the Santos-Sanz et al. (2012) and the present calibration and data reduction (e.g., different HIPE version, absolute calibration) the main difference is that in Santos-Sanz et al. (2012) a different kind of data product, namely supersky-subtracted images were used for final photometry. As discussed in Kiss et al. (2014) and Kiss & Müller (2016), double-differential (DDIFF) maps are superior in obtaining accurate and reliable photometry compared with supersky-subtracted maps, and we used these DDIFF maps for 1999 KR16 and 2005 QU182, reduced with the latest version of our pipeline (Kiss & Müller 2016). The supersky-subtracted images are more sensitive to the presence of background sources close to the target at one of the epochs considered. This was the case for the PACS measurements of both targets. By using these DDIFF images the 100 μm flux densities are now consistent with those in the two other bands, as confirmed by the subsequent radiometric modeling (see Sect. 3).
In addition to these objects, updated flux densities of 2007 UK126, along with albedo and size derived from a combination of radiometric modeling and occultation data, are available in Schindler et al. (2017). Similarly, a revised radiometric model is available for 2007 OR10 in Kiss et al. (2019a). All Herschel/PACS data are available in the “Small Bodies: Near and Far” database of thermal infrared observations of Solar System small bodies2 (Kiss et al. 2019a; Szakáts et al. 2020).
Herschel in-band fluxes at all three PACS bands for the “new” objects, and for two objects with updated fluxes, presented in this work.
Spitzer observations summary.
2.2 Spitzer/MIPS data
Spitzer/MIPS measurements were reduced using the same pipeline as was used for the reduction of MIPS data of Centaurs and trans-Neptunian objects by Mueller et al. (2012) and Stansberry et al. (2008, 2012). The MIPS instrument team data analysis tools (Gordon et al. 2005) were used to produce flux-calibrated images for each band, and the contribution of background objects were subtracted (see Stansberry et al. 2008). Aperture photometry was performed on the original images and on the final images, and the final flux values were obtained using the aperture corrections by Gordon et al. (2007) and Engelbracht et al. (2007). The flux densities obtained are presented in Table 2. In four cases Spitzer/MIPS flux densities were obtained in addition to the PACS fluxes (upper five rows in Table 2). We have three targets with Spitzer data only. In these cases the same methods were applied as in the case of PACS only and PACS/MIPS combined measurements. Spitzer-only targets were the plutinos 1995 QY9 and 2003 QX111 and the Neptune trojan 2001 QR322.
2.3 Radiometric modeling
In modeling the thermal emission of our targets we followed the main steps presented in the previous “TNOs are Cool” population-specific papers, in particular those used in Vilenius et al. (2014). We use the Near-Earth Asteroid Thermal Model (NEATM; Harris 1998) to obtain the temperature distribution on the surface of a body that is assumed to be airless, spherical, and in instantaneous equilibrium with the solar radiation. Deviations from the temperature distribution of a smooth surface and non-rotating body are considered through the beaming parameter η which reflects the combined effects of spin properties, thermal inertia and surface roughness (see, e.g., Spencer et al. 1989; Spencer 1990). With the application of the beaming parameter the temperature of the subsolar point Tss is calculated as
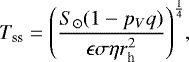 (1)
(1)
where S⊙ is the solar irradiation at 1 AU, q the phase integral, ɛ the bolometric emissivity, and rh the heliocentric distance of the target. The temperature distribution on the surface is obtained as
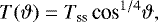 (2)
(2)
where ϑ is the angular distance form the subsolar point on the surface of the body.
We use a constant spectral emissivity of ɛ(λ) = 0.9 throughout the wavelength range of our measurements (24–160 μm), hence a bolometric emissivity of ɛ = 0.9 in the calculation of Tss. While the spectral emissivity has been shown to decrease for longer submillimeter wavelengths, its value is fairly constant below ~200 μm (Fornasier et al. 2013; Lellouch et al. 2017). We fit the free parameters of the NEATM model of a target (geometric albedo, pV ; effective diameter, Deff of an equal area sphere; and beaming parameter, η) by minimizing the reduced-χ2 values, calculated from the observed and modeled flux densities and the observed uncertainties.
Our NEATM model calculates in-band flux densities for our instrument–filter combinations in addition to the monochromatic flux densities that a NEATM model calculates by default. As the local blackbody temperature is known at each grid point of this computation (using the standard Tss cos1∕4ϑ assumption) it is possible to calculate the actual color-correction factors that have to be applied to obtain the in-band flux densities from the monochromatic flux densities (Müller et al. 2011; Stansberry et al. 2007). These in-band flux densities are integrated (summed) to obtain the total, disk-integrated in-band flux density of the target for that specific model and instrument–filter. In the χ2 minimization we use these in-band model flux densities with the measured in-band flux densities, instead of using color-corrected monochromatic values, as was done in previous similar studies (e.g., Mommert et al. 2012; Santos-Sanz et al. 2012; Vilenius et al. 2014). This eliminates the uncertainty in the determination of the color correction from measured in-band flux densities to monochromatic ones. The typical Cλ color-correction factors (used to transform the F′ monochromatic flux densities to the F in-band flux densities as Fλ =  ) are C70 = 0.98–1.03, C100 = 0.98–0.99, and C160 = 0.98–1.01 for the PACS band, and C24 = 1.00–1.15 and C71 = 0.89–0.97 for the MIPS bands. In some cases MIPS color-correction factors are significant (especially in the 24 μm band, due to the relatively low surface temperatures of the targets) resulting in a ~10% change between the in-band and monochromatic flux densities, in contrast to the PACS measurements for which the change in flux density is ≤3% in all bands.
) are C70 = 0.98–1.03, C100 = 0.98–0.99, and C160 = 0.98–1.01 for the PACS band, and C24 = 1.00–1.15 and C71 = 0.89–0.97 for the MIPS bands. In some cases MIPS color-correction factors are significant (especially in the 24 μm band, due to the relatively low surface temperatures of the targets) resulting in a ~10% change between the in-band and monochromatic flux densities, in contrast to the PACS measurements for which the change in flux density is ≤3% in all bands.
We consider the absolute magnitude HV of the object as a measurement constraining the relationship between the geometric albedo and the effective diameter, reducing the degrees of freedom. HV values were mostly taken from the literature (see Table 3), but for 2003 WU172 it was obtained from the data in the Minor Planet Center database.
The beaming parameter η is a complexfunction of the basic characteristics of the targets, including the spin-axis orientation via the corresponding subsolar latitude βss, the thermal parameter Θ, and the surface roughness, described by the root mean square surface slopes s. The thermal parameter Θ is defined as
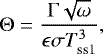 (3)
(3)
where Γ is the thermal inertia, ω is the spin rate of the target, and Tss1 is the subsolar temperature uncorrected for beaming (η ≡ 1):
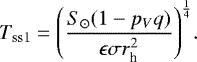 (4)
(4)
The dependence of η on these parameters is discussed in detail in Lellouch et al. (2013), based on Spencer et al. (1989) and Spencer (1990). In this approach η > 1 is caused by a combined effect of thermal inertia and rotation, and scales with the thermal parameter Θ and the subsolar latitude βss in the “no roughness” case; η < 1 is explained by surface roughness effects. We used the Brucker et al. (2009) formula to obtain a geometric albedo-dependent phase integral in the calculation of the Bond albedo, A = 1 − pVq.
In some cases our fits provided solutions with large error bars or converged to our lower and upper beaming parameter limits, η = 0.5 and 2.5. The lower limit of η = 0.5 was set considering the possible highest surface roughness correction in the beaming parameter for very low Θ values (Spencer 1990; Lellouch et al. 2013). Similarly, the upper limit of η = 2.5 is set according to the maximum possible values for βss = 0° subsolar latitude, Tss = 60-70 K (typical subsolar temperatures of our “high η” targets), and high Θ ≥ 100 thermal parameter values (Spencer 1990; Lellouch et al. 2013). In these cases we repeated the analysis with a “fixed” η of 1.25 ± 0.35, using this beaming parameter range to estimate the errors in pV and Deff (see also Vilenius et al. 2014). These cases are also listed in Table 4. This fixed beaming parameter value is slightly higher than the η = 1.2 used by Stansberry et al. (2008) and Lellouch et al. (2013) as in our sample the beaming parameters obtained from acceptable fits provided a higher average value (see Sect. 3.1). Flux density upper limits were treated in the same way as described in Vilenius et al. (2014). While the beaming parameter has a dependence on the phase angle (see, e.g., Delbo et al. 2003; Ali-Lagoa et al. 2018), this cannot be considered in our cases due to the very limited phase angle ranges.
2.4 Colors
In the final stage of our investigation we also used color information of our targets. Following the scheme in Lacerda et al. (2014) we use the spectral slope S′ in units of [%/(1000 Å)], to quantify the visible colors. This spectral slope is calculated as (Hainaut & Delsanti 2002)
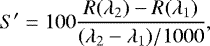 (5)
(5)
![\begin{equation*} R(\lambda) = 10^{-0.4[ (m(\lambda)-m_{\odot}(\lambda)) - (m(V)-m_{\odot}(V)) ]},\end{equation*}](/articles/aa/full_html/2020/06/aa36183-19/aa36183-19-eq7.png) (6)
(6)
where R is the reflectance normalized to the V band, and m and m⊙ are the magnitudes of the object and of the Sun at the wavelength λ.
Broadband colors are taken from the literature; these observations were usually executed in the Johnson-Cousins B, V, R, I bands or the SLOAN g′, r′, i′ bands. In Table 3 we present the V –R colors, the S′ spectral slopes, and the source of the data. SLOAN colors were transformed to Johnson-Cousins colors following Sheppard (2012).
3 Radiometric model results
3.1 General results
We derived new albedo, effective diameter, and beaming para- meter values for 20 trans-Neptunian resonant and scattered disk objects via NEATM radiometric modeling using mainly Herschel/PACS data, in some cases supplemented by Spitzer/MIPS measurements, and for 3 targets based solely on Spitzer/MIPS data. The results are presented in Table 4, and the best-fit radiometric model fits are shown in Fig. 1. Due to non-detections (upper limits) of the thermal emission at all bands in the case of some targets we were only able to derive an upper limit for the effective diameter and a lower limit for the geometric albedo.
The fitted beaming parameters of those targets for which we did not use fixed-η are plotted in Fig. 2 as a function of the heliocentric distance (red symbols). Compared with the Lellouch et al. (2013) beaming parameters (gray symbols in Fig. 2), in general the new targets present higher η values, with a mean value of η = 1.56 and standard deviation of dη = 0.53, while this is 1.18 for the Lellouch et al. (2013) objects. A sample compiled from the Lellouch et al. (2013) targets with heliocentric distances of rh ≥ 29 AU and from our floating-η fit targets gives an average beaming parameter of η = 1.25, and we used this value for the fixed-η radiometric fitting (see Sect. 2.3).
It should be noted that objects presented in this paper are among the faintest ones in the “TNOs are Cool” sample. This is reflected in the large flux density uncertainties, and also in the radiometric modeling in the large η uncertainties for many objects; in these cases the observed fluxes could be fitted with a large range of beaming parameters, as also shown in Fig. 1.
Absolute brightness values and colors of our targets.
3.2 Individual targets
The NEATM-fits of the individual targets are presented in Fig. 1.
(82075) 2000 YW134 was observed in the Science Verification Phase of the Herschel Space Observatory with the PACS photometer,in chop-nod mode (Müller et al. 2010). Those measurements provided only upper limits of F70 ≤ 5 mJy and F160 ≤ 8 mJy in the 70 and 160 μm bands, setting upper limits on the effective diameter, Deff ≤ 500 km, and a lower limit of pV ≥ 0.08 on the geometric albedo. These limits are in agreement with our newly derived, system-integrated values of Deff = 437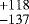 km and pV = 0.13
km and pV = 0.13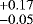 . 2000 YW134 is a binary, with a brightness difference of Δm = 1. m3 between thetwo components (Stephens & Noll 2006). This provides effective diameters of Deff = 382 and 210 km, assuming equal albedos for the primary and secondary.
. 2000 YW134 is a binary, with a brightness difference of Δm = 1. m3 between thetwo components (Stephens & Noll 2006). This provides effective diameters of Deff = 382 and 210 km, assuming equal albedos for the primary and secondary.
(139775) 2001 QG298 is a plutino showing a large amplitude light curve, suggesting that it is a contact binary system (Lacerda & Jewitt 2007). Due to the non-detections (upper limits) in all PACS bands, we were only able to derive an upper limit for the equivalent diameter Deff < 215 km for the system and a lower limit for the geometric albedo, pV > 0.07. Lacerda &Jewitt (2007) and Lacerda (2011) obtained a solution for the system from multi-epoch visible light curve observations that the density of the system (for both components) is ρ = 0.59 g cm−3 with a secondary-to-primary mass ratio of q = 0.84, and two triaxial ellipsoids with primary-to-secondary axis ratios of B∕A = 0.72, C∕A = 0.64, b∕a =0.45 and c∕a = 0.41, using a Roche model (lowest χ2 model with lunar-type scattering). Assuming that the two bodies have equal albedos and that the Herschel measurements represent a mean rotational and orbital phase configuration in terms of apparent cross sections of the components, the semi-axes of the ellipsoids are A = 115 km, B = 82 km, C = 72 km, a = 146 km, b = 66 km, and c = 60 km, using the upper limit of Deff < 215 km, from our radiometric solution.
2001 QR322 is the first Neptune Trojan discovered, and it may have a dynamically unstable orbit (Horner & Lykawka 2010). Our measurements suggest a very dark surface (pV = 0.03 ± 0.02) and an effective diameter of Deff = 178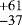 km.
km.
(42301) 2001 UR163 is one of the reddest objects known in the Solar System (B–R = 2.05 ± 0.10, Santos-Sanz et al. 2009). Our floating beaming parameter fit converges to a very low value of η = 0.5, the lowest limit in our calculations. These extremely low beaming parameters would be expected for a rough surface and low thermal parameters (Spencer et al. 1989; Spencer 1990). The corresponding albedo and diameter would be Deff = 261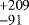 km and pV = 0.43
km and pV = 0.43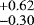 . We have repeated this calculation by applying a fixed beaming parameter of η = 1.25, as in previous “TNOs are Cool” sample papers (e.g., Santos-Sanz et al. 2012). This provides a size of Deff = 367
. We have repeated this calculation by applying a fixed beaming parameter of η = 1.25, as in previous “TNOs are Cool” sample papers (e.g., Santos-Sanz et al. 2012). This provides a size of Deff = 367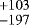 km and a geometric albedo of pV = 0.22
km and a geometric albedo of pV = 0.22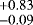 .
.
(126154) 2001 YH140 was also observed in the Science Verification Phase (SVP) of the Herschel Space Observatory with the PACS photometer, in chop-nod mode (Müller et al. 2010) in two bands, 70 and 160 μm. The monochromatic flux densities obtained are F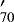 = 9.8 ± 2.9 mJy and F
= 9.8 ± 2.9 mJy and F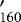 ≤ 13 mJy (i.e., an upper limit in the latter case). The in-band flux densities derived in our present work, F70 = 5.08 ± 1.40 mJy and F100 = 3.67 ± 1.70 mJy, are notably lower then suggested by the earlier measurements, and we provide a more strict upper limit of F160 ≤ 1.95 mJy (1σ). The high flux densities obtained in the SVP measurements may be a consequence of the weak reliability of the chop-nod observing mode that was superseded by the scan-map mode in the later phases of the Herschel mission (Nielbock et al. 2013), and are not necessarily true flux density changes between the two observational epochs. Based on our new radiometric fits 2001 YH140 is smaller and brighter, Deff = 252
≤ 13 mJy (i.e., an upper limit in the latter case). The in-band flux densities derived in our present work, F70 = 5.08 ± 1.40 mJy and F100 = 3.67 ± 1.70 mJy, are notably lower then suggested by the earlier measurements, and we provide a more strict upper limit of F160 ≤ 1.95 mJy (1σ). The high flux densities obtained in the SVP measurements may be a consequence of the weak reliability of the chop-nod observing mode that was superseded by the scan-map mode in the later phases of the Herschel mission (Nielbock et al. 2013), and are not necessarily true flux density changes between the two observational epochs. Based on our new radiometric fits 2001 YH140 is smaller and brighter, Deff = 252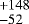 km and pV = 0.14
km and pV = 0.14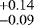 , than that derived from the Herschel SVP measurements (D ≈ 350 km and pV ≈ 0.08).
, than that derived from the Herschel SVP measurements (D ≈ 350 km and pV ≈ 0.08).
2003 UZ413 is a plutino with a rotation period of P = 4.13 ± 0.05 h and a light curve amplitude of Δm = 0.13 ± 0.03 mag (Perna et al. 2009). The observed fast rotation and the light curve amplitude might be compatible with a Jacobi ellipsoid with a/b ≈ 1.13; however, this would require a high density of ρ = 2.3–3.0 g cm−3, a peculiarly high value among trans-Neptunian objects. For 2003 UZ413, the floating η NEATM fit in our radiometric analysis cannot provide a well-defined solution (η converges to the minimum allowed value of 0.5). By applying a fixed beaming parameter of η = 1.25, we derived an effective diameter of Deff = 650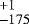 km and a geometric albedo of pV = 0.08
km and a geometric albedo of pV = 0.08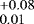 .
.
(145451) 2005 RM43 is a detached object that was also observed by Perna et al. (2009), who obtained a rotation period of P = 9.00 ± 0.06 h and a light curve amplitude of Δm = 0.12 ± 0.05 mag. A Jacobi ellipsoid model provides a density estimate of ρ ≈ 0.55g cm−3. According to our radiometric fit, the diameter is Deff = 524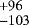 km with a geometric albedo of pV = 0.10
km with a geometric albedo of pV = 0.10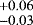 .
.
(40314) 1999 KR16 and 2005 QU182 were analyzed previously in Santos-Sanz et al. (2012), but the Herschel/PACS 100 μm data were inconsistent (too low) with the flux densities obtained in the 70 and 160 μm bands, and we therefore reanalyzed these measurements in the present work.
As discussed in Sect. 2.1, in our reduction we used double-differential images instead of supersky-subtracted images, as in Santos-Sanz et al. (2012), to minimize the effect of nearby background sources. In the case of 1999 KR16 Vilenius et al. (2018) reanalyzed the PACS measurements and found that there was a bright background source near the target at one of the epochs; due to this contamination they decided not to use the visit 2 measurements (i.e., their photometry is based on a single-epoch measurement, strongly affected by the background).
For 1999 KR16 Santos-Sanz et al. (2012) obtained the monochromatic flux densities of F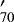 = 5.7 ± 0.7 mJy, F
= 5.7 ± 0.7 mJy, F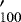 = 3.5 ± 1.0 mJy, and F
= 3.5 ± 1.0 mJy, and F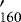 = 4.6 ± 2.2 mJy. Our in-band flux densities are F70 = 7.61 ± 1.44 mJy, F100 = 5.21 ± 2.29 mJy, and F160 < 1.98 mJy. The fixed beaming parameter fit of η = 1.2 in Santos-Sanz et al. (2012) provided Deff = 254 ± 37 km and pV = 0.20
= 4.6 ± 2.2 mJy. Our in-band flux densities are F70 = 7.61 ± 1.44 mJy, F100 = 5.21 ± 2.29 mJy, and F160 < 1.98 mJy. The fixed beaming parameter fit of η = 1.2 in Santos-Sanz et al. (2012) provided Deff = 254 ± 37 km and pV = 0.20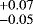 . This is similar to our floating η fit, Deff = 202
. This is similar to our floating η fit, Deff = 202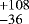 km and pV = 0.31
km and pV = 0.31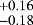 . However, in this latter case the best-fit beaming parameter is η = 0.53
. However, in this latter case the best-fit beaming parameter is η = 0.53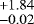 , an extremely low value. For 2005 QU182 Santos-Sanz et al. (2012) obtained F
, an extremely low value. For 2005 QU182 Santos-Sanz et al. (2012) obtained F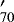 = 4.5 ± 0.9 mJy, F
= 4.5 ± 0.9 mJy, F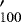 = 2.5 ± 1.1 mJy, and F
= 2.5 ± 1.1 mJy, and F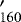 = 8.4 ± 3.0 mJy, providing Deff = 416 ± 73 km and pV = 0.33
= 8.4 ± 3.0 mJy, providing Deff = 416 ± 73 km and pV = 0.33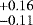 using a fixed η = 1.2 fit. In our photometry using the double-differential products, the monochromatic flux densities are F70 = 4.41 ± 1.28 mJy, F100 = 6.94 ± 2.11 mJy, and F160 < 2.73 mJy, and the corresponding effective diameter and geometric albedo are Deff = 584
using a fixed η = 1.2 fit. In our photometry using the double-differential products, the monochromatic flux densities are F70 = 4.41 ± 1.28 mJy, F100 = 6.94 ± 2.11 mJy, and F160 < 2.73 mJy, and the corresponding effective diameter and geometric albedo are Deff = 584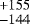 km and pV = 0.13
km and pV = 0.13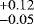 , with a best-fit beaming parameter of η = 2.08
, with a best-fit beaming parameter of η = 2.08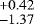 (i.e., a notably larger size and lower albedo).
(i.e., a notably larger size and lower albedo).
Radiometric fit results of our new targets.
 |
Fig. 1 NEATM fits of the thermal emission of our target sample. Black solid and dash-dotted curves represent the spectral energy distribution of the best-fit (lowest χ2) model for the epochs of the PACS and MIPS measurements, respectively. The gray area shows the zone of NEATM model curves that are compatible with the observed measurement uncertainties. In those cases when the floating η fits converged to one of the beaming parameter limits, the fit was repeated with a fixed beaming parameter of η = 1.25, represented by the green curves (not in all panels). Red and blue symbols represent the measured MIPS and PACS flux densities, respectively, color-corrected according to the best-fit NEATM model, at their respective epochs. In those cases when only flux density upper limits were available, we show the SED of the NEATM model with the diameter and geometric albedo limits presented in Table 4. |
 |
Fig. 1 continued. |
 |
Fig. 2 Beaming parameter vs. the heliocentric distance of the target at the time of the observation. Red symbols indicate the targets from the present paper for which the beaming parameter could be derived within the predefined limits. Gray symbols in the background indicate the beaming parameters from Lellouch et al. (2013). |
4 Discussion
4.1 Thermal intertia estimates
Lellouch et al. (2013) estimated thermal inertia from the η values derived and obtained a decrease in Γ from ~5 to ~2 J m−2 s−1∕2K−1 from ~25 AU to heliocentric distances beyond 40 AU. Following a similar approach we also estimated the thermal inertia values for our targets. The phase integral q was calculated applying both the standard Bowell et al. (1989) formula with a G = 0.15 slope parameter, and also using the geometric albedo dependent formula by Brucker et al. (2009). These two methods resulted in subsolar temperatures with negligible differences (typically ≲1 K, the largest difference is ~4 K for the high albedo target 2002 CY224) and with a negligible effect on the final results. We assumed a uniform P = 8 h rotation period for all targets. We used two subsolar latitudes, βss = 32.7° (average values of random orientation spin axis directions) and also βss = 0°, as some specific (high, η ≥ 2.0) beaming parameter values could not be reproduced with βss = 32.7°. We allowed a roughness from s = 0 to 60° (zero to high roughness). The thermal inertias obtained were similar in the two βss cases for a specific target, but showed a wide range of possible values, partly due to the typically large uncertainties in the η determination, and the ambiguity that different combinations of Θ, βss, and s can result in the same beaming parameter at the end. The median values for our sample were 1.9 J m−2 s−1∕2K−1 for βss = 0° and 3.1 J m−2 s−1∕2K−1 for βss = 32.7°; for the same target (albedo and heliocentric distance) a higher βss value results in a higher Γ, as a higher Θ is needed to obtain the same beaming parameter (see Fig. 4 in Lellouch et al. 2013). These thermal inertias are compatible with those obtained by Lellouch et al. (2013) for the same heliocentric distance range.
4.2 Albedo-color diagram
As was demonstrated in Lacerda et al. (2014) objects in the trans-Neptunian region can be divided into two main clusters based on their geometric albedo and visible color properties. We repeated this analysis using the mclust package in R (Fraley et al. 2018).
We used two main datasets. The first is the Lacerda et al. (2014) sample using mainly the geometric albedo and spectral slope data derived from the original papers, but using new albedo and color values in the cases when they were updated according to the latest reduction of the Herschel and Spitzer data – e.g., 2007 OR10 (Pál et al. 2016) and 2007 UK126 (Schindler et al. 2017)– or by new occultation measurements (Haumea, Ortiz et al. 2017; Müller et al. 2019). New targets given in the present paper are not included in this dataset.
The second dataset contains all objects, i.e., the Lacerda et al. (2014) sample and also our new targets, and two additional targets, 1996 TO66 and 1999 CD158 from Vilenius et al. (2018). 1996 TO66 is considered to be a Haumea collisional family member, while 1999 CD158 is thought to be dynamical interloper with this family. We also considered the relatively wide ranges obtained for the albedos and colors from the disk-resolved measurements of Pluto and Charon (Grundy et al. 2016) when drawing their data points in the corresponding figures.
In both cases we run the MClust package for a multiple number of cluster components assumed and also using different data models. Theresults are presented in Fig. 3 and summarized in Table 5. In the case of the first dataset (Lacerda et al. 2014 sample) the smallest residuals were obtained using an ellipsoidal, varying volume and shape data model (VVI) with three groups. These clusters are very closely identical with the clusters obtained by Lacerda et al. (2014), i.e., we can identify a dark-neutral group (DN, blue symbols in Fig. 3) and a bright-red group (BR, red symbols), and a third group at high albedos and nearly solar colors. This last group is not defined explicitly by Lacerda et al. (2014) as the related objects are essentially excluded from that analysis; these objects are the brightest dwarf planets (Pluto, Eris, Makemake) and the members of the Haumea collisional family. As we left these objects in the dataset, a third, “bright-neutral” (BN) group could be identified (Fig. 3, top panel, green symbols). We note that the objects with uncertain cluster identification are indicated by black symbols in the figure (located typically between two clusters).
We plotted the new targets over the clusters of the original sample in the middle panel of Fig. 3. These targets extend the spectral slope range to smaller values (close to solar) even in the pV > 0.1 region, where there were few objects in the original sample. Including the new targets in the cluster modeling results in somewhat different clusters (Fig. 3, bottom panel), but the main structure (the number, location, and extension of the groups) remains basically unchanged (see Table 5). The groups we identified both in the original and in the full sample match the clusters identified by Lacerda et al. (2014) very closely.
While most of our new objects follow the previously identified main groups, there is an important new feature. In the Lacerda et al. (2014) analysis the albedo–color range of 0.10 ≲pV ≲0.40 and 5 ≲S′ ≲15 [%/100 nm] remained empty, in our sample we have three objects, 2000 YW134, 1995 QY9, and 2005 RS43 that fall here. While many inner Solar System objects have surfaces matching the albedos and colors of our dark and neutral group (Lacerda et al. 2014), objects with these moderate albedos and slightly red colors cannot be found even in the inner Solar System beyond the 5:3 resonance with Jupiter (including Hildas and Jupiter Trojans), only at heliocentric distances of ≲3.5 au (DeMeo & Carry 2014). These objects seem to lack the red material that is common among most trans-Neptunian objects in this albedo range. We note that the Neptune irregular satellite Nereid has albedo and color similar to those of these objects (Kiss et al. 2016). Targets with nearly solar colors and medium albedos (0.08 ≲pV ≲ 0.30) all have ambiguous identifications in this clustering scheme.
We also found that the objects 2004 PG115 and 2005 RM43, although they are likely associated with the DN group, are located so far from the group center with their negative spectral slopes and pV ≈ 0.10 albedos thattheir group assignment can be considered ambiguous. Lacerda et al. (2014) found that objects in relic populations, i.e., those that formed and remained in the outer Solar System (cold classical KBOs and objects in the outer resonances), possess exclusively bright red surfaces, while populations with dynamically more complex origin (Centaurs, scattered disk objects, hot classical KBOs, plutinos) show mixed surfaces. Our new targets follow this general picture; for example, new scattered disk objects can be found both in the DN and the BR groups, while detached objects and targets from the outer resonances can exclusively be found among BR objects.
 |
Fig. 3 Albedo vs. visible color, quantified by the spectral slope S′. Upper panel: TNOs from Lacerda et al. (2014) using updated albedo and spectral slope values in some specific cases. The three clusters identified are indicated in blue, red, and green. Ellipses (distorted due to the logarithmic pV scale) with crosshairs indicating the centers and variance values of the clusters in the albedo–spectral slope plane. Objects indicated by black symbols have ambiguous identifications. Middle panel: same as the top panel (TNOs from Lacerda et al. 2014), but with the new objects of the present paper overplotted. The following symbols were used: ▿ – plutinos; ⊠ – detached objects; × – scattered disk objects; ◊ – outer resonants; ○ – inner resonants; ⋆ – middle resonants; □ – 1999 CD158 (Vilenius et al. 2018); ⊗ – 1996 TO66 (Vilenius et al. 2018). Bottom panel: clusters in the albedo vs. spectral slope plot using all 120 objects, including those from Lacerda et al. (2014) and the new targets from the present paper. |
4.3 Impact on size distributions
Size distribution is an essential characteristic of small body populations, providing information on the collisional history. As diameters of small bodies cannot be obtained directly in most cases, it is difficult to obtain a reliable size distribution.Usually it is necessary to rely on the absolute magnitude distribution that can be derived directly from the observationsof these objects (Gladman et al. 2001). Typically, a single, mean albedo value known from other measurements can be used (e.g., radiometry or occultations) to convert between the diameter and the absolute magnitude in the corresponding distributions. Mommert et al. (2012), among others, used an average albedo of 0.08 ± 0.03 to convert from absolute magnitude to effective diameter and to derive the size distribution of plutinos. However, as we have shown above, trans-Neptunian populations, including scattered disk and resonant objects show a bimodal albedo and color distribution;therefore, the application of a bimodal albedo (e.g., using the color as a proxy for the mean albedo) might be more appropriate.
In Fig. 4 we drew the plutinos, objects in other (not 3:2) resonances, and scattered disk and detached objects over the main groups identified by our cluster analysis. Bimodal and color-dependent albedo is clearly the case for scattered disk and detached objects (right panel). Here the objects in the specific groups, pV (SDO,DN) = 0.044 ± 0.008 and pV(SDO,BR) = 0.119 ± 0.054, follow the general albedos of the larger samples (Table 5). We note that there is no detached object in the DN group. The three objects with very low spectral slope values (S′ ≲ 0, 2000 YW134, 1995 QY9 and 2005 RS43) seem to have albedos similar to the BR group, pV ≈ 0.12. The case is different for the resonant objects, including the plutinos, due to the presence of several new objects in the range 0.10 ≲pV ≲0.40 and 5 ≲S′ ≲15 [%/100 nm] (see the discussion above), making the color-to-albedo assignment ambiguous. It is, however, still the case for the BR group that their colors correspond to a relatively well-defined albedo, pV (RTNO,BR) = 0.12 ± 0.04.
It is also an important question whether objects with different sizes have the same typical albedos, and whether the same mean albedo (or albedo distribution) can be used to convert from absolute magnitudes to effective diameters within the same albedo-color group. In Fig. 5 we plot the geometric albedos of resonant and scattered disk objects versus the effective diameter derived form radiometric data. We have to emphasis that this sample is not unbiased, as objects in the “TNOs are Cool” studies (where the majority of these data are from) were selected to cover different dynamic classes, sizes, or absolute magnitude ranges, and should have been foreseen to be detectable by the Herschel Space Observatory, assuming a uniform 8% geometric albedo (Müller et al. 2009; Kiss et al. 2014). In the present sample no obvious trend is visible within any of the albedo-color groups. There is a general trend, considering all objects together, that smaller objects are darker, but this is dominated by the presence of Centaurs (asterisks in Fig. 5) that are found at smaller heliocentric distances and remain observable above HV ≈ 9.0, which is an absolute limit for the targets in the other dynamical families. In addition, darker objects are observable at smaller sizes in thermal emission at the same heliocentric distance, and that was the main criterion when the “TNOs are Cool” object list was compiled. This indicates that to our present knowledge a color-dependent and dynamical class-dependent albedo is probably suitable to transform between absolute magnitude and size distributions, as discussed above.
Clusters identified by Lacerda et al. (2014, Col. 1), using the Lacerda et al. (2014) sample with updates (this work, Col. 2), and usingall targets (this work, Col. 3).
 |
Fig. 4 Spectral slope vs. geometric albedo for resonant (left), and scattered disk and detached objects (right). Regions delineated with dashed and dash-dotted lines correspond to the 1 σ contours of the clusters identified in our analysis using the original and full samples, respectively. Filled circles and stars mark plutinos (3:2 resonance) and other resonant objects, respectively, in the left panel. Filled squares and triangles indicate scattered disk and detached objects in the right panel. Black symbols indicate objects with ambiguous cluster assignments. |
 |
Fig. 5 Geometric albedo (pV) vs. diameter (D) for the full scattered disk and resonant sample. The clusters are color-coded: blue – DN; red – BR; green – BN; gray – ambiguous group assignment. Filled circles, stars, squares, and triangles indicate plutinos, other resonances, scattered disk objects, and detached objects, respectively. Open circles are any other dynamical class, except the Centaurs that are shown as asterisks. Dotted lines represent the constant absolute magnitudes, as labeled. Purple symbols with dashed lines indicate those targets for which only diameter upper- and albedo lower limits could be derived in this paper. |
5 Summary
We determined the size and albedo of 23 trans-Neptunian resonant and scattered disk objects using data mainly based on the “TNOs are Cool” Herschel open time key programme observations, supplemented in some cases by Spitzer Space Telescope data. Together with the previous studies based on the “TNOs are Cool” data, this is the largest reliable set of size and albedo estimates for objects in the outer resonances in the Kuiper belt. We confirm the results of a previous investigation (Lacerda et al. 2014) that trans-Neptunian objects can be divided into albedo-color groups and that objects in relic populations exclusively have bright-red surfaces, strengthening the evidence for a compositional discontinuity in the young Solar System. We suggest that size distribution studies based on absolute magnitude distributions use the bimodal albedos, specific for the dark-neutral and bright-red groups in all dynamical populations, for example using colors or spectral slopes as a proxy for albedo-color group membership (e.g., Ayala-Loera et al. 2018).
Acknowledgements
The research leading to these results has received funding from the European Union’s Horizon 2020 Research and Innovation Programme, under Grant Agreement no 687378; from the K-125015 and GINOP-2.3.2-15-2016-00003 grants of the National Research, Development and Innovation Office (NKFIH, Hungary). The work of G. Marton was supported by the NKFIH grant PD-128360. Part of this work was supported by the German DLR project number 50 OR 1108. We thank our reviewerfor the comments, especially those on the data reduction issues, which have certainly had an important impact on the final results of this paper.
References
- Ali-Lagoa, V., Müller, T. G., Usui, F., & Hasegawa, S. 2018, A&A, 612, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alvarez-Candal, A., Pinilla-Alonso, N., Licandro, J., et al. 2011, A&A, 532, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ayala-Loera, C., Alvarez-Candal, A., Ortiz, J. L., et al. 2018, MNRAS, 481, 1848 [NASA ADS] [CrossRef] [Google Scholar]
- Balog, Z., Müller, T., Nielbock, M., et al. 2014, Exp. Astron., 37, 129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bannister, M. T., Gladman, B. J., Kavelaars, J. J., et al. 2018, ApJS, 236, 18 [CrossRef] [Google Scholar]
- Barucci, M. A., & Doressoundiram, A. 1999, Icarus, 142, 476 [NASA ADS] [CrossRef] [Google Scholar]
- Boehnhardt, H., Schulz, D., Protopapa, S., & Götz, C. 2014, EM&P, 114, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Bowell, E. G., Hapke, B., Domingue, D., et al. 1989, Asteroids II, eds. Gehrels, T., Matthews, M. T., & Binzel, R. P. (Tucson, AZ: University of Arizona Press), 524 [Google Scholar]
- Brown, M. E., & Butler, B.J. 2018, AJ, 156, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Brucker, M. J., Grundy, W. M., Stansberry, J. A., et al. 2009, Icarus, 201, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Buie, M. W., Jordan, A. B., Wasserman, L. H., et al. 2003, MPEC 2003-H07 [Google Scholar]
- Delbo, M., Harris, A. W., Binzel, R. P., Pravec, P., & Davies, J. K. 2003, Icarus, 266, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Delbo, M., Mueller, M., Emery, J. P., Rozitis, B., & Capria, M. T. 2015, Asteroids IV, eds. P. Michel, F. E. DeMeo, & W. F. Bottke (Tucson, AZ: University of Arizonal Press), 107 [Google Scholar]
- DeMeo, F. E., & Carry, B. 2014, Nature, 505, 629 [NASA ADS] [CrossRef] [Google Scholar]
- DeMeo, F. E., Fornasier, S., & Barucci, M. A. 2009, A&A, 493, 283 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Doressoundiram, A., Peixinho, N., de Bergh, C., et al. 2002, AJ, 124, 2279 [NASA ADS] [CrossRef] [Google Scholar]
- Doressoundiram, A., Peixinho, N., Doucet, C., et al. 2005, Icarus, 174, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Doressoundiram, A., Peixinho, N., Moullet, A., et al. 2007, AJ, 134, 2186 [NASA ADS] [CrossRef] [Google Scholar]
- Duffard, R., Pinilla-Alonso, N., & Santos-Sanz, P. 2014, A&A, 564, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Engelbracht, C. W., Blaylock, M., & Su, K. Y. L. 2007, PASP, 119, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Farkas-Takács, A. I., Kiss, Cs., Pál, A., et al. 2017, AJ, 154, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Fornasier, S., Lellouch, E., Müller, T. G., et al. 2013, A&A, 555, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fraley, C., Raftery, A. E., Scrucca, L., Murphy, T. B., & Fop, M. 2018, Package ’mclust’, version Novermber 17, 2018 [Google Scholar]
- Fraser, W. C., Brown, M. E., & Schwamb, M. E. 2010, Icarus, 210, 944 [NASA ADS] [CrossRef] [Google Scholar]
- Fraser, W. C., Brown, M. E., Morbidelli, A., Parker, A., & Batygin, K. 2014, ApJ, 782, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Gladman, B., Kavelaars, J. J., Petit, J.-M., et al. 2001, AJ, 122, 1051 [NASA ADS] [CrossRef] [Google Scholar]
- Gladman, B., Lawler, S. M., Petit, J.-M., et al. 2012, AJ, 144, 23 [Google Scholar]
- Gomes, R. S., Fernández, J. A., Gallardo, T., et al. 2008, SSBN book, 259G [Google Scholar]
- Gordon, K. D., Rieke, G. H., Engelbracht, C. W., et al. 2005, PASP, 117, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, K. D., Engelbracht, C. W., Fadda, D., et al. 2007, PASP, 119, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Grundy, W. M., Binzel, R. P., Buratti, B. J., et al. 2016, Science, 351, 9189 [NASA ADS] [CrossRef] [Google Scholar]
- H1 Collaboration (Aaron, F. D., et al.) 2009, Eur. Phys. J. C, 63, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hainaut, O. R., & Delsanti, A. C. 2002, A&A, 389, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, A. W. 1998, Icarus, 131, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herschel Science Centre, Herschel Products and Tools Contributor’s Guide, HERSCHEL-HSC-DOC-1405 4 December 2009 [Google Scholar]
- Horner, J., & Lykawka, P. S. 2010, MNRAS, 405, 49 [NASA ADS] [Google Scholar]
- Jurić, M., Ivezić, Ž, Lupton, R.H., et al. 2002, AJ, 124, 1776 [NASA ADS] [CrossRef] [Google Scholar]
- Kiss, Cs., & Müller, T. G. 2016, User Provided Data Product upload of Herschel/PACS near-Earth asteroid observations, Release Note V, 1.0, available at: http://archives.esac.esa.int/hsa/legacy/UPDP/COOLTNOs/tnosarecool.pdf [Google Scholar]
- Kiss, Cs., Müller, Th. G., Vilenius, E., et al. 2014, Exp. Astron., 37, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Kiss, Cs., Pál, A., Farkas-Takács, A. I., et al. 2016, MNRAS, 457, 2908 [NASA ADS] [CrossRef] [Google Scholar]
- Kiss, Cs., Müller, T., & Varga-Verebélyi, E., et al. 2017, User Provided Data Products from the TNOs are Cool! - A Survey of the trans-Neptunian Region Herschel Open Time Key Program Version 1.0, May 5, 2017, Release Note 1.0, http://archives.esac.esa.int/hsa/legacy/UPDP/COOLTNOs/tnosarecool.pdf [Google Scholar]
- Kiss, Cs., Szakáts, R., Marton, G., et al. 2019a, “Small Bodies: Near and Far” database of thermal infrared measurements of small Solar System bodies, Release Note: Public Release 1.2, 2019 March 29 (http://ird.konkoly.hu) [Google Scholar]
- Kiss, C., Marton, G., Parker, A. H., et al. 2019b, Icarus, 334, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Lacerda, P. 2011, AJ, 142, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Lacerda P., & Jewitt, D. C. 2007, AJ, 133, 1393 [NASA ADS] [CrossRef] [Google Scholar]
- Lacerda, P., Fornasier, S., Lellouch, E., et al. 2014, ApJ, 793, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Lellouch, E., Santos-Sanz, P., Lacerda, P., et al. 2013, A&A 557, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lellouch, E., Moreno, R., Müller, T., et al. 2017 A&A 608, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mommert, M., Harris, W., Kiss, Cs., et al. 2012, A&A 541, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, T. G., Lellouch, E., Böhnhardt, H., et al. 2009, EM&P, 105, 209 [Google Scholar]
- Müller, T. G., Lellouch, E., Stansberry, J., et al. 2010, A&A, 518, L146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, T., Okumura, K., & Klaas, U. 2011, PACS Photometer Passbands and Colour Correction Factors for Various Source SEDs, Herschel/PACS technical report, PICC-ME-TN-038 [Google Scholar]
- Mueller, M., Stansberry, J., Mommert, M., & Grundy, W. 2012, TNO Diameters And Albedos: The Final MIPS Dataset, AAS DPS Meeting, 44, 310.13 [Google Scholar]
- Müller, T. G., Marciniak, A., Kiss, C., et al. 2018, Adv. Space Res., 62, 2326 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, T. G., Kiss, C., Ali-Lagoa, V., et al. 2019, Icarus, 334, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, T., Lellouch, E., & Fornasier, S., 2020, The Trans-Neptunian Solar System, eds. D. Prialnik, M. Antoinetta Barucci, & L. Young (Amsterdam: Elsevier), 153 [CrossRef] [Google Scholar]
- Nielbock, M., Müller, Th. G., Klaas, U., et al. 2013, Exp. Astron., 36, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Ortiz, J. L., Santos-Sanz, P., Sicardy, B., et al. 2017, Nature, 550, 219 [NASA ADS] [CrossRef] [Google Scholar]
- PACS Data Reduction Guide: Photometry, Issue user. Version 12 Nov. 2015 [Google Scholar]
- Pál, A., Kiss, C., & Müller, T. G. 2012, A&A 541, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pál, A., Kiss, C., & Müller, T. G. 2016, AJ, 151, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Perna, D., Dotto, E., Barucci, M. A., et al. 2009, A&A, 508, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perna, D., Barucci, M. A., Fornasier, S., et al. 2010, A&A, 510, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perna, D., Dotto, E., Barucci, M. A., et al. 2013, A&A, 554, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popesso, P., Magnelli, B., Buttiglione, S., et al. 2012, ArXiv e-prints [arXiv:1211.4257] [Google Scholar]
- Romanishin, W., & Tegler, S. C. 2005, Icarus, 179, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Santos-Sanz, P., Ortiz, J. L., Barrera, L., & Boehnhardt, H. 2009, A&A, 494, 693 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos-Sanz, P., Lellouch, E., & Fornasier, S. 2012, A&A, 541, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schindler, K., Wolf, J., Bardecker, J., et al. 2017, A&A, 600, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sheppard, S. S. 2012, AJ, 144, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Sheppard, S. S., & Jewitt, D. C. 2002, AJ, 124, 1757 [NASA ADS] [CrossRef] [Google Scholar]
- Sheppard, S. S., & Jewitt, D. C. 2004, AJ, 127, 3023 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Snodgrass, C., Carry, B., Dumas, C., & Hainaut, O. 2010, A&A 511, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spencer, J. R. 1990, Icarus, 83, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Spencer, J. R., Lebofsky, L. A., & Sykes, M. V. 1989, Icarus, 78, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Stansberry, J. A., Gordon, K. D., & Bhattacharya, B. 2007, PASP, 119, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Stansberry, J., Grundy, W. M., Brown, M. E., et al. 2008, in The Solar System Beyond Neptune, Physical Properties of Kuiper Belt and Centaur Objects: Constraints from the Spitzer Space Telescope (Tuscon, AZ: University of Arizona Press), 161 [Google Scholar]
- Stansberry, J. A., Grundy, W. M., Mueller, M., et al. 2012, Icarus, 219, 676 [NASA ADS] [CrossRef] [Google Scholar]
- Stephens, D. C., & Noll, K. S. 2006, AJ, 131, 1142 [NASA ADS] [CrossRef] [Google Scholar]
- Szakáts, R., Müller, T., Ali-Lagoa, V., et al. 2020, A&A, 635, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vilenius, E., Kiss, C., Mommert, M., et al. 2012, A&A, 541, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vilenius, E., Kiss, C., & Müller, T., 2014, A&A 564, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vilenius, E., Stansberry, J., Müller, T. G., et al. 2018, A&A, 618, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Volk, K., Murray-Clay, Gladman, B. J., et al. 2018, AJ, 155, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, T. Y. M., Murray-Clay, R., & Volk, K. 2018, AJ, 156, 33 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Herschel in-band fluxes at all three PACS bands for the “new” objects, and for two objects with updated fluxes, presented in this work.
Clusters identified by Lacerda et al. (2014, Col. 1), using the Lacerda et al. (2014) sample with updates (this work, Col. 2), and usingall targets (this work, Col. 3).
All Figures
 |
Fig. 1 NEATM fits of the thermal emission of our target sample. Black solid and dash-dotted curves represent the spectral energy distribution of the best-fit (lowest χ2) model for the epochs of the PACS and MIPS measurements, respectively. The gray area shows the zone of NEATM model curves that are compatible with the observed measurement uncertainties. In those cases when the floating η fits converged to one of the beaming parameter limits, the fit was repeated with a fixed beaming parameter of η = 1.25, represented by the green curves (not in all panels). Red and blue symbols represent the measured MIPS and PACS flux densities, respectively, color-corrected according to the best-fit NEATM model, at their respective epochs. In those cases when only flux density upper limits were available, we show the SED of the NEATM model with the diameter and geometric albedo limits presented in Table 4. |
| In the text | |
 |
Fig. 1 continued. |
| In the text | |
 |
Fig. 2 Beaming parameter vs. the heliocentric distance of the target at the time of the observation. Red symbols indicate the targets from the present paper for which the beaming parameter could be derived within the predefined limits. Gray symbols in the background indicate the beaming parameters from Lellouch et al. (2013). |
| In the text | |
 |
Fig. 3 Albedo vs. visible color, quantified by the spectral slope S′. Upper panel: TNOs from Lacerda et al. (2014) using updated albedo and spectral slope values in some specific cases. The three clusters identified are indicated in blue, red, and green. Ellipses (distorted due to the logarithmic pV scale) with crosshairs indicating the centers and variance values of the clusters in the albedo–spectral slope plane. Objects indicated by black symbols have ambiguous identifications. Middle panel: same as the top panel (TNOs from Lacerda et al. 2014), but with the new objects of the present paper overplotted. The following symbols were used: ▿ – plutinos; ⊠ – detached objects; × – scattered disk objects; ◊ – outer resonants; ○ – inner resonants; ⋆ – middle resonants; □ – 1999 CD158 (Vilenius et al. 2018); ⊗ – 1996 TO66 (Vilenius et al. 2018). Bottom panel: clusters in the albedo vs. spectral slope plot using all 120 objects, including those from Lacerda et al. (2014) and the new targets from the present paper. |
| In the text | |
 |
Fig. 4 Spectral slope vs. geometric albedo for resonant (left), and scattered disk and detached objects (right). Regions delineated with dashed and dash-dotted lines correspond to the 1 σ contours of the clusters identified in our analysis using the original and full samples, respectively. Filled circles and stars mark plutinos (3:2 resonance) and other resonant objects, respectively, in the left panel. Filled squares and triangles indicate scattered disk and detached objects in the right panel. Black symbols indicate objects with ambiguous cluster assignments. |
| In the text | |
 |
Fig. 5 Geometric albedo (pV) vs. diameter (D) for the full scattered disk and resonant sample. The clusters are color-coded: blue – DN; red – BR; green – BN; gray – ambiguous group assignment. Filled circles, stars, squares, and triangles indicate plutinos, other resonances, scattered disk objects, and detached objects, respectively. Open circles are any other dynamical class, except the Centaurs that are shown as asterisks. Dotted lines represent the constant absolute magnitudes, as labeled. Purple symbols with dashed lines indicate those targets for which only diameter upper- and albedo lower limits could be derived in this paper. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


