| Issue |
A&A
Volume 637, May 2020
|
|
|---|---|---|
| Article Number | A90 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202037609 | |
| Published online | 21 May 2020 | |
Effect of the 3D distribution on water observations made with the SWI
I. Ganymede
1
Department of Space, Earth, and Environment, Chalmers University of Technology, Onsala Space Observatory,
439 92
Onsala,
Sweden
e-mail: eva.wirstrom@chalmers.se
2
Max-Planck-Institut für Sonnensystemforschung,
Justus-von-Liebig-Weg 3,
37077
Göttingen,
Germany
3
Research Group for Genomic Epidemiology, National Food Institute, Technical University of Denmark,
Kgs. Lyngby
2800,
Denmark
Received:
24
January
2020
Accepted:
3
April
2020
Context. Characterising and understanding the atmospheres of Jovian icy moons is one of the key exploration goals of the Submillimetre Wave Instrument (SWI), which is to be flown on ESA’s Jupiter Icy Moons Explorer (JUICE) mission.
Aims. The aim of this paper is to investigate how and under which conditions a 3D asymmetric distribution of the atmosphere may affect the SWI observations. In this work we target the role of phase angle for both nadir and limb geometries for unresolved and partially resolved disc observations from large distances.
Methods. We adapted the LIME software package, a 3D non-local thermodynamical equilibrium radiative transfer model, to evaluate ortho-H2O populations and synthesise the simulated SWI beam spectra for different study cases of Ganymede’s atmosphere. The temperature and density vertical distributions were adopted from a previous work. The study cases presented here were selected according to the distance and operational scenarios of moon monitoring anticipated for SWI during the Jupiter phase of the JUICE mission.
Results. We demonstrate that nadir and limb observations at different phase angles will modify the line amplitude and width. Unresolved observations where both absorption against surface continuum and limb emission contributes within the beam will lead to characteristic line wing emission, which may also appear in pure nadir geometry for specific phase angles. We also find that for Ganymede, the 3D non-local thermodynamical equilibrium populations are more highly excited in the upper atmosphere near the sub-solar region than they are in 1D spherically symmetric models. Finally, the 3D radiative transfer is better suited to properly simulate spectral lines for cases where density or population gradients exist along the line of sight.
Key words: planets and satellites: atmospheres / planets and satellites: individual: Ganymede / submillimeter: planetary systems / radiative transfer / space vehicles: instruments
© ESO 2020
1 Introduction
The largest moon of Jupiter, Ganymede, has a surface composed mostly of water ice and a very tenuous atmosphere that is maintained by some combination of sublimation, sputtering, photon-stimulated desorption, and micro-meteorite impact vaporisation of the surface (Johnson et al. 2004; Marconi 2007; McGrath et al. 2013; Turc et al. 2014; Plainaki et al. 2015; Shematovich 2016; Leblanc et al. 2017). Direct observations of Ganymede’s atmosphere are scarce. Its molecular composition has largely been deduced from observations of atomic lines in the UV with the Hubble Space Telescope (Hall et al. 1998; Feldman et al. 2000; McGrath et al. 2013), indicating column densities up to about 1015 cm−2, and thereby a largely collision-less atmosphere, or exosphere. Oxygen and hydrogen appear to be the dominating elements, and water is considered one of the main components, especially close to the sub-solar point (SSP), where sublimation of water ice potentially creates a local density enhancement where collisions dominate interactions, in particular, molecular excitation.
The atmosphere of Ganymede will be one of the main targets for detailed scientific investigation by ESA’s Jupiter Icy Moons Explorer (JUICE) mission. In particular, the Submillimetre Wave Instrument1 (SWI) is able to observe rotational transitions of water and other molecular species in the frequency ranges 530–625 and 1080–1275 GHz at high spectral resolution (105–107), and will be well suited to characterise the key parameters of its atmosphere. Ganymede in particular will be observed from a wide range of distances throughout the mission, both from large distances of 280 Jupiter radii or more, when the moon is unresolved by the SWI beam (440′′ FWHM at 557 GHz), and up close from an orbit of 500 km altitude later in the mission (Grasset et al. 2013).
Simulating the water observations and making retrievals is complicated, especially for regions of low density where processes other than collisional excitation determine the rotational populations of molecules, and local thermodynamical equilibrium (LTE) is not applicable. Such conditions are expected to occur typically some distance away from the SSP (Marconi 2007) and/or in the upper regions of the atmosphere. Radially symmetric non-LTE models should be detailed enough to reproduce and interpret line profiles in the cases when the radial distribution does not vary significantly within the beam (see e.g. Yamada et al. 2018). However, for unresolved monitoring observations, or for observations when the moon is just resolved, it is unclear what the effects of observing angle with respect to the SSP, for instance, will be on the observed lines.
We use a non-spherically symmetric non-LTE radiative transfer code to investigate the effects of the expected asymmetric water distributions in the atmosphere of Ganymede on observed water line properties for different observing geometries relevant for the upcoming JUICE mission. We focus the comparisons on the ground-state ortho water transition H2O (110−101) at 557 GHz because at our current level of understanding of Ganymede’s atmosphere, this is the line that will primarily be used for monitoring and large-scale mapping of the water distribution.
2 Using LIME on planetary scales
The code LIME2 (Brinch & Hogerheijde 2010) is a parallelised 3D non-LTE line radiative transfer code. It allows for the radiative transfer to be solved in arbitrary geometries, and the densities, temperatures, and velocity fields are given analytically as input to the Monte Carlo code. In this work, version 1.43 was used. An unstructured Delaunay grid is generatedby random sampling of the input model. After the grid has been computed, LIME calculates the rotational level populations at each grid point in an iterative manner based on the local temperature, density, and radiation field. After the convergence criterion is fulfilled, the model is ray-traced, and fits files are produced 3.
2.1 Model of the Ganymede water atmosphere
Analytical approximations of the temperature and water density distribution are derived based on the kinetic atmosphere model by Marconi (2007). We used their vertical density and temperature profiles at 10° and 90° sub-solar latitudes (SSL), and interpolated profiles at 60° as input for a full 3D model of the Ganymede atmosphere. In our model, between the SSP and 90° we let the temperature and logarithm of the density at each altitude vary with the cosine of the SSL (see Fig. 1), while parameters on the dark side of Ganymede were kept at the SSL = 60° profile. Water-water collisional rate coefficients were adopted from Buffa et al. (2000), and the water ortho-to-para ratio (OPR) was assumed to take the thermalised value of 3. The radius of Ganymede was set to 2634 km, the height of the atmosphere was taken to be 450.5 km, and the computational domain was 3500 km in radius. In the region outside the atmosphere, the temperature was equal to TCMB and the density was kept at a very low value, that is, 10−3 cm−3. Below the atmosphere (i.e. from the surface and below), the temperature was kept equal to the surface temperature, in local equilibrium with the lower boundary of the atmosphere. In addition, the density was very high (1022 cm−3), while the gas-to-dust ratio was set to 10−70. This low ratio ensures that no photons propagate through the Ganymede model surface. This means that in this model, Ganymede is treated as a solid-sphere perfect absorber that emits at the local surface temperature. Thus, surface and subsurface properties such as reflectivity or dielectricity are not taken into account.
We used 100 000 grid points in the model. Test runs were carried out to ensure that these numbers were sufficient. When the number of grid points were reduced by a factor of two, line profiles were affected by less than 0.5%. In the case of Ganymede, where the density and temperature vary, the sampling probability for generating the Delaunay grid is weighted so that the grid is finer in regions of higher density (except below the surface of the moon). Each grid point was weighted based on the density, that is, 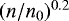 , where n0 = 109 cm−3. To ensure that no unnecessary grid points were located inside the surface radius of Ganymede, a weighting of 10−10 was used below 2550 km (84 km below the surface). This implies that the gridding is also sufficient in the region just below the surface and ensures that the sudden increase in density at the surface of the Ganymede model is properly sampled. Because the vertical and horizontal velocities of water in the lower Ganymede atmosphere are thought to be below 100 m s−1 (Marconi 2007), we set the Doppler parameter to zero. After calculation of the level populations, the model was ray-traced at a sufficiently high spatial resolution, that is, 3′′ for cases I and II, and 6′′ for case III (seebelow). A cut through the model is presented in Fig. 2.
, where n0 = 109 cm−3. To ensure that no unnecessary grid points were located inside the surface radius of Ganymede, a weighting of 10−10 was used below 2550 km (84 km below the surface). This implies that the gridding is also sufficient in the region just below the surface and ensures that the sudden increase in density at the surface of the Ganymede model is properly sampled. Because the vertical and horizontal velocities of water in the lower Ganymede atmosphere are thought to be below 100 m s−1 (Marconi 2007), we set the Doppler parameter to zero. After calculation of the level populations, the model was ray-traced at a sufficiently high spatial resolution, that is, 3′′ for cases I and II, and 6′′ for case III (seebelow). A cut through the model is presented in Fig. 2.
 |
Fig. 1 Maximum (lower atmospheric boundary, upper curves) and minimum (upper atmospheric boundary, lower curves) atmospherictemperatures (solid lines) and densities (dashed lines) in the model as a function of angular distance from the SSP. |
2.2 Validation
The LIME code has recently been applied to study 3D effects on the H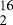 O line shape during the early activity of comet 67/Churyumov-Gerasimenko (67P/CG) measured from Rosetta (Zhao et al. 2020). However, LIME has not yet been applied to gravitationally bound atmospheres of moons or planets. Therefore additional details were taken into consideration for application to Ganymede. Distances are on metre scales, in contrast to astronomical unit scales that are used to model regions outside the Solar System. In the 1.43 version of LIME, there is a hard-coded minimum distance in the raytrace.c file that needs to be modified. For the models presented in this paper, we set this distance to 0.1 m instead of the standard 10 000 metres. 0.1 m is short enough to allow the generation of a grid of sufficient resolution, but at the same time, it is long enough to allow for the largest distances that need to be considered. We also note that densities in the Ganymede atmosphere are up to about 109 cm−3, which is higher than for typical star-forming environments.
O line shape during the early activity of comet 67/Churyumov-Gerasimenko (67P/CG) measured from Rosetta (Zhao et al. 2020). However, LIME has not yet been applied to gravitationally bound atmospheres of moons or planets. Therefore additional details were taken into consideration for application to Ganymede. Distances are on metre scales, in contrast to astronomical unit scales that are used to model regions outside the Solar System. In the 1.43 version of LIME, there is a hard-coded minimum distance in the raytrace.c file that needs to be modified. For the models presented in this paper, we set this distance to 0.1 m instead of the standard 10 000 metres. 0.1 m is short enough to allow the generation of a grid of sufficient resolution, but at the same time, it is long enough to allow for the largest distances that need to be considered. We also note that densities in the Ganymede atmosphere are up to about 109 cm−3, which is higher than for typical star-forming environments.
In order to have an independent check of the 3D LIME results, we compared the resulting excitation temperature and line profiles to a spherically symmetric non-LTE radiative transfer code developed by Per Bergman at Onsala Space Observatory. It uses an accelerated lambda iteration (ALI) scheme (Rybicki & Hummer 1991), has been used in several publications (e.g. Bjerkeli et al. 2011; Wirström et al. 2014), and was benchmarked by Maercker et al. (2008). The physical properties and data files for spectroscopy and excitation we used as input to the 100 shells spherically symmetric code are identical to those used for the LIME model, except for the density and temperature variation with phase angle in the LIME model.
First we ensured that the excitation was well reproduced under LTE and non-LTE conditions. The relative populations of two radiatively connected rotational energy levels (n1, n2) in a molecule can be described by a Boltzmann distribution at the excitation temperature, Tex, so that 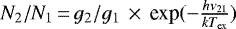 , where gi is the statistical weight, h is Planck’s constant, and ν21 the transition frequency. When collisional excitation completely dominates radiative excitation (LTE), all transitions locally are described by the same excitation temperature. In non-LTE this breaks down, however, and different radiative transitions will be described by different excitation temperatures. The density and temperature at which this transition between LTE and non-LTE excitation occurs thus depends on the efficiency of collisional excitation (collisional coefficients) versus the local radiative excitation. In Fig. 3 we therefore compare the variation in the excitation temperature of the 557 GHz water transition with atmospheric height in all grid points of the LIME model compared to the spherically symmetric ALI models for adopted radial temperature and density profiles at 10° from the SSP (densities high enough for collisionally dominated excitation closest to the surface) and at 60° from the SSP (non-LTE excitation from the surface and up) from Marconi (2007). As expected, the excitation temperature profile computed with ALI at 10° traces the grid points of highest excitation in the LIME model up to about 200 km altitude, where the density becomes low enough for the LTE condition to break down. The excitation temperatures in LIME can exceed those of the spherically symmetric ALI model at higher altitudes because ALI only takes (radially) local radiation into account, while LIME in its 3D geometry sums the total radiation that reaches and excites the molecules also from inner, warmer parts of the atmosphere. This of course only has an effect under non-LTE conditions and also causes the excitation temperature profile from ALI at 60° to coincide with the lower edge of the LIME excitation temperature distribution.
, where gi is the statistical weight, h is Planck’s constant, and ν21 the transition frequency. When collisional excitation completely dominates radiative excitation (LTE), all transitions locally are described by the same excitation temperature. In non-LTE this breaks down, however, and different radiative transitions will be described by different excitation temperatures. The density and temperature at which this transition between LTE and non-LTE excitation occurs thus depends on the efficiency of collisional excitation (collisional coefficients) versus the local radiative excitation. In Fig. 3 we therefore compare the variation in the excitation temperature of the 557 GHz water transition with atmospheric height in all grid points of the LIME model compared to the spherically symmetric ALI models for adopted radial temperature and density profiles at 10° from the SSP (densities high enough for collisionally dominated excitation closest to the surface) and at 60° from the SSP (non-LTE excitation from the surface and up) from Marconi (2007). As expected, the excitation temperature profile computed with ALI at 10° traces the grid points of highest excitation in the LIME model up to about 200 km altitude, where the density becomes low enough for the LTE condition to break down. The excitation temperatures in LIME can exceed those of the spherically symmetric ALI model at higher altitudes because ALI only takes (radially) local radiation into account, while LIME in its 3D geometry sums the total radiation that reaches and excites the molecules also from inner, warmer parts of the atmosphere. This of course only has an effect under non-LTE conditions and also causes the excitation temperature profile from ALI at 60° to coincide with the lower edge of the LIME excitation temperature distribution.
To further verify the modelled spectral line shapes, comparisons are required for an observing geometry in which properties do not vary significantly within the beam because we expect the two codes to produce the same result in these circumstance. Figure 4 thus shows the modelled 557 GHz lines with the 440′′ SWI beam from a distance of 5000 km altitude (7364 km from centre), where the beam footprint on the surface of Ganymede is about 10 km. We used the spherically symmetric code ALI for temperature and density profiles 10° from SSP and compared this to a particular LIME model with no variation in density and temperature with phase angle for a straightforward comparison. Furthermore, 200 000 grid points were used to avoid too coarse gridding when the ray-tracing was made from a very small distance. Integrated line emission from pointings through the exosphere at 50 km from limb agrees to within ~10%. The difference in absorption depth is consistent with the lower excitation temperatures of the 1D ALI code at higher altitudes (see Fig. 3) which results in stronger self-absorption. SWI is planned to perform observations under these geometrical conditions, in orbit around Ganymede, for example, as part of limb scans to investigate the vertical density and temperature profiles of the exosphere.
 |
Fig. 2 Cut through the Ganymede radiative transfer model, where colours show the density distribution in the atmosphere. This representation assumes that solar radiation heats the surface from the bottom in the figure, marked by SSP. Neither the moon itself nor the model grid points outside the atmosphere are included in this figure. |
 |
Fig. 3 Altitude vs. H2O (110−101) excitation temperaturefor the 100 000 grid points in the Ganymede LIME model. Red dots represents the part of the model within 45° from the SSP, while the remaining model is represented in blue. Excitation temperatures computed at locations that are not in the atmosphere are excluded in this figure. Grey and brown circles show the variation in the excitation temperaturewith altitude in the ALI SSL10 and SSL60 cases, respectively. |
 |
Fig. 4 Modelled ALI (dashed line) and LIME (solid line) spectra when Ganymede is viewed from 5000 km altitude, pointing at a tangent altitude of 50 km. |
Overview of the modelled test cases and their properties.
3 Simulation results
The goal of the following simulations is to assess the importance of 3D effects on the formation of the 557 GHz water line for observationsof the Ganymede disc by SWI. As described in the previous section, we used the self-consistent 3D code LIME to evaluate therotational populations that are subsequently used in the ray-tracing algorithm to calculate synthetic SWI spectra.
3.1 Test cases
First, we characterise the effect of the 3D non-LTE distribution of H2O rotational levels across the visible disc on the beam-averaged spectra as a function of phase angle (Sun-target-observer angle). Second, we determine whether there are notable differences between completely unresolved and partially resolved disc observations.
We chose three different test cases, corresponding to different distances to Ganymede, that is, 1.9 × 107 km, 2.7 × 106 km, and 1.2 × 106 km. Times and orbital distances were taken from the SPICE kernels juice_crema_404 and/or the JUICE_Red_Book_i1.05. The beam footprints on Ganymede for these three cases correspond to 13, 100, and 225% of the Ganymede diameter, respectively. For each test case, we considered a range of phase angles, from 0 to 135°. Table 1 provides an overview of the properties of the considered test cases, and Fig. 5 illustrates the beam sizes compared to Ganymede at the three different distances. Figure 6 further illustrates when and how frequently the three test cases are applicable during the mission, starting from just before Jupiter orbit insertion (JOI). The case I model is applicable even earlier, during the interplanetary transfer phase, by scaling the intensity by the square of the distance of interest.
For each test case, full spectral maps at high spatial resolution were computed for the H2O (110−101) line. Different maps were computed for different phase angles. These maps were then convolved using a 2D Gaussian with a full width at half-maximum (FWHM) of 440′′ in order to produce an oversampled map corresponding to what might be observed with SWI at each distance from Ganymede. From these maps, we extracted nadir and limb spectra for cases I and II and 5 by 5 maps for case III (where the Ganymede moon model is resolved). We defined the limb position to be at an atmospheric height of 225 km, that is, half the height of the model atmosphere. Consequently, the nadir and limb positions are separated by 2859 km.
 |
Fig. 5 Relative sizes of the SWI beam FWHM and the Ganymede projected disc for modelled test cases. The Ganymede image was obtained with the Galileo spacecraft, courtesy NASA/JPL. |
3.2 Case I: unresolved observations
The nominal case I uses an observing distance of 1.9e7 km, from which Ganymede has an angular size of ~57′′, thus about 13% of the SWI beam in the 600 GHz band (440′′). This observing geometry is applicable during the first orbit after JOI when the apojove distance is largest (see Fig. 6), but case I results are useful for all monitoring observations: they can be scaled for any other observing distances when Ganymede is not resolved in the beam.
The modelled spectra towards the nadir and limb positions are presented in Fig. 7. As expected, the nadir and limb spectra are very similar for such large observing distances. At 0° phase angle, the o-H2O line is only detected in absorption because the most abundant or warm part of the atmosphere is at the centre of the moon with respect to JUICE/SWI and the column through limb is comparatively small on all sides of the moon. The same roughly applies from a phase angle of 60°, although the change in continuum level between the 0° and 60° cases is significant. When the observation is made from a phase angle of 135°, the densest or warmest parts of the atmosphere are located at the edge of the moon, causing the H2O (110−101) line to also be partly seen in emission in the line wings, but only at a level <0.01 K. In comparison, a 1D model with high water abundance would predict deep absorption in combination with line wings, whileone with low water abundance could only predict shallow absorption and no line wings and thus would not reproduce this complex variation with phase angle. Another striking difference between observations from different phase angles is that the width of the absorption decreases with increasing phase angle, from about 0.80 km s−1 at 0° to barely 0.55 km s−1 at 135°. This is also an effect of emission blending with the absorption at larger phase angles, and it is particularly clear at 135°.
 |
Fig. 6 Distance between the JUICE spacecraft and Ganymede as a function of time from arrival in the Jupiter system, based on the CReMA 4.0 consolidated trajectory (black line). The approximate distances for which the three modelled test cases are applicable are shaded in blue (case I), red (case II), and pink (case III). |
 |
Fig. 7 Modelled spectra towards the nadir (solid lines) and limb (dashed lines) positions of the Ganymede moon model for case I. Red spectra represent a phase angle (viewing angle with respect to the SSP) of 0°, black spectra represent a phase angle of 60°, and blue spectra represent a phase angle of 135°. |
3.3 Case II: Ganymede fills the SWI beam
Case II uses an observing distance of 2.7 × 106 km, at which Ganymede fills the 557 GHz beam of the SWI. Such observations will be useful for planning five-point cross maps throughout the Jupiter tour part of the mission (see Fig. 6). In Fig. 8, five-point cross maps of simulated baseline-subtracted spectra at half-beam spacing for four different phase angles are presented: 0°, 60°, 90°, and 135°. When Ganymede is observed at this distance and towards the SSP, the expected difference in absorption depth between a direct nadir pointing and a FHWM/2 offset pointing is close to a factor of 2. Differences like this are expected to be easily distinguishable with the SWI.
When the phase angle is 60° (SSP rotated to the right, or east, in the upper right panel of Fig. 8), the absorption depth varies from ~7 K towards the west limb (position (220, 0)), through a maximum of about 15 K towards nadir, to ~11 K towards the east limb (position (−220, 0)). Variations like this are expected to be detectable by the SWI in about 5–10 min integration per pointing. Already at these distances, we can therefore determine whether water-ice sublimation is the dominating source in the water atmosphere of Ganymede, as assumed in the model of Marconi (2007).
When the non-illuminated side of Ganymede is observed (phase angles 90° and 135° in the lower panels of Fig. 8), absorption depths are similar because most of the observed region is well separated from the SSP. Similar to case I, when the non-illuminated side is observed, the H2O (110−101) line profiles show emission in the line wings, most pronounced towards the limb closest to the SSP, position (−220,0). At this low spatial resolution, the beam here covers both the strong emission from high water column densities just outside the moon limb, shown in red in the full-resolution colour-scale background image, and weaker absorption from lower column densities towards the moon background (cyan). This results in spectral line profiles with this mix of absorption and emission. The intensity of the line wing emission above the continuum is at most 1 K under these conditions, which is at the limit of what is detectable with SWI within a reasonable observing time.
In the same way as for case I, the line widths decrease with phase angle from about 0.8 km s−1 for 0° to about 0.55 km s−1 for 135°. The SWI high-resolution spectrometer (CTS) will provide a channel separation of 100 kHz, and thus a velocity resolution at 557 GHz better than 0.1 km s−1. These differences will therefore be measurable.
3.4 Case III: resolved 5 × 5 maps
Case III used an observing distance of 1.2 × 106 km, which is more than a factor of two closer than in case II. When observations are made from this distance, Ganymede can be resolved with the SWI, and planning for spatially resolved maps may be justified. As an example, we present four 5 by 5 maps in Fig. 9. They show half-beam-spaced baseline-subtracted spectra towards Ganymede for four different phase angles, 0, 60, 90, and 135°. The absorption depths vary strongly across the disc, and maximum absorption is almost 60 K in nadir towards the SSP. In a 60–90° phase angle observation, the strongest absorption is expected to be observed not at nadir or limb, but towards the mapping position (−220,0) in between, where the absorption can be as high as 10 K stronger than towards either of these.
As in case II, the H2O (110−101) line wings appear in emission when the beam covers the limb close to the SSP where the line-of-sight water column density is highest (see position (−440,0) in the 90 and 135° phase angle maps of Fig. 9). At this higher spatial resolution, the intensity of the line wings above the continuum is increased to ~3 K, which would be detectable with the SWI using dedicated longer integrations.
The modelled continuum level also varies significantly across the disc (see Fig. A.1), from 20 K at the map edges to more than 120 K in nadir towards the SSP. However, no local temperature variations due to surface properties such as albedo or roughness are included in this model. These will also be investigated by the SWI, however, through dedicated continuum detectors of 4 GHz bandwidth.
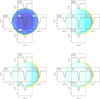 |
Fig. 8 Upper left panel: five-point map towards Ganymede at a distance of 2.7 × 106 m (case II). The phase angle is 0°. Baseline-subtracted spectra are overlaid on a moment-zero map, where light cyan to dark blue regions correspond to increasing absorption, and light yellow to dark red regions correspond to increasing emission. The linear colour scale is normalised to either the position where the integrated intensity is highest or lowest, depending on which attains the greatest absolute value (hence the varying colours in the figures throughout this paper), and white always corresponds to neither absorption nor emission. The moment-zero map is presented at full resolution where each pixel correspond to 6′′. Upper right panel: same as the upper left panel, but for a phase angle of 60°. Lower left panel: same as the upper left panel, but for a phase angle of 90°. Lower right panel: same as the upper left panel, but for a phase angle of 135°. |
4 Discussion
The SWI/JUICE instrument will provide the JUICE mission with the unique ability to monitor the atmospheres of Ganymede and other Jovian moons already during the Jupiter orbit phase (distances of ~20 RJ). With a full beam width of 0.002 radians at 600 GHz, the projected beam size is about the radius of Ganymede (2600 km), allowing distinguishing atmospheric sources in north-south and east-west regions of the disc using the five-point-mapping mode. In addition, with proper timing, the phase dependence of atmospheric water variability can be determined. Therefore, this work is the first step in understanding the line formation in 3D through simulating different phase-angle observations for nadir and limb geometries.
The current Ganymede atmospheric model only takes into account collisions between water molecules in ortho and para form. The inclusion of 3D distributions of other collisional partners known to be present in the atmosphere (H, H2, O2, and e−) may affect the water populations to a significantly higher degree than demonstrated here and thus affect the water line profiles. This remains to be investigated with future improvements of the model.
Currently, the characteristics of the Ganymede atmosphere are poorly constrained, but it is known that several mechanisms might contribute to the Ganymede atmosphere, and the overall outgassing geometry of a species will be coupled to these: If thermal sublimation dominates, the highest concentrations will be observed around the SSP where the surface can reach the highest temperatures. Sputtering by energetic atomic ions, however, produces highest concentrations in the open magnetic field line regions around the poles. In addition, local variations in surface properties such as ice abundance and albedo can affect the outgassing distribution.
The kinetic atmosphere model by Marconi (2007) assumes that the sources of atmospheric water are a combination of sublimation and sputtering of a homogeneous surface of water ice, which produces the highest density of atmospheric water in the region around the SSP. Together, the modelled spectra presented in this paper show that already from SWI five-point cross maps, performed from distances when Ganymede approximately fills the telescope beam, it will be possible to determine whether thermal sublimation of water is the driving process, as assumed by Marconi (2007).
The Marconi scenario is in stark contrast to more recent full orbital simulations of the Ganymede atmosphere and its seasonal variation by Leblanc et al. (2017). These simulations showed that when a lower water sublimation rate is assumed (depending on surface structure and temperature), the atmospheric density of water will generally be highest around the poles and lowest on the trailing hemisphere, except at phase 90° (when the SPP is in the leading hemisphere) where the highest column is predicted around ±45° latitude at the leading hemisphere. The simulated difference between leading and trailing hemisphere is due to asymmetries in the magnetosphere of Ganymede, allowing for efficient sputtering by Jovian ions at lower latitudes on the leading hemisphere, as indicated by auroral emission maps by McGrath et al. (2013). The SWI will have many opportunities to observe both the leading and trailing hemispheres in all case I, II, and III configurations, as demonstrated in Fig. 6, where the short-period oscillations correspond to the ~7-day orbital period of Ganymede.
Finally, we note that an even more interesting case to investigate is the detectability of localised and transient outburst of water from beneath the icy surface of Ganymede, as were recently detected for Europa (Paganini et al. 2019). This requires a more advanced 3D model based on unconfirmed assumptions about the density and abundance of water, velocity structure, vent size and shape, etc., however, and will be addressed in detail in a forthcoming paper.
 |
Fig. 9 Upper left panel: 5 by 5 map towards Ganymede at a distance of 1.2 × 106 km. The phase angle is 0°. Moment-zero maps are similar to those presented in Fig. 8, and spectra are baseline subtracted. Upper right panel: same as the upper left panel, but for a phase angle of 60°. Lower left panel: same as the upper left panel, but for a phase angle of 90°. Lower right panel: same as the upper left panel, but for a phase angle of 135°. |
5 Conclusions
We attempted to identify 3D distribution effects on the excitation and line formation for the 557 GHz water transition in the context of the SWI/JUICE instrument. In particular, we studied these effects for observations that will be performed for daily moon monitoring during the Jupiter phase, when the Ganymede disc is unresolved or partially resolved, at scales of ~350–6000 km. Because Ganymede (and other moons) will be viewed at different phases (illumination) and geometries (limb and/or nadir), the role of 3D effects is highly relevant.
We presented several study cases built around three relevant distances (also Fig. 6) from Ganymede and assumptionsabout the phase angles, as outlined in Table 1. The 3D distribution of water and kinetic temperature inputs required for the LIME radiative transfer model were built from Marconi (2007).
Our main results on the effect of the 3D distribution on the ground-state ortho-water line for unresolved and partially resolved observations by SWI/JUICE can be summarised as follows:
- 1.
The predicted H2O spectral line profiles are strongly affected by atmospheric gradients within the beam. Such variations are naturally accounted for in 3D calculations, but not in 1D calculations. Our modelling shows that this has to be accounted for when the SWI observations are interpreted.
- 2.
Absorption depth and width of the 557-GHz transition varies with phase angle in nadir observations from all distances we simulated (from 1.9 × 107 to 1.2 × 106 km).
- 3.
Under conditions when sufficient atmospheric limb emission is present within the SWI beam (i.e. from distances of about a million kilometers or closer), the observed line profiles show emission features. It is assumed that these features may be substantially stronger with proper surface continuum emission modelling.
- 4.
SWI five-point mapping is expected to clearly detect east-west variations for certain phase angles. The same applies to north-south variations if the atmosphere turns out not to be symmetric around the SSP, as assumed in this model.
- 5.
From distances shorter than ~106 km, the 5 by 5 mapping provides sufficient spatial resolution to discern large-scale variations on the Ganymede surface. Spectral line profiles are therefore expected to show varying characteristics as a function of phase angle. These variations may be valuable in the post-processing of measurements for pointing reconstruction, if necessary.
We also find that SWI five-point cross maps, performed at a range of phase angles from distances when Ganymede approximately fills the telescope beam, should enable determining whether the dominating driving process for the water atmosphere is thermal sublimation or sputtering.
This work provides evidence that with the technological capabilities of missions such as JUICE, providing unprecedented observational opportunities for the icy moons, we are also required to update our tools for interpretation of the future data. In the case of SWI/JUICE, adapted 3D radiative transfer models will not be enough for interpretation, but it will be equally important to obtain good input data (first guess) from 3D kinetic models. Finding a speedy and reliable way to couple such models may prove to be key in future studies of tenous atmospheres, both with space missions and from ground-based observatories such as the Atacama Large Millimetre Array (ALMA).
Acknowledgements
E.S.W. and P.B. acknowledge generous support from the Swedish National Space Agency. The astrophysics HPC facility at the University of Copenhagen, supported by a research grant (VKR023406) from VILLUM FONDEN, was used for carrying out the radiative transfer modeling.
Appendix A Supplementary material
References
- Bjerkeli, P., Liseau, R., Nisini, B., et al. 2011, A&A, 533, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brinch, C., & Hogerheijde, M. R. 2010, A&A, 523, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buffa, G., Tarrini, O., Scappini, F., & Cecchi-Pestellini, C. 2000, ApJS, 128, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Feldman, P. D., McGrath, M. A., Strobel, D. F., et al. 2000, ApJ, 535, 1085 [NASA ADS] [CrossRef] [Google Scholar]
- Grasset, O., Dougherty, M. K., Coustenis, A., et al. 2013, Planet. Space Sci., 78, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Hall, D. T., Feldman, P. D., McGrath, M. A., & Strobel, D. F. 1998, ApJ, 499, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, R. E., Carlson, R. W., Cooper, J. F., et al. 2004, Radiation effects on the Surfaces of the Galilean Satellites, eds. F. Bagenal, T. E. Dowling, & W. B. McKinnon (Cambridge, UK: Cambridge University Press), 1, 485 [Google Scholar]
- Leblanc, F., Oza, A. V., Leclercq, L., et al. 2017, Icarus, 293, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Maercker, M., Schöier, F. L., Olofsson, H., Bergman, P., & Ramstedt, S. 2008, A&A, 479, 779 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marconi, M. L. 2007, Icarus, 190, 155 [NASA ADS] [CrossRef] [Google Scholar]
- McGrath, M. A., Jia, X., Retherford, K., et al. 2013, J. Geophys. Res. Space Phys., 118, 2043 [NASA ADS] [CrossRef] [Google Scholar]
- Paganini, L., Villanueva, G. L., Roth, L., et al. 2019, Nat. Astron., 4, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Plainaki, C., Milillo, A., Massetti, S., et al. 2015, Icarus, 245, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Rybicki, G. B., & Hummer, D. G. 1991, A&A, 245, 171 [NASA ADS] [Google Scholar]
- Shematovich, V. 2016, Sol. Syst. Res., 50, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Turc, L., Leclercq, L., Leblanc, F., Modolo, R., & Chaufray, J.-Y. 2014, Icarus, 229, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Wirström, E. S., Charnley, S. B., Persson, C. M., et al. 2014, ApJ, 788, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Yamada, T., Rezac, L., Larsson, R., et al. 2018, A&A, 619, A181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhao, Y., Rezac, L., Hartogh, P., et al. 2020, MNRAS, 494, 2374 [NASA ADS] [CrossRef] [Google Scholar]
Parallel mode, using 32 threads, was utilised in LIME to limit the number of required wall-clock hours. All computations were performed at the High Performance Computing Centre (HPCC) at the University of Copenhagen: https://hpc.ku.dk
All Tables
All Figures
 |
Fig. 1 Maximum (lower atmospheric boundary, upper curves) and minimum (upper atmospheric boundary, lower curves) atmospherictemperatures (solid lines) and densities (dashed lines) in the model as a function of angular distance from the SSP. |
| In the text | |
 |
Fig. 2 Cut through the Ganymede radiative transfer model, where colours show the density distribution in the atmosphere. This representation assumes that solar radiation heats the surface from the bottom in the figure, marked by SSP. Neither the moon itself nor the model grid points outside the atmosphere are included in this figure. |
| In the text | |
 |
Fig. 3 Altitude vs. H2O (110−101) excitation temperaturefor the 100 000 grid points in the Ganymede LIME model. Red dots represents the part of the model within 45° from the SSP, while the remaining model is represented in blue. Excitation temperatures computed at locations that are not in the atmosphere are excluded in this figure. Grey and brown circles show the variation in the excitation temperaturewith altitude in the ALI SSL10 and SSL60 cases, respectively. |
| In the text | |
 |
Fig. 4 Modelled ALI (dashed line) and LIME (solid line) spectra when Ganymede is viewed from 5000 km altitude, pointing at a tangent altitude of 50 km. |
| In the text | |
 |
Fig. 5 Relative sizes of the SWI beam FWHM and the Ganymede projected disc for modelled test cases. The Ganymede image was obtained with the Galileo spacecraft, courtesy NASA/JPL. |
| In the text | |
 |
Fig. 6 Distance between the JUICE spacecraft and Ganymede as a function of time from arrival in the Jupiter system, based on the CReMA 4.0 consolidated trajectory (black line). The approximate distances for which the three modelled test cases are applicable are shaded in blue (case I), red (case II), and pink (case III). |
| In the text | |
 |
Fig. 7 Modelled spectra towards the nadir (solid lines) and limb (dashed lines) positions of the Ganymede moon model for case I. Red spectra represent a phase angle (viewing angle with respect to the SSP) of 0°, black spectra represent a phase angle of 60°, and blue spectra represent a phase angle of 135°. |
| In the text | |
 |
Fig. 8 Upper left panel: five-point map towards Ganymede at a distance of 2.7 × 106 m (case II). The phase angle is 0°. Baseline-subtracted spectra are overlaid on a moment-zero map, where light cyan to dark blue regions correspond to increasing absorption, and light yellow to dark red regions correspond to increasing emission. The linear colour scale is normalised to either the position where the integrated intensity is highest or lowest, depending on which attains the greatest absolute value (hence the varying colours in the figures throughout this paper), and white always corresponds to neither absorption nor emission. The moment-zero map is presented at full resolution where each pixel correspond to 6′′. Upper right panel: same as the upper left panel, but for a phase angle of 60°. Lower left panel: same as the upper left panel, but for a phase angle of 90°. Lower right panel: same as the upper left panel, but for a phase angle of 135°. |
| In the text | |
 |
Fig. 9 Upper left panel: 5 by 5 map towards Ganymede at a distance of 1.2 × 106 km. The phase angle is 0°. Moment-zero maps are similar to those presented in Fig. 8, and spectra are baseline subtracted. Upper right panel: same as the upper left panel, but for a phase angle of 60°. Lower left panel: same as the upper left panel, but for a phase angle of 90°. Lower right panel: same as the upper left panel, but for a phase angle of 135°. |
| In the text | |
 |
Fig. A.1 Same as Fig. 9, but without continuum subtraction. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


