| Issue |
A&A
Volume 636, April 2020
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 9 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201935423 | |
| Published online | 17 April 2020 | |
Twisted quasar light curves: implications for continuum reverberation mapping of accretion disks
Institute of Physics, Laboratory of Astrophysics, École Polytechnique Fédérale de Lausanne (EPFL), Observatoire de Sauverny, 1290 Versoix, Switzerland
e-mail: hung-hsu.chan@epfl.ch
Received:
6
March
2019
Accepted:
10
October
2019
With the advent of high-cadence and multi-band photometric monitoring facilities, continuum reverberation mapping is becoming of increasing importance for the measurement of the physical size of quasar accretion disks. The method is based on measuring the time it takes for a signal to propagate from the center to the outer parts of the central engine, assuming the continuum light curve at a given wavelength has a time shift of the order of a few days with respect to light curves obtained at shorter wavelengths. We show that with high-quality light curves, this assumption is no longer valid and that light curves at different wavelengths are not only shifted in time, but also distorted: in the context of the lamp-post model and thin-disk geometry, the multi-band light curves are, in fact, convolved by a transfer function whose size increases with wavelength. We illustrate the effect with simulated light curves in the Large Synoptic Survey Telescope (LSST) ugrizy bands and examine the impact on the delay measurements when using three different methods, namely JAVELIN, CREAM, and PyCS. We find that current accretion disk sizes estimated from JAVELIN and PyCS are underestimated by ∼30% and that unbiased measurements are only obtained with methods that properly take the skewed transfer functions into account, as the CREAM code does. With the LSST-like light curves, we expect to achieve measurement errors below 5% with a typical two-day photometric cadence.
Key words: accretion, accretion disks / quasars: general
© ESO 2020
1. Introduction
Active galactic nuclei (AGNs) are astrophysical sources powered by the accretion of hot gas onto super-massive black holes (SMBHs) at the center of galaxies. Gas or dust around a SMBH orbits in a plane around the SMBH center, forming a so-called accretion disk. In current models, the central accretion disk is considered to be optically thick and geometrically thin (Shakura & Sunyaev 1973). Its emission is a combination of the internal heat from viscous dissipation and external heat from the reprocessing of the UV/X-ray source near the SMBH. Considering that the disk luminosity is produced by blackbody radiation, the temperature profile at large distance, R, follows T ∝ R−3/4.
Understanding the growth and evolution of SMBH in AGNs requires studying the structure of their accretion disk. Currently, size measurements are carried out either using microlensing in lensed AGNs (e.g., Schechter & Wambsganss 2002; Kochanek 2004; Morgan et al. 2010, 2018), or reverberation mapping (e.g. Fausnaugh et al. 2016; Jiang et al. 2017; Mudd et al. 2018; Yu et al. 2020a). The basic idea of reverberation mapping is to measure the time lag τlag between broad-line and continuum fluxes from spectroscopic monitoring (Blandford & McKee 1982). Assuming that the broad-line emission is triggered by the central emission, the lag is considered as the light-travel time from the central illuminating source to the broad-line region (BLR), that is, RBLR = cτlag, and provides a measurement of the BLR’s size. Similarly, it is natural to use the same method to measure the disk size itself, since the continuum emission across the disk is also driven by the central source.
Early studies have obtained continuum lags for several targets, particularly using the Swift data (Gehrels et al. 2004), such as NGC 2617 (Shappee et al. 2014), NGC 5548 (McHardy et al. 2014; Edelson et al. 2015; Fausnaugh et al. 2016; Starkey et al. 2017), NGC 4151 (Edelson et al. 2017), MCG+08-11-011, and NGC 2617 (Fausnaugh et al. 2018). More recently, other studies have used large quasar samples from various wide field surveys to measure accretion disk sizes: Jiang et al. (2017) use 39 quasars from Pan-STARRS; Mudd et al. (2018) have 15 quasars on the supernova fields from the Dark Energy Survey (DES); and Homayouni et al. (2019) use 95 quasars from the Sloan Digital Sky Survey (SDSS). Most notablym Yu et al. (2020a), present measurements using high-cadence light curves (over one day) in a sample of 23 quasars in the standard star fields and in the supernova C fields of DES. However, each study finds different systematic trends for the measured sizes and prediction of the thin-disk model. A plausible explanation might be a bias in the time-delay measurements between multi-band light curves when using methods based on interpolated cross-correlation function (ICCF; Peterson et al. 1998) and JAVELIN (Zu et al. 2011, 2013). Both curve-shifting techniques are capable of capturing the appropriate lags when the line light curve is a smoothed and shifted version of the continuum (Yu et al. 2020b) but may not be valid when the transfer function of light curves becomes asymmetric. Notably, an algorithm that directly fits the reprocessing disk model does exist: the Continuum REprocessed AGN Markov chain Monte Carlo code (CREAM, Starkey et al. 2016, 2017) that Fausnaugh et al. (2018) reports to be in agreement with JAVELIN’s measurement.
In this paper, we simulate such realistic light curves as can be obtained with the Large Synoptic Survey Telescope (LSST) in order to test and compare several tools used for measuring time lags between light curves taken in multiple photometric bands. In addition to ICCF, JAVELIN, and CREAM, we also use PyCS (Tewes et al. 2013; Bonvin et al. 2016), a toolbox for time-delay measurements in strongly-lensed AGNs, developed by the COSMOGRAIL collaboration1.
We present our simulations in Sect. 2 and our results in Sect. 3, along with their implications for future observational strategies. The conclusions are described in Sect. 4. Throughout this paper, we use ΛCDM cosmology with H0 = 70 km s−1 Mpc−1, Ωm = 0.3, and ΩΛ = 0.7.
2. Simulating continuum light curves
Here we introduce the models for our light-curve simulations and the related asymmetric transfer functions which distort multi-band light curves. We then use LSST-like light curves to compare disk-size measurements using JAVELIN, CREAM, and PyCS, and to evaluate the biases in these measurements.
2.1. Thin-disk and lamp-post model
We considered a non-relativistic thin-disk model emitting black-body radiation (Shakura & Sunyaev 1973) where the central source is assumed to be a lamp-post located close above the black hole (Cackett et al. 2007; Starkey et al. 2016). The time-variable temperature profile of disk can be expressed as
where f(t − tlag) is the small fluctuation lagged by the light traveling time tlag = (1 + z)R/c. In other words, f(t) is a driving variable source at the center of the AGN. The unperturbed temperature profile T0 at rest wavelength λ can be expressed as
where h and k are the Planck and the Boltzmann constants, respectively, and we ignore the inner edge of the disk. Rλ is the radius where the disk temperature matches the photon wavelength (kT = hc/λ):
where L/LE is the luminosity in unit of the Eddington luminosity LE and η is the accretion efficiency (Morgan et al. 2010). We assume the accretion disk flux arises from the blackbody radiation described by Planck’s law
where
when the temperature variations are small, we have δT∝ f(t − tlag)/ξ and the time-variable surface brightness can be expressed as (Tie & Kochanek 2018)
where
The observed flux is the sum of photons emitted by all points on the disk, the observed photons from the outer disk being responses to irradiation emitted from the central region at earlier times, due to the lamp-post delay tlag. We can express the variation in the flux as:
Therefore, Gλ(ξ) plays the role of a weight function and we can now construct a distribution of photon lag, δt as a transfer function for an accretion disk:
2.2. Properties of the simulated light curves
In order to investigate how the source-size measurements are biased due to imperfect time-delay estimates, we designed two types of light curves. First, a single Gaussian to illustrate how the peak positions shift when convolving with the time-delay transfer function. Second. we used light curves represented by a damped random walk (DRW) model, which is currently thought to aptly describe AGN variability (Kelly et al. 2009; Kozłowski et al. 2010; Zu et al. 2013).
We generated multi-band light curves based on the LSST ugrizy bands (Fig. 1). In our toy simulation, we chose a quasar redshift of z = 0.5, a black hole mass Mbh = 2 × 108 M⊙, an Eddington ratio of L/LE = 0.1, and an accretion efficiency of η = 0.1. Using Eq. (3), the corresponding disk size in the u band is RLSST − u = 5.078 × 1014 cm = 0.196 light-day. We note that when calculating Rλ with Eq. (3), we accounted for the quasar redshift, i.e. λ = λobs/(1 + z). The mean delay of each transfer function given by the thin-disk with lamp-post model can be obtained from:
 |
Fig. 1. Top: transfer functions for LSST filters. Mean delays ⟨δt⟩λ of each transfer function Eq. (10) are represented as dot-dashed vertical lines. Bottom: light curves generated using single Gaussian as driving source (shown in black). Peak positions are represented as vertical dotted lines. The inset highlights with colored wedges the difference between the peak position and the mean delay for each band. |
which is called the geometric delay as it is related to a delayed emission from the different regions of the source (Bonvin et al. 2019). We displayed the transfer function in each band on the top panel of Fig. 1 with ⟨δt⟩λ, the mean of these distributions, labelled as vertical dot-dashed lines. Here we show the effect for a face-on disk, but we note that larger inclination angle would introduce even larger bias between the peak and mean values (Starkey et al. 2016). Furthermore, we ignore the emission lines from the BLR as the latter does not contaminate the continuum lag measurements much (e.g., Yu et al. 2020a).
We first simulated a single Gaussian as a driving-source emission of the lamp-post model, f(t). The black curve on the bottom panel of Fig. 1 was generated using a mean of 0 day and σ = 1 day. The observed flux is the integrated flux of the photons traveling from each region of the disk with a time lag of tlag = (1 + z)R/c.
We then constructed a transfer function for each filter, and we convolved it with the source emission function, as presented on the bottom panel of Fig. 1. The new curves are not only shifted in time, but also smeared asymmetrically, indicating that they are skewed. The observed peaks of emission intensity for each curve are indicated as vertical dotted lines. In the inset, we highlight the differences between the peak positions and the mean delays with colored wedges. We note that for a sharper source function (i.e., σ < 1 day), the differences between the peaks and the mean intensities are larger. As a consequence, any method measuring time lags from sharp “peaky” structures of similar size to the transfer function will be biased as they are not measuring the mean lag, ⟨δt⟩λ, which is the physically relevant quantity.
Next, we created more realistic light curves using a DRW model from astroML (Vanderplas et al. 2012; Ivezić et al. 2014) for the driving source emission with a characteristic timescale τ = 200 days at the rest frame and a structure function at infinity SFinf = 2 (flux unit), which describes the long-term variability of the light curve. These DRW parameters are typical of the quasars in the DES sample (Yu et al. 2020a). Using the same transfer functions as before, we then generated the light curves shown on the top panel of Fig. 2. In the middle panel of Fig. 2, we shift the curves back by ⟨δt⟩λ to show that the positions in time of the minima and maxima are earlier than in the original DRW light curve.
 |
Fig. 2. Top: simulated light curves for LSST filters before time sampling. Black curve is a DRW using τ = 200 days and SFinf = 2 as a centrally-driven source. Transfer functions shown on the top panel of Fig. 1 are applied to simulate distorted (skewed) multi-band light curves. Middle: curves are shifted back by their mean delay, ⟨δt⟩λ, showing that there are residual misalignments due to convolution by skewed kernel that may bias delay measurements toward the peak of asymmetric delay distribution rather than its mean. Bottom: example of simulated data as may be obtained with LSST g, r, and y bands. We simulate the light curves over a period of 1000 days with a one-day cadence. The error bars are all Δm = 0.01 mag rms. The color code is the same as in Fig. 1. |
In practice, light curves are not perfectly continuous. To mimic real-life observations, we sampled our light curves using photometric noise with a rms scatter of Δm = 0.01 mag over a period of 1000 days with a one-day cadence. We also removed data falling in season gaps of 120 days every 240 days. In a first experiment, we did not include data loss due to bad weather or technical problems as our purpose was to illustrate measurement biases even with fairly ideal data. These light curves are presented as the data points on the bottom panels of Fig. 2 and the right panels of Fig. A.2.
We generated 25 DRW realizations of simulated light curves for PyCS considering 25 noise realizations and JAVELIN/JAVELIN-Ext considering one noise realization. We ran CREAM with one of the simulations due to the slow speed computation. This still allows us to demonstrate the impact of skewed transfer functions.
3. Result
The conventional approach to estimating disk sizes is to measure the time delay between light curves observed in different bands and then fit the lags according to a given disk model. In this work, we chose the u band as the reference band since its light curve is less distorted and we employed PyCS and JAVELIN to measure time lags.
PyCS is a publicly available python package developed by the COSMOGRAIL collaboration (Tewes et al. 2013; Bonvin et al. 2016) which includes two main point-estimators of time delays. One of them is the free-knot splines estimator that we use here. PyCS does not assume any physical AGN model, and its use is, thus, completely data-driven.
JAVELIN models the variability of AGNs as DRW, assuming light curves at various wavelengths are shifted, scaled, and smoothed versions of the central variability. In practice, the shift is done using a convolution of the central DRW by time-shifted top-hat functions (Zu et al. 2011, 2013). The width of top-hat of each filter is a free parameter. As a top-hat function is obviously not skewed, we expect a bias in time-lag measurements when applied to continuum light curves.
JAVELIN has been used widely in emission-line and continuum reverberation mapping observations (Shappee et al. 2014; Fausnaugh et al. 2016; Jiang et al. 2017). Due to the difficulty of measuring short delays, Mudd et al. (2018) have developed an extension of JAVELIN to implement the τ ∝ λ4/3 scaling of thin-disk models (hereafter JAVELIN-Ext), which can directly fit for a disk size Rλ using all the available photometric light curves simultaneously.
Furthermore, we applied CREAM to our simulated light curves. CREAM is designed to fit the more realistic transfer functions of the lamp-post model, for which it infers a posterior probability distribution for the AGN disk size. In this work, we limited ourselves to face-on disk for both CREAM and JAVELIN-Ext. In doing so, we fixed the scaling relation of disk size as Rλ ∝ λ4/3 in accordance to our simulations. We note that in real-life applications, these parameters are not necessarily known and it’s necessary to marginalize over them.
Finally, we also tested the conventional interpolated cross-correlation function (ICCF) method (Peterson et al. 1998; Sun et al. 2018). This led to the same conclusion as reported by Jiang et al. (2017) and Yu et al. (2020a), meaning that the lag distributions from ICCF are significantly wider (≳0.8 day) than the distributions from the previous three methods to the point that statistical error vastly dominates the systematic errors we wish to study here. Therefore, we do not further consider the ICCF method here.
In the top row of Fig. 3, we display the probability distributions of the measured time lags τλ relative to the reference band (λ0 = LSST − u in this work) from PyCS and JAVELIN. We indicate the true delays as red vertical lines, i.e., ⟨δt⟩λ − ⟨δt⟩λ0 using Eq. (10). To estimate the disk size, we adopt least-square fitting using the measured delays τλ between the LSST bands. This is
 |
Fig. 3. Probability distributions of measured time lags τLSST − grizy (top-row), relative to reference band LSST-u, and source size RLSST − u (bottom-left), using PyCS (blue), JAVELIN (orange), JAVELIN-Ext (green), and CREAM (purple). True delays and sizes are shown as red lines. In the table, the values represent the 50th, 16th, and 84th percentiles of the respective probability distributions. The last column (Truth) shows the input value of ⟨δt⟩LSST − grizy − ⟨δt⟩LSST − u using Eq. (10). The results from PyCS and JAVELIN are comparable and are 20% smaller than the true size. JAVELIN-Ext leads to even smaller sizes (30% smaller) but CREAM leads to unbiased measurements. |
where
and where σλ are the standard deviations of the distributions. The probability distributions for the source size at the reference band RLSST − u are shown on the bottom-left panel of Fig. 3. Evidently, the smaller-size measurements of PyCS and JAVELIN come from the underestimation of time lags in comparison with the mean delays of the transfer function ⟨δt⟩λ − ⟨δt⟩λ0. The effect is stronger for light curves displaying sharp peaks, that is, when the driving light curve is dominated by high-frequency structures acting on timescales similar to the (temporal) size of the transfer function. Both PyCS and JAVELIN seem sensitive to such structures, which are most affected by the skewed transfer functions. This results in estimated source sizes about 20% smaller than the true size for our simulations but this should degrade even more with the increasing level of sharp structures in the DRW, hence, the level of bias depends on every object.
In contrast to the previous methods, both CREAM and JAVELIN-Ext fit the source size directly, but the main differences are: 1- JAVELIN-Ext adopts a shifted top-hat transfer function while CREAM has a realistic thin-disk model, and 2- CREAM represents the driving source with a prior on the Fourier power density spectrum while JAVELIN-Ext assumes that the driving light curve is a DRW. The posteriors of DRW parameters from JAVELIN are shown in Fig. A.1.
Consequences on future observational strategies. CREAM outputs the posterior of accretion rate Ṁ and the mean delay of each transfer function ⟨δt⟩λ. The number of total iterations is 20 000, and only the samples after iteration larger than 5000 are used for size measurement. To avoid confusion in converting CREAM’s measurement of Ṁ to Rλ, we use ⟨δt⟩LSST−u as our estimate to measure the disk size, using Eq. (3). The Markov chain Monte Carlo (MCMC) fit of CREAM is illustrated in Fig. A.2. More inputs/outputs of CREAM are discussed in Appendix A.
The results of JAVELIN-Ext and CREAM are also shown in Fig. 3. We note an even larger bias for JAVELIN-Ext which leads to an underestimation of the size by 30%. The result of JAVELIN-Ext has the same trend as shown in Fig. 11 of Mudd et al. (2018). CREAM obtains the unbiased measurement with an rms uncertainty of ∼4%. However, there are so far very few direct comparisons of different time lag measurement algorithms using real data. Based on the present experiment, we conclude that it is crucial to consider asymmetric transfer functions to infer the disk size using continuum reverberation mapping data.
We then investigated the precision of the disk size measurement from simple observational strategies using CREAM, as this is the method giving the best performances in the previous sections. We used the same light curve simulation as for CREAM, as shown in Fig. A.2 (Δm = 0.01), but we increased the cadence gradually from one day to five days. Furthermore, we randomly added three inter-night gaps to each observation season (240 days) and 10% loss of observation to mimic bad weather or technical issues with the telescope. Each inter-night gap is one week. These observing conditions are typical for the COSMOGRAIL program and should also apply to such instruments as the LSST. The numbers of epochs for each observation strategy is listed in Table 1. The total number of iterations is 20 000. We choose the samples after the iteration of 5000 and then measured the probability distributions for ⟨δt⟩LSST − u. The corresponding source sizes at the reference band RLSST − u from CREAM are shown in Fig. 4. In general, CREAM can measure disk sizes with an rms error below 10%, even for a cadence of five days and with data loss. A cadence of over two days can even achieve errors below the 5% level.
 |
Fig. 4. Probability distributions for source size RLSST − u using CREAM. Simulated light curves are the same as shown on the right panels of Fig. A.2 and we increase cadence (cdn) from one to five days (Top), and further add inter-night gaps and 10% loss of time (Bottom). CREAM measures disk size with an uncertainty below 10% even when a cadence is five days with data loss. |
Number of epochs for each observation strategy using CREAM.
4. Conclusions
We show that most current methods for analyzing continuum reverberation mapping data leads to underestimates of accretion-disk sizes if the transfer function is skewed.
To illustrate our finding, we simulate light curves using an AGN model based on a combination of thin-disk, lamp-post, and damped random walk for the driving function. We estimate the time lags using both PyCS’s free-knot splines estimator and JAVELIN and we use the measured lags to derive the disk size. We also use JAVELIN-Ext and CREAM to directly fit the disk size, with the former adopting a shifted top-hat transfer function. Our findings are as follows.
-
As the transfer function of thin-disk model is asymmetric, multi-band continuum light curves are not only shifted and smoothed with regard to each other, but they are also skewed.
-
Curve-shifting techniques that are sensitive to sharp features, acting on similar timescales as the transfer function, underestimate multi-band time delays by up to 20%, hence, they translate into a source size estimate that is also 20% smaller than in actuality. We note that the figure quoted here depends on the level of high-frequency structures (e.g., sharp peaks) in the actual DRW used.
-
Direct disk size estimates using JAVELIN-Ext do not perform better given their fitted size is 30% smaller than in actuality.
-
Taking the proper transfer functions into account, such as CREAM, is essential to reach an unbiased measurement of the disk size.
-
In order to achieve a size measurement with errors below 5%, a cadence of at least one observation every two days is needed, assuming photometric errors of the order of Δm = 0.01 mag rms over a period of ∼ three years.
A long-standing problem in quasar accretion disk studies is that measurements of their sizes are larger than the predictions of the thin-disk model by factors as large as two to three. Yu et al. (2020a) report that the measured disk sizes are consistent with the predictions after the disk variability is taken into account, assuming that disks illuminate following the lamp-post model because this increases the flux-weighted mean disk size by up to 50% (see Eqs. (8) and (9) in Yu et al. 2020a). However, the discrepancy still exists if the effect of the skewed transfer function is ignored. In this work, we chose the traditional disk model to demonstrate the effect. Although the details of the transfer function may vary from other models, we show that accounting for its skewness, which is a general property shared by many models, is necessary to converge towards unbiased measurements of the disk size.
Our results based on numerical experiments suggest that future generations of continuum reverberation mapping studies should consider the transfer function shape in detail, or potentially attempt to reconstruct it during the time-lag measurement process.
Acknowledgments
This research is supported by the Swiss National Science Foundation (SNSF) and by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (COSMICLENS: grant agreement No 787866). We thank Dominique Sluse for the useful discussion. We would also like to thank the anonymous referee for the constructive comments on this work.
References
- Blandford, R. D., & McKee, C. F. 1982, ApJ, 255, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonvin, V., Tewes, M., Courbin, F., et al. 2016, A&A, 585, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonvin, V., Tihhonova, O., Millon, M., et al. 2019, A&A, 621, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cackett, E. M., Horne, K., & Winkler, H. 2007, MNRAS, 380, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Edelson, R., Gelbord, J. M., Horne, K., et al. 2015, ApJ, 806, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Edelson, R., Gelbord, J., Cackett, E., et al. 2017, ApJ, 840, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Fausnaugh, M. M., Denney, K. D., Barth, A. J., et al. 2016, ApJ, 821, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Fausnaugh, M. M., Starkey, D. A., Horne, K., et al. 2018, ApJ, 854, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Homayouni, Y., Trump, J. R., Grier, C. J., et al. 2019, ApJ, 880, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezić, Ž., Connolly, A., Vanderplas, J., & Gray, A. 2014, Statistics, Data Mining and Machine Learning in Astronomy (Princeton, NJ: Princeton University Press) [CrossRef] [Google Scholar]
- Jiang, Y.-F., Green, P. J., Greene, J. E., et al. 2017, ApJ, 836, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Kelly, B. C., Bechtold, J., & Siemiginowska, A. 2009, ApJ, 698, 895 [Google Scholar]
- Kochanek, C. S. 2004, ApJ, 605, 58 [Google Scholar]
- Kozłowski, S., Kochanek, C. S., Udalski, A., et al. 2010, ApJ, 708, 927 [NASA ADS] [CrossRef] [Google Scholar]
- McHardy, I. M., Cameron, D. T., Dwelly, T., et al. 2014, MNRAS, 444, 1469 [NASA ADS] [CrossRef] [Google Scholar]
- Morgan, C. W., Kochanek, C. S., Morgan, N. D., & Falco, E. E. 2010, ApJ, 712, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Morgan, C. W., Hyer, G. E., Bonvin, V., et al. 2018, ApJ, 869, 106 [Google Scholar]
- Mudd, D., Martini, P., Zu, Y., et al. 2018, ApJ, 862, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., Wanders, I., Horne, K., et al. 1998, PASP, 110, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Schechter, P. L., & Wambsganss, J. 2002, ApJ, 580, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shappee, B. J., Prieto, J. L., Grupe, D., et al. 2014, ApJ, 788, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Starkey, D. A., Horne, K., & Villforth, C. 2016, MNRAS, 456, 1960 [NASA ADS] [CrossRef] [Google Scholar]
- Starkey, D., Horne, K., Fausnaugh, M. M., et al. 2017, ApJ, 835, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, M., Grier, C. J., & Peterson, B. M. 2018, Astrophysics Source Code Library [record ascl:1805.032] [Google Scholar]
- Tewes, M., Courbin, F., & Meylan, G. 2013, A&A, 553, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tie, S. S., & Kochanek, C. S. 2018, MNRAS, 473, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Vanderplas, J., Connolly, A., Ivezić, Ž., & Gray, A. 2012, Conf. Intell. Data Understanding, 47 [Google Scholar]
- Yu, Z., Martini, P., Davis, T. M., et al. 2020a, ApJS, 246, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, Z., Kochanek, C. S., Peterson, B. M., et al. 2020b, MNRAS, 491, 6045 [NASA ADS] [CrossRef] [Google Scholar]
- Zu, Y., Kochanek, C. S., & Peterson, B. M. 2011, ApJ, 735, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Zu, Y., Kochanek, C. S., Kozłowski, S., & Udalski, A. 2013, ApJ, 765, 106 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: The fits from JAVELIN and CREAM
The posterior distribution of the DRW’s parameters from JAVELIN are shown in Fig. A.1.
 |
Fig. A.1. Posterior distributions of DRW parameters from JAVELIN: structure function at infinity SFinf (left) and characteristic timescale τ at rest frame (right). The values on the top-right of each panel represent the 50th, 16th, and 84th percentiles of the respective probability distribution. The result shows that JAVELIN can recover the input parameters SFinf = 2 (lnSFinf = 0.69) and τ = 200 ( |
In the case of CREAM, we model the driving light curve with frequencies in the range 0.0005–0.4 cycles day−1. The number of Fourier frequencies is ∼800. The time sampling both for light curves and for the transfer functions is 0.1 days.
We set the black hole mass Mbh = 2 × 108 M⊙ and the initial mass accretion rate is Ṁ = 0.5 M⊙ yr−1, varying with a step 0.01 M⊙ yr−1. We ignore the inner edge in CREAM to match our simplified model. In practice, the position of the inner edge is outside the Schwarzschild radius, Rs = 2GMbh/c2. A full account of the size of the inner edge is beyond the scope of this work. The power law indices of the viscous and irradiation components of the temperature-radius profile are fixed to be −3/4. We also fix the inclination to be 0 degree as the results do not change qualitatively by changing this parameter.
The MCMC fit of CREAM is shown in Fig. A.2. The left column shows the inferred transfer functions with vertical lines showing the mean time delay. The right column shows the response light curves in the LSST ugrizy filters including 1σ uncertainty envelopes. CREAM outputs the posterior of accretion rate Ṁ and the mean delay of each transfer function ⟨δt⟩λ, and the samples. These are shown in Fig. A.3. We notice that in Fig. A.2 the light curve error envelopes do not sufficiently expand and contract in the seasonal gaps, indicating that the number of MCMC samples do not adequately cover the posterior parameter distribution, due to the computational limit on this high cadence and high accuracy data set. As a consequence, the accuracy of the disk size measurement is insensitive to the number of MCMC samples, but some of the error distributions of the CREAM parameters are likely to be underestimated and biased, as shown in Figs. 3 and 4.
 |
Fig. A.2. Left: transfer functions in each filter, as recovered with CREAM, along with their means in observed frame, represented as dot-dashed vertical lines. Input transfer functions are shown as black curves and the means are labelled as black dot lines, which agrees well with the CREAM’s outputs. Right: inferred light curves from CREAM, plotted as mean and rms envelope of the MCMC samples, along with simulated data, which are sampled with Δm = 0.01 mag over a period of 1000 days using a one-day cadence and adding season gaps of 120 days every 240 days. |
 |
Fig. A.3. Samples for accretion rate, Ṁ, and mean delays ⟨δt⟩λ from CREAM. |
One can convert Ṁ to the source size following the convention adopted in the CREAM code:
where δ = 0 is the ratio of lamp-post height and inner edge in Schwarzschild radius units Rs = 2GM/c2, and A = 0 is the disk albedo. We note at this stage that users of CREAM do not have access to all of the code parameters. Therefore, we use the mean output delays to infer the source size according to Eq. (3). Although we use only LSST − u as a reference to estimate the disk size, we still find that using other filters as a reference leads to consistent results. We fix the nominal error bars of the input light curves.
All Tables
All Figures
 |
Fig. 1. Top: transfer functions for LSST filters. Mean delays ⟨δt⟩λ of each transfer function Eq. (10) are represented as dot-dashed vertical lines. Bottom: light curves generated using single Gaussian as driving source (shown in black). Peak positions are represented as vertical dotted lines. The inset highlights with colored wedges the difference between the peak position and the mean delay for each band. |
| In the text | |
 |
Fig. 2. Top: simulated light curves for LSST filters before time sampling. Black curve is a DRW using τ = 200 days and SFinf = 2 as a centrally-driven source. Transfer functions shown on the top panel of Fig. 1 are applied to simulate distorted (skewed) multi-band light curves. Middle: curves are shifted back by their mean delay, ⟨δt⟩λ, showing that there are residual misalignments due to convolution by skewed kernel that may bias delay measurements toward the peak of asymmetric delay distribution rather than its mean. Bottom: example of simulated data as may be obtained with LSST g, r, and y bands. We simulate the light curves over a period of 1000 days with a one-day cadence. The error bars are all Δm = 0.01 mag rms. The color code is the same as in Fig. 1. |
| In the text | |
 |
Fig. 3. Probability distributions of measured time lags τLSST − grizy (top-row), relative to reference band LSST-u, and source size RLSST − u (bottom-left), using PyCS (blue), JAVELIN (orange), JAVELIN-Ext (green), and CREAM (purple). True delays and sizes are shown as red lines. In the table, the values represent the 50th, 16th, and 84th percentiles of the respective probability distributions. The last column (Truth) shows the input value of ⟨δt⟩LSST − grizy − ⟨δt⟩LSST − u using Eq. (10). The results from PyCS and JAVELIN are comparable and are 20% smaller than the true size. JAVELIN-Ext leads to even smaller sizes (30% smaller) but CREAM leads to unbiased measurements. |
| In the text | |
 |
Fig. 4. Probability distributions for source size RLSST − u using CREAM. Simulated light curves are the same as shown on the right panels of Fig. A.2 and we increase cadence (cdn) from one to five days (Top), and further add inter-night gaps and 10% loss of time (Bottom). CREAM measures disk size with an uncertainty below 10% even when a cadence is five days with data loss. |
| In the text | |
 |
Fig. A.1. Posterior distributions of DRW parameters from JAVELIN: structure function at infinity SFinf (left) and characteristic timescale τ at rest frame (right). The values on the top-right of each panel represent the 50th, 16th, and 84th percentiles of the respective probability distribution. The result shows that JAVELIN can recover the input parameters SFinf = 2 (lnSFinf = 0.69) and τ = 200 ( |
| In the text | |
 |
Fig. A.2. Left: transfer functions in each filter, as recovered with CREAM, along with their means in observed frame, represented as dot-dashed vertical lines. Input transfer functions are shown as black curves and the means are labelled as black dot lines, which agrees well with the CREAM’s outputs. Right: inferred light curves from CREAM, plotted as mean and rms envelope of the MCMC samples, along with simulated data, which are sampled with Δm = 0.01 mag over a period of 1000 days using a one-day cadence and adding season gaps of 120 days every 240 days. |
| In the text | |
 |
Fig. A.3. Samples for accretion rate, Ṁ, and mean delays ⟨δt⟩λ from CREAM. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} T^4(R,t)=T^4_0(R)\left[1+f(t-t_{\rm lag})\right], \end{aligned} $$](/articles/aa/full_html/2020/04/aa35423-19/aa35423-19-eq1.gif)
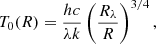
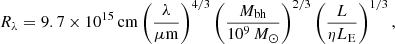
![$$ \begin{aligned} I(R,t)\propto \frac{1}{\exp (\frac{hc}{\lambda kT})-1}= \left[\exp (\xi )-1\right]^{-1}, \end{aligned} $$](/articles/aa/full_html/2020/04/aa35423-19/aa35423-19-eq4.gif)
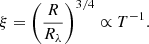
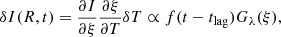
![$$ \begin{aligned} G_{\lambda }(\xi )=\frac{\xi \exp (\xi )}{\left[\exp (\xi )-1\right]^2}\cdot \end{aligned} $$](/articles/aa/full_html/2020/04/aa35423-19/aa35423-19-eq7.gif)
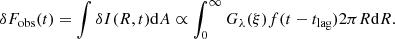
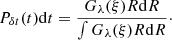
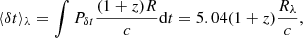
![$$ \begin{aligned} \chi ^2 = \sum _{\lambda }\frac{\left[ \Delta t_{\lambda }-\langle \delta t\rangle _{\lambda } \right]^2}{\sigma _{\lambda }^2}, \end{aligned} $$](/articles/aa/full_html/2020/04/aa35423-19/aa35423-19-eq11.gif)
![$$ \begin{aligned} \Delta t_{\lambda }-\langle \delta t\rangle _{\lambda } = \tau _{\lambda }+ 5.04(1+z)\frac{R_{\lambda _0}}{c} [1-(\lambda /\lambda _0)^{4/3}] \end{aligned} $$](/articles/aa/full_html/2020/04/aa35423-19/aa35423-19-eq12.gif)

![$$ \begin{aligned} R_{\lambda }&= 5.16\times 10^{12}\,\mathrm{cm}\nonumber \\&\times \left[3+4\delta \eta (1-A)\right]^{1/3} \left(\frac{\lambda }{\mu \mathrm{m}} \right)^{4/3} \left(\frac{M_{\rm bh}\dot{M}}{M_{\odot }^2\,\mathrm{yr}^{-1}} \right)^{1/3} \end{aligned} $$](/articles/aa/full_html/2020/04/aa35423-19/aa35423-19-eq24.gif)