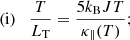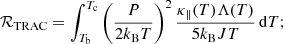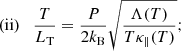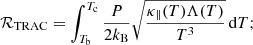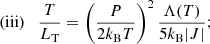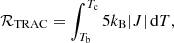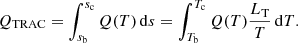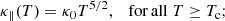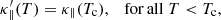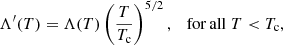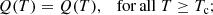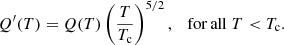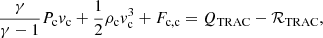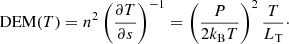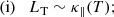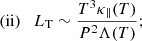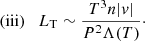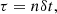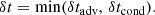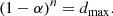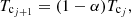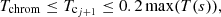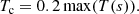| Issue |
A&A
Volume 635, March 2020
|
|
|---|---|---|
| Article Number | A168 | |
| Number of page(s) | 19 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/201936979 | |
| Published online | 30 March 2020 | |
Modelling the solar transition region using an adaptive conduction method
1
School of Mathematics and Statistics, University of St Andrews, St Andrews, Fife KY16 9SS, UK
e-mail: cdj3@st-andrews.ac.uk
2
Space and Atmospheric Physics, The Blackett Laboratory, Imperial College, London SW7 2BW, UK
3
Rosseland Centre for Solar Physics, University of Oslo, PO Box 1029, Blindern 0315 Oslo, Norway
4
Department of Physics and Astronomy, Rice University, Houston, TX 77005, USA
Received:
23
October
2019
Accepted:
25
February
2020
Modelling the solar Transition Region with the use of an Adaptive Conduction (TRAC) method permits fast and accurate numerical solutions of the field-aligned hydrodynamic equations, capturing the enthalpy exchange between the corona and transition region, when the corona undergoes impulsive heating. The TRAC method eliminates the need for highly resolved numerical grids in the transition region and the commensurate very short time steps that are required for numerical stability. When employed with coarse spatial resolutions, typically achieved in multi-dimensional magnetohydrodynamic codes, the errors at peak density are less than 5% and the computation time is three orders of magnitude faster than fully resolved field-aligned models. This paper presents further examples that demonstrate the versatility and robustness of the method over a range of heating events, including impulsive and quasi-steady footpoint heating. A detailed analytical assessment of the TRAC method is also presented, showing that the approach works through all phases of an impulsive heating event because (i) the total radiative losses and (ii) the total heating when integrated over the transition region are both preserved at all temperatures under the broadening modifications of the method. The results from the numerical simulations complement this conclusion.
Key words: hydrodynamics / magnetohydrodynamics (MHD) / Sun: transition region / Sun: chromosphere / Sun: corona / Sun: flares
© ESO 2020
1. Introduction
The computational modelling of the plasma response to either impulsive or quasi-steady coronal heating has a long history and it has become an essential tool in understanding flares of all sizes, as well as active region and quiet Sun heating (see e.g. Reale 2014, for a review). A widely used approach to investigate the energy release involves studying the response of the plasma along a flux element (or field-line or loop) to an imposed heating function. Such one-dimensional (1D) hydrodynamic models have the benefit of being relatively simple to implement and run and can readily generate observables such as emission line intensities and profiles. However, they suffer from major computational limitations brought about by the very narrow transition region (TR), between chromosphere and corona.
Bradshaw & Cargill (2013, hereafter BC13) demonstrated that inadequate TR spatial resolution leads to a potentially major underestimate of the coronal density in numerical simulations. The very steep temperature gradients in the TR are associated with thermal conduction between the corona and chromosphere. Resolving these gradients requires a highly resolved grid which, in turn, acts as a major constraint on the time step (Δt). Stability in an explicit numerical scheme that models thermal conduction requires,
where κ∥(T) = κ0T5/2 is the field-aligned Spitzer-Härm (SH) coefficient of thermal conduction (Spitzer & Härm 1953) with κ0 = 10−11, T the plasma temperature, n the number density, Δs the numerical grid cell width and the time step is limited by the minimum of the bracketed quantity across the entire grid.
For a uniform grid, this condition is always set by the coronal properties, and so is grossly inefficient. Thus, a highly non-uniform mesh that puts grid points preferentially in the TR is of considerable benefit in reducing the time a given simulation takes to run. However, an additional problem is that the TR moves in response to coronal heating and cooling, so ideally the most highly resolved region should be able to move upward or downward as required. Adaptive grid codes have been developed that can address this problem satisfactorily (Betta et al. 1997; Antiochos et al. 1999; Bradshaw & Mason 2003, BC13) so that for a single loop, a brute force approach can be implemented, given adequate computational facilities.
Some authors also avoid the conduction stability condition, defined in Eq. (1), by using either implicit methods (e.g. Hansteen 1993) or operator splitting methods (e.g. Botha et al. 2011; Gudiksen et al. 2011). Such operator splitting methods enable the advection terms to be integrated in time using an explicit numerical scheme while treating thermal conduction separately with an implicit method. However, with both approaches, spatial convergence to the correct solution in the TR may still require a very fine grid, as discussed further in Sect. 4.2 of BC13.
Therefore, for studies of multiple loops forming an active region (Bradshaw & Viall 2016; Barnes et al. 2019) and for long simulations (Froment et al. 2018; Winebarger et al. 2018), it is desirable to develop methods that mitigate the need for highly resolved numerical grids. Further, there is also a need for a 1D code that can be run quickly in order to assess the viability of physical ideas. The same considerations obviously also apply to the difficulties of modelling thermal conduction in multi-dimensional magnetohydrodynamic (MHD) models, where machine limitations dictate the number of grid points run in a simulation (e.g. Hood et al. 2016; Reale et al. 2016; Warnecke et al. 2017; Reid et al. 2018; Martínez-Sykora et al. 2018; Howson et al. 2019; Knizhnik et al. 2019)
In recent years, two approaches have been proposed. One, by Johnston et al. (2017a,b, 2019), was tested in a field-aligned hydrodynamic code, and modelled the TR as an unresolved discontinuity using a physically motivated jump condition across it. Comparison with fully resolved 1D simulations of impulsive heating and the development of thermal non-equilibrium (TNE) showed good agreement (Johnston et al. 2019).
A second approach is due, in its original form, to Linker et al. (2001) and, subsequently Lionello et al. (2009, hereafter L09) and Mikić et al. (2013). In order to decrease the mesh resolution requirements (and so increase the conduction time step), they chose to broaden the TR by setting the parallel thermal conductivity (κ∥(T)) to be constant below a fixed temperature, defined herein as Tc, with Tc = 2.5 × 105 K a typical value used. At the same time, they modified the optically thin radiative loss function (Λ(T)) below Tc such that κ∥(T)Λ(T) gave the same function of temperature as for T ≥ Tc. The method is discussed in more detail in Sect. 2.2, but for a static loop, L09 showed that this approach gave almost identical coronal conditions to those obtained using the classical SH heat flux formulation at all temperatures. In addition, a range of tests on, in particular, TNE (Mikić et al. 2013), showed that the method worked for dynamically evolving loops as well.
However, further investigation has revealed that for a more general class of problems, in particular involving strong impulsive heating, the L09 method with a fixed Tc and coarse spatial resolution has shortcomings similar to those identified by BC13 when the entire TR was under-resolved. In a recent paper (Johnston & Bradshaw 2019, hereafter JB19), we proposed an important modification to their approach, to model the Transition Region using an Adaptive Conduction (TRAC) method. In TRAC, Tc was allowed to vary throughout the simulation in a way that adapted to the resolution requirements at any time. This permitted the modelling of very dynamic phenomenon such as strong flares, and we found (i) excellent agreement between our approach and a fully resolved 1D model and (ii) extremely significant savings in computation time.
JB19 presented just a sample of results. In this paper, we examine how well the TRAC method works for a wider range of problems, why it works through all phases of an impulsive heating event, and what other physics can be included in the approach. Section 2 outlines the TRAC method, Sect. 3 describes the numerical model and an extensive analysis of our test problems is presented in Sect. 4. We conclude with a discussion of the TRAC method in Sect. 5 and a series of Appendices contain supplementary material.
2. The TRAC method
In the JB19 Letter, we introduced the ideas behind the TRAC method but space did not permit a full description. This is presented in the following subsections.
We model the plasma response to heating by considering the single fluid, field-aligned hydrodynamic equations for a coronal loop, with uniform cross-section,
Here, s is the spatial coordinate along the magnetic field, ρ is the mass density, P is the gas pressure, T is the temperature, kB is the Boltzmann constant, ϵ = P/(γ − 1)ρ is the specific internal energy density, n is the number density (n = ρ/1.2mp, mp is the proton mass), v is the velocity parallel to the magnetic field, g∥ is the field-aligned gravitational acceleration (for which we use a profile that corresponds to a semi-circular strand), ν is the dynamic viscosity, Fc = −κ∥(T)∂T/∂s is the SH heat flux with κ∥(T) defined following Eq. (1), Q is a heating function, Λ(T) is the radiative loss function in an optically thin plasma, which we approximate using the piecewise continuous function defined in Klimchuk et al. (2008), and ρν(∂v/∂s)2 is a viscous heating term which is added to the heating function Q.
Throughout this paper, we assume equilibrium ionization and use the SH conductivity. We note that this form of thermal conduction assumes that the mean free path of the electrons remains small compared to the characteristic scale lengths (see e.g. Lie-Svendsen et al. 1999). However, a radiative loss function that depends on the history of the plasma (e.g. Hansteen 1993) and alternative conductivity models also can potentially be implemented with the TRAC method.
2.1. Identification of an adaptive cutoff temperature
For impulsive heating, the evolution of a loop can be divided into three phases (e.g. Cargill 1994; Klimchuk 2006; Cargill et al. 2015). As the loop is heated, a strong enhancement of thermal conduction from corona to chromosphere arises. This leads to the TR moving downwards, and the excessive conductive flux leads to an enthalpy flux upwards into the corona, increasing the coronal density (Antiochos & Sturrock 1978; Klimchuk et al. 2008). This phase has the most severe requirements on TR numerical resolution. Following the termination of the heating, the coronal temperature declines, but the density continues to increase until a balance between downward conduction and TR radiation is reached with only small mass motions. This is the time of maximum coronal density. After this, as the corona cools further, its density decreases, leading to a downward enthalpy flux whose magnitude is determined by the TR radiation requirements (Bradshaw & Cargill 2010a,b). These three phases are demonstrated very simply in the approximate methods developed by Klimchuk et al. (2008) and Cargill et al. (2012a,b).
The essence of the TRAC method is to ensure that the TR is resolved at all times in the most effective way while ensuring that these three phases, as well as intervening times, are modelled correctly. The first part of achieving this is to identify the locations in the simulation where the temperature profile is unresolved, and the second part (described in subsequent subsections) is to modify κ∥(T), Λ(T) and Q(T) in such a way that the temperature profile becomes resolved at these locations.
We define the adaptive cutoff temperature (Tc) such that Tc is the temperature associated with the upper location on the grid of any unresolved grid cells (i.e. the temperature is under-resolved below Tc). Here we assume a symmetric loop but the method can be adapted readily to consider asymmetry between the footpoints by performing the following calculation at each footpoint. This is done using an algorithm based on the method employed by Johnston et al. (2017a,b) for locating the top of an unresolved transition region, and is restated here for completeness.
The temperature length scale is defined as,
and the local resolution in the simulation is given by,
where s is the spatial coordinate along the magnetic field and Δs is the local grid cell width. We note that these definitions can be used on either a uniform or non-uniform grid.
Using these definitions, the cutoff temperature is defined as the maximum temperature that violates the resolution criteria of Johnston et al. (2017a,b),
which corresponds to having an insufficient number of grid cells across the temperature length scale (i.e. unresolved temperature gradients). The choice of δ = 1/2 is the minimum resolution criteria. However, we note that choosing n grid points across LT (δ = 1/n) will result in higher cutoff temperatures for increasing values of n > 2.
An upper bound for the cutoff temperature is set as 20% of the peak coronal temperature in the loop at that time, but for the simulations we have performed, the results are only weakly dependent on this upper bound. A lower bound is set as the temperature value of the isothermal chromosphere, taken as Tchrom = 2 × 104 K. Therefore, we dynamically adjust Tc with the criteria that it should also satisfy,
One important aspect of the model that could not be discussed in JB19 for reasons of space is that Tc can undergo sudden jumps when the entire TRAC region becomes temporarily resolved. In that case, Tc briefly defaults to the minimum value, introducing significant changes in the radiative properties of the TRAC region for a limited number of time steps. While this does not have any effect on the coronal quantities, it is aesthetically unpleasing, and is easily removed. This is discussed in Appendix A and in this paper we use the cutoff temperature limiter that is described there.
2.2. Analytical assessment of the TRAC region modifications
We now turn to an analytical assessment of the TRAC method in order to (i) justify the broadening modifications that are used and (ii) demonstrate how the approach works through all phases of an impulsive heating event.
As noted in the introduction, Linker et al. (2001) introduced an artificial TR broadening by modifying κ∥(T) such that it was constant for temperatures below 0.25 MK. For static loops, they found that while the coronal temperature of the loop was roughly the same when compared with a full SH solution, the density was larger by up to a factor of two. This difference in the coronal density indicates that the approximation underestimates the TR radiation when compared to SH conduction.
Subsequently, L09 demonstrated that modifying κ∥(T) such that κ∥(T)Λ(T) was the same function of temperature in both the SH and modified models gave excellent agreement with the coronal temperature and density. We now show that this result has generality through all phases of the evolution of a heated loop.
It is required that the radiative losses integrated across the TRAC region be independent of the specific form of κ∥(T), Λ(T) and Q(T). These integrated losses are defined as,
where sb (sc) is the spatial coordinate at the base (top) of the TRAC region and LT is as defined in Eq. (6).
To demonstrate this in a simple way, we start by writing the energy Eq. (4) in the TRAC region in the following conservative form,
where E = P/(γ − 1)+ρv2/2. We note that Eq. (11) applies to the fluid in single species codes such as the Lagrangian remap code (Arber et al. 2001; Johnston et al. 2017a,b) and electrons in multi-species codes such as HYDRAD (Bradshaw & Mason 2003; Bradshaw & Cargill 2006, BC13).
Next, following Klimchuk et al. (2008), we assume that the TRAC region is quasi-steady, gravity is neglected and any flows are subsonic. These assumptions are made only to derive the analytical approximations that follow. They are not imposed on the TRAC region in numerical simulations, as is discussed in Sect. 2.3. Then we can solve for LT by writing Eq. (11) in the form,
where J = nv is the mass flux and here we retain the TR heating term. J is positive (negative) for an upflow (downflow). This can be solved for T/LT as,
where the positive (negative) root corresponds to the increasing (decreasing) temperature gradient found at the left-hand (right-hand) leg of the loop. Substituting this into Eq. (10) shows that only the combinations κ∥(T)Λ(T) and κ∥(T)Q(T) occur in the expression for the radiative losses integrated across the TRAC region (ℛTRAC). Hence, so long as these combinations are properly adjusted, the same integrated radiative losses, ℛTRAC, arise for both the TRAC and SH conduction models.
Adopting the approach of Klimchuk et al. (2008) and neglecting TR heating, we can further simplify Eq. (13) into three limits: (i) strong evaporation (neglect radiation); (ii) peak density (neglect dynamics); and (iii) radiative cooling (neglect thermal conduction). For these three phases we find:
and,
where J is negative (a downflow) in the third regime. Since the product κ∥(T)Λ(T) is assumed to be the same function of temperature for both models, then the integrated radiative losses at all temperatures in the TRAC region are the same for both the SH and TRAC methods.
Furthermore, a similar analysis also holds for the heating integrated across the TRAC region,
In particular, as long as the combination κ∥(T)Q(T) is properly adjusted, then QTRAC is independent of the specific form of κ∥(T) and Q(T), so that the integrated heating at all temperatures in the TRAC region is also the same for both the SH and TRAC methods.
2.3. Broadening the TRAC region
Having identified the adaptive cutoff temperature, the second part of the TRAC method is to broaden the steep temperature and density gradients in the TRAC region. This is achieved using an extension of the approach developed by Linker et al. (2001), L09 and Mikić et al. (2013) as discussed in detail in the preceding section.
Using the results presented in Sect. 2.2, below the cutoff temperature (Tc):
(i) the parallel thermal conductivity (κ∥(T)) is set to a constant value 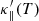 , so that,
, so that,
(ii) the radiative loss rate (Λ(T)) is modified to Λ′(T) to preserve 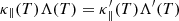 ,
,
and,
(iii) the heating rate (Q(T)) is modified to Q′(T) to preserve 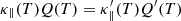 ,
,
When TRAC is employed in the numerical simulations in Sects. 3 and 4, we solve the full set of Eqs. (2)–(5) in the TRAC region (e.g. Johnston et al. 2017b) and corona, but with the use of the modified 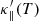 , Λ′(T) and Q′(T) in the TRAC region. Thus the assumptions, such as subsonic flows made in the analytic solutions, are not present, enabling us to assess their validity by a comparison between the analytical and numerical solutions (see Appendix B).
, Λ′(T) and Q′(T) in the TRAC region. Thus the assumptions, such as subsonic flows made in the analytic solutions, are not present, enabling us to assess their validity by a comparison between the analytical and numerical solutions (see Appendix B).
As we show further on in this paper, increasing the parallel thermal conductivity while decreasing the radiative loss and heating rates, at temperatures below Tc, has the desired effect of broadening the temperature length scales in the TRAC region. This helps TRAC prevent the heat flux jumping across any unresolved regions while maintaining accuracy in the properly resolved parts of the atmosphere. Further, we note that the formulation of TRAC: (i) makes no assumptions about the spatial resolution in a simulation; (ii) reduces to the classical SH conduction model when the TR is properly resolved (e.g. see JB19); and (iii) may still be implemented in both explicit and implicit numerical schemes that model thermal conduction.
3. Numerical model and experiments
In JB19, we demonstrated the viability of the TRAC method with two examples, namely a 600 s (long) and 60 s (short) heating pulse in a loop of total length 100 Mm, including a 10 Mm chromosphere at each end. The heating pulse was triangular, uniformly distributed along the loop, with a peak value of 2 × 10−2 Jm−3 s−1. The 600 (60) s pulse thus had 4.8 × 108(7) Jm−2, which for an aspect ratio of 10, gives a total energy release of 1023(22) J.
As in JB19, the TRAC results for these two examples are compared with the SH results that are obtained using the adaptive mesh refinement code HYDRAD (Bradshaw & Mason 2003; Bradshaw & Cargill 2006, BC13). HYDRAD has been extensively described elsewhere (e.g. BC13) so we only restate the details relevant to the results presented here.
We run the HYDRAD code in single fluid mode to solve Eqs. (2)–(5). The largest grid cell in all of our calculations has a width of 106 m (1000 km) and each successive refinement splits the cell into two. Thus, a refinement level of RL leads to cell widths decreased by 1/2RL. In this study, the adaptive mesh in HYDRAD is limited to 14 levels of refinement, defined as RL = [0, 1, 2, …, 13, 14]. A mesh with RL = 14 has a minimum grid cell size 214 = 16384 times smaller than a uniform grid with RL = 0, corresponding to a grid cell width of 61 m in the most highly resolved parts of the TR.
BC13 demonstrated that the value of RL needed for a “converged” solution depended on the problem being solved (Table 1 there), but here we work with RL = 14 as the benchmark for comparison. Hereafter we refer to the (benchmark) HYDRAD solutions computed with RL = 14 and the SH conduction method as the SH solutions. When TRAC is implemented in HYDRAD, we use RL = 5 so that the minimum grid size of 31.25 km is a factor 29 = 512 times larger than the corresponding SH solution. These simulations are identical in all respects except for the value of RL and the conduction method used. However, this leads to TRAC run times for a typical problem being of order 500−1000 times faster. We focus on the TRAC solutions that are computed with RL = 5 here because of the improvement in the accuracy of the temperature evolution that is accessible with minimal increase in computation time, when compared with the RL = 3 simulations (see Sect. 4.3).
The results of two uniform heating cases, namely the long and short heating pulses, are presented in Sects. 4.1 and 4.2, respectively. While these experiments are representative of reasonably powerful flares, it is also important to consider how the TRAC method performs for a wider range of uniform heating events and spatially non-uniform heating functions in order for future users to have confidence in the method. The latter is addressed in Sect. 4.4 through the consideration of both impulsive and steady footpoint heating. The former involves a parameter study for uniform heating, which we present in Sect. 4.3, that covers several orders of magnitude for the total energy released.
4. Results
4.1. Long pulse
We first consider the details of the 600 s heating pulse simulations. In particular, we present a comprehensive description of certain aspects of the loop evolution in order to demonstrate and explain why the TRAC simulations are so successful in describing the coronal response to heating while using such large grid cell widths. Furthermore, a detailed analysis of the global evolution of the loop, during the three key phases discussed in Sect. 2.2, is also presented in Appendix B.
4.1.1. Coronal response to heating
Starting with the coronal response, the upper two panels (row 1) of Fig. 1 show the coronal averaged temperature and density as a function of time, where the averaging is calculated over the 50% of the loop nearest the apex. The three curves are the SH solution with RL = 14 (solid red line), the TRAC solution with RL = 5 (dashed blue line) and the SH solution with RL = 5 (dashed red line). In the time-dependent plots in Fig. 1 all of the quantities are shown with 1 s temporal resolution.
 |
Fig. 1. Results for the 600 s heating pulse simulations (Sect. 4.1). Upper four panels: coronal averaged temperature and density as functions of time, and their respective normalised differences. The lines are colour coded in a way that reflects the conduction method used and different values of RL are separated by different line styles as shown in the right-hand panels. Central two panels: comparison of the energetically dominant quantities that are associated with the TRAC region, namely, the heat (Fc, c, blue line) and enthalpy (Fe, c, orange line) fluxes at the top of the TRAC region, and the radiative losses (ℛTRAC, red line) and heating (QTRAC, green line) integrated across the TRAC region. Solid (dashed) lines indicate where the enthalpy flux is upflowing (downflowing). Lower four panels: time evolution of the cutoff temperature (Tc), TRAC region thickness (ℓ), radiative losses integrated across the TRAC region (ℛTRAC) and total over half of the loop (ℛTOTAL), and the ratio between these losses (℔TRAC/℔TOTAL). We note that the temperature of the TRAC(RL = 5) and SH(RL = 14) solutions overlay in the top left-hand panel. |
As expected, the under-resolved SH solution shows major differences in the density from the resolved one (BC13). On the other hand, the TRAC and resolved SH solutions show excellent agreement and both show the familiar pattern described in Sect. 2.1 of a rapid temperature increase, followed by a slower density increase, then a cooling and draining (Bradshaw & Cargill 2006; Cargill et al. 2012a,b, 2015; Reale 2016). We note that in Fig. 1, the TRAC and resolved SH temperatures lie on top of each other.
The second pair of panels (row 2) in Fig. 1 show the normalised difference between the resolved SH and TRAC solutions (e.g. (TTRAC − TSH)/TSH). The TRAC solution shows a slightly higher density throughout the simulation, which will be discussed later, but the difference at any time is less than 5%. The rapid increase in the percentage temperature difference towards the end of the simulation reflects the slightly more rapid decrease of TTRAC as the cooling tries to return to its initial equilibrium. This is a common feature in the late radiative phase when comparing accurate numerical solutions with approximate methods (e.g. Cargill et al. 2012a).
4.1.2. Energy balance in the TRAC region
We now turn to a consideration of how the TRAC modifications to the parallel thermal conductivity, radiative loss and heating rates affect the local energy balance and subsequent dynamics inside the TRAC region. Using the approach of Johnston et al. (2017a,b), Eq. (11) can be rewritten to describe the energy balance in the TRAC region as,
where the subscripts “c” and “TRAC” indicate quantities evaluated at the top of and integrated across the TRAC region, respectively. This location is determined by the temperature value of Tc and the temperature domain is the same for SH and TRAC results, although may correspond to different spatial locations (e.g. see Figs. B.1–B.3).
The fifth and sixth panels (row 3) in Fig. 1 show the dominant terms in the integrated energy Eq. (27) for the TRAC solution (left) and SH (right). In these panels, the blue and orange curves are the downward heat flux (Fc, c = −κ∥(∂T/∂s) evaluated at Tc), and downward or upward enthalpy flux (Fe, c = γ/(γ − 1)Pcvc) respectively, with dashed (solid) lines corresponding to a downflow (upflow). The red (green) curve is the total radiative loss (heating) integrated across the TRAC region.
Both methods show the standard picture of an initial phase where the downward heat flux is balanced by an upward enthalpy flux (evaporation), a density maximum at 900 s when the heat flux is balanced by radiative losses and a decay phase when the radiation is driven by a downward enthalpy flux. These figures show that, even though there is good agreement between the coronal quantities, there are significant fluctuations in, and at the top of the TRAC region, especially during the decay phase in the SH solution. These can be attributed to the continual relocation of Tc(s) as the top of the TRAC region retreats back upwards.
4.1.3. TRAC region cutoff temperature and thickness
Next we focus on the dynamic evolution of the cutoff temperature and the effect this has on the broadening of the TRAC region. The panels in row 4 of Fig. 1 show Tc and the thickness of the TRAC region (ℓ) as a function of time, with the same colour coding as before. Tc evolves in approximately the same manner as the coronal temperature, beginning at 0.12 MK and rising to 1.45 MK at peak heating. Thus, the ability to vary Tc is an important aspect of obtaining the correct coronal properties: retaining this at a fixed value of 0.25 MK would have led to a major under-resolution of the TR (e.g. see JB19).
The impact of the TRAC approach can also be seen in the right-hand panel. Here the TRAC region thickness is increased by an order of magnitude when the TRAC method is applied. The artificial broadening is at a maximum at the time of peak heating, which is associated with the most extreme downward heat flux (see panel 5), and subsequently settles down to being roughly a factor 10 larger than the SH thickness. We note that the spikes in the SH model thickness are approximately the width of the minimum grid size in the TRAC simulation. They arise due to the motion of Tc(s).
4.1.4. Integrated radiative losses
Finally, in order to test the analytical predictions made in Sect. 2.2, we now consider the details of the integrated radiative losses from the SH and TRAC models. The lower two panels (row 5) of Fig. 1 show the integrated radiative losses in the TRAC region (lower pair of curves) and the total over half of the loop (upper pair of curves), and the ratio of these quantities in the left and right-hand panels, respectively. In Appendix B, we discuss in detail the agreement and discrepancies between the results of Sect. 2.2 and these numerical simulations. Here we note the good agreement of the integrated losses after 600 s (the end of the heating phase), and Appendix B outlines the causes of the discrepancy prior to this time; in particular, amongst other things, the violation of the subsonic assumption made in Sect. 2.2. The smaller integrated TRAC region losses up to this time lead to a slightly higher coronal density due to enhanced evaporation and accounts for the difference in the coronal densities shown in the second and fourth panels. The spikes in the SH radiation are due to the upward and downward motion at the base of the TRAC region.
4.2. Short pulse
Figure 2 shows the outcome of the 60 s heating pulse simulations in the same format as Fig. 1. For such a strongly impulsive heating event, the evolution is much more dynamic than for the long pulse, with the coronal plasma sloshing to and fro within the loop (Reale 2016). But the agreement between the T and n obtained with the SH and TRAC models remains good (the errors are less than 5% throughout the simulation), with even the oscillations seen in the coronal density showing reasonable timing agreement.
 |
Fig. 2. Results for the 60 s heating pulse simulations (Sect. 4.2). Notation is the same as that in Fig. 1. |
The plasma sloshing is also reflected in the continual change of sign in the enthalpy flux at the top of the TRAC region (Fe, c), superposed on the fluctuations described earlier. The agreement between the integrated radiative losses is good, once again with the exception of the times around peak heating, which then leads to a slightly larger TRAC density. This happens because the downflows at the base of the TR are supersonic during this period. However, even though the analytical model does not work as well during the heating phase, it has little consequence for the coronal evolution because the radiative losses are small compared to the other terms in Eq. (27) at that time.
4.3. Parameter study for uniform heating
We have also carried out a comparison between TRAC and the fully resolved SH simulations for a wider range of uniform heating events, using the suite of twelve examples first established by BC13 and further analysed in Johnston et al. (2017a). These are in addition to the two examples presented in detail above. The parameter study focusses on short (60 Mm) and long (180 Mm) loops with a range of heating functions.
Table 1 summarises the results. The columns are, from left to right: the case number and stage of evolution, the heating event parameters 2L, QH and τH, the sample time then the average temperature using SH(RL = 14) and TRAC(RL = 5,[3]), the percentage difference between these, and the corresponding density values at the same time. The survey focuses on three times: peak heating, peak density and during the decay phase. The first two are readily identifiable from the simulations, and the third is chosen to be representative of a time when the coronal part of the loop is cooling largely by radiation to space and an enthalpy flux to the TR.
In all cases, the discrepancy between the TRAC(RL = 5) and SH(RL = 14) models is small. For the temperature, there are just five occasions when the normalised difference is greater than 1%, all occurring in the decay phase. The errors are larger for the density, with the majority over 1%, but there are only two instances when the difference is greater than 5%.
The heating events in the longer loop show better agreement than the shorter loop and the largest discrepancies are for the strongest heating events. The first of these happens because shorter loops require greater spatial resolution than longer loops for a given peak temperature (BC13). The second arises because the heat flux that hits the TR and subsequent evaporation is systematically larger for stronger heating events (Johnston et al. 2017b), which in turn increases the difficulty of capturing accurately the corona and TR enthalpy exchange. It is also widely known (e.g. Cargill et al. 2012b) that modelling the coronal density with approximate methods is much more challenging than the temperature. This can be attributed to the temperature being set initially by the direct in-situ heating, while the density evolution relies on the difficult interplay in the TR between downward conduction and upward enthalpy.
We also show the equivalent results when the TRAC simulations are computed with 125 km grid cells (RL = 3) in Table 1 in square brackets. These are the simulations that correspond to the same spatial resolution as those presented in Fig. 3 of JB19. The density errors are of similar order to TRAC(RL = 5). Once again, there are only two instances when the normalised difference is greater than 5%. On the other hand, the temperature errors do show significant variation, with the TRAC(RL = 3) differences consistently larger than TRAC(RL = 5). The latter is associated with a higher cutoff temperature having more influence on the coronal temperature evolution, while the former, in contrast, is indicative of the rapid convergence of the TRAC method when modelling the enthalpy exchange.
4.4. Footpoint heating
Footpoint heating of coronal loops, either steady or impulsive, is a topic of considerable importance. Steady footpoint heating can be associated with phenomena such as coronal rain (e.g. Schrijver 2001; Antolin et al. 2010, 2015; Antolin 2020) and long-period extreme ultra-violet (EUV) pulsations (e.g. Auchère et al. 2014, 2018; Froment et al. 2015, 2017, 2018; Froment et al. 2020; Pelouze et al. 2020), while unsteady footpoint heating can arise due to, for example, precipitation of energetic particles during flares (Testa et al. 2014) and chromospheric reconnection during surface magnetic flux cancellation (Chitta et al. 2018).
In order to model the coronal response to footpoint heating accurately, the TRAC method must include the modification of the heating rate (Q(T)) as described in Sect. 2.3. This is an important extension to the technique developed by L09 for broadening the TR because when this modification is not included, there can be large discrepancies in the total energy injected into the loop (and subsequent evolution) between the TRAC and SH models.
4.4.1. Impulsive energy release
In Johnston et al. (2017b), we examined a number of impulsive footpoint heating examples in the context of the jump condition model. The most challenging were those involving heating at the base of the TR (i.e. s = sb in the initial equilibrium, referred to as the “fp2” examples in that paper). We consider two such examples here, namely a loop with 2L = 60 Mm, and a heating function comprised of a Gaussian pulse centred at the base of each TR with a half-width of 0.75 Mm, lasting for 600 and 60 s. The former (latter) has a peak heating rate of 0.21 (2.1) Jm−3 s−1 at the maximum of the Gaussian profile.
The results are summarised in Figs. 3 and 4, which are of the same format as Figs. 1 and 2. They show little difference from the previous cases of uniform coronal energy release, indicating the robustness of the method. In particular, consistent with the analytical assessment of the TRAC method presented in Sect. 2.2, both the integrated radiative losses and integrated heating show good agreement between the TRAC and SH models, but as before there is discrepancy between the radiative losses at times during the heating phase. We have also tested impulsive footpoint heating in loops of total length 180 Mm. These simulations show the same fundamental properties as the 60 Mm loop.
 |
Fig. 3. Results for the 600 s footpoint heating simulations (Sect. 4.4.1). Notation is the same as that in Fig. 1. |
 |
Fig. 4. Results for the 60 s footpoint heating simulations (Sect. 4.4.1). Notation is the same as that in Fig. 1. |
4.4.2. Steady energy release
Thermal non-equilibrium (TNE) is a phenomenon that can occur in coronal loops when the heating is quasi-steady and concentrated towards the footpoints (e.g. Müller et al. 2003; Antolin et al. 2010; Peter et al. 2012; Mikić et al. 2013; Froment et al. 2018). The response of a loop to such heating conditions is to undergo evaporation and condensation cycles with a period on the timescale of hours.
For the case of steady footpoint heating, Johnston et al. (2019) demonstrated that with the SH conduction model inadequate TR resolution can lead to significant discrepancies in TNE cycle behaviour, with TNE being suppressed in under-resolved loops. To compare this influence of numerical resolution on TNE (in coronal loops) with the TRAC method, we repeat those steady footpoint heating simulations here.
Figure 5 contrasts the TRAC model with the SH results. The upper two rows show the coronal averaged temperature (T) as a function of time, for selected values of RL, for the SH and TRAC methods, respectively. The TRAC solutions are significantly less dependent on the spatial resolution than the SH results, with cyclic TNE (Froment et al. 2018; Winebarger et al. 2018; Klimchuk & Luna 2019) arising for all values of RL, while maintaining high levels of accuracy throughout. The details of the time evolution of the temperature as a function of position are representative of those described fully in Johnston et al. (2019).
 |
Fig. 5. Results for the steady footpoint heating simulations run with the Spitzer-Härm (SH) and TRAC conduction methods (Sect. 4.4.2). Upper two panels: coronal averaged temperature as a function of time, for six values of RL, for each method. Lower two panels: TNE cycle frequency and computation time dependency on the minimum permitted spatial resolution (coarser resolution is associated with smaller RL). The lines are colour-coded in a way that reflects the conduction method used. |
The lower two rows show the dependence of TNE cycle frequency (row 3) and simulation computation time (row 4) on the minimum spatial resolution. In these plots the blue (red) lines correspond to the TRAC (SH) model. Convergence of the TNE cycle period and thermodynamic evolution (i.e. the same temperature extrema) is seen with TRAC for RL ≥ 5 (corresponding to a TR grid cell width of 31.25 km), while the SH model requires a TR grid resolution of 1.95 km or better (RL ≥ 9). This relaxation of the resolution requirements represents a substantial saving in the computation time. The improvement in run time is comparable to that described in JB19, which we note is achieved in all of the simulations presented in this paper. Even if computationally one can only achieve a TR resolution of 500 km (RL = 1), then with TRAC method, the error in the cycle period is just 10% whereas without TRAC there is no cycle detected.
5. Discussion
This paper extends the work of JB19 and demonstrates the versatility and robustness of the TRAC method over a range of impulsive and quasi-steady footpoint heating events, as well as the theoretical underpinning of its success. Furthermore, the method should prove amenable to extension in multi-dimensional MHD simulations, though a more sophisticated treatment will be required; in particular, how the magnetic field evolution modifies the prescription of the cutoff temperature along a field-line. Flux tube area expansion will also form part of such an extension.
The main consequence of not adequately resolving the transition region (TR) in numerical simulations of impulsive heating is that the resulting coronal density is artificially low (BC13). This happens because the downward heat flux is forced to“jump” across an under-resolved TR to the chromosphere, where the incoming energy is then strongly radiated. Hence, the integrated radiative losses are significantly overestimated with a lack of spatial resolution on use of the SH conduction method (see e.g. Johnston et al. 2017a).
In contrast, when using the TRAC method, the integrated radiative losses are accurately accounted for which helps ensure that the energy balance across the TRAC region is an accurate approximation of the properly resolved SH solution. This is achieved by enforcing certain conditions on the parallel thermal conductivity, radiative loss and heating rates that are not met physically (e.g. by the SH conduction method), but do enable the TR to be broadened so that the steep gradients are spatially resolved even when using coarse numerical grids.
The resulting accuracy of the coronal plasma evolution means that simulations using TRAC can be used to follow coronal observables with confidence. However, despite the method conserving both the integrated radiative losses and integrated heating across the TRAC region, caution is needed with any forward modelling below the cutoff temperature (Tc). This can be seen by examining the dependence of the differential emission measure (DEM) on temperature. Using the expressions for LT from Sect. 2.2, we can calculate the temperature distribution of the DEM for each model,
In the three limits, (i) strong evaporation, (ii) peak density and (iii) decay, we find:
and,
Therefore, the temperature dependence of the DEM now differs significantly between TRAC and SH in all regimes since the combination κ∥(T)Λ(T) no longer appears. Thus, observables cannot be calculated below Tc with confidence. However, for all temperatures above Tc, including the majority of the upper TR, the emission can be synthesised accurately.
In summary, the TRAC method allows the highly efficient numerical integration of the hydrodynamic equations through the computationally demanding TR. The outcome is an accurate and time-dependent “boundary condition” for the domain of interest, which is comprised of all the plasma in the corona and above Tc. Below the cutoff temperature, the modifications to the heat flux, heating and cooling rates broaden the steep gradients in the TR while conserving key quantities in the energy equation.
Acknowledgments
This work has received support from the European Union Horizon 2020 research and innovation programme (grant agreement No. 647214), from the UK Science and Technology Facilities Council through the consolidated grant ST/N000609/1 and the Research Council of Norway through its Centres of Excellence scheme, project number 262622. S.J.B. is grateful to the National Science Foundation for supporting this work through CAREER award AGS-1450230. C.D.J. acknowledges support from the International Space Science Institute (ISSI), Bern, Switzerland to the International Team 401 “Observed Multi-Scale Variability of Coronal Loops as a Probe of Coronal Heating”. We also acknowledge useful discussions with Dr. Z. Mikić and very constructive comments from the referee, Dr. Philip Judge.
References
- Antiochos, S. K., & Sturrock, P. A. 1978, ApJ, 220, 1137 [NASA ADS] [CrossRef] [Google Scholar]
- Antiochos, S. K., MacNeice, P. J., Spicer, D. S., & Klimchuk, J. A. 1999, ApJ, 512, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Antolin, P. 2020, Plasma Phys. Control. Fusion, 62, 014016 [Google Scholar]
- Antolin, P., Shibata, K., & Vissers, G. 2010, ApJ, 716, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Antolin, P., Vissers, G., Pereira, T. M. D., Rouppe van der Voort, L., & Scullion, E. 2015, ApJ, 806, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Arber, T. D., Longbottom, A. W., Gerrard, C. L., & Milne, A. M. 2001, J. Comput. Phys., 171, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Auchère, F., Bocchialini, K., Solomon, J., & Tison, E. 2014, A&A, 563, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Auchère, F., Froment, C., Soubrié, E., et al. 2018, ApJ, 853, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, W. T., Bradshaw, S. J., & Viall, N. M. 2019, ApJ, 880, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Betta, R., Peres, G., Reale, F., & Serio, S. 1997, A&AS, 122, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Botha, G. J. J., Arber, T. D., & Hood, A. W. 2011, A&A, 525, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bradshaw, S. J., & Cargill, P. J. 2006, A&A, 458, 987 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bradshaw, S. J., & Cargill, P. J. 2010a, ApJ, 710, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Bradshaw, S. J., & Cargill, P. J. 2010b, ApJ, 717, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Bradshaw, S. J., & Cargill, P. J. 2013, ApJ, 770, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Bradshaw, S. J., & Mason, H. E. 2003, A&A, 407, 1127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bradshaw, S. J., & Viall, N. M. 2016, ApJ, 821, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Cargill, P. J. 1994, ApJ, 422, 381 [Google Scholar]
- Cargill, P. J., Bradshaw, S. J., & Klimchuk, J. A. 2012a, ApJ, 752, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Cargill, P. J., Bradshaw, S. J., & Klimchuk, J. A. 2012b, ApJ, 758, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Cargill, P. J., Warren, H. P., & Bradshaw, S. J. 2015, Trans. R. Soc. London Ser. A, 373, 20140260 [NASA ADS] [CrossRef] [Google Scholar]
- Chitta, L. P., Peter, H., & Solanki, S. K. 2018, A&A, 615, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Froment, C., Auchère, F., Bocchialini, K., et al. 2015, ApJ, 807, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Froment, C., Auchère, F., Aulanier, G., et al. 2017, ApJ, 835, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Froment, C., Auchère, F., Mikić, Z., et al. 2018, ApJ, 855, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Froment, C., Antolin, P., Henriques, V. M. J., Kohutova, P., & Rouppe van der Voort, L. H. M. 2020, A&A, 633, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gudiksen, B. V., Carlsson, M., Hansteen, V. H., et al. 2011, A&A, 531, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hansteen, V. 1993, ApJ, 402, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Hood, A. W., Cargill, P. J., Browning, P. K., & Tam, K. V. 2016, ApJ, 817, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Howson, T. A., De Moortel, I., Reid, J., & Hood, A. W. 2019, A&A, 629, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnston, C. D., & Bradshaw, S. J. 2019, ApJ, 873, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, C. D., Hood, A. W., Cargill, P. J., & De Moortel, I. 2017a, A&A, 597, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnston, C. D., Hood, A. W., Cargill, P. J., & De Moortel, I. 2017b, A&A, 605, A8 [Google Scholar]
- Johnston, C. D., Cargill, P. J., Antolin, P., et al. 2019, A&A, 625, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klimchuk, J. A. 2006, Sol. Phys., 234, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Klimchuk, J. A., & Luna, M. 2019, ApJ, 884, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Klimchuk, J. A., Patsourakos, S., & Cargill, P. J. 2008, ApJ, 682, 1351 [Google Scholar]
- Knizhnik, K. J., Antiochos, S. K., Klimchuk, J. A., & DeVore, C. R. 2019, ApJ, 883, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Lie-Svendsen, Ø., Holzer, T. E., & Leer, E. 1999, ApJ, 525, 1056 [NASA ADS] [CrossRef] [Google Scholar]
- Linker, J. A., Lionello, R., Mikić, Z., & Amari, T. 2001, J. Geophys. Res., 106, 25165 [NASA ADS] [CrossRef] [Google Scholar]
- Lionello, R., Linker, J. A., & Mikić, Z. 2009, ApJ, 690, 902 [CrossRef] [Google Scholar]
- Martínez-Sykora, J., De Pontieu, B., De Moortel, I., Hansteen, V. H., & Carlsson, M. 2018, ApJ, 860, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Mikić, Z., Lionello, R., Mok, Y., Linker, J. A., & Winebarger, A. R. 2013, ApJ, 773, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, D. A. N., Hansteen, V. H., & Peter, H. 2003, A&A, 411, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pelouze, G., Auchère, F., Bocchialini, K., et al. 2020, A&A, 634, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peter, H., Bingert, S., & Kamio, S. 2012, A&A, 537, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reale, F. 2014, Liv. Rev. Sol. Phys., 11, 4 [Google Scholar]
- Reale, F. 2016, ApJ, 826, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Reale, F., Orlando, S., Guarrasi, M., et al. 2016, ApJ, 830, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, J., Hood, A. W., Parnell, C. E., Browning, P. K., & Cargill, P. J. 2018, A&A, 615, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schrijver, C. J. 2001, Sol. Phys., 198, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L., & Härm, R. 1953, Phys. Rev., 89, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Testa, P., De Pontieu, B., Allred, J., et al. 2014, Science, 346, 1255724 [NASA ADS] [CrossRef] [Google Scholar]
- Vesecky, J. F., Antiochos, S. K., & Underwood, J. H. 1979, ApJ, 233, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Warnecke, J., Chen, F., Bingert, S., & Peter, H. 2017, A&A, 607, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winebarger, A. R., Lionello, R., Downs, C., Mikić, Z., & Linker, J. 2018, ApJ, 865, 111 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Alternative TRAC method options
A.1. JB19 formulation of the TRAC method
As noted in Sect. 2.1, the algorithm described in JB19 to identify the adaptive cutoff temperature (Tc) can give rise to oscillations in the Tc value prescribed. However, these oscillations do not affect the ability of the TRAC method to accurately capture the coronal response to heating but they can introduce errors in the TRAC region integrated radiative losses (and other TRAC region integrated quantities too).
In particular, the algorithm for moving from time step j to j + 1 allows the cutoff temperature to drop on occasions. For example, to calculate Tj + 1 etc, we first scan through the solution at time step j to calculate Tc. Once this is obtained, we then modify the parallel thermal conductivity, radiative loss rate and heating rate at time step j as specified in Sect. 2.3, and then calculate Tj + 1 in the usual way. This gives the TRAC region diagnostics at j + 1. Therefore, the solution and diagnostics at time step j + 1 (j) are based on the cutoff temperature calculated at time step j (j − 1). Thus, it is possible that at time step j the TR has become fully (or partially) resolved as a result of the broadening below Tc(j − 1) (i.e. no (or significantly fewer) grid points violate the resolution criteria Eq. (8)) and so the cutoff temperature drops to the minimum value Tc(j) = Tchrom (or to a lower unresolved temperature in the TR) for the update to time step j + 1.
The response of the integrated radiative losses, to the drop in Tc, is to significantly increase in magnitude. This happens because Λ′(T) scales with (T/Tc)5/2 and the density stratification at time step j + 1 remains identical to that at time step j, since the lower atmosphere has not had time to respond to the changing TR conditions.
The upper six panels of Fig. A.1 show the results of the 600 s heating pulse simulations considered in Sect. 4.1, when run with the JB19 formulation of the TRAC method. The format is similar to Fig. 1.
 |
Fig. A.1. Results for the 600 s for heating pulse simulations (Sect. 4.1) when run with the JB19 formulation of the TRAC method (upper six panels) and a fixed percentage cutoff temperature (lower six panels). The panels show the coronal averaged temperature and density, as functions of time, the time evolution of the cutoff temperature (Tc), the normalised differences between the coronal quantities, and the radiative losses integrated across the TRAC region (ℛTRAC) and total over half of the loop (ℛTOTAL). The lines are colour coded in a way that reflects the conduction method used with dashed blue (solid red) representing the TRAC (SH) solution. Each set of six panels (upper and lower) can be compared with Fig. 1, which shows the results when TRAC is run with the cutoff temperature limiter. Starting from the top left, the corresponding panels in Fig. 1 are a, b, g, c, d and i, respectively. |
It is clear that oscillations in the cutoff temperature and spikes in the integrated radiative losses occur throughout the evolution. The characteristics of these oscillations and spikes are similar during periods of (i) strong evaporation (0−300 s) and (ii) peak density (600−1200 s), with the drops in the Tc triggered by the TR becoming either fully or partially resolved. We note that these oscillations are short lived (<1 s) because the TR re-steepens when the radiative losses spike. On the other hand, the oscillations seen in the decay phase (1800−2400 s) are driven by increases in the Tc when the TR becomes temporarily under-resolved as the loop cools.
The main aim of the TRAC method is to provide coronal diagnostics and the TRAC solutions converge to the coronal response of the properly resolved SH solution. However, if one is interested in improved TRAC region diagnostics, then the subsequent section provides a solution.
A.2. Cutoff temperature limiter
It is possible to remove the jumps in the cutoff temperature and thus the radiation spikes, described in the previous section, by limiting the decreases in the Tc to a small percentage per time step. This can be achieved by imposing the following limiter on the cutoff temperature.
We define the time interval over which we limit decreases in Tc as,
where δt is the current time step in the simulation, given by the minimum of the advection and conduction time steps,
Confining the compound reduction in Tc over the n time steps in τ to a maximum percentage (dmax) then takes the form,
In this paper, we have taken the time interval as τ = 1 s and the maximum percentage change in Tc over this interval is prescribed as dmax = 0.1 (i.e. 10%).
Using these definitions, when Tcj + 1 < Tcj, decreases in the cutoff temperature are then limited as follows,
where Tcj + 1 (Tcj) is the cutoff temperature at time step j + 1 (j) and 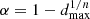 . This corresponds to limiting the decreases in Tc to 10% over any 1 s interval. However, we note that Tcj + 1 is also required to satisfy the criteria,
. This corresponds to limiting the decreases in Tc to 10% over any 1 s interval. However, we note that Tcj + 1 is also required to satisfy the criteria,
which we outlined previously in Eq. (9).
Figure 1 shows the results of the 600 s heating pulse simulations when TRAC is run with the cutoff temperature limiter described above. The figure clearly demonstrates the benefit of imposing such a limiter: the removal of the radiation spikes enables the TRAC method to provide accurate diagnostics from both the TRAC region and TR (e.g. the total radiative losses integrated across the TR). Furthermore, limiting the decreases in the cutoff temperature does not influence the accuracy of the coronal evolution and so the method also retains the ability to provide accurate coronal diagnostics.
A.3. Fixed percentage cutoff temperature
An alternative option for the TRAC method is just to set the cutoff temperature as a fixed percentage of the peak coronal temperature. For example, one can prescribe the adaptive Tc to be the upper bound value,
The lower six panels of Fig. A.1 show the results when using this approach of a fixed 20% cutoff temperature. The main compromise made for simplicity in the implementation is that the method no longer reduces to the SH formulation when the TR is fully resolved (i.e. when running with high spatial resolution). The outcome is that the error in the coronal response does not scale with the resolution (i.e. the RL value). On the other hand, (i) the error in the coronal response at the particular times of interest (peak heating, peak density and during the decay phase) remains bounded by around 5%, (ii) the temporal evolution of the cutoff temperature is smooth and so (iii) the TRAC region diagnostics show good agreement with the fully resolved SH solution.
Appendix B: Details of the long heating pulse results – global evolution
Figures B.1–B.3 show the evolution of a number of variables as a function of position along the loop, in response to the 600 s heating pulse considered in Sect. 4.1, through a series of snapshots at three different times: t = 300 s (Fig. B.1), t = 900 s (Fig. B.2) and t = 2000 s (Fig. B.3). These correspond to the time of maximum heating, maximum density, and during the loop’s draining phase. Therefore, the snapshots are representative of the three main phases for which it is valid to compare the global evolution of the loop with the analytical predictions presented in Sect. 2.2.
 |
Fig. B.1. Results for the 600 s heating pulse simulations (Sect. 4.1). Upper four panels: temperature, density, Mach number and velocity as functions of position along the loop, at the time of peak heating (t = 300 s). Lower four panels: heat flux, local radiative losses, enthalpy flux and integrated radiative losses as functions of temperature. A change in line style indicates a change in sign of the enthalpy flux. The lines are colour coded in a way that reflects the conduction method used with dashed blue (solid red) representing the TRAC (SH) solution. The dashed red (blue) vertical line indicates the base of the TRAC (SH) TR and the dot-dashed red (blue) vertical line the TRAC cutoff temperature, Tc, at the top of the TRAC region (the SH temperature at the top of the TR). |
 |
Fig. B.2. Results for the 600 s heating pulse simulations (Sect. 4.1). The panels show snapshots at the time of peak density (t = 900 s). Notation is the same as that in Fig. B.1. |
 |
Fig. B.3. Results for the 600 s heating pulse simulations (Sect. 4.1). The panels show snapshots during the loop’s decay phase (t = 2000 s). Notation is the same as that in Fig. B.1. |
In the upper four panels of these figures we focus on 20 Mm of the loop around the TR, showing the temperature, density, local Mach number and velocity respectively. An enlargement about the TRAC region is also shown inset on the temperature and density panels. In the lower four panels, we show the heat flux, local radiative loss, enthalpy flux and integrated radiative losses as a function of temperature. The integrated losses are defined as being from the top of the loop downwards to the base of the TR region and are shown on a linear scale. In these panels, the red and blue lines are the SH and TRAC solutions respectively. For SH (TRAC) solid (dashed) lines indicate positive quantities and dashed (solid) negative. Starting from the left, the first dashed red (blue) vertical line at the base of the TR shows its location for TRAC (SH), and the next dot-dashed red line the top of the TRAC region (Tc). The rightmost vertical dot-dashed blue line is the top of the actual TR, defined by where the sum of the downward conduction and enthalpy flux changes from a loss to a gain (e.g. Vesecky et al. 1979; Klimchuk et al. 2008).
First we examine the temperature and density structure in the lower TR region. The upper two panels (row 1) in Figs. B.1–B.3 show the extent of the TR broadening that is associated with the TRAC method. As noted in Sect. 4.1.3, the extent of the TRAC region diminishes as the loop evolves, and this region extends the TR both below and above the SH location, as was also shown for a static loop by L09.
The velocity and Mach number results are also of interest. At t = 300 s, while the mass flux out of the TRAC region is the same, the location of maximum velocity is displaced upwards because of the effect the TR broadening has on the density profile in this region. The Mach number indicates that the peak velocity is a significant fraction of the local sound speed and, hence at this time, the subsonic approximation is only marginally valid. This is the reason for the discrepancy between the solutions presented in Sect. 2.2 and the simulations as discussed shortly.
Again, this is indicative that while the details of the plasma as a function of temperature and density differ between the SH and TRAC models, the result is to maintain good agreement between the two in the corona. This can also be seen in the panel that shows the local radiative losses as a function of temperature. For example, the coronal properties of the two models converge despite the differences in the local radiative losses below Tc.
The heat flux plots in Figs. B.1–B.3 show that the top of the TR is at 10.1, 4.45 and 2.31 MK, corresponding to roughly 75%, 60% and 80% of the maximum loop temperature, consistent with the detailed expectations of Cargill et al. (2012a). In all cases Tc, as shown in Fig. 1g, is significantly smaller than the temperature at the top of the TR, with Tc of order 1.25 MK at peak heating, declining to 0.94 MK at peak density and 0.53 MK at 2000 s, so that Tc just follows the coronal average (but limited to 20% of the maximum temperature). The thickness of the TRAC region is thus a small fraction of the TR thickness. Furthermore, the SH and TRAC temperature and density profiles converge a short distance above the top of the TRAC region (see the upper two panels (row 1) of Figs. B.1–B.3), significantly below the top of the TR, again suggestive of the limited influence of the TRAC method on the corona.
The lower right plot of Figs. B.1–B.3 show that at t = 900 and 2000 s, the integrated radiative losses show good agreement between the TRAC and SH methods, as predicted in Sect. 2.2. However, the agreement is less satisfactory at t = 300 s. While this is of little consequence for the coronal behaviour since the radiative losses are a relatively small fraction of the total energy budget at that time, it is of interest to understand why this occurs. Analysis of the output shows that the subsonic assumption is violated, as is the steady mass flux, implying a dynamic TRAC region. The outcome is that the TRAC region integrated radiative losses in the simulation deviate from the analytical expression given in Eq. (15), during this short period. Further, the smaller integrated TRAC losses are responsible for the slightly larger coronal density at that time, as discussed above in Sect. 4.1.4.
All Tables
All Figures
 |
Fig. 1. Results for the 600 s heating pulse simulations (Sect. 4.1). Upper four panels: coronal averaged temperature and density as functions of time, and their respective normalised differences. The lines are colour coded in a way that reflects the conduction method used and different values of RL are separated by different line styles as shown in the right-hand panels. Central two panels: comparison of the energetically dominant quantities that are associated with the TRAC region, namely, the heat (Fc, c, blue line) and enthalpy (Fe, c, orange line) fluxes at the top of the TRAC region, and the radiative losses (ℛTRAC, red line) and heating (QTRAC, green line) integrated across the TRAC region. Solid (dashed) lines indicate where the enthalpy flux is upflowing (downflowing). Lower four panels: time evolution of the cutoff temperature (Tc), TRAC region thickness (ℓ), radiative losses integrated across the TRAC region (ℛTRAC) and total over half of the loop (ℛTOTAL), and the ratio between these losses (℔TRAC/℔TOTAL). We note that the temperature of the TRAC(RL = 5) and SH(RL = 14) solutions overlay in the top left-hand panel. |
| In the text | |
 |
Fig. 2. Results for the 60 s heating pulse simulations (Sect. 4.2). Notation is the same as that in Fig. 1. |
| In the text | |
 |
Fig. 3. Results for the 600 s footpoint heating simulations (Sect. 4.4.1). Notation is the same as that in Fig. 1. |
| In the text | |
 |
Fig. 4. Results for the 60 s footpoint heating simulations (Sect. 4.4.1). Notation is the same as that in Fig. 1. |
| In the text | |
 |
Fig. 5. Results for the steady footpoint heating simulations run with the Spitzer-Härm (SH) and TRAC conduction methods (Sect. 4.4.2). Upper two panels: coronal averaged temperature as a function of time, for six values of RL, for each method. Lower two panels: TNE cycle frequency and computation time dependency on the minimum permitted spatial resolution (coarser resolution is associated with smaller RL). The lines are colour-coded in a way that reflects the conduction method used. |
| In the text | |
 |
Fig. A.1. Results for the 600 s for heating pulse simulations (Sect. 4.1) when run with the JB19 formulation of the TRAC method (upper six panels) and a fixed percentage cutoff temperature (lower six panels). The panels show the coronal averaged temperature and density, as functions of time, the time evolution of the cutoff temperature (Tc), the normalised differences between the coronal quantities, and the radiative losses integrated across the TRAC region (ℛTRAC) and total over half of the loop (ℛTOTAL). The lines are colour coded in a way that reflects the conduction method used with dashed blue (solid red) representing the TRAC (SH) solution. Each set of six panels (upper and lower) can be compared with Fig. 1, which shows the results when TRAC is run with the cutoff temperature limiter. Starting from the top left, the corresponding panels in Fig. 1 are a, b, g, c, d and i, respectively. |
| In the text | |
 |
Fig. B.1. Results for the 600 s heating pulse simulations (Sect. 4.1). Upper four panels: temperature, density, Mach number and velocity as functions of position along the loop, at the time of peak heating (t = 300 s). Lower four panels: heat flux, local radiative losses, enthalpy flux and integrated radiative losses as functions of temperature. A change in line style indicates a change in sign of the enthalpy flux. The lines are colour coded in a way that reflects the conduction method used with dashed blue (solid red) representing the TRAC (SH) solution. The dashed red (blue) vertical line indicates the base of the TRAC (SH) TR and the dot-dashed red (blue) vertical line the TRAC cutoff temperature, Tc, at the top of the TRAC region (the SH temperature at the top of the TR). |
| In the text | |
 |
Fig. B.2. Results for the 600 s heating pulse simulations (Sect. 4.1). The panels show snapshots at the time of peak density (t = 900 s). Notation is the same as that in Fig. B.1. |
| In the text | |
 |
Fig. B.3. Results for the 600 s heating pulse simulations (Sect. 4.1). The panels show snapshots during the loop’s decay phase (t = 2000 s). Notation is the same as that in Fig. B.1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



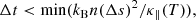
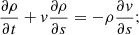
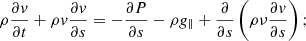
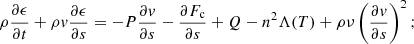
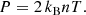
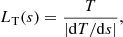
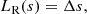
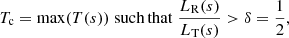
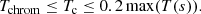
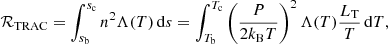
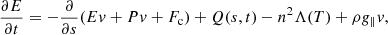
![$$ \begin{aligned} \dfrac{\kappa _\parallel (T)}{T} \left( \dfrac{T}{L_{\rm T}} \right)^{2} - 5k_{\rm B} J \left( \dfrac{T}{L_{\rm T}} \right) - \left[\left(\dfrac{P}{2k_{\rm B}T}\right)^{2} \Lambda (T) - Q \right] = 0, \end{aligned} $$](/articles/aa/full_html/2020/03/aa36979-19/aa36979-19-eq12.gif)
![$$ \begin{aligned} \dfrac{T}{L_{\rm T}} = \dfrac{5k_{\rm B} J \pm \sqrt{25k_{\rm B}^2J^2 + 4\dfrac{\kappa _\parallel (T)}{T} \left[\left(\dfrac{P}{2k_{\rm B}T}\right)^{2} \Lambda (T)-Q \right]}}{2\dfrac{\kappa _\parallel (T)}{T}}, \end{aligned} $$](/articles/aa/full_html/2020/03/aa36979-19/aa36979-19-eq13.gif)