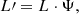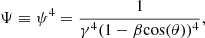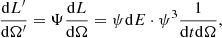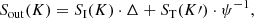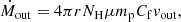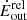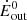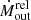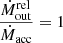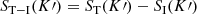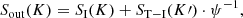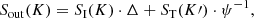EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 633 (January 2020) A&A, 633 (2020) A55 Full HTML
Free Access
Issue
A&A
Volume 633, January 2020
Article Number A55
Number of page(s) 5
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/201936797
Published online 10 January 2020

© ESO 2020

1. Introduction

Outflows are ubiquitously observed from a variety of astrophysical sources, and their impact on the surrounding environment depends on their energy. In particular, mildly relativistic and ionised outflows from the innermost regions of active galactic nuclei (AGNs) are often seen in UV and X-ray absorption spectra (e.g. Chartas et al. 2002; Tombesi et al. 2010; Rodríguez Hidalgo et al. 2011; Bruni et al. 2019) and may carry sufficient energy to regulate both the growth of the central super-massive black hole (SMBH) and the evolution of the surrounding host galaxy (Costa et al. 2014; Faucher-Giguère & Quataert 2012; Tombesi et al. 2015; Zubovas & King 2012). This critically depends on the kinetic power of these outflows, which in turn depends on their velocity and on their mass flux (Di Matteo et al. 2005; King & Pounds 2015).

The line-of-sight (LOS) velocity is typically inferred via the blueshift of the absorption features imprinted by the outflowing material onto the continuum emission of the central source, compared to the systemic redshift of the host galaxy. The mass outflow rate ̇Mout, instead, for a given covering factor and distance of the outflow, is estimated by measuring the optical depth of the absorption features. The observed optical depth is considered a proxy of the outflow column density NH along the LOS, independently of its outflow velocity vout.

In this work we show that this assumption no longer holds for outflows escaping the central continuum source of radiation with velocities corresponding to a fraction of the speed of light c (e.g. vout ≳ 0.05c). For these outflows the observed (i.e. apparent) optical depth of the spectral features produced by the absorbing material significantly underestimates the intrinsic NH and, consequently, the mass transfer rate of the outflows. Therefore, a velocity-dependent correction must be adopted in the estimate of NH to account for this effect.

This pure special-relativistic effect is universal (i.e. it applies to any fast-moving outflow intercepting the LOS), and affects not only our estimate of the kinetic power of the outflow, but also the ability of the radiative source to effectively accelerate the outflow outwards. For AGN outflows, this may have deep implications on the feedback mechanism and the co-evolution with respect to the host galaxy (Kormendy & Ho 2013).

The paper is organised as follows. In Sect. 2 we give an overview of the special relativity treatment for a fast-moving gas embedded in a radiation field. In Sect. 3 we show how to incorporate this treatment in modelling outflow spectra. In Sect. 4 we discuss the results and their implications on estimating Ṁout and Ėout, and we summarise in Sect. 5.

2. Special relativistic transformation in the outflow reference frame

According to special relativity, the luminosity L′ seen by a clump of gas moving at relativistic speed is reduced of a factor Ψ, with respect to a static gas, as

L ′ = L · Ψ , $$ \begin{aligned} L\prime =L\cdot \Psi , \end{aligned} $$(1)

where L is the luminosity seen by an observer at rest and Ψ (i.e. the de-boosting factor) is defined as

Ψ ≡ ψ 4 = 1 γ 4 ( 1 − β cos ( θ ) ) 4 , $$ \begin{aligned} \Psi \equiv \psi ^4= \frac{1}{\gamma ^4 (1-\beta \mathrm{cos}(\theta ))^4} , \end{aligned} $$(2)

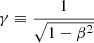where γ ≡ 1 1 − β 2 $ \gamma \equiv \frac{1}{\sqrt{1-\beta^2}} $, β = vout/c, vout is the gas velocity, and θ is the angle between the incident luminosity L and the direction of motion of the gas. Figure 1 shows Ψ as a function of vout for θ = 180°, corresponding to a radial outward motion of the gas. The deboosting factor is due to the combination of the space-time dilatation in the gas reference frame K′, and the relativistic Doppler shift of the received radiation (Rybicki & Lightman 1986).

thumbnail Fig. 1.

Deboosting factor Ψ in the gas reference frame K′ as a function of vout assuming θ = 180°. For speeds lower than 0.1c, the radiation intercepted by the outflow and by the (rest-frame) observer at infinity are virtually the same. For higher speeds, the fraction of intercepted radiation drops dramatically due to special relativistic effects.

Using Eq. (1), the radiative intensity (i.e. the luminosity per solid angle) 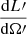d L ′ d Ω ′ $ \frac{\mathrm{d}L\prime}{\mathrm{d}\Omega\prime} $ received by the outflowing gas in K′ can be written as a function of the intensity in the rest frame K, as

d L ′ d Ω ′ = Ψ d L d Ω = ψ d E · ψ 3 1 d t d Ω , $$ \begin{aligned} \frac{\mathrm{d}L^{\prime }}{\mathrm{d}\Omega ^{\prime }}= \Psi \frac{\mathrm{d}L}{\mathrm{d}\Omega } =\psi \mathrm{d}E\cdot \psi ^3\frac{1}{\mathrm{d}t \mathrm{d}\Omega } , \end{aligned} $$(3)

where dE, dt, and dΩ corresponds to the energy, time, and solid angle intervals in K. Specifically, in Eq. (3), ψdE is the energy transformation term, which represents the Doppler shift of the wavelengths in K′. The second term, 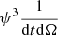ψ 3 1 d t d Ω $ \psi^3\frac{1}{\mathrm{d}t \mathrm{d}\Omega} $, indicates a reduction of the intensity due to the space-time dilatation in K′.

It should be noted that Eqs. (1) and (3) also describe the emission from gas moving at relativistic velocity, as usually observed in high-velocity systems such as jets in blazars and gamma-ray burts (Urry & Padovani 1995; Ghisellini et al. 1993). When radiation is emitted along the direction of motion (i.e. θ ≈ 0°), Ψ increases with increasing vout, while Ψ ≤ 1 when it is emitted perpendicularly or backward (θ = 90° and 180°, respectively). The overall result is to concentrate the emitted radiation into a narrow cone along the direction of motion, an effect known as relativistic beaming (Rybicki & Lightman 1986; Event Horizon Telescope Collaboration 2019).

Another way of describing the reduction of the luminosity seen by the outflowing gas is the following. In K′, the luminosity source appears to be moving away with velocity vout and θ = 180° (for a pure radial motion), which results in a de-boosting of the received luminosity due to the relativistic beaming, according to Eq. (1).

3. Modelling outflow absorption spectra including special relativistic effects

We include these special relativistic corrections in modelling spectral absorption features from the outflowing gas, according to the following procedure (see Appendix A for a detailed description):

  • The incident spectrum SI(K) is transformed from K to K′, obtaining SI(K′), according to Eq. (3);

  • SI(K′) is given as input to the radiative transfer code to calculate the transmitted spectrum in the outflowing gas frame K′, ST(K′);

  • The relativistic-corrected transmitted spectrum in K (i.e. Sout(K)) is given by

    S out ( K ) = S I ( K ) · Δ + S T ( K ′ ) · ψ − 1 , $$ \begin{aligned} S_{\rm out}(K)=S_{\rm I}(K)\cdot \Delta + S_{\rm T}(K\prime )\cdot \psi ^{-1}, \end{aligned} $$(4)

where Δ ≡ 1 − ψ3. The term ST(K′) ⋅ ψ−1 indicates the spectrum ST(K′) in Doppler-shifted frequencies (from K′ to K).

We note that in the low-velocity limit vout ≪ c, Ψ ≈ 1, Δ ≈ 0, and the resulting spectrum is Sout(K) = ST(K′) ⋅ ψ−1, as is usually calculated. For the opposite high-velocity regime vout → c, Ψ ≈ 0, and the outflowing gas does not interact with the ionising radiation. In fact, SI(K′) and ST(K′) have null intensity (see Eq. (3)), Δ ≈ 1, and Sout(K)≈SI(K).

We use the radiative transfer code XSTAR, v2.5 (Kallman & Bautista 2001) to calculate Sout(K), which is the spectrum as seen by a rest frame observer in K.

Figure 2 shows the X-ray spectrum in the range 6 − 16 keV of a power-law continuum source with Γ = 2 and an ionising luminosity Lion = 5 × 1046 erg s−1 in the 1–1000 Ry (1 Ry = 13.6 eV) energy interval, modified by an absorber with vout = 0.0, 0.3, and 0.5c. In all cases, we assume an absorbing column density of NH = 6 × 1023cm−2 and an ionisation parameter 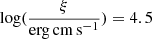log ( ξ erg cm s − 1 ) = 4.5 $ \mathrm{log}(\frac{\xi}{\mathrm{erg}\,\mathrm{cm}\,\mathrm{s}^{-1}})=4.5 $, which are typical of ultra-fast outflows (UFOs) observed in AGNs (Reeves et al. 2009; Tombesi et al. 2011; Gofford et al. 2013). The middle and right panels of Fig. 2 also report the vout = 0 case for an easier comparison. It can be seen that the absorption features related to the relativistically outflowing gas are both blueshifted and are significantly weaker than the v = 0 case. This effect dramatically increases for increasing velocity, as shown in a more quantitative way in Fig. 3, which displays the column density NH necessary to reproduce outflow absorption features with a fixed optical depth, as a function of vout. The required column density corresponds to NH = 1023 cm−2 for vout = 0, and it increases by an order of magnitude for vout = 0.8c. It is interesting to note that this effect may introduce an observational bias in current X-ray data, which are typically restricted to E <  10 keV, making outflows at higher velocity more difficult to detect due to the weakening of their spectral features at E <  10 keV.

thumbnail Fig. 2.

Absorption spectra for increasing outflow velocity: vout = 0.00 (left panel), = 0.30 (centre panel), = 0.50c (right panel). For comparison, in the centre and right panels we show the absorption spectrum for vout = 0.00c (in light grey). See Sect. 3 for details on the spectral parameters used in this simulation.

We also note that Schurch & Done (2007) and Saez & Chartas (2011) presented AGN outflow models including special relativistic effects to provide an estimate of both NH and ξ. However, the two studies seem not to account properly for the reduction of the optical depth in the calculation of Sout(K). In Eq. (4) the relativistic-corrected optical depth of the wind is preserved by transforming the transmitted spectrum back to the source rest frame K, while this aspect has not been considered in these studies.

4. Discussion

Mass and kinetic energy transfer rates of the outflow (Ṁout and Ėout, respectively), linearly depends on NH. Specifically, Ṁout can be calculated as (Crenshaw & Kraemer 2012)

M ˙ out = 4 π r N H μ m p C f v out , $$ \begin{aligned} \dot{M}_{\rm out} = 4 \pi r N_{\rm H} \mu m_{\rm p} C_{\rm f} { v}_{\rm out}, \end{aligned} $$(5)

where r, μ, mp, and Cf are the distance from the source, the mean atomic weight (≈1.4 for solar abundances), the proton mass, and the covering factor of the outflow, respectively, and Ėout is defined as 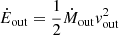E ˙ out = 1 2 M ˙ out v out 2 $ \dot{E}_{\mathrm{out}}=\frac{1}{2} \dot{M}_{\mathrm{out}} \mathit{v}_{\mathrm{out}}^2 $. Correct estimates of Ṁout and Ėout are of fundamental importance to testing theoretical models of two-phase expansion of AGN outflows towards galaxy scales, in which kiloparsec-scale galactic outflows are the result of the shock of ultra-fast, accretion disc-scale outflows onto the ISM (Faucher-Giguère & Quataert 2012; Zubovas & King 2012; Menci et al. 2019).

We find that neglecting special relativistic effects will result in an underestimate of NH and, in turn, of Ṁout and Ėout. As an example, we correct for these effects in the reported values of Ṁout, Ėout for the UFOs observed in AGNs from Gofford et al. (2015) and Fiore et al. (2017) (see Fig. 3). Specifically, for the UFOs in Gofford et al. (2015) we use the average values between the reported Ṁout, Ėout calculated using rmin and those using rmax, where rmin (rmax) is the minimum (maximum) inferred launching radius. Values of Ṁout, Ėout reported in Fiore et al. (2017) are calculated in the same way. In Fig. 4 we plot the ratio of the relativistic-corrected energy rates 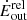E ˙ out rel $ \dot{E}_{\mathrm{out}}^{\mathrm{rel}} $ to the original values 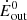E ˙ out 0 $ \dot{E}_{\mathrm{out}}^0 $ as a function of vout. The value of 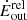E ˙ out rel $ \dot{E}_{\mathrm{out}}^{\mathrm{rel}} $ is a factor of > 2 higher than 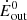E ˙ out 0 $ \dot{E}_{\mathrm{out}}^0 $ for the fastest observed outflows (vout ≥ 0.3c).

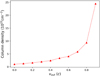thumbnail Fig. 3.

Absorbing gas NH required to reach a given value of the optical depth as a function of vout. Spectral parameters are as in Fig. 2.

As shown in Fig. 3, we expect even higher ratios for higher velocity outflows. In this respect, the improved sensitivity and resolution of the new generation of X-ray telescopes, such as XRISM and Athena, will be particularly promising and it will allow us to partially overcome the observational bias discussed in Sect. 3. Interestingly, evidence for velocities ≥0.4 − 0.5c have indeed already been reported for some high-luminosity quasars, such as PDS 456 and APM 08279+5255 (see e.g. Reeves et al. 2018; Chartas et al. 2009).

Figure 5 shows the ratio of the relativistic-corrected mass loss rate 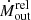M ˙ out rel $ \dot{M}_{\mathrm{out}}^{\mathrm{rel}} $ to the mass accretion rate Ṁacc, as a function of λEdd ≡ Lbol/LEdd (i.e. the ratio of the bolometric and Eddington luminosities). We derive the mass accretion rate as 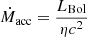M ˙ acc = L Bol η c 2 $ \dot{M}_{\mathrm{acc}}=\frac{L_{\mathrm{Bol}}}{\eta c^2} $, assuming η = 0.1 as in a standard Shakura & Sunyaev (1973) accretion disc. We note that for almost half of the sources 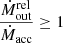M ˙ out rel M ˙ acc ≥ 1 $ \frac{\dot{M}_{\mathrm{out}}^{\mathrm{rel}}}{\dot{M}_{\mathrm{acc}}}\geq1 $, indicating that 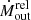M ˙ out rel $ \dot{M}_{\mathrm{out}}^{\mathrm{rel}} $ is comparable to (or higher than) the mass accretion rate of the disc. This may indicate a limit for the outflow lifetime, after which the accretion disc is depleted and it can no longer sustain the outflow (see e.g. Belloni et al. 1997). The plot also shows an apparent lack of sources with 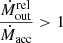M ˙ out rel M ˙ acc > 1 $ \frac{\dot{M}_{\mathrm{out}}^{\mathrm{rel}}}{\dot{M}_{\mathrm{acc}}} > 1 $ at high λEdd. However, the sample is too small to allow us to draw any conclusions. Future observations of high λEdd AGNs are needed to shed light on this aspect.

Finally, we compare the outflow momentum rate, defined as Ṗout = Ṁoutvout, with the momentum rate of the radiation of the AGN (i.e. 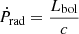P ˙ rad = L bol c $ \dot{P}_{\mathrm{rad}}= \frac{L_{\mathrm{bol}}}{c} $). We obtain a median 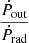P ˙ out P ˙ rad $ \frac{\dot{P}_{\mathrm{out}}}{\dot{P}_{\mathrm{rad}}} $ value of 0.64 for the original sample, and 0.96 after the relativistic correction. Interestingly, the latter value is consistent with unity, as expected for outflows accelerated through the continuum radiation pressure (the so-called Eddington winds; see e.g. King & Pounds 2015).

It is worth noting that in Eq. (2) we use the total gas velocity vout. We assume that the velocity vlos along the LOS coincides with vout. As a result, the derived relativistic correction must be regarded as a conservative limit. The correction would increase in the presence of an additional velocity component v⊥ perpendicular to the LOS, which implies 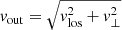v out = v los 2 + v ⊥ 2 $ \mathit{v}_{\mathrm{out}}=\sqrt{\mathit{v}_{\mathrm{los}}^2+\mathit{v}_{\perp}^2} $.

As an example, we consider the MHD model presented by Fukumura et al. (2010, 2014), where the outflowing gas is launched from the accretion disc at Keplerian velocity. Close to the launching radius, most of the velocity is in the direction of the disc rotation ϕ, and it is converted to radial velocity at higher distances (i.e. close to the Alfven point) thanks to MHD effects. For a wind launched at r0 = 10rG1, the rotational speed has a roughly constant value of vϕ = 0.3c until r ≈ 100rG, while the radial velocity (i.e. the component parallel to the LOS) has an average value of vLOS ≈ 0.2c. In Fig. 1 we show that when vout = 0, Ψ = 1 and the relativistic effects are absent. On the other hand, when vout → c, Ψ ≈ 0 and the effects are the highest. Using vLOS as a proxy for vout in Eq. (2) yields Ψ = 0.8, while using the total velocity (i.e. the composition between vr and vϕ) gives Ψ = 0.6, a factor of 0.25 lower.

It is worth noting, as Abramowicz et al. (1991) already pointed out, that the observed optical depth of the gas depends on the velocity of the outflow relative to the source of radiation (see their Eqs. (2.1) and (2.2)). Specifically, they concentrated on an outflowing wind that is optically thick with respect to Thompson scattering, and calculated the integrated luminosity of its photosphere. Moreover, Sumitomo et al. (2007) and Fukue & Sumitomo (2009) considered the impact of special relativistic effects on the emitted radiation from a fast spherical wind in stars and accreting sources, such as quasars and ULXs. These works further underline the importance of relativistic effects for radiation-matter interaction at high speeds, along with the photo-electric and resonant absorption we investigate in this work.

5. Conclusions

In this work we have shown that special relativistic effects are of fundamental importance for a correct modelling of the outflow spectral features, even for mildly relativistic velocities (vout ≳ 0.05c, see Fig. 1). We have also provided a simple procedure that can be implemented in any radiative transfer code to take into account these effects.

We observe a significant reduction of the optical depth of the outflowing gas for fixed NH and increasing vout (Figs. 2 and 3). This indicates that it is necessary to include a velocity-dependent correction when estimating NH of the outflow from the optical depth derived by spectral fitting. This correction is already significant (a factor of ≈0.5) for an outflow velocity of vout = 0.1c and reaches values of a factor of ≳10 for vout ≥ 0.8c (see Fig. 3).

The derived mass and kinetic energy transfer rates linearly depend on NH (see Eq. (5)), and hence must be corrected accordingly. For AGN outflows, this correction can significantly increase both Ṁout and Ėout and, in turn, the impact of the outflow on the surrounding environment and on the feedback mechanism. We plot in Figs. 4 and 5 the relativistic-corrected Ėout, Ṁout for a sample of ultra-fast outflows (UFOs) in AGNs reported in the literature. These pictures further underline the importance of relativistic corrections for a correct assessment of the outflow properties. Furthermore, these corrections are increasingly important in view of the next generation of high-sensitivity X-ray telescopes, which will increase the accuracy of the detection of mildly relativistic outflows, as discussed in Sect. 4.

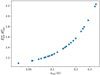thumbnail Fig. 4.

Ratio of the relativistic-corrected energy transfer rates E ˙ out rel $ \dot{E}^{\mathrm{rel}}_{\mathrm{out}} $ to the original values E ˙ out 0 $ \dot{E}^0_{\mathrm{out}} $ as a function of vout, for a sample of ultra-fast outflows observed in AGNs (see Sect. 4 for details).

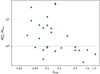thumbnail Fig. 5.

Ratio of the relativistic-corrected outflow mass rate M ˙ out rel $ \dot{M}_{\mathrm{out}}^{\mathrm{rel}} $ to the inflow mass rate Ṁacc, as a function of λEdd ≡ Lbol/LEdd. The sample is as in Fig. 4. The dotted line corresponds to M ˙ out rel M ˙ acc = 1 $ \frac{\dot{M}_{\mathrm{out}}^{\mathrm{rel}}}{\dot{M}_{\mathrm{acc}}}=1 $.

The effects discussed in Sect. 2 have further implications on the radiative driving exerted on the outflowing gas, which will be discussed in a separate work (Luminari et al., in prep.). Moreover, we also plan to present a new version of the X-ray spectral modelling code WINE (Luminari et al. 2018), which includes a relativistic-corrected radiative transfer treatment according to the procedure of Sect. 3.

1

The gravitational radius rG is defined as rG = GM/c2, where G is the gravitational constant and M is the black hole mass.

2

Moreover, in some of the most popular codes, such as XSTAR, the emissivity of all the atomic lines listed in the atomic database is saved in a separated file. Emissivities can be used to build relativistic-corrected outflow emission spectra, as we will illustrate in detail in a forthcoming paper.

Acknowledgments

We thank Stefano Ascenzi for useful discussions and Tim Kallman for having provided custom XSTAR packages. AL, EP, FT, LZ acknowledge financial support from the Italian Space Agency (ASI) under the contract ASI-INAF n.2017-14-H.0. FT acknowledges support by the Programma per Giovani Ricercatori – anno 2014 “Rita Levi Montalcini”. FF acknowledges support from INAF under the contract PRIN-INAF-2016 FORECAST, and ASI/INAF contract I/037/12/0.

References

  1. Abramowicz, M. A., Novikov, I. D., & Paczynski, B. 1991, ApJ, 369, 175 [NASA ADS] [CrossRef] [Google Scholar]
  2. Belloni, T., Méndez, M., King, A. R., et al. 1997, ApJ, 488, L109 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bruni, G., Piconcelli, E., Misawa, T., et al. 2019, A&A, 630, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Chartas, G., Brandt, W. N., Gallagher, S. C., et al. 2002, ApJ, 579, 169 [NASA ADS] [CrossRef] [Google Scholar]
  5. Chartas, G., Saez, C., Brandt, W. N., et al. 2009, ApJ, 706, 644 [Google Scholar]
  6. Costa, T., Sijacki, D., & Haehnelt, M. G. 2014, MNRAS, 444, 2355 [NASA ADS] [CrossRef] [Google Scholar]
  7. Crenshaw, D. M., & Kraemer, S. B. 2012, ApJ, 753, 75 [NASA ADS] [CrossRef] [Google Scholar]
  8. Di Matteo, T., Springel, V., & Hernquist, L. 2005, Nature, 433, 604 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  9. Event Horizon Telescope Collaboration(Akiyama, K., et al.) 2019, ApJ, 875, L1 [NASA ADS] [CrossRef] [Google Scholar]
  10. Faucher-Giguère, C.-A., & Quataert, E. 2012, MNRAS, 425, 605 [NASA ADS] [CrossRef] [Google Scholar]
  11. Feruglio, C., Fiore, F., Carniani, S., et al. 2015, A&A, 583, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Fiore, F., Feruglio, C., Shankar, F., et al. 2017, A&A, 601, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Fukue, J., & Sumitomo, N. 2009, PASJ, 61, 615 [NASA ADS] [CrossRef] [Google Scholar]
  14. Fukumura, K., Kazanas, D., Contopoulos, I., et al. 2010, ApJ, 715, 636 [NASA ADS] [CrossRef] [Google Scholar]
  15. Fukumura, K., Tombesi, F., Kazanas, D., et al. 2014, ApJ, 780, 120 [Google Scholar]
  16. Ghisellini, G., Padovani, P., Celotti, A., et al. 1993, ApJ, 407, 65 [Google Scholar]
  17. Gofford, J., Reeves, J. N., Tombesi, F., et al. 2013, MNRAS, 430, 60 [Google Scholar]
  18. Gofford, J., Reeves, J. N., McLaughlin, D. E., et al. 2015, MNRAS, 451, 4169 [Google Scholar]
  19. Kallman, T., & Bautista, M. 2001, ApJS, 133, 221 [NASA ADS] [CrossRef] [Google Scholar]
  20. King, A., & Pounds, K. 2015, ARA&A, 53, 115 [Google Scholar]
  21. Kormendy, J., & Ho, L. C. 2013, ARA&A, 51, 511 [Google Scholar]
  22. Luminari, A., Piconcelli, E., Tombesi, F., et al. 2018, A&A, 619, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Menci, N., Fiore, F., Feruglio, C., et al. 2019, ApJ, 877, 74 [NASA ADS] [CrossRef] [Google Scholar]
  24. Rodríguez Hidalgo, P., Hamann, F., & Hall, P. 2011, MNRAS, 411, 247 [NASA ADS] [CrossRef] [Google Scholar]
  25. Reeves, J. N., O’Brien, P. T., Braito, V., et al. 2009, ApJ, 701, 493 [NASA ADS] [CrossRef] [Google Scholar]
  26. Reeves, J. N., Braito, V., Nardini, E., et al. 2018, ApJ, 854, L8 [NASA ADS] [CrossRef] [Google Scholar]
  27. Rybicki, G. B., & Lightman, A. P. 1986, Radiative Processes in Astrophysics, Chapter 4 [Google Scholar]
  28. Saez, C., & Chartas, G. 2011, ApJ, 737, 91 [Google Scholar]
  29. Schurch, N. J., & Done, C. 2007, MNRAS, 381, 1413 [Google Scholar]
  30. Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 500, 33 [Google Scholar]
  31. Sumitomo, N., Nishiyama, S., Akizuki, C., et al. 2007, PASJ, 59, 1043 [NASA ADS] [CrossRef] [Google Scholar]
  32. Tombesi, F., Cappi, M., Reeves, J. N., et al. 2010, A&A, 521, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Tombesi, F., Cappi, M., Reeves, J. N., et al. 2011, ApJ, 742, 44 [Google Scholar]
  34. Tombesi, F., Meléndez, M., Veilleux, S., et al. 2015, Nature, 519, 436 [Google Scholar]
  35. Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
  36. Zubovas, K., & King, A. 2012, ApJ, 745, L34 [Google Scholar]

Appendix A: Algorithm for special relativity corrections

In this appendix we provide a detailed description of the procedure for special relativity corrections outlined in Sect. 3. Following Eq. (3), the incident spectrum in the outflowing gas reference frame SI(K′) is obtained from SI(K) by multiplying the frequencies by a factor ψ and the intensity by a factor ψ3.

For a given set of outflow parameters (NH, log(ξ0),n0, vout), we run a radiative transfer simulation by using SI(K′) as incident spectrum. As a result we obtain the transmitted spectrum ST(K′) displaying the absorption features due to the outflowing gas2.

We then calculate the difference spectrum as follows:

S T − I ( K ′ ) = S T ( K ′ ) − S I ( K ′ ) $$ \begin{aligned} S_{\rm T-I}(K\prime )=S_{\rm T}(K\prime )-S_{\rm I}(K\prime ) \end{aligned} $$(A.1)

Accordingly, ST − I(K′) represents the absorption features produced by the outflowing gas, with the relativistic-corrected optical depth. As the next step we calculate the relativistic-corrected, rest-frame absorbed spectrum as

S out ( K ) = S I ( K ) + S T − I ( K ′ ) · ψ − 1 , $$ \begin{aligned} S_{\rm out}(K)=S_{\rm I}(K)+S_{\rm T-I}(K\prime )\cdot \psi ^{-1} , \end{aligned} $$(A.2)

where ST − I(K′) ⋅ ψ−1 represents the difference spectrum in rest frame (K) frequencies, which is obtained by dividing the frequencies by a factor ψ. Using Eq. (A.1), we can thus rewrite Eq. (A.2) as

S out ( K ) = S I ( K ) · Δ + S T ( K ′ ) · ψ − 1 , $$ \begin{aligned} S_{\rm out}(K)= S_{\rm I}(K)\cdot \Delta +S_{\rm T}(K\prime ) \cdot \psi ^{-1} , \end{aligned} $$(A.3)

where Δ ≡ 1 − ψ3 and SI(K)⋅Δ indicates a scaling of the intensity of the spectrum SI(K) of a factor Δ.

In our calculations we assume that the outflow has a net velocity vout and direction θ. From a physical point of view, vout and θ correspond to the average velocity and direction of the outflow, respectively. Therefore, if a turbulent velocity component is present, the above discussion is still valid, provided that vturb ≪ vout. Furthermore, if the outflowing velocity is a function of the spatial coordinates (i.e. 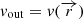v out = v ( r → ) $ \mathit{v}_{\mathrm{out}}=\mathit{v}(\overrightarrow{r}) $) the above procedure can be implemented by dividing the outflow into small slabs, and assuming vout to be constant in each of them. Finally, the treatment of more complicated scenarios for 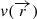v ( r → ) $ \mathit{v}(\overrightarrow{r}) $ requiring a first-principle approach are beyond the scope of the present paper.

All Figures

thumbnail Fig. 1.

Deboosting factor Ψ in the gas reference frame K′ as a function of vout assuming θ = 180°. For speeds lower than 0.1c, the radiation intercepted by the outflow and by the (rest-frame) observer at infinity are virtually the same. For higher speeds, the fraction of intercepted radiation drops dramatically due to special relativistic effects.
In the text
thumbnail Fig. 2.

Absorption spectra for increasing outflow velocity: vout = 0.00 (left panel), = 0.30 (centre panel), = 0.50c (right panel). For comparison, in the centre and right panels we show the absorption spectrum for vout = 0.00c (in light grey). See Sect. 3 for details on the spectral parameters used in this simulation.
In the text
thumbnail Fig. 3.

Absorbing gas NH required to reach a given value of the optical depth as a function of vout. Spectral parameters are as in Fig. 2.
In the text
thumbnail Fig. 4.

Ratio of the relativistic-corrected energy transfer rates E ˙ out rel $ \dot{E}^{\mathrm{rel}}_{\mathrm{out}} $ to the original values E ˙ out 0 $ \dot{E}^0_{\mathrm{out}} $ as a function of vout, for a sample of ultra-fast outflows observed in AGNs (see Sect. 4 for details).
In the text
thumbnail Fig. 5.

Ratio of the relativistic-corrected outflow mass rate M ˙ out rel $ \dot{M}_{\mathrm{out}}^{\mathrm{rel}} $ to the inflow mass rate Ṁacc, as a function of λEdd ≡ Lbol/LEdd. The sample is as in Fig. 4. The dotted line corresponds to M ˙ out rel M ˙ acc = 1 $ \frac{\dot{M}_{\mathrm{out}}^{\mathrm{rel}}}{\dot{M}_{\mathrm{acc}}}=1 $.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.