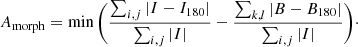| Issue |
A&A
Volume 633, January 2020
|
|
|---|---|---|
| Article Number | A131 | |
| Number of page(s) | 11 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201935527 | |
| Published online | 22 January 2020 | |
Kinematics of disk galaxies in (proto-)clusters at z = 1.5⋆
1
Institute for Astronomy (IfA), University of Vienna, Türkenschanzstrasse 17, 1180 Vienna, Austria
e-mail: asmus.boehm@univie.ac.at
2
Astronomical Institute, Tohoku University, Aramaki, Aoba-ku, Sendai 980-8578, Japan
3
National Astronomical Observatory of Japan, Osawa, Mitaka, Tokyo 181-8588, Japan
4
Subaru Telescope, National Astronomical Observatory of Japan, 650 North A’ohoku Place, Hilo, HI 96720, USA
5
Department of Astronomical Science, SOKENDAI (The Graduate University for Advanced Studies), Mitaka, Tokyo 181-8588, Japan
Received:
24
March
2019
Accepted:
4
December
2019
Aims. While many aspects of the impact of dense environments on late-type galaxies at redshifts below unity have been scrutinized in the past few decades, observational studies of the interplay between environment and disk galaxy evolution at z > 1 are still scarce. We observed star-forming galaxies at z ≈ 1.5 selected from the HyperSuprimeCam Subaru Strategic Program. The galaxies are part of two significant overdensities of [O II] emitters identified via narrowband imaging and photometric redshifts from grizy photometry.
Methods. We used the K-band Multi-Object Spectrograph (KMOS) to carry out Hα integral field spectroscopy of 46 galaxies in total. Ionized gas maps, star formation rates, and velocity fields were derived from the Hα emission line. We quantified morphological and kinematical asymmetries in order to look for potential gravitational (e.g., galaxy-galaxy) or hydrodynamical (e.g., ram-pressure) interactions.
Results. Hα emission was detected in 36 of our targets. Of these galaxies, 34 are members of two (proto-)clusters at z = 1.47, confirming our selection strategy to be highly efficient. By fitting model velocity fields to the observed ones, we determined the intrinsic maximum rotation velocity Vmax of 14 galaxies. Utilizing the luminosity–velocity (Tully–Fisher) relation, we find that these galaxies are more luminous than their local counterparts of similar mass by up to ∼4 mag in the rest-frame B-band. In contrast to field galaxies at z < 1, the offsets of the z ≈ 1.5 (proto-)cluster galaxies from the local Tully–Fisher relation are not correlated with their star formation rates but with the ratio between Vmax and gas velocity dispersion σg. This probably reflects that fewer disks have settled to purely rotational kinematics and high Vmax/σg ratios, as is observed in the field at similar redshifts. Tests with degraded low-redshift cluster galaxy data show that we cannot identify purely hydrodynamical interactions with the imaging currently at hand. Due to relatively low galaxy velocity dispersions (σv < 400 km s−1) of the (proto-)clusters, gravitational interactions are likely more efficient, resulting in higher kinematical asymmetries than in present-days clusters.
Key words: galaxies: spiral / galaxies: evolution / galaxies: kinematics and dynamics / galaxies: high-redshift
© ESO 2020
1. Introduction
The evolution of galaxies is affected by their environment in various ways. Observations show that the galaxy population in clusters has changed substantially during the past 5−6 Gyr, with the fraction of spirals decreasing and the fraction of lenticulars (but also dwarf ellipticals) increasing towards z ≈ 0 (e.g., Desai et al. 2007). Galaxies in dense regions have redder colors on average (e.g., Blanton et al. 2005) and are less frequently star-forming (e.g., Verdugo et al. 2008) than in the field. In the cluster environment, galaxies are subject to a plethora of interaction processes, such as harassment (e.g., Moore et al. 1996), ram-pressure stripping (RPS, e.g., Kronberger et al. 2008), and strangulation (e.g., Balogh et al. 2000). The latter two refer to the impact of the hot intra-cluster medium (ICM) on the interstellar medium of a galaxy moving within a cluster. Strangulation occurs when only the gaseous halo of a galaxy is removed, followed by a phase of gas consumption via star formation on a time-scale of gigayears. First discussed by Gunn & Gott (1972), RPS affects not only the hot gas halo but also the cold gas disk. Quilis et al. (2000) used hydrodynamical simulations to show that ram-pressure plays an important role in the transformation of field spirals into cluster S0 galaxies. More recently, Steinhauser et al. (2016) for example demonstrated that in extreme cases, RPS can quench star formation within ∼0.5 Gyr.
As part of the Space Telescope A901/902 Galaxy Evolution Survey (STAGES; Gray et al. 2009) of the multiple cluster system A901/902 at z = 0.17, we were able to show in Bösch et al. (2013a) that so-called red spirals are probably produced by the impact of RPS. Red spirals, which show weaker spiral arms and a four-times-lower specific star formation rate than normal, blue spirals, might be an intermediate stage in the transformation of blue field spirals into cluster S0s. Red spirals are the dominant population in clusters at intermediate cluster-centric radii and galaxy masses, while they are almost absent in the field at z ≈ 0.2 (e.g., Wolf et al. 2009). In Bösch et al. (2013b), we used the Tully–Fisher relation (TFR; Tully & Fisher 1977) – the scaling relation linking the maximum rotation velocity Vmax of disk galaxies to their luminosity – to confirm that red spirals are in the process of quenching and that the TFR scatter is increasing towards the inner cluster regions. Other studies investigated the mass–size relation, for example, finding smaller sizes of star-forming galaxies in clusters at z ≈ 0.5 than in the field (Kuchner et al. 2017).
In the past few decades, a large number of studies have utilized the TFR. Using field spirals at 0.1 < z < 1.0, Böhm & Ziegler (2016) found that, at a given Vmax, disk galaxies were brighter ∼8 Gyr ago by 1.2 mag in rest-frame B and smaller by a factor of ∼1.5 than spirals in the present-day universe. Based on the stellar-mass TFR, Miller et al. (2012) found only a very small evolution of its zero point, corresponding to stellar masses that are smaller by 0.06 dex at z ≈ 1.7 and fixed Vmax. While these two former studies relied on slit spectroscopy, the usage of integral field units (IFUs) like the K-band Multi-Object Spectrograph (KMOS) of the Very Large Telescope (VLT) has become more common for kinematic studies of distant galaxies. Übler et al. (2017), for example, found no evolution in the stellar-mass TFR up to z ≈ 2.3 using KMOS.
For several years, the results from studies investigating whether or not the TFR differs between the field and the cluster environment were somewhat heterogeneous. Ziegler et al. (2003) and Nakamura et al. (2006), for example, did not find differences between the two regimes, while Milvang-Jensen et al. (2003) and Bamford et al. (2005) found that late-type galaxies in dense environments are more luminous than in the field. Other studies, like Moran et al. (2007), deduced that the TFR scatter in clusters is higher than in low-density environments. It became clearer later that one key factor in such kinematical studies is to compare only galaxies with similar properties. Since various cluster-specific interactions can affect the kinematics of cluster disk galaxies, the fraction of disturbed rotation curves or velocity fields is found to be higher in clusters than in the field (e.g., Vogt et al. 2004). This can introduce an environmental dependence of the TFR unless the same criteria are applied to all kinematic data by using only symmetric rotation velocity fields in the TFR analysis (e.g., Bösch et al. 2013b).
Galaxy clusters at high redshifts z > 1 show important differences from those at lower redshifts. While galaxies in the central regions of low-redshift clusters are mostly passive, clusters at high-z frequently show strongly star-forming galaxies in their central regions. For example, Hayashi et al. (2010) found a high number density of [O II] emitters in the core of XMMXCS J2215.9−1738 at z = 1.46. Some clusters at these early cosmic epochs already show a well-established ICM in hydrostatic equilibrium (e.g., IDCS1426+358 at z = 1.75, Brodwin et al. 2016). Studies of TFR in z > 1 clusters remain scarce. Based on a small sample of disk galaxies in a z = 1.4 cluster, we found a moderate luminosity evolution of high-mass cluster galaxies, while low-mass cluster galaxies were much brighter than their field counterparts at similar redshifts (Pérez-Martínez et al. 2017).
Multiple observations have shown that even in the absence of cluster-specific interaction processes, disk galaxies become more kinematically hot towards higher redshifts in the sense that the ratio between their gas maximum rotation velocity Vmax and velocity dispersion σv decreases. The settling of disks, that is, Vmax/σv ratios above a certain threshold, occurs at earlier cosmic epochs for disks of higher mass (e.g., Kassin et al. 2012). As Simons et al. (2016) have found at redshifts z ≈ 2, this behavior is also reflected in the stellar-mass TFR, where galaxies with low Vmax/σv ratios tend to show overly slow rotation for their stellar mass.
In this paper, we aim to shed light on the impact of dense environments on the kinematic evolution of disk galaxies 9 Gyr ago. The paper is organized as follows: In Sect. 2 we outline the target selection and observations, Sect. 3 briefly describes the data reduction, in Sect. 4 we detail all steps of the analysis, Sect. 5 comprises a discussion, and Sect. 6 summarizes our main results.
In the following, we assume a flat concordance cosmology with ΩΛ = 0.7, Ωm = 0.3 and H0 = 70 km s−1 Mpc−1. All magnitudes are given in the Vega system.
2. Target selection and observations
Our target selection relied on the HyperSuprime-Cam Subaru Strategic Program (HSC-SSP, see Aihara et al. 2018a). The HSC (Miyazaki et al. 2018; Komiyama et al. 2018; Kawanomoto et al. 2018; Furusawa et al. 2018) is an optical imaging camera operated at the prime focus of Subaru that, with a diameter of 1.5°, features the largest field-of-view of all 10 m-class telescopes. The HSC offers five broad-band filters, g, r, i, z, and y, and several narrowband filters of which the filter NB921 probes the 3727 Å [O II] emission line doublet of galaxies at a redshift z ≈ 1.5 (Hayashi et al. 2018). The HSC-SSP spans a total of 300 nights at Subaru over 5−6 years. The first data release took place 1.7 years into the survey and is described in Aihara et al. (2018b).
The two target (proto-)clusters for our spectroscopic follow-up, which we refer to as HSC-CL2329 and HSC-CL2330 in the following, were identified as strong overdensities (with a significance of 5.7σ and 7.2σ, resp.) of [O II] emitters at z = 1.47 using the narrowband filter NB921. Clusters or (proto-)clusters at these redshifts often show star-forming galaxies in their central regions, while they are preferentially located between intermediate cluster-centric radii and the outskirts of local clusters (Dressler 1980). Since HSC-SSP also comprises photometric redshifts (derived using various methods, including SED fitting, machine learning, etc.; see Tanaka et al. 2018), we were able to rule out contamination by other emission lines, such as for example Hα or [O III], from galaxies at different redshifts. This was later confirmed by the spectroscopic redshift distribution of our sample (see Sect. 4). Since the width of the NB921 filter corresponds to a redshift range of z = 1.471 ± 0.018, or a velocity width of ±2200 km s−1, we were expecting that (i) the majority of the [O II] emitters are physically associated (proto-)cluster members and that (ii) the (proto-)cluster sample will be nearly complete within the covered field of view, given that the typical velocity dispersion of rich clusters is 1000 km s−1.
The KMOS is a second-generation VLT instrument capable of observing 24 science targets simultaneously in the near-infrared. Each of the individual IFUs offers a field of view of 2.8 × 2.8 arcsec2 (with spaxels sizes of 0.2 arcsec), corresponding to 23.7 kpc on a side at z = 1.47, and can be placed within a patrol field of 7.2 arcmin in diameter. In the H-band, which we chose for our observations, the typical spectral resolution of KMOS is R ≈ 4000.
We selected our target galaxies to have Hα fluxes fHα > 6 × 10−17 erg s−1 cm−2. Predicted Hα fluxes were converted from the observed [O II] fluxes following Kennicutt (1998), assuming the Hα fluxes to be on average a factor of two larger than the [O II] fluxes. The KMOS H-band observations were carried out between June and September 2017 with a stare and nod-to-sky strategy. Each observation block consisted of an ABA ABA sequence, where “A” denotes that the IFUs were placed on the science targets, and “B” indicates that the IFUs were observing blank sky. The integration time of each exposure was 420 s, the total integration time per (proto-)cluster was ∼2.8 h, and the total observing time per (proto-)cluster, including overheads, was four hours. Seeing conditions measured in the optical with the Differential Image Motion Monitor (DIMM) ranged between 0.7″ and 1.0″ for (proto-)cluster HSC-CL2330, which was executed first, and between 0.5 and 1.2 arcsec for (proto-)cluster HSC-CL2329. We note that the seeing full width at half maximum (FWHM) in the H-band used for the KMOS spectroscopy is considerably smaller, with a median around 0.3 arcsec.
3. Data reduction
The data reduction was carried out with the official ESO-KMOS pipeline version 1.4.3. We conducted a range of tests to see whether or not the default settings of the pipeline could be improved. In these tests, we aimed to optimize the S/N in the continuum close to the Hα line and in the Hα line itself, and to minimize night-sky OH residuals in the vicinity of the Hα line. We decided to deviate from the default reduction settings in two respects. Firstly, we detected significant offsets between the IFU object positions from the individual observation blocks (OBs) of (proto-)cluster HSC-CL2329: typically only 1−2 pixels but in three cases as large as four pixels (0.8 arcsec). Although these offsets do not compromise the spatial coverage of our targets, they are much larger than expected based on the IFU-positioning accuracy. They are probably related to a re-calibration of the IFU positioning system during the observation epoch of HSC-CL2329 (M. Hilker, priv. comm.). We accounted for these offsets during the co-addition of the individual exposures. Secondly, the best data quality in the co-addition of individual exposures is achieved using sigma clipping. The default setting of the pipeline is to first combine exposures from within a single OB before then combining these OBs into final data cubes. However, the sigma clipping is much more effective when the number of frames used for the final co-addition is maximized, so we modified the default approach and ran the sigma clipping and cube combination on all exposures from all OBs in one go.
After some further tests, we disregarded the two OBs with the worst seeing of around one arcsec FWHM in the final data cube combination in both (proto-)clusters; that is, one OB was rejected for each (proto-)cluster. Due to this, the average DIMM seeing was 0.7 arcsec FWHM for HSC-CL2330 and 0.5 arcsec FWHM for HSC-CL2329, and the total time on target 5040 s for all galaxies.
4. Analysis
We detected Hα in 36 out of 46 targets. Only two galaxies are foreground objects probably not physically associated with the (proto-)clusters. Our combined narrowband/photo-z selection strategy was thus confirmed as highly efficient. The redshift distributions and sky positions of our sample are shown in Fig. 1. Given that the projected separation of the two (proto-)clusters is approximately 19 Mpc, their z-distributions are remarkably similar with peaks at z ≈ 1.46 and z ≈ 1.475. This probably suggests that both (proto-)clusters are part of a large-scale structure. The gap in the redshift distribution of both (proto-)clusters (corresponding to ∼16 200 Å) is very unlikely to be due to problems with strong night-sky residuals. Three strong OH lines are located in the vicinity of z ≈ 1.47 Hα emission: at 16 129 Å, 16 195 Å, and 16 235 Å, with the first and last one being much stronger than the middle one. Among the galaxies with determined redshifts, we have six cases each where the Hα line profile was affected by residuals of the line at 16 129 Å or 16 235 Å, but no spectra where Hα is affected by the OH line at 16 195 Å. The gap in the z-distribution of both (proto-)clusters is therefore most probably physical.
 |
Fig. 1. Top: spatial distribution of our target candidates (small dots), galaxies without Hα detections (open circles), and Hα-detected galaxies (filled circles) for the two observed (proto-)clusters. The large dotted circle in both plots denotes the available KMOS patrol field with a diameter of 7.2 arcmin or ∼3.7 Mpc at the redshifts of the (proto-)clusters. Bottom: redshift distribution of all 36 Hα detections for both (proto-)clusters combined (large plot) and for the two (proto-)clusters individually (inset graphs). Only two field galaxies are found (shown as gray filled circles in the upper panel), demonstrating the efficiency of the target selection. Both (proto-)clusters reside at a redshift z = 1.47, which we aimed for by selecting overdensities of [O II] emitters at z ≈ 1.5 with combined broad- and narrowband data. Interestingly, the two (proto-)clusters show similar substructure in redshift space. |
Twelve of the Hα detections are weak and extend over only a few spaxels in the data cubes. These data only allow to determine the redshift. In the remaining 24 detections, the Hα emission was more spatially extended, meaning that we could use them to extract velocity fields (VFs).
Hα luminosities were transformed into star formation rates (SFRs) following Kennicutt (1998). Since the only prominent emission feature in the data is the Hα line (+ [N II]), the extinction coefficient could not be determined from a traditional source like the Balmer decrement. Instead, we used chemical enrichment models from Ferreras et al. (2014) to determine the mass- and disk-inclination-dependent E(B − V) extinction. This was then converted into the A(Hα) extinction coefficient following Ly et al. (2012). In Fig. 2, the SFRs computed from Hα are compared to the [O II]-based ones derived from the NB photometry following Gilbank et al. (2010). We find good agreement between the two (with a scatter of ∼0.31 dex), even for cases where the Hα line is affected by night sky residuals.
 |
Fig. 2. Comparison between the star formation rates from [O II] fluxes estimated with HSC SSP NB imaging and the new, Hα-based SFRs from the KMOS data. Open symbols depict objects for which the Hα line was affected by night sky residuals, which could lead to underestimation of the SFRs; however, there is no clear indication for this. |
For the determination of the intrinsic maximum rotation velocity Vmax, synthetic VFs were created based on gas disk inclination, kinematic center, kinematic position angle, turnover radius, and maximum rotation velocity for a given galaxy. Intrinsically, the rotation velocity is assumed to rise linearly with radius and turn over into a regime of constant rotation velocity Vmax at a turnover radius rt that is linked to the stellar disk scale length rd via rt = 2.2 rd. This turnover radius, strictly speaking, follows from the surface mass density profile of a pure exponential disk (Binney & Tremaine 1987) and is often used in the literature to fit observed rotation curves of spiral galaxies (e.g., Courteau 1997). The synthetic VFs take into account blurring due to seeing during spectroscopy. The optical DIMM seeing monitor values were transformed into the corresponding H-band values following prescriptions provided by ESO. For our data, the H-band seeing ranged from 0.25 to 0.3 arcsec. The VF models also account for beam smearing stemming from the finite pixel size of 0.2 arcsec.
Velocity fields covering 30−40 spaxels allow us to use all parameters listed above as free fitting parameters. However, for the VFs with the smallest number of information elements, Vmax is the only free parameter, while all other parameters were determined from the i-band imaging with the GALFIT package (Peng et al. 2002). As a cross-check, we used the output of Source Extractor (Bertin & Arnouts 1996). Position angles and axial ratios b/a were in good agreement between GALFIT and SExtractor for most objects, but in a few cases, very low ratios b/a < 0.1 were yielded by GALFIT, coinciding with significant fit residuals. This was solved by using a synthetic Gaussian profile as input point spread function (PSF) instead of a PSF constructed from averaged stellar images, which was used for all other objects. For the measurement of these structural parameters, we used the best-seeing HSC-SSP images, which are i-band frames with a total integration time of 30 min and a FWHM of 0.7 arcsec.
Our Vmax derivation algorithm does not perform a Levenberg-Marquard minimization, nor does it use the Monte Carlo Markov chain approach; instead, it probes the entire parameter space. This is computationally expensive but avoids running into any local χ2 minima. Fourteen velocity fields yielded a robust value for Vmax, while the remaining 10 VFs could not be properly fitted due to insufficient extent, strong perturbations, or a total lack of a velocity gradient. All 14 galaxies stem from the (proto-)clusters; neither of the two foreground field galaxies yielded a Vmax. Four examples of observed and model VFs, along with i-band images and Hα maps, are shown in Fig. 3.
 |
Fig. 3. Four examples of z ≈ 1.47 (proto-)cluster galaxies for which the maximum rotation velocity Vmax could be determined. In each row, the plots show from left to right: best-seeing i-band image from the Subaru HSC survey, ionized gas map as observed in Hα with VLT/KMOS, observed rotation velocity field, best-fit model rotation velocity field used for the determination of the intrinsic Vmax, and fit residuals after subtracting the best-fit model from the observed velocity field. We note that the galaxy to the southeast of HSC-232978 (top panel, leftmost figure) is a foreground galaxy with a photometric redshift in the range 0.7 < zphot < 0.8, depending on the method, and undetected in the KMOS data. |
Rest-frame absolute B-band magnitudes were computed from the apparent magnitudes in the y-filter which, among the available HSC-SSP filters, best probes the rest-frame B-band at the redshifts of the KMOS targets. The k-corrections for the transformation y → B were derived via synthetic photometry. Intrinsic absorption was taken into account using the inclination- and Vmax-dependent prescription from Tully et al. (1998). We also use this work as a local comparison sample to ensure consistency.
We note that by adopting the Tully et al. (1998) approach up to z = 1.5, we assume that there is no redshift dependence of the dust mass fraction at a given mass or of the dust properties such as typical grain sizes. Based on the data at hand, we cannot infer the amount of intrinsic dust absorption by means of SED fitting (e.g., Wolf et al. 2009) or Balmer decrement (e.g., Kennicutt et al. 2009). High-redshift galaxies have higher SFRs, and in turn a higher production of dust (e.g., Calzetti 2001). It would therefore be possible that by using the Tully et al. (1998) method at z ≈ 1.5, we underestimate the B-band luminosities of our KMOS targets and in turn the evolution in luminosity compared to z ≈ 0. On the other hand, Scoville et al. (2015) for example find that the attenuation curve of 2 < z < 4 galaxies is similar to that of local starburst galaxies from Calzetti et al. (2000). Furthermore, Whitaker et al. (2017) find that the fraction of obscured star formation at a given stellar mass shows little evolution over the redshift range 0 < z < 2.5.
The B-band Tully–Fisher diagram comprising the z = 1.47 (proto-)cluster galaxies, 1 < z < 1.5 field spirals (taken from Epinat et al. 2009; Miller et al. 2011), and the local TFR is shown in Fig. 4. The distant (proto-)cluster galaxies as well as almost all distant field galaxies fall on the high-luminosity side of the local TFR. Computing the offsets ΔMB (for a given Vmax) from the local relation, we find median values of ⟨ΔMB⟩ = − 1.87 mag for the (proto-)cluster galaxies and ⟨ΔMB⟩ = − 1.37 mag for the field sample. Given the lower average redshift of the field galaxies (⟨z⟩ = 1.10) compared to the (proto-)cluster sample (⟨z⟩ = 1.47), the difference in the TF offsets could be due to the difference in look-back time and the corresponding difference in luminosity evolution. Adopting the redshift-dependent luminosity evolution reported for redshifts 0.1 < z < 1.0 in Böhm & Ziegler (2016) and projecting it to higher redshifts, we find that the expected TF offsets of the field galaxies at ⟨z⟩ = 1.10 would be ΔMB = −1.38 mag. This is a stronger evolution than predicted from combined N-body simulations and semi-analytic models of Dutton et al. (2011; ⟨ΔMB⟩ = − 0.90 mag), but is in excellent agreement with the observed value ⟨ΔMB⟩ = − 1.37 mag we find for the combined samples of Miller et al. and Epinat et al. For z = 1.5, the expected luminosity evolution would be ΔMB = −1.65 mag. The average TF offset of the (proto-)cluster sample is therefore only slightly larger (by 0.2 mag) than what would be expected for field galaxies at z = 1.5. This indicates that, at least in a statistical sense, the impact of the dense environment on the average luminosity evolution of disk galaxies is small at that epoch.
 |
Fig. 4. B-band Tully–Fisher diagram showing our (proto-)cluster galaxy sample at z = 1.47 (filled black circles). We also show field galaxies at 1.0 < z < 1.3 (open squares) from Miller et al. (2011) and 1.2 < z < 1.5 (open triangles) from Epinat et al. (2009) for comparison. The local Tully–Fisher relation from Tully et al. (1998) is depicted by a dashed line; the dotted lines indicate the 1σ scatter. The dash-dotted line denotes the expected TFR for field galaxies at z = 1.5, adopting the luminosity evolution found in Böhm & Ziegler (2016). |
We note that the stellar-mass TFR is not part of the scope of this paper. The currently available photometry of the HSC-SSP is comprising filters that probe only up to rest-frame wavelengths λ ≈ 4300 Å for galaxies at z = 1.47. Stellar mass determinations based on the UV or blue part of the spectral energy distribution carry very large systematic errors. Without NIR imaging at our disposal, we prefer to restrict our TFR analysis to the B-band.
As an additional tool in our kinematic analysis, we use a measure for the kinematical asymmetry Akin. To this end, we rely on the formalism used in Bösch et al. (2013a), which is a variation of the formalism presented by Dale et al. (2001). It quantifies the asymmetry of the rotation curve (rotation velocity as a function of radius) of a galaxy.
For a given rotation curve, Akin is computed via:
Here, v(ri) and v(−ri) are the observed rotation velocities at a galactocentric radius ri on either side of the center of the galaxy, while σv(ri) and σv(−ri) are the errors on the rotation velocity at those positions. The total area between the kinematically folded, approaching and receding side of the rotation curve is normalized to the average area under the rotation curve. Additionally, the contribution of each velocity pair (v(ri),v(−ri)) is weighted by its error (σv(ri),σv(−ri)). The asymmetry Akin is then minimized by varying the kinematic center within ±2 pixels of the photometric center (corresponding to ∼3.4 kpc at z = 1.47). Numerically, Akin can vary between a value of zero for a perfectly symmetric rotation curve and a maximum value of two if all line-of-sight velocities v(ri) have the same sign at all covered radii ri.
Our main motivation to use rotation curves instead of the full 2D velocity fields to quantify kinematic asymmetries is the ability that this method confers to compare the results obtained in the HSC (proto-)clusters with the cluster system A901/902 at z = 0.17, for which our team carried out multi-object spectroscopy with VLT/VIMOS (Bösch et al. 2013a). We extracted rotation curves from the velocity fields of our KMOS data by placing mock slits along the photometric major axis, using an apparent slit width of 0.4 arcsec. At z = 1.5, this corresponds to a physical slit width of 3.4 kpc, which is the same physical width of the slits used in our VIMOS spectroscopy of z = 0.17 A901/902 galaxies, where the apparent slit width was 1.2 arcsec. The spatial resolution of the VIMOS observations (taken under an optical FWHM ∼ 1 arcsec) is, in physical units, very similar to the resolution of the KMOS observations (H-band FWHM ∼ 0.3 arcsec), given the difference in redshift. A comparison between the z = 0.17 and z = 1.5 data is presented in Sect. 5.
We also computed morphological asymmetries Amorph on the best-seeing i-band images, following the definition of Conselice (Conselice 2003). The asymmetry compares the original image to a version of itself that is rotated by 180°. To account for contributions by sky noise, a blank sky region B that has the same size as the object image is included in the computation:
Here, I is the original image, I180 is the image rotated by 180° about the adopted galaxy center, and B and B180 are the background and rotated background. The sum is computed over all pixels within the 1σ isophotes of the galaxy, as determined using Source Extractor. Here, B covers the same number of pixels as I. Amorph is minimized by allowing small shifts of the assumed position of the rotation axis (i.e., the galaxy center), by a maximum of ±2 pixels in x- or y-direction.
We furthermore derived the gas velocity dispersion σg in the disk by measuring the velocity dispersion in each spaxel (corresponding to ∼1.7 kpc on a side) across the entire velocity field of a given galaxy and then computing its median. Taking into account the spectral resolution of KMOS in the H-band (R ≈ 4000), we found gas disk velocity dispersions in the range 16.8 km s−1 < σg < 33.7 km s−1. We note that for our data set, the conclusions drawn in the following discussion would not change if the gas velocity dispersion σg were instead determined in the center of a given galaxy.
The main parameters derived in our analysis are given in Table 1.
Main parameters of the 14 galaxies from our sample for which a derivation of the maximum rotation velocity Vmax was feasible.
5. Discussion
The partly very large TFR over-luminosities we found for the z = 1.47 (proto-)cluster galaxies could be due to several reasons. The high-z galaxies form stars at much higher rates than local galaxies of similar mass, and the higher fraction of young, high-mass stars arising from a higher SFR translates into a lower rest-frame B-band mass-to-light ratio M/LB. This effect is the most probable explanation for the redshift-dependent B-band TFR offsets at 0 < z < 1 discussed in Böhm & Ziegler (2016).
In a dense environment, gravitational (e.g., tidal forces) or hydrodynamical interactions (ram-pressure) can act in addition to the evolution in mass-to-light ratio. Tidal interactions can invoke an increase of the star formation rate provided that relative velocities between the galaxies are not too high and distances between them not too large (e.g., Lambas et al. 2003). Moreover, tidal forces can perturb the velocity field and induce noncircular motions of the gas and stars in a galaxy. Both effects (higher SFR and/or a stronger contribution from nonordered motions) would lead to shifts towards higher luminosity in the Tully–Fisher diagram as long as the perturbations of the rotation velocity field are not too strong and Vmax can still be derived. The effect of ram pressure on the other hand, can either increase or decrease the luminosity at a given Vmax, depending on whether the interaction is observed at an early or a later stage. Simulations have shown that ram-pressure can initially lead to an enhanced SFR for several 100 Myr via compression of the gaseous disk, followed by the quenching of star formation via massive gas loss (e.g., Ruggiero & Lima Neto 2017).
Based on Focal Reducer and Spectrograph (FORS) slit spectroscopy, our group previously carried out a Tully–Fisher analysis of cluster disk galaxies at slightly lower redshift z ≈ 1.4 (Pérez-Martínez et al. 2017). There, we targeted the massive cluster XMMU J2235−2557, which has a well-established ICM as confirmed with X-ray observations (Mullis et al. 2005). The average offset from the local B-band TFR found by Pérez-Martínez et al. (2017) (∼ − 1.6 mag) is similar to what we report here (∼ − 1.8 mag), and also the scatter of the TF offsets is similar between the two samples (1.0 mag at z = 1.4 vs. 1.1 mag at z = 1.5). Moreover, the average luminosity evolution observed in the cluster/(proto-)cluster environment is only slightly stronger (by ∼0.2 mag) than what is expected in the field at the same redshifts (adopting Eq. (4) from Böhm & Ziegler 2016). This is in agreement with earlier studies such as Ziegler et al. (2003) which have found that little difference is found between dense environments and the field on average, provided that only undisturbed velocity fields and/or rotation curves are utilized in a Tully–Fisher analysis.
However, some individual HSC (proto-)cluster galaxies have much stronger TF offsets – up to four magnitudes in rest-frame B – than what was found in the J2235−2557 cluster, where the largest offsets are ΔMB ≈ −2.5 mag. This suggests that there are other factors that have an impact on the Tully–Fisher analysis of the (proto-)cluster galaxies, such as for example noncircular gas motions; we address this again further below.
To investigate the influence of star-formation on the distribution in Tully–Fisher space for our KMOS sample, we show the TFR offsets Δ MB plotted against SFR in Fig. 5 compared to the field sample from Böhm & Ziegler (2016). For field spirals at z < 1, there is a clear correlation between the TFR offsets and SFRs: a Spearman test yields ρ = −0.46 and p = 10−4. However, for the (proto-)cluster galaxies, we find no clear correlation: ρ = 0.27 and p = 0.35. The galaxy with the highest SFR of over 100 M⊙ yr−1 is a slight outlier in the KMOS distribution, but even if one neglects this object in the statistical analysis, the Spearman test result does not change significantly: for the remaining 13 galaxies, we find ρ = 0.09 and p = 0.78. We note that the SFRs are also not correlated with the kinematical asymmetry Akin (ρ = 0.19 and p = 0.37); it is therefore unlikely that star formation in many of the galaxies is enhanced by tidal interactions.
 |
Fig. 5. Hα-based star formation rates vs. offsets Δ MB from the local B-band Tully–Fisher relation. In contrast to field disk galaxies at z < 1 (small open squares; taken from Böhm & Ziegler 2016), the TFR offsets of the z = 1.47 (proto-)cluster galaxies (filled circles) are not correlated with star formation rate. See text for details. |
The KMOS sample has some overlap in SFR and Δ MB with the highest-SFR field galaxies at z < 1, but the above tests indicate that star formation rate is not the only parameter that drives the offsets of the z ≈ 1.5 galaxies from the local TFR. Indeed, we find that the TFR offsets depend on the contributions of noncircular motions to the gas kinematics of the z = 1.47 (proto-)cluster galaxies. Figure 6 shows the TFR offsets versus the ratio Vmax/σg between maximum rotation velocity and gas velocity dispersion. This figure demonstrates that galaxies with lower Vmax/σg ratios (less rotation-dominated kinematics) have larger TFR offsets, confirmed by a Spearman test which returns ρ = 0.77 and p = 0.001. A relatively large velocity dispersion does not necessarily imply gravitational perturbations, for example by galaxy–galaxy interactions, but could also indicate kinematically “hotter” disks that have also been found in the field regime at similar redshifts (e.g., Simons et al. 2016). However, we cannot compare this result to our own z < 1 field sample as we did in Fig. 5, because the relatively low spectral resolution of the VLT/FORS data from Böhm & Ziegler (2016) corresponds to a lower limit σg ≈ 100 km s−1.
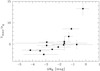 |
Fig. 6. Offsets from the local Tully–Fisher relation Δ MB vs. ratio between maximum rotation velocity Vmax and gas velocity dispersion σg. Galaxies which are more rotation dominated show smaller TFR offsets. This indicates that significant noncircular motions in the gas kinematics are contributing to the deviations from the local TFR. |
Independent of whether the low Vmax/σg ratios of some objects are due to gravitational interactions or a general trend towards kinematically hotter, thicker disks at higher redshifts (e.g., Wisnioski et al. 2015), we would expect more massive galaxies to be more rotation-dominated than lower-mass ones: higher-mass galaxies are less susceptible to external gravitational forces, and they also settle to high Vmax/σg ratios at earlier cosmic times than low-mass disks (e.g., Kassin et al. 2012). Figure 7 shows the ratio Vmax/σg between maximum rotation velocity and gas velocity dispersion as a function of Vmax, which is a proxy for total mass, for our z = 1.5 (proto-)cluster sample; also shown for comparison are local field galaxies from the GHASP survey (Epinat et al. 2010), which comprises Fabry-Pérot Hα observations of local isolated spiral galaxies. For the purpose of this plot, we restricted the local sample to the Vmax range covered by the HSC (proto-)cluster galaxies. In both samples, the kinematics of galaxies with higher Vmax, and therefore higher mass, are more rotation dominated than the kinematics of low-mass ones. However, the Vmax/σg ratio is slightly lower for the distant (proto-)cluster galaxies; we find a median ⟨Vmax/σg⟩ = 4.9 compared to ⟨Vmax/σg⟩ = 6.2 in the GHASP sample. This could reflect the increase in gas velocity dispersion with look-back time (e.g., Wisnioski et al. 2015) or velocity field perturbations due to galaxy–galaxy interactions in the z = 1.5 (proto-)cluster environment. As we discuss further below, the relative velocities of the (proto-)cluster galaxies in our sample are probably much lower than would be typical in low-redshift clusters. From a theoretical perspective, besides more frequent gravitational interactions, several scenarios exist to explain the increasing gas velocity dispersion in disks towards higher redshifts. Hung et al. (2019) used cosmological simulations to show that higher gas inflow rates and subsequently enhanced star formation rates lead to larger σg at earlier cosmic times.
 |
Fig. 7. Ratio between maximum rotation velocity Vmax and gas velocity dispersion σg as a function of maximum rotation velocity for our (proto-)cluster sample at z = 1.5 (filled circles) and local disk galaxies from Epinat et al. (2010, open circles). In both samples, faster rotators (i.e., disk galaxies of higher mass) have more rotation-dominated kinematics than galaxies of lower mass. |
We now want to include morphological information in our analysis, in an attempt to disentangle various possible interaction processes in the high-redshift (proto-)clusters. In Fig. 8, we show the kinematical asymmetry Akin as a function of morphological asymmetry Amorph. The Y-axis of this parameter space is sensitive both to hydrodynamical and gravitational interactions, while the X-axis only probes gravitational interactions; stars are not affected by ram pressure (e.g., Kronberger et al. 2008). We first want to focus on the z = 1.5 (proto-)cluster data. Filled circles denote galaxies with a determined Vmax, while open circles show galaxies with disturbed and/or nonrotating velocity fields, for which Vmax could not be derived. As would be expected, galaxies with velocity fields that could be used for the determination of Vmax generally have lower kinematic asymmetries Akin (median ⟨Akin⟩ = 0.44) than galaxies that did not yield a value for Vmax (⟨Akin⟩ = 0.76). No correlation between Akin and Amorph is found using a Spearman test: ρ = 0.05 and p = 0.79.
 |
Fig. 8. Morphological asymmetry Amorph vs. kinematic asymmetry Akin for our z = 1.5 (proto-)cluster sample. Filled circles denote galaxies with determined Vmax, and open circles represent galaxies with disturbed or nonrotating velocity fields for which Vmax could not be derived. For comparison, we also show spirals from the low-redshift cluster A901/902 at z = 0.17 (small open squares), using data from Bösch et al. (2013a). The imaging of the z = 0.17 galaxies has been degraded to match the image quality of the z = 1.5 data, and also the derivation of Akin ensured comparable spatial resolutions in the two data sets. |
For further interpretation, we now compare the morphological and kinematical asymmetries at z = 1.5 to a dense environment at low redshift: the cluster system A901/902 at z ≈ 0.17. In this system, we previously found a population of disk galaxies that, despite having regular morphologies with low Amorph values, show high gas kinematical asymmetries (cf. Fig. 17 in Bösch et al. 2013a). This is evidence for hydrodynamical interaction, as this is the sole process in dense environments that only affects the gas distribution and gas kinematics, but not the stellar light morphology. To be able to directly compare the A901/902 data to our new z = 1.5 observations, we degraded the Hubble Space Telescope Advanced Camera for Surveys (HST/ACS) imaging of galaxies in A901/902 to match the physical pixel scale (1.7 kpc pix−1), spatial resolution (PSF FWHM of 5.9 kpc), and noise properties of the HSC i-band imaging of the z = 1.5 (proto-)clusters. The morphological asymmetries Amorph of the z = 0.17 cluster galaxies were then re-computed on these degraded images. As explained in the last section, we also extracted rotation curves and derived kinematical asymmetries Akin from the KMOS data cubes such that this parameter is directly comparable between the low- and high-redshift data. The A901/902 sample was restricted to star-forming galaxies with stellar masses of log(M*/M⊙) > 9.5, which is the expected stellar mass range of the KMOS sample given its distribution of Vmax values and the observed stellar mass TFR at z ≈ 1.5 reported by Übler et al. (2017). This mass-restricted part of the A901/902 sample is depicted in Fig. 8 by open squares.
As is the case for the z = 1.5 (proto-)cluster galaxies, no correlation between Amorph and Akin is found in the degraded A901/902 sample (Spearman test: ρ = 0.12 and p = 0.54). Moreover, the strongly limited spatial resolution of the degraded imaging camouflages the hydrodynamical interactions reported in Bösch et al. (2013a): dividing the z = 0.17 sample into two equally sized parts with low and high morphological asymmetry (Amorph < 0.12 and Amorph > 0.12, resp.), the low-asymmetry sample does not yield a correlation between Amorph and Akin (ρ = 0.19 and p = 0.51), or, in particular, an anti-correlation, as was found based on the fully resolved imaging (cf. Bösch et al. 2013a). We therefore conclude that hydrodynamical interactions cannot be identified at the resolution of the HSC imaging of the (proto-)clusters, at least at our current sample size.
Nevertheless, we do find that both the morphological and kinematical asymmetries are higher on average in the z = 1.5 sample (median ⟨Amorph⟩ = 0.23 and ⟨Akin⟩ = 0.60) than in the z = 0.17 data (⟨Amorph⟩ = 0.12 and ⟨Akin⟩ = 0.22), probably due to much more efficient galaxy–galaxy interactions in the (proto-)clusters arising from the low relative velocities between the galaxies, as we show further below. We note that part of the difference in average morphological asymmetries between the A901/902 and the (proto-)cluster galaxies might stem from the difference in rest-frame wavelength of the imaging (∼5100 Å for A901/902, taken with the F606W filter of HST/ACS, versus ∼3200 Å for the z = 1.5 galaxies; i-band data). The sensitivity of the NUV to clumpy star-forming regions generally leads to higher Amorph than rest-frame optical or NIR images (that are currently not at hand for the (proto-)clusters sample). Irrespective of this, the lack of a correlation between morphological and kinematical asymmetry suggests that a mixture of hydrodynamical and gravitational interactions might be present in HSC-2329 and HSC-2330 (as in A901/902), but the limited spatial resolution of the available imaging does not allow us to disentangle these processes.
We estimated the galaxy velocity dispersions in the two (proto-)clusters, assuming that the two peaks in their redshift distributions are physical, since it seems unlikely that strong night-sky residuals are the cause of the observed “gap” at z = 1.468 in both (proto-)clusters. For the two peaks in the z-distribution of HSC-CL2329, we find velocity dispersions of σv = 304 km s−1 and σv = 364 km s−1; the distribution in HSC-CL2330 yields values of σv = 385 km s−1 and σv = 361 km s−1, resp.
If all structures were virialized, these velocity dispersions would be equivalent to virial masses of 1.6 × 1014 M⊙ < Mvir < 3.2 × 1014 M⊙. These estimates follow Crook et al. (2007) and are based on the observed velocity dispersions and projected pairwise galaxy–galaxy separations of the (proto-)cluster members. However, it is much more likely that these numbers are overestimating the (proto-)cluster masses due to their nonvirialized state. The large average pairwise galaxy–galaxy separations in the observed overdensities result in projected virial radii between 1.4 and 2 Mpc for the four structures. This is very large given the observed range in velocity dispersions: following Finn et al. (2005), the σv values given above, under the assumption of virialization, would correspond to virial radii of only 0.33 Mpc < R200 < 0.42 Mpc.
Rather than being virialized, it is therefore much more likely that the targeted overdensities are in the process of formation. To reflect this in our nomenclature, we refer to them as (proto-)clusters throughout this paper. Further characterization of HSC-CL2329 or HSC-CL2330 is difficult on the basis of our current data. No prominent Brightest Cluster Galaxy is observed in either (proto-)cluster, which is in compliance with an early dynamical state, but we cannot test for the presence or absence of a red sequence with the current imaging that probes only rest-frame UV and blue wavelengths. Since we are lacking deep X-ray data, a direct detection of the ICM is also not feasible.
Irrespective of the dynamical status of HSC-CL2329 and HSC-CL2330, the σv values show that the relative velocities between the (proto-)cluster galaxies in our sample are low compared to those observed in virialized clusters, and tidal interactions between the galaxies are therefore much more efficient than would be expected in a typical cluster environment at later cosmic epochs. This strengthens the interpretation that galaxy–galaxy interactions contribute to the distribution shown in Fig. 8, though we would expect a clear correlation between morphological and kinematical asymmetry if tidal forces were the only interaction process in action.
To summarize, our morpho-kinematical analysis of galaxies in dense environments at z ≈ 1.5, corresponding to a look-back time of ∼9 Gyr, reveals some similarities to the field galaxy population at this epoch, in particular with regard to a high fraction of disks with significant contributions from noncircular motions. However, two points have to be stressed. Firstly, our sample stems from a cosmic phase that represents the onset of environmental influence on galaxy evolution, and not the clear impact observed at lower redshifts. Secondly, the complex redshift distributions of HSC-2329 and HSC-2330 indicate that both structures are in an early, nonvirialized stage, and might lack a dense ICM at the time of observation, which would weaken the effects from hydrodynamical interactions. More IFU observations of galaxies in clusters, including more evolved structures at high redshifts, will be necessary to shed more light on the impact of environment on galaxy evolution at early cosmic stages.
6. Summary
We used VLT/KMOS to perform integral field spectroscopy on the Hα emission from 46 galaxies in two (proto-)clusters at redshift z = 1.47 detected as overdensities of [O II] emitters in HSC-SSP data. In the KMOS data cubes, the Hα line was detected in 36 galaxies, of which 34 are (proto-)cluster members; only two objects are located in the field, demonstrating the efficiency of our selection strategy. Twenty-four galaxies show spatially extended Hα emission from which velocity fields could be extracted, while in the remaining 12 objects, the Hα emission is spread over only a few pixels and/or is affected by strong residuals of OH night sky lines.
By fitting the observed velocity fields with simulated velocity fields that take into account geometrical effects like disk inclination and position angle as well as seeing and beam smearing, we were able to derive the maximum rotation velocity Vmax of 14 galaxies. The velocity fields of the remaining 10 galaxies with extended Hα are disturbed or nonrotating. We computed quantitative morphological and kinematical asymmetries to compare the z = 1.47 (proto-)cluster galaxy data to our own studies of the galaxy population in low-redshift clusters. Our main findings can be summarized as follows.
-
Based on the TFR, all (proto-)cluster disk galaxies at z ≈ 1.5 are more luminous than local spirals at a given Vmax, by up to ∼4 mag in rest-frame B. However, the average evolution in B-band luminosity between z = 1.5 and z = 0 only weakly depends on environment, since we find little difference in the average offsets from the local TFR between the field and the (proto-)clusters. We did not consider the stellar-mass TFR here as the currently available photometry does not cover rest-frame red optical or NIR colors, which are mandatory for the derivation of robust stellar masses.
-
The deviations from the local TFR are not correlated with star formation rate, but with the ratio between Vmax and gas velocity dispersion σg. In turn, this ratio Vmax/σg is larger towards higher Vmax, that is, higher total mass. Besides possible gravitational interactions between (proto-)cluster members, this might reflect that many low-mass disks have not yet settled to purely rotational kinematics by z ≈ 1.5. This has also been observed in the field at this epoch.
-
Tests with degraded low-redshift cluster galaxy data show that we cannot detect purely hydrodynamical interactions within the limitations of the ground-based HSC imaging. Gravitational interactions on the other hand are likely to be more efficient in the (proto-)clusters than in dense environments at low redshifts due to rather small relative velocities between the z = 1.5 (proto-)cluster members. This would explain the higher kinematical asymmetries that we find at z = 1.5 in comparison to cluster galaxies at low redshift.
Acknowledgments
BLZ is grateful for an NAOJ visitorship in 09/2018, which was supported by the grant of Visiting Scholar Program funded by the Research Coordination Committee, National Astronomical Observatory of Japan (NAOJ), National Institutes of Natural Sciences (NINS).
References
- Aihara, H., Arimoto, N., Armstrong, R., et al. 2018a, PASJ, 70, S4 [NASA ADS] [Google Scholar]
- Aihara, H., Armstrong, R., Bickerton, S., et al. 2018b, PASJ, 70, S8 [NASA ADS] [Google Scholar]
- Balogh, M. L., Navarro, J. F., & Morris, S. L. 2000, ApJ, 540, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Bamford, S. P., Milvang-Jensen, B., Aragón-Salamanca, A., & Simard, L. 2005, MNRAS, 361, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binney, J., & Tremaine, S. 1987, Galactic Dynamics: Second Edition (Princeton: Princeton University Press) [Google Scholar]
- Blanton, M. R., Eisenstein, D., Hogg, D. W., Schlegel, D. J., & Brinkmann, J. 2005, ApJ, 629, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm, A., & Ziegler, B. L. 2016, A&A, 592, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brodwin, M., McDonald, M., Gonzalez, A. H., et al. 2016, ApJ, 817, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Bösch, B., Böhm, A., Wolf, C., et al. 2013a, A&A, 549, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bösch, B., Böhm, A., Wolf, C., et al. 2013b, A&A, 554, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calzetti, D. 2001, PASP, 113, 1449 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. 2003, ApJS, 147, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Courteau, S. 1997, AJ, 114, 2402 [NASA ADS] [CrossRef] [Google Scholar]
- Crook, A. C., Huchra, J. P., Martimbeau, N., et al. 2007, ApJ, 655, 790 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, D. A., Giovanelli, R., Haynes, M. P., Hardy, E., & Campusano, L. E. 2001, AJ, 121, 1886 [Google Scholar]
- Desai, V., Dalcanton, J. J., Aragón-Salamanca, A., et al. 2007, ApJ, 660, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A. 1980, ApJ, 236, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Dutton, A. A., van den Bosch, F. C., Faber, S. M., et al. 2011, MNRAS, 410, 1660 [NASA ADS] [Google Scholar]
- Epinat, B., Contini, T., Le Févre, O., et al. 2009, A&A, 504, 789 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Epinat, B., Amram, P., Balkowski, C., & Marcelin, M. 2010, MNRAS, 401, 2113 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreras, I., Böhm, A., Ziegler, B. L., & Silk, J. 2014, MNRAS, 437, 1872 [NASA ADS] [CrossRef] [Google Scholar]
- Finn, R. A., Zaritsky, D., McCarthy, Jr., D. W., et al. 2005, ApJ, 630, 206 [NASA ADS] [CrossRef] [Google Scholar]
- Furusawa, H., Koike, M., Takata, T., et al. 2018, PASJ, 70S, 3 [Google Scholar]
- Gilbank, G., Baldry, I. K., Balogh, M. L., Glazebrook, K., & Bower, R. G. 2010, MNRAS, 405, 2594 [NASA ADS] [Google Scholar]
- Gray, M. E., Wolf, C., Barden, M., et al. 2009, MNRAS, 393, 1275 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., & Gott, J. R. 1972, ApJ, 176, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, M., Kodama, T., Koyama, Y., et al. 2010, MNRAS, 402, 1980 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, M., Tanaka, M., Shimkawa, R., et al. 2018, PASJ, 70, 17 [NASA ADS] [Google Scholar]
- Hung, C.-L., Hayward, C. C., Yuan, T., et al. 2019, MNRAS, 482, 5125 [NASA ADS] [CrossRef] [Google Scholar]
- Kassin, S. A., Weiner, B. J., Faber, S. M., et al. 2012, ApJ, 758, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Kawanomoto, S., Uraguchi, F., Komiyama, Y., et al. 2018, PASJ, 70, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. 1998, ARA&A, 36, 189 [Google Scholar]
- Kennicutt, R., Hao, C.-N., Calzetti, D., et al. 2009, ApJ, 703, 1672 [NASA ADS] [CrossRef] [Google Scholar]
- Komiyama, Y., Obuchi, Y., Nakaya, H., et al. 2018, PASJ, 70S, 2 [Google Scholar]
- Kronberger, T., Kapferer, W., Unterguggenberger, S., Schindler, S., & Ziegler, B. L. 2008, A&A, 483, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuchner, U., Ziegler, B. L., Verdugo, M., Bamford, S., & Häußler, B. 2017, A&A, 604, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambas, D. G., Tissera, P. B., Sol Alonso, M., & Coldwell, G. 2003, MNRAS, 346, 1189 [NASA ADS] [CrossRef] [Google Scholar]
- Ly, C., Malkan, M. A., Kashikawa, N., et al. 2012, ApJ, 747, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, S. H., Bundy, K., Sullivan, M., Ellis, R. S., & Treu, T. 2011, ApJ, 741, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, S. H., Ellis, R. S., Sullivan, M., et al. 2012, ApJ, 753, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Milvang-Jensen, B., Aragón-Salamanca, A., Hau, G. K. T., Jørgensen, I., & Hjorth, J. 2003, MNRAS, 339, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Miyazaki, S., Komiyama, Y., Kawanomoto, S., et al. 2018, PASJ, 70, S1 [NASA ADS] [Google Scholar]
- Moran, S. M., Miller, N., Treu, T., Ellis, E. S., & Smith, G. P. 2007, ApJ, 659, 1138 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B., Katz, N., Lake, G., Dressler, A., & Oemler, A. 1996, Nature, 379, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Mullis, C. R., Rosati, P., Lamer, G., et al. 2005, ApJ, 623, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Nakamura, O., Aragón-Salamanca, A., Milvang-Jensen, B., et al. 2006, MNRAS, 366, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-Martínez, J. M., Ziegler, B. L., Verdugo, M., Böhm, A., & Tanaka, M. 2017, A&A, 605, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quilis, V., Moore, B., & Bower, R. 2000, Science, 288, 1617 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ruggiero, R., & Lima Neto, G. B. 2017, MNRAS, 468, 4107 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N., Faisst, A., Capak, P., et al. 2015, ApJ, 800, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Simons, R. C., Kassin, S. A., Trump, J. R., et al. 2016, ApJ, 830, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Steinhauser, D., Schindler, S., & Springel, V. 2016, A&A, 591, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tanaka, M., Coupon, J., Hsieh, B.-C., et al. 2018, PASJ, 70, S9 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B., & Fisher, J. R. 1977, A&A, 54, 661 [NASA ADS] [Google Scholar]
- Tully, R. B., Pierce, M. J., Huang, J.-S., et al. 1998, AJ, 115, 2264 [NASA ADS] [CrossRef] [Google Scholar]
- Übler, H., Förster-Schreiber, N., Genzel, R., et al. 2017, ApJ, 842, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Verdugo, M., Ziegler, B. L., & Gerken, B. 2008, A&A, 486, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vogt, N. P., Haynes, M. P., Giovanelli, R., & Herter, T. 2004, AJ, 127, 330 [Google Scholar]
- Whitaker, K. E., Pope, A., Cybulski, R., et al. 2017, ApJ, 850, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Wisnioski, E., Förster-Schreiber, N., Wuyts, S., et al. 2015, ApJ, 799, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, C., Aragón-Salamanca, A., Balogh, M., et al. 2009, MNRAS, 393, 1302 [NASA ADS] [CrossRef] [Google Scholar]
- Ziegler, B. L., Böhm, A., Jäger, K., Heidt, J., & Möllenhoff, C. 2003, ApJ, 598, L87 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Main parameters of the 14 galaxies from our sample for which a derivation of the maximum rotation velocity Vmax was feasible.
All Figures
 |
Fig. 1. Top: spatial distribution of our target candidates (small dots), galaxies without Hα detections (open circles), and Hα-detected galaxies (filled circles) for the two observed (proto-)clusters. The large dotted circle in both plots denotes the available KMOS patrol field with a diameter of 7.2 arcmin or ∼3.7 Mpc at the redshifts of the (proto-)clusters. Bottom: redshift distribution of all 36 Hα detections for both (proto-)clusters combined (large plot) and for the two (proto-)clusters individually (inset graphs). Only two field galaxies are found (shown as gray filled circles in the upper panel), demonstrating the efficiency of the target selection. Both (proto-)clusters reside at a redshift z = 1.47, which we aimed for by selecting overdensities of [O II] emitters at z ≈ 1.5 with combined broad- and narrowband data. Interestingly, the two (proto-)clusters show similar substructure in redshift space. |
| In the text | |
 |
Fig. 2. Comparison between the star formation rates from [O II] fluxes estimated with HSC SSP NB imaging and the new, Hα-based SFRs from the KMOS data. Open symbols depict objects for which the Hα line was affected by night sky residuals, which could lead to underestimation of the SFRs; however, there is no clear indication for this. |
| In the text | |
 |
Fig. 3. Four examples of z ≈ 1.47 (proto-)cluster galaxies for which the maximum rotation velocity Vmax could be determined. In each row, the plots show from left to right: best-seeing i-band image from the Subaru HSC survey, ionized gas map as observed in Hα with VLT/KMOS, observed rotation velocity field, best-fit model rotation velocity field used for the determination of the intrinsic Vmax, and fit residuals after subtracting the best-fit model from the observed velocity field. We note that the galaxy to the southeast of HSC-232978 (top panel, leftmost figure) is a foreground galaxy with a photometric redshift in the range 0.7 < zphot < 0.8, depending on the method, and undetected in the KMOS data. |
| In the text | |
 |
Fig. 4. B-band Tully–Fisher diagram showing our (proto-)cluster galaxy sample at z = 1.47 (filled black circles). We also show field galaxies at 1.0 < z < 1.3 (open squares) from Miller et al. (2011) and 1.2 < z < 1.5 (open triangles) from Epinat et al. (2009) for comparison. The local Tully–Fisher relation from Tully et al. (1998) is depicted by a dashed line; the dotted lines indicate the 1σ scatter. The dash-dotted line denotes the expected TFR for field galaxies at z = 1.5, adopting the luminosity evolution found in Böhm & Ziegler (2016). |
| In the text | |
 |
Fig. 5. Hα-based star formation rates vs. offsets Δ MB from the local B-band Tully–Fisher relation. In contrast to field disk galaxies at z < 1 (small open squares; taken from Böhm & Ziegler 2016), the TFR offsets of the z = 1.47 (proto-)cluster galaxies (filled circles) are not correlated with star formation rate. See text for details. |
| In the text | |
 |
Fig. 6. Offsets from the local Tully–Fisher relation Δ MB vs. ratio between maximum rotation velocity Vmax and gas velocity dispersion σg. Galaxies which are more rotation dominated show smaller TFR offsets. This indicates that significant noncircular motions in the gas kinematics are contributing to the deviations from the local TFR. |
| In the text | |
 |
Fig. 7. Ratio between maximum rotation velocity Vmax and gas velocity dispersion σg as a function of maximum rotation velocity for our (proto-)cluster sample at z = 1.5 (filled circles) and local disk galaxies from Epinat et al. (2010, open circles). In both samples, faster rotators (i.e., disk galaxies of higher mass) have more rotation-dominated kinematics than galaxies of lower mass. |
| In the text | |
 |
Fig. 8. Morphological asymmetry Amorph vs. kinematic asymmetry Akin for our z = 1.5 (proto-)cluster sample. Filled circles denote galaxies with determined Vmax, and open circles represent galaxies with disturbed or nonrotating velocity fields for which Vmax could not be derived. For comparison, we also show spirals from the low-redshift cluster A901/902 at z = 0.17 (small open squares), using data from Bösch et al. (2013a). The imaging of the z = 0.17 galaxies has been degraded to match the image quality of the z = 1.5 data, and also the derivation of Akin ensured comparable spatial resolutions in the two data sets. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} A_{\rm kin} = \sum _{i}\frac{|{ v}(r_{i})+{ v}(-r_{i})|}{\sqrt{\sigma _{{ v}}^{2}(r_{i})+\sigma _{{ v}}^{2}(-r_{i})}}\cdot \left[ \frac{1}{2}\sum _{i}\frac{|{ v}(r_{i})|+|{ v}(-r_{i})|}{\sqrt{\sigma _{{ v}}^{2}(r_{i})+\sigma _{{ v}}^{2}(-r_{i})}}\right]^{-1}\cdot \end{aligned} $$](/articles/aa/full_html/2020/01/aa35527-19/aa35527-19-eq1.gif)